POLITECHNIKA BIAŁOSTOCKA

WYDZIAŁ MECHANICZNY

KATEDRA MECHANIKI I INFORMATYKI STOSOWANEJ

LABORATORIUM MECHANIKI

INSTRUKCJA

BADANIE DYNAMIKI RUCHU UKŁADU
MECHANICZNEGO

ROBERT UŚCINOWICZ

BIAŁYSTOK 2009

2

1. CEL DWICZENIA

Celem dwiczenia jest doświadczalne wyznaczenie maksymalnej i średniej wartości siły

napięcia w lince łączącej dwa ciała układu mechanicznego poruszającego się w polu sił
ciężkości. Dwiczenie powinno również dostarczyd informacji o wpływie sił tarcia na wartośd
siły w lince łączącej ciała układu mechanicznego.

2. OPIS STANOWISKA

Stanowisko do badania dynamiki ruchu układu mechanicznego przedstawiono na

poniższej fotografii (

rys. 1

) i schematycznie na

rys. 2

. Składa się ono z następujących

elementów: równi pochyłej (1), prowadnicy (2), ułożyskowanego bloczka (3), kątomierza (4),
linki (5), klocka (6) (z wymiennymi wkładkami ciernymi), szalki z ciężarem G (7),
wzmacniacza tensometrycznego Spider 8 (8). Komputer PC współpracujący ze
wzmacniaczem, który jest wymagany do zarejestrowania i wizualizacji danych nie został
przedstawiony na rysunkach.

Rys. 1. Stanowisko do badania dynamiki ruchu układu mechanicznego

Stanowisko pomiarowe, którego ilustrację zamieszczono na

rys. 1 i 2

składa się z

dwóch ciał powiązanych ze sobą wiotką linką. Ruch układu jest wymuszany przez ciężarek G
, który to za pośrednictwem linki wprawia w ruch obrotowy ułożyskowany bloczek (linkę
nawinięto jednokrotnie na bloczek) i wymusza ruch klocka Q w górę równi. Klocek Q (

rys. 3

)

ślizga się po prowadnicy zamontowanej na równi pochyłej, której kąt nachylenia można
zmieniad za pomocą pokrętła umieszczonego pod płytą równi pochyłej (

rys. 4

). W trakcie

eksperymentu rejestrowana jest wartośd siły S w lince. Pomiar ten realizowany jest przy

3

pomocy tensometrycznego przetwornika siły, do którego jest zaczepiona linka. Przetwornik
siły, zbudowany jest w oparciu o tensometryczny układ półmostkowy, naklejony na stalowej
belce i zamontowany na górnej powierzchni klocka. Sygnał z przetwornika siły, w postaci
względnych zmian napięcia jest przesyłany do wzmacniacza tensometrycznego Spider 8 (

rys.

5

) i dalej w formie cyfrowej do komputera PC w celu archiwizacji i późniejszej wizualizacji

wyników pomiarów. W realizowanym dwiczeniu zastosowanie wzmacniacza pomiarowego
Spider 8 pozwala na rejestrację siły napięcia linki w czasie rzeczywistym oraz dokładny
pomiar czasu ruchu klocka na prowadnicy. Klocek posiada wymienne wkładki wykonane z
różnych materiałów. Poprzez wymianę wkładek możliwa jest ocena wpływu rodzaju
ślizgających się po sobie tworzyw na wartośd siły S w lince. Możliwe do zastosowania w
dwiczeniu pary trące materiałów zestawiono w

tab. 1

.

a)

b)

c)

d)

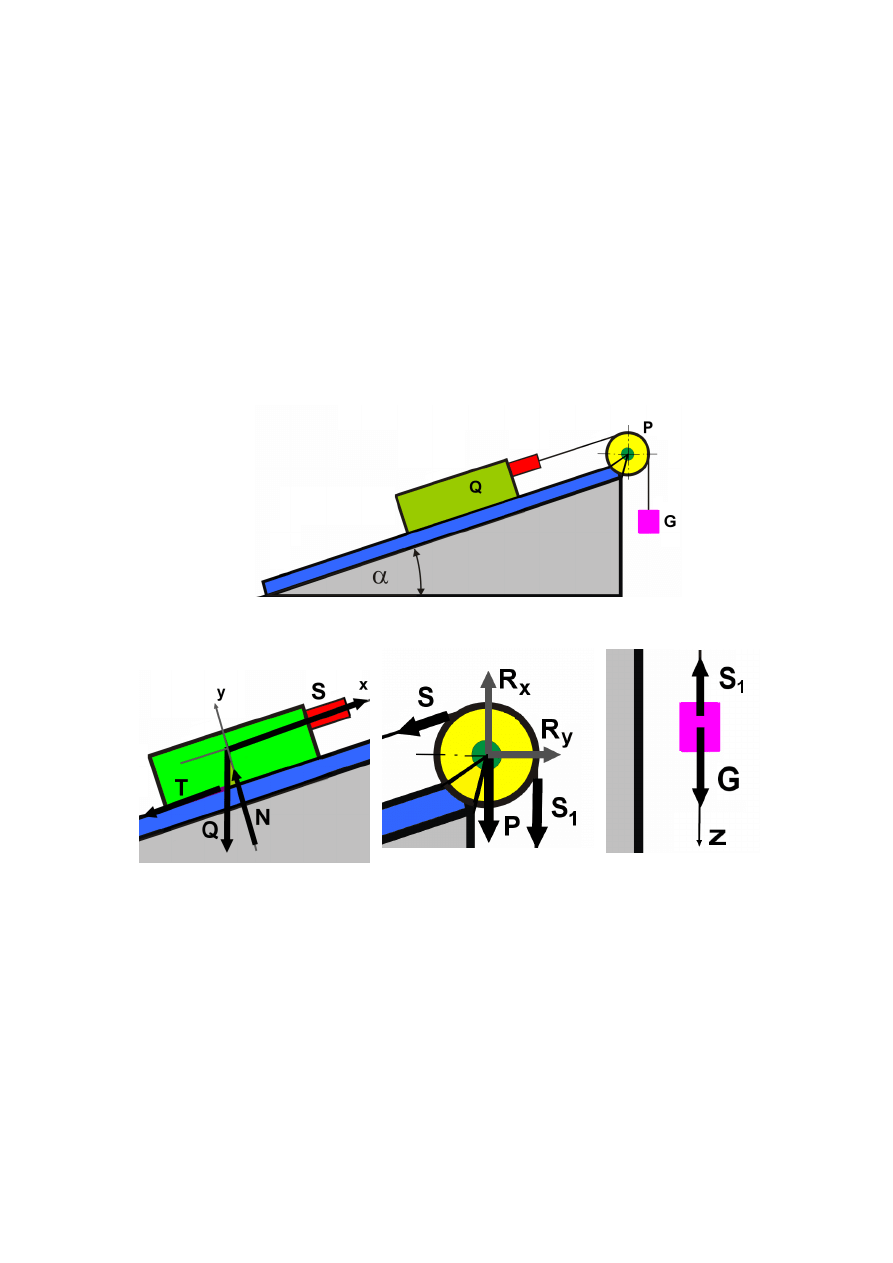
Rys. 2. Schemat badanego układu mechanicznego: a) schemat ogólny stanowiska, b) obciążenie siłowe klocka

o ciężarze

Q

, c) obciążenie bloczka, d) obciążenie ciężarka

G

4

Rys. 3. Klocek

Q

z wymiennymi wkładkami: 1 – tensometryczny przetwornik siły, 2 – płytka mocująca

wkładki , 3 – linka łącząca klocek z ciężarkiem, 4 – wymienna para wkładek

Tab. 1. Zastosowane w dwiczeniu pary trących materiałów

powierzchnia prowadnicy

wkładka klocka

stal

stal

stal

stop aluminium,

stal

tworzywo sztuczne (poliamid)

stal

mosiądz

Rys. 4. Pomiar kąta nachylenia równi

Rys. 5. Wzmacniacz tensometryczny Spider 8

Tensometryczny przetwornik siły jest cienkościenną, jednostronnie utwierdzoną stalową

belką, na której naklejono dwa tensometry opornościowe w układzie półmostkowym. W
trakcie doświadczenia dochodzi do sprężystego ugięcia belki (pod wpływem siły

5

występującej w lince). Jeden z tensometrów (tzw. czynny) naklejony na belce doznaje
sprężystego odkształcenia zmieniając swoją opornośd. Drugi tensometr ma kompensowad w
układzie półmostkowym zmiany temperatury zachodzące w strefie działania przetwornika.
Jeżeli do układu tensometrycznego doprowadzi się stałe napięcie (w gałęzi zasilania) to
zmiana oporności tensometru czynnego wywoła zmianę napięcia w gałęzi pomiarowej. Aby
określid zależnośd pomiędzy wielkościami mechanicznymi (siła) i wielkościami elektrycznymi
(względny przyrost napięcia) należy dokonad procesu wzorcowania i zbudowad tzw.
charakterystykę statyczną przetwarzania. Najczęściej jest to prosta przechodząca przez
początek układu współrzędnych. Jeżeli zastosowany w dwiczeniu przetwornik
tensometryczny będzie obciążało się (monotonicznie) znanymi, coraz większymi wartościami
siły (odważniki o znanym ciężarze) i mierzyło odpowiadające im względne przyrosty napięcia
(we wzmacniaczu Spider 8), to w prosty sposób można zbudowad potrzebną charakterystykę
statyczną przetwornika i określid jej równanie. Posłuży ona później do wyznaczenia wartości
siły S (w lince) w trakcie przebiegu klocka po prowadnicy równi.

3. WIADOMOŚCI OGÓLNE

Dynamiczne równania różniczkowe dla klocka o ciężarze Q i masie

Q

m

mają postad:

sin

Q

m

x

T

S

Q



     

,

(1)

cos

0

Q

m

y

N

Q



 





,

(2)

gdzie:

Q

m

– masa klocka Q , S – siła napięcia nici,

T

– siła tarcia, N – reakcja normalna

podłoża,



– kąt nachylenia równi.

Drugie równanie jest równaniem statyki (

0

y



) i wyznaczamy z niego siłę normalną N ,

będącą składową pionową reakcji równi pochyłej na spoczywające na niej ciało:

cos

N

Q





.

(3)

Wykorzystując prawo tarcia Coulomba przyjmujemy wartośd siły tarcia

T

dla granicznego

przypadku, zatem

cos

T

N

Q











.

(4)

Wstawiając równanie (4) do różniczkowego równania (1) opisującego ruch klocka Q mamy:

cos

sin ,

cos

sin ,

Q

Q

Q

Q

m x

Q

S

Q

m x

m

g

S

m

g













  

  

  

 

 

 

(5)

6





cos

sin

Q

S

x

g

m







 





.

(6)

Dynamiczne równanie różniczkowe dla bloczka o ciężarze

P

jest następujące:

1

o

J

S R

S R



    

,

(7)

gdzie:

o

J

– masowy moment bezwładności bloczka względem osi obrotu,

R

– promieo

walca (bloczka);

0.5

z

R

d



,

1

S

– siła w nici od strony ciężarka G wymuszającego ruch układu

mechanicznego.

Dynamiczne równanie różniczkowe dla ciężarka

G

G

m

g





wymuszającego ruch układu

mechanicznego jest następujące:

1

G

G

m

z

m g

S

 



.

(8)

Zakładając brak poślizgów linki na bloczku i jej nierozciągliwośd można zapisad, że z

x



,

więc z

x



. Z równania (8) wyznaczono

1

S

i podstawiono do równania (7) otrzymując:

(

)

o

G

G

J

S R

m g

m x R



   





.

(9)

Uwzględniając w równaniu (6), zależnośd między przyspieszeniem liniowym klocka Q , a

przyspieszeniem kątowym bloczka, x

R



 

oraz mając na uwadze równanie (9) otrzymamy

układ równao z dwiema niewiadomymi S i



:





cos

sin

,

(

)

Q

o

G

G

S

R

g

m

J

S R

m g

m

R R













  











   









(10)

Po rozwiązaniu układu równao ze względu na S będziemy mieli następujące wyrażenie na
poszukiwaną siłę napięcia linki:





2

2

2

2

cos

sin

2

2

2

2

z

z

G

o

G

z

o

G

z

Q

d

d

m g

g

J

m

S

d

J

m

d

m





















 



































































.

(11)

7

gdzie:



– współczynnik tarcia,

g

– przyspieszenie ziemskie. Współczynnik tarcia wyznaczony

został eksperymentalnie w dwiczeniu „Doświadczalne wyznaczenie współczynnika tarcia
kinetycznego”.

W

tab. 4

podano wartości niektórych współczynników tarcia suchego (statycznego i

kinetycznego), które można wykorzystad w dwiczeniu dla wybranych par trących. Bloczek jest
cienkościenną aluminiową rurą o długości h i średnicy wewnętrznej

53.5

 

oraz

zewnętrznej

z

d

. Otwory w rurze są zaślepione 2 tarczami. Wzdłuż osi bloczka biegnie

stalowa oś obrotowa o średnicy

5

 

i długości

137

l



, która jest zespolona z bloczkiem

(na wcisk).

Do wyznaczenia momentu bezwładności całego bloczka (wraz z osią) można

wykorzystad następujące wzory:



moment bezwładności rury względem osi geometrycznej:





4

4

1

32

rury

z

w

J

h d

d

 



   



,

(12)



moment bezwładności walca względem osi geometrycznej:

4

1

32

walca

z

J

h

d







   

,

(13)

gdzie:



– gęstośd materiału,

z

d

– średnica zewnętrzna,

w

d

– średnica wewnętrzna, h -

wysokośd walca.

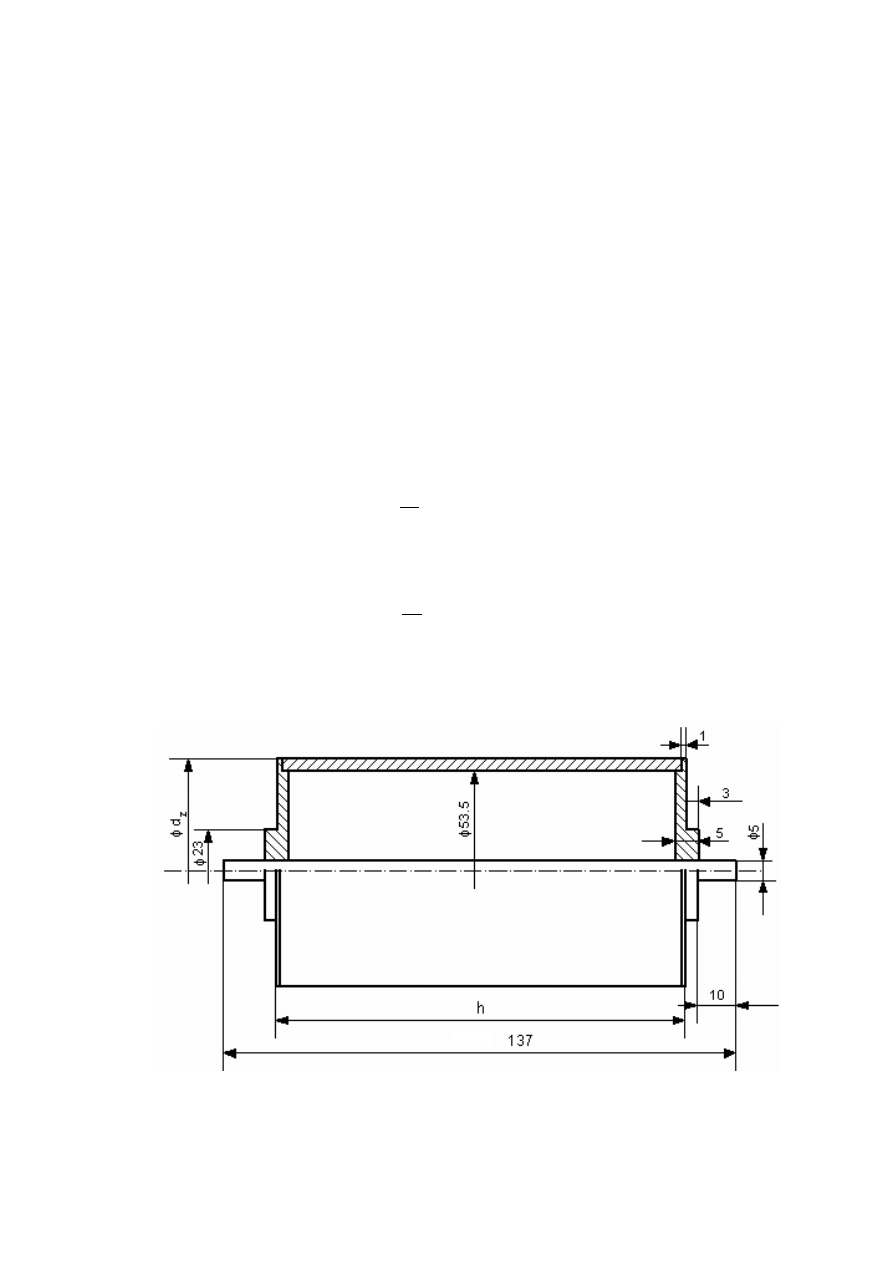
Rys. 6. Wymiary geometryczne bloczka

8

4. PRZEBIEG DWICZENIA

W celu przeprowadzenia dwiczenia należy:

1. Zapoznad się z budową stanowiska i sposobem pomiaru naciągu linki.

2. Uruchomid wzmacniacz pomiarowy Spider 8 i program Catman Express 3.1 –

rejestrujący sygnały pomiarowe (względne przyrosty napięcia). Do obsługi
wzmacniacza pomiarowego Spider 8 i programu Catman Express 3.1 wymagane jest
przeczytanie oddzielnej instrukcji [1].

3. Wyznaczyd charakterystykę statyczną przetwarzania przetwornika obciążając go

odważnikami o znanej masie oraz mierząc odpowiadające im względne przyrosty
napięd.

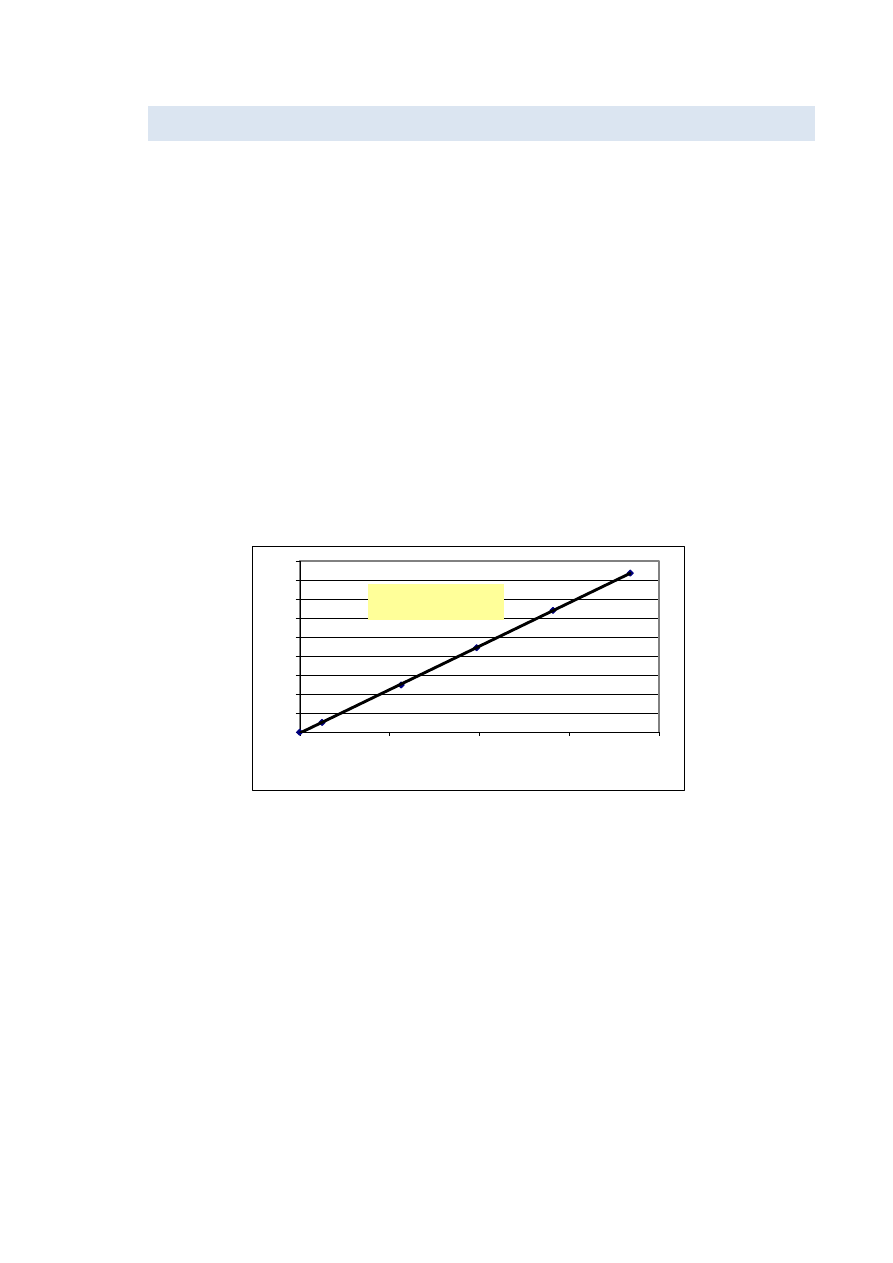
4. W programie MS Excel [2] sporządzid wykres przedstawiający uzyskane zależności, tj.

względny przyrost napięcia – siła (

rys. 7

). Otrzymany zbiór punktów aproksymowad

równaniem prostej i wyznaczyd jej równanie.

Rys. 7. Charakterystyka statyczna przetwarzania przetwornika siły

5. Zmierzyd średnicę

z

d

i szerokośd h bloczka.

6. Zamocowad wkładki cierne z wybranego materiału w gnieździe klocka.

7. Określid masę klocka Q łącznie z wkładkami oraz ciężarka G (wraz z szalką) wpisując

wartości do

tab. 2

. Zawiesid na szalce ciężarek G o takiej masie, aby wywołał ruch

klocka Q w górę.

8. Ustawid równię pochyłą pod kątem



(za pomocą pokrętła umieszczonego pod

torem pomiarowym); wartośd kąta odczytad ze skali i wpisad do

tab. 2

.

9. Ustawid klocek na prowadnicy w pozycji dolnej skrajnej.

y = 22.827x - 0.0442

R² = 0.9999

0

1

2

3

4

5

6

7

8

9

0

0.1

0.2

0.3

0.4

S

[

N

]

D

u/u [mV/V]

9

10. Zwolnid klocek o ciężarze Q , zarejestrowad wartości względnych przyrostów napięd

generowanych w tensometrycznym przetworniku siły (pośrednio jest mierzona
wartości siły S ).

11. Próbę powtórzyd trzykrotnie dla wybranego rodzaju okładzin ciernych klocka Q .

Uzyskane z pomiarów dane zapisad w arkuszu MS Excela, przeprowadzid konwersję
wartości wielkości elektrycznych na mechaniczne według wyznaczonego uprzednio
równania prostej (punkt 3 i 4).

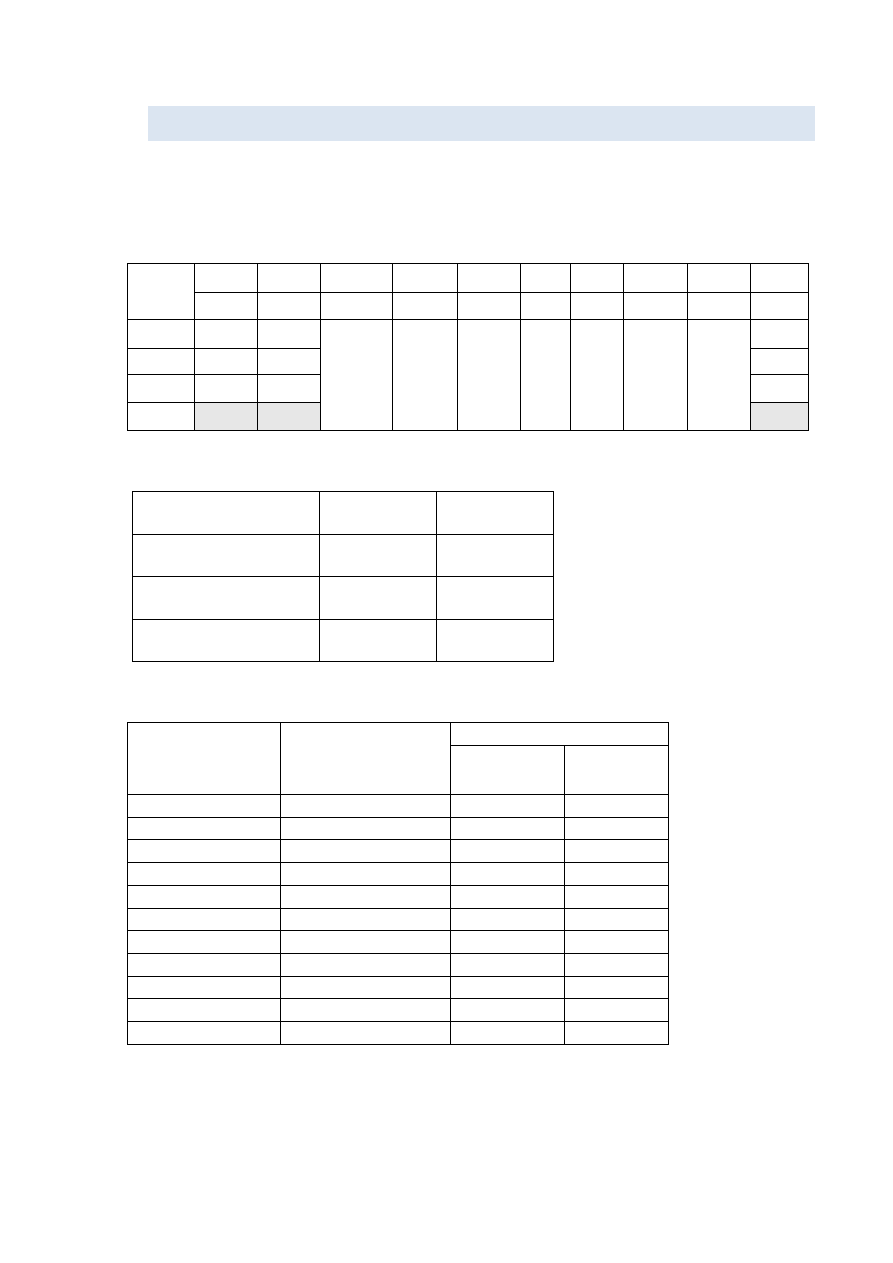
12. Sporządzid w arkuszu MS Excel wykres przedstawiający zależnośd siły S od czasu (

rys.

8

); wyznaczyd maksymalną wartośd siły w czasie eksperymentu, a otrzymane wyniki

zamieścid w

tab. 2

.

Rys. 8. Wykres zmienności siły napięcia linki w czasie doświadczenia

13. Zrealizowad serię pomiarów dla różnych par materiałów powtarzając punkty 6–12.

14. Obliczyd wartośd momentu bezwładności bloczka

o

J

wykorzystując wzory (12) – (13)

i znaną gęstośd stopu aluminium i stali (

Al



i

stal



).

15. Wyznaczyd wartości siły napięcia linki

.

analit

S

ze wzoru (11) i porównad ją z

maksymalną wartością siły

.

eksp

S

uzyskaną z pomiarów (dla różnych rodzajów

materiałów wkładek klocka Q ).

16. Wartości sił

.

eksp

S

i

.

analit

S

dla testowanych rodzajów materiałów zamieścid w

tab. 3

.

0

2

4

6

8

10

12

0

0.2

0.4

0.6

0.8

1

Si

ła

S

eksp

.

[N

]

czas t [s]

10

5. WYNIKI POMIARÓW I OBLICZEO

Wyniki uzyskane z eksperymentu oraz obliczone ze wzorów zestawid w poniższych tabelach.

Tab. 2. Wyniki pomiarów

Numer
pomiaru

z

d

h

Al



stal



o

J

i





G

m

Q

m

.

eksp

S

[m]

[m]

[kg/m

3

]

[kg/m

3

]

[kg m

2

]

*°+

–

[kg]

[kg]

[N]

1

2

3

Średnia

Tab. 3. Zestawienie wyników obliczeo

Materiał wkładki

.

eksp

S

[N]

.

analit

S

[N]

równanie (11)

equation

reference goes

hereequation

reference goes

here

Stal – stal

Stop aluminium –stal

Tworzywo sztuczne – stal

Tab. 4. Wartości statycznych i kinetycznych współczynników tarcia suchego [3]

Materiał 1

Materiał 2

współczynnik tarcia

statyczny

kinetyczny

stal miękka

stal miękka

0.74

0.57

aluminium

stal miękka

0.61

0.47

miedź

stal miękka

0.53

0.36

stal

poliamid 66

–

0.25

stal

mosiądz

0.35

–

stal miękka

mosiądz

0.51

0.44

stal miękka

żeliwo

–

0.23

stal twarda

polietylen

0.2

stal twarda

polistyren

0.3-0.35

–

stal twarda

stal twarda

0.78

0.42

stal miękka

ołów

0.95

0.95

11

6. WNIOSKI

Przeanalizowad ewentualne przyczyny, które mogą mied wpływ na różnicę między

wartością siły napięcia

.

analit

S

w lince wyznaczoną z równania (11), a jej odpowiednikiem

eksperymentalnym

.

eksp

S

. Jak moment bezwładności bloczka

o

J

wpływa na wartośd siły

.

analit

S

wyznaczonej z równania (11)?

Literatura

1. Uścinowicz Robert: Instrukcja obsługi wzmacniacza Spider 8 i programu Catman

Express 3.1, Białystok, 2007.

2. Instrukcja obsługi programu Microsoft Office Excel, 2000.

3. Strona

internetowa

f-my

Roymech.

Dostępna

w

Internecie:

http://www.roymech.co.uk/Useful_Tables/Tribology/co_of_frict.htm