2008-05-09 11:23

Wykład: Analiza wariancji prosta (jednoczynnikowa)(ANOVA)

Analiza zmienności została opracowana przez uczonego angielskiego, biologa i genetyka Ronalda
A. Fishera. Istota jego teorii opiera się na podziale zmienności głównej na pewne frakcje i na
analizowaniu tych poszczególnych zmienności.
W oparciu o pogląd Fishera wyróżniamy 3 rodzaje zmienności:
a) zmienność ogólna - wyraża się zróżnicowaniem wszystkich kolejnych wartości zmiennej
w stosunku do ogólnej średniej (obliczonej dla całej zbiorowości)
b) zmienność międzygrupowa - występuje na skutek różnic powstałych między grupami
doświadczalnymi, wywołana jest działaniem czynnika doświadczalnego na poszczególne grupy
doświadczalne, wyraża się zróżnicowaniem średnich poszczególnych grup doświadczalnych
w stosunku do ogólnej średniej
c) zmienność wewnątrzgrupowa - istnieje między poszczególnymi wartościami zmiennej
wewnątrz każdej grupy, wywołana jest czynnikami osobniczymi czyli indywidualnymi cechami
poszczególnych osobników, wyraża się zróżnicowaniem poszczególnych zmiennych wewnątrz
każdej grupy w stosunku do średniej dla tej grupy

Analizą wariancji posługujemy się przy badaniu istotności różnic między grupami

doświadczalnymi. W tym celu wykorzystujemy wykryte przez Fishera prawo, że stosunek
kwadratów odchyleń międzygrupowych do wewnątrzgrupowych kształtuje się według określonego
rozkładu (rozkład F) i stąd możliwa jest ocena prawdopodobieństwa wystąpienia pewnych wartości
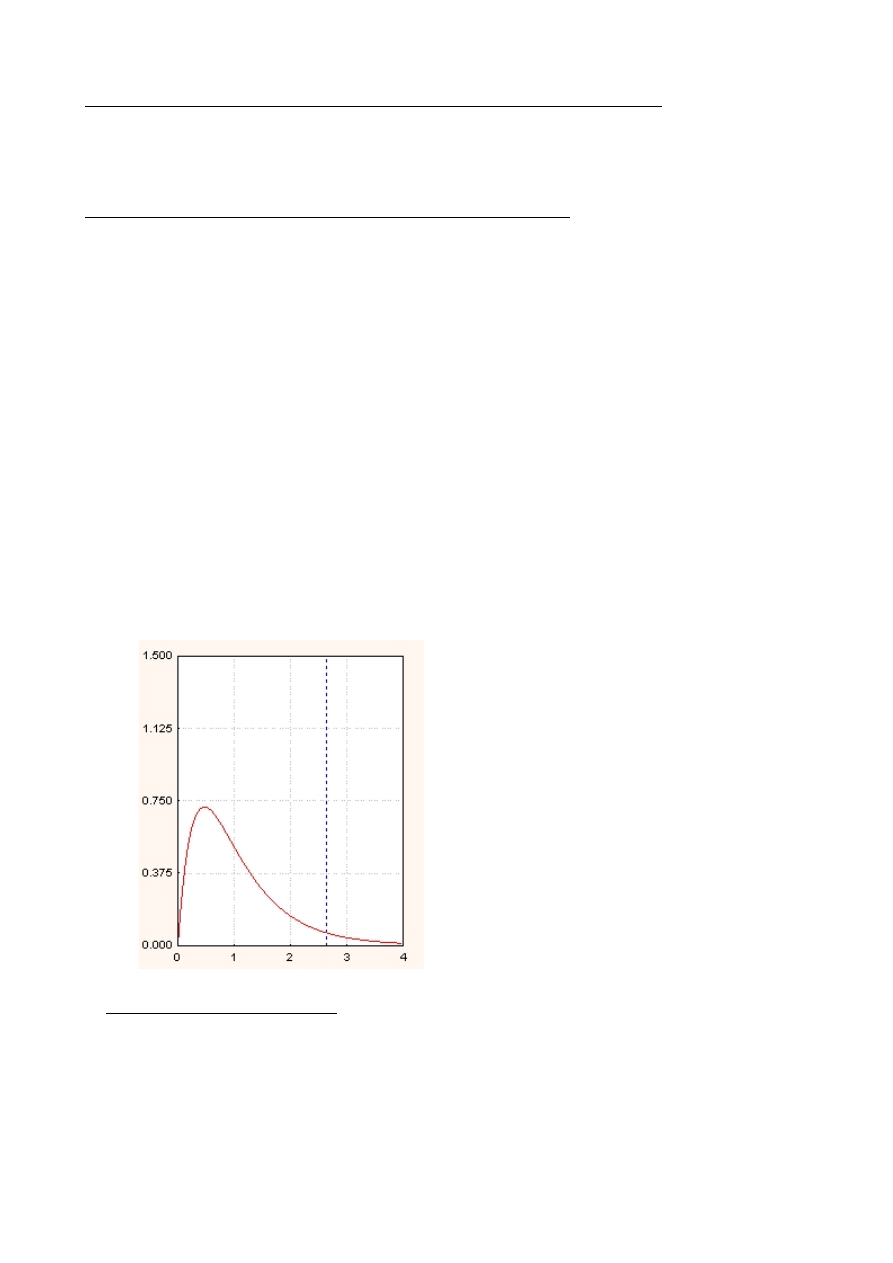
F. Sytuację tę można wyobrazić sobie w następujący sposób. Jeśli z populacji o rozkładzie
normalnym wybieralibyśmy losowo po dwie próby i badalibyśmy wzajemne relacje ich wariancji
(iloraz), to ten stosunek miałby rozkład zgodny z rozkładem F. Jest to rozkład prawoskośny, tj.
średnia arytmetyczna jest większa od mediany.

Hipoteza zerowa i alternatywna:

H

0

: Wszystkie średnie są równe.

H

0

:

µ

1

=

µ

2

=

µ

3

=

µ

4

=

µ

5

=

µ

6

...

H

1

: Istnieje co najmniej jedna para średnich, które różnią się ze sobą.

H

1

:

µ

1

≠µ

2

lub

µ

1

≠µ

3

lub

µ

2

≠µ

3

itd....

Autor: Dariusz Piwczyński

1

2008-05-09 11:23

Kolejność obliczeń (Analiza wariancji prosta)

1. Obliczanie stopni swobody (rodzaj zmienności) (

DF

)

a)

Ogólna

N-1

(N – liczebność populacji)

b)

Międzygrupowa

k-1

(k - liczba grup doświadczalnych)

c)

Wewnątrzgrupowa

N-k

2. Sumy kwadratów odchyleń (

SKO

)

a) Ogólna

( )

∑

∑

−

=

N

x

x

S

o

2

2

b) Międzygrupowa

c) Wewnątrzgrupowa: Sw=S

o

- S

m

3. Średnie kwadraty odchyleń (

ŚKO

)

a)

zmienność międzygrupowa: S

m

2

=S

m

/(k-1)

b) zmienność wewnątrzgupowa: S

w

2

=S

w

/(N-k)

4. F empiryczne

2

2

w

m

emp

S

S

F

=

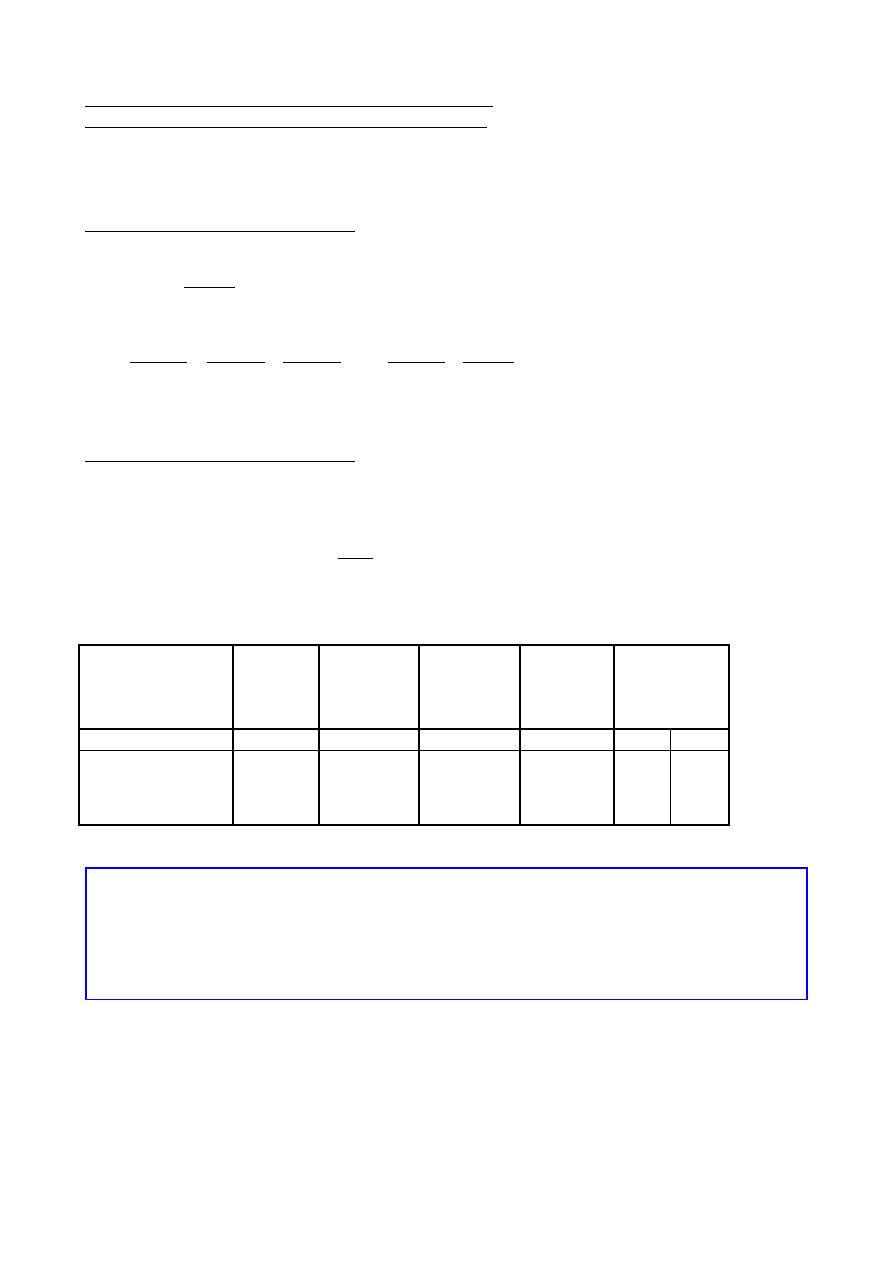
Tabela analizy zmienności

Rodzaj zmienności

Liczba

stopni

swobody

DF

Suma

kwadratów

odchyleń

SKO

Średni

kwadrat

odchyleń

ŚKO

F

emp

F

tab

0,05

0,01

Ogólna

Międzygrupowa

Wewnątrzgrupowa

N-1

k-1

N-k

S

o

S

m

S

w

S

m

2

S

w

2

F

emp

Obliczoną wartość statystyki F (tzw. F empiryczne - F

emp.

) odnosimy do wartości krytycznej z

rozkładu F-Snedecora dla założonego poziomu istotności (

α

) i określonej liczby stopni swobody

(

ν

1

=k-1 oraz

ν

2

=N-k) (F tabelaryczne - F

tab.

). Jeżeli F

emp.

≥

F

tab.

- to mamy podstawę do odrzucenie

hipotezy zerowej i stwierdzenia, iż istnieje co najmniej jedna para średnich, które różnią się ze
sobą. Zatem czynnik doświadczalny wpływa statystycznie na cechę. W przeciwnym przypadku,
nie mamy podstaw do odrzucenia H

0

.

Autor: Dariusz Piwczyński

2

(

) (

) (

)

(

) ( )

N

x

n

x

n

x

n

x

n

x

S

i

i

m

2

2

3

2

3

2

2

2

1

2

1

...

∑

∑

∑

∑

∑

−

+

+

+

+

=

2008-05-09 11:23

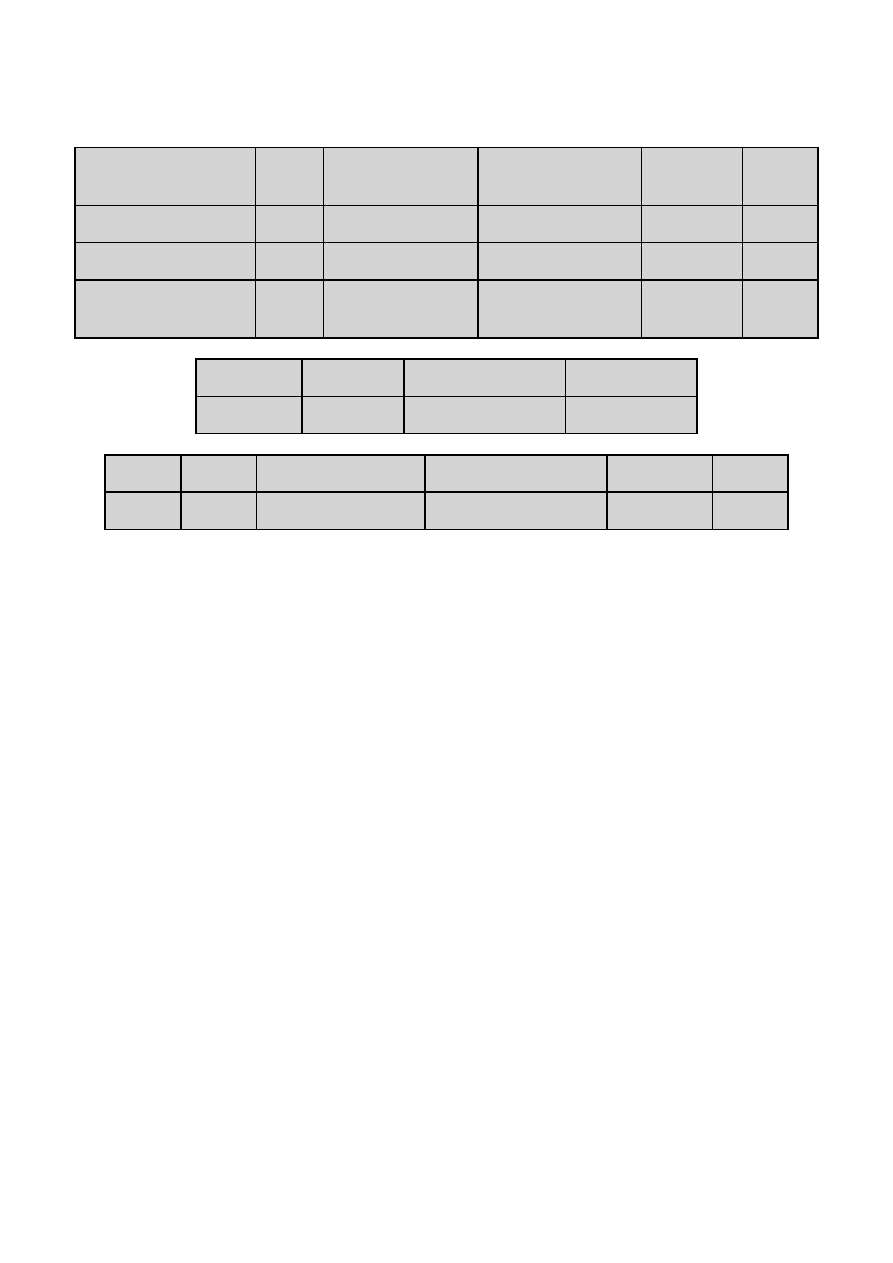
Wynik analizy wariancji jednoczynnikowej w SAS

Zmienna zależna: nGat

Źródło

St.

sw.

Suma

kwadratów

Średnia

kwadratów

Wartość

F

Pr > F

Model

6

3729.08593

621.51432

42.95

<.0001

Błąd

990

14327.22500

14.47194

Razem

skorygowane

996

18056.31093

R-kwadrat Wsp. war. Pierwiastek MSE Średnia nGat

0.206525

26.69850

3.804201

14.24875

Źródło St. sw. Type III Suma kw. Średnia kwadratów Wartość F

Pr > F

Zaklad 6

3729.085933

621.514322

42.95

<.0001

Autor: Dariusz Piwczyński

3