Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–1

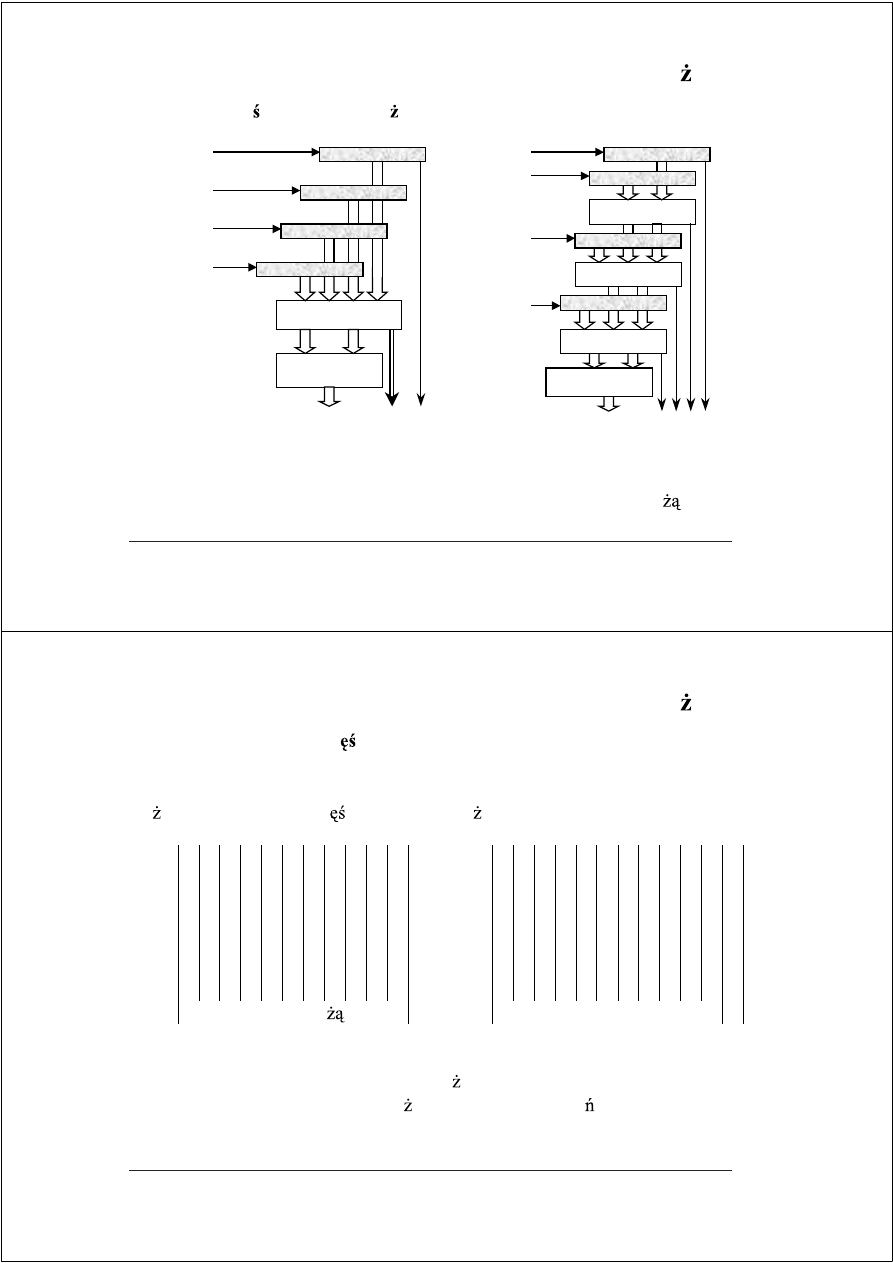
Schematy przy pieszonego mno enia

CSA

CPA

CPA

x

0

A

x

1

A

x

2

A

x

3

A

x

0

A

x

1

A

x

2

A

x

3

A

akumulacja równoległa

CSA

CSA

akumulacja sekwencyjna

CSA

•

akumulacja równoległa – drzewiasta struktura CSA,

•

akumulacja sekwencyjna – liniowa struktura CSA, matryca mno

ca

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–2

Akumulacja iloczynów cz ciowych

•

sumatory wielooperandowe CSA

ró ne wagi iloczynów cz ciowych

ró na liczba operandów jednej wagi

A 9 8 7 6 5 4 3 2 1 0 A 9 8 7 6 5 4 3 2 1 0
o o o o o o o o o o o o o o o o o
o o o o o o o o o o o o o o o
o o o o o o o o o o o o o
o o o o o o o o o o o
o o o o o o o o o
o o o o o o o

matryca mno

ca

drzewo CSA

drzewo CSA

•

szybka redukcja operandów w najdłu szej kolumnie

•

redukcja do 1 operandów najni szych wag (krótsze ko cowe dodawanie)

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–3

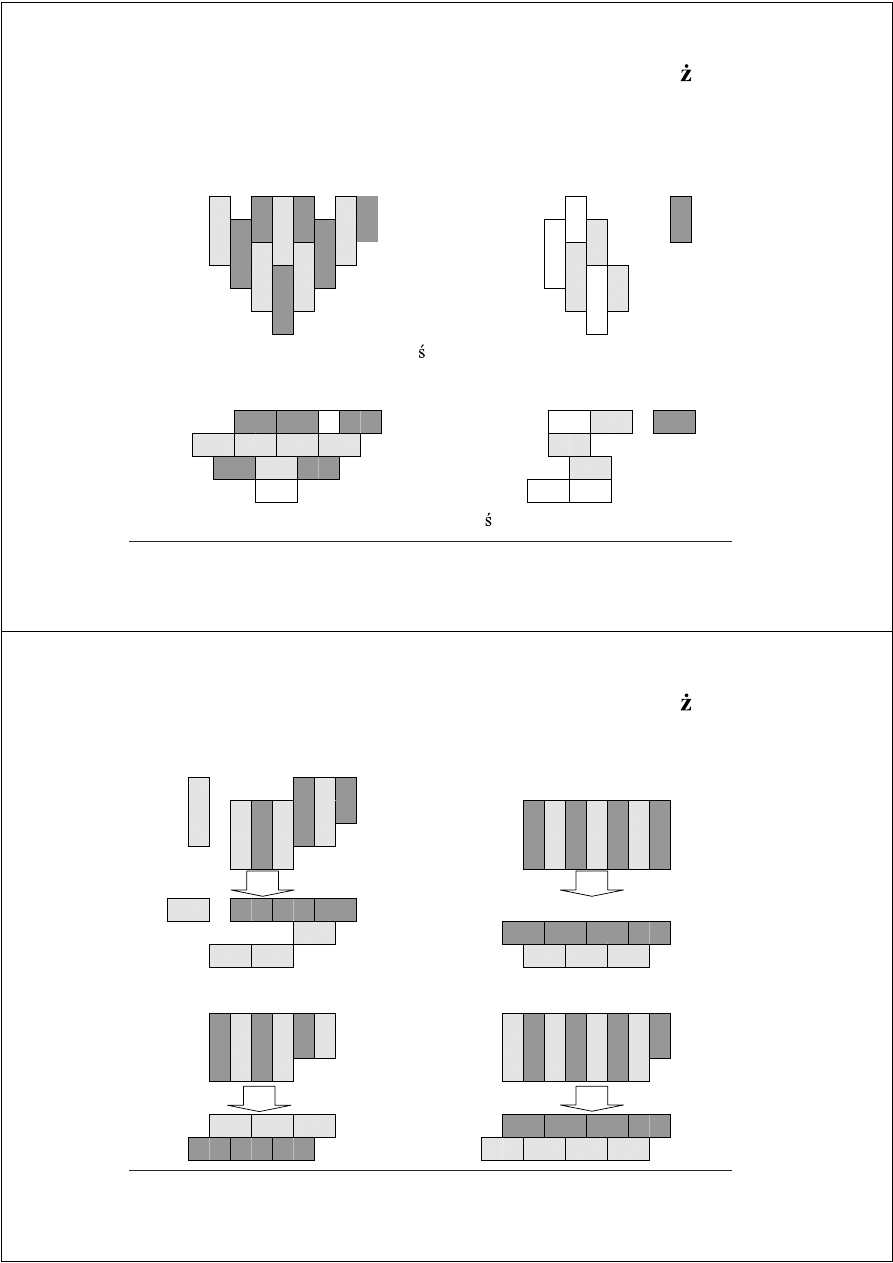
Optymalizacja struktury CSA (1)

redukcja maksymalna

drzewo Wallace’a

A 9 8 7 6 5 4 3 2 1 0

A 9 8 7 6 5 4 3 2 1 0

o o o o o o o o o o o o o o o o o o o o o o
o o o o o o o o o o o o o o o o o o
o o o o o o o o o o o o o o
o o o o o o o o o o
o o o o o o
o o

CSA, poziom 3 – wej cia układów (3,2) lub (2,2)

A 9 8 7 6 5 4 3 2 1 0

A 9 8 7 6 5 4 3 2 1 0

o o o o o o o o o o o o o o o o o o o o o
o o o o o o o o o o o o o o o o
o o o o o o o o o o o o o o
o o o o o o o o o o

CSA, poziom 3 – wynik redukcji: wyj cia układów (3,2) lub (2,2)

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–4

Optymalizacja struktury CSA (1)

A 9 8 7 6 5 4 3 2 1 0

A 9 8 7 6 5 4 3 2 1 0

o o o o o o o o o o o o o o o o o o o o o o
o o o o o o o o o o o o o o o o
o o o o o o o o o o o o o
o o o o o o o o o o

o o o o o o o o o o o o o o o o o o o o o o
o o o o o o o o o o o o o o o
o o o o o o o o o o o

CSA, poziom 2

o o o o o o o o o o o o o o o o o o o o o o
o o o o o o o o o o o o o o o
o o o o o o o o o o o

o o o o o o o o o o o o o o o o o o o o o o
o o o o o o o o o o o o o o o

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–5

Redukcja liczby iloczynów cz ciowych – przekodowanie kanoniczne

Minimaln dla danego mno nika liczb dodawa lub odejmowa okre la waga

|)

|

...

|

|

|

|

(

0

2

1

y

y

y

n

n

+

+

+

−

−

jego minimalnej reprezentacji w kodzie SD.

}

,

,...,

{

0

1

1

x

x

x

n

−

=

X

U2

→

}

,

,...,

{

0

1

1

min

y

y

y

n

−

=

Y

SD

– przekodowanie kanoniczne

Przekodowanie kanoniczne –algorytm (p

0

=0)

x

i–1

x

i

p

i

p

i+1

y

i

Komentarz

0

0

0

0

0

ci g zer

0

1

0

0

1

izolowana jedynka

1

0

0

0

0

ci g zer

1

1

0

1

1

Pocz tek ci gu jedynek

0

0

1

0

1

koniec ci gu jedynek

0

1

1

1

0

ci g jedynek

1

0

1

1

1

izolowane zero

1

1

1

1

0

ci g jedynek

Skomplikowana i czasochłonna procedura przekodowania

→

rzadko stosowane

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–6

Przekodowanie Bootha

•

zast pienie serii dodawa jednym odejmowaniem i jednym dodawaniem

l

s

l

l

s

s

2

2

2

2

...

2

2

1

2

1

−

=

+

+

+

+

+

−

−

|{...0[11...11]0... }

U2

| = |{...1[00...00]0... }

U2

| – |{...0[00...01]0...}

U2

,

|{...0[11...11]0... }

SD

| = |{

...

0

]

1

0

...

00

[

1

...

}

SD

|

→

reguła Bootha

≡

przekodowanie mno

ż

nika na kod SD

•

reprezentacja w systemie NB lub U2 jest reprezentacj w systemie SD, ale

przekodowanie według reguły Bootha:

•

U2

→

SD – wykonalne, bo [x1...11]0... = [(1

−

x)0...00]0...

−

[00...01]0...

•

NB

→

SD – niewykonalne bez rozszerzenia gdy {1,1,… ,1,0, x ,…}, bo

x

≥

0

∧

z

≠

1

⇒

|{1, x,..., x, x}

SD

| > |{z, y, y,..., y}

SD

|

⇒

konieczne rozszerzenie {1,… ,1,0, x ,…}

NB

= {0,1, … ,1,0, x ,…}

U2

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–7

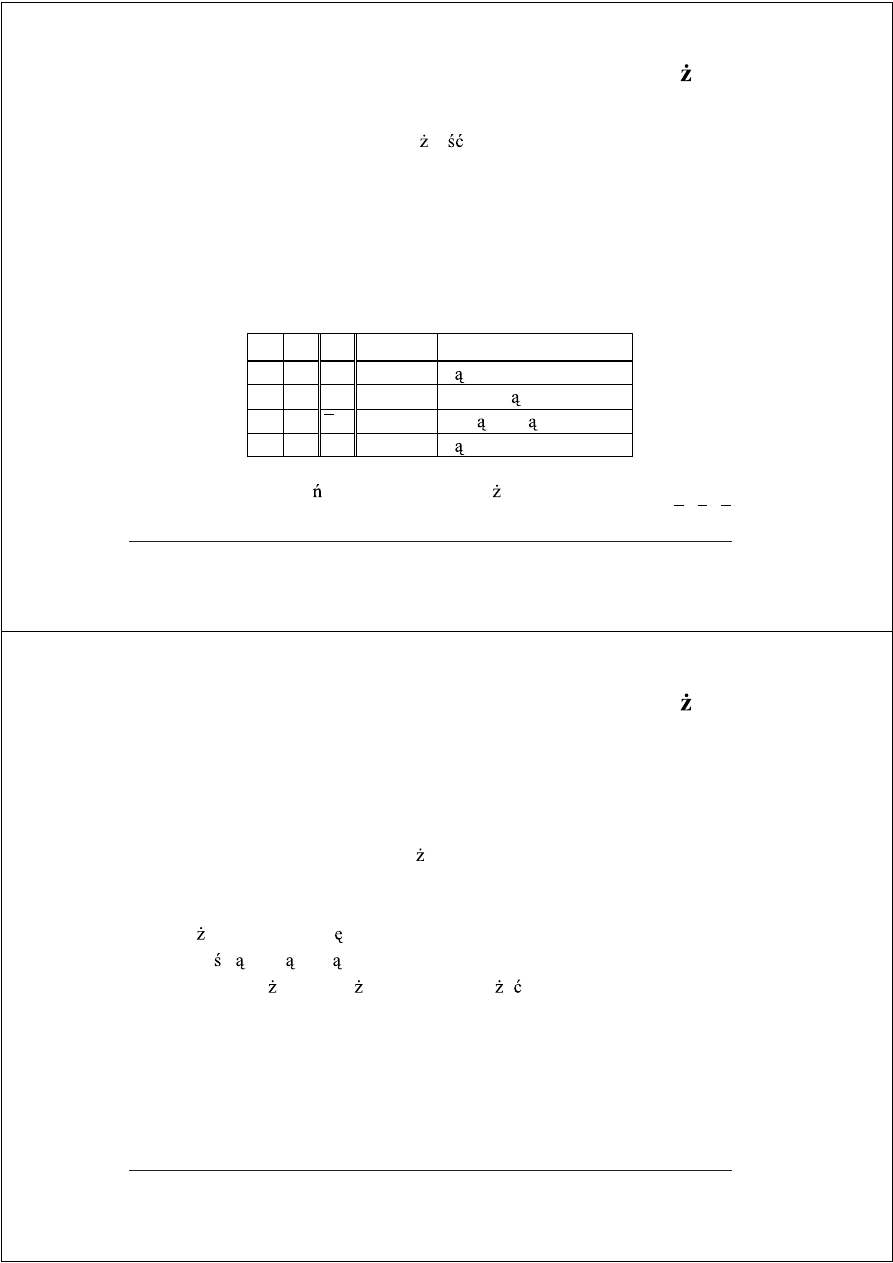
Algorytm Bootha

Uzasadnienie teoretyczne – równowa no X = 2X

−

X

1

1

0

1

2

0

1

1

1

2

0

1

2

)

(

2

2

2

2

−

−

=

−

−

=

−

−

+

−

=

−

−

−

=









+

−

−









+

−

=

∑

∑

∑

x

x

x

x

x

x

x

X

i

n

i

i

i

i

n

i

i

n

n

i

n

i

i

n

n

}

1

,

0

{

∈

i

x

⇒

}

1

,

0

,

1

{

1

−

∈

−

=

−

i

i

i

x

x

y

(x

–1

= 0)

|{x

n–1

, x

n–2

, x

n–1

, …, x

1

, x

0

}

U2

| = |{(x

n–2

– x

n–1

), (x

n–3

– x

n–2

), …, (x

0

– x

1

), (x

– 1

– x

0

)}

SD

|

Przekodowanie Bootha (

i

i

i

x

x

y

−

=

−

1

)

x

i

x

i–1

y

i

operacja komentarz

0

0

0

—

ci g zer

0

1

1

+

A

koniec ci gu jedynek

1

0

1

−

A

pocz tek ci gu jedynek

1

1

0

—

ci g jedynek

Wady:
– zmienna liczba działa arytmetycznych, zale na od kodu liczby,
– nieefektywne kodowanie izolowanych jedynek –...010101(0)

→

1

1

1

1

1

1

...

.

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–8

Alternatywne przekodowanie Bootha

0

2

0

1

1

1

0

1

2

)

(

2

2

)

(

x

x

x

x

x

x

X

i

n

i

i

i

i

n

i

i

i

−

−

=

−

−

=

∑

∑

−

=

+

−

−

=

−

.

⇒

alternatywne przekodowanie mno nika

}

,

,...,

{

0

1

1

y

y

y

n

−

=

Y

1

0

,

1

−

≤

≤

−

=

+

n

i

x

x

y

i

i

i

,

Poniewa

0

2

x

Y

X

−

=

, wi c

•

warto ci pocz tkow akumulowanej sumy iloczynów jest

A

x

0

−

,

•

zamiast mno nej A nale y w algorytmie u y jej podwojenia 2A,

•

y

i

(przekodowanie alternatywne) = y

i+1

(przekodowanie proste)

Przekodowanie alternatywne NB/U2

→

SD zawsze wykonalne:

•

U2

→

SD – rozszerzenie

1

−

=

n

n

x

x

,

⇒

0

1

=

−

n

y

•

NB

→

SD – rozszerzenie

0

=

n

x

⇒

1

1

−

−

=

n

n

x

y

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–9

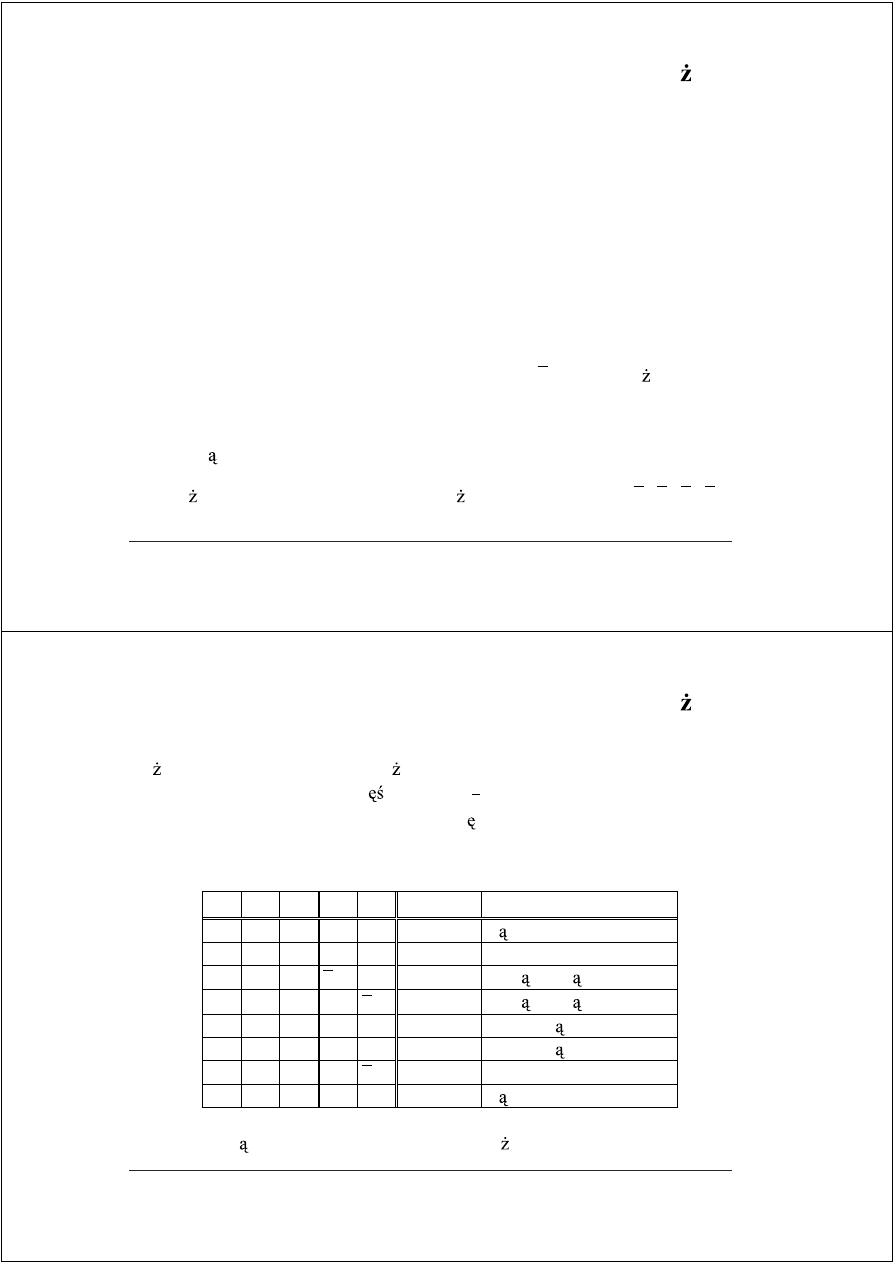
Przekodowanie rozszerzone (w bazie 2

2

) – algorytm Bootha-McSorleya

Na podstawie

1

1

0

1

2

)

(

−

−

=

−

−

−

=

∑

x

x

x

X

i

n

i

i

i

mamy (





2

/

n

k

=

)

1

2

1

0

1

2

2

1

2

1

2

1

0

1

2

2

2

1

2

1

1

2

1

0

1

2

2

2

1

0

2

1

2

2

)

2

(

2

)

2

2

(

2

)

(

2

)

(

−

−

=

−

+

−

−

=

+

−

−

+

−

=

+

−

=

−

−

+

+

−

=

−

−

+

−

=

=

−

−

+

−

=

∑

∑

∑

∑

x

x

x

x

x

x

x

x

x

x

x

x

x

x

X

j

k

j

j

j

j

j

k

j

j

j

j

j

j

k

j

j

j

j

k

j

j

j

}

1

,

0

{

∈

i

x

⇒

}

2

,

1

,

0

,

1

,

2

{

2

1

2

2

1

2

+

+

−

−

∈

+

+

−

=

−

+

j

j

j

i

x

x

x

y

(x

−

1

= 0)

⇒

wynik przekształce

ń

:

SD

0

1

1

}

,

,...,

{

y

y

y

n

−

=

Y

})

1

,

0

,

1

{

(

#

∈

y

takie, e

i

i

i

i

i

y

y

x

x

x

2

1

2

1

2

2

1

2

2

2

+

=

+

+

−

+

−

+

•

rozwi zanie jednoznaczne gdy

0

2

1

2

=

+

j

j

y

y

(

≥

połowa cyfr

Y to zera)

•

mo liwe zmniejszenie liczby zer mno nika (00101010

→

1

0

1

0

1

0

1

0

).

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

FAM–10

Algorytm Bootha-McSorleya – praktyczna realizacja

Ka da z kolejnych par bitów mno nika zawiera co najmniej jedno 0

⇒

liczba iloczynów cz ciowych

≤

n

2

1

.

•

dla pary pozycji

i

i

x

x

2

1

2

,

+

wykonuje si dodawanie

A

x

x

x

i

i

i

)

2

(

1

2

1

2

2

+

−

−

+

Przekodowanie rozszerzone (Bootha-McSorleya)

x

2i+1

x

2i

x

2i–1

y

2i+1

y

2i

działanie komentarz

0

0

0

0

0

—

ci g zer

0

1

0

0

1

+A

izolowana jedynka

1

0

0

1

0

−

2A

pocz tek ci gu jedynek

1

1

0

0

1

−

A

pocz tek ci gu jedynek

0

0

1

0

1

+A

koniec ci gu jedynek

0

1

1

1

0

+2A

koniec ci gu jedynek

1

0

1

0

1

−

A

izolowane zero

1

1

1

0

0

—

ci g jedynek

analizowane s pary bitów

⇒

rozszerzenie mno nika do parzystej liczby bitów

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

FAM–11

Alternatywne przekodowanie Bootha-McSorleya





0

2

2

1

2

2

2

1

2

/

0

0

2

0

1

2

)

2

(

2

2

)

(

2

x

x

x

x

x

x

x

X

i

i

i

i

n

i

j

n

j

j

j

−

+

+

−

=

−

−

=

+

+

−

=

−

=

+

∑

∑

.

}

2

,

1

,

0

,

1

,

2

{

)

2

(

2

1

2

2

2

−

−

∈

+

+

−

+

+

i

i

i

x

x

x

→

wynik przekodowania:

Y

SD

taka, e

i

i

i

i

i

y

y

x

x

x

2

1

2

2

1

2

2

2

2

2

+

=

+

+

−

+

+

+

oraz

0

2

1

2

=

+

i

i

y

y

Alternatywne przekodowanie Bootha-McSorleya

x

2i+2

x

2i+1

x

2i

y

2i+1

y

2i

działanie komentarz

0

0

0

0

0

—

ci g zer

0

0

1

0

1

+2A

pocz tek ci gu jedynek

0

1

0

0

1

+2A

izolowana jedynka

0

1

1

1

0

+4A

pocz tek ci gu jedynek

1

0

0

1

0

−

4A

koniec ci gu jedynek

1

0

1

0

1

−

2A

izolowane zero

1

1

0

0

1

−

2A

koniec ci gu jedynek

1

1

1

0

0

—

ci g jedynek

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

FAM–12

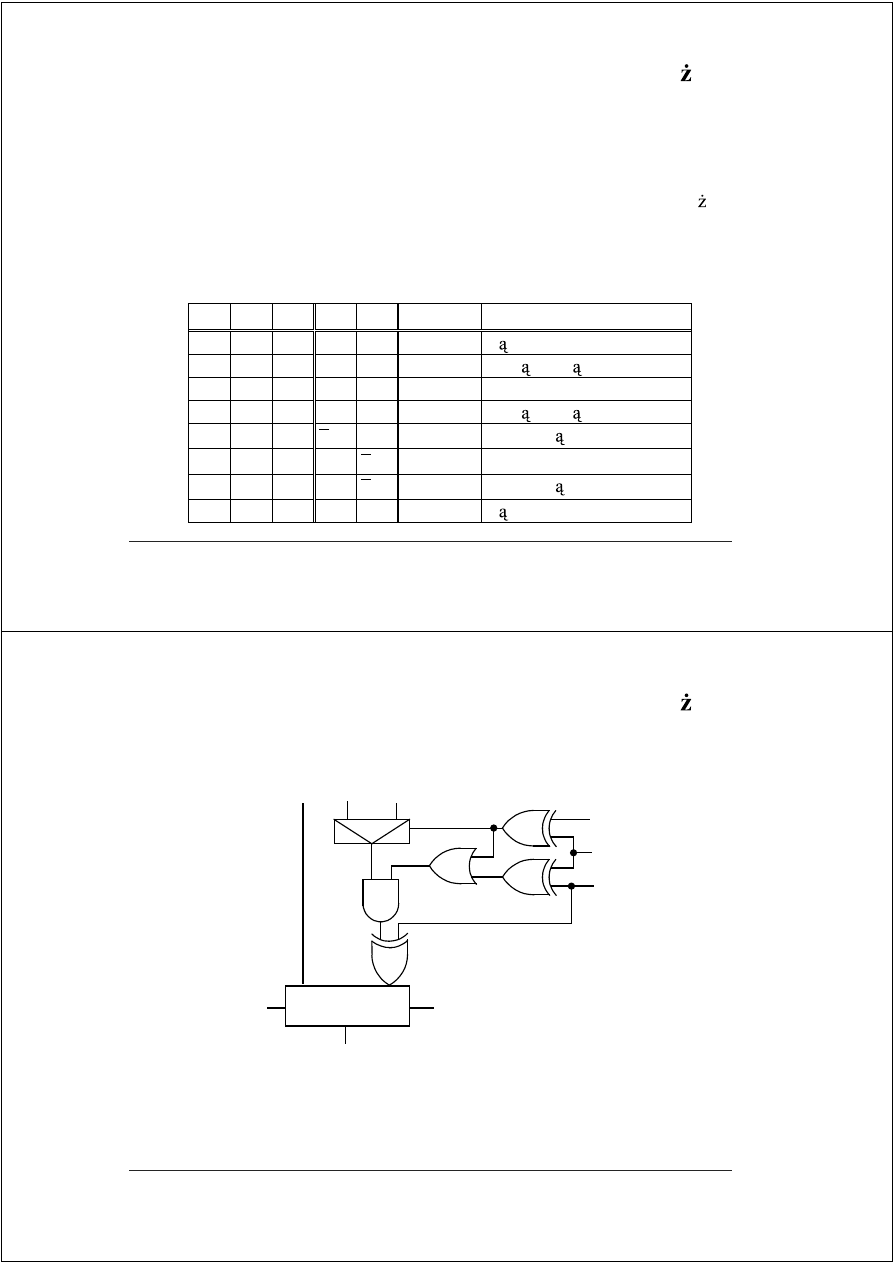
Realizacja przekodowania Bootha-McSorleya

a

v+1

x

r+1

x

r

x

r–1

a

v

s

r+v

FA

s

r+v+2

r = 2i + p, v = j + p

( p = 0 – prosty))

( p = 1 – alternatywny))

•

„brak podwojenia” = x

r

⊕

x

r–1

,

•

„odejmowanie” = x

r+1

,

•

„brak zerowania” = (x

r

⊕

x

r+1

) + (x

r

⊕

x

r–1

),

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

FAM–13

Algorytm Bootha/Bootha-McSorleya – przykłady

X

= {1,1,0,1,0,1}

U2

– w bazie 2 –

}

1

1

,

1

,

1

,

1

,

0

{

=

Y

,

– alternatywne w bazie 4 –

}

1

0

,

1

0

,

00

{

=

Y

, P

0

=–x

0

A

Y

(2)

Y

(4R)

A

=−3

1 1 1 1 0 1

1 1 1 1 0 1

X

=−11

0

1

1

1

1

1

0 0 0

1

0

1

P

0

=

0 0 0 0 0 0 0 0 0 0 0 0

–x

0

A 0 0 0 0 0 0 0 1 1

–A 0 0 0 0 0 0 0 0 0 1 1

–2A 0 0 0 0 0 0 1 1

+A 1 1 1 1 1 1 1 1 0 1

–2A 0 0 0 0 1 1

–A 0 0 0 0 0 0 0 1 1

0 0 0 1 0 0 0 0 1

+A 1 1 1 1 1 1 0 1

–A 0 0 0 0 0 0 1

XA

=

33

0 0 0 0 1 0 0 0 0 0 1

Uwaga: W polach zacienionych wpisano cyfry rozszerzenia znakowego.

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

FAM–14

Przekodowanie mno nika w systemie uzupełnie do 1

W systemie U1, na podstawie równowa no ci X = 2X

−

X mamy









+

−

−

−









+

−

−

=

∑

∑

−

=

−

−

+

−

=

−

i

n

i

i

n

n

i

n

i

i

n

n

x

ulp

x

x

ulp

x

X

2

)

2

(

2

)

2

2

(

2

0

1

1

1

2

0

1

,

sk d wynika

ulp

x

x

x

x

X

n

i

n

i

i

i

1

1

1

0

1

2

)

(

−

−

−

=

−

+

−

−

=

∑

.

Poniewa ulp = 1, a rozszerzeniem liczby w kodzie U1 jest

1

1

−

−

=

n

x

x

, zatem

i

n

i

i

i

x

x

X

2

)

(

1

0

1

∑

−

=

−

−

=

.

Podobnie

)

(

2

)

(

2

0

1

2

0

1

x

x

x

x

X

n

i

n

i

i

i

−

+

−

=

−

−

=

+

∑

.

•

algorytm analogiczny jak w U2, lecz inna warto pocz tkowa akumulacji

•

sumowanie z uwzgl dnieniem rozszerze prawo- i lewostronnych

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

FAM–15

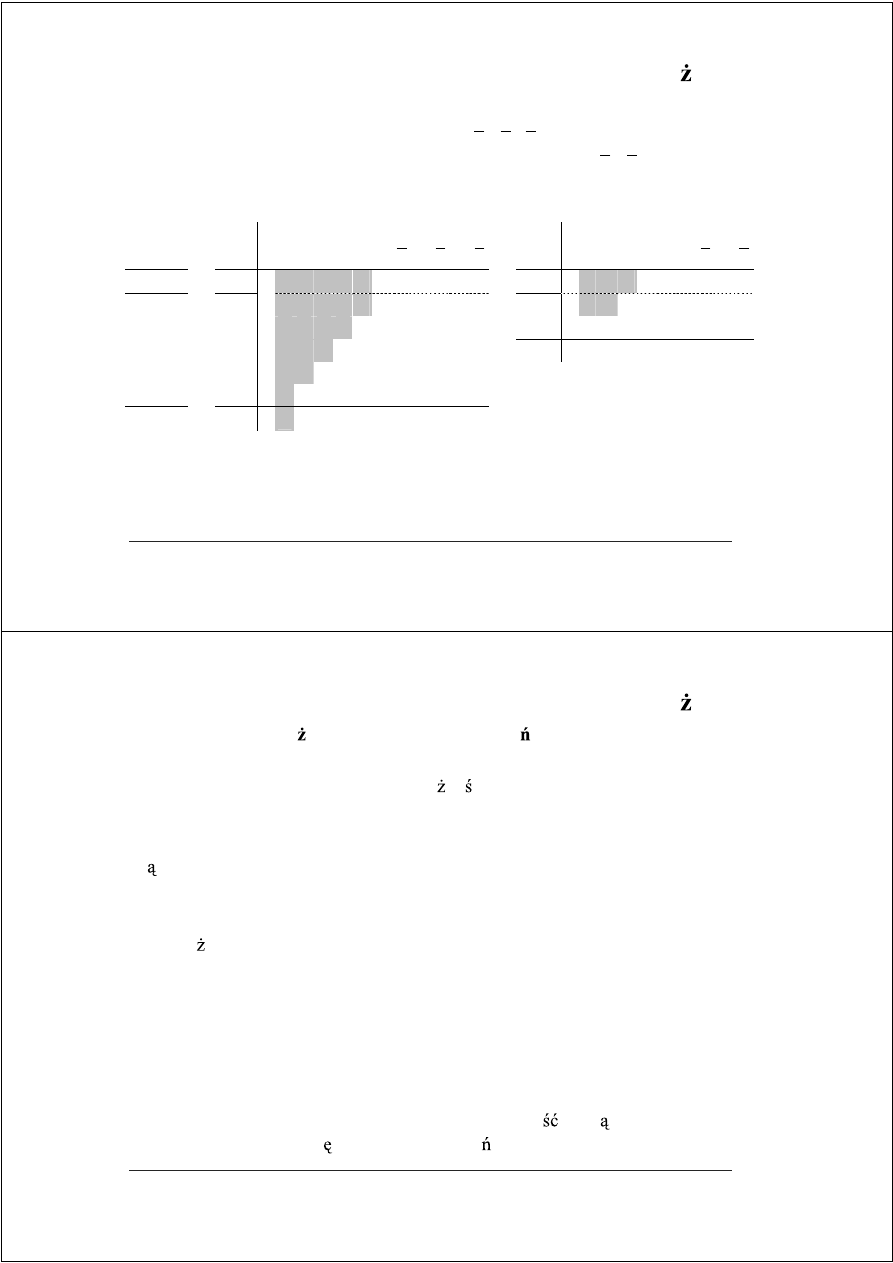
Matrycowe układy mno

ce – schemat mno enia

a

4

a

3

a

2

a

1

a

0

×

x

4

x

3

x

2

x

1

x

0

a

4

x

0

a

3

x

0

a

2

x

0

a

1

x

0

a

0

x

0

+

a

3

x

1

a

2

x

1

a

1

x

1

a

0

x

1

a

4

x

1

s

41

s

31

s

21

s

11

c

41

c

31

c

21

c

11

+

a

3

x

2

a

2

x

2

a

1

x

2

a

0

x

2

a

4

x

2

s

52

s

42

s

32

s

22

c

52

c

42

c

32

c

22

+

a

3

x

3

a

2

x

3

a

1

x

3

a

0

x

3

a

4

x

3

s

63

s

53

s

43

s

33

c

63

c

52

c

42

c

32

+

a

3

x

3

a

2

x

3

a

1

x

3

a

0

x

3

a

4

x

3

s

74

s

64

s

54

s

44

+

c

74

c

64

c

54

c

44

s

9

s

8

s

7

s

6

s

5

s

4

s

3

s

2

s

1

s

0

sji oraz cji – sumy i przeniesienia na pozycji j w i-tym kroku akumulacji

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

FAM–16

Matryca mno

ca kodu naturalnego (Brauna)

a

4

x

0

HA

a

0

x

1

HA

a

1

x

1

HA

a

2

x

1

HA

a

3

x

1

a

4

x

1

FA

a

0

x

2

FA

a

1

x

2

FA

a

2

x

2

FA

a

3

x

2

a

4

x

2

FA

a

0

x

3

FA

a

1

x

3

FA

a

2

x

3

FA

a

3

x

3

a

4

x

3

FA

a

0

x

4

FA

a

1

x

4

FA

a

2

x

4

FA

a

3

x

4

a

4

x

4

HA

FA

FA

FA

p

9

p

8

p

7

p

6

p

5

p

4

p

3

p

2

p

1

p

0

CSA

CSA

CSA

CPA

a

0

x

0

a

1

x

0

a

2

x

0

a

3

x

0

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

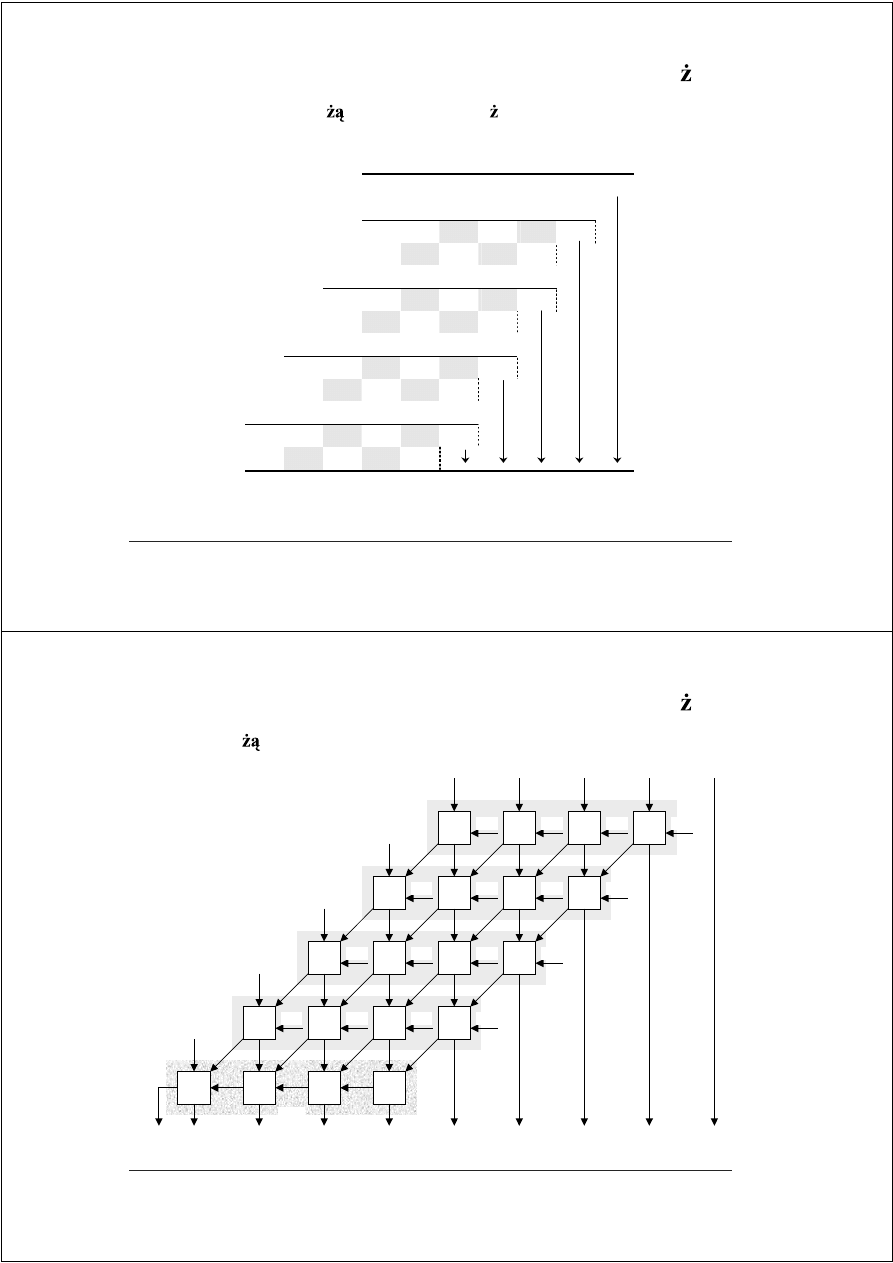
FAM–17

Multiplikator Brauna (Braun multiplier)

HA

HA

HA

HA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

HA

x

0

x

1

x

2

x

3

x

4

a

4

a

2

a

1

a

3

a

0

s

0

s

1

s

3

s

2

s

4

s

5

s

6

s

7

s

8

s

9

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

FAM–18

Matrycowe układy mno

ce kodu U2

iloczyny cz ciowe lub iloczyny elementarne mog by liczbami ujemnymi

.

2

2

2

2

2

2

2

2

2

2

2

0

1

1

2

0

1

1

2

0

2

0

2

1

1

2

0

1

1

2

0

1

1













−

+













−

+

+

=

=













+

−

⋅













+

−

∑

∑

∑

∑

∑

∑

−

=

−

−

−

=

−

−

−

=

+

−

=

−

+

−

−

−

=

−

−

−

=

−

−

k

i

i

i

m

m

m

j

j

j

k

k

k

i

j

i

i

j

m

j

k

m

k

m

m

j

j

j

m

m

k

i

i

i

k

k

a

x

x

a

a

x

a

x

x

x

a

a

•

wagi operandów (1-bitowych iloczynów) mog by ujemne

→

wystarczy zmieni znaki wag wej i wyj niektórych sumatorów

•

zast pienie sumatorów FA realizuj cych dodawanie x

+

y

+

z = 2c

+

s

układami odejmuj cymi FS (x

−

y

−

z =

−

2c

+

s) lub FS

D

(x

+

y

−

z = 2c

−

s)

•

struktura logiczna FS i FS

D

identyczna

•

przeciwne wagi wej i wyj , bo

x

−

y

−

z =

−

(z

+

y

−

x) oraz

−

(2c

−

s) =

−

2c + s

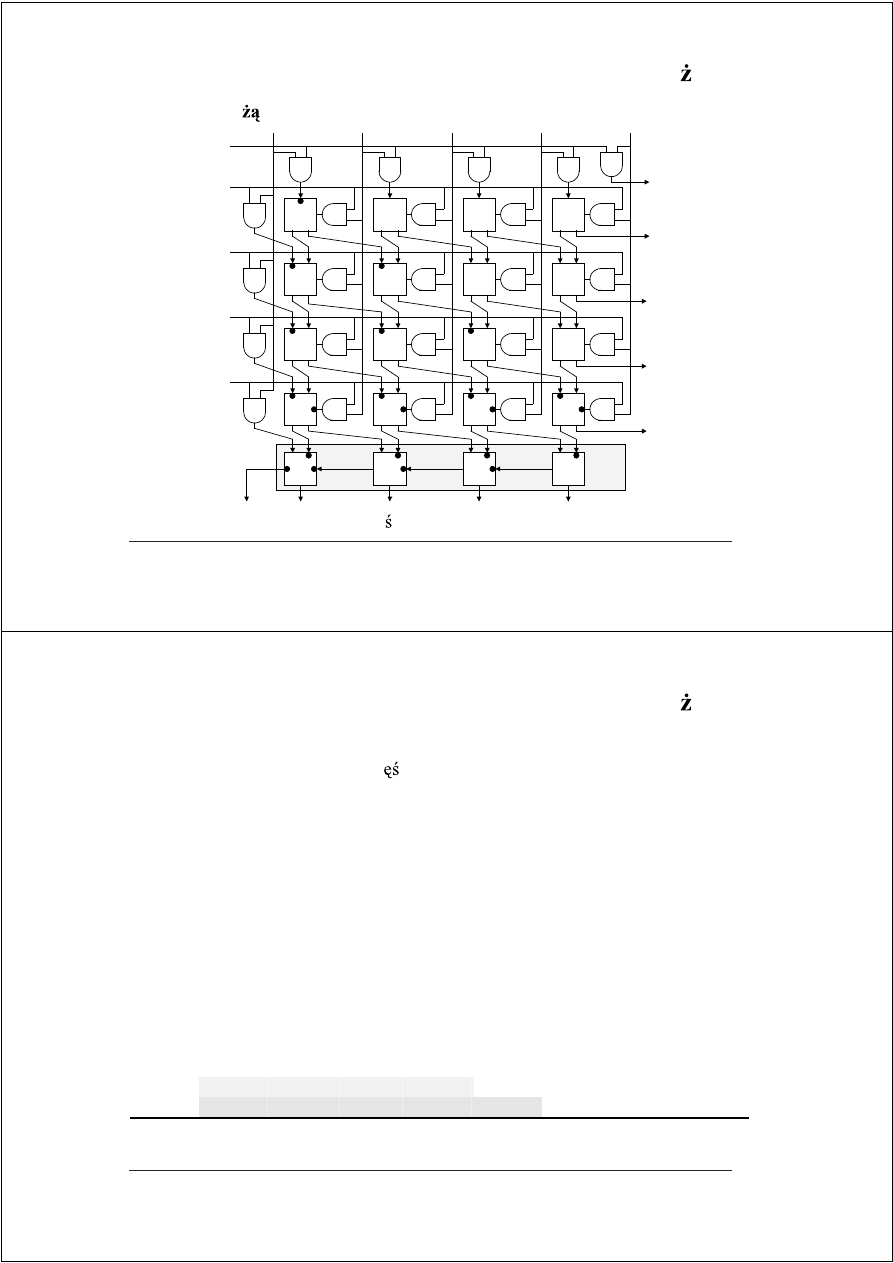
Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

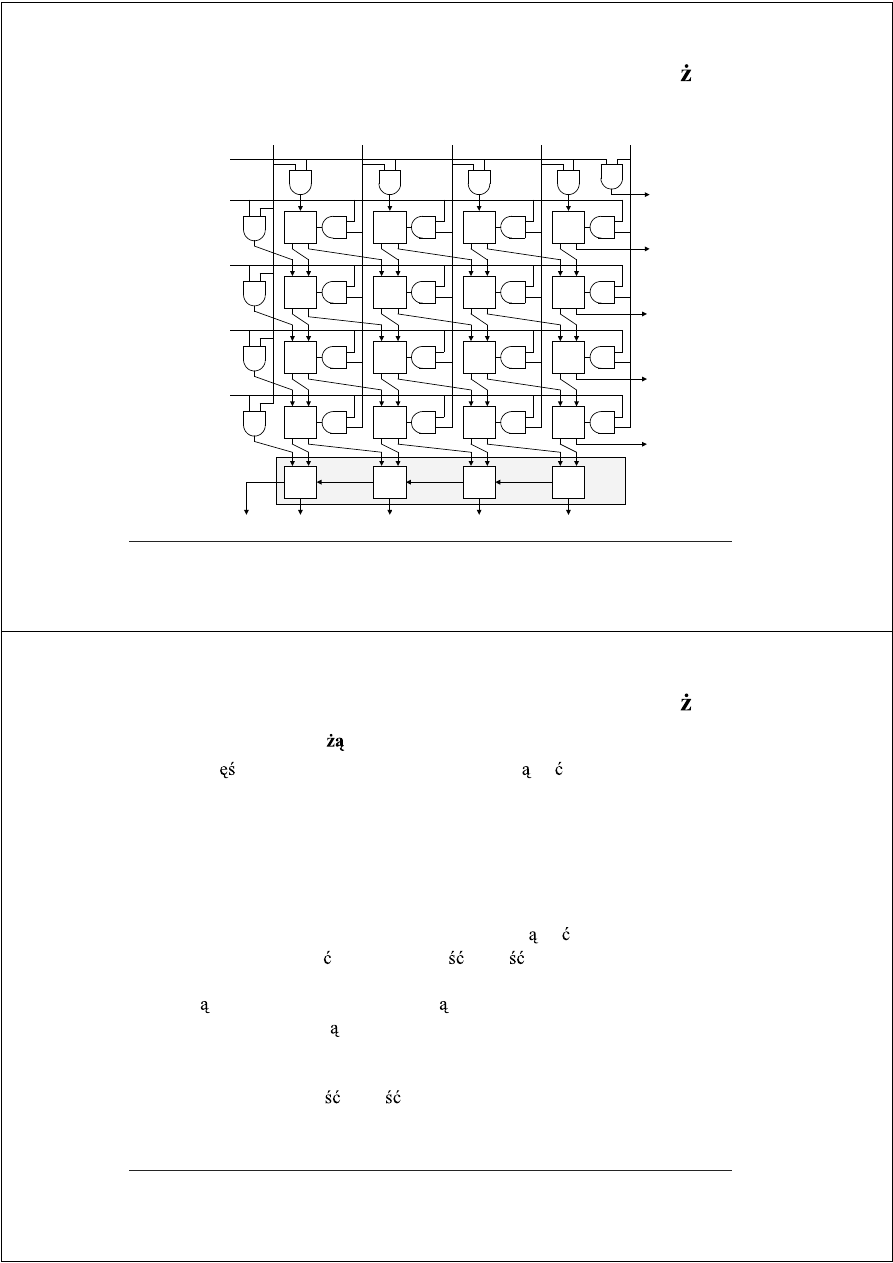
FAM–19

Matryca mno

ca kodu uzupełnieniowego

HS

HA

HA

HA

FS

FS

FA

FA

FS

FS

FS

FA

FS

FS

FS

FS

FS

FS

FS

HS

x

0

x

1

x

2

x

3

x

4

a

4

a

2

a

1

a

3

a

0

s

0

s

1

s

3

s

2

s

4

s

5

s

6

s

7

s

8

s

9

(

•

– wej cia o ujemnej wadze)

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–20

Algorytm Baugha-Wooley’a

zamiana ujemnych iloczynów cz ciowych na dodatnie:













+

−

+

−

=

−

−

−

=

−

+

−

+

−

−

=

−

−

∑

∑

1

2

0

1

2

1

2

0

1

1

2

2

)

1

(

2

2

2

m

k

i

m

i

i

m

k

m

k

i

i

i

m

m

a

x

a

x

,













+

−

+

−

=

−

−

−

=

−

+

−

+

−

−

=

−

−

∑

∑

1

2

0

1

2

1

2

0

1

1

2

2

)

1

(

2

2

2

k

m

j

k

j

j

m

k

k

m

j

j

j

k

k

x

a

x

a

.

korekcyjne dodawanie argumentów:

(1–a

k–1

) 2

k+m–2

+ a

k–1

2

k–1

2

k+m–1

+ (1–x

m–1

) 2

k+m–2

+ x

m–1

2

m–1

a

4

(1–x

0

)

a

3

x

0

a

2

x

0

a

1

x

0

a

0

x

0

a

4

(1–x

1

)

a

3

x

1

a

2

x

1

a

1

x

1

a

0

x

1

a

4

(1–x

2

)

a

3

x

2

a

2

x

2

a

1

x

2

a

0

x

2

a

4

(1–x

3

)

a

3

x

3

a

2

x

3

a

1

x

3

a

0

x

3

(1–a

4

)

a

4

1

(1–x

3

)

x

3

s

8

s

7

s

6

s

5

s

4

s

3

s

2

s

1

s

0

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

FAM–21

Akumulacja iloczynów cz ciowych w kodzie U2

Poniewa

∑

∑

−

=
=

−

−

−

−

=
=

−

−

+

−

+

−

=

+

−

2

0

1

1

1

2

0

1

1

2

2

)

1

(

2

2

2

p

i

i

i

i

p

p

p

p

i

i

i

i

p

p

z

z

z

z

,

wi c ka dy iloczyn cz ciowy 2

i

x

i

A mo na zast pi przez:

)

(

1

2

0

1

1

2

2

]

2

)

(

2

))

(

1

[(

2

i

i

m

i

m

j

j

j

j

i

m

m

i

i

i

A

a

x

a

x

A

x

+

−

+

−

=
=

−

−

+

−

=

+

−

=

∑

Iloczyn mo na wi c obliczy jako (

0

gdy

0

;

1

gdy

)

(

=

=

=

=

i

i

j

i

j

i

j

x

x

a

x

a

a

):

=













+

−

+













+

−

−

=

⋅

∑

∑

∑

−

=

−

−

−

=

−

=

−

−

−

−

−

2

0

1

1

2

0

2

0

1

1

1

1

1

2

2

2

2

2

2

k

j

j

i

j

k

i

k

m

i

i

k

j

j

m

j

k

m

k

m

x

a

x

a

x

a

x

a

X

A













−

+

−

+













−

−

+

=

−

−

=

−

−

−

=

−

=

−

=

−

−

−

−

−

∑

∑

∑

∑

1

2

0

)

(

1

)

(

1

2

0

2

0

2

0

)

1

(

1

)

1

(

1

1

2

2

2

)

1

(

2

2

2

)

1

(

2

2

k

k

j

j

i

j

k

i

k

m

i

i

k

j

j

k

j

j

m

j

k

m

k

m

a

a

a

a

,

Ostatecznie otrzymujemy:

1

1

2

0

2

0

)

(

1

)

(

1

2

0

)

1

(

1

)

1

(

1

1

2

2

2

2

)

1

(

2

1

2

)

1

(

2

2

−

+

−

−

=

−

=

−

−

−

=

−

−

−

−

−

−

+













+

−

+













+

−

+

=

∑

∑

∑

k

m

k

m

i

k

j

j

i

j

k

i

k

i

k

j

j

m

j

k

m

k

m

a

a

a

a

X

A

czyli:

1

2

0

)

(

)

1

(

1

1

2

2

)

~

(

2

2

−

−

=

+

−

+

−

−

+

+

+

−

+

−

=

∑

k

m

i

i

i

m

m

k

m

A

A

AX

Szybkie mno enie

© Janusz Biernat

, Szybkie mnozenie'04

FAM–22

Konstrukcja matrycy mno

cej

•

negowanie bitów najwy szego iloczynu cz ciowego (dopełnianie),

•

dodanie stałych koryguj cych

1

2

−

k

i –

1

2

−

+

m

k

oraz

1

2

−

m

(uzupełnianie)

(1) 0 0 0 1

1

♦

o o o o o o o

♦

o o o o o o o

♦

o o o o o o o

♦

o o o o o o o

(

♦

– negacja najbardziej znacz cego bita operandu, o – negacja bita)

•

koryguj ca „1” na pozycji k–1 (2

k–1

) ⇒ s + 1 = 2c

+

+ s* ⇒ s* = 1

⊕

s

, c

+

= s

•

dodanie 2

m–1

– modyfikacja półsumatora pozycji m–1 w pierwszej linii

x

+ y + 1 = 2c

+

+ s ⇒

y

x

s

⊕

=

,

y

x

c

+

=

+

lub

y

x

s

⊕

=

,

y

x

c

⋅

=

+

•

dodanie –2

n+l–1

– korekcja przeniesienia z najwy szej pozycji iloczynu ,

zgodnie z zale no ci c

–

+ 1 = 2c

+

+ s, czyli c

+

= c

–

oraz s = 1

⊕

c

–

•

matryca kwadratowa

(k = m) – (2

k–1

+2

k–1

=2

k

) ⇒ korekcja na pozycji k

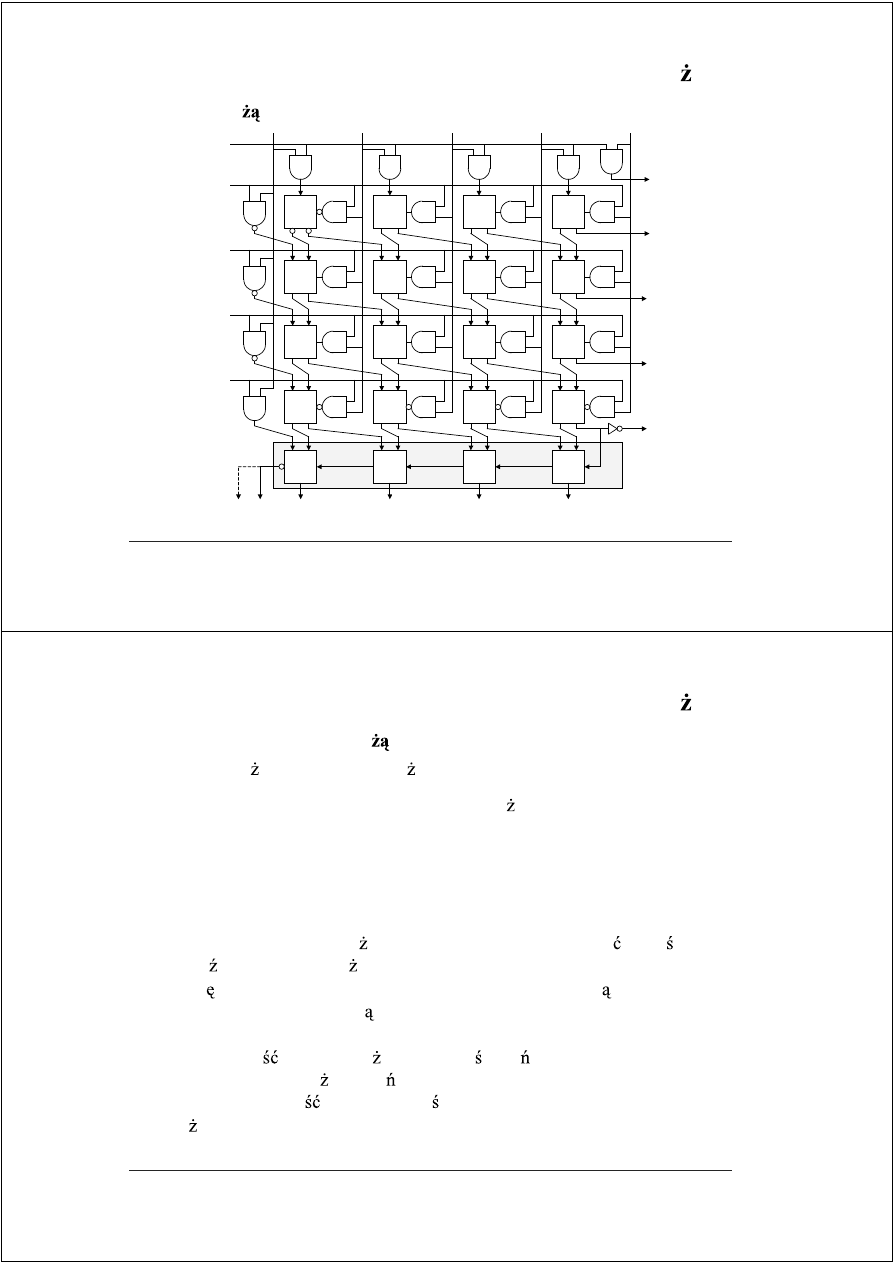
Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–

23

Matryca mno

ca kodu uzupełnieniowego

HA

HA

HA

HA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

FA

x

0

x

1

x

2

x

3

x

4

a

4

a

2

a

1

a

3

a

0

s

0

s

1

s

3

s

2

s

4

s

5

s

6

s

7

s

8

s

9

c

9

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–

24

Charakterystyki matryc mno

cych

zło

ż

ono

ś

ć

(mno nik m-bitowy, mno na k-bitowa)

•

A

= 8(m–1)k (dodatkowa bramka AND na ka dy akumulowany bit)

•

T

= 4(m – 1) + T

CPA(k)

≥

2(2m + log k–2)

podatno

ś

ć

na przetwarzanie potokowe

(pipelining)

•

dla danej pary operandów w danej chwili jest wykonywane dodawanie

tylko na jednym poziomie układu matrycowego,

•

na innych poziomach mo na w tym samym czasie wykona wcze niejsze

lub pó niejsze fazy mno enia innych par operandów

•

niezb dne rozbudowanie o dodatkowe układy transmituj ce wyniki

dodawania na mniej znacz cych pozycjach oraz układ synchronizacji.

•

przepustowo układu zale y od szybko ci ko cowego dodawania

w seryjnym mno eniu ko cowy CPA jako kaskada CSA

szybko bliska szybko ci dodawania 1-bitowego!

•

mo liwe zastosowanie algorytmu Bootha/McSorleya

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–

25

Strukturalizacja układów mno

cych

•

układ mno

cy kn

×

kn

– zło enie układów mno

cych n

×

n

:

∑

∑

∑

∑

∑

∑

−

=

−

+

−

=

−

−

=

=

−

−

=

−

=

+

=

























=

2

2

1

1

1

0

0

1

0

1

0

2

2

2

2

k

k

j

k

k

j

i

i

j

i

jn

k

j

j

i

i

j

i

jn

k

s

sn

s

k

s

sn

s

X

A

X

A

X

A

AX

,

albo w postaci skróconej

∑

∑

−

=

−

+

−

=

−

=

2

2

0

)

1

,

min(

)

1

,

0

max(

2

k

j

k

j

k

j

i

i

j

i

jn

X

A

AX

gdzie

∑

−

=

+

=

1

0

2

n

j

j

j

ni

i

a

A

,

∑

−

=

+

=

1

0

2

n

j

j

j

ni

i

x

X

.

wyrównywanie

(alignment)

•

ka dy 2n-pozycyjny iloczyn

i

s

i

X

A

−

ma wag

s

n

2

]

,

,...,

,

[

)

(

0

1

1

1

1

0

s

s

s

s

s

X

A

X

A

X

A

X

A

−

−

=

AX

•

efekt – akumulacja 2k

−

1 wielooperandów ró nego rozmiaru

zamiast k

2

operandów o identycznej wielko ci

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–

26

Wyrównanie operandów

2

7n

2

6n

2

5n

2

4n

2

3n

2

2n

2

n

2

0

0

3

X

A

1

3

X

A

0

2

X

A

2

3

X

A

1

2

X

A

0

1

X

A

3

3

X

A

2

2

X

A

1

1

X

A

0

0

X

A

3

2

X

A

2

1

X

A

1

0

X

A

3

1

X

A

2

0

X

A

3

0

X

A

Wyrównanie operandów w układzie mno

cym 4n

×

4n

•

w kodzie U2 i U1 – niezb dne uwzgl dnienie rozszerzenia znakowego

efekt – liczba operandów w j-ej grupie wynosi 2j

+

1 osi gaj c maksimum 4k

−

3,

→

niweczy to zysk wynikaj cy ze strukturalizacji.

→

przekonstruowanie sumatora wielooperandowego CSA.

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–

27

Mno enie wielokrotnej precyzji

Mno enie liczb dodatnich

•

bezpo rednie zastosowanie schematu wyrównania

Mno enie długich liczb znakowanych (U2)

•

najwy sze iloczyny (... A

3

X

#

oraz A

#

X

3

)

– mno enie liczby dodatniej przez znakowan !
– dodawanie dodatniej i znakowanej !

Rozwi zanie 1:

•

przekodowanie na dodatnie (podobnie jak w mno eniu bez rozszerze )

•

korekcja (podobnie jak w mno eniu bez rozszerze )

Rozwi zanie 2:

•

przekodowanie na warto ci bezwzgl dne

•

mno enie dodatnich i wytworzenie znaku

•

przekodowanie iloczynu na kod uzupełnieniowy

Szybkie mno enie

© Janusz Biernat, Szybkie mnozenie'04

FAM–

28

Mno enie U2 – jeszcze inne przekodowanie

Zast pienie ujemnych iloczynów w













+

−

⋅













+

−

∑

∑

−

=

−

−

−

=

−

−

2

0

1

1

2

0

1

1

2

2

2

2

m

j

j

j

m

m

k

i

i

i

k

k

x

x

a

a

1

2

0

1

1

2

2

0

1

1

2

0

1

1

2

2

)

1

(

2

2

2

2

−

−

=

−

+

−

−

+

−

=

−

+

−

−

=

−

−

+

−

+

−

=

−

=

−

∑

∑

∑

m

k

i

m

i

m

i

m

k

k

i

m

i

m

i

k

i

i

i

m

m

x

a

x

a

a

x

,

1

2

0

1

1

2

2

0

1

1

2

0

1

1

2

2

)

1

(

2

2

2

2

−

−

=

−

+

−

−

+

−

=

−

+

−

−

=

−

−

+

−

+

−

=

−

=

−

∑

∑

∑

k

m

j

k

j

j

k

m

k

m

j

k

j

j

k

m

j

j

j

k

k

x

a

x

a

x

a

,