12

12

13. OBLICZENIA WYTRZYMAŁO CIOWE PRZEKŁADNI WALCOWEJ

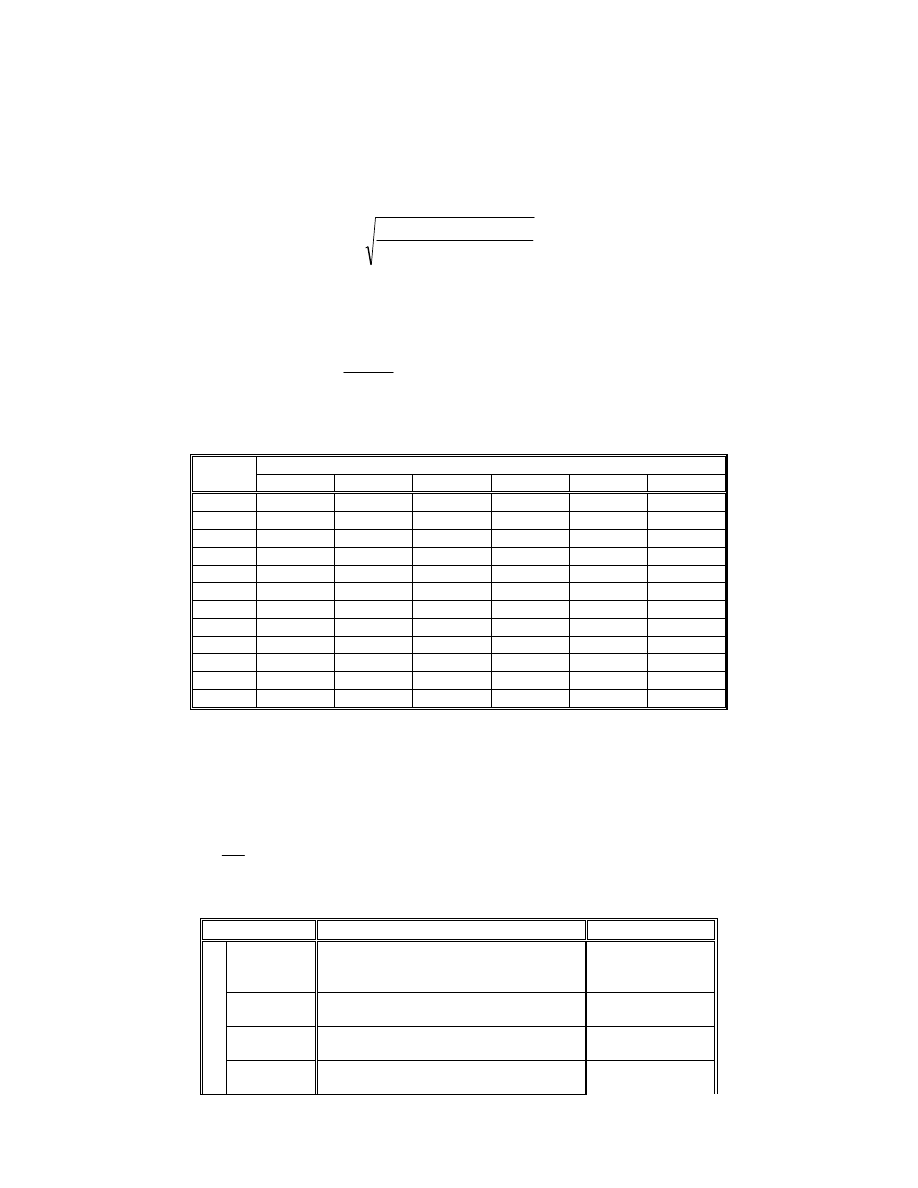
13.1. Obliczanie modułu normalnego z warunku na wytrzymało z ba u pod-

stawy

3

1

gj

1

zast

n

C

k

n

z

cos

N

267

)

zg

(

m

β

λ

ψ

β

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

, (20)

gdzie

λ

zast

- współczynnik wytrzymało ci z ba u podstawy;

λ

zast

dla

zast pczej liczby z bów (21) lub

λ

dla z bów

prostych, odczytujemy z tablicy 8:

β

3

1

zsst

cos

z

z

====

, (21)

Tablica 8

Współczynniki

λ

, (

λ

zast

) wg L.D. Czasownikowa dla z bów normalnych, korygowanych

α = 20

o

,

c = 0,25 m

x – współczynnik przesuni cia zarysu

z

(z

zast

)

- 0,6

- 0,2

0

+0,2

+0,4

+0,6

12

0,325

0,406

0,487

0,565

14

0,345

0,420

0,490

0,565

16

0,296

0,362

0,430

0,498

0,565

18

0,314

0,378

0,442

0,504

0,565

20

0,333

0,395

0,452

0,509

0,565

24

0,367

0,420

0,470

0,519

0,565

30

0,303

0,401

0,444

0,498

0,530

0,564

36

0,333

0,421

0,463

0,501

0,537

0,564

42

0,355

0,436

0,475

0,510

0,543

0,563

50

0,378

0,451

0,488

0,520

0,546

0,562

80

0,435

0,488

0,510

0,528

0,545

0,556

100 i >

0,454

0,498

0,513

0,528

0,542

0,552

C

β

- współczynnik zale ny od skokowej liczby przyporu:

C

β

= 1,1 dla

ε

β

≤ 1,5 ,

C

β

= 1,2 dla

ε

β

> 1,5 ,

n

m

b

=

ψ

- współczynnik szeroko ci wie ca - tablica 15.

Tablica 9

Warto ci współczynnika szeroko ci wie ca

ψ

Wykonanie z bów

Uło yskowanie

ψ

max

b. dokładne

Bardzo staranne uło yskowanie na ło yskach

tocznych lub lizgowych, sztywna obudowa,

sztywne wały

30

÷ 40

rednio

dokładnie

Dobre uło yskowanie w skrzynkach

do 25

do

dokładnie

Uło yskowanie na konstrukcjach stalowych,

kształtownikach itp.

do 15

O

br

ob

io

ne

niezbyt

dokładnie

Jednostronne uło yskowanie

(koło zwisaj ce )

do 10

13

13

Odlane

Koła ze starannie odlanymi z bami, do

staranne uło yskowanie

do 10

Przy wyborze wielko ci k ta pochylenia linii z ba nale y kierowa si przede wszystkim tym, aby
poskokowy stopie pokrycia

ε

β

> 1, przy czym przyjmuje si dla z bów rubowych

β

= 8 ÷ 30

0

(20

0

).

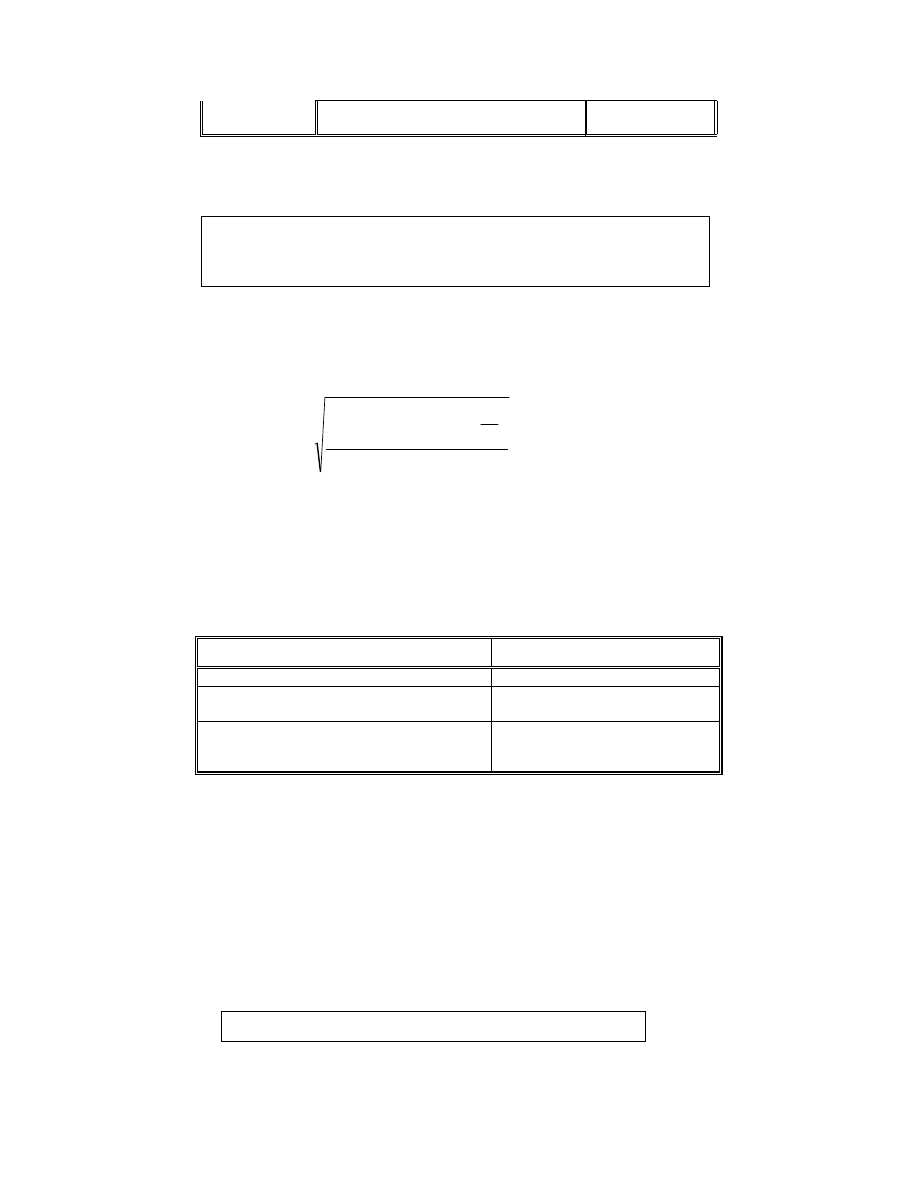
13.2. Obliczanie modułu normalnego z warunku na naciski Hertza w

punkcie C.

3

II

2

2

H

2

2

1

2

2

II

2

,

m

n

n

k

z

z

z

1

cos

N

C

267

)

H

(

m

α

α

ε

ψ

β

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

(22)

gdzie
stał C

m,

α

- przyjmujemy z tablicy 10,

ε

α

- czołowy stopie pokrycia .

Na tym etapie oblicze , nie znaj c wymiarów koła przyjmujemy

ε

α

= 1.

Tablica 10

Warto ci stałych C

m,

α

dla

α

=

20

0

Materiały na koła

α

,

m

C

[N/mm

2

]

1/2

Stal na stali E

1

= E

2

= 210 000 [N/mm

2

]

478,2

Stal na eliwie E

1

= 210 000 [N/mm

2

]

lub br zie E

2

= 105 000 [N/mm

2

]

390,6

eliwo na eliwie lub br z na br zie

E

1

= E

2

=105 000

[N/mm

2

]

338,5

Na podstawie obliczonych modułów ze wzorów (20) i (22) przyj najbli szy wi kszy z ci gu mo-

dułów znormalizowanych m

n

(PN).

m

n

(PN) > max{m

n

(zg), m

n

(H)}+(0,5÷1) .

13.3. Przyj cie modułu znormalizowanego

Ci g modułów uprzywilejowanych wg PN-78/M-88502 (cyfry pogrubione) i modułów dopuszczal-

nych (uj te w nawiasy)

Dla kół o z bach sko nych, rubowych i łukowych modułem znormalizowanym jest

moduł redni

w przekroju normalnym !

W przypadku, gdy wytrzymało zm czeniowa na zginanie koła na Z

gj2

<

Z

gj1

, nale y obliczy moduł równie dla koła z

2

ze wzoru (20) wstawia-

j c odpowiednio N

II

, n

II

, z

2

.

0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; (3,5); 4; (4,5); 5; (5,5); 6; 7 ....

14

14

Dla kół o z bach sko nych, rubowych lub łukowych jako moduł znormalizowany przyjmujemy

wi kszy od najwi kszego modułu obliczonego wg (28 ) i (31).

Moduł czołowy

β

=

cos

)

PN

(

n

t

m

m

(23)

13.4. Sprawdzenie napr e maksymalnych na zginanie u podstawy

1

gj

n

zast

zast

max

g

k

C

m

b

P

≤≤≤≤

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

β

λ

σ

, (24)

gdzie:
P

zast

= P

stat

⋅

c

p

⋅

c

d

, (25)

c

p

- współczynnik przeci enia - tablica 11,

Tablica 11

Współczynnik przeci enia c

p

wg Niemanna

Silnik nap dowy

Nap dzane maszyny

lub mechanizmy

elektryczny

turbina, siln.

wielocyl.

Siln.

jednocylindr.

Pr dnice, przeno niki, dmuchawy, wy-

ci gi, mieszalniki

1,0

1,25

1,5

Obrabiarki, suwnice, pompy tłokowe

1,25

1,50

1,75

Prasy, no yce, walcarki, koparki

1,75

2,0

2,25

c

d

- współczynnik nadwy ek dynamicznych - tablica 12,

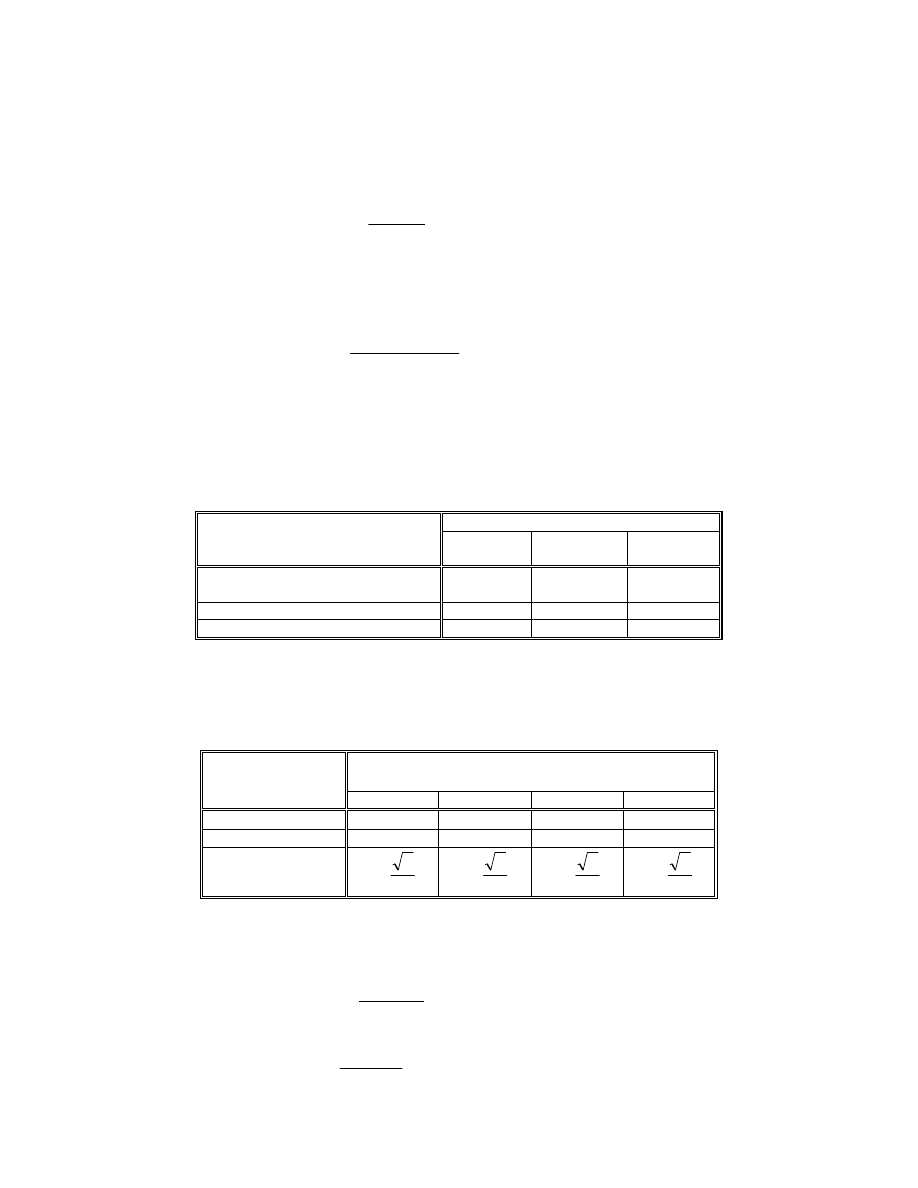
Tablica 12

Współczynnik nadwy ek dynamicznych c

d

wg Henriota

Grupa dokładno ci

Wielko ci

I

II

III

IV

v [m/s]

100

50

20

5

÷ 10

Klasy dokładno ci kół

2

÷ 5

4

÷ 6

6

÷ 8

8

÷ 10

c

d

30

1

ν

+

12

1

ν

+

6

1

ν

+

3

1

ν

+

v

N

1000

P

stat

⋅⋅⋅⋅

====

[N], (26)

pr dko obwodowa

60000

n

d

v

1

⋅⋅⋅⋅

⋅⋅⋅⋅

====

π

[m/s], (27)

15

15

d

1

= z

1

⋅

m

t ,

(28)

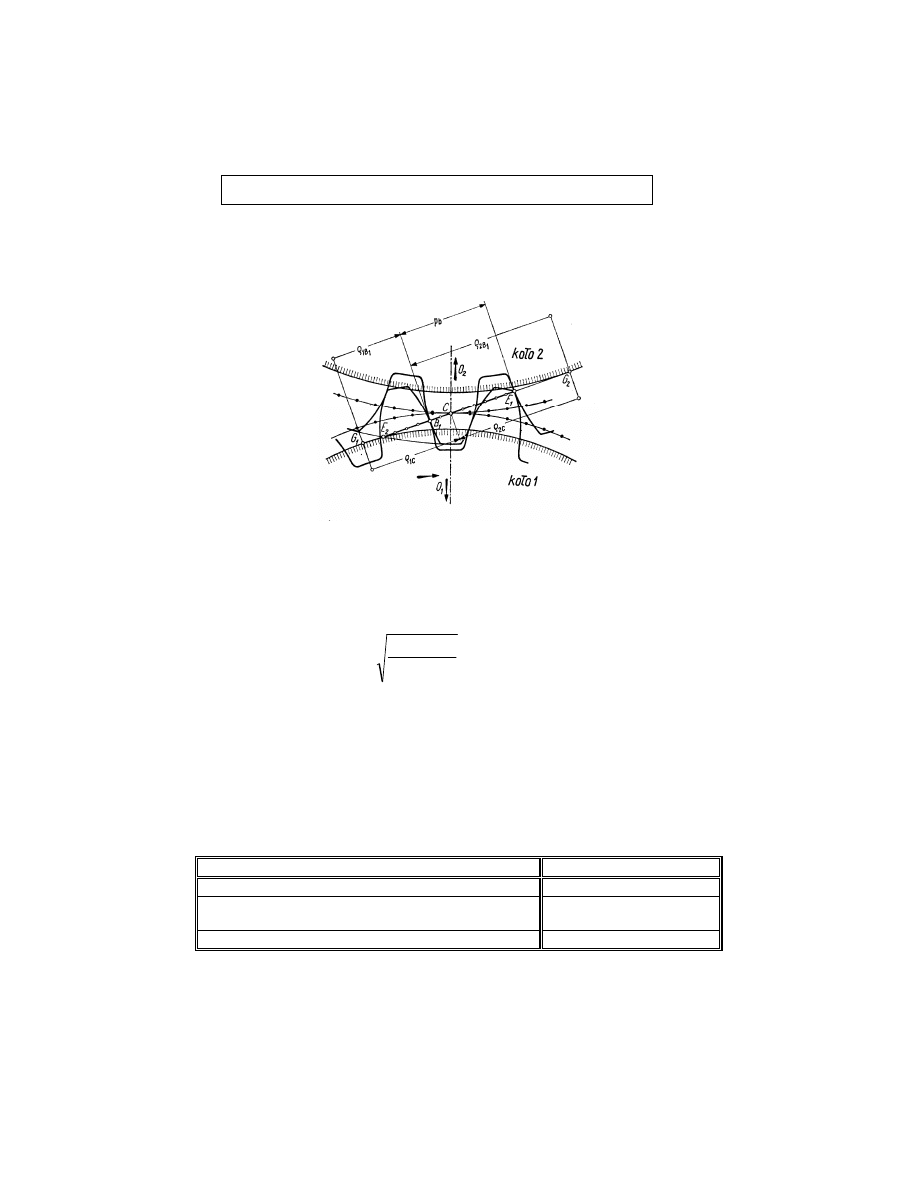
13.5. Sprawdzenie napr e na docisk powierzchniowy w

punkcie jednoparowego zaz bienia B

1

- rys. 4.

Rys.4. Punkt B

1

jednoparowego zaz bienia – rozpoczyna

si w nim współpraca jednej pary z bów, a w pun-

kcie E

1

ko czy si współpraca drugiej pary z bów.

Maksymalne napr enia na docisk liczymy ze wzoru

1

H

1

1

zast

m

max

1

c

k

C

d

b

P

C

≤≤≤≤

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

ρ

σ

, (29)

gdzie
C

ρ1

– współczynnik zale ny od wielko ci promieni krzywizn zarysów

współpracuj cych boków z bów w punkcie B

1

– tablica 14 lub

wzory (30), (31) podane przez Niemanna.

Tablica 13

Warto ci stałej C

m

Materiały kół współpracuj cych

C

m

[N/mm

2

]

1/2

Stal na stali E

1

= E

2

= 210 000 [N/mm

2

]

271

Stal na eliwie E

1

= 210 000 [N/mm

2

]

E

2

= 105 000 [N/mm

2

]

221

eliwo na eliwie (lub br zie ) E

1

=E

2

= 105 000 [N/mm

2

]

192

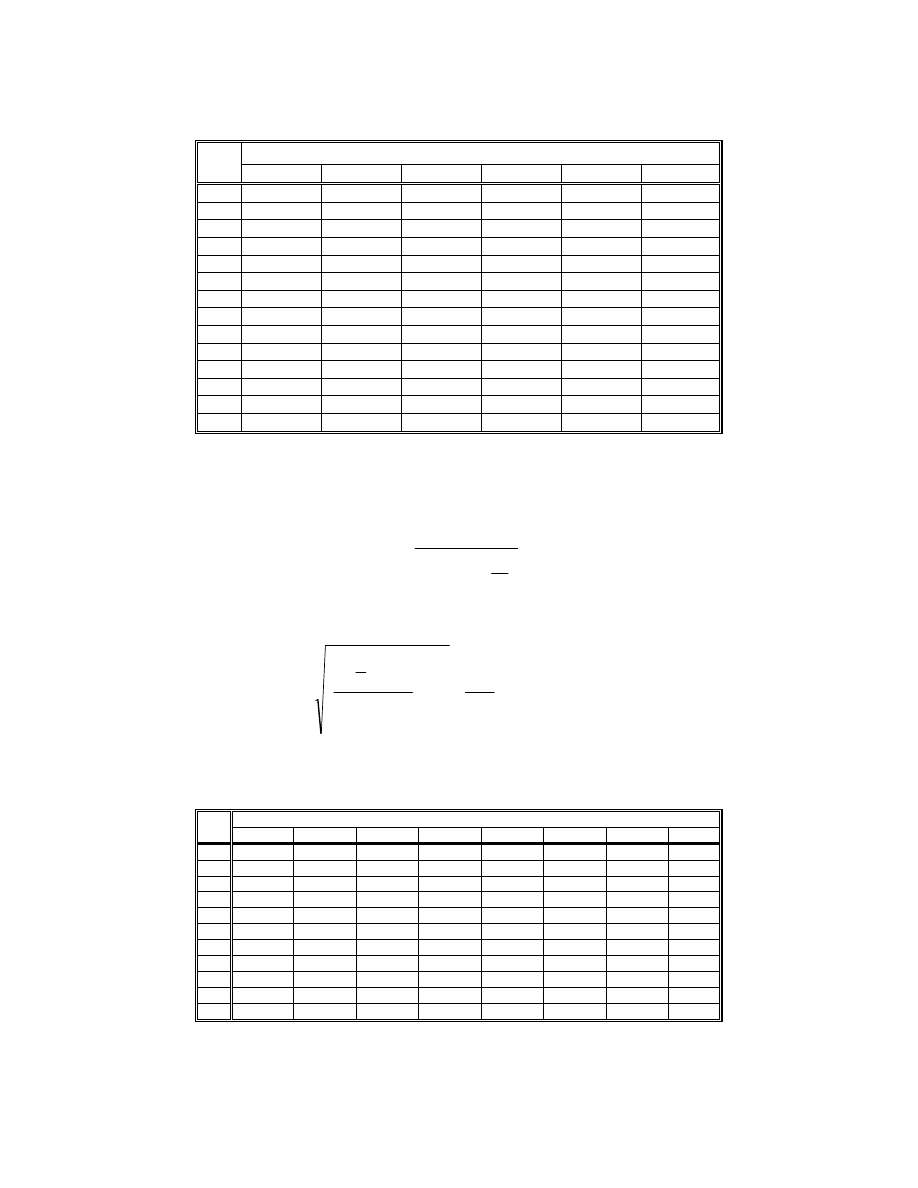
Tablica 14

Warto ci współczynnika C

ρ1

- uz bienie normalne -zerowe (y = 1, x = 0,

α = 20

0

)

Gdy k

gj2

< k

gj1

– sprawdzi napr enia dla koła (z

2

)

16

16

C

ρ1

dla z

2

/z

1

z

1

1

1,4

2

3

5

10

9

0,103

0,107

0,111

0,114

10

0,117

0,122

0,130

0,135

0,141

11

0,130

0,137

0,147

0,154

0,162

12

0,098

0,140

0,148

0,169

0,167

0,177

13

0,126

0,148

0,158

0,171

0,181

0,192

14

0,142

0,154

0,165

0,179

0,190

0,203

15

0,146

0,158

0,171

0,186

0,199

0,211

17

0,150

0,165

0,180

0,197

0,212

0,227

20

0,155

0,172

0,189

0,207

0,225

0,241

24

0,157

0,177

0,196

0,216

0,236

0,254

30

0,159

0,180

0,201

0,224

0,246

0,266

45

0,160

0,184

0,207

0,232

0,256

0,278

70

0,161

0,186

0,211

0,237

0,263

0,286

150

0,162

0,187

0,213

0,239

265

0,289

Współczynnik C

ρ1

mo na oblicza wg wzorów podanych przez Niemanna:

+

⋅

−

⋅

⋅

=

1

2

2

1

1

tg

1

cos

z

z

f

f

C

w

α

α

ρ

, (30)

gdzie

(

)

z

x

y

z

f

π

α

⋅

−

−

+

+

=

2

1

cos

2

1

2

. (31)

Przy korekcji P-0 ,

α

w

=

α

.

Tablica 15

Warto ci współczynnika f. Z by normalne y = 1,

α = 20

0

y + x =1+x

1)

z

0,5

0,75

1,0

1,2

1,4

1,6

1,8

2,0

10

0,01980

0,07717

0,16591

0,24264

0,29659

0,35821

0,41794

0,47606

12

0,05006

0,13465

0,21221

0,27062

0,32648

0,38027

0,43237

0,48303

14

0,09896

0,17423

0,24343

0,30525

0,34543

0,39344

0,43991

0,48505

16

0,13499

0,20293

0,26555

0,32017

0,35799

0,40152

0,44362

0,48452

20

0,18440

0,24146

0,29436

0,33436

0,37274

0,40936

0,44535

0,48006

24

0,21655

0,26689

0,31186

0,34672

0,38019

0,41244

0,44369

0,47401

28

0,23909

0,28262

0,323335

0,35435

0,38412

0,41288

0,44073

0,46782

32

0,25572

0,29470

0,33134

0,35927

0,38618

0,41217

0,43739

0,46782

60

0,30826

0,33097

0,35270

0,36952

0,38583

0,40175

0,41725

0,43242

100

0,3318

0,34528

0,35933

0,37017

0,38076

0,39116

0,40137

0,41141

∞

0,36397

0,36397

0,36397

0,36397

0,36397

0,36397

0,36397

0,36397

Uwaga: dla koła 1 - z = z

1

, dla koła 2 - z = z

2

1)

gdy y = 1, x = - 0,5 , wówczas y + x = 0,5

17

17

13.6. Sprawdzenie przekładni walcowej na grzanie

Przy obrotach n

≥ 1500 [1/min], w przekładniach silnie obci onych pomimo smarowania

mo e wyst pi zbyt du e grzanie małego koła (z bnika), , je li straty energetyczne s zbyt du e przy

przyj tych wymiarach przekładni.

Obliczenia na grzanie polegaj na sprawdzeniu warunku podanego przez Hofera:

1

N

1836

b

d

x

t

1

t

>>>>

⋅⋅⋅⋅

⋅⋅⋅⋅

====

, (32)

gdzie moc tarcia

v

2

2

1

t

z

7

z

z

1

N

N

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

====

[kW] , (33)

zast pcza liczba z bów

β

3

1

v

cos

z

z

====

(34)

x

t

> 1 zapewnia prawidłow pod wzgl dem cieplnym prac przekładni.

14. Wymiary geometryczne przekładni walcowej

14.1. Koła o z bach prostych nie korygowanych

Dane: z

1

, z

2

, m , y , c*,

α

1. Podziałka

m

p

⋅

=

π

.

2. Podziałka na kole zasadniczym

α

cos

p

p

b

⋅

=

.

3. rednice kół podziałowych

m

z

d

1

1

⋅⋅⋅⋅

====

,

m

z

d

2

2

⋅⋅⋅⋅

====

.

4. Odległo osi kół

((((

))))

2

1

0

d

d

2

1

a

a

++++

====

====

5. rednice kół zasadniczych

α

cos

d

d

1

1

b

⋅⋅⋅⋅

====

,

α

cos

d

d

2

2

b

⋅⋅⋅⋅

====

.

6. Luz wierzchołkowy

m

c

c

*

⋅

=

.

7. Wysoko głów z bów

m

y

h

h

2

a

1

a

⋅⋅⋅⋅

====

====

18

18

8. Wysoko stóp z bów

c

m

y

h

h

2

f

1

f

++++

⋅⋅⋅⋅

====

====

9. rednice wierzchołków

1

a

1

1

a

h

2

d

d

⋅⋅⋅⋅

++++

====

,

2

a

2

2

a

h

2

d

d

⋅⋅⋅⋅

++++

====

10. rednice stóp

1

f

1

1

f

h

2

d

d

⋅⋅⋅⋅

−−−−

====

,

2

f

2

2

f

h

2

d

d

⋅⋅⋅⋅

−−−−

====

11. K t przyporu na wierzchołku

1

d

d

tg

2

1

b

2

1

a

1

a

−−−−

====

α

,

1

d

d

tg

2

2

b

2

2

a

2

a

−−−−

====

α

.

12. Cz ciowy wska nik przyporu

((((

))))

α

α

π

ε

tg

tg

2

z

1

a

1

1

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

,

((((

))))

α

α

π

ε

tg

tg

2

z

2

a

2

2

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

13. Całkowity wska nik przyporu

2

1

ε

ε

ε

++++

====

14.2. Koła o z bach rubowych nie korygowane

Dane: z

1

, z

2

, m

n

,

α

n

,

β

, y

n

=1

1. Wysoko głowy narz dzia

h

a0

= 1.25 m

n

.

2. Moduł czołowy

β

cos

m

m

n

t

=

.

3. rednice kół podziałowych

t

1

1

m

z

d

⋅⋅⋅⋅

====

,

t

2

2

m

z

d

⋅⋅⋅⋅

====

.

4. K t przyporu w przekroju czołowym

====

β

α

α

cos

tg

artg

n

t

.

5. K t pochylenia linii z ba na walcu zasadniczym

19

19

(

)

β

α

β

sin

cos

sin

⋅

=

n

b

ar

.

6. Zast pcza liczba z bów na kole zasadniczym

β

β cos

cos

z

z

b

2

1

1

v

⋅⋅⋅⋅

====

.

7. rednica koła wierzchołków

n

1

1

a

m

2

d

d

⋅⋅⋅⋅

++++

====

,

n

2

2

a

m

2

d

d

⋅⋅⋅⋅

++++

====

.

8. rednica koła stóp

0

a

1

1

f

h

2

d

d

⋅⋅⋅⋅

−−−−

====

,

0

a

2

2

f

h

2

d

d

⋅⋅⋅⋅

−−−−

====

.

9. rednica koła zasadniczego

t

1

1

b

cos

d

d

α

⋅⋅⋅⋅

====

,

t

2

2

b

cos

d

d

α

⋅⋅⋅⋅

====

.

10. K t przyporu na rednicy wierzchołków

1

d

d

tg

2

1

b

2

1

a

1

a

−−−−

====

α

,

1

d

d

tg

2

2

b

2

2

a

2

a

−−−−

====

α

.

11. Cz ciowy wska nik przyporu

((((

))))

t

a

tg

tg

z

α

α

π

ε

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

1

1

1

2

,

((((

))))

t

a

tg

tg

z

α

α

π

ε

−−−−

⋅⋅⋅⋅

⋅⋅⋅⋅

====

2

2

2

2

.

12. Czołowy wska nik przyporu

2

1

ε

ε

ε

α

++++

====

.

13. Poskokowy wska nik przyporu

n

m

sin

b

⋅

⋅

=

π

β

ε

β

.

14. Całkowity wska nik przyporu

β

α

γ

ε

ε

ε

+

=

.

15. SIŁY W PRZEKŁADNI WALCOWEJ O Z BACH SKO NYCH

( RUBOWYCH)

20

20

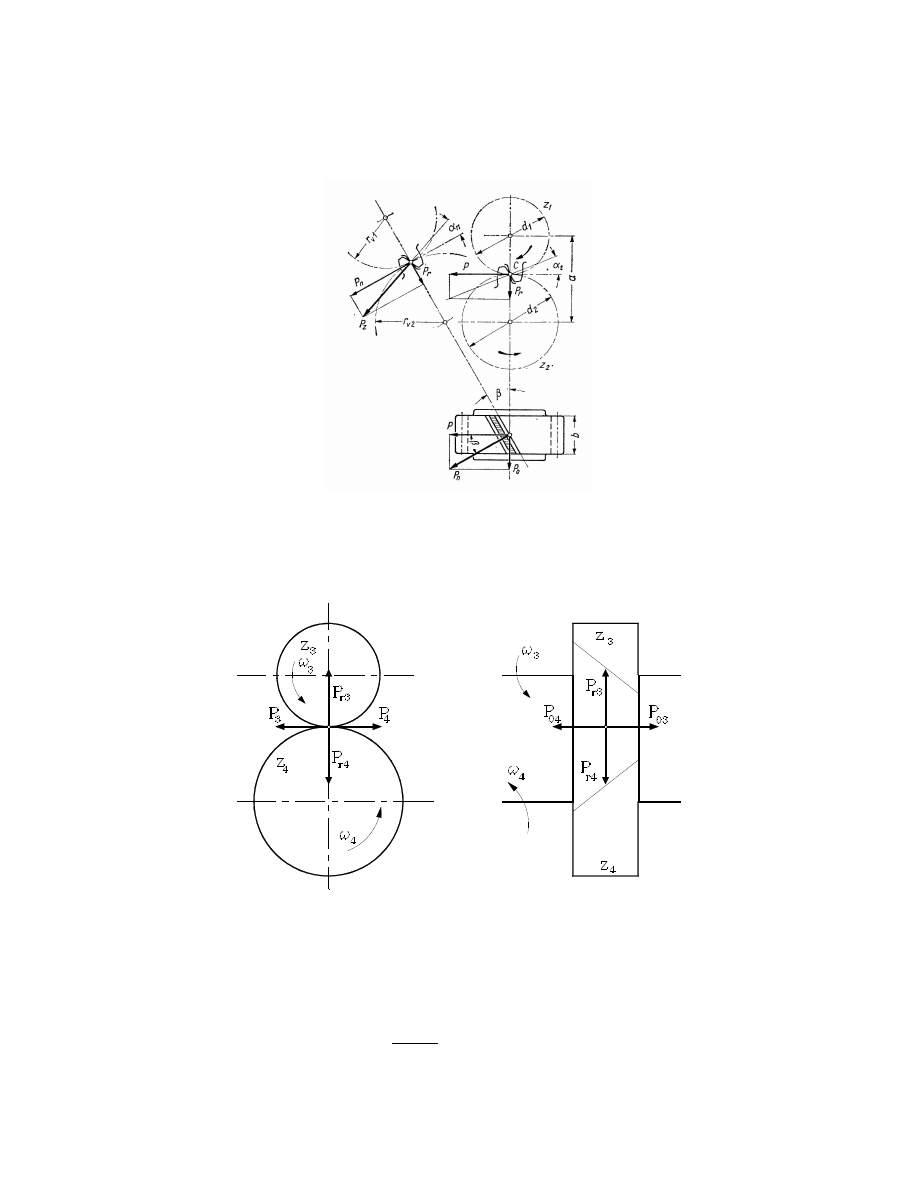
Na rys. 5 pokazano rozkład sił w przekładni walcowej o z bach sko nych ( rubowych) dla

obrotów prawych i dla prawego kierunku pochylenia linii z bów z bnika .

Rys.5. Rozkład sił w przekładni walcowej o z bach

sko nych ( rubowych)

Dla obrotów lewych i prawego pochylenia linii z bów z bnika , rozkład sił na kołach z

1

i z

2

pokazano na rys 6.

Rys.6. Rozkład sił na z bniku i kole

Siły w przekładni walcowej obliczymy wg poni szych wzorów:

Siła obwodowa

3

II

4

3

2

d

M

P

P

P

⋅

=

=

=

. (35)

Siła osiowa

21

21

β

tg

4

3

⋅

=

=

=

P

P

P

P

o

o

o

. (36)

Siła promieniowa

t

r

r

r

P

P

P

P

α

tg

4

3

⋅

=

=

=

. (37)