Wstęp do programowania
wykład 2
Agata Półrola
Wydział Matematyki i Informatyki UŁ
sem. zimowy 2010/2011
Agata Półrola Wydział Matematyki i Informatyki UŁ
Liczby
Korzystanie z liczb
Ada “zna” różne rodzaje liczb (różne
typy
liczbowe) i potrafi
wykonywać na nich podstawowe operacje arytmetyczne.
Nie jest
do tego potrzebne dołączanie żadnego pakietu
Jeśli w programie chcemy dodatkowo takie liczby wprowadzać (np.
z klawiatury) lub wyprowadzać (np. na ekran), to musimy dołączyć
pakiet odpowiedni dla danego typu liczbowego.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Liczby
Korzystanie z liczb
Ada “zna” różne rodzaje liczb (różne
typy
liczbowe) i potrafi
wykonywać na nich podstawowe operacje arytmetyczne.
Nie jest
do tego potrzebne dołączanie żadnego pakietu
Jeśli w programie chcemy dodatkowo takie liczby wprowadzać (np.
z klawiatury) lub wyprowadzać (np. na ekran), to musimy dołączyć
pakiet odpowiedni dla danego typu liczbowego.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład (Liczby (całkowite) - bez wypisywania)
p r o c e d u r e w02 p1 i s
a , b :
i n t e g e r ;
b e g i n
a : = 1 2 ;
b:=10+a ;
end w02 p1 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład (Liczby (całkowite) - z wypisywaniem)
with ada . i n t e g e r t e x t i o ;
p r o c e d u r e w02 p2 i s
a , b :
i n t e g e r ;
b e g i n
a : = 1 2 ;
b:=10+a ;
ada . i n t e g e r t e x t i o . p u t ( b ) ;
end w02 p2 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały numeryczne
Literały
reprezentują wartości (liczbowe, znakowe, napisy) za
pomocą odpowiedniej notacji.
Literały numeryczne
reprezentują
wartości liczbowe.
Literały numeryczne to
literały całkowite
i
literały rzeczywiste
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały numeryczne
Literały
reprezentują wartości (liczbowe, znakowe, napisy) za
pomocą odpowiedniej notacji.
Literały numeryczne
reprezentują
wartości liczbowe.
Literały numeryczne to
literały całkowite
i
literały rzeczywiste
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały całkowite
przykłady
literałów całkowitych
:
13, 0, -2, +4,
1 234, 23 45, 15E5, 1e8,
2#100 111#, 16#1a#, 2#11 001#e2.
Znaczenie:
podkreślenie zastępuje spację (1 234 567 zapiszemy jako
1 234 567)
literały postaci 15e5 (z małą lub wielką literą E) przedstawiają
liczby
w postaci wykładniczej
. Interpretacja liczby postaci aEb
to a · 10
b
(czyli 15e5 to 15 · 10
5
)
literały 2#100 111#, 16#1a#, 2#11001#e2 to
literały z
podstawą
, umożliwiające zapisywanie liczb w różnych
systemach pozycyjnych. Ostatni z literałów ma dodatkowo
postać wykładniczą.
Ogólna postać takiego literału to
podstawa#liczba#[wykładnik]
(nawiasy kwadratowe oznaczają że wykładnik jest opcjonalny)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały całkowite
przykłady
literałów całkowitych
:
13, 0, -2, +4, 1 234, 23 45,
15E5, 1e8,
2#100 111#, 16#1a#, 2#11 001#e2.
Znaczenie:
podkreślenie zastępuje spację (1 234 567 zapiszemy jako
1 234 567)
literały postaci 15e5 (z małą lub wielką literą E) przedstawiają
liczby
w postaci wykładniczej
. Interpretacja liczby postaci aEb
to a · 10
b
(czyli 15e5 to 15 · 10
5
)
literały 2#100 111#, 16#1a#, 2#11001#e2 to
literały z
podstawą
, umożliwiające zapisywanie liczb w różnych
systemach pozycyjnych. Ostatni z literałów ma dodatkowo
postać wykładniczą.
Ogólna postać takiego literału to
podstawa#liczba#[wykładnik]
(nawiasy kwadratowe oznaczają że wykładnik jest opcjonalny)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały całkowite
przykłady
literałów całkowitych
:
13, 0, -2, +4, 1 234, 23 45, 15E5, 1e8,
2#100 111#, 16#1a#, 2#11 001#e2.
Znaczenie:
podkreślenie zastępuje spację (1 234 567 zapiszemy jako
1 234 567)
literały postaci 15e5 (z małą lub wielką literą E) przedstawiają
liczby
w postaci wykładniczej
. Interpretacja liczby postaci aEb
to a · 10
b
(czyli 15e5 to 15 · 10
5
)
literały 2#100 111#, 16#1a#, 2#11001#e2 to
literały z
podstawą
, umożliwiające zapisywanie liczb w różnych
systemach pozycyjnych. Ostatni z literałów ma dodatkowo
postać wykładniczą.
Ogólna postać takiego literału to
podstawa#liczba#[wykładnik]
(nawiasy kwadratowe oznaczają że wykładnik jest opcjonalny)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały całkowite
przykłady
literałów całkowitych
:
13, 0, -2, +4, 1 234, 23 45, 15E5, 1e8,
2#100 111#, 16#1a#,
2#11 001#e2.
Znaczenie:
podkreślenie zastępuje spację (1 234 567 zapiszemy jako
1 234 567)
literały postaci 15e5 (z małą lub wielką literą E) przedstawiają
liczby
w postaci wykładniczej
. Interpretacja liczby postaci aEb
to a · 10
b
(czyli 15e5 to 15 · 10
5
)
literały 2#100 111#, 16#1a#, 2#11001#e2 to
literały z
podstawą
, umożliwiające zapisywanie liczb w różnych
systemach pozycyjnych. Ostatni z literałów ma dodatkowo
postać wykładniczą.
Ogólna postać takiego literału to
podstawa#liczba#[wykładnik]
(nawiasy kwadratowe oznaczają że wykładnik jest opcjonalny)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały całkowite
przykłady
literałów całkowitych
:
13, 0, -2, +4, 1 234, 23 45, 15E5, 1e8,
2#100 111#, 16#1a#, 2#11 001#e2.
Znaczenie:
podkreślenie zastępuje spację (1 234 567 zapiszemy jako
1 234 567)
literały postaci 15e5 (z małą lub wielką literą E) przedstawiają
liczby
w postaci wykładniczej
. Interpretacja liczby postaci aEb
to a · 10
b
(czyli 15e5 to 15 · 10
5
)
literały 2#100 111#, 16#1a#, 2#11001#e2 to
literały z
podstawą
, umożliwiające zapisywanie liczb w różnych
systemach pozycyjnych. Ostatni z literałów ma dodatkowo
postać wykładniczą.
Ogólna postać takiego literału to
podstawa#liczba#[wykładnik]
(nawiasy kwadratowe oznaczają że wykładnik jest opcjonalny)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały całkowite
przykłady
literałów całkowitych
:
13, 0, -2, +4, 1 234, 23 45, 15E5, 1e8,
2#100 111#, 16#1a#, 2#11 001#e2.
Znaczenie:
podkreślenie zastępuje spację (1 234 567 zapiszemy jako
1 234 567)
literały postaci 15e5 (z małą lub wielką literą E) przedstawiają
liczby
w postaci wykładniczej
. Interpretacja liczby postaci aEb
to a · 10
b
(czyli 15e5 to 15 · 10
5
)
literały 2#100 111#, 16#1a#, 2#11001#e2 to
literały z
podstawą
, umożliwiające zapisywanie liczb w różnych
systemach pozycyjnych. Ostatni z literałów ma dodatkowo
postać wykładniczą.
Ogólna postać takiego literału to
podstawa#liczba#[wykładnik]
(nawiasy kwadratowe oznaczają że wykładnik jest opcjonalny)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały całkowite
przykłady
literałów całkowitych
:
13, 0, -2, +4, 1 234, 23 45, 15E5, 1e8,
2#100 111#, 16#1a#, 2#11 001#e2.
Znaczenie:
podkreślenie zastępuje spację (1 234 567 zapiszemy jako
1 234 567)
literały postaci 15e5 (z małą lub wielką literą E) przedstawiają
liczby
w postaci wykładniczej
. Interpretacja liczby postaci aEb
to a · 10
b
(czyli 15e5 to 15 · 10
5
)
literały 2#100 111#, 16#1a#, 2#11001#e2 to
literały z
podstawą
, umożliwiające zapisywanie liczb w różnych
systemach pozycyjnych. Ostatni z literałów ma dodatkowo
postać wykładniczą.
Ogólna postać takiego literału to
podstawa#liczba#[wykładnik]
(nawiasy kwadratowe oznaczają że wykładnik jest opcjonalny)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały całkowite
przykłady
literałów całkowitych
:
13, 0, -2, +4, 1 234, 23 45, 15E5, 1e8,
2#100 111#, 16#1a#, 2#11 001#e2.
Znaczenie:
podkreślenie zastępuje spację (1 234 567 zapiszemy jako
1 234 567)
literały postaci 15e5 (z małą lub wielką literą E) przedstawiają
liczby
w postaci wykładniczej
. Interpretacja liczby postaci aEb
to a · 10
b
(czyli 15e5 to 15 · 10
5
)
literały 2#100 111#, 16#1a#, 2#11001#e2 to
literały z
podstawą
, umożliwiające zapisywanie liczb w różnych
systemach pozycyjnych. Ostatni z literałów ma dodatkowo
postać wykładniczą.
Ogólna postać takiego literału to
podstawa#liczba#[wykładnik]
(nawiasy kwadratowe oznaczają że wykładnik jest opcjonalny)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały całkowite
przykłady
literałów całkowitych
:
13, 0, -2, +4, 1 234, 23 45, 15E5, 1e8,
2#100 111#, 16#1a#, 2#11 001#e2.
Znaczenie:
podkreślenie zastępuje spację (1 234 567 zapiszemy jako
1 234 567)
literały postaci 15e5 (z małą lub wielką literą E) przedstawiają
liczby
w postaci wykładniczej
. Interpretacja liczby postaci aEb
to a · 10
b
(czyli 15e5 to 15 · 10
5
)
literały 2#100 111#, 16#1a#, 2#11001#e2 to
literały z
podstawą
, umożliwiające zapisywanie liczb w różnych
systemach pozycyjnych. Ostatni z literałów ma dodatkowo
postać wykładniczą.
Ogólna postać takiego literału to
podstawa#liczba#[wykładnik]
(nawiasy kwadratowe oznaczają że wykładnik jest opcjonalny)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Jeszcze o literałach z podstawą:
Dopuszczalne (w języku Ada) podstawy to liczby całkowite od 2 do 16. Cyfry używane
do zapisu liczb to 0..9, A, B, ..., F, gdzie litery A..F reprezentują cyfry 10..16. W
zapisie liczby o podstawie X używamy cyfr 0..X-1.
Interpretacja liczby zapisanej w dowolnym systemie pozycyjnym o
podstawie p:
liczba c
i
c
i −1
...c
1
c
0
(gdzie c
i −1
, ..., c
0
to cyfry) jest interpretowana
jako c
i
· p
i
+ c
i −1
· p
i −1
+ . . . + c
1
· p
1
+ c
0
· p
0
Przykład
2#111011#, czyli liczba 111011
2
to
1 · 2
5
+ 1 · 2
4
+ 1 · 2
3
+ 0 · 2
2
+ 1 · 2
1
+ 1 · 2
0
, czyli 59
16#AE#, czyli liczba AE
16
, to 10 · 16
1
+ 15 · 16
0
, czyli 174.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Jeszcze o literałach z podstawą:
Dopuszczalne (w języku Ada) podstawy to liczby całkowite od 2 do 16. Cyfry używane
do zapisu liczb to 0..9, A, B, ..., F, gdzie litery A..F reprezentują cyfry 10..16. W
zapisie liczby o podstawie X używamy cyfr 0..X-1.
Interpretacja liczby zapisanej w dowolnym systemie pozycyjnym o
podstawie p:
liczba c
i
c
i −1
...c
1
c
0
(gdzie c
i −1
, ..., c
0
to cyfry) jest interpretowana
jako c
i
· p
i
+ c
i −1
· p
i −1
+ . . . + c
1
· p
1
+ c
0
· p
0
Przykład
2#111011#, czyli liczba 111011
2
to
1 · 2
5
+ 1 · 2
4
+ 1 · 2
3
+ 0 · 2
2
+ 1 · 2
1
+ 1 · 2
0
, czyli 59
16#AE#, czyli liczba AE
16
, to 10 · 16
1
+ 15 · 16
0
, czyli 174.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Jeszcze o literałach z podstawą:
Dopuszczalne (w języku Ada) podstawy to liczby całkowite od 2 do 16. Cyfry używane
do zapisu liczb to 0..9, A, B, ..., F, gdzie litery A..F reprezentują cyfry 10..16. W
zapisie liczby o podstawie X używamy cyfr 0..X-1.
Interpretacja liczby zapisanej w dowolnym systemie pozycyjnym o
podstawie p:
liczba c
i
c
i −1
...c
1
c
0
(gdzie c
i −1
, ..., c
0
to cyfry) jest interpretowana
jako c
i
· p
i
+ c
i −1
· p
i −1
+ . . . + c
1
· p
1
+ c
0
· p
0
Przykład
2#111011#, czyli liczba 111011
2
to
1 · 2
5
+ 1 · 2
4
+ 1 · 2
3
+ 0 · 2
2
+ 1 · 2
1
+ 1 · 2
0
, czyli 59
16#AE#, czyli liczba AE
16
, to 10 · 16
1
+ 15 · 16
0
, czyli 174.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Jeszcze o literałach z podstawą:
Dopuszczalne (w języku Ada) podstawy to liczby całkowite od 2 do 16. Cyfry używane
do zapisu liczb to 0..9, A, B, ..., F, gdzie litery A..F reprezentują cyfry 10..16. W
zapisie liczby o podstawie X używamy cyfr 0..X-1.
Interpretacja liczby zapisanej w dowolnym systemie pozycyjnym o
podstawie p:
liczba c
i
c
i −1
...c
1
c
0
(gdzie c
i −1
, ..., c
0
to cyfry) jest interpretowana
jako c
i
· p
i
+ c
i −1
· p
i −1
+ . . . + c
1
· p
1
+ c
0
· p
0
Przykład
2#111011#, czyli liczba 111011
2
to
1 · 2
5
+ 1 · 2
4
+ 1 · 2
3
+ 0 · 2
2
+ 1 · 2
1
+ 1 · 2
0
, czyli 59
16#AE#, czyli liczba AE
16
, to 10 · 16
1
+ 15 · 16
0
, czyli 174.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały rzeczywiste
Literał rzeczywisty
to literał numeryczny zawierający kropkę
dziesiętną (literały całkowite nie zawierają kropek).
Przykłady literałów rzeczywistych:
13.3, 0.0, -2.1, +4.2, 1 234.2, 23 45.3, 15.4E5,
1.2e8, 2#100 111.11#, 16#1a.b#, 2#11 001.1#e2.
Interpretacja powyższych zapisów jest analogiczna jak dla literałów
całkowitych.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały rzeczywiste
Literał rzeczywisty
to literał numeryczny zawierający kropkę
dziesiętną (literały całkowite nie zawierają kropek).
Przykłady literałów rzeczywistych:
13.3, 0.0, -2.1, +4.2,
1 234.2, 23 45.3, 15.4E5,
1.2e8, 2#100 111.11#, 16#1a.b#, 2#11 001.1#e2.
Interpretacja powyższych zapisów jest analogiczna jak dla literałów
całkowitych.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały rzeczywiste
Literał rzeczywisty
to literał numeryczny zawierający kropkę
dziesiętną (literały całkowite nie zawierają kropek).
Przykłady literałów rzeczywistych:
13.3, 0.0, -2.1, +4.2, 1 234.2, 23 45.3,
15.4E5,
1.2e8, 2#100 111.11#, 16#1a.b#, 2#11 001.1#e2.
Interpretacja powyższych zapisów jest analogiczna jak dla literałów
całkowitych.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały rzeczywiste
Literał rzeczywisty
to literał numeryczny zawierający kropkę
dziesiętną (literały całkowite nie zawierają kropek).
Przykłady literałów rzeczywistych:
13.3, 0.0, -2.1, +4.2, 1 234.2, 23 45.3, 15.4E5,
1.2e8,
2#100 111.11#, 16#1a.b#, 2#11 001.1#e2.
Interpretacja powyższych zapisów jest analogiczna jak dla literałów
całkowitych.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały rzeczywiste
Literał rzeczywisty
to literał numeryczny zawierający kropkę
dziesiętną (literały całkowite nie zawierają kropek).
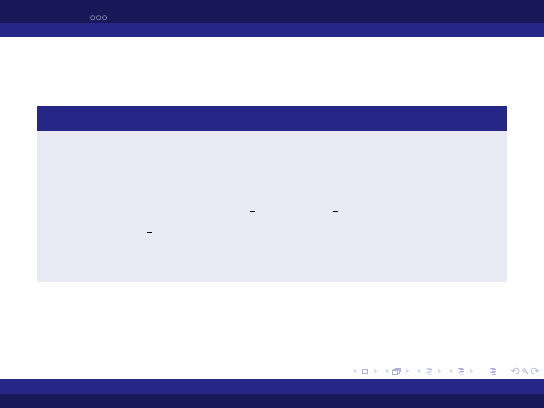
Przykłady literałów rzeczywistych:
13.3, 0.0, -2.1, +4.2, 1 234.2, 23 45.3, 15.4E5,
1.2e8, 2#100 111.11#, 16#1a.b#,
2#11 001.1#e2.
Interpretacja powyższych zapisów jest analogiczna jak dla literałów
całkowitych.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały rzeczywiste
Literał rzeczywisty
to literał numeryczny zawierający kropkę
dziesiętną (literały całkowite nie zawierają kropek).
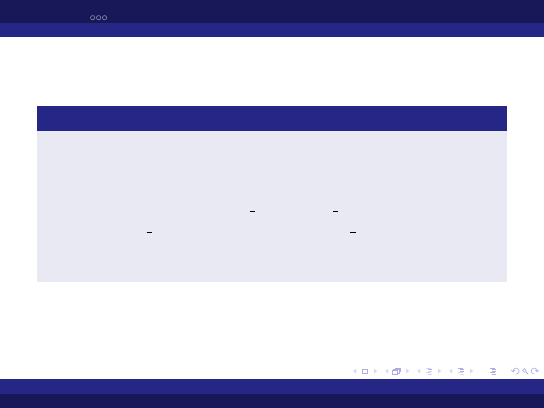
Przykłady literałów rzeczywistych:
13.3, 0.0, -2.1, +4.2, 1 234.2, 23 45.3, 15.4E5,
1.2e8, 2#100 111.11#, 16#1a.b#, 2#11 001.1#e2.
Interpretacja powyższych zapisów jest analogiczna jak dla literałów
całkowitych.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Literały rzeczywiste
Literał rzeczywisty
to literał numeryczny zawierający kropkę
dziesiętną (literały całkowite nie zawierają kropek).
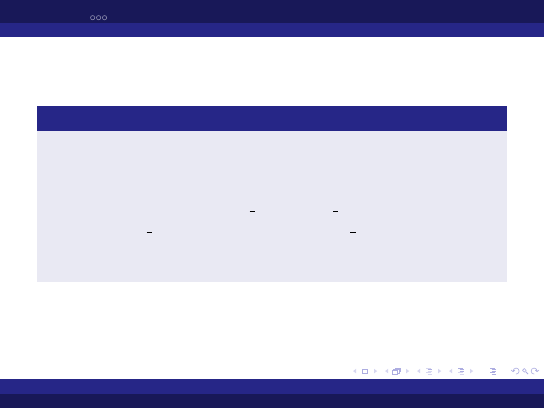
Przykłady literałów rzeczywistych:
13.3, 0.0, -2.1, +4.2, 1 234.2, 23 45.3, 15.4E5,
1.2e8, 2#100 111.11#, 16#1a.b#, 2#11 001.1#e2.
Interpretacja powyższych zapisów jest analogiczna jak dla literałów
całkowitych.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Wypisywanie literałów
W celu wypisania literałów numerycznych musimy użyć zasobów
odpowiedniego pakietu.
Literały całkowite są typu
universal integer
. Do ich
wypisywania używamy procedury
put
z pakietu
ada.integer text io
Literały rzeczywiste są typu
universal real
. Do ich wypisywania
używamy procedury
put
z pakietu
ada.float text io
.
Agata Półrola Wydział Matematyki i Informatyki UŁ
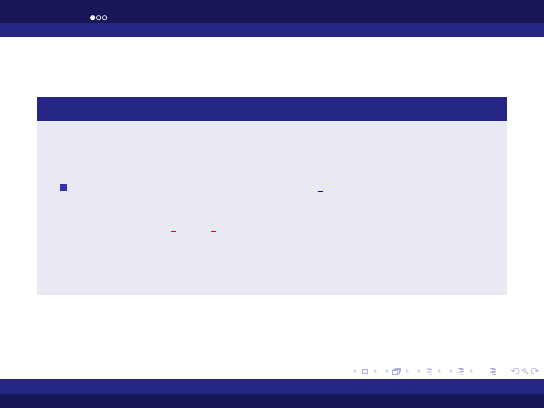
Wypisywanie literałów
W celu wypisania literałów numerycznych musimy użyć zasobów
odpowiedniego pakietu.
Literały całkowite są typu
universal integer
. Do ich
wypisywania używamy procedury
put
z pakietu
ada.integer text io
Literały rzeczywiste są typu
universal real
. Do ich wypisywania
używamy procedury
put
z pakietu
ada.float text io
.
Agata Półrola Wydział Matematyki i Informatyki UŁ
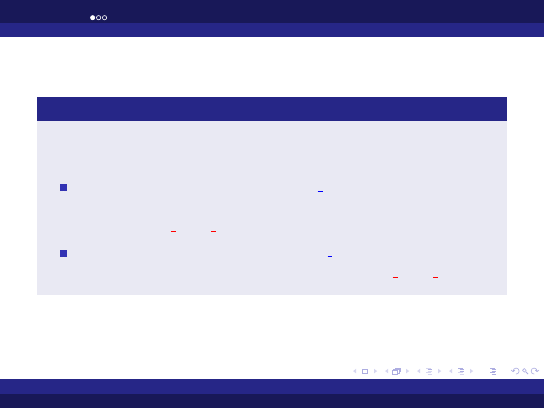
Wypisywanie literałów
W celu wypisania literałów numerycznych musimy użyć zasobów
odpowiedniego pakietu.
Literały całkowite są typu
universal integer
. Do ich
wypisywania używamy procedury
put
z pakietu
ada.integer text io
Literały rzeczywiste są typu
universal real
. Do ich wypisywania
używamy procedury
put
z pakietu
ada.float text io
.
Agata Półrola Wydział Matematyki i Informatyki UŁ
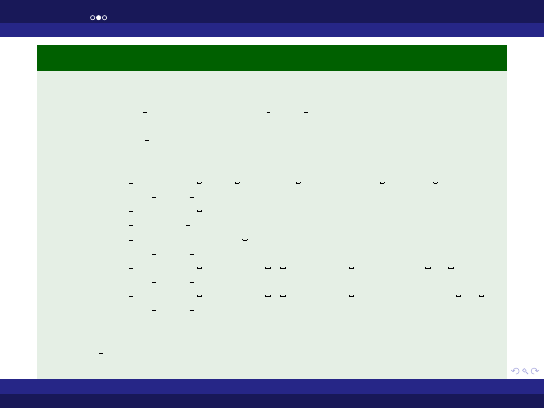
Przykład (Literały całkowite)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w02 p4
i s
b e g i n
ada . t e x t i o . p u t ( ” −−−− p r o g r a m w y p i s u j a c y
l i c z b e ” ) ;
ada . i n t e g e r t e x t i o . p u t ( 2 2 ) ;
ada . t e x t i o . p u t ( ” −−−−” ) ;
ada . t e x t i o . n e w l i n e ( 2 ) ;
ada . t e x t i o . p u t ( ” l i c z b a ” ) ;
ada . i n t e g e r t e x t i o . p u t ( 2 2 ,
w i d t h =>0);
ada . t e x t i o . p u t ( ” z a p i s a n a w s y s t e m i e dwojkowym t o ” ) ;
ada . i n t e g e r t e x t i o . p u t ( i t e m => 2 2 , w i d t h =>0, b a s e =>2);
ada . t e x t i o . p u t ( ” z a p i s a n a w s y s t e m i e
s z e s n a s t k o w y m t o ” ) ;
ada . i n t e g e r t e x t i o . p u t ( 2 2 , 0 , 1 6 ) ;
end w02 p4 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
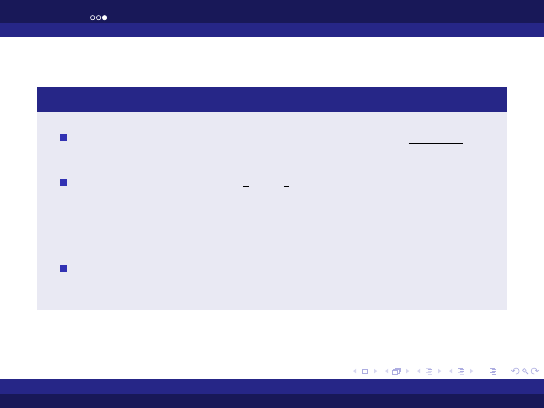
Uwagi do przykładu
we wszystkich trzech przypadkach została użyta ta sama
procedura
procedura ada.integer text io.put ma trzy
parametry
o
nazwach item, width i base. Item to wypisywana wartość,
width to szerokość obszaru wypisywania, base to podstawa
wypisywanej liczby.
dwa ostatnie parametry procedury mają wartości domyślne,
więc można ich nie podawać
Agata Półrola Wydział Matematyki i Informatyki UŁ
Podawanie wartości parametrów procedur
Procedury mają często kilka parametrów. Każdy parametr ma swoją
nazwę. Niektóre parametry mają ponadto wartości domyślne.
put(item, width, base), gdzie width i base mają wartości domyślne
Używając procedury (
wywołując
ją), musimy podać wartości dla
parametrów nie mających wartości domyślnych, i możemy podać
wartości dla pozostałych
jeśli przy podawaniu wartości nie użyjemy nazw parametrów -
istotna jest kolejność (
notacja pozycyjna
)
put(14, 4, 2) oznacza, że item ma wartość 14, width wartość 4, a
base wartość 2
jeśli użyjemy nazw wszystkich parametrów - kolejność
podawania wartości nie ma znaczenia (
notacja nazywana
)
put(base=>2, item=>14, width=>4), put(width=>2, item=>12)
można użyć notacji mieszanej - dla początkowych parametrów
pozycyjnej, dla dalszych nazywanej (
put(12, base=>2)
)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Podawanie wartości parametrów procedur
Procedury mają często kilka parametrów. Każdy parametr ma swoją
nazwę. Niektóre parametry mają ponadto wartości domyślne.
put(item, width, base), gdzie width i base mają wartości domyślne
Używając procedury (
wywołując
ją), musimy podać wartości dla
parametrów nie mających wartości domyślnych, i możemy podać
wartości dla pozostałych
jeśli przy podawaniu wartości nie użyjemy nazw parametrów -
istotna jest kolejność (
notacja pozycyjna
)
put(14, 4, 2) oznacza, że item ma wartość 14, width wartość 4, a
base wartość 2
jeśli użyjemy nazw wszystkich parametrów - kolejność
podawania wartości nie ma znaczenia (
notacja nazywana
)
put(base=>2, item=>14, width=>4), put(width=>2, item=>12)
można użyć notacji mieszanej - dla początkowych parametrów
pozycyjnej, dla dalszych nazywanej (
Agata Półrola Wydział Matematyki i Informatyki UŁ
Rozróżnianie procedur
W przykładzie dołączaliśmy pakiety ada.text io i
ada.integer text io; oba zawierają procedury put
Jeśli użyjemy klauzuli use i pominiemy przy wywołaniach
nazwy pakietów z których pochodzą procedury, program nadal
będzie poprawny.
Kompilator “domyśla się” którą procedurę mieliśmy na myśli w
danym wywołaniu na podstawie typów wartości przypisanych
parametrom, lub na podstawie liczby parametrów.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Rozróżnianie procedur
W przykładzie dołączaliśmy pakiety ada.text io i
ada.integer text io; oba zawierają procedury put
Jeśli użyjemy klauzuli use i pominiemy przy wywołaniach
nazwy pakietów z których pochodzą procedury, program nadal
będzie poprawny.
Kompilator “domyśla się” którą procedurę mieliśmy na myśli w
danym wywołaniu na podstawie typów wartości przypisanych
parametrom, lub na podstawie liczby parametrów.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Rozróżnianie procedur
W przykładzie dołączaliśmy pakiety ada.text io i
ada.integer text io; oba zawierają procedury put
Jeśli użyjemy klauzuli use i pominiemy przy wywołaniach
nazwy pakietów z których pochodzą procedury, program nadal
będzie poprawny.
Kompilator “domyśla się” którą procedurę mieliśmy na myśli w
danym wywołaniu na podstawie typów wartości przypisanych
parametrom, lub na podstawie liczby parametrów.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ;
p r o c e d u r e w 0 2 p 4 1
i s
b e g i n
p u t ( ” −−−− p r o g r a m w y p i s u j a c y
l i c z b e ” ) ;
p u t ( 2 2 , 8 ) ;
p u t ( ” −−−−” ) ;
n e w l i n e ( 2 ) ;
p u t ( ” l i c z b a ” ) ;
p u t ( 2 2 ,
w i d t h =>0);
p u t ( ” z a p i s a n a w s y s t e m i e dwojkowym t o ” ) ;
p u t ( 2 2 , 0 , 2 ) ;
end w 0 2 p 4 1 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład (Literały rzeczywiste)
w i t h ada . t e x t i o ,
ada . f l o a t t e x t i o ;
p r o c e d u r e w02 p5
i s
b e g i n
ada . t e x t i o . p u t ( ” −−−− p r o g r a m w y p i s u j a c y
l i c z b e ” ) ;
ada . f l o a t t e x t i o . p u t ( 2 2 . 2 ) ;
ada . t e x t i o . p u t ( ” −−−−” ) ;
ada . t e x t i o . n e w l i n e ( 2 ) ;
ada . t e x t i o . p u t ( ” l i c z b a ” ) ;
ada . f l o a t t e x t i o . p u t ( 2 2 . 2 ,
e x p =>0);
ada . t e x t i o . p u t ( ” moze b y c w y p i s a n a t a k : ” ) ;
ada . f l o a t t e x t i o . p u t ( 2 2 . 2 ) ;
ada . t e x t i o . p u t ( ” a l b o np .
t a k : ” ) ;
ada . f l o a t t e x t i o . p u t ( i t e m = >22.2 , f o r e =>4, a f t =>2, e x p =>0);
ada . t e x t i o . p u t ( ” a l e
n i e moze b y c np .
w y p i s a n a ” &
”w s y s t e m i e dwojkowym : ” ) ;
end w02 p5 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Uwagi do przykładu
Procedura ada.float text io.put ma cztery parametry, o
nazwach item, fore, aft i exp. Tylko pierwszy nie ma wartości
domyślnej.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Typy liczbowe
W języku zdefiniowane są pewne (tzw.
predfiniowane
typy
liczbowe. Podstawowe to:
typ całkowity -
integer
(służący do reprezentowania liczb
całkowitych)
typ zmiennoprzecinkowy -
float
(służący do reprezentowania
liczb rzeczywistych)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Zakresy typów
Wartości danego typu T są zapamiętywane przy użyciu pewnej
określonej dla danego typu liczby bitów
Z tego powodu każdy typ ma swój
zakres
- istnieje w nim wartość
największa i najmniejsza
Najmniejsza liczba w typie T to T’first, największa to T’last
Agata Półrola Wydział Matematyki i Informatyki UŁ
Zakresy typów
Wartości danego typu T są zapamiętywane przy użyciu pewnej
określonej dla danego typu liczby bitów
Z tego powodu każdy typ ma swój
zakres
- istnieje w nim wartość
największa i najmniejsza
Najmniejsza liczba w typie T to T’first, największa to T’last
Agata Półrola Wydział Matematyki i Informatyki UŁ
Zakresy typów
Wartości danego typu T są zapamiętywane przy użyciu pewnej
określonej dla danego typu liczby bitów
Z tego powodu każdy typ ma swój
zakres
- istnieje w nim wartość
największa i najmniejsza
Najmniejsza liczba w typie T to T’first, największa to T’last
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład (Jak poznać zakres typu integer?)
w i t h ada . i n t e g e r t e x t i o ,
ada . t e x t i o ;
u s e
ada . i n t e g e r t e x t i o ,
ada . t e x t i o ;
p r o c e d u r e w02 p6
i s
b e g i n
p u t ( ” n a j m n i e j s z a
l i c z b a w t y p i e
i n t e g e r
t o ” ) ;
p u t ( i n t e g e r ’ f i r s t , w i d t h =>0);
p u t ( ” a n a j w i e k s z a
t o ” ) ;
p u t ( i n t e g e r ’ l a s t ) ;
end w02 p6 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Inne predefiniowane typy liczowe
typy całkowite (zależnie od implementacji):
long integer
long long integer
short integer
short short integer
typy rzeczywiste (zależnie od implementacji):
long float
long long float
short float
short short float
(tego w naszym przypadku nie ma)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Zmienne
Aby móc zapamiętać (przechować) wprowadzoną z klawiatury lub
wyliczoną w programie wartość pewnego typu, musimy
zadeklarować
zmienną
tego typu
w tym celu w części deklaracyjnej programu piszemy
nazwa zmiennej:
typ;
(np. i:
integer; )
wynik: w odpowienim momencie uruchamiania programu w
pamięci zostaje zarezerwowany pewien obszar o rozmiarze
odpowiednim dla przechowania wartości danego typu.
Odwołujemy się do niego przez nazwę zmiennej.
można zadeklarować na raz kilka zmiennych tego samego
typu:
j, f, ile :
integer;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Zmienne
Aby móc zapamiętać (przechować) wprowadzoną z klawiatury lub
wyliczoną w programie wartość pewnego typu, musimy
zadeklarować
zmienną
tego typu
w tym celu w części deklaracyjnej programu piszemy
nazwa zmiennej:
typ;
(np. i:
integer; )
wynik: w odpowienim momencie uruchamiania programu w
pamięci zostaje zarezerwowany pewien obszar o rozmiarze
odpowiednim dla przechowania wartości danego typu.
Odwołujemy się do niego przez nazwę zmiennej.
można zadeklarować na raz kilka zmiennych tego samego
typu:
j, f, ile :
integer;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Wartość zmiennej może ulegać zmianie podczas działania
programu
Instrukcja przypisania
(
:=
) pozwala nadać zmiennej pewną
wartość
Przypisywana wartość musi mieścić się w zakresie typu,
inaczej dostaniemy błąd
zmienna, której nie przypisano w programie żadnej wartości,
ma wartość przypadkową
Agata Półrola Wydział Matematyki i Informatyki UŁ
Wartość zmiennej może ulegać zmianie podczas działania
programu
Instrukcja przypisania
(
:=
) pozwala nadać zmiennej pewną
wartość
Przypisywana wartość musi mieścić się w zakresie typu,
inaczej dostaniemy błąd
zmienna, której nie przypisano w programie żadnej wartości,
ma wartość przypadkową
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład (Użycie instrukcji przypisania)
deklaracje zmiennych: a,b,i:
integer;
i := 2;
a := 2+2;
b := a+i;
weź wartość zmiennej a, dodaj do niej wartość zmiennej i, otrzymany wynik
przypisz zmiennej b
a := a + 5;
weż wartość zmiennej a, dodaj do niej 5, otrzymany wynik przypisz z powrotem
zmiennej a
Agata Półrola Wydział Matematyki i Informatyki UŁ
Wartość początkowa zmiennej
Zmiennej możemy przypisać wartość już w momencie jej
deklarowania (
inicjalizacja zmiennej
). Przypisywana wartość musi
mieścić się w zakresie typu, inaczej dostaniemy błąd.
Postać:
nazwa zmiennej :
typ := wyrażenie;
Przykład
i:
integer := 0;
s:
float := 2.5234 + 3.234;
k,l,m :
integer := 100;
wszystkie trzy zmienne zostaną zainicjowane wartością 100
zmienna oczywiście nadal pozostaje zmienną, czyli jej wartość może ulegać zmianie
podczas działania programu
Agata Półrola Wydział Matematyki i Informatyki UŁ
Wartość początkowa zmiennej
Zmiennej możemy przypisać wartość już w momencie jej
deklarowania (
inicjalizacja zmiennej
). Przypisywana wartość musi
mieścić się w zakresie typu, inaczej dostaniemy błąd.
Postać:
nazwa zmiennej :
typ := wyrażenie;
Przykład
i:
integer := 0;
s:
float := 2.5234 + 3.234;
k,l,m :
integer := 100;
wszystkie trzy zmienne zostaną zainicjowane wartością 100
zmienna oczywiście nadal pozostaje zmienną, czyli jej wartość może ulegać zmianie
podczas działania programu
Agata Półrola Wydział Matematyki i Informatyki UŁ
Stałe
Oprócz zmiennych możemy w programie używać także
stałych
.
Stałe nie mogą zmieniać swojej wartości. Wartość nadajmy im w
momencie deklaracji.
w części deklaracyjnej programu piszemy
nazwa stałej : constant typ := wyrażenie;
lub
nazwa stałej : constant := wyrażenie;
w drugim przypadku stała przyjmuje typ universal integer lub
universal real, zależnie od rodzaju wyrażenia
Przykład
Deklaracje stałych
procent podatku :
constant integer := 18;
przyspieszenie ziemskie :
constant := 9.80665;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Stałe
Oprócz zmiennych możemy w programie używać także
stałych
.
Stałe nie mogą zmieniać swojej wartości. Wartość nadajmy im w
momencie deklaracji.
w części deklaracyjnej programu piszemy
nazwa stałej : constant typ := wyrażenie;
lub
nazwa stałej : constant := wyrażenie;
w drugim przypadku stała przyjmuje typ universal integer lub
universal real, zależnie od rodzaju wyrażenia
Przykład
Deklaracje stałych
procent podatku :
constant integer := 18;
przyspieszenie ziemskie :
constant := 9.80665;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Operacje wejścia/wyjścia dla zmiennych i stałych
Pobieranie i wypisywanie wartości zmiennych
Aby pobrać wartość zmiennej (np. z klawiatury) lub wypisać
wartość zmiennej albo stałej (np. na ekran) musimy użyć zasobów
odpowiedniego pakietu
dla typu integer - pakietu ada.integer text io
dla typu float - pakietu ada.float text io
dla typu long integer - pakietu
ada.long integer text io
dla typu long float - pakietu ada.long float text io itd.
Niektóre implementacje Ady mogą nie udostępniać gotowych pakietów dla wszystkich
w/w typów. Musimy wtedy dokonać odpowiedniej
konkretyzacji
pakietu
ada.text io.integer io lub ada.text io.float io.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Operacje wejścia/wyjścia dla zmiennych i stałych
Pobieranie i wypisywanie wartości zmiennych
Aby pobrać wartość zmiennej (np. z klawiatury) lub wypisać
wartość zmiennej albo stałej (np. na ekran) musimy użyć zasobów
odpowiedniego pakietu
dla typu integer - pakietu ada.integer text io
dla typu float - pakietu ada.float text io
dla typu long integer - pakietu
ada.long integer text io
dla typu long float - pakietu ada.long float text io itd.
Niektóre implementacje Ady mogą nie udostępniać gotowych pakietów dla wszystkich
w/w typów. Musimy wtedy dokonać odpowiedniej
konkretyzacji
pakietu
ada.text io.integer io lub ada.text io.float io.
Agata Półrola Wydział Matematyki i Informatyki UŁ
Każdy z w/w pakietów zawiera:
procedurę
put
dla odpowiedniego typu, umożliwiającą
wypisanie na ekran wartości zmiennej lub stałej tego typu
procedurę
get
dla odpowiedniego typu, umożliwiającą
pobranie z klawiatury wartości zmiennej tego typu
działanie procedury get: jeśli bufor klawiatury jest pusty, procedura
zatrzymuje program do momentu wprowadzenia do bufora danych
(zakończonych znakiem końca linii, czyli klawiszem Enter); jeśli bufor nie
jest pusty - czyta wartość z bufora bez oczekiwania na podanie danych
przez użytkownika. Czytanie przebiega następująco: początkowe białe
znaki (spacje, znaki końca linii, znak tabulatora) są pomijane, czytana
zmienna przyjmuje wartość odpowiadającą literałowi złożonemu ze
znaków przeczytanych do napotkania pierwszego “nieodpowiedniego”
znaku. Wprowadzone z klawiatury “nieodpowiednie” znaki (np. końcowy
znak końca linii wprowadzony przy wciskaniu Enter) zostają w buforze
Agata Półrola Wydział Matematyki i Informatyki UŁ
Wyrażenia arytmetyczne
Wyrażenia
konstruuje się z literałów, nazw obiektów (tj. nazw
stałych i zmiennych) oraz operatorów arytmetycznych.
Wyrażenia służą do obliczania wartości, które przypisujemy stałym
lub zmiennym, lub wyprowadzamy np. na ekran.
pojedyncza zmienna lub literał to także wyrażenie
Agata Półrola Wydział Matematyki i Informatyki UŁ
Operatory używane w wyrażeniach
Podstawowe operatory używane w wyrażeniach
arytmetycznych to
+ - * /
Kolejność działań jest standardowa (standardowy priorytet
operatorów), można używać także nawiasów grupujących
Ada nie pozwala na “mieszanie” w jednym wyrażeniu
elementów różnych typów
np. wyrażenie 2.3*2 jst niepoprawne, poprawna wersja to
2.3*2.0
Typ wyniku jest taki sam jak typ argumentów użytych w
wyrażeniu
uwaga -
dzielenie dwóch liczb całkowitych jest w takim
razie dzieleniem całkowitym
Agata Półrola Wydział Matematyki i Informatyki UŁ
Operatory używane w wyrażeniach
Podstawowe operatory używane w wyrażeniach
arytmetycznych to
+ - * /
Kolejność działań jest standardowa (standardowy priorytet
operatorów), można używać także nawiasów grupujących
Ada nie pozwala na “mieszanie” w jednym wyrażeniu
elementów różnych typów
np. wyrażenie 2.3*2 jst niepoprawne, poprawna wersja to
2.3*2.0
Typ wyniku jest taki sam jak typ argumentów użytych w
wyrażeniu
uwaga -
dzielenie dwóch liczb całkowitych jest w takim
razie dzieleniem całkowitym
Agata Półrola Wydział Matematyki i Informatyki UŁ
Inne operatory arytmetyczne
operator
rem
(remainder) pozwala na znalezienie reszty z
dzielenia całkowitego
definicja operatora: A = (A/B) · B + (AremB)
przy czym | A rem B |<| B | i A rem B ma ten sam znak co A
operator
mod
działa w podobny sposób
definicja operatora: A = B · N + (AmodB) dla pewnego
całkowitego N
przy czym | A mod B |<| B | i A mod B ma ten sam znak co B
Powyższe operatory zdefiniowane są tylko dla typów całkowitych
Agata Półrola Wydział Matematyki i Informatyki UŁ
Inne operatory arytmetyczne
operator
rem
(remainder) pozwala na znalezienie reszty z
dzielenia całkowitego
definicja operatora: A = (A/B) · B + (AremB)
przy czym | A rem B |<| B | i A rem B ma ten sam znak co A
operator
mod
działa w podobny sposób
definicja operatora: A = B · N + (AmodB) dla pewnego
całkowitego N
przy czym | A mod B |<| B | i A mod B ma ten sam znak co B
Powyższe operatory zdefiniowane są tylko dla typów całkowitych
Agata Półrola Wydział Matematyki i Informatyki UŁ
Inne operatory arytmetyczne
operator
rem
(remainder) pozwala na znalezienie reszty z
dzielenia całkowitego
definicja operatora: A = (A/B) · B + (AremB)
przy czym | A rem B |<| B | i A rem B ma ten sam znak co A
operator
mod
działa w podobny sposób
definicja operatora: A = B · N + (AmodB) dla pewnego
całkowitego N
przy czym | A mod B |<| B | i A mod B ma ten sam znak co B
Powyższe operatory zdefiniowane są tylko dla typów całkowitych
Agata Półrola Wydział Matematyki i Informatyki UŁ
Inne operatory arytmetyczne - cd
Ada umożliwia również potęgowanie (operator **)
podstawa potęgi może być typu całkowitego lub
zmiennoprzecinkowego
wykladnik potęgi musi być liczbą całkowitą (dla
podstawy całkowitej - dodatkowo nieujemną)
Agata Półrola Wydział Matematyki i Informatyki UŁ
Konwersja typów
Zastosowanie w jednym wyrażeniu zmiennych różnych typów
wymaga
konwersji typów
.
Konwersja do typu T:
T(wyrażenie innego typu)
oczywiście nie każda konwersja jest możliwa i nie każda jest
sensowna
Agata Półrola Wydział Matematyki i Informatyki UŁ
Podtypy
Jeśli chcemy ograniczyć zakres zmiennej, możemy zdefiniować
podtyp pewnego typu. Operacje wejścia/wyjścia dla podtypu
obsługiwane są przez pakiet dla typu bazowego
Agata Półrola Wydział Matematyki i Informatyki UŁ
Document Outline
Wyszukiwarka
Podobne podstrony:
1011z wdprog ww07
1011z wdprog ww05
1011z wdprog w01
1011z wdprog ww06
1011z wdprog ww08
1011z wdprog ww03
1011z wdprog ww04
1011z wdprog ww09
1011z wdprog ww07
1011z wdprog ww05
1011z wdprog ww07
więcej podobnych podstron