
Wstęp do programowania
wykład 9
Agata Półrola
Wydział Matematyki i Informatyki UŁ
sem. zimowy 2010/2011
Agata Półrola Wydział Matematyki i Informatyki UŁ
Tablice wielowymiarowe
Tablice wielowymiarowe, podobnie jak jednowymiarowe,
przechowują elementy tego samego typu
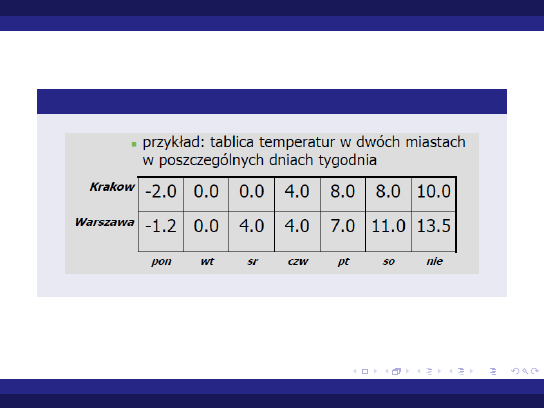
przykłady:
tablica temperatur w dwóch miastach w poszczególnych
dniach tygodnia
szachownica
plansza do gry w okręty
...
Agata Półrola Wydział Matematyki i Informatyki UŁ
Przykład tablicy dwuwymiarowej
Agata Półrola Wydział Matematyki i Informatyki UŁ
Deklaracja tablic wielowymiarowych
Zmienne tablicowe możemy deklarować jako będące
anonimowego typu tablicowego:
zmienna : array (określenie_indeksu_1, określenie_indeksu_2,
... określenie_indeksu_n) of typ_składowych ;
Przykłady
sudoku : array (1..9, 1..9) of integer;
dwa_na_trzy_na_cztery: array (integer range 1..2, integer range 1..3,
integer range 10..13) of float;
type miasta is (Krakow, Warszawa, Lodz, Poznan);
type miesiace is (sty,lut, mar, kwie);
type TablicaOpadow is array (miasta, miesiace range sty..mar)
of integer;
opady: TablicaOpadow;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Deklaracja tablic wielowymiarowych - cd
kolejna możliwość to zdefiniowanie typu tablicowego
posiadającego własną nazwę, a potem zadeklarowanie
zmiennej tego typu:
type nazwa_typu is array (określenie_indeksu_1, określenie_indeksu_2,
... określenie_indeksu_n) of typ_składowych ;
zmienna_tablicowa: nazwa_typu;
Przykłady
type TypDlaSudoku is array (1..9, 1..9) of integer;
sudoku: TypDlaSudoku;
type Tablice_2_3_4 is array (integer range 1..2, integer range 1..3,
integer range 10..13) of float;
dwa_na_trzy_na_cztery: Tablice_2_3_4;
type miasta is (Krakow, Warszawa, Lodz, Poznan);
type miesiace is (sty,lut, mar, kwie);
opady: array (miasta, miesiace range sty..mar) of integer;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Indeksy tablic wielowymiarowych - uwagi
każde określenie indeksu może być postaci takiej jak w
przypadku tablic jednowymiarowych
każdy indeks musi być typu dyskretnego
każdy z indeksów tablicy wielowymiarowej może być innego
typu (por. tablicę opady z przykładów)
jeśli typ któregoś indeksu nie jest podany jawnie, to przyjmuje
się że jest on odpowiedniego typu dyskretnego
krańce zakresu indeksu mogą być zadane dowolnym
wyrażeniem
Agata Półrola Wydział Matematyki i Informatyki UŁ

Odwołania do elementów tablic
Do elementów tablic odwołujemy się przez nazwę zmiennej
tablicowej i wartości indeksów umieszczone w okrągłych nawiasach
(przy czym wartości mogą być dane dowolnymi wyrażeniami).
Przykłady
sudoku(1,2):=7;
dwa_na_trzy_na_cztery(1,3,4):= 0.12;
opady(Warszawa,sty):=12;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Wypełnianie tablic wartościami
nie wypełniona “jawnie” danymi tablica wielowymiarowa
zawiera wartości przypadkowe
tablica może zostać wypełniona danymi przez kolejne
przypisywanie wartości wszystkim jej składowym
często wykorzystuje się wówczas pętle zagnieżdżone (po jednej pętli dla każdego
indeksu, czyli “wymiaru”)
inną metodą jest przypisanie wartości wszystkim składowym
równocześnie, jedną instrukcją, co wymaga użycia agregatu
tablicy
Agata Półrola Wydział Matematyki i Informatyki UŁ

Agregaty tablic wielowymiarowych
Mamy tablice:
type miasta is (Krakow, Lodz);
t: array (miesiace range lipiec..wrzesien, miasta) of float;
m: array(integer range 1..2, integer range 1..2) of integer
notacja pozyzyjna:
t:=((20.1,23.0), (20.2, 19.4), (19.0, 19.0));
m := ((0,1), (4,2));
notacja nazywana i mieszana
t:=(lipiec => (Krakow =>20.1, Lodz => 23.0),
sierpien => (Krakow => 20.2, Lodz => 19.4),
wrzesien => (others=>19.0));
m := (1=>(1=>0, 2=> 1), 2=>(1=> 4,2=> 2));
t:=(lipiec=>(20.1,23.0), sierpien => (20.2, 19.4),
wrzesien => (others=>19.0));
m := (1=>(0,1), 2=>(4,2));
Agata Półrola Wydział Matematyki i Informatyki UŁ

Tablice wielowymiarowe - operacje i atrybuty
z tablic wielowymiarowych nie można “wykrawać”
wielowymiarowych podtablic
tablice wielowymiarowe tego samego typu można porównać za
pomocą = i /=
można używać atrybutów takich jak dla tablic
jednowymiarowych, ale trzeba dodać do którego indeksu
(wymiaru) dany atrybut się odnosi (przykłady: t’first(1) -
zwróci lipiec, t’last(2) - zwróci Lodz). Bez określenia jak
powyżej atrybut (np. t’first) odnosi się do pierwszego
wymiaru.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Użycie tablicy dwuwymiarowej)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ,
ada . f l o a t t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ,
ada . f l o a t t e x t i o ;
p r o c e d u r e w09 tab2wym
i s
s u b t y p e
f l t d o d
i s
f l o a t
r a n g e
0 . 0 . . f l o a t ’ l a s t ;
t y p e
d n i
i s
( pon , wt , s r , czw , pt , so , n i e ) ;
p a c k a g e d n i o
i s new ada . t e x t i o . E n u m e r a t i o n I O ( d n i ) ;
u s e d n i o ;
t y p e
w y d a t k i w r o k u
i s
a r r a y ( i n t e g e r
r a n g e
1 . . 5 3 , d n i ) o f
f l t d o d ;
mojewyd2010 :
w y d a t k i w r o k u ;
n r t y g :
i n t e g e r ;
c z y :
c h a r a c t e r ;
b e g i n
mojewyd2010 : = ( o t h e r s=>(o t h e r s = >0.0));
l o o p
p u t ( ” c z y
w y p e l n i a s z
j a k i s
t y d z i e n ? t−t a k ,
i n n e − k o n i e c ” ) ;
g e t ( c z y ) ;
e x i t when c z y /= ’ t ’ and c z y /= ’T ’ ;
p u t ( ” p o d a j numer t y g o d n i a do w y p e l n i e n i a ” ) ;
g e t ( n r t y g ) ;
f o r
i
i n mojewyd2010 ’ r a n g e ( 2 )
l o o p
p u t ( i ) ;
p u t ( ”> ” ) ;
g e t ( mojewyd2010 ( n r t y g , i ) ) ;
end l o o p ;
end l o o p ;
p u t l i n e ( ” w y d a t k i w r o k u 2 0 1 0 : ” ) ;
f o r
i
i n mojewyd2010 ’ r a n g e ( 1 )
l o o p
f o r
j
i n mojewyd2010 ’ r a n g e ( 2 )
l o o p
p u t ( mojewyd2010 ( i , j ) , a f t =>2, e x p =>0, f o r e =>4);
end l o o p ;
n e w l i n e ;
end l o o p ;
end w09 tab2wym ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Tablice dynamiczne wielowymiarowe
Dynamiczne tablice wielowymiarowe tworzymy tak samo jak
jednowymiarowe (korzystając z bloku deklaracyjnego)
Dynamicznie ustana może być dowolna liczba wymiarów.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Użycie dynamicznej tablicy dwuwymiarowej)
w i t h ada . t e x t i o ,
ada . i n t e g e r t e x t i o ,
ada . f l o a t t e x t i o ;
u s e ada . t e x t i o ,
ada . i n t e g e r t e x t i o ,
ada . f l o a t t e x t i o ;
p r o c e d u r e w09 tab2wymd
i s
s u b t y p e
f l t d o d
i s
f l o a t
r a n g e
0 . 0 . . f l o a t ’ l a s t ;
t y p e
d n i
i s
( pon , wt , s r , czw , pt , so , n i e ) ;
p a c k a g e d n i o
i s new ada . t e x t i o . E n u m e r a t i o n I O ( d n i ) ;
u s e d n i o ;
n r t y g ,
i t :
i n t e g e r ;
c z y :
c h a r a c t e r ;
b e g i n
p u t ( ” i l e
t y g o d n i
c h c e s z m i e c w t a b l i c y ? ” ) ;
g e t ( i t ) ;
d e c l a r e
t y p e
w y d a t k i w r o k u
i s
a r r a y ( i n t e g e r
r a n g e
1 . . i t , d n i ) o f
f l t d o d ;
mojewyd2010 :
w y d a t k i w r o k u ;
b e g i n
mojewyd2010 : = ( o t h e r s=>(o t h e r s = >0.0));
l o o p
p u t ( ” c z y
w y p e l n i a s z
j a k i s
t y d z i e n ? t−t a k ,
i n n e − k o n i e c ” ) ;
g e t ( c z y ) ;
e x i t when c z y /= ’ t ’ and c z y /= ’T ’ ;
p u t ( ” p o d a j numer t y g o d n i a do w y p e l n i e n i a ” ) ;
g e t ( n r t y g ) ;
f o r
i
i n mojewyd2010 ’ r a n g e ( 2 )
l o o p
p u t ( i ) ;
p u t ( ”> ” ) ;
g e t ( mojewyd2010 ( n r t y g , i ) ) ;
end l o o p ;
end l o o p ;
p u t l i n e ( ” w y d a t k i w r o k u 2 0 1 0 : ” ) ;
f o r
i
i n mojewyd2010 ’ r a n g e ( 1 )
l o o p
f o r
j
i n mojewyd2010 ’ r a n g e ( 2 )
l o o p
p u t ( mojewyd2010 ( i , j ) , a f t =>2, e x p =>0, f o r e =>4); end l o o p ;
n e w l i n e ;
end l o o p ;
end ;
end w09 tab2wymd ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Tablice niezawężone
Istnienie niezawężonych typów tablicowych (ang. unconstrained
array types) umożliwia tworzenie tablic należących do jednego
typu, ale mających różne rozmiary i zakresy indeksów.
Tablice niezawężone mogą byc jedno- lub wielowymiarowe.
Agata Półrola Wydział Matematyki i Informatyki UŁ

Definiowanie jednowymiarowego niezawężonego typu tablicowego
Niezawężony typ tablicowy dla tablic jednowymiarowych
definiujemy następująco:
type nazwa_typu is array (typ_indeksu range <>)
of typ_składowych;
Przykład
type ciag is array (integer range <>) of integer;
Rozmiar zmiennej tego typu jest określany dopiero w momencie jej
deklaracji - podajemy wtedy zakres indeksu tablicy
Przykład
c1 :
ciag(1..100);
c2 :
ciag(1..3);
Agata Półrola Wydział Matematyki i Informatyki UŁ

Definiowanie jednowymiarowego niezawężonego typu tablicowego
Niezawężony typ tablicowy dla tablic jednowymiarowych
definiujemy następująco:
type nazwa_typu is array (typ_indeksu range <>)
of typ_składowych;
Przykład
type ciag is array (integer range <>) of integer;
Rozmiar zmiennej tego typu jest określany dopiero w momencie jej
deklaracji - podajemy wtedy zakres indeksu tablicy
Przykład
c1 :
ciag(1..100);
c2 :
ciag(1..3);
Agata Półrola Wydział Matematyki i Informatyki UŁ

Deklarowanie zmiennych
Zmienne o wartościach należących do niezawężonego typu
tablicowego możemy deklarować:
podając zakres indeksu, np. c1:
ciag(1..100);
tablica c1 jest indeksowana wartościami od 1 do 100 i zawiera wartości
przypadkowe
ograniczając zakres indeksu przez nadanie zmiennej wartości
początkowej
Przykłady
type tab is array (integer range <>) of integer;
t0: tab(5..6) := (1,2);
t1: tab := (1=> 100, 2=> 200, 3=> 300);
-- indeks t1: 1..3
t2: tab := (1,2,3);
-- indeks t2: integer’first..integer’first+2
t4: tab:=t0;
-- indeks t4: taki jak indeks t0 czyli 5..6
Agata Półrola Wydział Matematyki i Informatyki UŁ

Podtypy typów niezawężonych
Możliwe jest definiowanie
podtypów
niezawężonego typu
tablicowego. Podtyp nie jest już niezawężony - obejmuje tablice
mające konkretny rozmiar.
Przykład
type ciag is array (integer range <>) of integer;
subtype ciag100 is ciag(1..100);
c1, c2: ciag;
Każda zmienna zadeklarowana jako należąca do niezawężonego
typu tablicowego należy właściwie do pewnego jego podtypu
określonego poprzez dane ograniczenie zakresu indeksu
Agata Półrola Wydział Matematyki i Informatyki UŁ

Podtypy typów niezawężonych
Możliwe jest definiowanie
podtypów
niezawężonego typu
tablicowego. Podtyp nie jest już niezawężony - obejmuje tablice
mające konkretny rozmiar.
Przykład
type ciag is array (integer range <>) of integer;
subtype ciag100 is ciag(1..100);
c1, c2: ciag;
Każda zmienna zadeklarowana jako należąca do niezawężonego
typu tablicowego należy właściwie do pewnego jego podtypu
określonego poprzez dane ograniczenie zakresu indeksu
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przesuwanie agregatów (slicing)
Prypisywanie zmiennej tablicowej wartości przy użyciu agregatu
może spowodować niejawną konwersję tego agregatu do
odpowiedniego podtypu (czyli zmianę zakresu indeksu w tym
agregacie - jest to tzw.
przesuwanie
(slicing)).
Zjawisko to nie występuje np. w przypadku agregatów
zawierających słowo others
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przesuwanie agregatów (slicing)
Prypisywanie zmiennej tablicowej wartości przy użyciu agregatu
może spowodować niejawną konwersję tego agregatu do
odpowiedniego podtypu (czyli zmianę zakresu indeksu w tym
agregacie - jest to tzw.
przesuwanie
(slicing)).
Zjawisko to nie występuje np. w przypadku agregatów
zawierających słowo others
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykłady (Przesuwanie agregatów)
type tab is array (positive range <>) of integer;
t: tab(1..5);
t:=(10..11=>1, 12..14=>4);
-- agregat przesuwa sie tak, ze t(1) i t(2) maja wartosc 1
-- pozostale - wartosc 4
t:=(5..6=>9, others=>0);
-- nie ma przesuniecia
-- przy wykonaniu nastapiloby przekroczenie zakresu
-- (proba odwolania do t(6))
t:=(3..5=>9, others=>0);
-- nie ma przesuniecia - t(3) do t(5) maja wartosc 9
-- pozostale - wartosc 0
t:=(8,8,8,others=>0);
-- nie ma przesuniecia - t(1) do t(3) maja wartosc 8,
-- pozostale - wartosc 0
Agata Półrola Wydział Matematyki i Informatyki UŁ

Jednowymiarowe niezawężone typy tablicowe - atrybuty
atrybuty ’first, ’last, ’range i ’length działają w
standardowy sposób, tzn. zwracają odpowiednio najmniejszy
indeks, największy indeks, zakres indeksu i długość tablicy do
której się odnoszą
(dokładniej: zwracają odpowiednie wartości dla podtypu
typu niezawężonego do którego należy rozpatrywana tablica)
Przykład
type tab is array (integer range <>) of integer;
t0: tab(5..6) := (1,2);
put(t0’first);
--- wypisze 5
put(t0’last);
--
wypisze 6
for K in t0’range loop ... end loop;
-- K przebiega zakres 5..6
put(t0’length);
-- wypisze 2
Agata Półrola Wydział Matematyki i Informatyki UŁ

Jednowymiarowe niezawężone typy tablicowe - operacje
operacje logiczne not, and, or, xor są zdefiniowane tylko dla
jednowymiarowych tablic o składowych typu boolean; tablice
muszą być tego samego typu (niezawężonego - mogą należeć
do jego różnych podtypów) i być tej samej długości
Przykład
type tabb is array (integer range <>) of boolean;
t1: tabb(1..3) :=(others => false);
t2: tabb(0..2) := (false, true, true);
t3: tabb := t1 and t2;
konkatenacja (&) jest zdefiniowana tylko dla tablic tego
samego typu (niezawężonego)
Przykład
t4:
tabb := t3 & t1 ;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Jednowymiarowe niezawężone typy tablicowe - operacje
z tablic jednowymiarowych można “wycinać” fragmenty -
podtablice
Przykład
type ciag is array (integer range <>) of integer;
t1: ciag(1..10) := (others=> 0);
t2: ciag(1..5) := (others=>2);
t2(1..3) := t2(2..5);
operacja przypisania (:=) umożliwia przypisywanie dla tablic
tego samego typu i rozmiaru
Agata Półrola Wydział Matematyki i Informatyki UŁ

Jednowymiarowe niezawężone typy tablicowe - operacje
operatory = i /= umożliwiają porównywanie tablic tego
samego typu (niezawężonego); dwie tablice są równe jeśli
mają tę samą liczbę składowych, a ich odpowiednie składowe
są jednakowe
Przykład
type tabb is array (integer range <>) of boolean;
t1: tabb(1..3) :=(others => false);
t2: tabb(0..2) := (others => false);
if t1=t2 then put("rowne"); else put("rozne"); end if;
-- wypisze rowne
Agata Półrola Wydział Matematyki i Informatyki UŁ

Jednowymiarowe niezawężone typy tablicowe - operacje
relacje <, <=, >=, > określone są dla jednowymiarowych tablic
(niezawężonych) o składowych typu dyskretnego
porównywanie kolejnych elementów, “od lewej do prawej”, do
momentu znalezienia składowych o różnych wartościach lub do
zakończenia którejś tablicy
tablica “mniejsza” to tablica krótsza lub taka, w której
pierwszy różniący się element jest mniejszy
Przykład
type tab is array (integer range <>) of integer;
t1: tab(1..20):=(others=>0);
t2: tab(1..3) :=(others=>0);
t3: tab(1..3) := (1,2,3);
if t1<t2 then put("t1 mniejsza"); else put("t1 nie mniejsza");
end if;
-- wypisze ’t1 nie mniejsza’
if t2<t3 then put("t2 mniejsza"); else put("t2 nie mniejsza");
end if;
Agata Półrola Wydział Matematyki i Informatyki UŁ

Jednowymiarowe niezawężone typy tablicowe - operacje
test przynależności do podtypu (in): testowana tablica i
podtyp muszą należeć do tego samego typu bazowego
(niezawężonego)
Przykład
type tab is array (integer range <>) of integer;
t1: tab(1..20):=(others=>0);
t2: tab(1..3) :=(others=>0);
t3: tab(1..3) := (1,2,3);
t4: tab(0..19);
subtype ttt is tab(1..20);
put(t3 in ttt);
-- wypisze FALSE
put(t1 in ttt);
-- wypisze TRUE
put (t4 in ttt); -- wypisze FALSE
Agata Półrola Wydział Matematyki i Informatyki UŁ

Przykład (Tablice niezawężone - podtypy, operacje)
w i t h ada . t e x t i o ;
u s e ada . t e x t i o ;
p r o c e d u r e
p r 4 4 c o n u n c o n
i s
t y p e t y p 1
i s
a r r a y
( i n t e g e r
r a n g e <>) o f
i n t e g e r ;
s u b t y p e t a b 1
i s
t y p 1 ( 1 . . 1 0 ) ;
s u b t y p e t a b 2
i s
t y p 1 ( 1 . . 5 ) ;
t 1 : t a b 1 : = ( o t h e r s =>0);
t 2 : t a b 2 : = ( o t h e r s =>2);
b e g i n
t 1 ( 1 ) : = t 2 ( 1 ) ;
t 1 ( 1 . . 3 ) : = t 2 ( 1 . . 3 ) ;
i f
t 1 ( 1 . . 5 ) = t 2 ( 1 . . 5 )
t h e n
p u t ( ” p o c z a t k o w e
k a w a l k i
t a b l i c
s a r o w n e ” ) ;
end
i f ;
i f
t 1=t 2 t h e n
p u t ( ” c a l e
t a b l i c e
s a r o w n e ” ) ;
end
i f ;
i f
t 1 ( 1 . . 5 ) > t 2 ( 1 . . 5 )
t h e n
p u t ( ” p o c z a t k o w y k a w a l e k 1− s z e j
t a b l i c y
j e s t
w i e k s z y ” ) ;
end
i f ;
i f
t 1>t 2 t h e n
p u t ( ” c a l e − p i e r w s z a
w i e k s z a ” ) ;
end
i f ;
end p r 4 4 c o n u n c o n ;
Agata Półrola Wydział Matematyki i Informatyki UŁ
Konwersja tablic
Tablicę można przekonwertować do innego typu tylko w przypadku,
gdy obie tablice mają ten sam rozmiar, typ elementów, typ indeksu
i długość
Przykład
type tab is array (integer range <>) of integer;
t1: tab(1..20):=(others=>0);
type tab2 is array(integer range <>) of integer;
t21: tab2(100..119);
t1:=t21; -- niewykonalne - niezgodość typów
t21:=tab2(t1);
-- wykonalne dzięki konwersji
Agata Półrola Wydział Matematyki i Informatyki UŁ

Wielowymiarowe tablice niezawężone
Niezawężone typy tablicowe mogą być rownież niezawężone
Brak zawężenia musi występować dla wszystkich zakresów
(indeksów)
Przykład
poprawne:
type macierz is array (positive range <>, positive range <>)
of integer;
m: macierz(1..2, 1..3);
niepoprawne:
type ZlyTyp is array (positive range <>, positive range 1..10)
of integer;
Atrybuty - jak w przypadku tablic niezawężonych
Operacje - dozwolone jest podstawianie, porównywanie = i /=,
konwersja i test przynależności
Agata Półrola Wydział Matematyki i Informatyki UŁ

Wielowymiarowe tablice niezawężone
Niezawężone typy tablicowe mogą być rownież niezawężone
Brak zawężenia musi występować dla wszystkich zakresów
(indeksów)
Przykład
poprawne:
type macierz is array (positive range <>, positive range <>)
of integer;
m: macierz(1..2, 1..3);
niepoprawne:
type ZlyTyp is array (positive range <>, positive range 1..10)
of integer;
Atrybuty - jak w przypadku tablic niezawężonych
Operacje - dozwolone jest podstawianie, porównywanie = i /=,
konwersja i test przynależności
Agata Półrola Wydział Matematyki i Informatyki UŁ
Document Outline
Wyszukiwarka
Podobne podstrony:
1011z wdprog ww07
1011z wdprog ww05
1011z wdprog w01
1011z wdprog ww06
1213z wdprog ww09
1011z wdprog ww08
1011z wdprog ww03
1011z wdprog ww04
1011z wdprog w02
1011z wdprog ww07
1011z wdprog ww05
1011z wdprog ww07
więcej podobnych podstron