
Wykład 6
Czesław Jasiukiewicz
Katedra Fizyki
Politechnika Rzeszowska
Semestr I Rok 2010/2011
Wykład 6
Wykład 6
Wykład 6
Wykład 6
Wykład 6

Wykład 6
Wykład 6
Wykład 6
Wykład 6
Wykład 6
Wykład 6
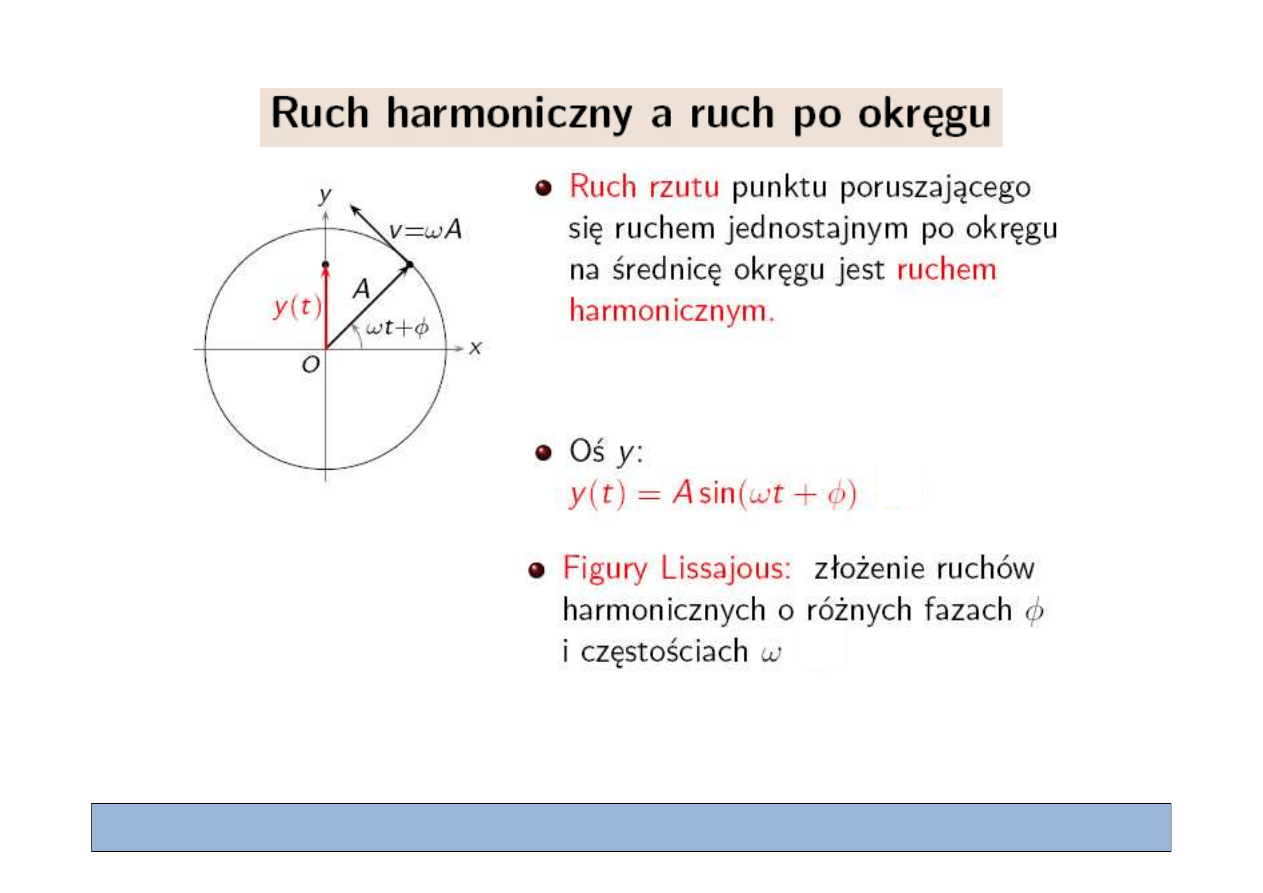
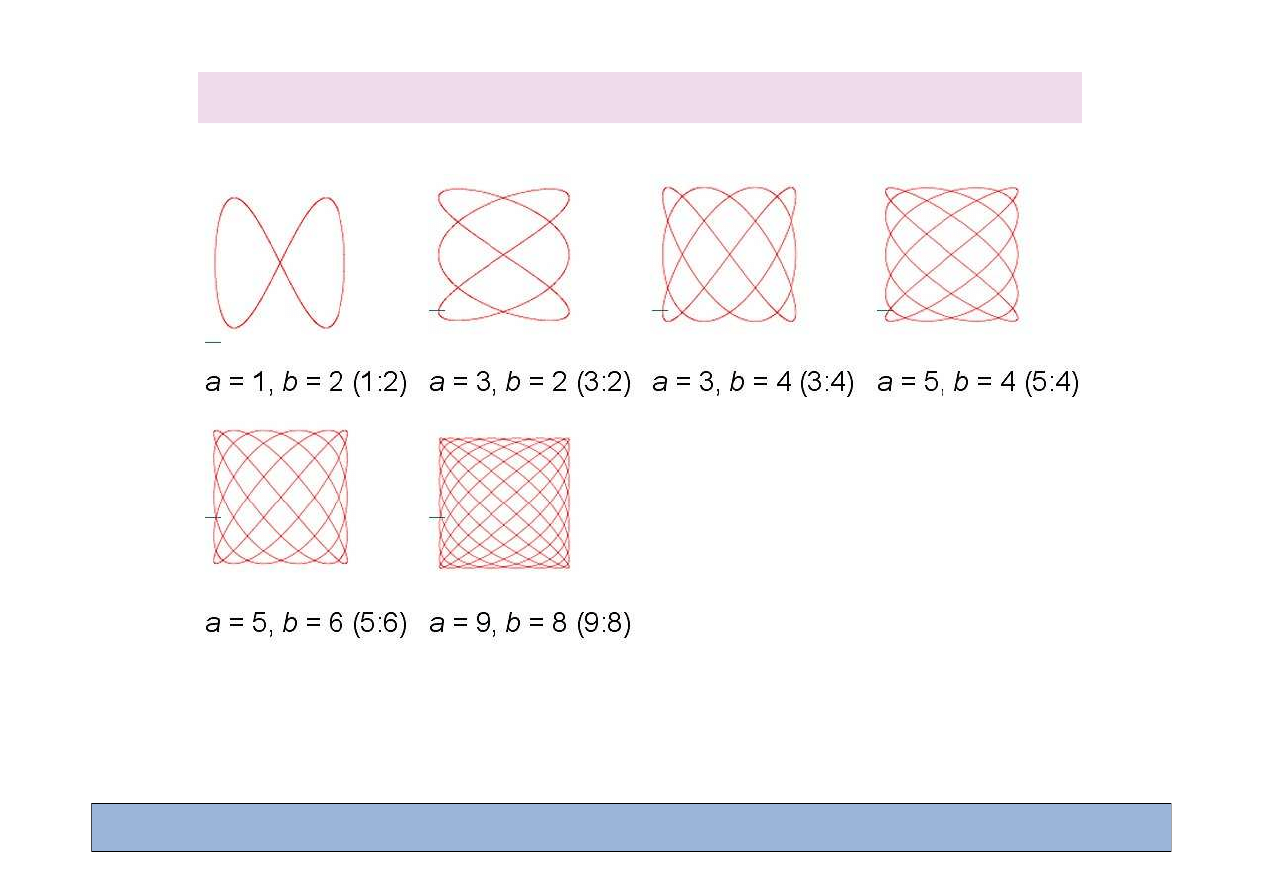
Figury Lissajous
http://ibiblio.org/e-notes/Lis/Lissa.htm
Wykład 6
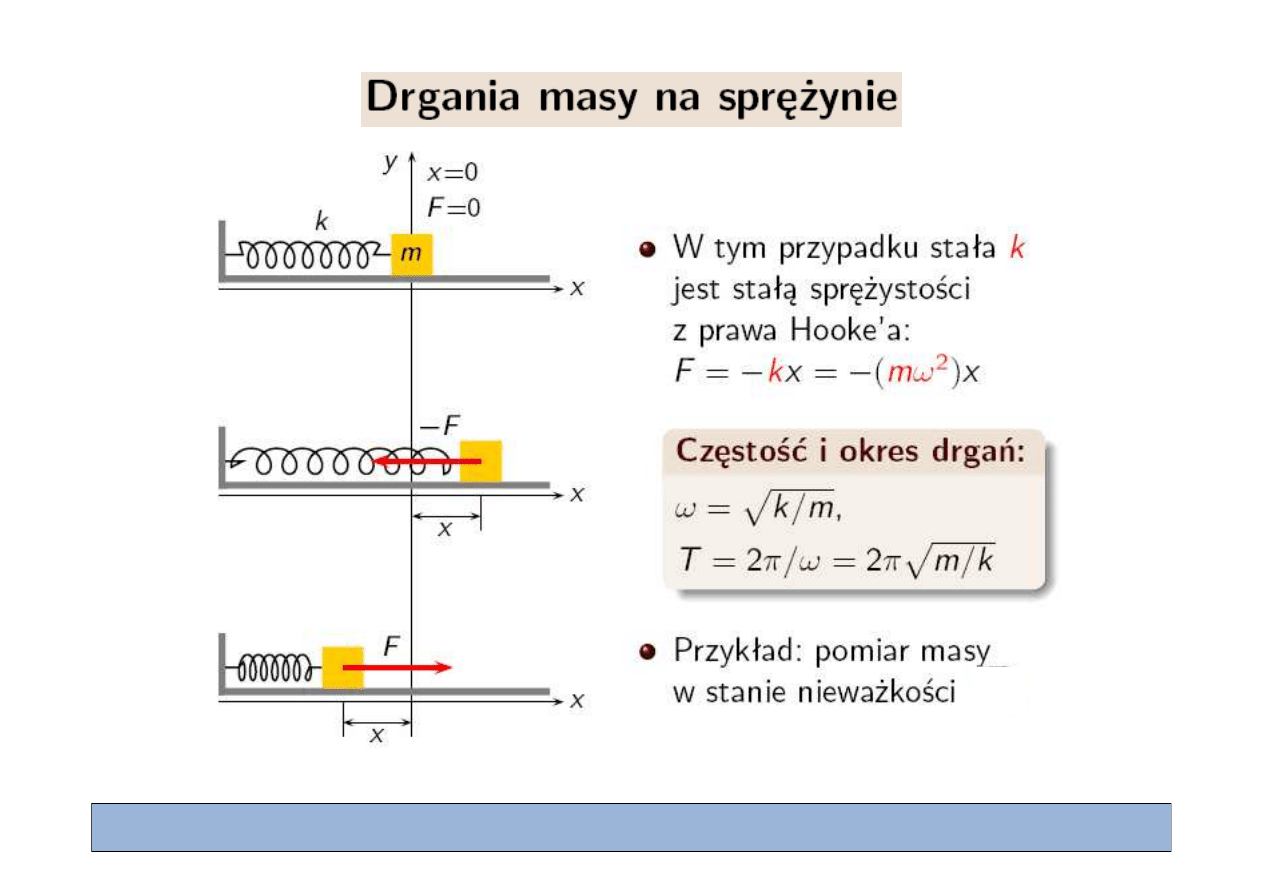
Rozwi
ą
zanie równa
ń
ruchu
2
2
,
d x
m
F
F
kx
dt
=
= −
Druga zasada dynamiki Newtona:
Równanie ró
ż
niczkowe:
2
2
0
d x
m
kx
dt
+
=
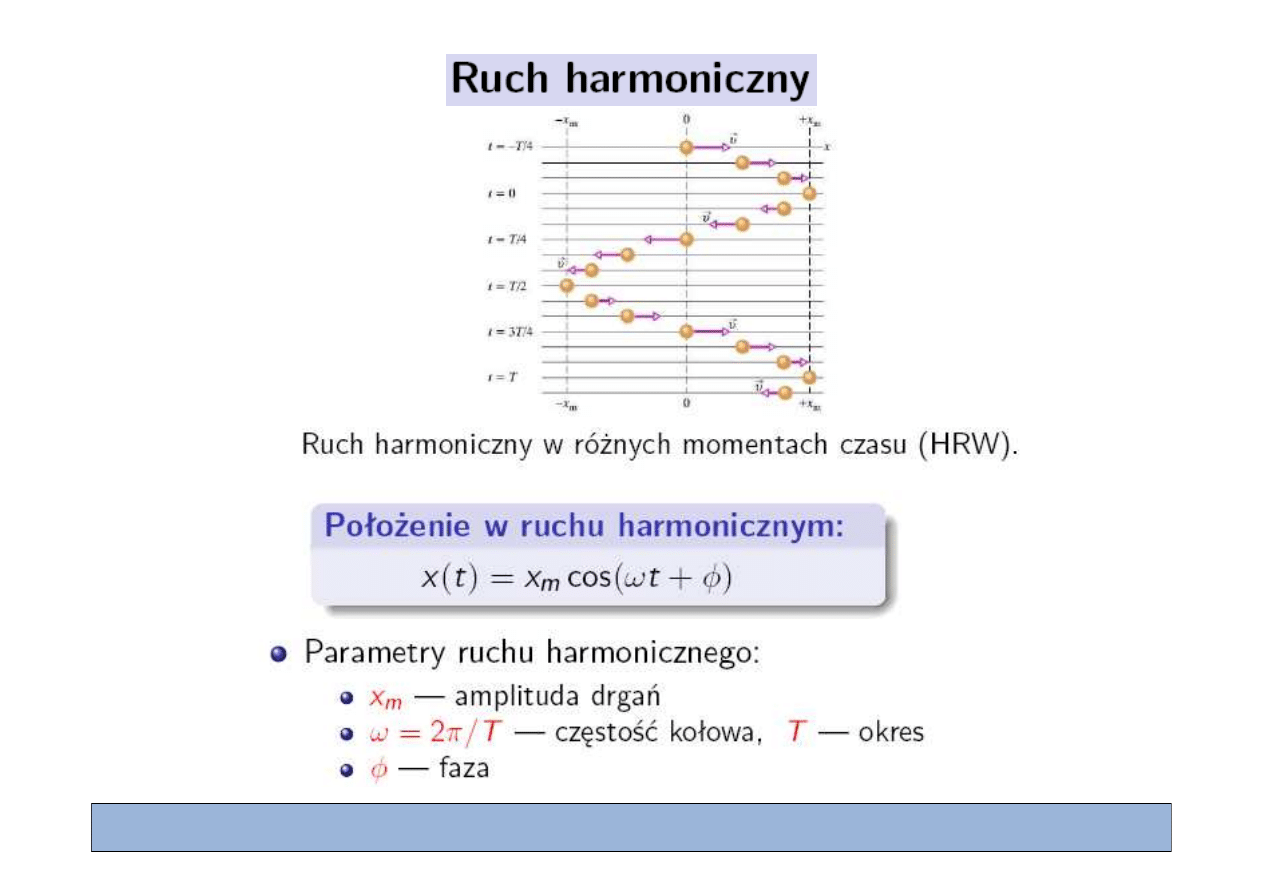
Rozwi
ą
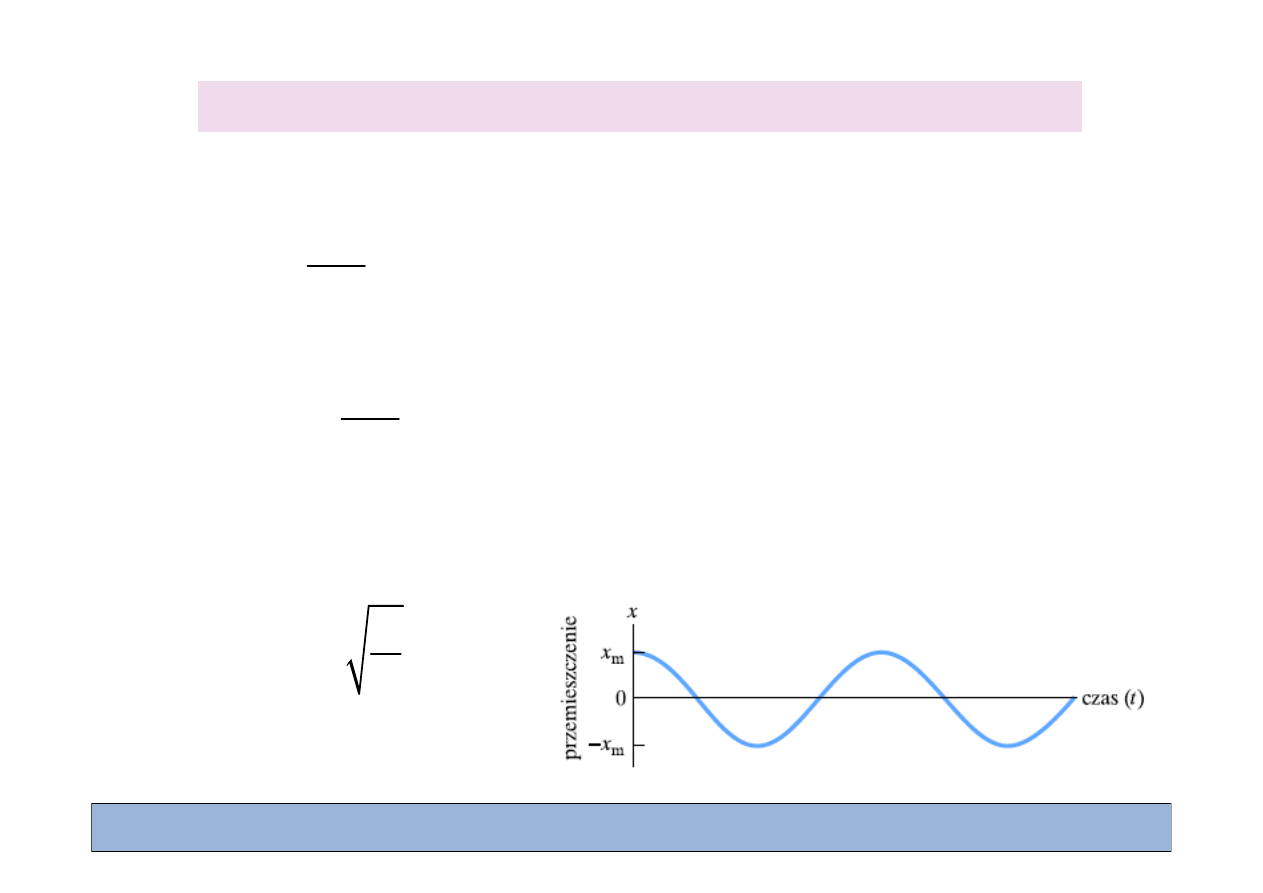
zanie:
(
)
( )
cos
m
x t
x
t
k
m
ω φ
ω
=
+
=
Wykład 6
Rozwi
ą
zanie równa
ń
ruchu (ruch tłumiony)
2
2
,
,
o
o
d x
m
F
F
F
kx
F
bv
dt
= +
= −
= −
Druga zasada dynamiki Newtona:
Równanie ró
ż
niczkowe:
2
2
0
d x
dx
m
b
kx
dt
dt
+
+
=
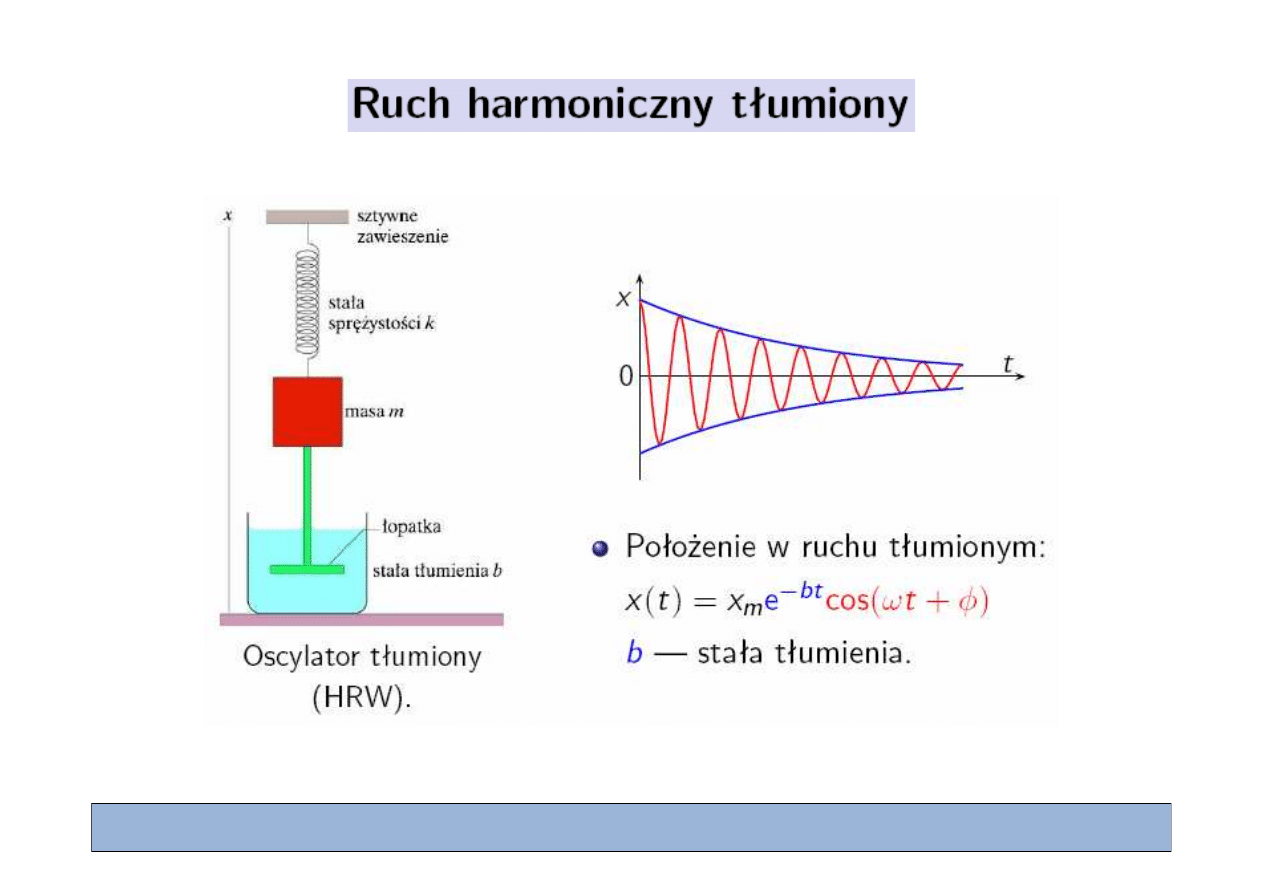
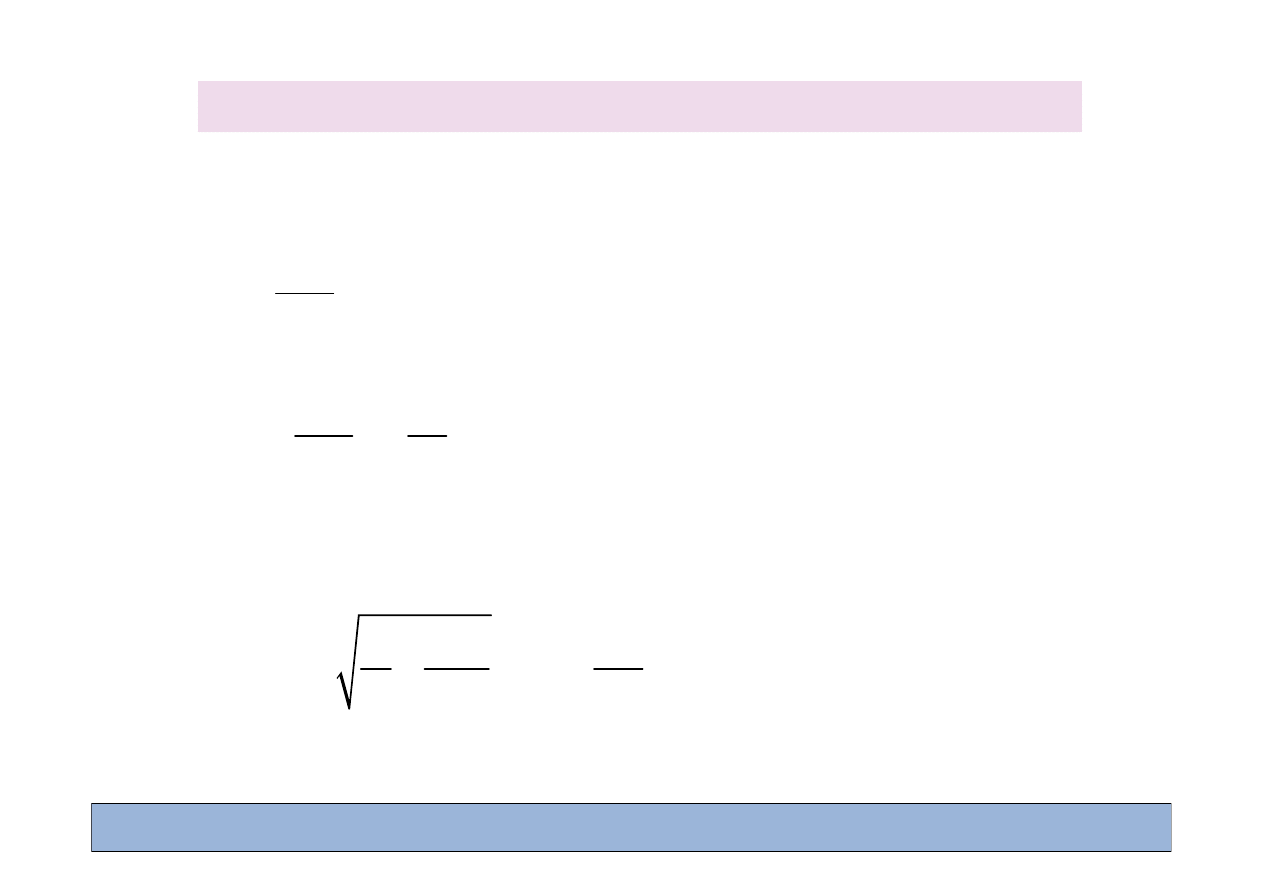
Rozwi
ą
zanie:
(
)
2
2
( )
cos
,
2
4
t
m
x t
x e
t
k
b
b
m
m
m
λ
ω φ
ω
λ
−
=
+
=
−
=
Wykład 6
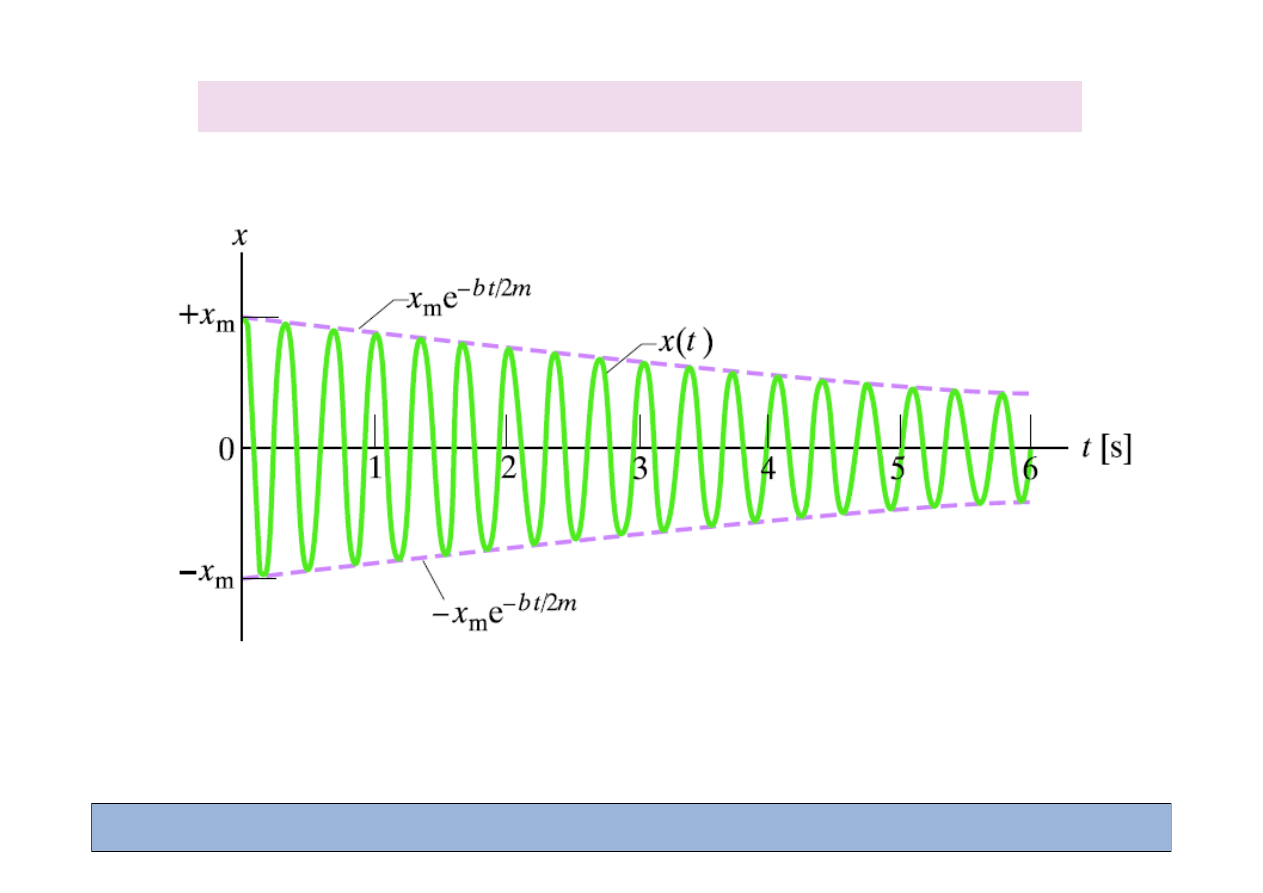
Rozwi
ą
zanie równa
ń
ruchu (ruch tłumiony)

Wykład 6

Wykład 6
Wykład 6
Wykład 6
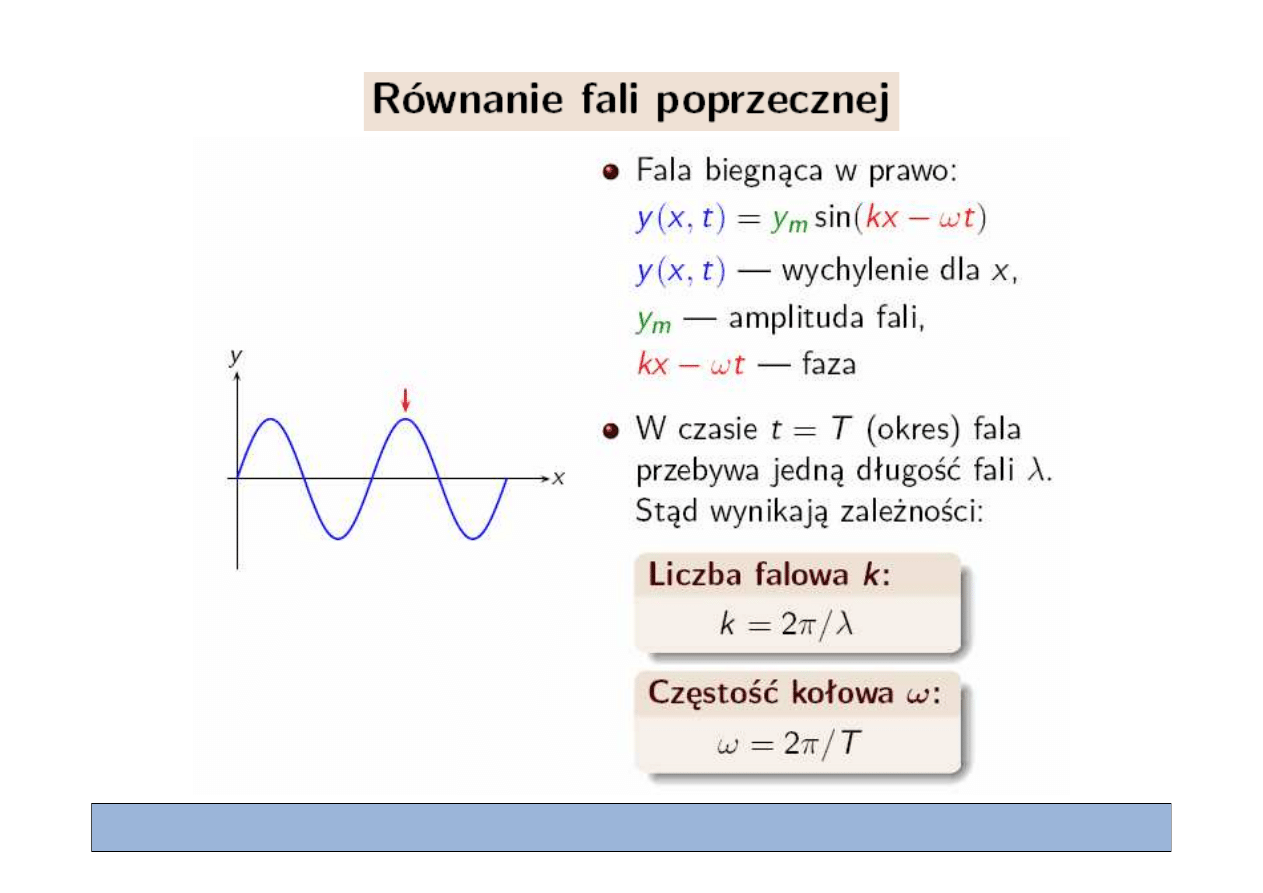
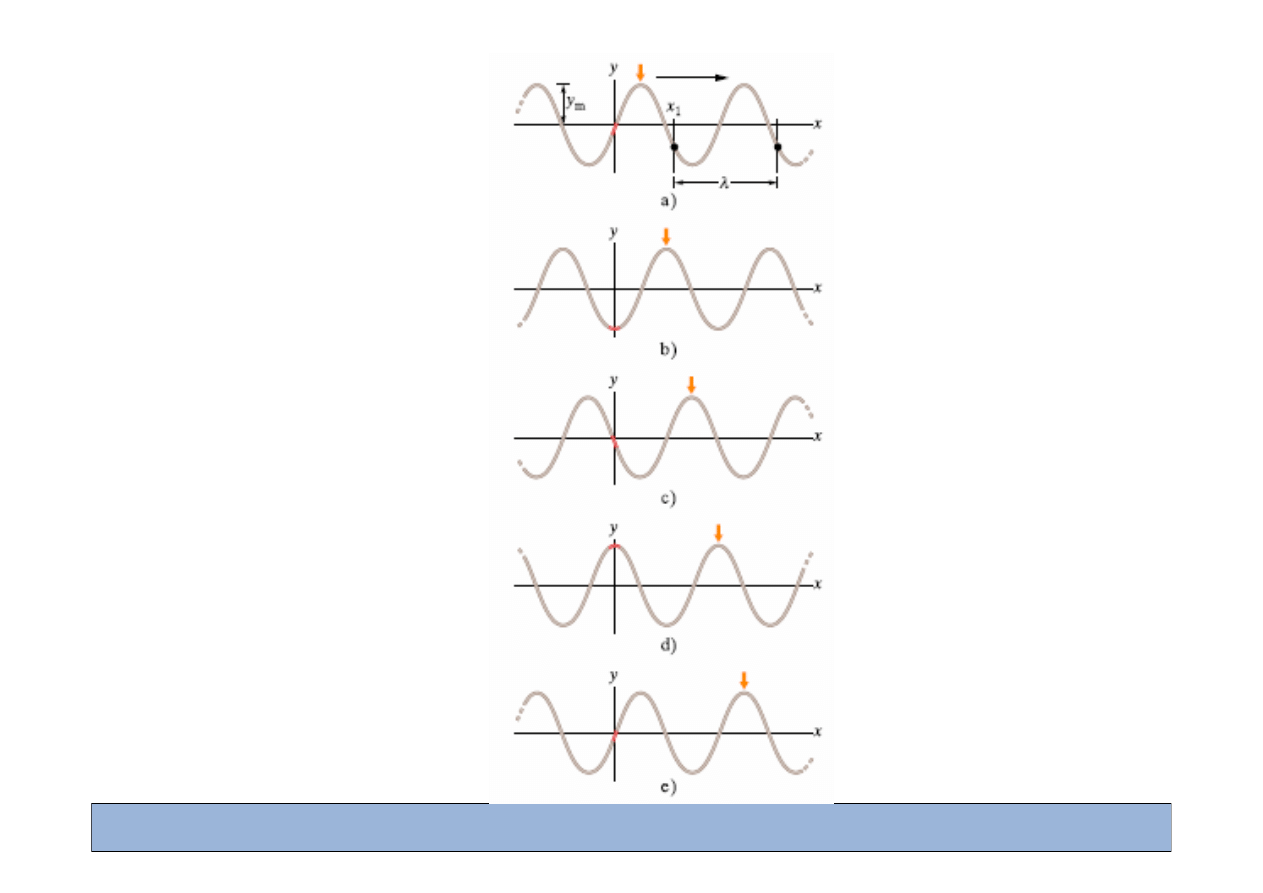
Fala biegn
ą
nca

Wykład 6
Wykład 6
Wykład 6
Wykład 6
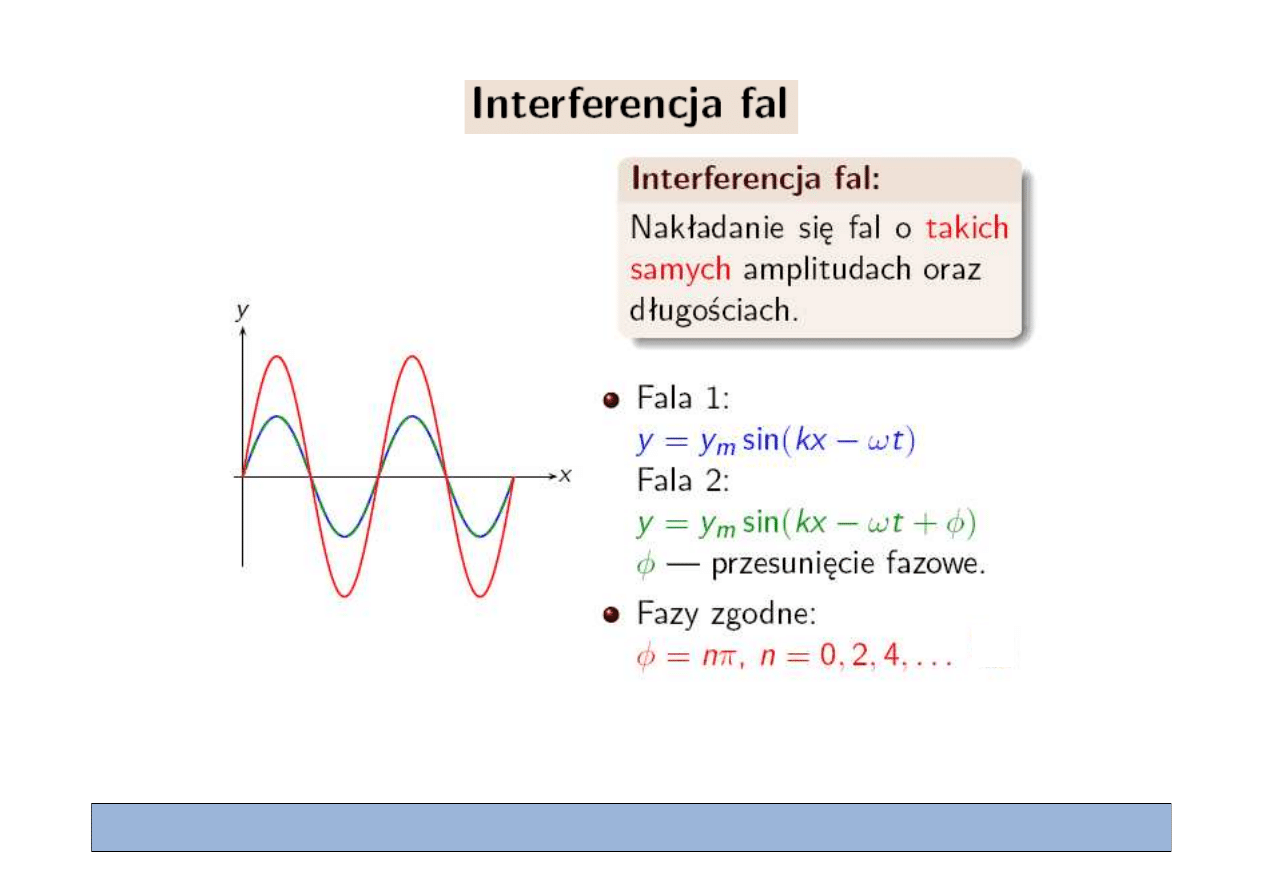
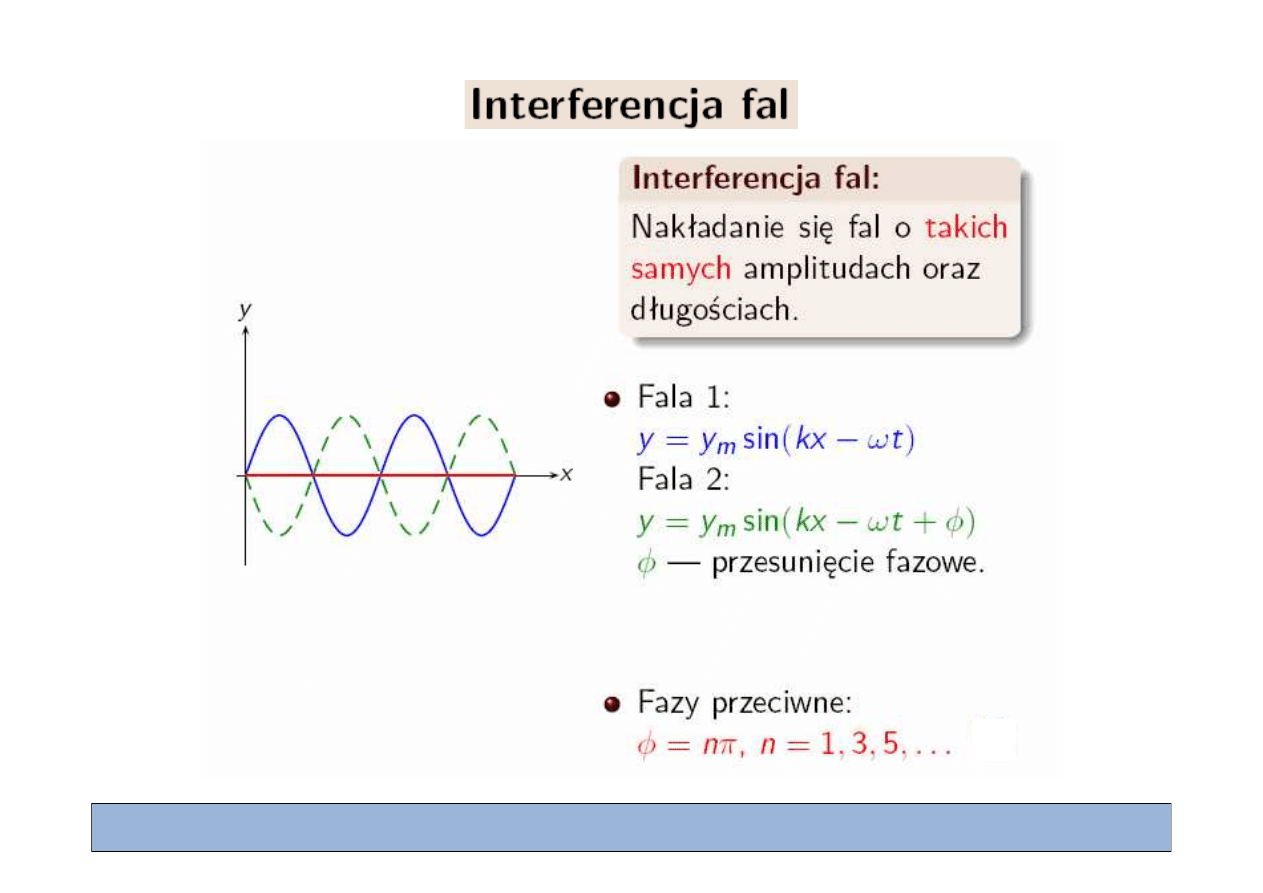
Superpozycja fal
1
2
( , )
( , )
( , )
y x t
y x t
y x t
′
=
+
1
( , )
sin(
)
m
y x t
y
kx
t
ω
=
−
2
( , )
sin(
)
m
y x t
y
kx
t
ω φ
=
−
+
(
)
(
)
( , )
sin
sin
m
m
y x t
y
kx
t
y
kx
t
ω
ω φ
′
=
−
+
−
+
sin
sin
2sin
cos
2
2
α β
α β
α
β
+
−
+
=
( ,
2
cos
sin
2
2
m
y x t
y
kx
t
φ
φ
ω
′
=
−
+
Wykład 6
Fale stoj
ą
ce
1
2
( , )
( , )
( , )
y x t
y x t
y x t
′
=
+
1
( , )
sin(
)
m
y x t
y
kx
t
ω
=
−
2
( , )
sin(
)
m
y x t
y
kx
t
ω
=
+
( , )
sin(
)
sin(
)
m
m
y x t
y
kx
t
y
kx
t
ω
ω
′
=
−
+
+
( , )
2
cos
sin
m
y x t
y
t
kx
ω
′
=

Wykład 6
Wykład 6
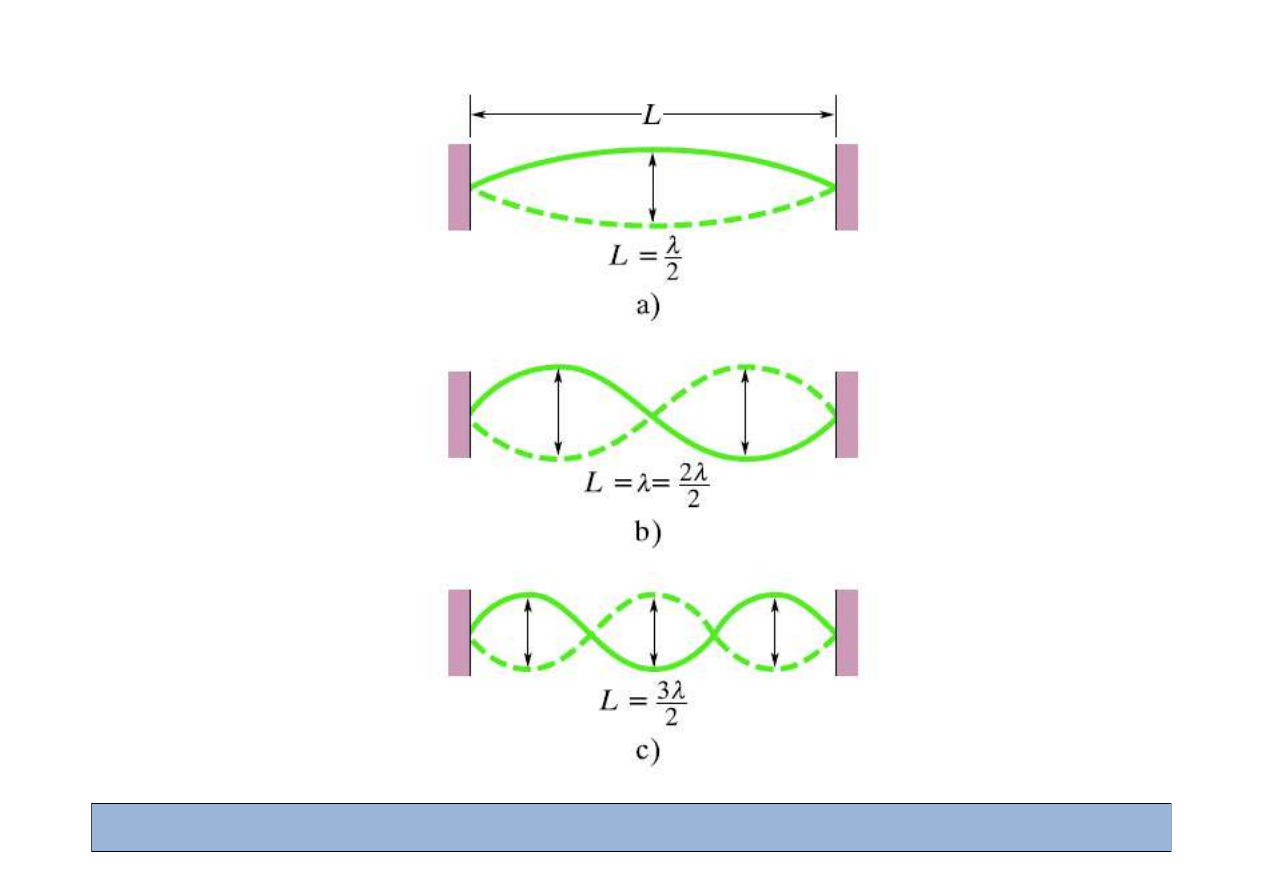
Fala stoj
ą
ca
Wykład 6
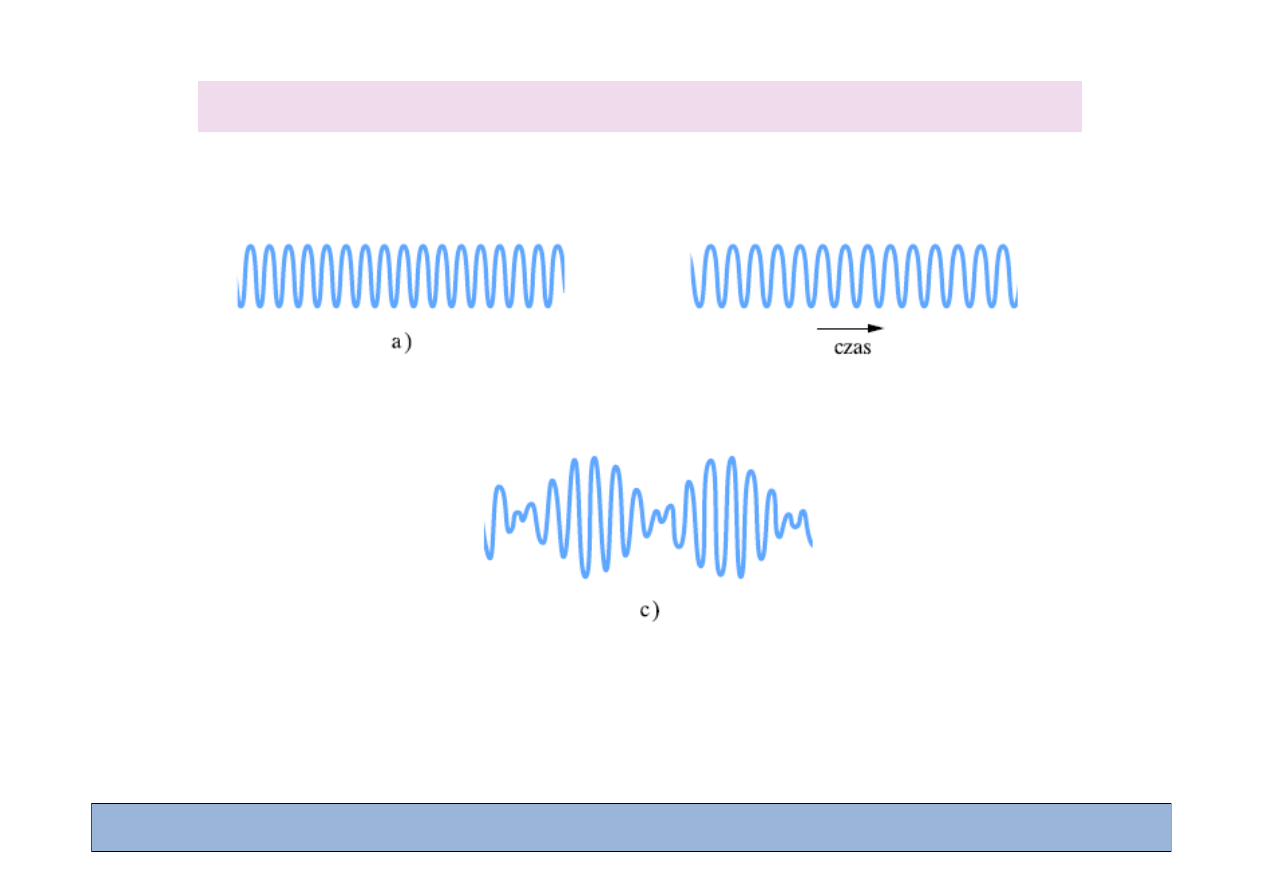
Dudnienia
1
1
( )
cos
m
s t
s
t
ω
=
(
)
1
2
1
2
( )
( )
( )
cos
cos
m
s t
s t
s t
s
t
t
ω
ω
=
+
=
+
cos
cos
2 cos
cos
2
2
α β
α β
α
β
−
+
+
=
(
)
(
)
1
2
1
2
( )
2
cos
cos
2
2
m
t
t
s t
s
ω ω
ω ω
−
+
=
2
2
( )
cos
m
s t
s
t
ω
=
Wykład 6
Dudnienia

Wykład 6
Wykład 6
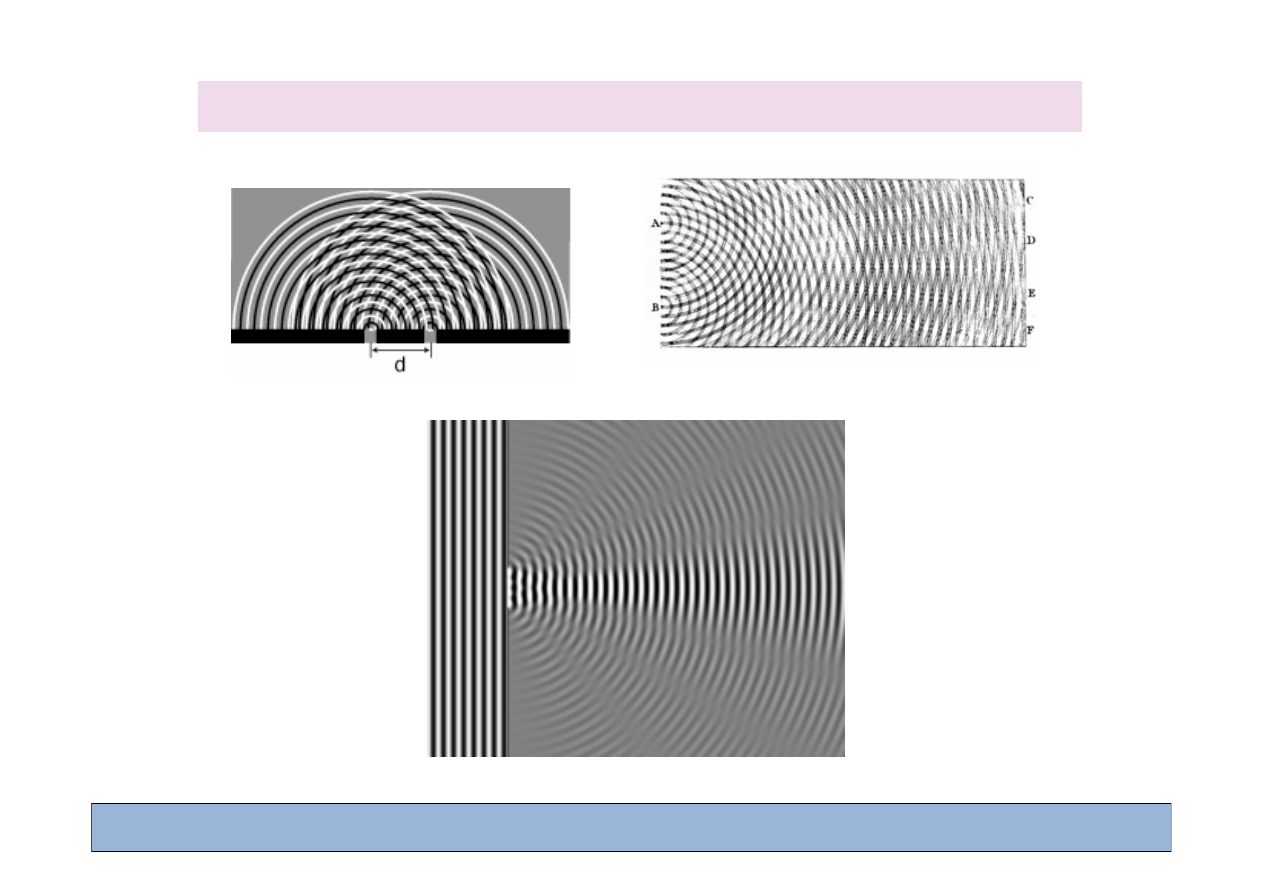
Dyfrakcja i interferencja

Wykład 6
Dyfrakcja i interferencja
Wykład 6
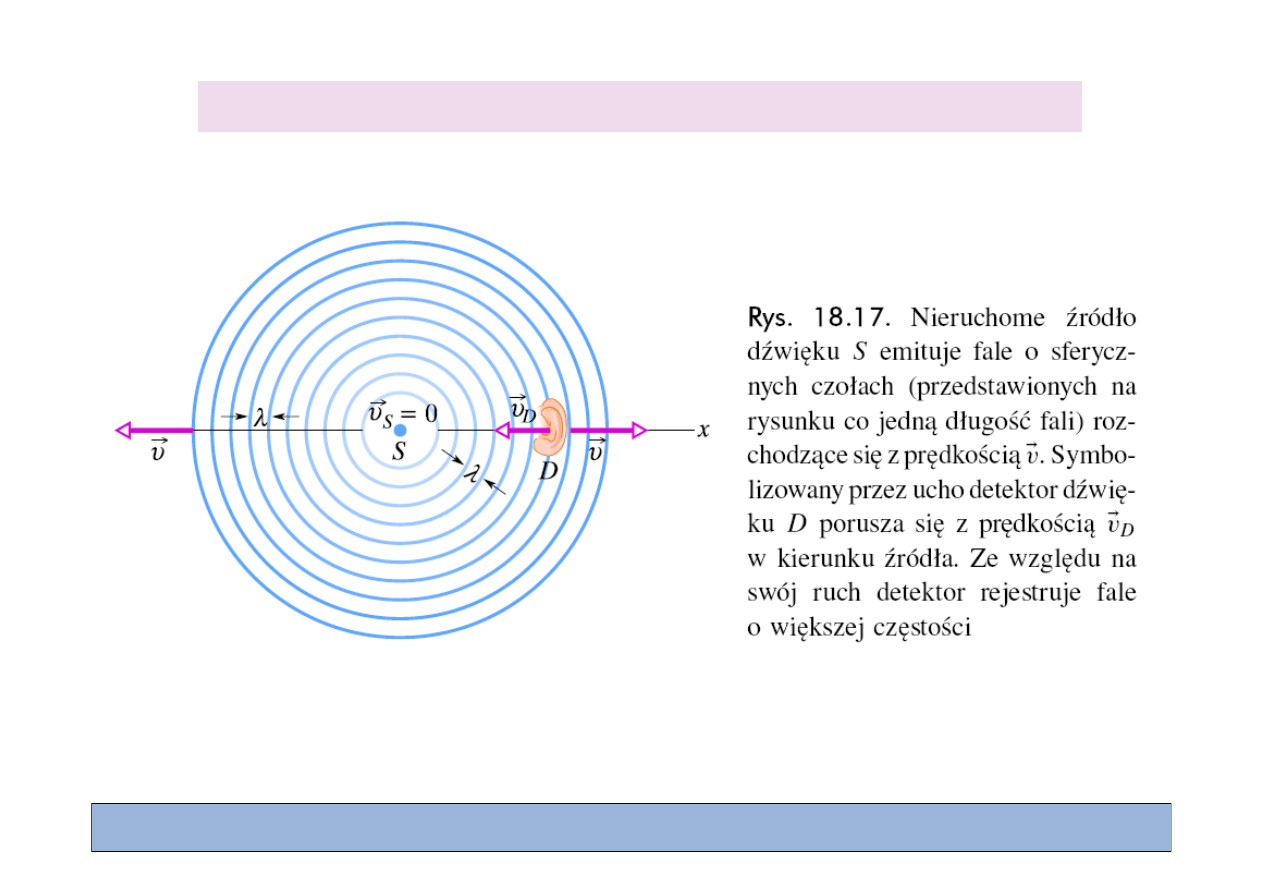
Zjawisko Dopplera
Wykład 6
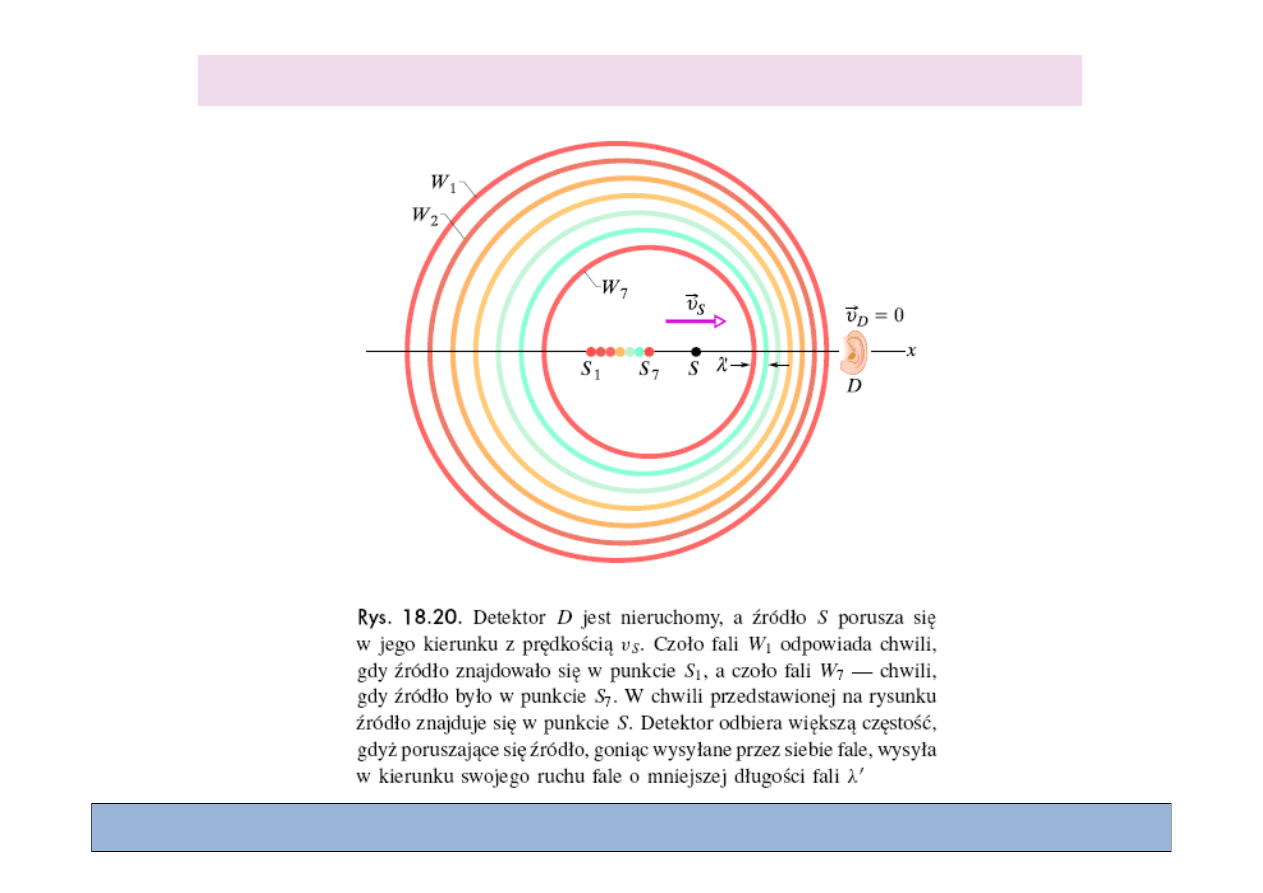
Zjawisko Dopplera
Wyszukiwarka
Podobne podstrony:
CJ Lecture 10
CJ Lecture 5
CJ Lecture 4
CJ Lecture 3
CJ Lecture 1
CJ Lecture 8
CJ Lecture 7
CJ Lecture 2
CJ Lecture 10
CJ Lecture 5
CJ Lecture 4
IR Lecture1
więcej podobnych podstron