
Instytut Radioelektroniki
Materiały do wykładu
ANTENY
I
PROPAGACJA FAL
Parametry anten
dr inż. Jacek Jarkowski
(Na prawach rękopisu)
Marzec 2003r.
Parametry anten.
Jacek Jarkowski
1
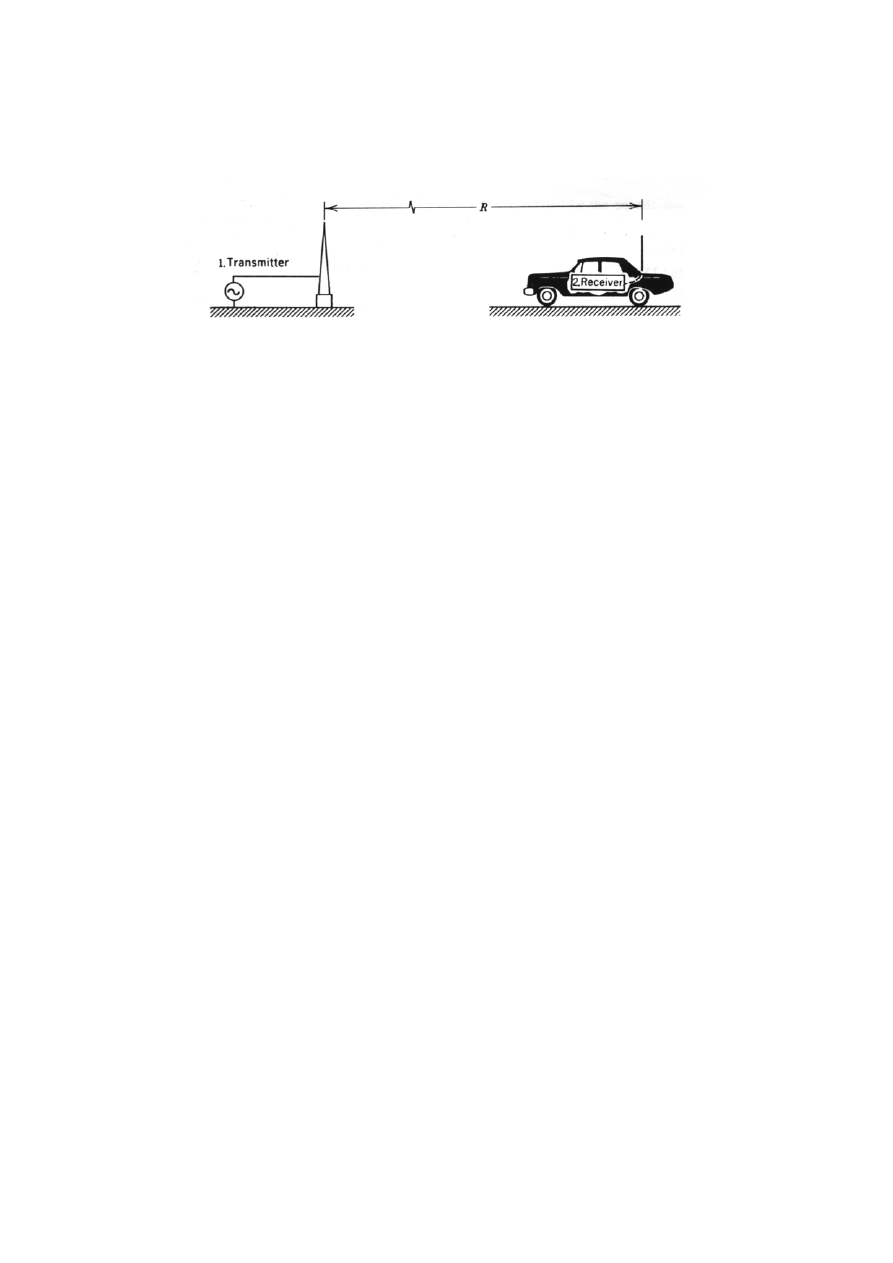
1. Wprowadzenie
1.
Dla generatora antena nadawcza jest obciążeniem
charakteryzującym się impedancją lub admitancją wejściową. Dla
optymalnej transmisji energii konieczne jest dopasowanie na każdym styku.
2. Ilość energii odebranej przez antenę z nadajnika jest w większości
wypromieniowana. Część jest wydzielona w postaci ciepła jako energia strat.
3. Antena nadawcza nie promieniuje jednakowo we wszystkich
kierunkach. Znajomość charakterystyki promieniowania anteny nadawczej
pozwala na znalezienie wektora gęstości mocy (wektora Poyntinga) w
miejscu odbioru.
4. Dla odbiornika antena odbiorcza objawia się źródłem napięciowym
(lub prądowym), którego siła elektromotoryczna jest określona przez wektor
natężenia pola elektrycznego fali padającej oraz przez parametr anteny
zwany długością skuteczną anteny. Moc odebrana przez antenę i wydzielona
w obciążeniu anteny mogą być określone za pomocą parametrów
odpowiednio: powierzchni czynnej i skuteczne anteny.
5. Droga fali em. z anteny nadawczej do odbiorczej nie musi być
bezpośrednia lecz może wynikać z odbicia od powierzchni ziemi,
wielodrogowości w jonosferze, albo tak jak to ma miejsce w systemach
radarowych od kształtu obiektów (celów) odbijających
6. Moc doprowadzona do odbiornika zależna jest od tłumienia w
ośrodku rozchodzenia się fali, jak również od własności polaryzacyjnych
anten i ośrodka.
7. Wyżej wymienione parametry zależą od częstotliwości co w
konsekwencji prowadzi do faktu, że anteny charakteryzują się szerokością
pasma.
Parametry anten.
Jacek Jarkowski
2
2. Podstawowe zasady antenowe.
2.1. Zasada
Huyhensa.
Podczas propagacji fali elektromagnetycznej (i nie tylko) każdy punkt
przestrzeni, do którego dotrze fala, staje się źródłem nowej fali kulistej.
2.2. Zasada
ekwiwalentności.
Każdą strukturę antenową wywołującą znany rozkład pola elektrycznego K i
pola magnetycznego H można zamienić powierzchnią zamkniętą, otaczającą tą
strukturę , na powierzchni której możemy określić zastępczy rozkład prądów
powierzchniowych:
s
s
i
n H
m
E
= ×
= × n
r
r
r
r
r
r
Powierzchnia ta zastępuje strukturę antenową poddawaną analizie. Prądy na
powierzchni odpowiednio dobranej wyznacza się poprzez przeprowadzenie
pomiarów. Dalszą analizę anteny przeprowadza się w oparciu o rozkład prądów
zastępczych. W ten sposób również wprowadza się hipotetyczne prądy
magnetyczne.
2.3. Zasada
superpozycji.
2.4. Zasada
wzajemności.
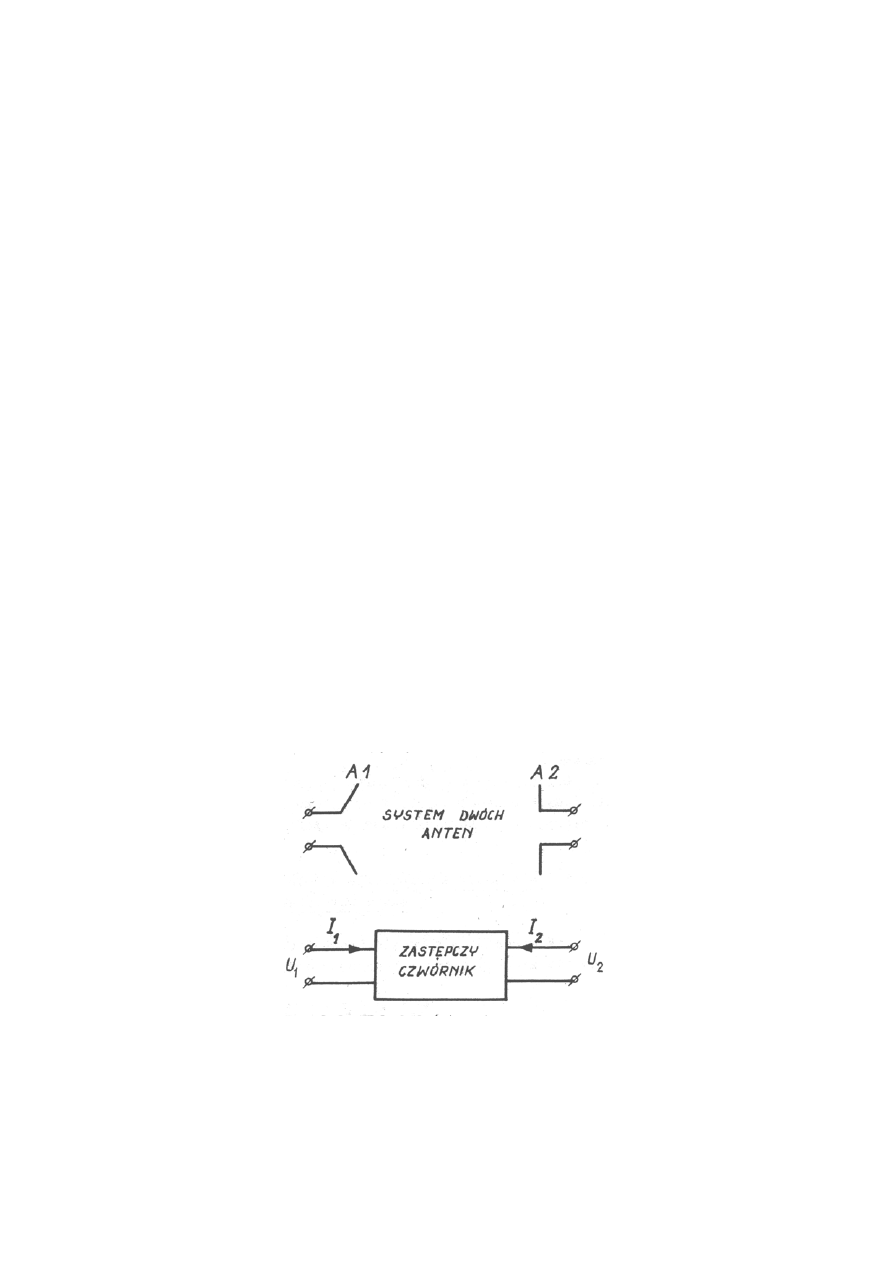
Anteny nadawczą i odbiorczą i ośrodek pomiędzy nimi możemy czwórnik
liniowy i bierny.
Czwórnik taki możemy opisać w znany sposób odpowiednimi macierzami.
Własności czwórnika nie zależą od tego, które zaciski uznamy za wejściowe, a
które za wyjściowe. Antenę nadawczą możemy traktować jako odbiorczą i
odwrotnie. Takie podejście jest niezmiernie użyteczne podczas projektowania i
pomiarów anten.
Parametry anten.
Jacek Jarkowski
3
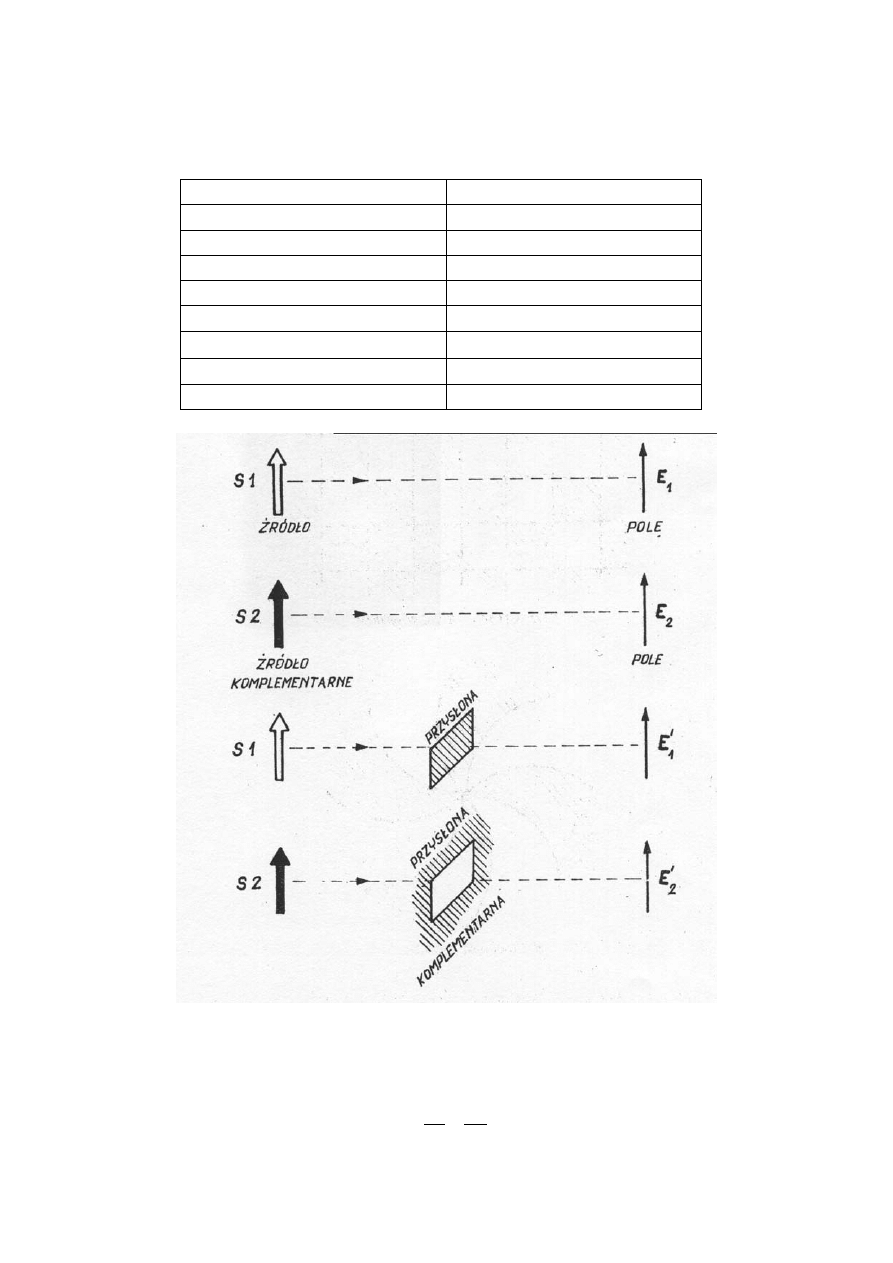
2.5. Zasada
Babineta.
Zasada ta dotyczy struktur komplementarnych (dualnych), czyli wzajemnie się
uzupełniających się.
System elektryczny
System magnetyczny
ρ
ρ
m
i
v
, i
s
I
m
v
, m
s
M
K
e
H
m
H
e
-K
m
µ
ε
ε
µ
δ
e
δ
m
Z, Y
Y, Z
Rys. 2.1 Ilustracja zasady Babineta.
Dla układu przedstawionego na rys. 2.1 obowiązuje zależność według
zasady Babineta.
1
2
2
1
1
=
′
+
′
E
E
E
E
Parametry anten.
Jacek Jarkowski
4
3. Propagacja w wolnej przestrzeni.
2
4 d
P
S
N
π
=
S- gęstość mocy w
1Wm
-2
P
N
- moc w
1W
d- odległość w
m
Albo w postaci logarytmicznej,
d
P
S
N
log
20
41
−
+
−
=
gdzie wielkości podawana są w decybelach;
S- gęstość mocy w stosunku do
1Wm
-2
P
N
- moc w stosunku do
1kW
d- odległość w
km
Natężenie pola elektrycznego fali promieniowanej izotropowo jest dane przez:
d
P
S
E
N
30
120
=
=
π
Natomiast w jednostkach praktycznych kW, km, mV/m itp.
km
kW
k
m
mV
d
P
G
E
173
=
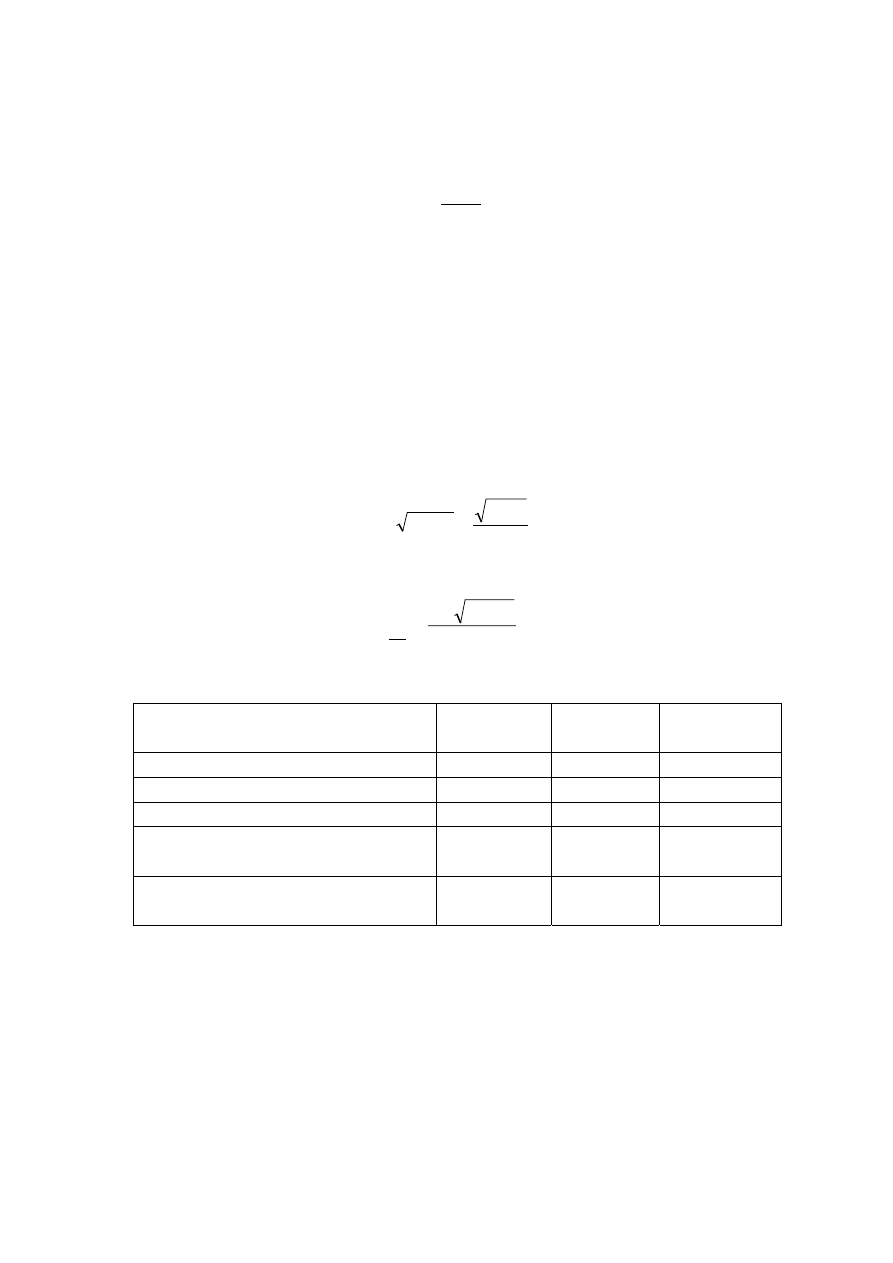
Tabela 3.1 Objaśnienia do wzoru
Rodzaj anteny
G
k
G
k
(dB)
Siła em.
(1kW) [V]
Antena izotropowa
1
0
173
Dipol Hertza w wolnej przestrzeni
1,5
1,75
212
Dipol półfalowy 1,65
2,15
222
Dipol Hertza pionowy nad ziemią.
doskonale przewodzącą
3 4,8 300
Antena pionowa ćwierćfalowa nad
ziemią doskonale przewodzącą
3,3 5,2 314
4. Podstawowe
własności i parametry anten.
4.1 Pojęcia podstawowe.
4.1.1. Wektor Poyntinga.
Antena promieniując moc P
N
wytwarza wokół siebie w tzw. strefie dalekiej pole
wektorowe gęstości mocy charakteryzowane wektorem Poyntinga S.
Zespolony wektor Poyntinga jest opisany wzorem
r
r
r
H
E
S
×
=
a jego część rzeczywista
Parametry anten.
Jacek Jarkowski
5

( )
S
S
r
Re
2
1
=
reprezentuje uśrednioną w czasie powierzchniową gęstość mocy.
Dla anteny izotropowej moduł wektora Poyntinga można obliczyć ze wzoru:
2
4 d
P
S
N
π
=
[W/m
2
]
4.1.2. Intensywność promieniowania
Wektor Poyntinga określa gęstość powierzchniową mocy w odległości d od
anteny, natomiast aby określić intensywność promieniowania anteny stosuje się
wielkość określająca moc promieniowana w jednostkowym kącie bryłowym. Ta
wielkość określona jest wzorem:
π
4
N
P
U
=
[W/sr]
nietrudno zauważyć, że
2
d
S
=
U
.
4.1.3. Strumień wektora pola.
Jeżeli w polu wektorowym umieścimy ramkę o powierzchni A, to strumień
wektora pola określa moc przepływającą przez tą powierzchnię.
r
r
ϕ
cos
A
S
A
S
P
str
=
•
=
5. Podstawowe parametry anten.
5.1. Charakterystyka
promieniowania.
Definicja. Charakterystyka promieniowania jest to figura geometryczna opisana
końcem wektora, którego początek umieszczony jest w początku biegunowego
układu współrzędnych, a jego długość jest proporcjonalna do intensywności
promieniowania anteny w jego zwrocie.
Rys. 5.1. Przykład charakterystyki promieniowania anteny.
Jednostką charakterystyki promieniowania tak zdefiniowanej jest W/sr. Przykład
charakterystyki promieniowania przedstawiony jest na Rys. 1.
Parametry anten.
Jacek Jarkowski
6
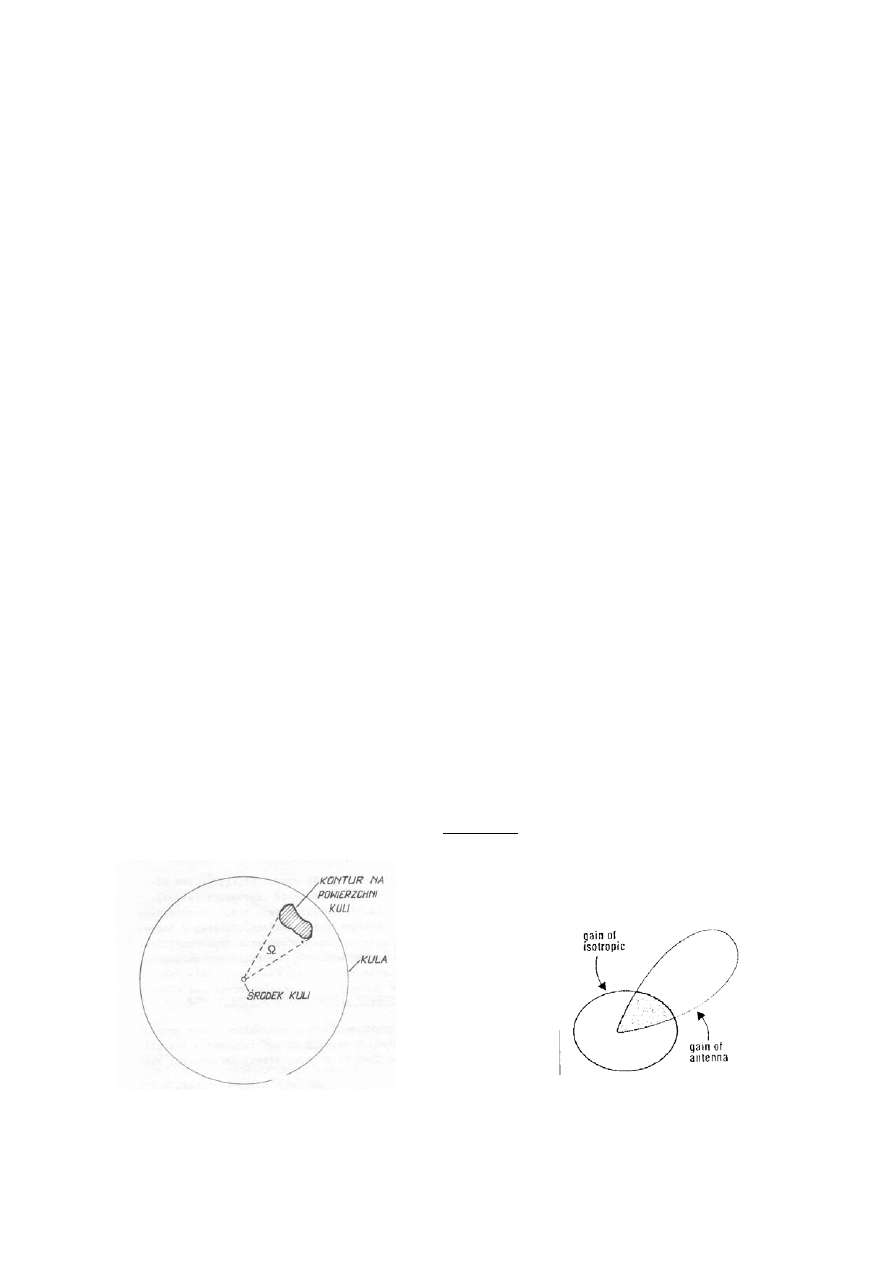
Całka charakterystyki promieniowania w układzie bezstratnym, po pełnym kącie
bryłowym jest równa mocy wypromieniowanej przez antenę.
W praktyce często stosuje się charakterystyki promieniowania znormowane do
jej wartości maksymalnej, wtedy gdy istotne jest przedstawienie własności
kierunkowych anteny a nie jej stanu elektrycznego.
Alternatywnie stosuje się charakterystyki promieniowania określające natężenie
pola elektrycznego w funkcji kierunku i odległości.
5.2.
Charakterystyka kierunkowa fazowa określa różnicę faz fali
promieniowanej w danym kierunku i fali promieniowanej w kierunku
odniesienia. Charakterystyka kierunkowa polaryzacyjna określa zależność od
kierunku polaryzacji fali promieniowanej.
Charakterystyka kierunkowa anteny odbiorczej dotyczy fali płaskiej padającej
na antenę i dopasowanej polaryzacyjnie (patrz: polaryzacja anteny).
Charakterystyka ta jest zależnością mocy dysponowalnej na obciążaniu anteny
vi zależności od kierunku padania fali płaskiej. Na podstawie zasady wzajemno-
ści można wykazać, że charakterystyki kierunkowe (nadawca i • odbiorcza tej
samej anteny) są jednakowe.
W praktyce diagramy kierunkowości są przedstawiane nie tylko we
współrzędnych sferycznych, a na inne sposoby, np. we współrzędnych
prostokątnych, gdzie na osi odciętych odkłada się kąt (
ϕ lub
θ
, a na osi
rzędnych w skali logarytmicznej wartość E lub S
5.2. Zysk
kierunkowy.
Definicja:
Zysk kierunkowy jest to stosunek maksymalnej intensywności
promieniowania danej anteny do maksymalnej intensywności
promieniowania anteny odniesienia.
( )
( )
max
max
,
,
−
=
odn
U
U
G
φ
θ
φ
θ
Rys. 5.1. Ilustracje definicji zysku kierunkowego
Parametry anten.
Jacek Jarkowski
7
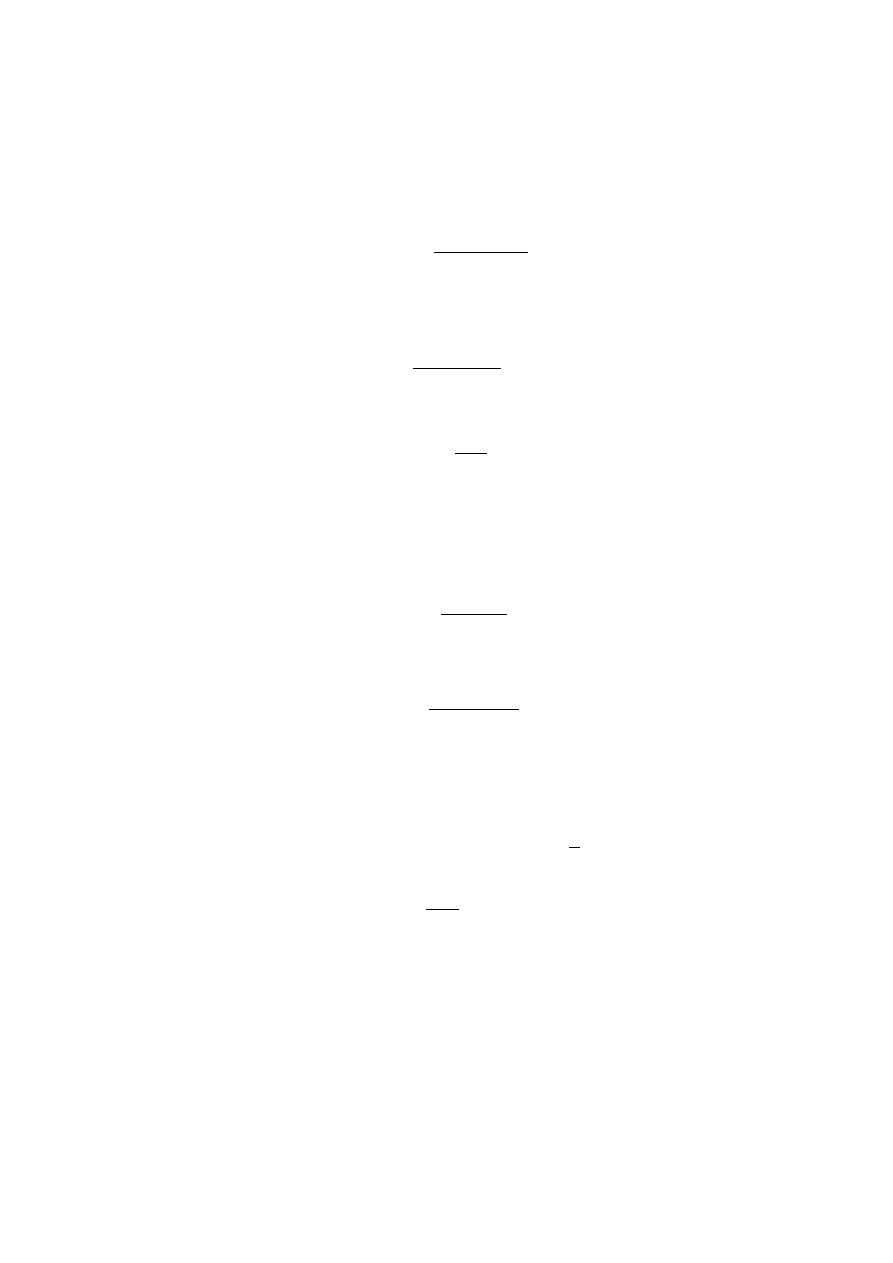
Najczęściej anteną odniesienia jest antena izotropowa i wtedy maksymalna
intensywności promieniowania anteny odniesienia jest równa mocy średniej
anteny w kącie bryłowym.
( )
( )
( )
∫∫
Ω
=
π
φ
θ
φ
θ
π
φ
θ
4
max
,
,
4
,
d
U
U
G
Wprowadzając pojęcie zastępczego kąta bryłowego B
( )
(
)
Ω
=
∫
d
U
U
B
π
φ
θ
φ
θ
4
0
0
max
,
,
otrzymujemy:
4
k
G
B
π
=
Interpretacją zastępczego kąta bryłowego jest kąt, w którym antena promieniuje
równomiernie ze swoją intensywnością maksymalną.
Dla regularnych charakterystyk promieniowania:
φ
θ
π
∆
∆
=
4
k
G
albo w stopniach
0
0
41253
φ
θ
∆
∆
=
k
G
Przykład
Zysk kierunkowy dipola elementarnego.
( )
( )
∫∫
∫
=
=
Ω
=
π π
π
π
φ
θ
θ
θ
2
0 0
3
4
2
3
8
sin
sin
d
d
d
B
5
,
1
4 =
=
B
G
π
5.3. Zysk
energetyczny:
Dla anten stratnych definiuje się zysk energetyczny G
e
. jako:
k
e
G
G
η
=
Paradoks anten superkierunkowych
5.4. Powierzchnia czynna anteny (powierzchnia skuteczna)
Parametry anten.
Jacek Jarkowski
8
Dla określenia własności odbiorczych anten definiuje się tzw. powierzchnię
czynną anteny.
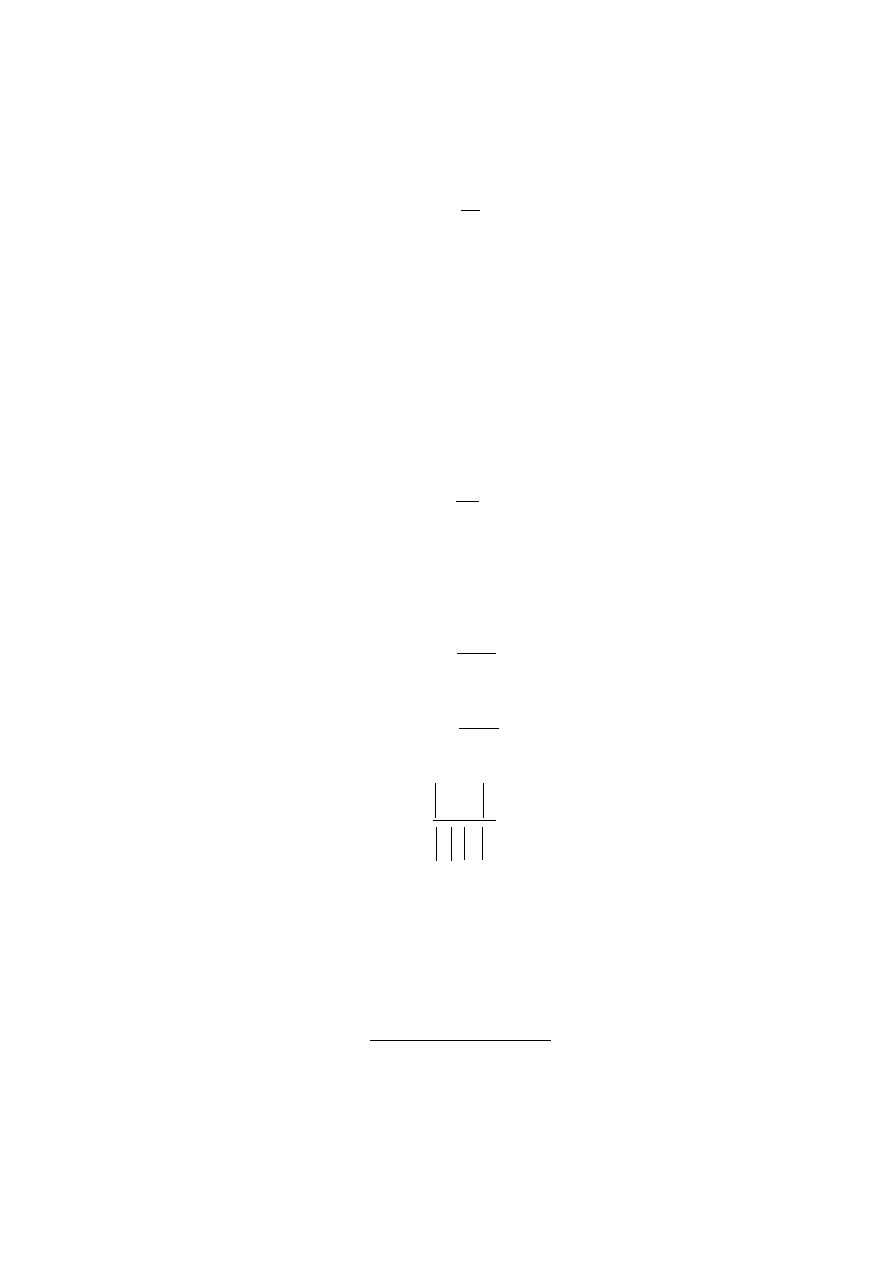
Wielkość tę definiuje się wzorem:
S
A
c
=
P
α
=
•
=
W postaci wektorowej wzór powyższy przybiera postać:
r
r
cos
S
A
S
A
P
c
c
Powyższe wzory pozwalają na wyznaczenie mocy odebranej przez antenę, a w
przypadku anteny bezstratnej moc tę można uważać za dostarczona do
obciążenia.
Jednak w przypadku anteny ze stratami moc użyteczna jest pomniejszona o
moc strat.
str
uż
P
P
P
−
=
Dla takiego przypadku stosujemy pojęcie powierzchni skutecznej.
S
A
sk
=
c
sk
A
A
P
uż
η
=
Łatwo zauważyć, że
gdzie
η
jest sprawnością anteny.
Jeśli antena wykazuje własności kierunkowe, to w kierunku wartościi
maksymalnej charakterystyki promieniowania obowiązuje zależność:
π
4
k
c
pq
A
=
λ
2
G
oraz
π
4
p
sk
pq
A
=
λ
2
G
gdzie p jest współczynnikiem dopasowania polaryzacyjnego
2
2
E
h
E
h
p
r
r
•
=
2
r
r
w którym jest wysokością skuteczną anteny, określającą związek pola
elektrycznego z siłą elektromotoryczną e zaindukowaną w antenie w obecności
pola elektromagnetycznego E.
h
v
α
cos
E
h
E
h
e
=
•
=
sk
sk
r
r
q jest natomiast jest współczynnikiem dopasowania energetycznego wyrażonego
wzorem:
(
) (
)
2
2
L
A
L
A
X
X
R
R
q
+
+
+
=
4
L
A
R
R
jX
R
Z
+
=
gdzie:
jest impedancją obciążenia anteny,
L
L
L
A
A
A
jX
R
Z
+
=
jest impedancja wewnętrzna anteny.
Parametry anten.
Jacek Jarkowski
9

5.5. Impedancja wejściowa anteny.
Impedancję wejściową anteny definiuje się analogicznie jak dwójnika. Dla linii
transmisyjnej TEM wielkość impedancji definiuje się jako stosunek wartości
zespolonej napięci do prądu na zaciskach anteny.
we
we
we
I
Z
ˆ
ˆ
=
Uˆ
W przypadku linii falowodowej, impedancje wejściowa definiujemy dla modu
podstawowego.
5.6. Rezystancja
promieniowania, rezystancja strat i sprawność anteny.
Rezystancję promieniowania anteny definiujemy wzorem
2
pr
pr
R
P
I
=
gdzie
P
pr
jest mocą promieniowaną,
I
prądem zasilania anteny (ewentualnie prądem mierzonym w innym
określonym przewodzie anteny).
Moc promieniowaną P
pr
można wyliczyć ze wzoru
r
r
n
A
pr
[
]
dA
H
E
dA
n
S
P
∫
∫
×
=
×
=
r
r
gdzie
S
jest wektorem Poyntinga reprezentującym gęstość-mocy
przepływającej przez element powierzchni dA (n - wektor normalny).
A
jest
powierzchnią zamkniętą, na której określony jest rozkład
wektora Poyntinga S.
Całka dotyczy powierzchni otaczającej antenę kulistą o dostatecznie dużym
promieniu.
Rezystancję strat anteny definiujemy wzorem
2
str
str
R
P
I
=
gdzie
P
str
jest mocą strat anteny,
Rezystancja strat reprezentuje moc przetworzoną na ciepło w strukturze
anteny i jej najbliższym otoczeniu, np. w uziemieniu anteny masztowej lub w
otaczających antenę przedmiotach stratnych.
Parametry anten.
Jacek Jarkowski
10

Sprawność energetyczna anteny określona jest wzorem
pr
str
pr
str
R
P
P P
R
R
η
=
=
+
+
5.7. Dobroć anteny
Każda antena, oprócz pola promieniowania, wytwarza pole bliskie. Energia
elektromagnetyczna pola bliskiego jest energią reaktywną. Traktując antenę jako
rezonator, można przypisać temu rezonatorowi dobroć zdefiniowaną ilorazem
mocy reaktywnej i mocy wypromieniowanej – czynnej wraz z mocą strat.
5.8. Polaryzacja
anteny.
Polaryzację anteny definiuje się zgodnie z rodzajem polaryzacji fali, jaka
antena emituje. Rozróżnia się polaryzację liniową (pionową, poziomą i
ukośną), kołową (prawoskrętna i lewoskrętną) oraz eliptyczną jako przypadek
ogólny polaryzacji.
Każdą falę o określonej polaryzacji można traktować jako superpozycję fal o
podstawowych rodzajach polaryzacji.
5.9. Inne parametry anten.
Definiuje się szereg innych parametrów anten, do których można zaliczyć:
- szerokość listka głównego
- szerokość pasma,
- poziom listków bocznych,
- współczynnik odbicia na wejściu anteny,
- współczynnik fali stojącej,
- itp.
5.9. Temperatura szumowa anten.
Gęstość mocy dysponowalnej szumu rezystora zrównoważonego cieplnie:
( )
1
−
=
kT
hf
e
hf
f
ρ
gdzie
h=6,623*10
-34
[Joula*s] - stała Plancka
k=1,380*10
-23
[Joula/K] - stała Boltzmana
f – częstotliwość [Hz]
T- temperatura rezystora [K]
dla T=290K i dla f= 140THz
kT
hF
=
więc dla zakresu częstotliwości radiowych można przyjąć
kT
hf
<<
i z tego wynika, że
Parametry anten.
Jacek Jarkowski
11
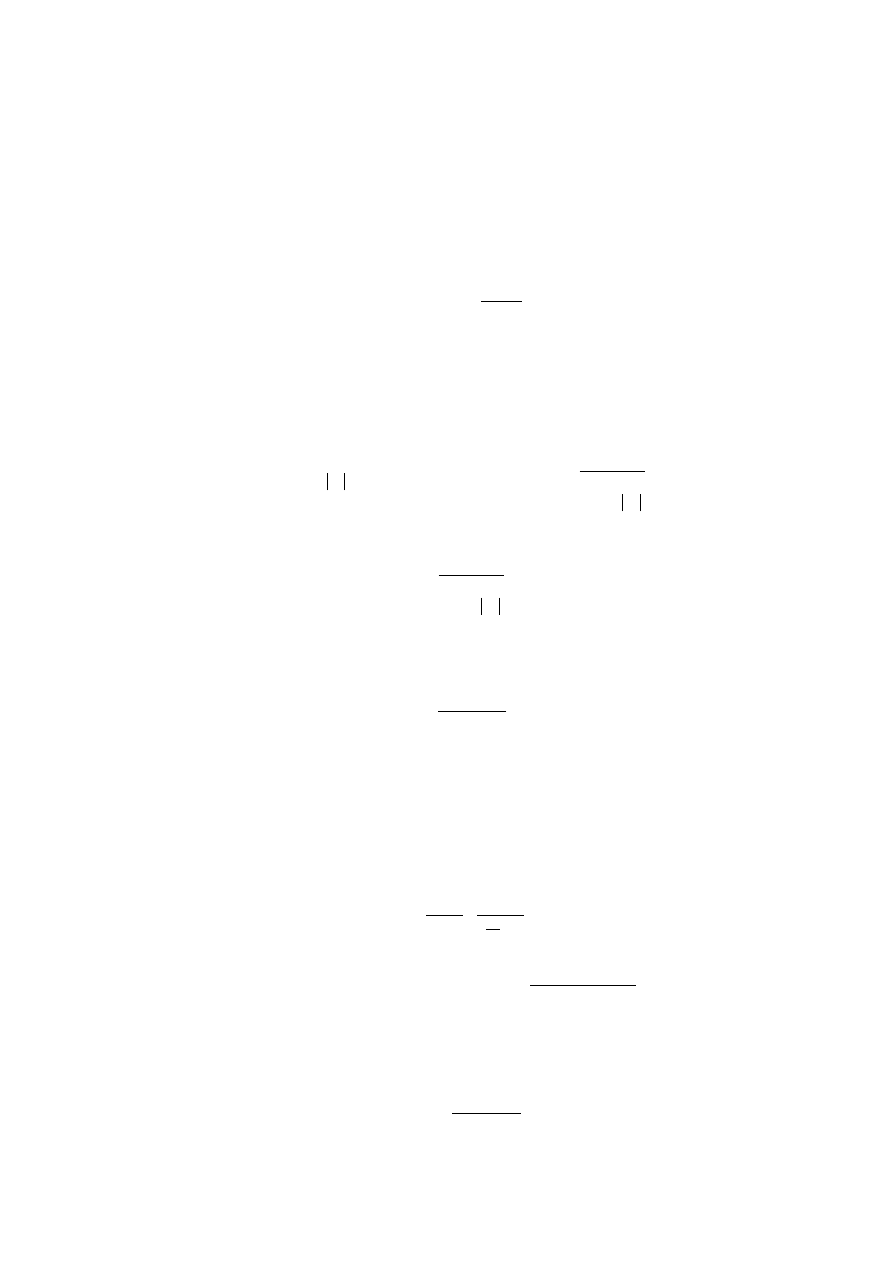
kT
=
ρ
Powyższy wzór służy jako wzór definicyjny zastępczej temperatury szumowej
dwójnika, jeżeli na jego zaciskach występuje gęstość mocy dysponowalnej
( )
f
ρ
W przypadku czwórnika, temperaturę szumową definiujemy w odniesieniu do
wyjścia czwórnika.
( )
k
k
N
f
T
P
SK
Z
=
gdzie N jest gęstością mocy szumów na wyjściu [W/Hz]
k
p
wzmocnienie mocy
Definiuje się również współczynnik szumów F czwórnika
(
1
290
)
−
=
F
T
K
Z SK
gdzie
1
+
=
K
SK
290
Z
T
F
Używamy również pojęcia względnej temperatury szumowej.
K
SK
290
Z
W
T
t
=
Wtedy
1
+
=
W
t
F
Wzór definiujący temperaturę szumową anteny.
( )
k
f
T
A
A
ρ
=
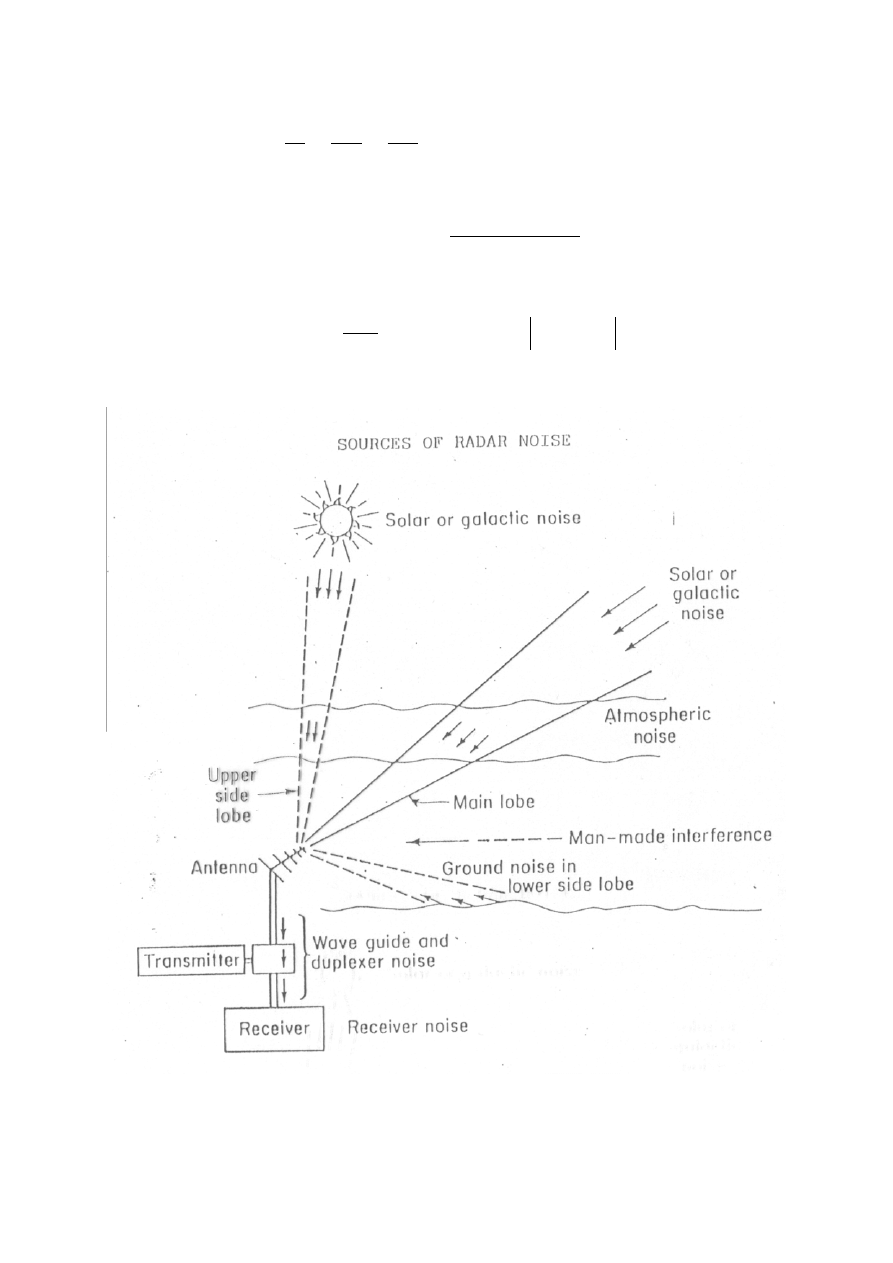
Szumy anteny głównie są odbierane z otoczenia.
W celu określenia promieniowania szumów odbieranych przez antenę
określamy temperaturę szumową nieboskłonu jako powierzchnię ciała
doskonale czarnego.
Gęstość mocy promieniowania przez ciało doskonale czarne określa wzór
Plancka.
( )
3
2
2
1
1
hf
kT
hf
B f
c
e
=
∗
−
gdzie B jest tzw. jaskrawością promieniowania.
Hz
str
m
W
2
gdy
hf
kT
>>
wzór Plancka przyjmuje postać wzoru Rayleigha-Jeansa.
( )
2
2
2
c
T
kf
f
B
=
Parametry anten.
Jacek Jarkowski
12
ponieważ
1
<<
+
+
+
+
=
α
α
α
α
α
dla
.........
!
3
!
2
!
1
1
3
2
e
Zastępcza temperatura nieboskłonu opisana jest wzorem:
(
)
(
)
2
2
2
,
,
,
,
kf
c
f
B
f
T
Z
γ
θ
γ
θ
=
Uśredniona temperatura skuteczna anteny:
( )
(
) (
)
Ω
=
∫∫
d
E
f
T
f
T
A
A
2
4
ŚR
,
,
,
4
1
ψ
θ
ψ
θ
π
π
gdzie
(
)
ψ
θ
,
E
jest względną charakterystyką promieniowania anteny
Rys.5.2 Źródła szumów w systemach odbiorczych
Parametry anten.
Jacek Jarkowski
13
Gęstość mocy padającej na antenę w elementarnym kącie bryłowym i w
elementarnym paśmie częstotliwości:
(
)
(
)
=
Hz
str
W
f
T
k
f
..
........
,
,
4
2
,
,
ψ
θ
π
ψ
θ
σ
Moc szumów odbierana przez antenę
(
)
df
d
f
P
Ω
=
∫∫∫
ψ
θ
σ
,
,
2
1
więc
(
) (
)
df
d
E
f
T
k
P
Ω
=
∫∫∫
2
,
,
,
4
ψ
θ
ψ
θ
π
a w paśmie odbieranym W
(
) (
)
Ω
=
∫∫
d
E
T
kW
P
2
,
,
4
ψ
θ
ψ
θ
π
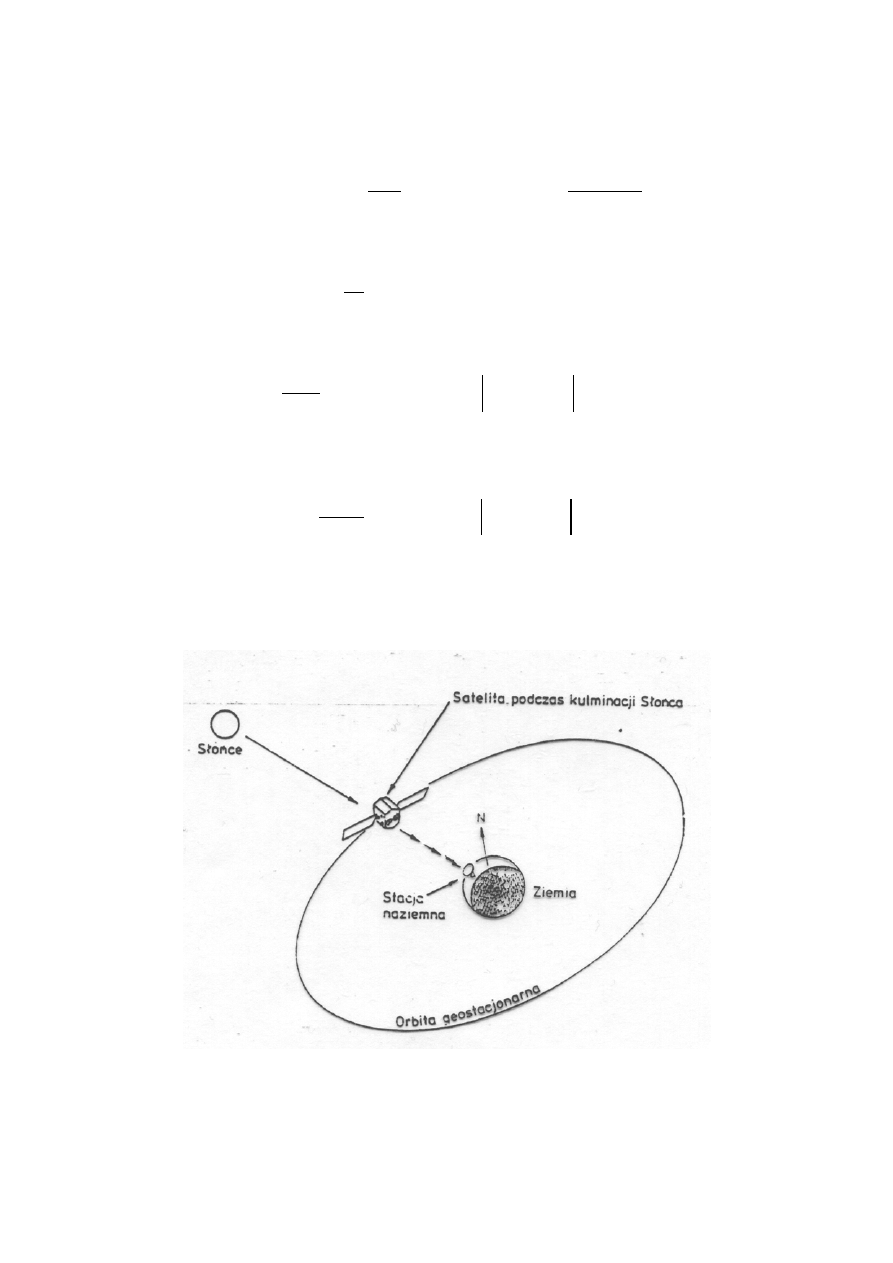
Rys.5.3 Efekt oślepiania anteny naziemnej przez słońce.
Parametry anten.
Jacek Jarkowski
14
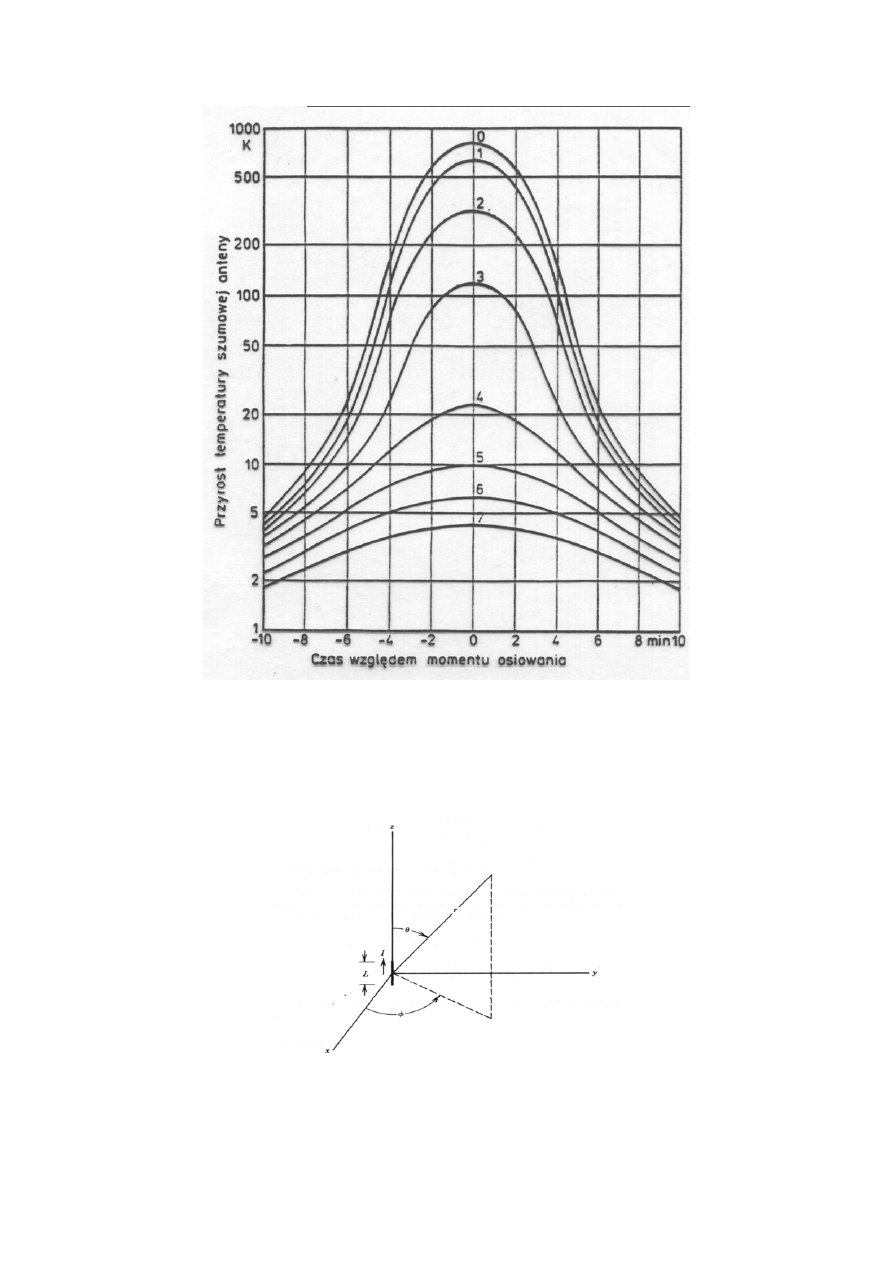
Rys.5.4 Przyrost temperatury szumów w zależności od położenia słońca
względem anteny odbiorczej.
6. Anteny elementarne.
6.1. Dipol
elementarny
Rys. 6.1. Dipol elementarny o długości L z prądem I umieszczony w układzie współrzędnych
prostokątnych.
Parametry anten.
Jacek Jarkowski
15
Dipol elementarny jest strukturą liniową, bardzo krótką z równomiernym rozkładem prądu.
W strefie dalekiej rozkład pola ma dwie składowe elektryczną i magnetyczną:
sin
4
j r
IL e
E
j
r
β
θ
ωµ
θ
π
−
=
r
sin
4
j r
IL e
H
j
r
β
φ
β
φ
π
−
=
r
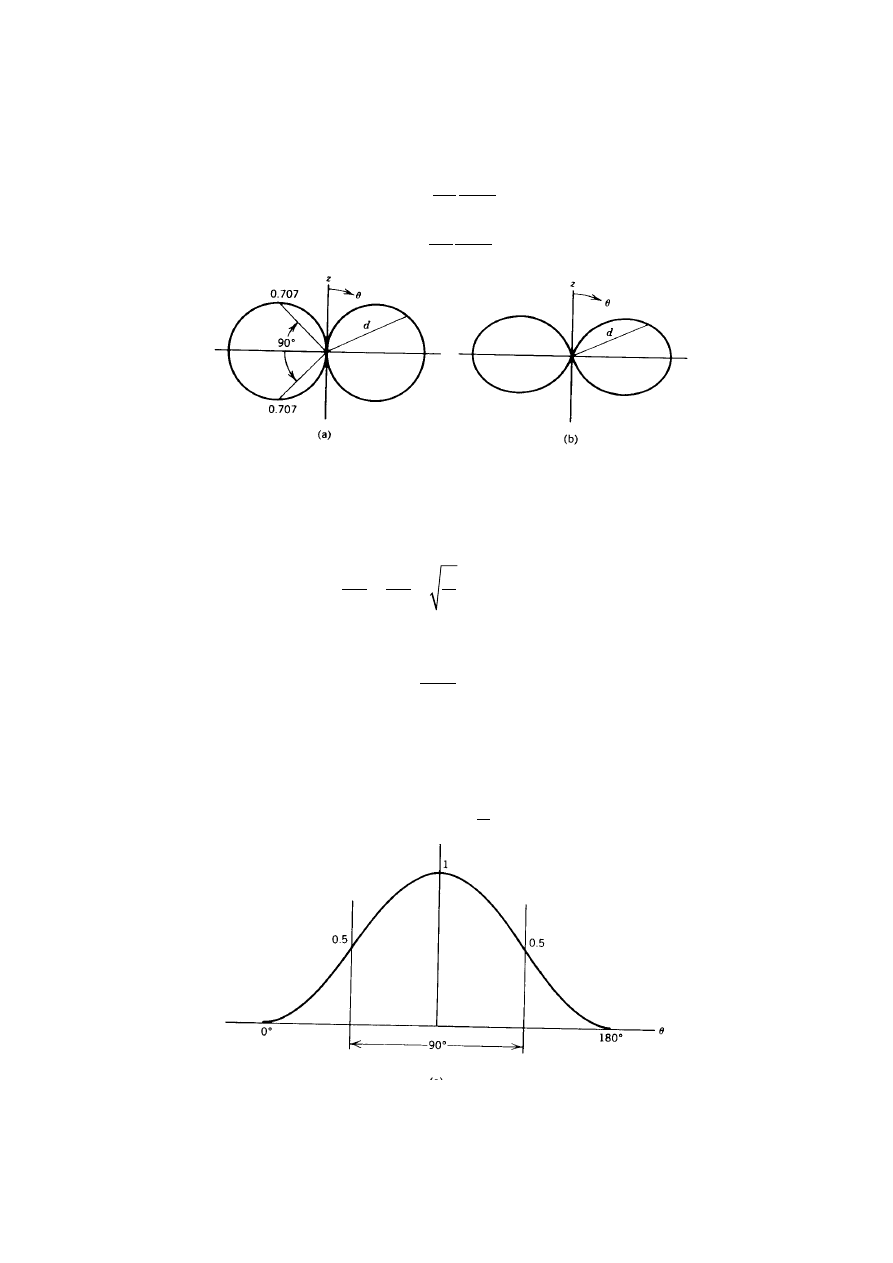
Rys. 6.2 Charakterystyki promieniowania dipola elementarnego
a) charakterystyka napięciowa (sin
θ),
b) charakterystyka energetyczna (sin
2
θ)
Należy pamiętać o zależności:
[ ]
120
E
H
θ
φ
ωµ
µ
π
β
ε
=
=
=
Ω
Uwzględniając te zależności rozkład pola elektrycznego można przedstawić w formie:
0
sin
2
r
Z IL
K
j
e
r
β
θ
θ
λ
−
=
Unormowana charakterystyka promieniowania dipola elementarnego
sin
F
θ
=
Rezystancja promieniowania natomiast wyraża się wzorem:
2
2
80
pr
L
R
π
λ
=
Rys. 6.3 Charakterystyka dipola elementarnego z Rys. 6.2a w układzie współrzędnych
prostokątnych.
Parametry anten.
Jacek Jarkowski
16

6.2. Dipole
symetryczne
Rys. 6.4. Przykłady dipoli symetrycznych
Rys. 6.5 Rozkład prądu w dipolach symetrycznych
6.3. Dipol
półfalowy.
Charakterystyka promieniowania jest zbliżona kształtem do dipola elementarnego i wyraża
się wzorem:
( )
cos
cos
2
sin
F
π
θ
θ
θ
=
Parametry anten.
Jacek Jarkowski
17
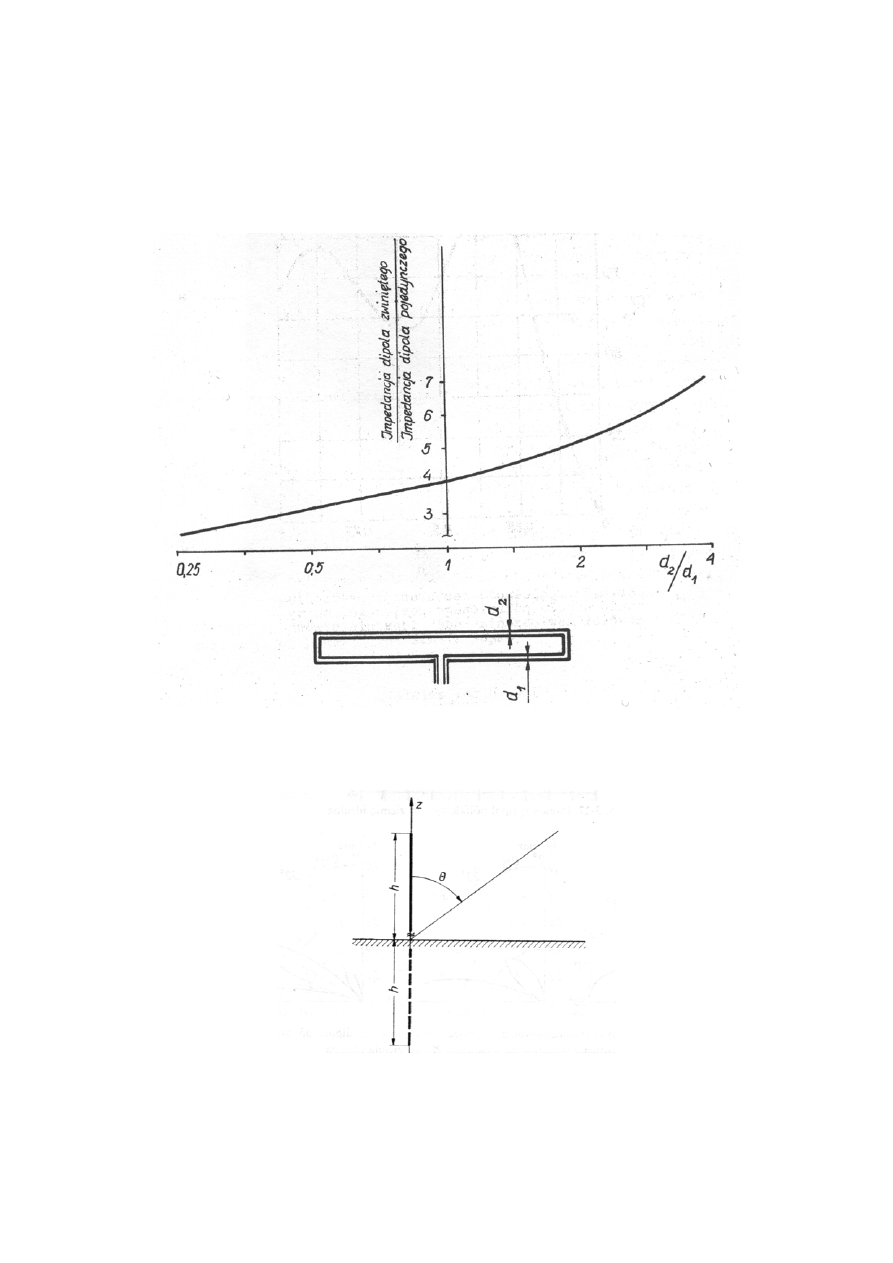
Podstawowe parametry dipola półfalowego
Rezystancja promieniowania
R
pr
= 73,2
Ω
Impedancja wejściowa Z
we
=73+j42,5
Ω
Zysk kierunkowy
G
k
=1,64
Rys. 6.6.Dipol półfalowy zwinięty i jego rezystancja wejściowa
6.4. Antena
pionowa
Rys. 6.7. Szkic anteny pionowej z odbiciem zwierciadlanym.
Parametry anten.
Jacek Jarkowski
18
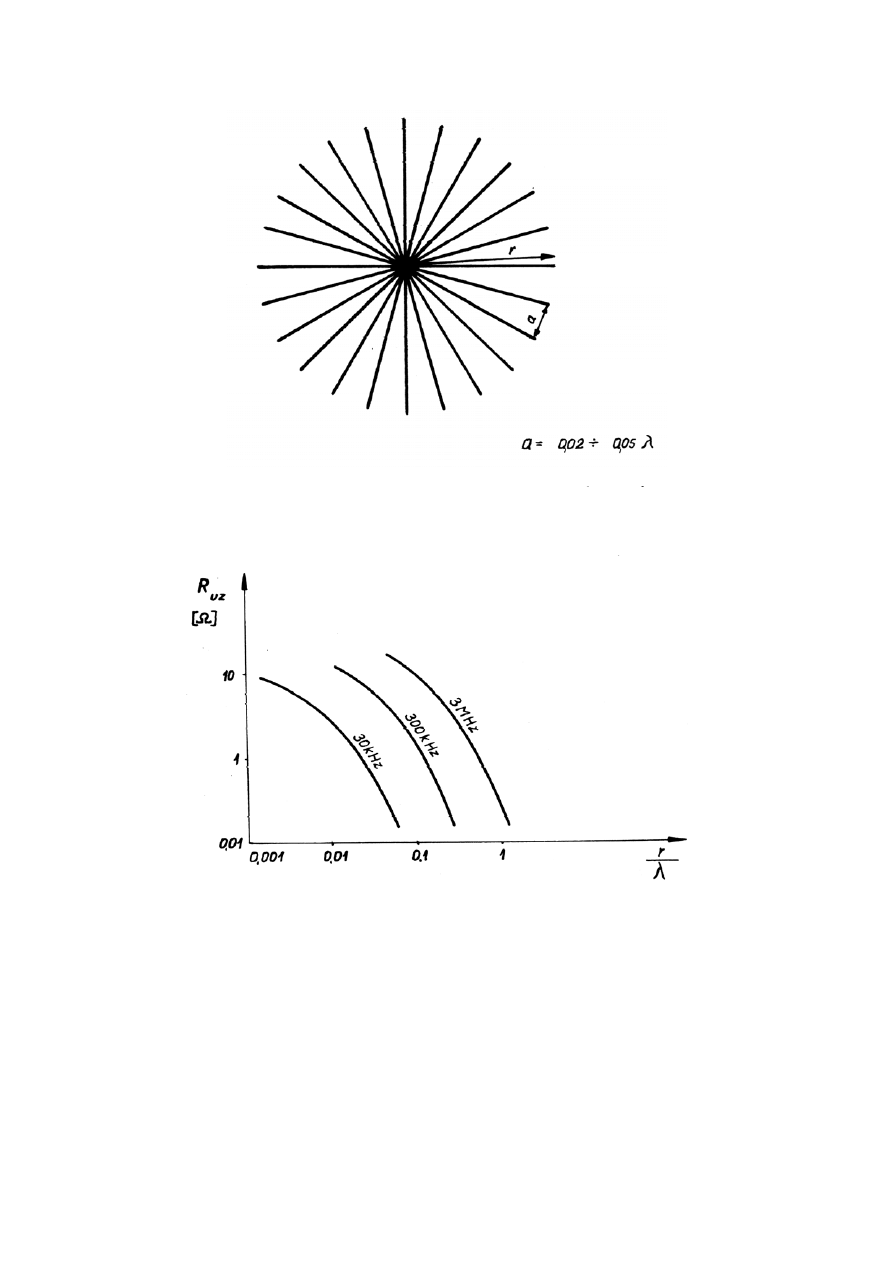
Rys. 6.8
Uziemienie masztu pionowego
Rys. 6.9. Rezystancja uziemienia anteny masztowej.
Parametry anten.
Jacek Jarkowski
19
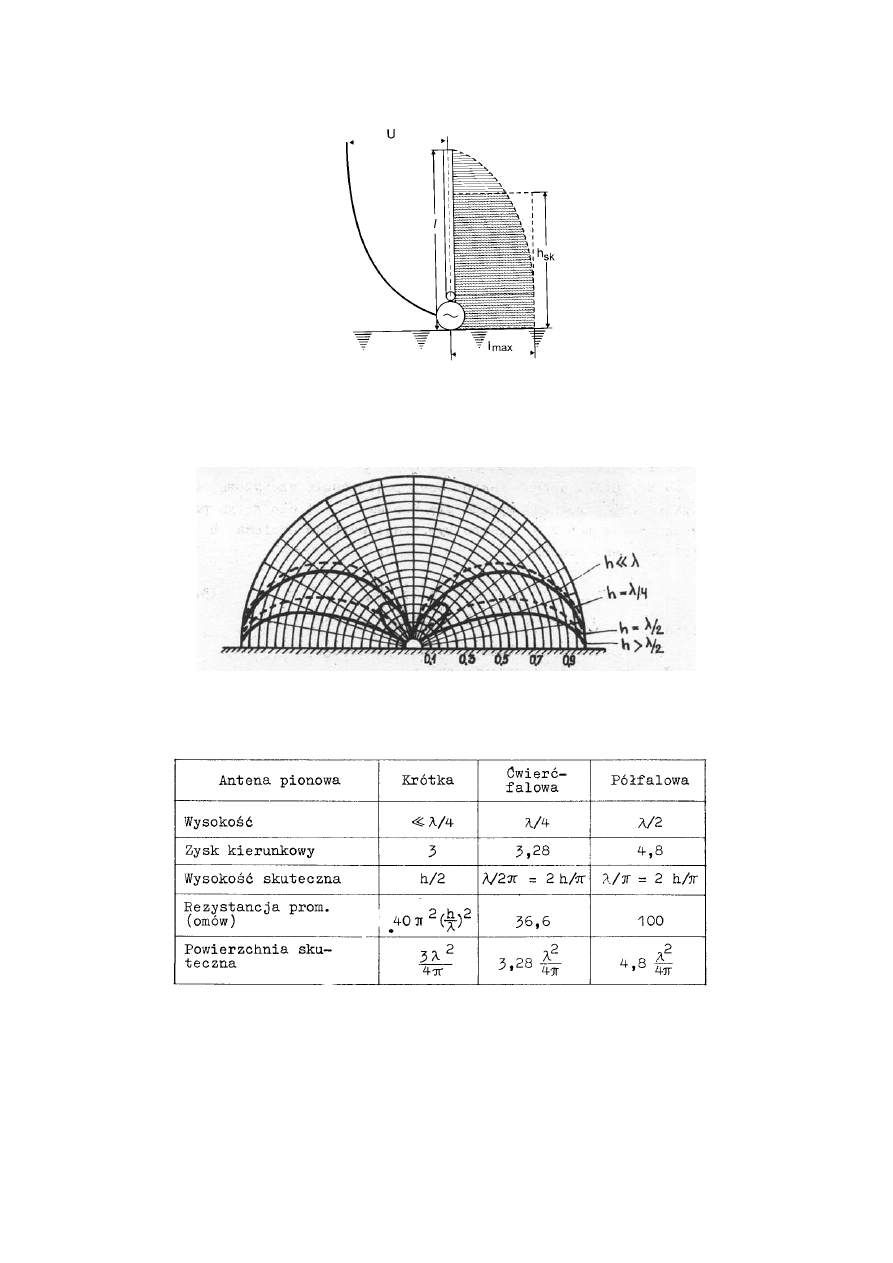
Rys. 6.10 Rozkład prądu i potencjału w antenie pionowej
oraz interpretacja wysokości skutecznej anteny
Rys. 6.11 Charakterystyki promieniowania anten pionowych (masztów)
Tabela 6.1 Wykaz ważniejszych parametrów anten pionowych.
Parametry anten.
Jacek Jarkowski
20
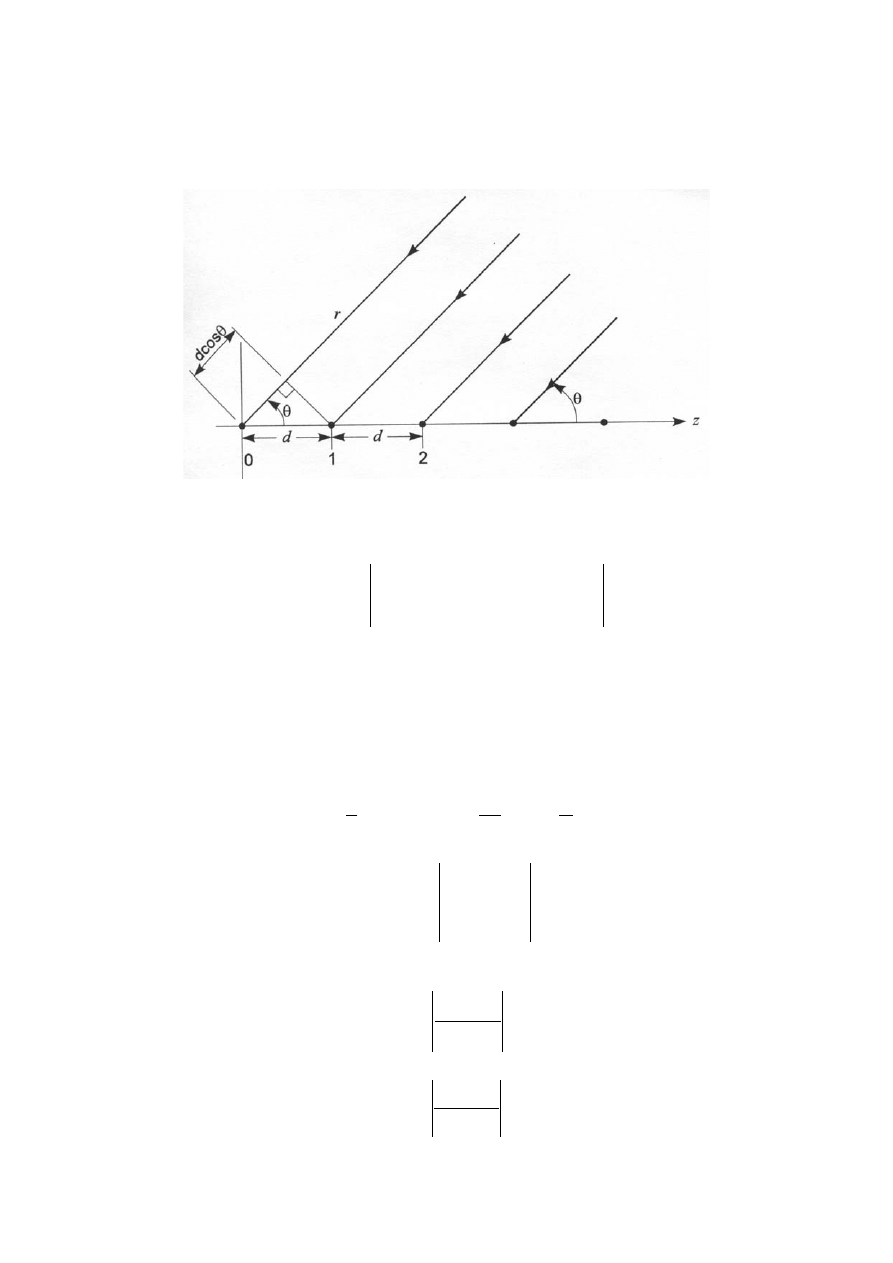
7. Grupy liniowe.
7.1. Charakterystyka promieniowania grupy liniowej.
Rys. 7.1 Układ grupy liniowej.
Charakterystyka promieniowania grupy liniowej w ogólnym przypadku może być opisana
wzorem:
( )
( )
[
]
θ
µ
β
µ
ϕ
µ
θ
φ
θ
φ
dcoc
j
m
j
e
e
A
F
E
1
1
,
,
−
=
∑
=
gdzie F(
φ
,
θ
) jest charakterystyką promieniowania elementu grupy liniowej,
jest zespoloną amplitudą prądu w
µ
-tym elemencie.
µ
ϕ
µ
j
e
A
Dla przypadku, w którym
A
1
=A
2
=A
µ
=1
ϕ
n
=
µϕ
gdzie
ϕ
jest stałym poskokiem fazy
oraz wprowadzając nową zmienną
(
)
2
cos
cos
2
1
ϕ
θ
λ
π
ϕ
θ
β
+
=
+
=
d
d
u
otrzymujemy
( )
∑
=
=
m
u
j
e
u
E
1
2
µ
µ
jest to suma m elementów postępu geometrycznegoz ilorazem e
2ju
.
Suma ta jest wyrażona wzorem
( )
u
mu
u
E
sin
sin
a po znormowaniu
( )
u
m
mu
u
E
sin
sin
Parametry anten.
Jacek Jarkowski
21
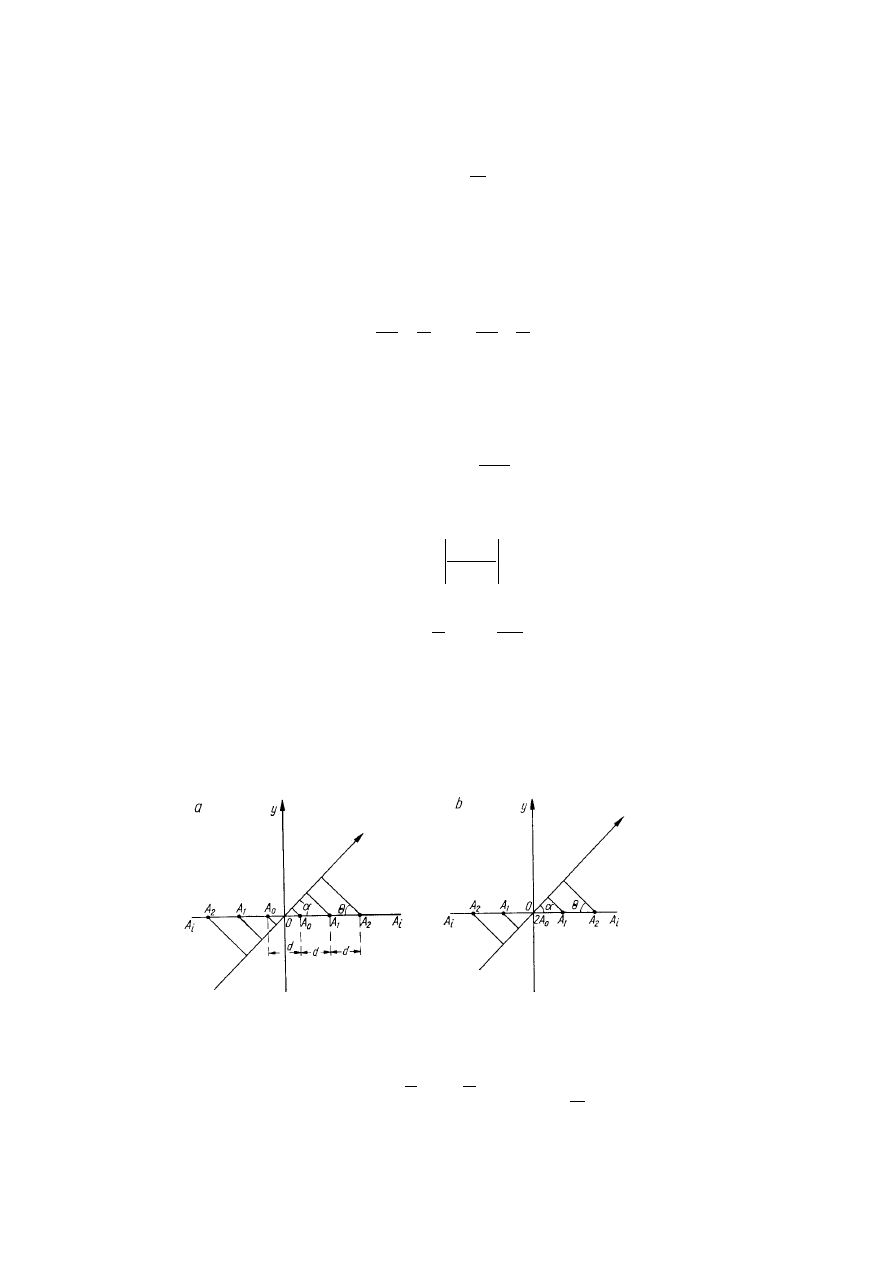
Funkcja ta jest periodyczna z okresem
π, i symetryczna względem ponktu u=0, oraz wykazuje
maksima w punktach u=0; ±
π; ± 2π ...i punkty zerowe:
+
±
=
π
π
m
n
k
u
dla k=0,1,2,...m-2, oraz n=0,1,2,....(m-1).
Charakterystyka promieniowania jest określona dla
0
0
180
0
≤
≤
θ
a więc
2
2
ϕ
λ
π
ϕ
λ
π
+
≤
≤
+
−
d
u
d
Dla układu synfazowego
ϕ
=0, u=0
, i wtedy kierunek maksymalnego promieniowania jest
poprzeczny.
natomiast gdy
ϕ≠0
−
=
d
m
π
ϕλ
θ
2
arccos
Warunek promieniowania wzdłużnego przybiera postać:
d
β
ϕ
−
=
Dla dużej liczby elementów sin u≈u i wtedy
( )
mu
mu
u
E
sin
≈
Szerokość listka głównego przy promieniowaniu poprzecznym (φ=0) wynosi:
md
L
λ
λ
α
88
,
0
88
,
0
=
≈
Zysk kierunkowy grupy liniowej, synfazowej składającej się z elementów izotropowych, w
przybliżeniu równa się liczbie elementów.
7.2. Synteza grupy liniowej (Według L Thourel'a)
Rys. 7.1 Ilustracja do obliczeń charakterystyki grupy liniowej
( )
=
+
=
−
2
2
0
2
2
0
0
ψ
θ
ψ
ψ
cos
A
e
e
A
f
j
j
Parametry anten.
Jacek Jarkowski
22
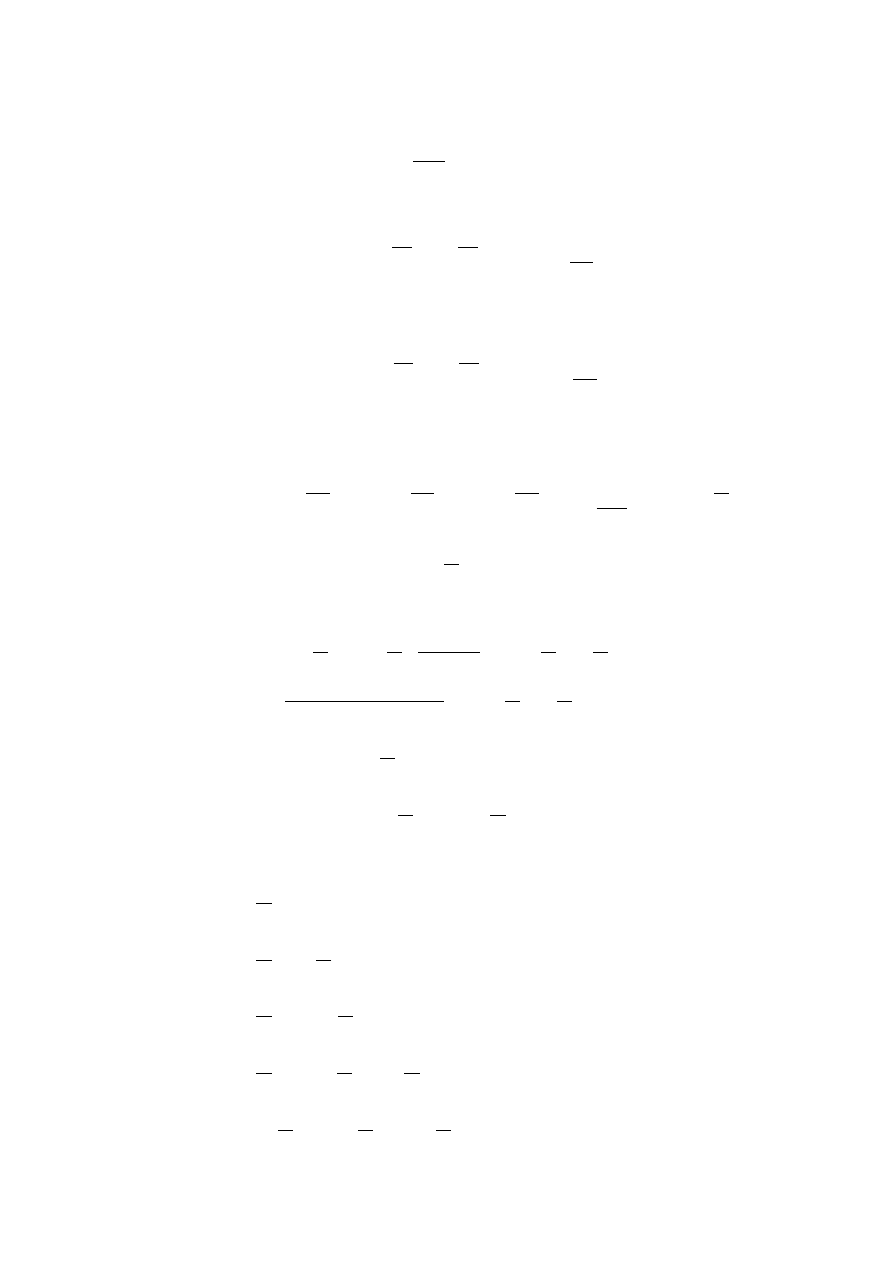
gdzie
ϕ
φ
λ
π
ψ
+
=
cos
d
2
Dla następnej pary źródeł mamy
( )
=
+
=
−
2
3
2
1
2
3
2
3
1
1
ψ
θ
ψ
ψ
cos
A
e
e
A
f
j
j
i następnej
( )
=
+
=
−
2
5
2
2
2
5
2
5
2
2
ψ
θ
ψ
ψ
cos
A
e
e
A
f
j
j
Całkowite pole układu
( )
(
)
−
+
+
+
+
=
−
2
1
2
7
2
5
2
3
2
2
1
3
2
1
0
ψ
ψ
ψ
ψ
θ
N
cos
A
.....
cos
A
cos
A
cos
A
A
f
N
Pole więc zależy od mnożnika w formie
2
ψ
m
cos
.
Czynnik ten można rozwinąć w szereg według wzoru de Moivre:
(
)
(
)(
)(
)
.....
sin
cos
!
m
m
m
m
sin
cos
!
m
m
cos
m
cos
m
m
m
2
2
4
3
2
1
2
2
2
1
2
2
4
4
2
2
ψ
ψ
ψ
ψ
ψ
ψ
−
−
−
−
−
+
+
−
−
=
Podstawiając
x
cos
=
2
ψ
Oraz pamiętając, że
2
1
2
2
2
ψ
ψ
cos
sin
−
=
Obliczamy wartości wielomianu dla różnych m:
Dla m=0,
1
1
2
=
=
ψ
m
cos
Dla m=1,
x
cos
m
cos
=
=
2
2
ψ
ψ
Dla m=2,
1
2
1
2
2
2
2
2
−
=
−
=
x
cos
m
cos
ψ
ψ
Dla m=3,
x
x
cos
cos
m
cos
8
4
2
3
2
4
2
3
3
−
=
−
=
ψ
ψ
ψ
Dla m=4,
1
8
8
1
2
8
2
8
2
2
4
2
4
+
−
=
+
−
=
x
x
cos
cos
m
cos
ψ
ψ
ψ
itd.
Parametry anten.
Jacek Jarkowski
23
Taki wielomian nazywa się wielomianem Czebyszewa:
( )
( )
( )
( )
( )
( )
( )
( )
x
x
x
x
x
T
x
x
x
x
T
x
x
x
x
T
x
x
x
T
x
x
x
T
x
x
T
x
x
T
x
T
7
56
112
64
1
18
48
32
5
20
16
1
8
8
3
4
1
2
1
3
5
7
7
2
4
6
6
3
5
5
2
4
4
3
3
2
2
1
0
−
+
−
=
−
+
−
=
+
+
=
+
+
=
−
=
−
=
=
=
Tak więc otrzymujemy dla
parzystej liczby elementów w grupie:
( )
( )
( )
( )
( )
[
]
x
T
A
x
T
A
x
T
A
x
T
A
f
N
i
1
5
2
3
1
1
0
2
−
+
+
+
=
.....
φ
nieparzystej liczby elementów w grupie:
( )
( )
( )
( )
( )
[
]
x
T
A
x
T
A
x
T
A
x
T
A
f
N
i
1
4
2
2
1
0
0
2
−
+
+
+
=
.....
φ
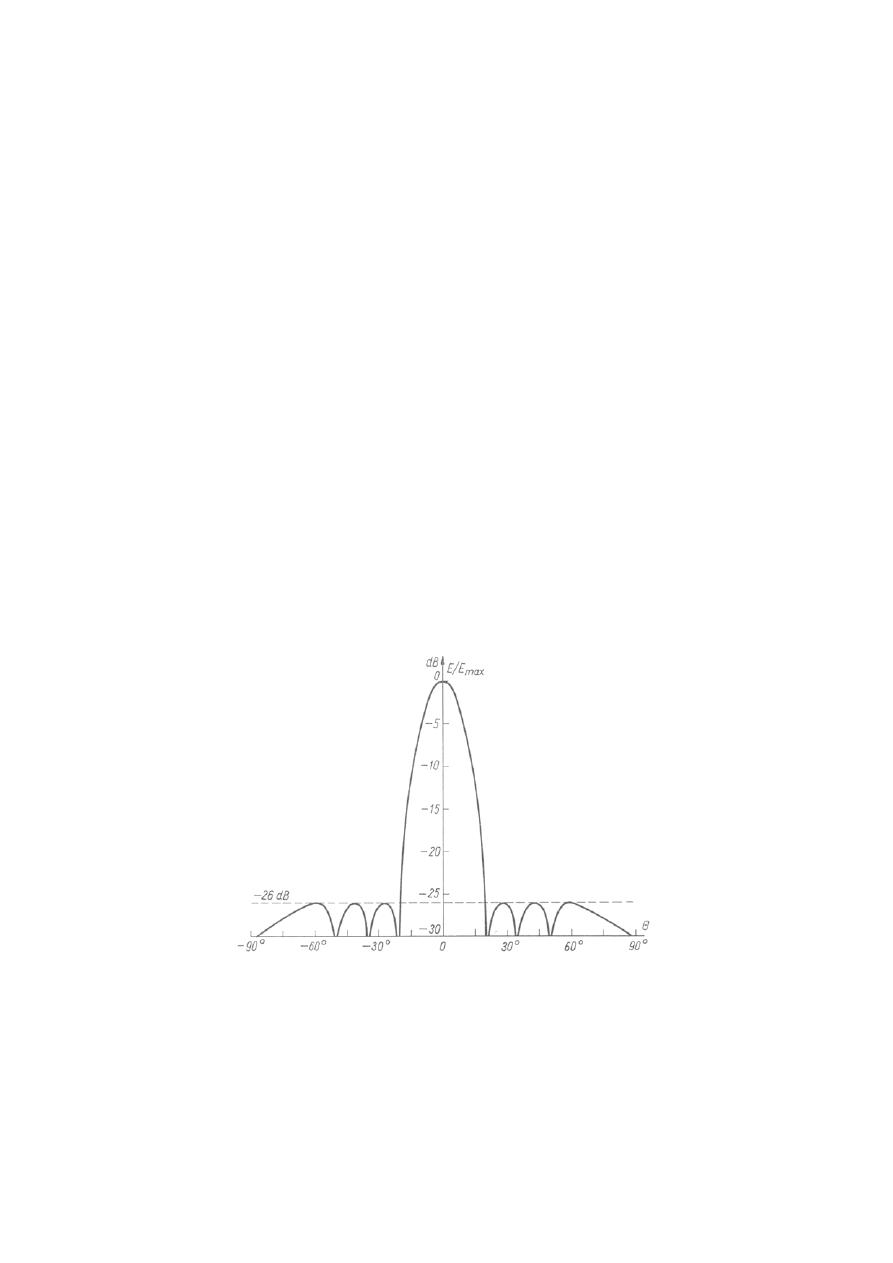
Rys.7.2. Charakterystyka promieniowania układu Czebyszewa ułożonego z 8 izotropowych
elementów antenowych; poziom listków bocznych wynosi –26dB. (według Bema)
Parametry anten.
Jacek Jarkowski
24
Wyszukiwarka
Podobne podstrony:
Charakterystyki i parametry anten
Kopia cw 3 nasze, pwr-eit, Anteny i propagacja fal radiowych, ćw.3 - Pomiary parametrów polowych ant
cw 3 nasze, pwr-eit, Anteny i propagacja fal radiowych, ćw.3 - Pomiary parametrów polowych anten w p
antena yagi pro, pwr-eit, Anteny i propagacja fal radiowych, ćw.2 - Pomiar parametrów obwodowych ant
Parametry życiowe dla WCEM
PARAMETRY STATYSTYCZNE Aktualne
Obliczanie i pomiary parametrów obwodów prądu jednofazowego
Zwiazki korelacyjne parametrow zageszczenia wyznaczonych VSS i LFG
Instrukcja 07 Symbole oraz parametry zaworów rozdzielających
05 Pomiar paramet zrodel U I
dobór parametru klotoidy
parametry.prv, fizjologia notatki
Hipoteza o istotności parametrów strukturalnych, Wykłady rachunkowość bankowość
Urządzenia 101 - parametry łączników protokół (tylko dla ZAO, Politechnika Lubelska, Studia, semestr
Gubin parametry, AGH, Semestr X, stateczność skarp i zboczy, Stateczność skarp TOEZ
Gen Czaban brakuje zapisu z rejestratora parametrów lotu
sprawozdanie mikroklimat i pomiary jego parametrów w środowisku górniczym
3 Parametry i usługi sieci dostępu do Internetu – teraz i w przyszłości
więcej podobnych podstron