EN- w04
1
Przekształtniki tyrystorowe (ac/dc)
Struktury (najczęściej stosowane)
Uproszczona analiza ( L
s
= 0, i
d
= const )
Przebiegi napięć , prądów i mocy
Wzory na wartości średnie , skuteczne, harmoniczne
Komutacja ( L
s
> 0 , i
d
= const )
Przebiegi i wzory jak poprzednio
Analiza symulacyjna ( L
s
> 0 , i
d
= i
d
(t) )
Przewodzenie przerywane
Przekształtnik jako element układu regulacji
Schemat blokowy, właściwości regulacyjne
EN- w04
2
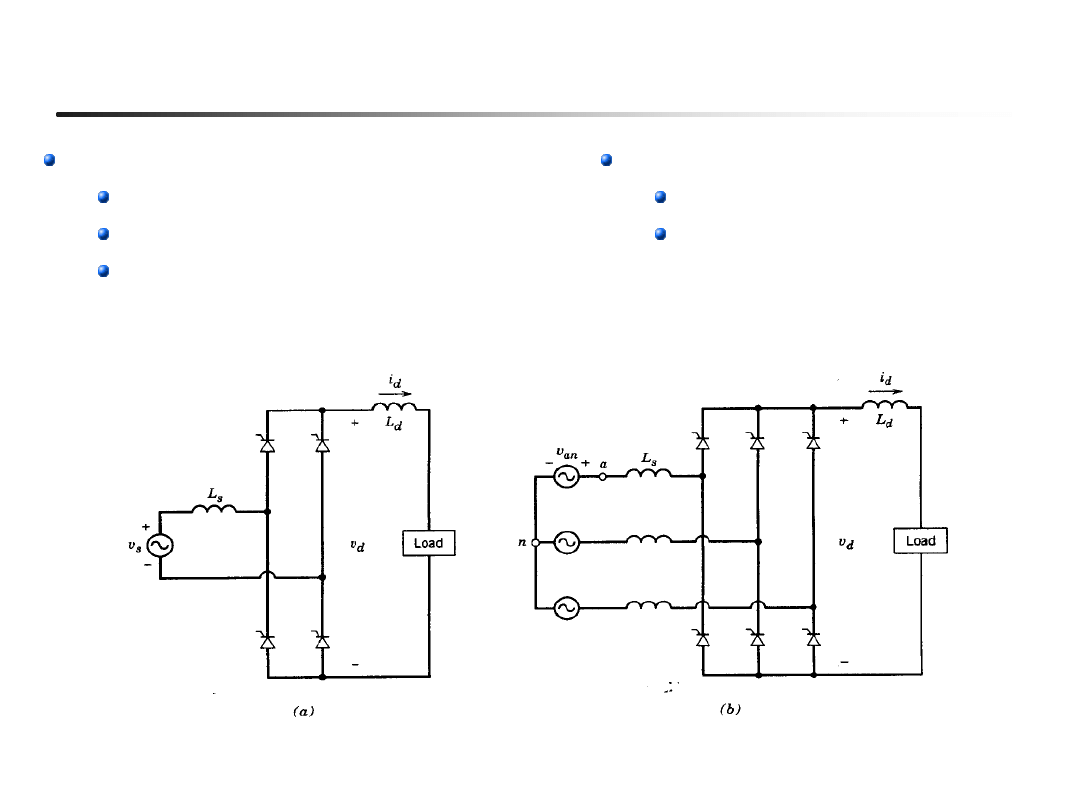
Prostowniki tyrystorowe – schematy praktyczne
Indukcyjność L
d
po stonie prądu stałego:
wygładza prąd wyjściowy
może być częścią obciążenia
obciążenie można zastąpić
źródłem prądowym
Indukcyjność L
s
po stronie zasilania:
wpływa na komutację
ogranicza di/dt
EN- w04
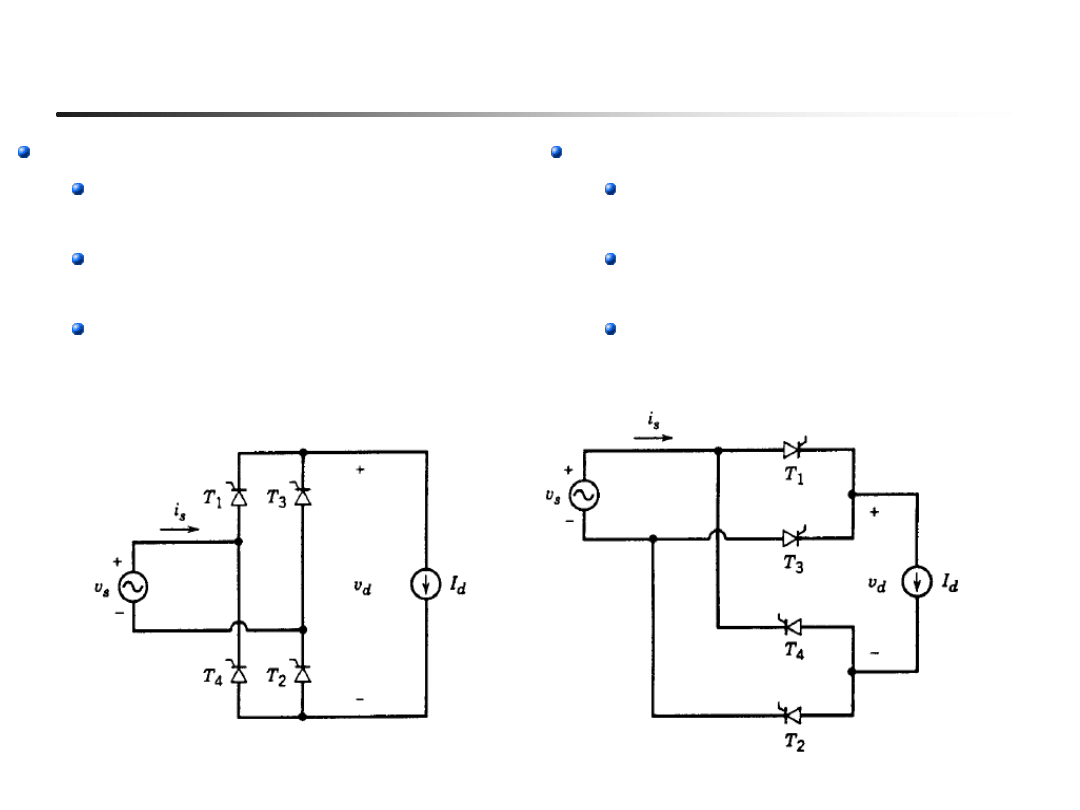
3
Zasady działania – model uproszczony (Ls=0, id=const)
Grupa komutacyjna katodowa
Katody T1 i T3 połączone
w punkcie P (+)
Przewodzi tyrystor o wyższym
napięciu anodowym
Wybierane jest najwyższe
napięcie
Grupa komutacyjna anodowa
anody T2 i T4 połączone
w punkcie N (-)
Przewodzi tyrystor o niższym
napięciu katodowym
Wybierane jest najniższe
napięcie
EN- w04
4
Prostownik 2-pulsowy mostkowy (Ls=0, Rd,Ld = var)
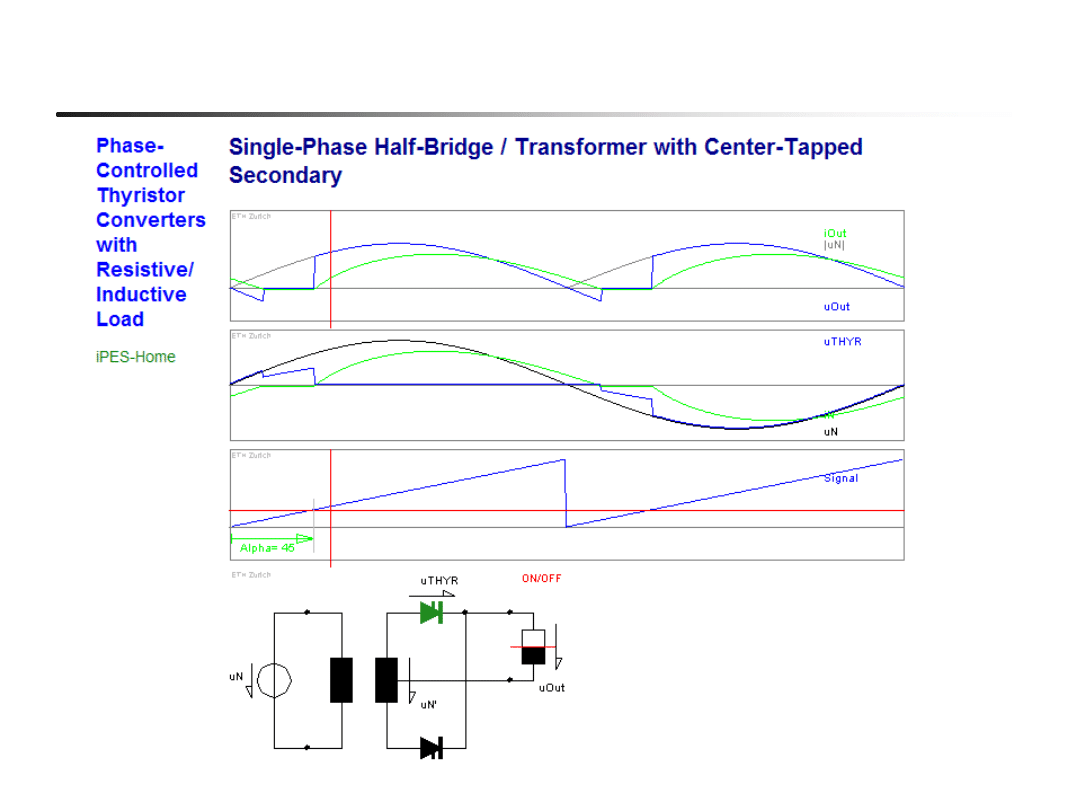
EN- w04
5
Prostownik 2-pulsowy jednokierunkowy (Ls=0, Rd,Ld = var)
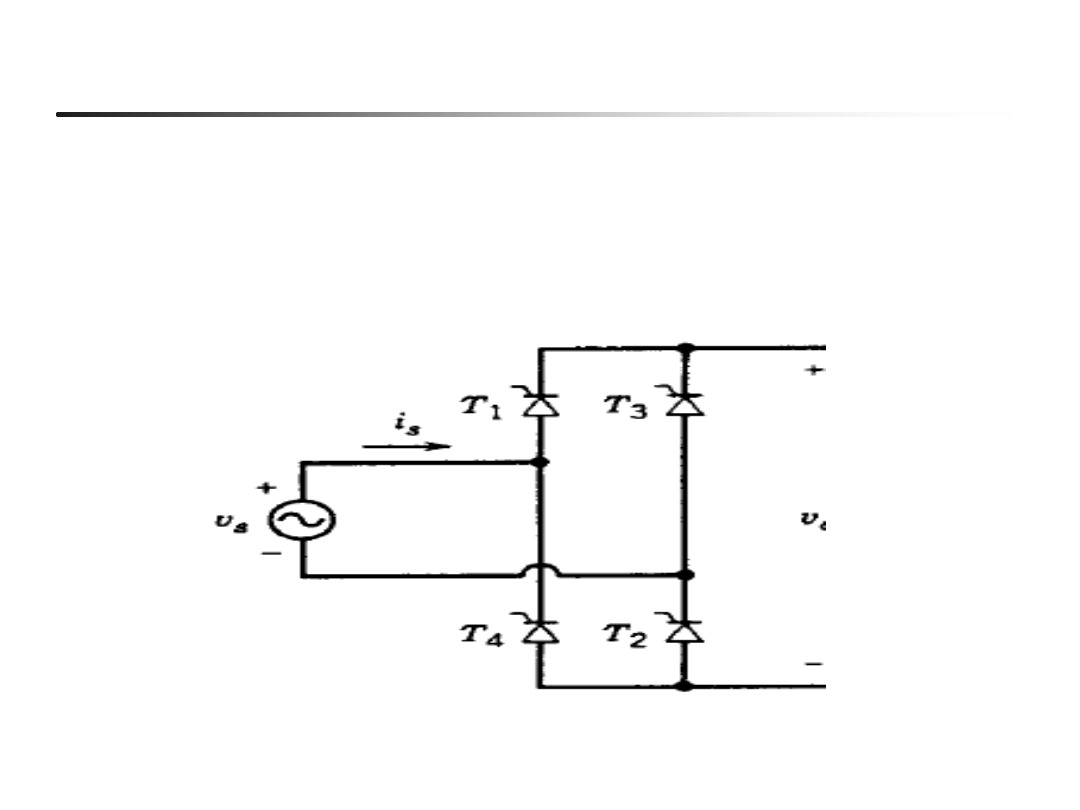
EN- w04
6
Zasady działania – model uproszczony (Ls=0, id=const)
Analiza przebiegów i wzory wyprowadzone na
następnych 8-miu slajdach dotyczą uproszczonego
modelu prostownika, w którym zakłada się stały
prąd obciążenia i
d
= I
d
EN- w04
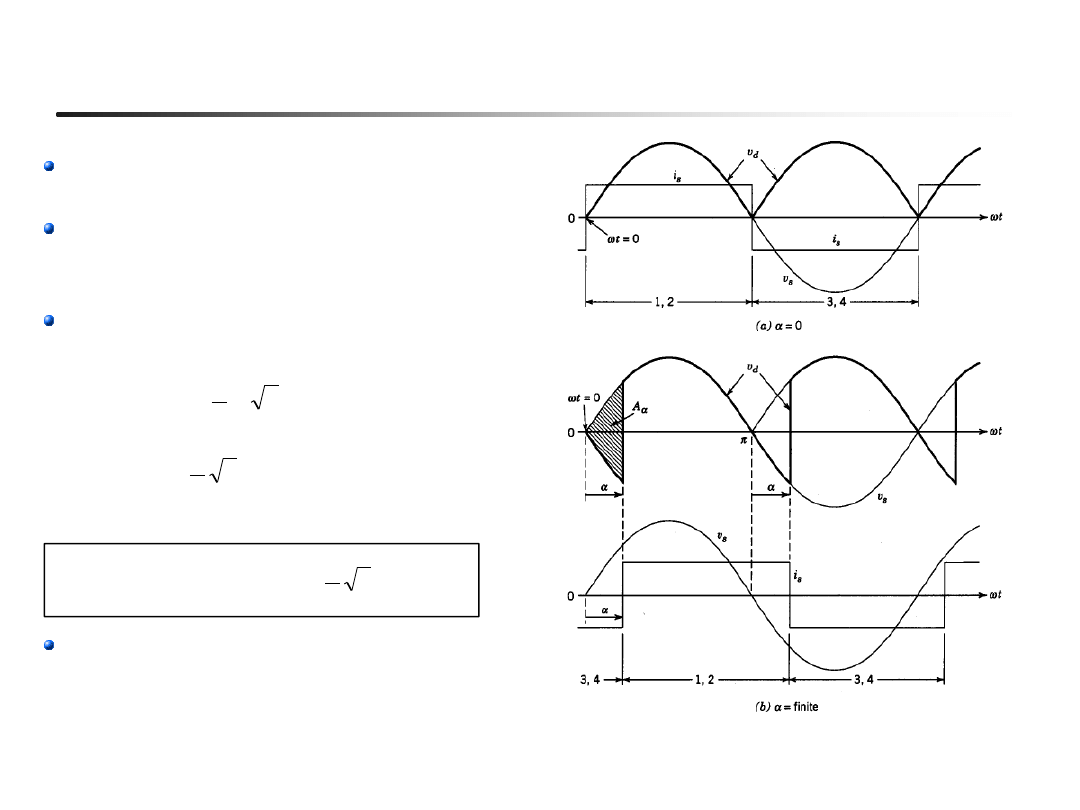
7
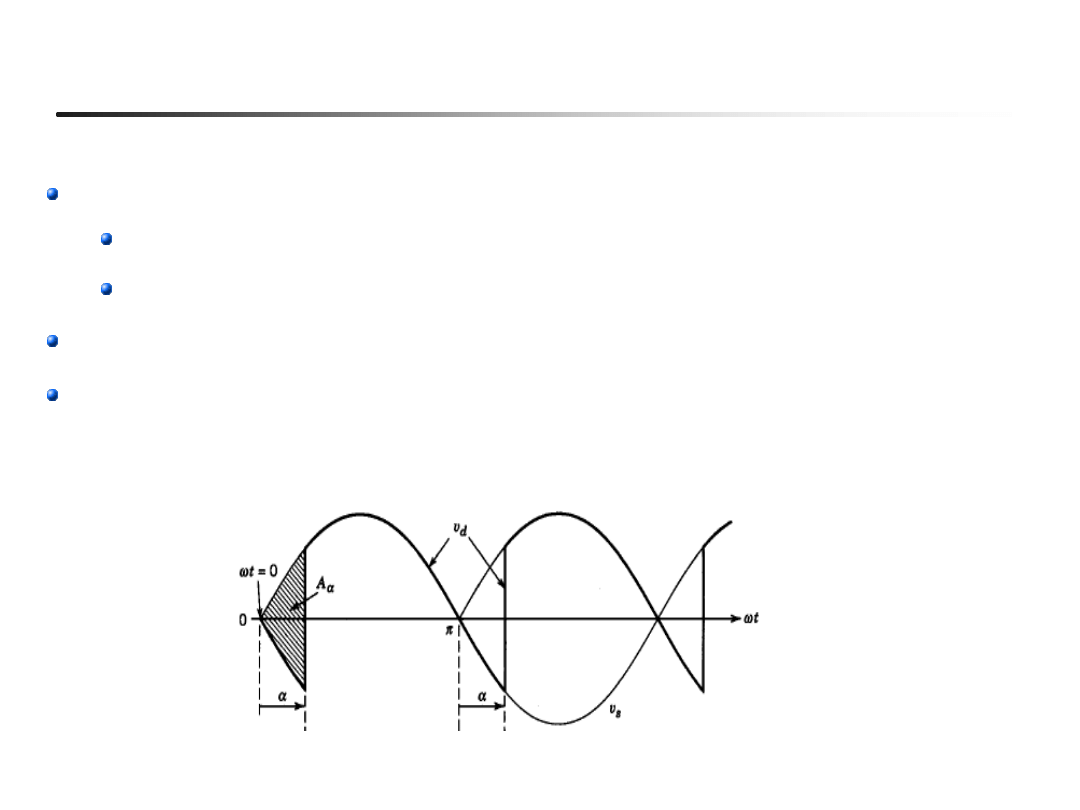
Średnie napięcie wyprostowane V
d
(
a
)
Takie samo jak w mostku diodowym,
o ile
a
= 0
Wartości chwilowe oraz średnie
napięcia mogą być ujemne (dzięki
źródłu prądowemu)
Wzór na napięcie średnie:
Prąd sieci jest opóźniony o kąt
a
α
α
V
π
=
α
V
ωt
d
ωt
V
π
=
α
V
s
d
s
α
+
π
α
d
0.9cos
cos
2
2
sin
2
1
s
d0
d0
d
V
π
=
V
α
V
=
α
V
2
2
cos
EN- w04
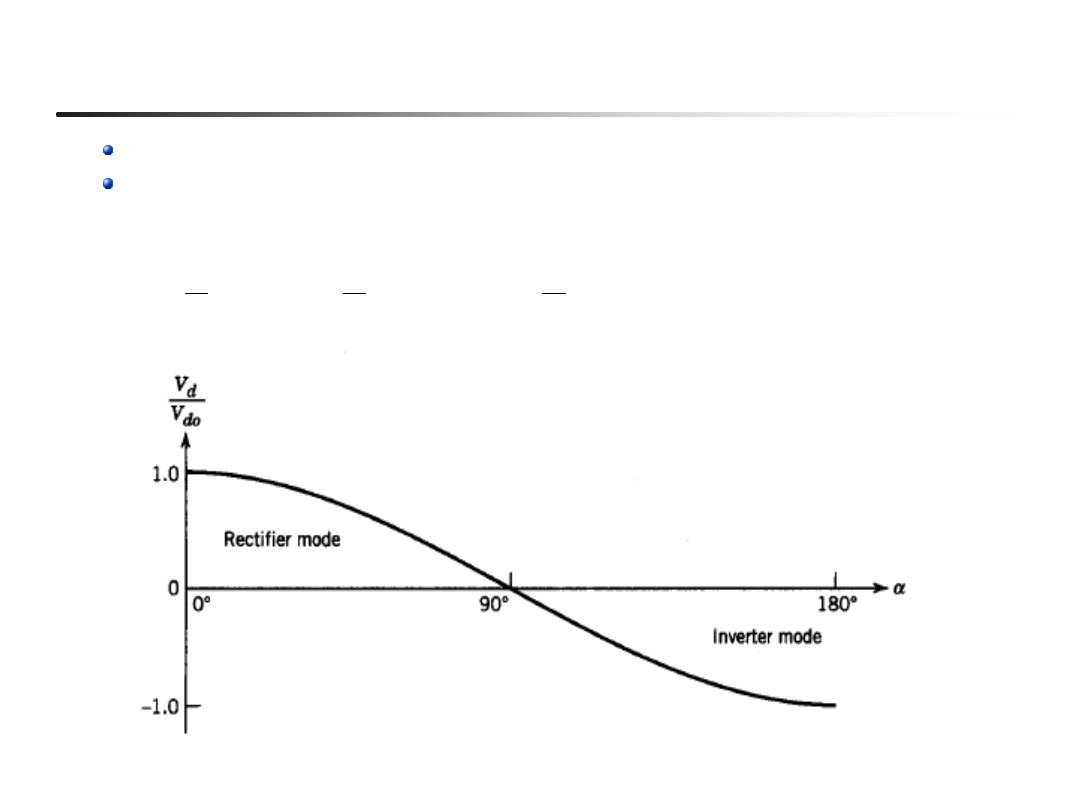
8
Praca prostownikowa i falownikowa , moc średnia
Średnie napięcie Vd jest ujemne, gdy 90
o
<
a
<180
o
; jest to praca falownikowa
Wzór na moc średnią:
α
I
V
I
V
=
dt
v
T
I
=
dt
i
v
T
=
dt
t
p
T
=
P
d
s
d
d
T
d
d
d
T
d
T
cos
0.9
1
1
1
0
0
0
EN- w04
9
Harmoniczne napięcia wyjściowego v
d
Przebieg powtarza się po połowie okresu napiecia sieci
Częstotliwości harmoniczne są wielokrotnościami 2f
s
Można je obliczyć za pomocą szeregu Fouriera
Maksimum harmonicznych występuje gdy
a
jest równe
p
/2
Wzory na harmoniczne można znaleźć w literaturze;
na wykładzie nie będziemy ich omawiać
EN- w04
10
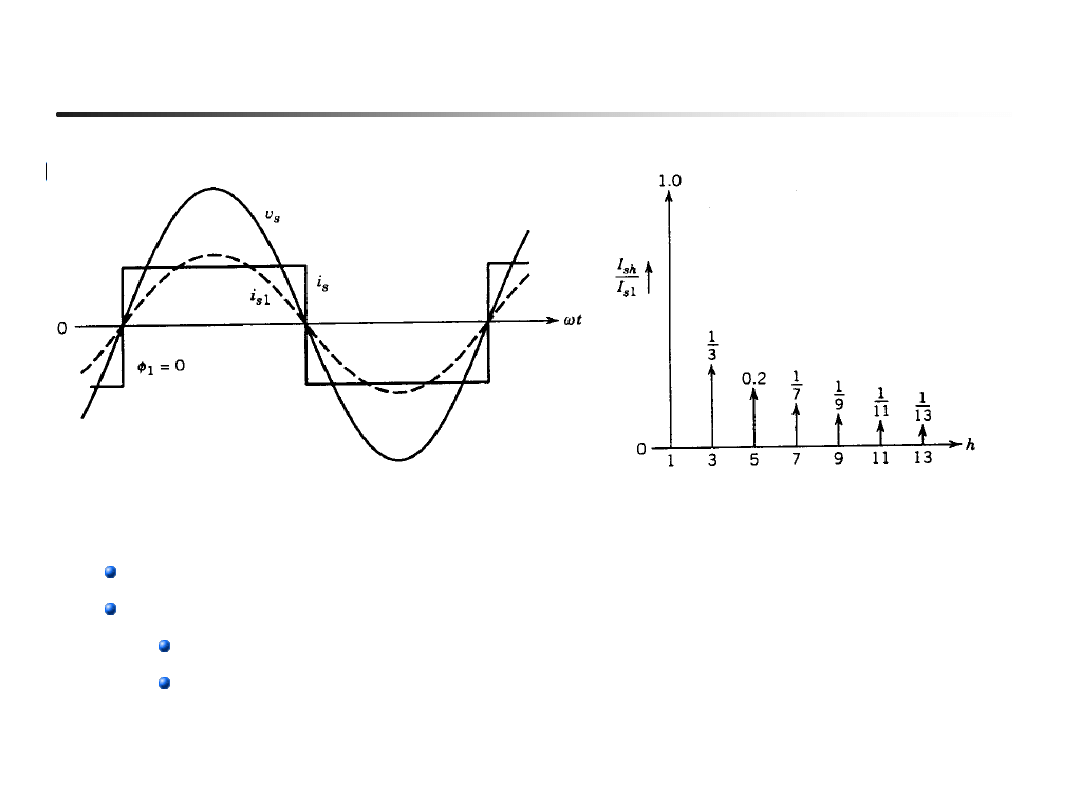
Prąd wejściowy (
a
=0 lub prostownik diodowy)
Współczynnik zniekształceń harmonicznych THD = 48,4%
Podstawowa składowa jest w fazie z napięciem
Współczynnik przesunięcia (displacement factor, cos
j
) =1
Współczynnik mocy PF = DPF Ish / Is ≈ 0.9
EN- w04
11
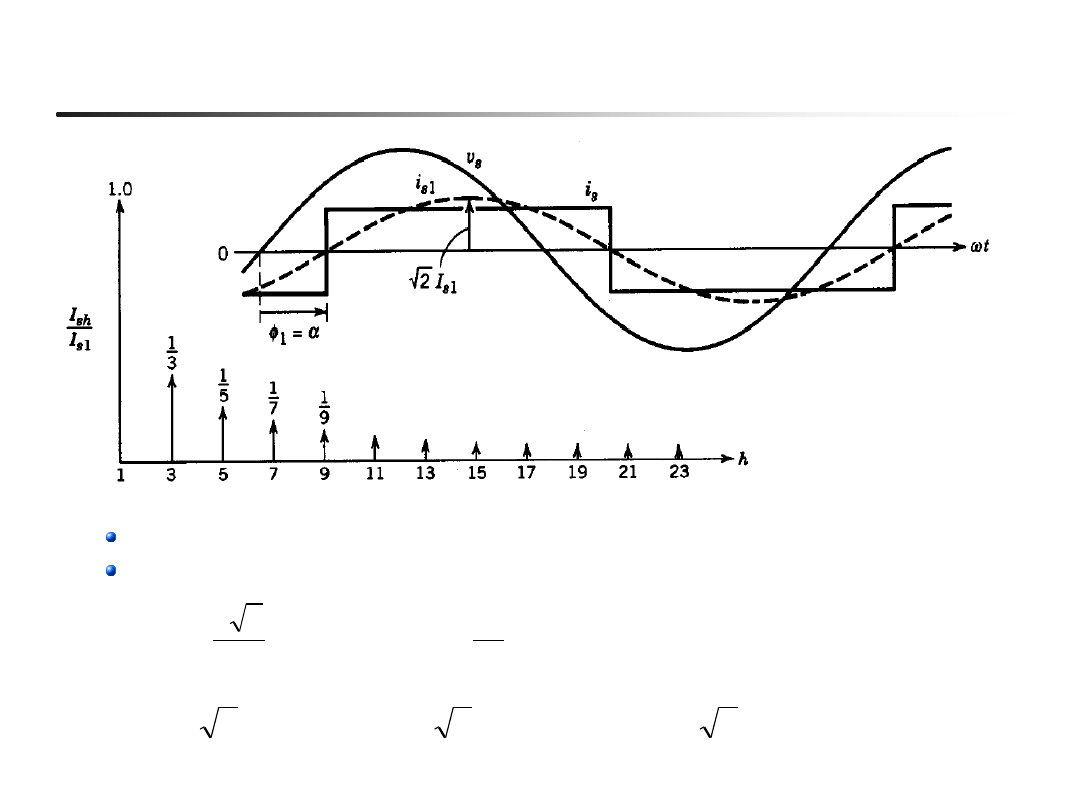
Prąd wejściowy i
s
(
a >
0 ) , rozkład na harmoniczne
Kąt przesunięcia składowej podstawowej
F
1
równy
a
Wartości skuteczne składowej podstawowej i harmonicznych:
...
1,2
1,
2k
0.9
2
2
,
=
k
+
=
h
,
h
I
=
I
,
I
I
π
=
I
s1
sh
d
d
s1
+
α
ωt
I
+
α
ωt
I
+
α
ωt
I
=
i
s5
s3
s1
s
5
sin
2
3
sin
2
sin
2
EN- w04
12
Współczynniki mocy:
DPF, THD, PF
Wartość skuteczna prądu :
I
s
= I
d
Przesunięcie podstawowej harmonicznej równe
a ,
zatem:
Współczynniki :
THD
i
, PF
α
=
Φ
=
DPF
cos
cos
1
0.484
2
2
s1
s1
s
I
I
I
=
THD
α
π
=
DPF
I
I
=
PF
s
s1
cos
2
2
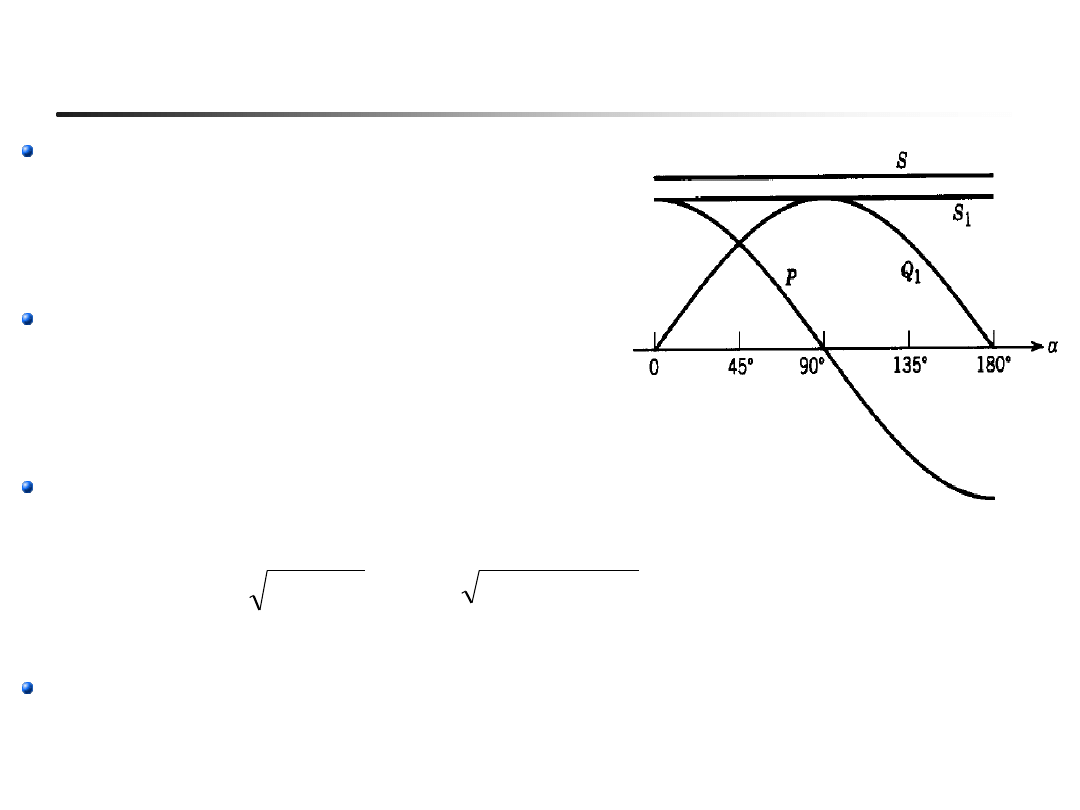
EN- w04
13
Moce: czynna P, bierna Q
1
, Q , pozorna S
1
, S
Moc czynna (równa po obu stronach):
Moc bierna składowej podstawowej:
Moc pozorna składowej podstawowej
(nie zależy od
a
):
Całkowita moc pozorna :
( S > S
1
)
α
I
V
=
Φ
I
V
=
P
d
d
s1
s
cos
cos
0
1
α
I
V
=
Φ
I
V
=
Q
d
d
s1
s
sin
sin
0
1
1
d
s
d
d
d
d
s1
s
I
V
I
V
=
α
+
α
I
V
=
Q
+
P
=
I
V
=
S
0.9
sin
cos
0
2
2
0
2
1
2
1
d
s
s
s
I
V
=
I
V
=
S
EN- w04
14
Komutacja
(rozważania wstępne)
W układach praktycznych indukcyjność Ls jest zawsze > 0
Prąd nie może przemieścić się z jednej gałęzi do drugiej natychmiastowo
Zmiana prądów, czyli komutacja zajmuje pewien przedział czasu:
t
m
Zamiast czasu częściej posługujemy się kątem komutacji:
m
=
w
t
m
Zakłada się , że prąd
i
d
nie zmienia się w czasie komutacji :
i
d
= I
d
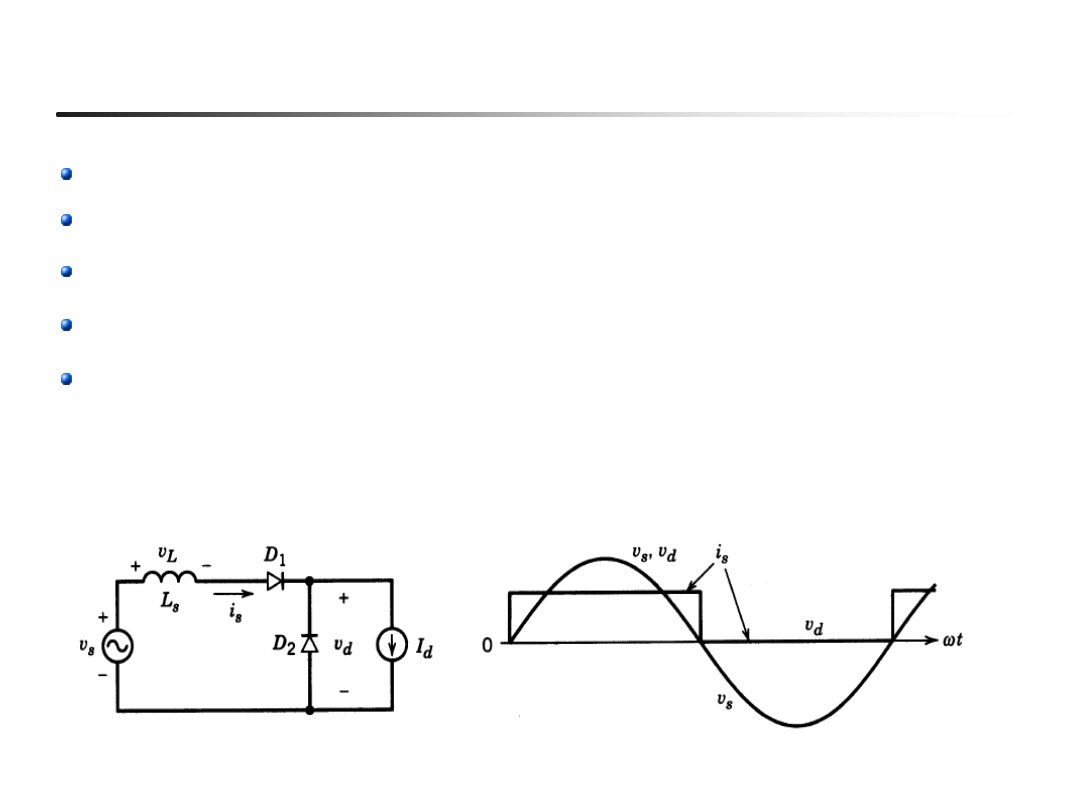
Przykład (przypomnienie komutacji natychmiastowej,
L
s
=0
→
t
m
=0
,
m
=0)
:
EN- w04
15
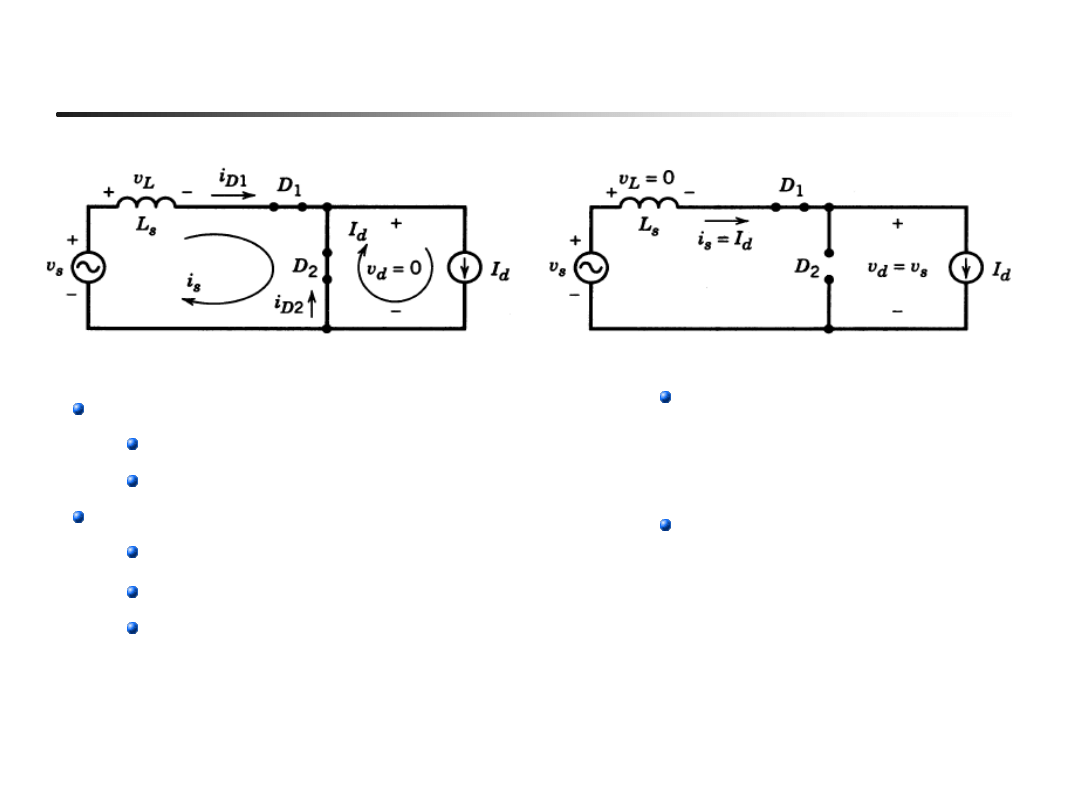
Komutacja
(przykład , Ls > 0)
V
s
< 0
D
2
przewodzi prąd I
d
Napięcie v
d
= 0
V
s
zmienia znak na dodatni
Zaczyna przewodzić D
1
L
s
spowalnia zmiany prądu
D
1
i D
2
przewodzą równocześnie
D
2
przestaje przewodzić
gdy prąd i
D2
spadnie do
zera
Po komutacji prądy oraz
napięcia źródła i
odbiornika są sobie
równe
EN- w04
16
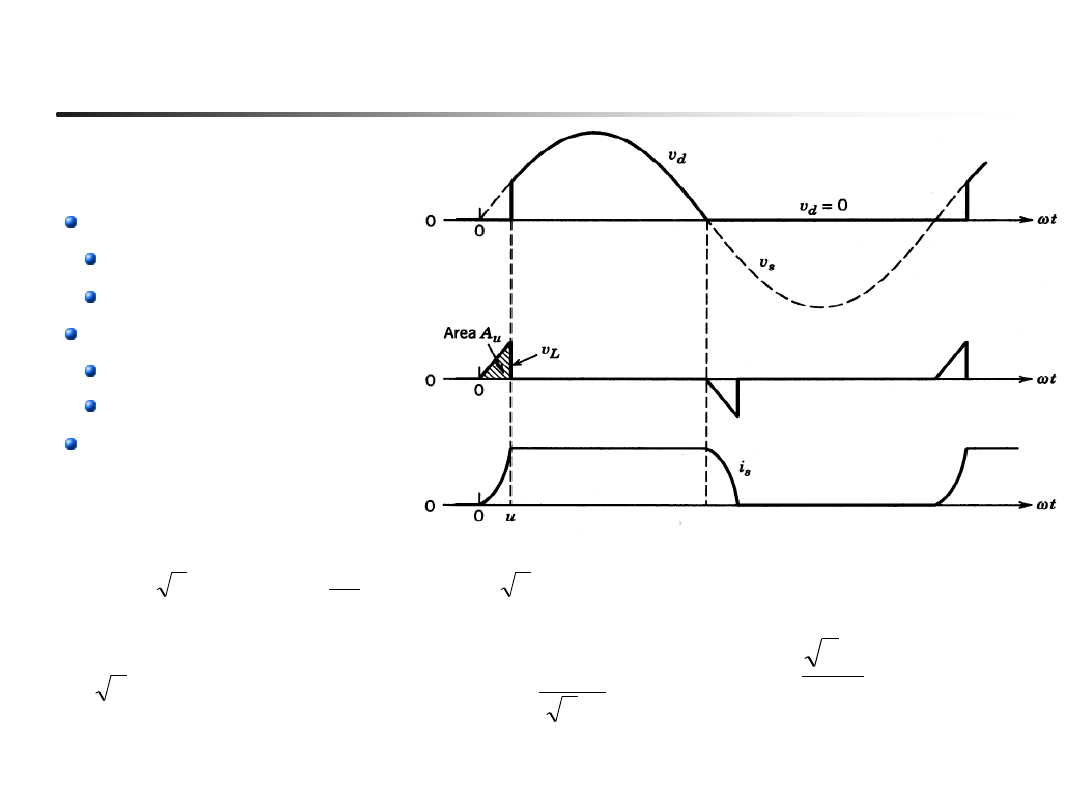
Przebiegi podczas komutacji (przykład , Ls > 0)
Podczas komutacji
(dwie na 1 okres sieci):
Prąd i
s
:
rośnie od 0 do I
d
maleje od I
d
do 0
Napięcie v
d
:
Pozostaje zerowe
Pozostaje zerowe
Napięcie v
L
oraz
A
m
(całka z v
L
):
d
I
s
s
s
μ
μ
s
s
s
L
di
ωL
=
ωt
d
ωt
V
=
A
dt
di
L
=
ωt
V
=
v
0
0
sin
2
sin
2
s
d
s
d
s
s
μ
V
I
ωL
=
μ
I
ωL
=
μ
V
=
A
2
1
cos
cos
1
2
μ
i
=
I
μ
ωL
V
=
I
k
d
s
s
d
cos
1
ˆ
cos
1
2
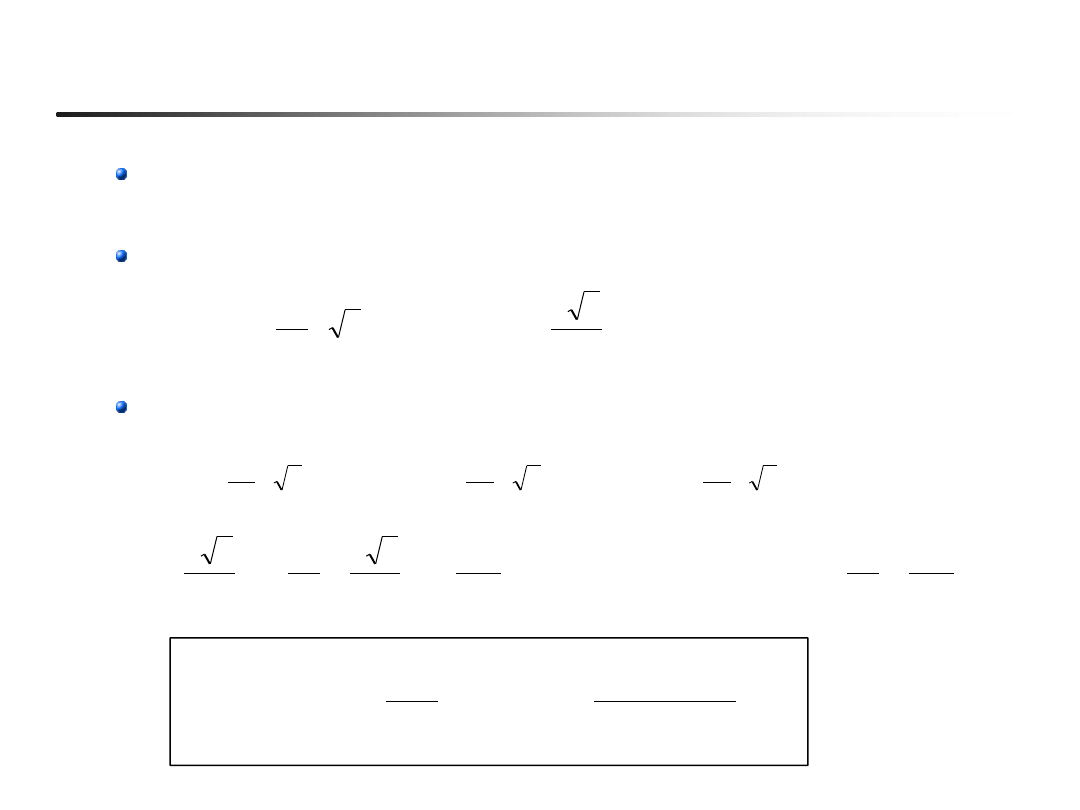
EN- w04
17
Średnie napięcie wyprostowane V
d
(przykład)
Podczas komutacji v
d
= 0 i dlatego średnie napięcie V
d
zmniejsza się
w porównaniu z przypadkiem komutacji natychmiastowej (L
s
=0)
Średnia wartość napięcia przy komutacji natychmiastowej:
Średnia wartość napięcia po uwzględnieniu komutacji:
s
s
s
π
d0
V
V
π
=
ωt
d
ωt
V
π
=
V
0.45
2
2
2
sin
2
2
1
0
ωt
d
ωt
V
π
ωt
d
ωt
V
π
=
ωt
d
ωt
V
π
=
V
s
μ
s
π
s
π
μ
d
sin
2
2
1
sin
2
2
1
sin
2
2
1
0
0
d
s
μ
d
d
s
s
μ
s
d
I
π
ωL
=
π
A
=
ΔV
ęcia
spadeknapi
,
I
π
ωL
V
π
=
π
A
V
π
=
V
2
2
:
2
2
2
2
2
2
2
2
2
cos
1
2
μ
+
V
=
I
π
ωL
V
=
V
d0
d
s
d0
d
EN- w04
18
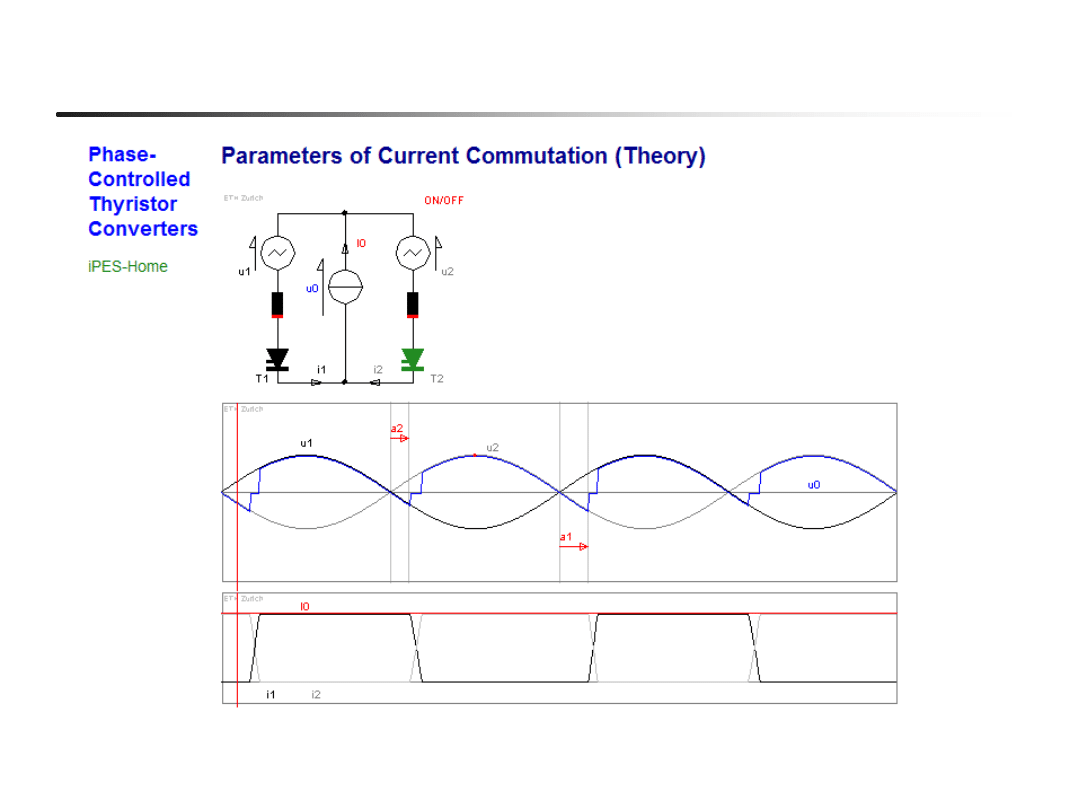
Komutacja w prostowniku 2-pulsowym – ćwiczenie iPES
EN- w04
19
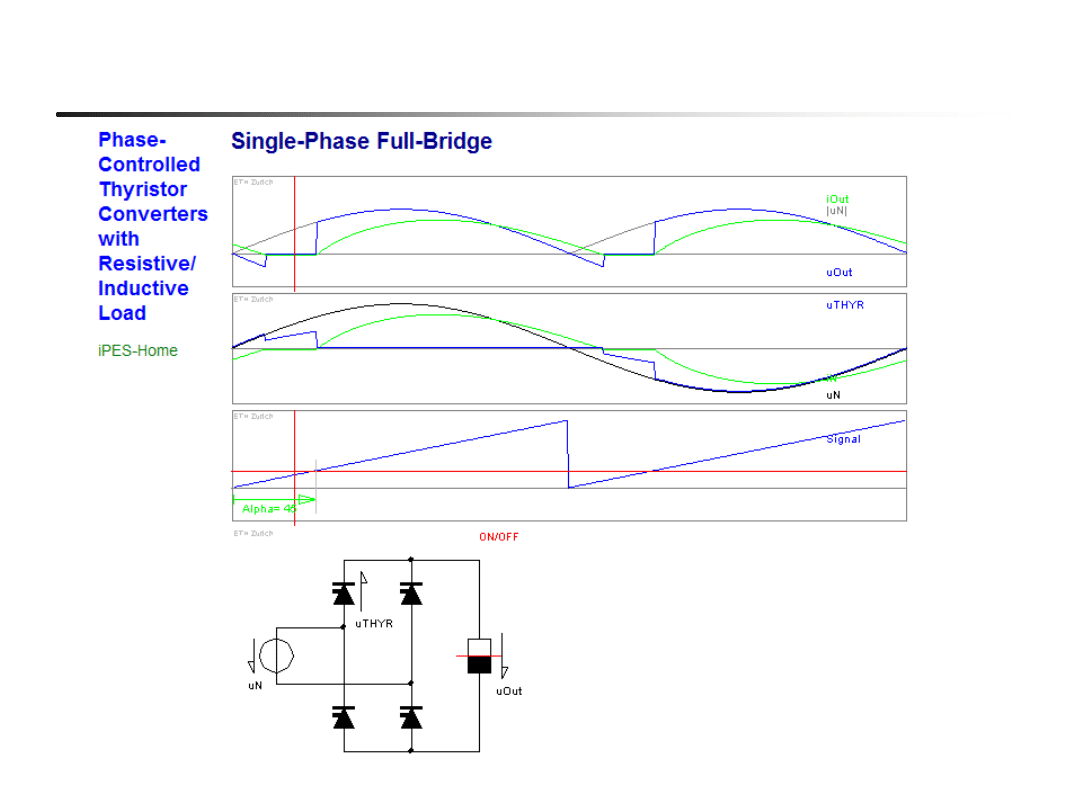
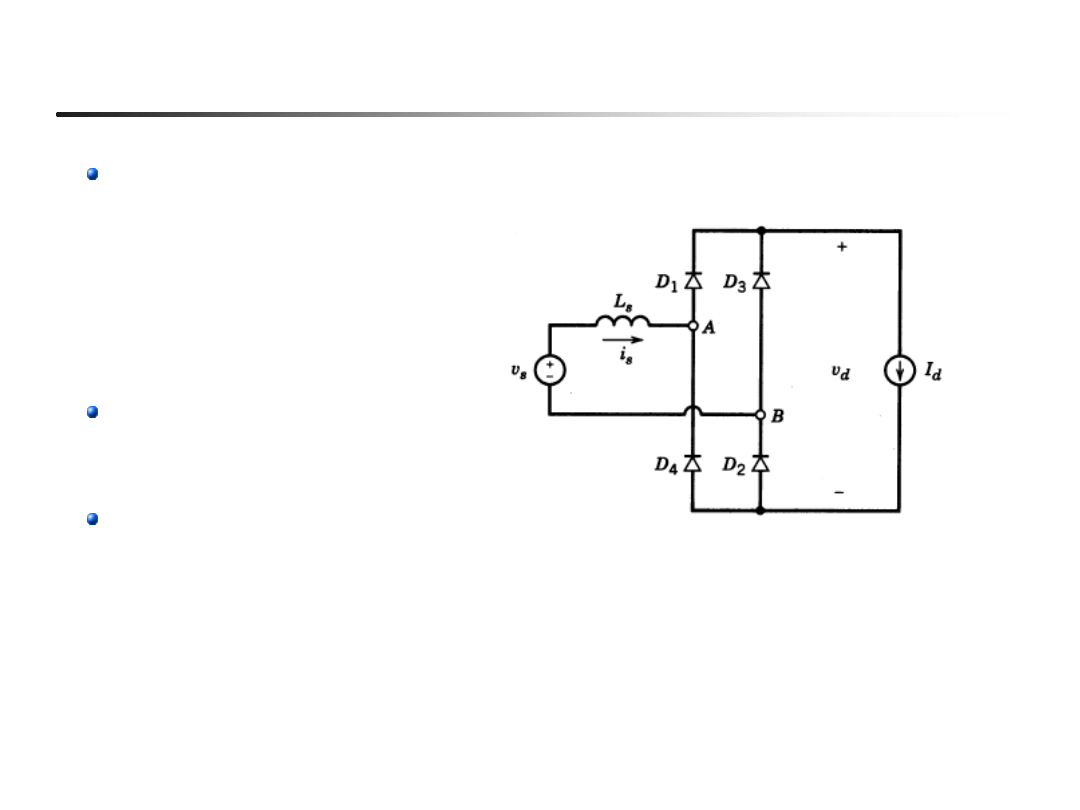
Przekształtnik mostkowy, 1-fazowy
Komutacja powoduje
podobne efekty, jak
poprzednio opisane
(zmniejszenie szybkości
zmian prądu i
s
, spadek
średniego napięcia
wyjściowego V
d
)
Podczas komutacji
przewodzą wszystkie cztery
tyrystory (diody)
Wzory na średnie napięcie
wyprostowane są podobne
(ale nie identyczne!)
EN- w04
20
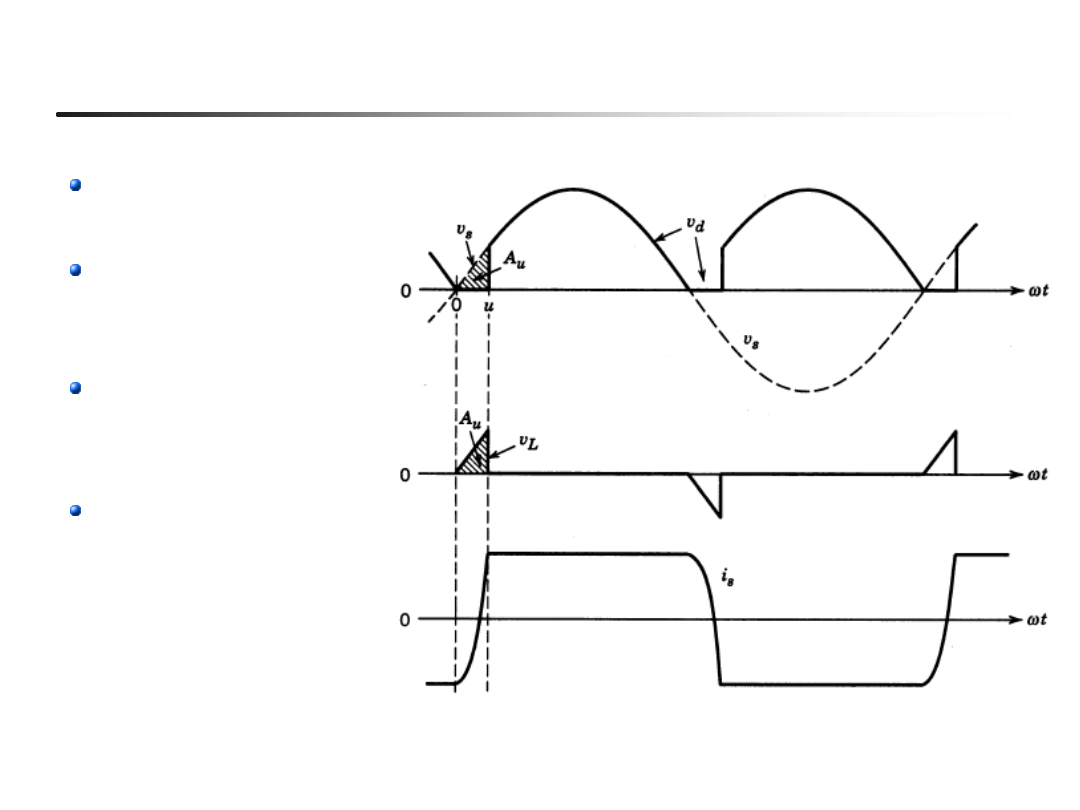
Komutacja w 1-fazowym mostku diodowym
Gdy
v
s
< 0
przewodzą D3 i D4
Gdy
v
s
staje się
dodatnie przewodzą
również D1 i D2
Prąd sieci
i
s
zmienia
się w granicach od -
I
d
do
I
d
Napięcie
v
d
jest
podczas komutacji
zerowe
EN- w04
21
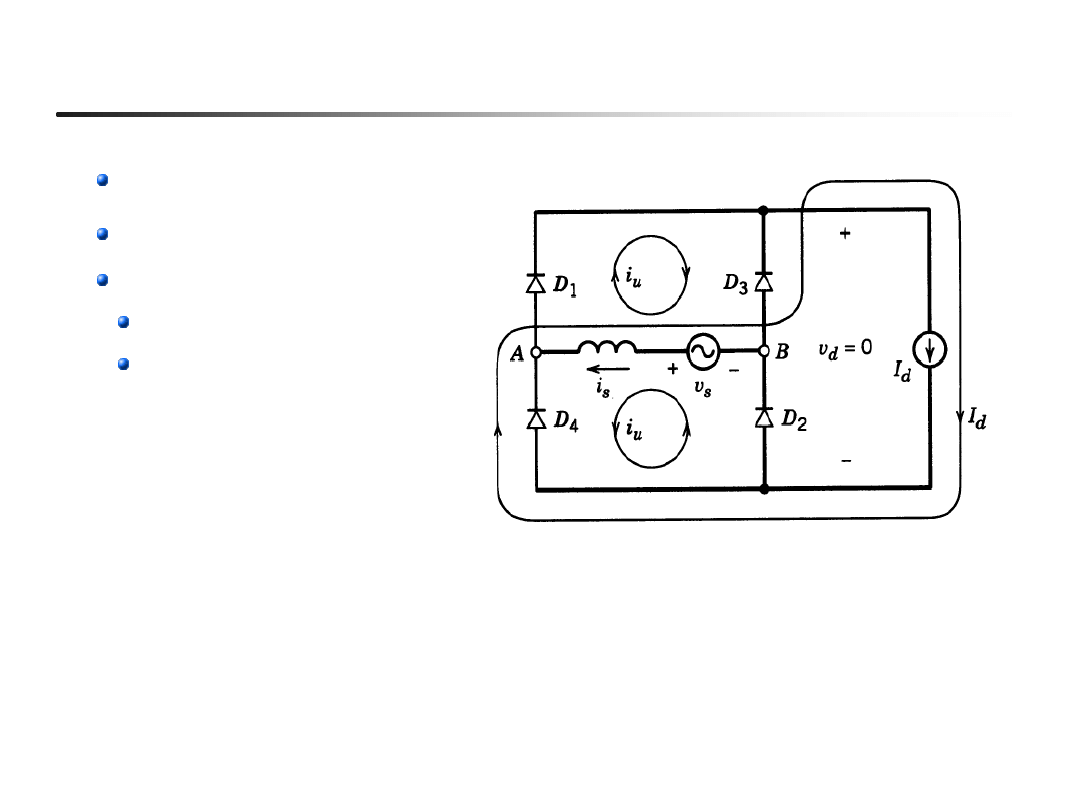
Analiza komutacji metodą prądów oczkowych
Schemat ważny dla:
Przewodzą 4 zawory:
D3 i D4 kontynuują,
D1 i D2 zaczynają
μ
<
ωt
<
0
komutacji
obwodu
oczkowy
prad
=
i
μ
μ
d
s
μ
d
D4
D3
μ
D2
D1
I
=
i
i
I
=
i
=
i
i
=
i
=
i
2i
0
0
=
v
;
>
v
d
s
EN- w04
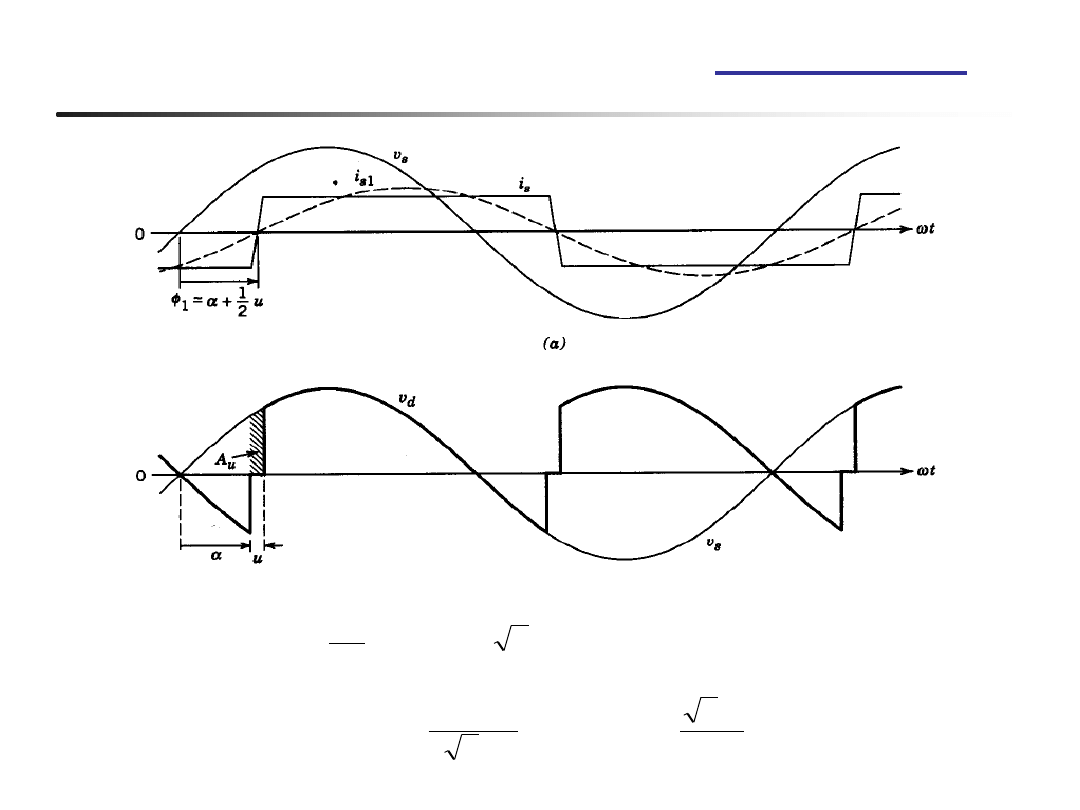
22
Kąt komutacji
m
w 1-fazowym mostku tyrystorowym
μ
+
α
α
ωL
V
=
I
lub
V
I
ωL
α
=
μ
+
α
I
ωL
=
I
di
ωL
=
dωω
ωt
V
=
A
dt
di
L
=
v
=
v
s
s
d
s
d
s
d
s
d
d
I
s
s
s
μ
+
α
α
μ
s
s
Ls
s
cos
cos
2
2
:
2
2
cos
cos
2
sin
2
EN- w04
23
Średnie napięcie wyprostowane
Spadek napięcia proporcjonalny do powierzchni A
m
Wzór na średnie napięcie wyjściowe i komutacyjny spadek napięcia
(w zależności od kąta
a
i pradu I
d
):
( wzór na średnie napięcie w funkcji kątów
a
i
m
)
s
k
s
d0
d
k
d0
d
ωL
π
=
X
;
V
π
=
V
;
I
X
α
V
=
V
2
2
2
cos
μ
+
α
+
α
V
=
μ
+
α
+
α
π
V
=
V
μ
+
α
α
ωL
V
π
ωL
α
π
V
=
V
d0
s
d
s
s
s
s
d
cos
cos
2
cos
cos
2
cos
cos
2
2
2
cos
2
2
d
s
μ
d
d
s
s
d
I
π
ωL
=
π
=
ΔV
π
I
ωL
α
π
V
=
V
2
2
2A
2
cos
2
2
EN- w04
24
Przesunięcie podstawowej składowej prądu sieci
Z powodu komutacji przesunięcie jest większe niż
a
Gdyby założyć liniowy przebieg prądu w czasie komutacji, to:
Z równowagi mocy (brak strat w przekształtniku):
Inne współczynniki muszą być liczone z uwzględnieniem kształtu prądu
2
/
cos
μ
+
α
DPF
2
/
cos
/
2
cos
2
μ
+
α
V
I
ωL
π
α
I
V
I
I
V
=
DPF
I
V
=
P
s
d
s
d
d0
s1
d
d
s1
s
EN- w04
25
Przesunięcie podstawowej składowej prądu sieci
Z powodu komutacji przesunięcie jest większe niż a
Gdyby założyć liniowy przebieg prądu w czasie komutacji, to:
Z równowagi mocy (brak strat w przekształtniku):
Inne współczynniki muszą być liczone z uwzględnieniem kształtu prądu
2
/
cos
μ
+
α
DPF
2
/
cos
/
2
cos
2
μ
+
α
V
I
ωL
π
α
I
V
I
I
V
=
DPF
I
V
=
P
s
d
s
d
d0
s1
d
d
s1
s
EN- w04
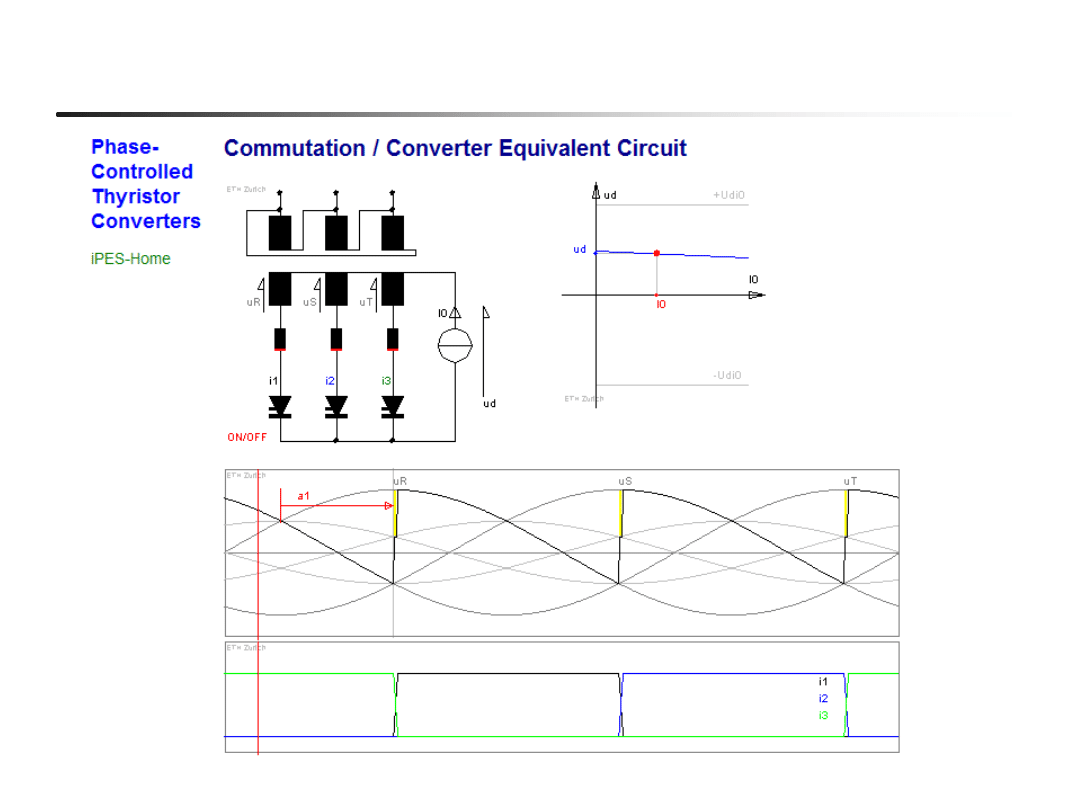
26
Komutacja w prostowniku 3-pulsowym; charakterystyka Vd(Id)
EN- w04
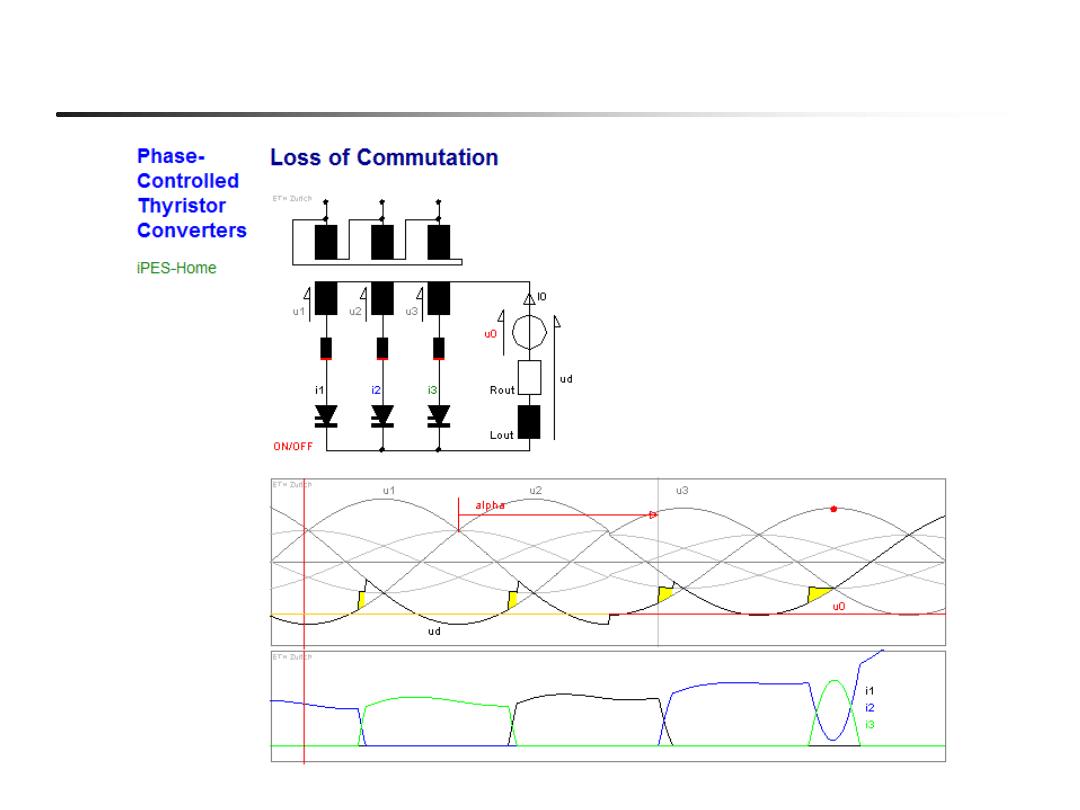
27
Przekształtnik 3-pulsowy w pracy falownikowej; przewrót
EN- w04
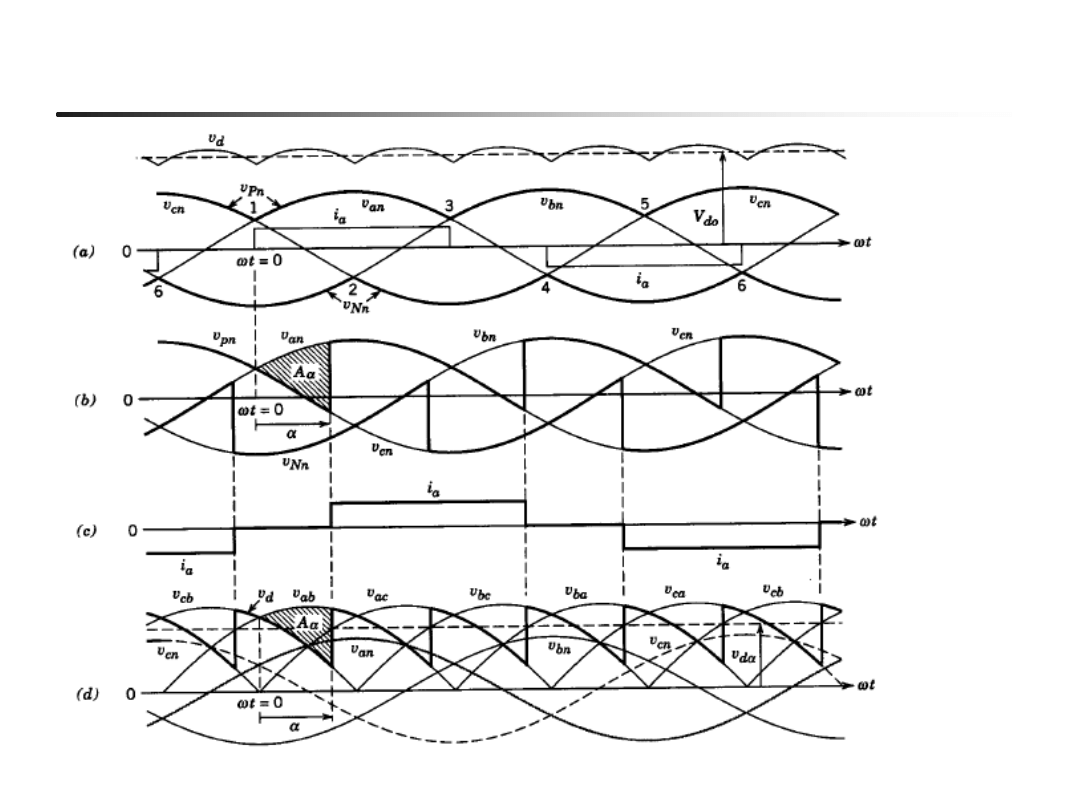
29
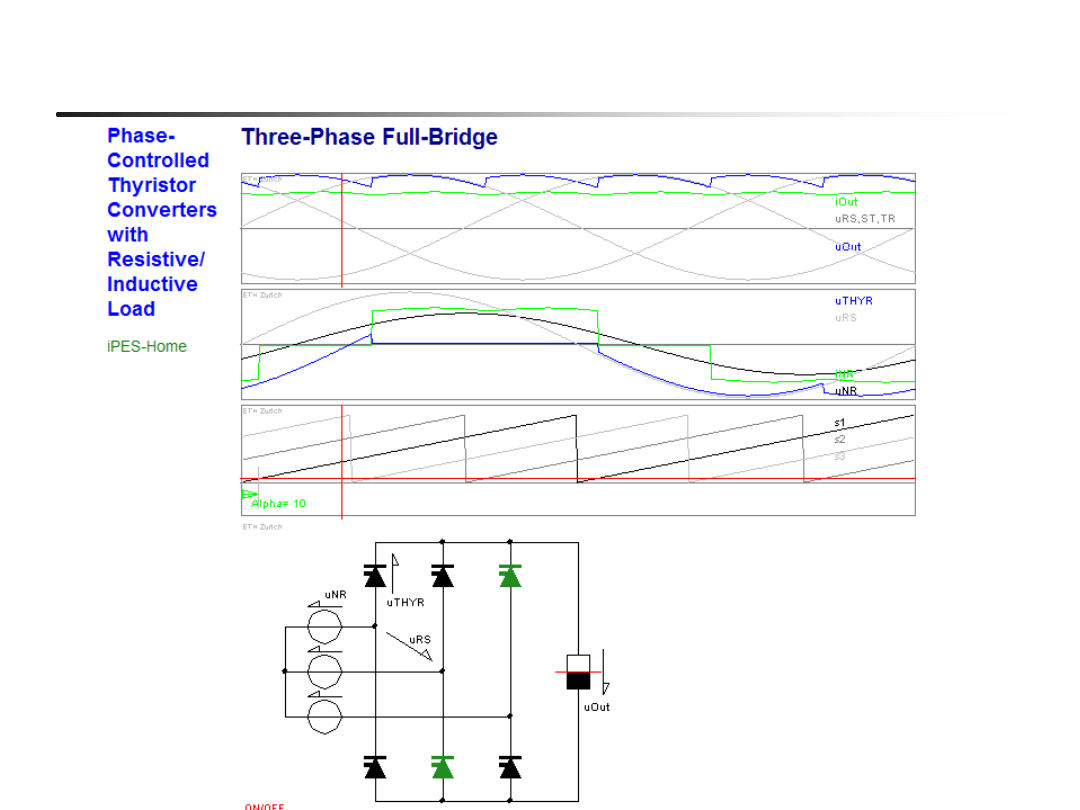
Przekształtnik 6-pulsowy mostkowy (Ls=0,id=const)
EN- w04
30
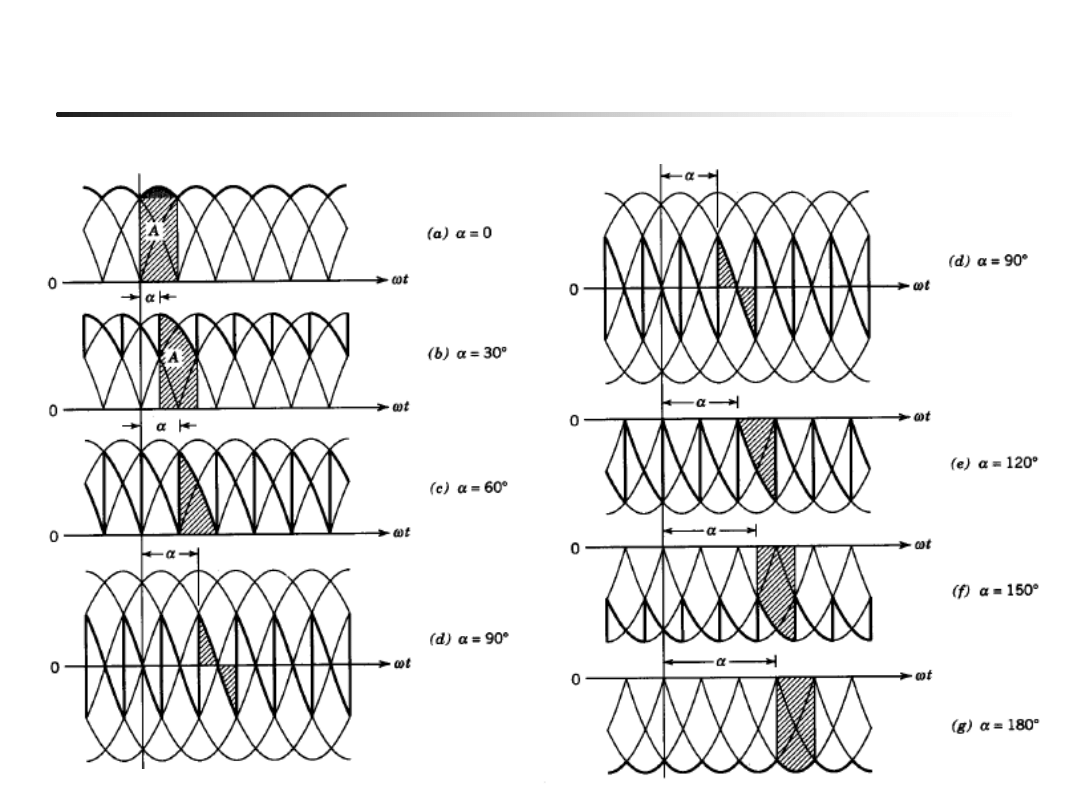
Przekształtnik 6-pulsowy : przebiegi napięcia vd
praca prostownikowa
praca falownikowa
EN- w04
31
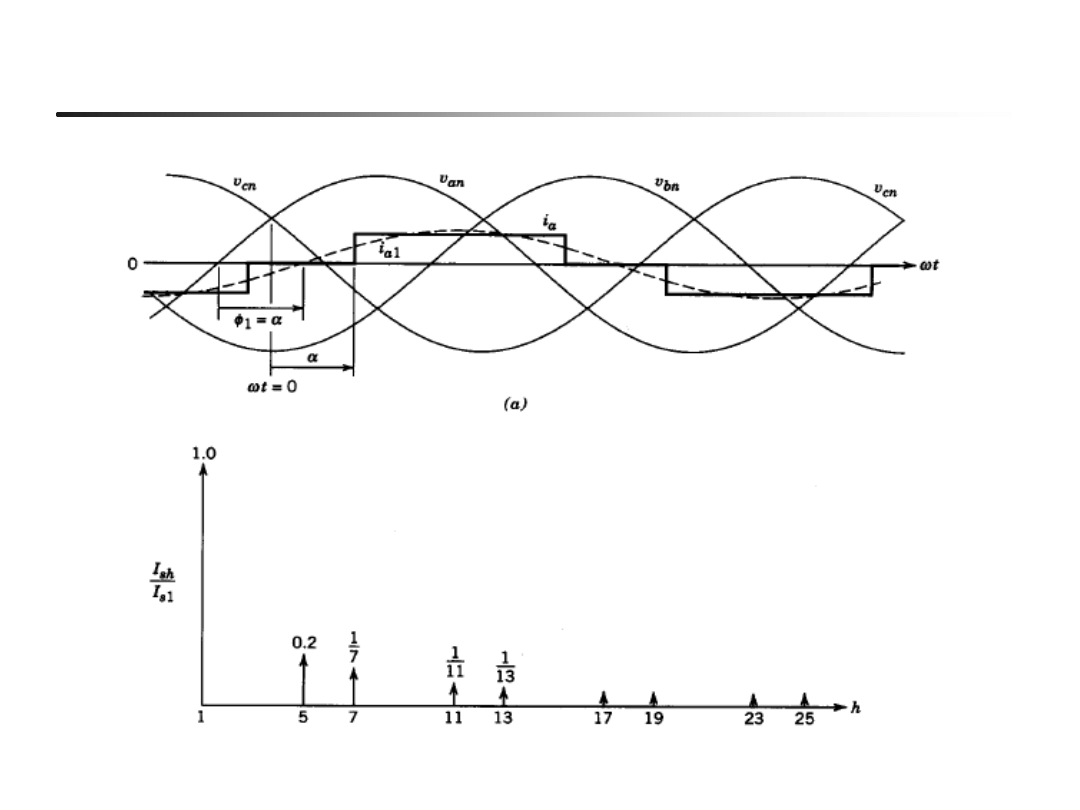
Przekształtnik 6-pulsowy : przebiegi prądu sieci
EN- w04
32
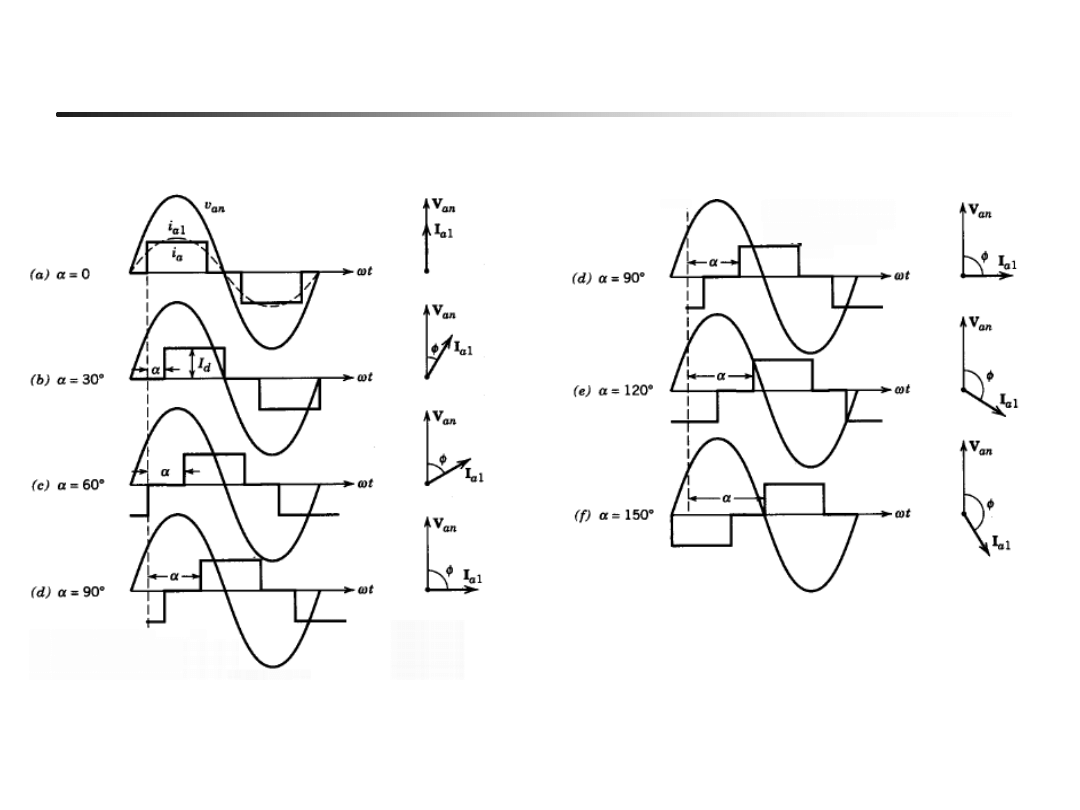
Przekształtnik 6-pulsowy : prąd sieci dla różnych kątów
a
praca prostownikowa
praca falownikowa
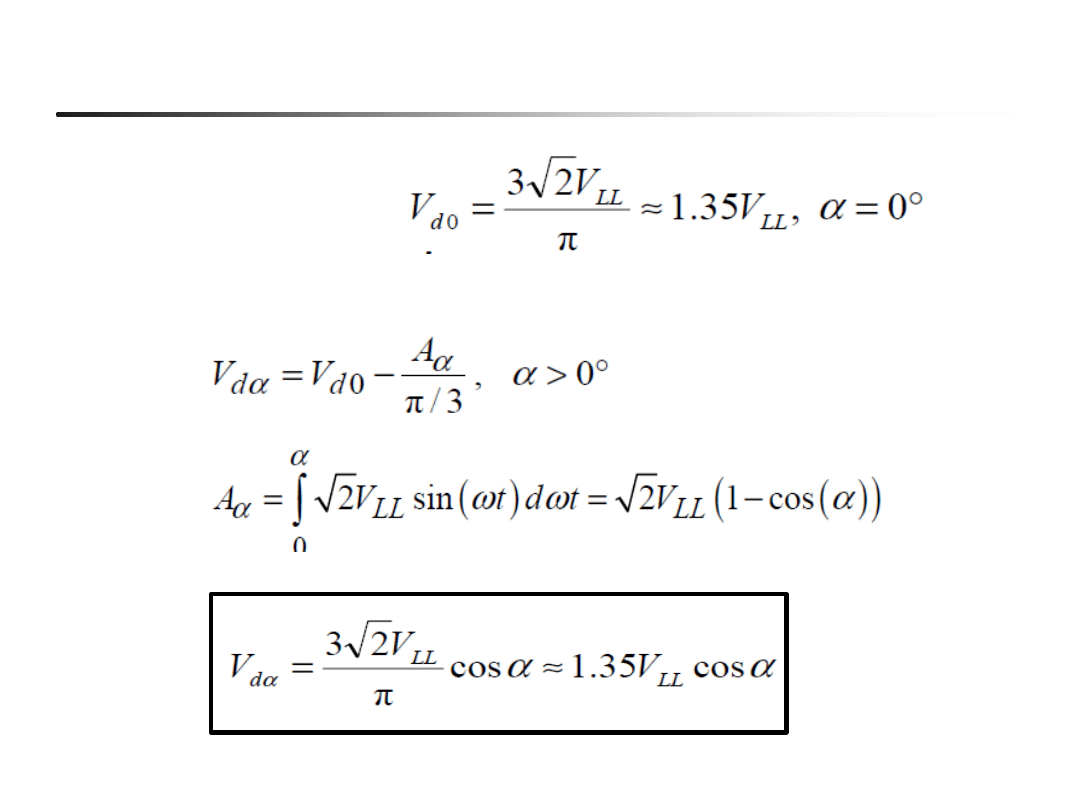
EN- w04
33
Przekształtnik 6-pulsowy : charakterystyka sterowania V
d
(
a
)
Diodowy, lub
a
=0 :
efekt sterowania :
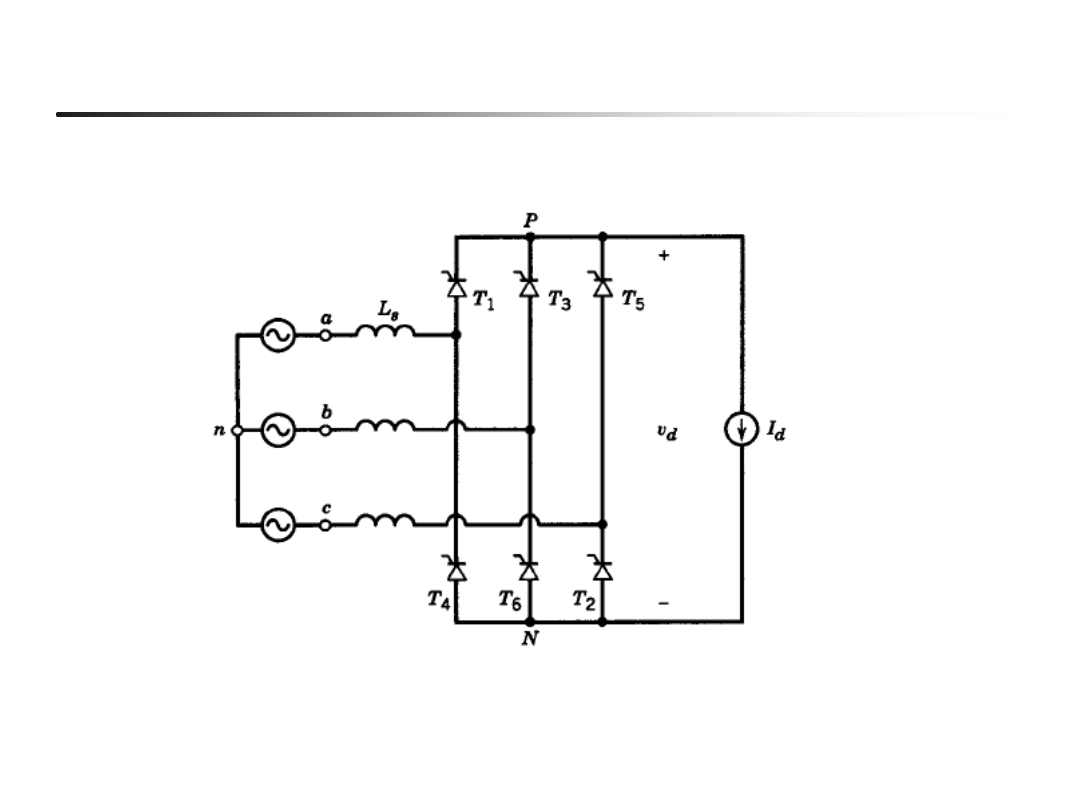
EN- w04
34
Przekształtnik 6-pulsowy (Ls >0; id=const)
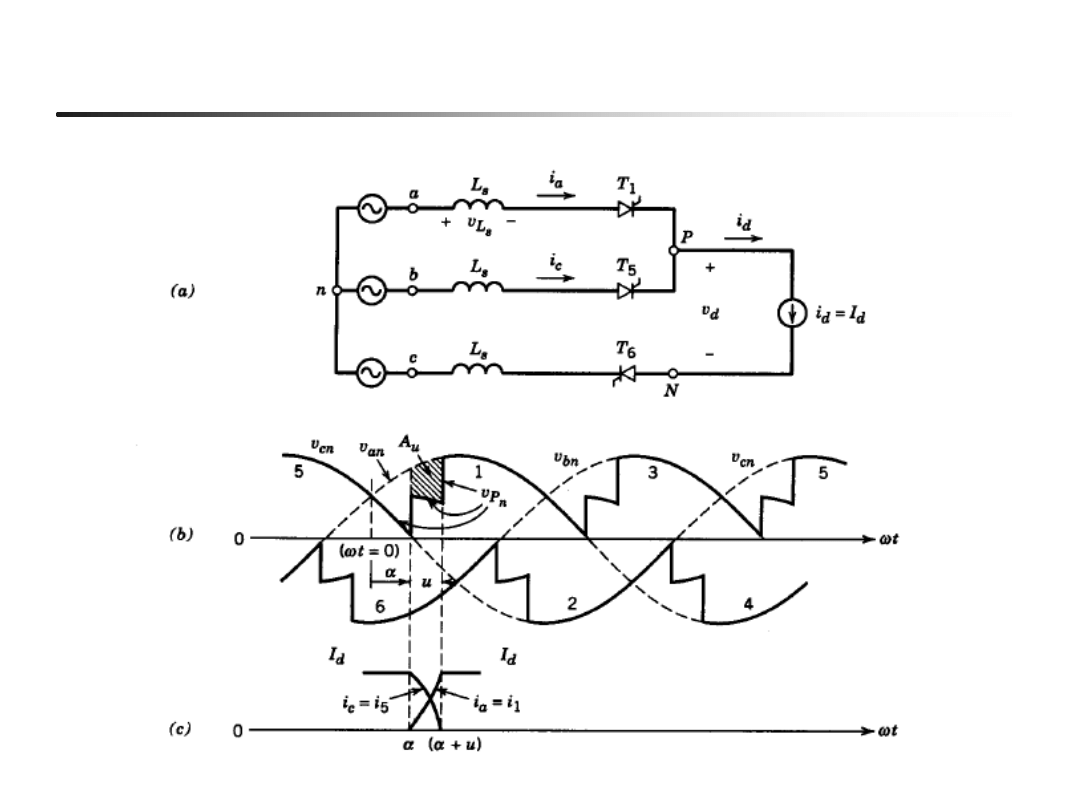
EN- w04
35
Napięcie i prądy podczas komutacji
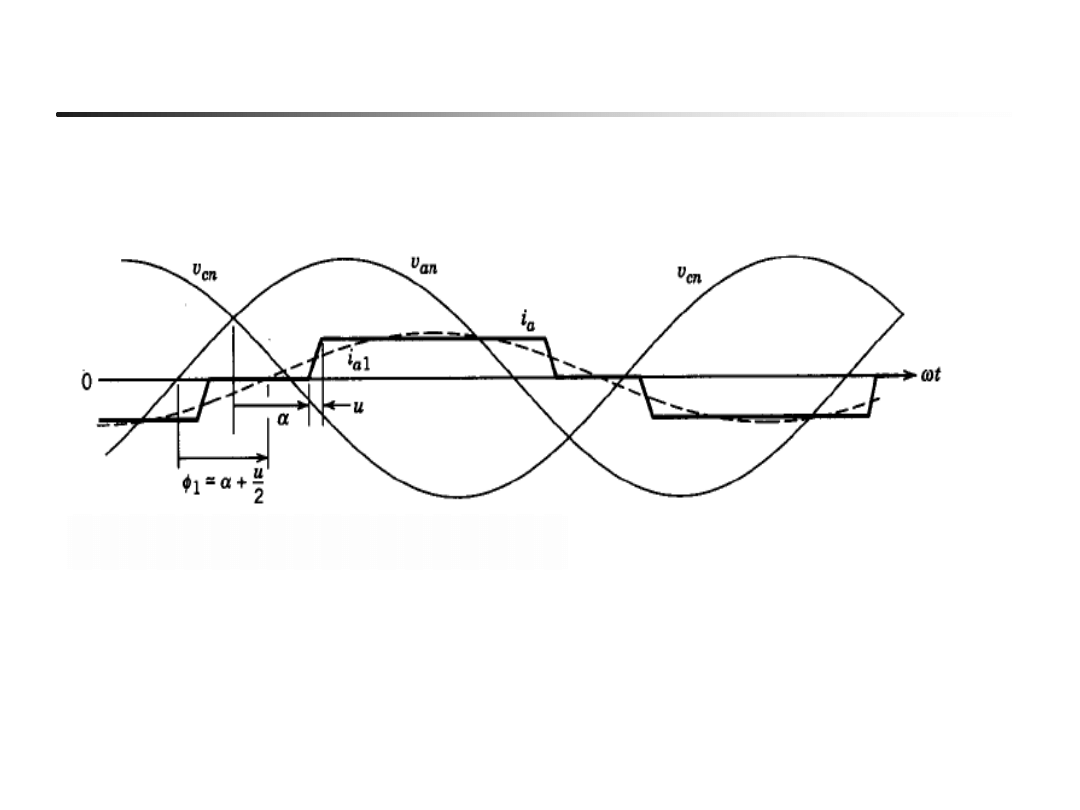
EN- w04
36
Prąd pobierany z sieci przez przekształtnik 6-pulsowy (Ls>0)
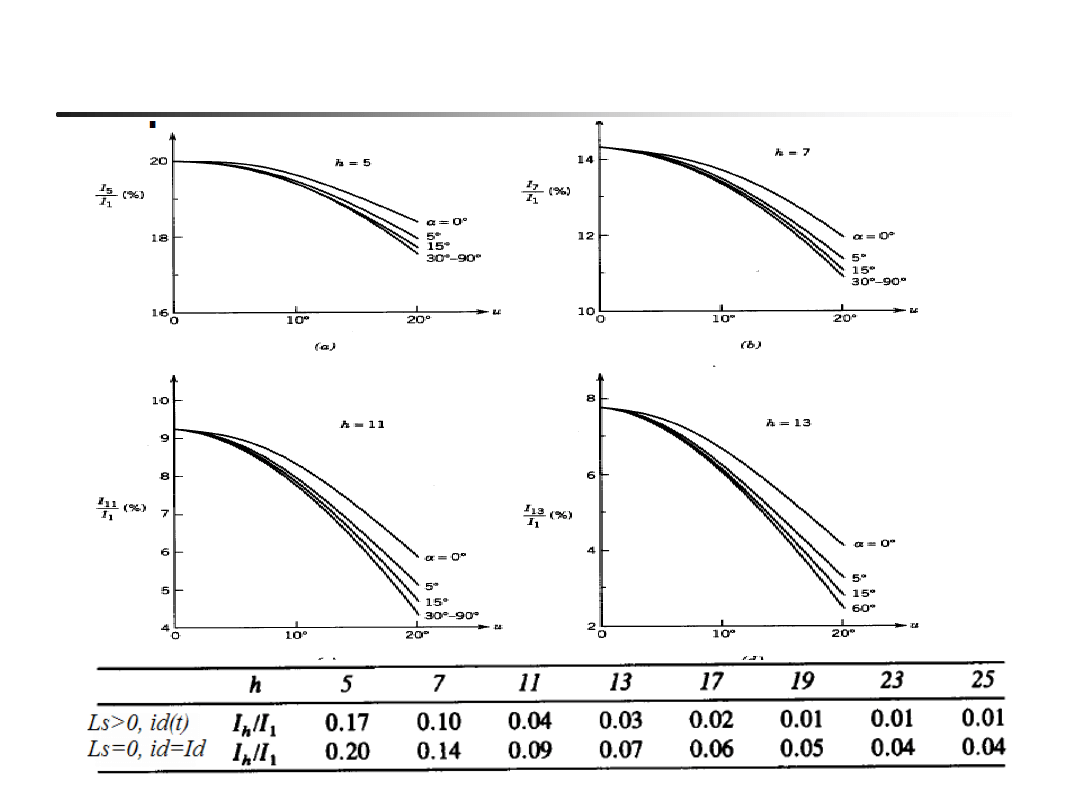
EN- w04
37
Harmoniczne prądu sieci (p=6, Ls>0)
EN- w04
38
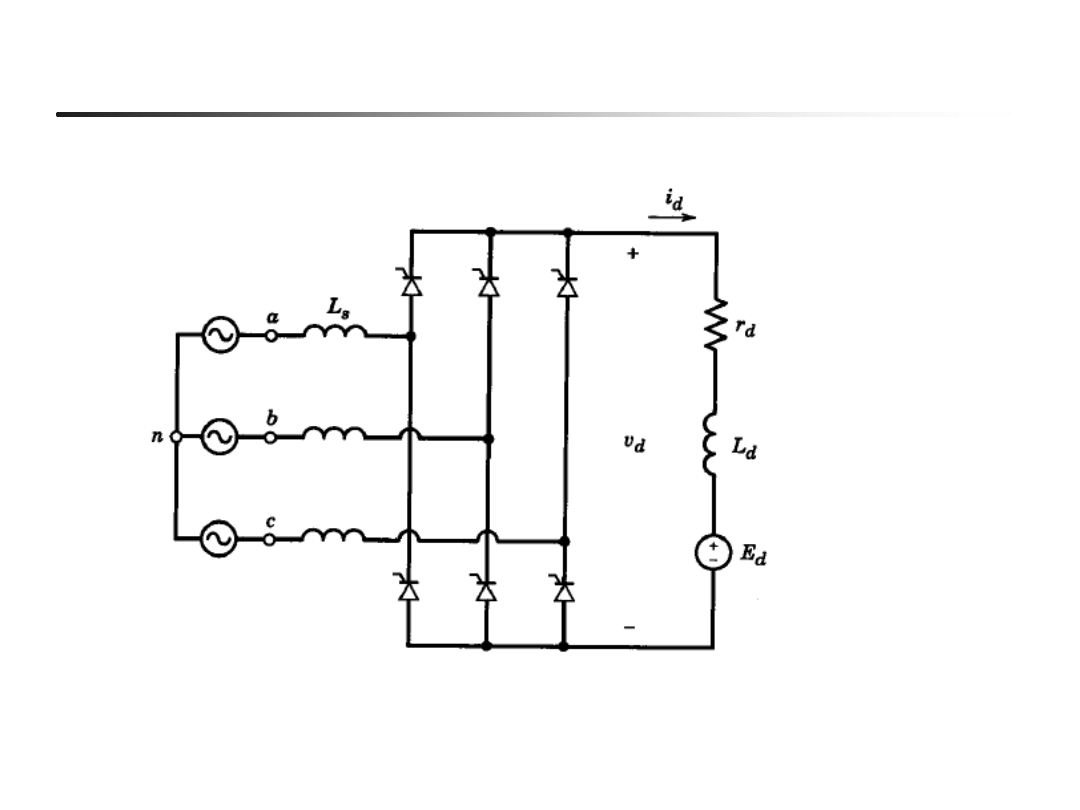
Przekształtnik 6-p, realistyczny model obciążenia (Rd-Ld-Ed))
EN- w04
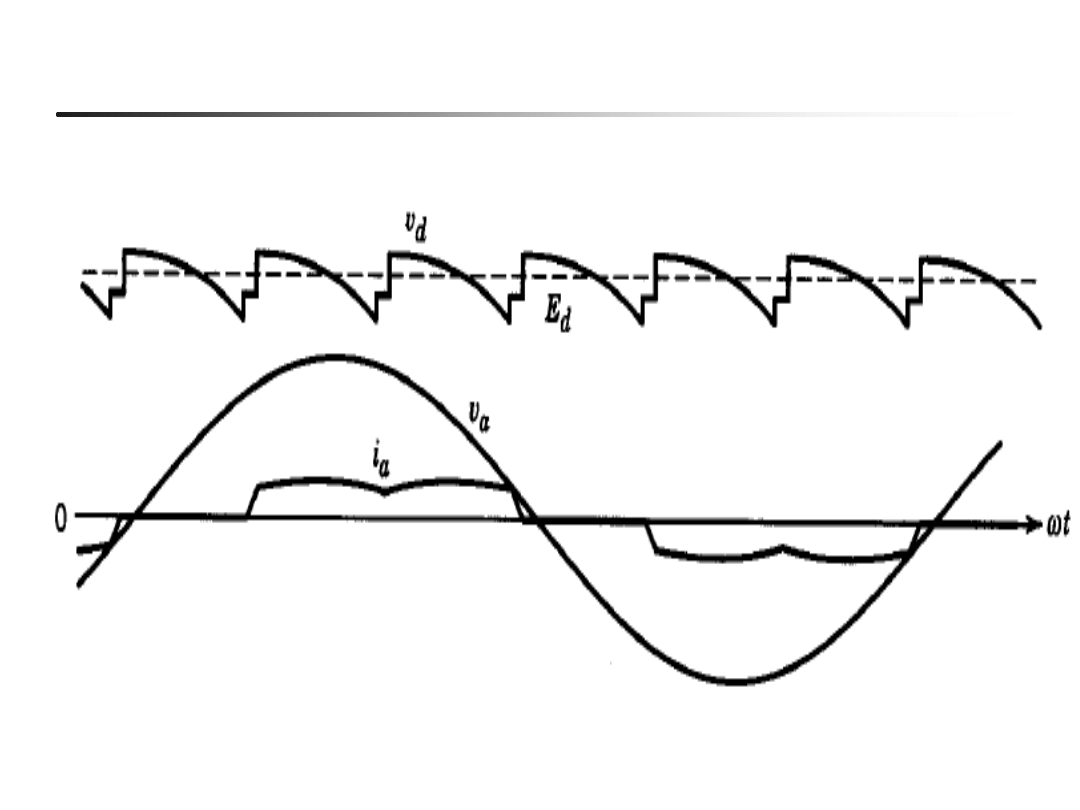
39
Napięcia i prądy zbliżone do realnych (p=6, Ls>0, Rd-Ld-Ed)
(przewodzenie ciągłe)
EN- w04
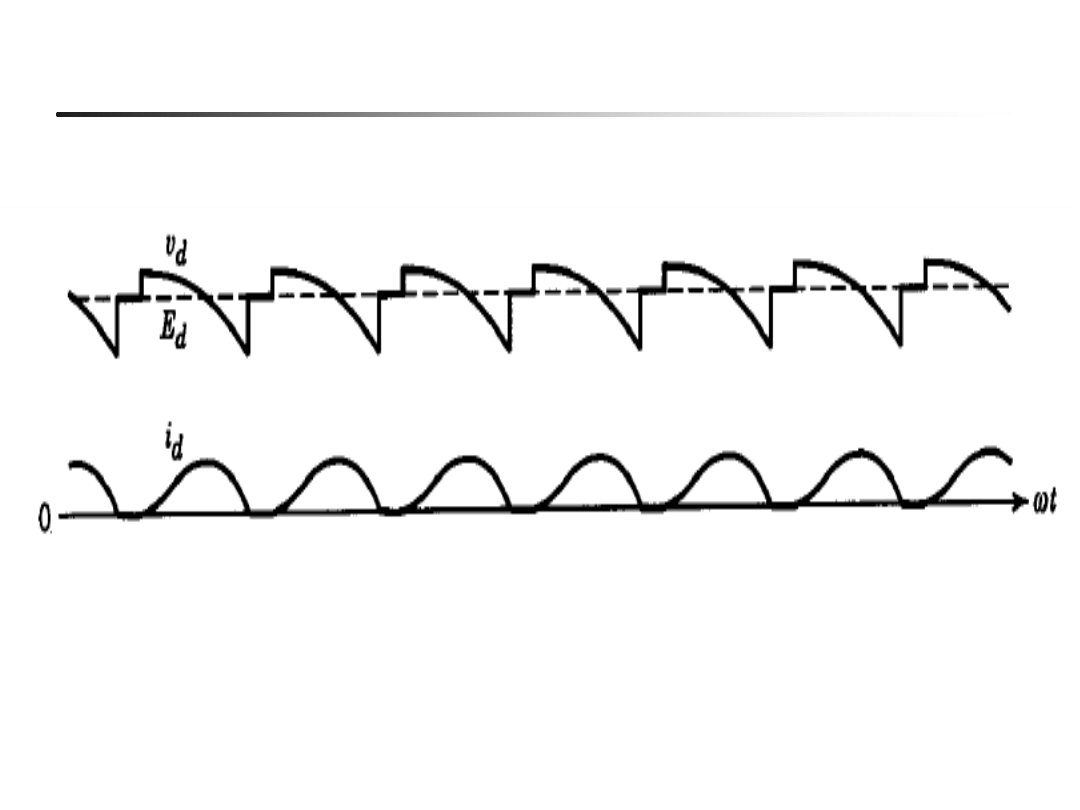
40
Napięcia i prądy zbliżone do realnych (p=6, Ls>0, Rd-Ld-Ed)
(przewodzenie przerywane)
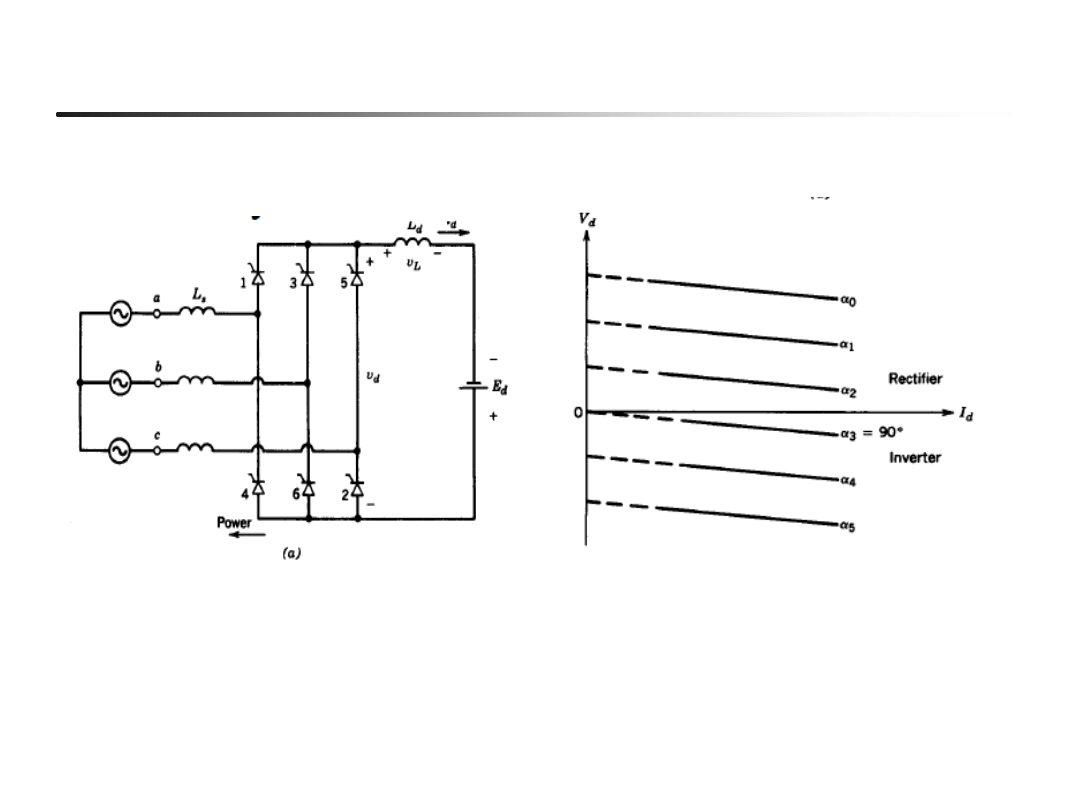
EN- w04
41
Charakterystyki zewnętrzne Vd(Id) przy różnych kątach
a
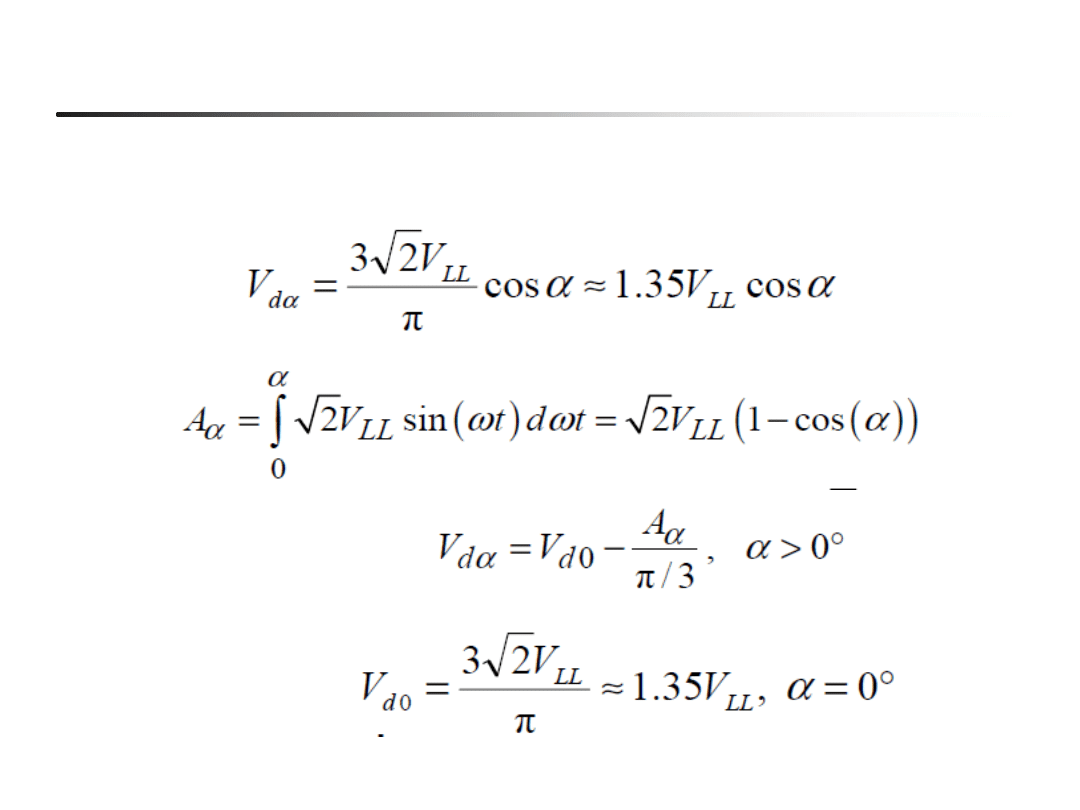
EN- w04
42
Średnie napięcie wyjściowe przy przewodzeniu
ciągłym
EN- w04
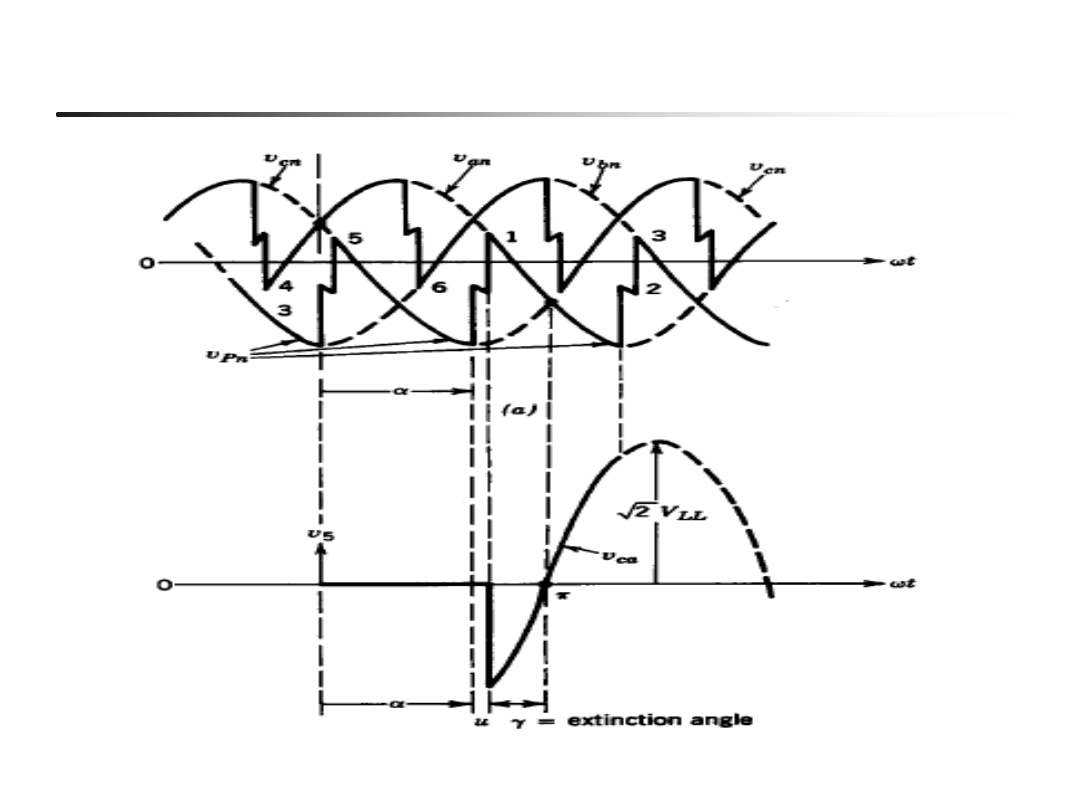
43
Kąt dysponowany na wyłączenie (zapas kątowy) przy pracy
falownikowej
EN- w04
44
Wzory na napięcie wyjściowe przekształtnika p-pulsowego
przy przewodzeniu ciągłym
s
k
s
d0
d
k
d0
dα
ωL
π
p
=
X
V
p
π
π
p
=
V
I
X
α
V
=
V
2
2
sin
cos
EN- w04
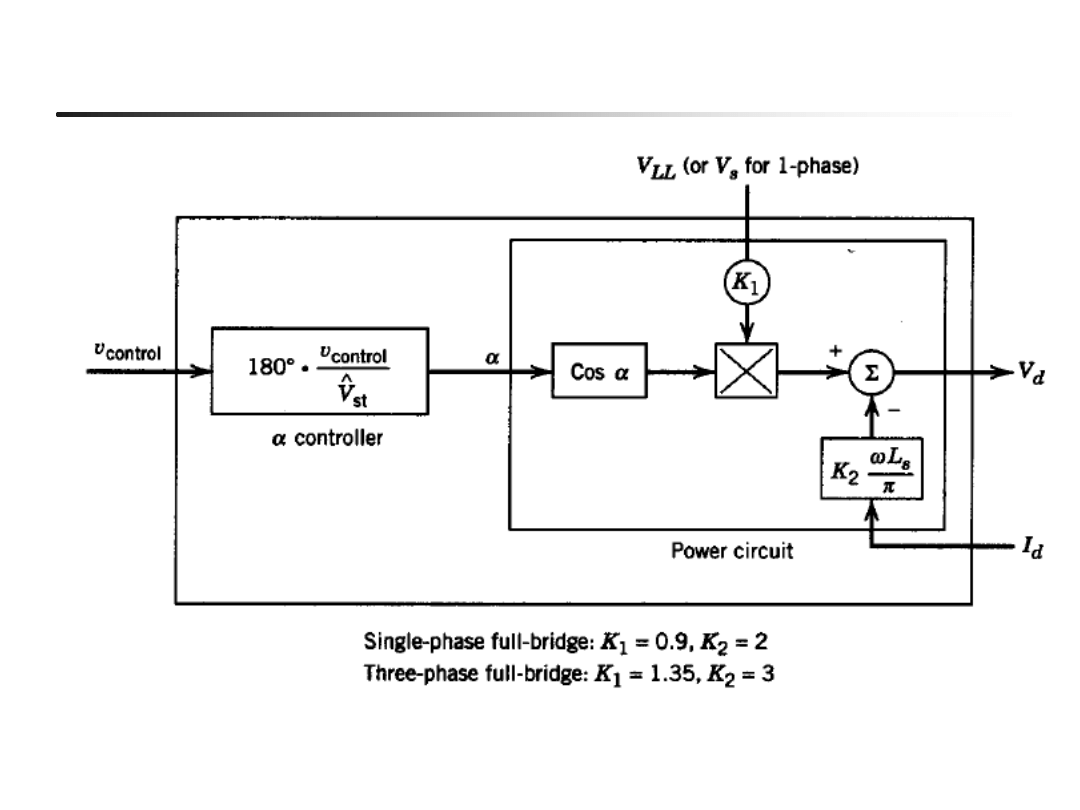
45
Schemat blokowy przekształtnika (przy przewodzeniu
ciągłym)
