Laboratorium Podstaw Informatyki

Kierunek Elektrotechnika

Ćwiczenie 8.1

Matlab

Narzędzie obliczeń numerycznych

Część I

Operatory i funkcje

Zakład Metrologii AGH

Kraków 1998

Laboratorium Podstaw Informatyki

Strona 2

1. Wprowadzenie

Matlab jest uniwersalnym środowiskiem obliczeń numerycznych. Podstawowym typem na
którym operuje użytkownik jest macierz wartości zespolonych. Jej szczególne przypadki to
macierz rzeczywista, wektor, wartość skalarna, macierz rzadka. Zestaw operatorów i
gotowych funkcji jest dostosowany do tego typu, dzięki czemu użytkownik może liczyć na
wykorzystanie wektoryzacji obliczeń, co skutkuje dużą szybkością tego rodzaju obliczeń w
porównaniu z analogicznymi skalarnymi, wykonywanymi iteracyjnie. W początkach
istnienia Matlab był łatwym w użytkowaniu interfejsem do bibliotek numerycznych
Fortranu LINPACK i EISPACK. Z czasem zawartość przyborników Matlaba (ang. toolbox)
przekroczyła zakres tych bibliotek.
Możliwe jest oczywiście zbudowanie w językach ogólnego przeznaczenia, typu C czy język
obiektowy C++, systemu operatorów i funkcji analogicznego do Matlaba. W czym więc
tkwi jego przewaga nad językami programowania ogólnego przeznaczenia ? Podobnie jak
Basic zyskał dużą popularność dzięki możliwości szybkiego zaprogramowania prostych
aplikacji, tak Matlab dzięki konstrukcji interpretera, dostarczaniu zestawu gotowych
operatorów i dużej ilości specjalizowanych funkcji nadaje się dobrze do szybkiego
rozwiązywania krótkich problemów numerycznych, a w szczególności macierzowych. Te
cechy, które dają efekt w postaci łatwości programowania (interpretacja, brak konieczności
deklarowania zmiennych, ubogi zestaw konstrukcji sterujących) ograniczają rozmiar
użytecznego kodu aplikacji pisanych w tym środowisku do kilkuset linii.
Dużym ograniczeniem tego środowiska jest umiarkowana szybkość działania w porównaniu
z kodem kompilowanym w języku ogólnego przeznaczenia. Mała pociechą, ze względu na
pracochłonność i konieczność zachowania ustalonego sposobu przekazywania parametrów,
jest przy tym możliwość dołączania funkcji w postaci kompilowanych modułów typu DLL.
Podsumować to wprowadzenie można więc słowami, że Matlab jest dobrym środowiskiem
do tworzenia i testowania prototypów aplikacji z dziedziny przetwarzania danych
numerycznych.

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 3

2. Zadanie 1 - operacje macierzowe

2.1

Inicjowanie macierzy

Inicjowanie macierzy przez przypisanie wartości początkowych zapisuje się w Matlabie w
sposób naturalny, przez podanie kolejnych odseparowanych wartości. Kolejne wartości
rozdzielone przecinkiem lub spacją tworzą wiersz macierzy. Przejście do nowego wiersza
macierzy wymusza się znakiem średnika lub końca linii. Np. macierz kwadratową o
wartościach A(1,1)=1.0, A(1,2)=2.0, A(2,1)=3.0, A(2,2)=4.0 można utworzyć przez ciąg
przypisań do elementów lub jedną instrukcją:

A=[
1 2
3 4];
% Równoważny zapis w jednej linii
A=[1 2; 3 4];

Załóżmy że naszym zadaniem jest utworzenie wektora zawierającego wartości od 0 do 1 co
0.1. Ręczne wpisywanie wartości jak w powyższym przykładzie jest zbyt męczące.
Przyzwyczajenie z języka C każe zbudować pętlę programową inicjującą wektor. W
Matlabie będzie ona miała postać:

V=[]; % Czyszczenie zawartości wektora
for i=0:10
V(i+1)=i/10;
end

Indeksowanie przy przypisaniu poza aktualny rozmiar wektora powoduje automatyczne
rozszerzenie rozmiaru wektora. Pierwsze udoskonalenie tego sposobu inicjowania to
wykorzystanie faktu, że zmienna sterującą w pętli for może mieć dowolne wartości
zmieniane z dowolnym przyrostem. Nowa postać instrukcji inicjujących wektor ma postać:

V=[]; % Zaczynamy od pustego wektora
for i=0:0.1:1
V=[V; i]; % Nowy element na koniec
end

Zmienna sterująca nie może być już indeksem w wektorze ponieważ przyjmuje wartości
rzeczywiste i byłaby zaokrąglana do najbliższej liczby całkowitej. Stąd rozszerzanie
rozmiaru wektora przez dodawanie nowego elementu na koniec. Zapis i=0:0.1:1 można
rozumieć nie tylko jako podanie wartości początkowej dla zmiennej sterującej, przyrostu i
wartości końcowej. W istocie jest to podanie wektora wartości, które będzie przyjmowała
zmienna sterująca. Zapis 0:0.1:1 oznacza wektor wartości od 0 do 1 co 0.1. Nasza instrukcja
inicjująca może więc mieć postać:

V=0:0.1:1;

Zysk z takiego zapisu wektorowego to szybkość wykonania operacji. Stosowany zapis
generuje wektor wierszowy. Żeby otrzymać wektor kolumnowy można transponować
wygenerowany wektor operatorem transpozycji, lub zastosować zapis transformujący
macierz do wektora kolumnowego.

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 4

V=V’;

% Transponowanie macierzy

V=V(:);

% Wymuszenie postaci kolumnowej

Inicjowanie na najczęściej wykorzystywane wartości 0 i 1 wykonują funkcje tworzenia
specyficznych macierzy. Funkcja zeros() generuje macierz zerową o podanych wymiarach,
ones() macierz jedynkową, eye() macierz jednostkową a diag() macierz diagonalną.

Utwórz wektor kolumnowy x o wartościach od -1 do 1 co 0.1 i wektor y o dwukrotnie
większych wartościach niż x i dodatkowo pomniejszonych o wartość 0.5. Utwórz wektor x1
o takim samym wymiarze jak wektor x (poda go funkcja size()) zawierający same jedynki.
Połącz wektory x i x1 w jednej macierzy xx o dwóch kolumnach.

2.2

Obliczanie wyrażeń macierzowych

Podobnie do inicjowania wektorów wyznaczenie np. sumy kwadratów elementów wektora
można wykonać w pętli z sumowaniem, ale prostszy zapis i szybsze wykonanie ma
instrukcja z operatorem mnożenia macierzowego.

x=x(:)

% Wymuszenie postaci kolumnowej wektora

% Mnożenie w pętli
wynik=0;
for i=1:length(x)
wynik=wynik+x(i)*x(i);
end
% Z wykorzystaniem operatora mnożenia skalarnego i funkcji sumowania elementów
wynik=sum(x.*x);
% Z wykorzystaniem operatora mnożenia macierzowego
wynik=x’*x; % Iloczyn wektorowy z macierzą transponowaną da ten sam efekt

Ze względu na różnice definicji operatorów działających na poszczególnych elementach
macierzy i operatorów macierzowych zestaw operatorów Matlaba zawiera operatory
skalarne i macierzowe. Operatory skalarne wykonują operacje na elementach macierzy. Są
to operator mnożenia poszczególnych elementów dwóch macierzy „.*”, operator dzielenia
elementów „./” i operator podnoszenia do potęgi poszczególnych elementów macierzy „.^”.
Operatory macierzowe mają zapis bez kropki. Istnieją dwa operatory dzielenia
odpowiadające mnożeniu lewo (\) i prawostronnemu (/) przez odwrotność macierzy.
Dla przykładowych macierzy a=[1 2;3 4] i b=[5 4;6 8] operacje skalarne i wektorowe dadzą
różne wyniki.

a.*b=[5 8; 18 32], a./b=[0.2 0.5; 0.5 0.5],
a*b=[17 20; 39 44], a/b=[-0.25 0.375; 0 0.5], a\b=[-4 0; 4.5 2]
a+b=[6 6; 9 12], a-b=[-4 -2; -3 -4]

Operatory dodawania i odejmowania mają takie samo znaczenie dla obydwu rodzajów
operacji więc mają tylko jedną postać.

Dla macierzy xx i y wygenerowanych w poprzednim zadaniu oblicz wartość wyrażenia:
(xx

T

*xx)

-1

*xx

T

*y

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 5

3. Zadanie 2 - m-pliki czyli skrypty i funkcje Matlaba

3.1

Algorytm najmniejszej sumy kwadratów

Wzór podany w poprzednim zadaniu opisuje algorytm najmniejszej sumy kwadratów LS.
Podaje on wartości współczynników zależności liniowej między wektorami danych
wejściowych i wyjściowych wyznaczone przy warunku najmniejszej sumy kwadratów
odległości wartości z wektora danych wyjściowych i wartości wyznaczonych na podstawie
danych wejściowych i wyliczonych parametrów. Przyjęta w zadaniu postać wektora xx
odpowiada założonej zależności funkcyjnej między danymi wejściowymi x i wyjściowymi
y w postaci y=a*x+b, gdzie a i b są poszukiwanymi parametrami. Ponieważ przy
generowaniu wektorów x i y przyjęliśmy, że y=2*x-0.5, stąd parametry otrzymane przez
wyznaczenie wartości wyrażenia LS są równe współczynnikom przyjętej zależności, a
dopasowanie prostej opisanej wyznaczonymi parametrami do danych jest dokładne (suma
kwadratów odległości jest równa zero).
Algorytm LS najczęściej stosuje się dla danych zawierających zakłócenia losowe, jak np.
dla danych pomiarowych. W tym przypadku daje on współczynniki prostej w przestrzeni
najlepiej dopasowanej do danych (w sensie LS). Ze względu na to, że algorytm ten jest
często wykorzystywany, wygodnie będzie zawrzeć go w postaci funkcji operującej na
danych przekazanych w parametrach. Inna możliwość to utworzenie skryptu, ale wtedy
przekazanie parametrów i odebranie wyników musi nastapić przez zmienne globalne.
Dane testowe znajdują się w pliku dyskowym w formacie ASCII czyli w zapisie znakowym
dziesiętnym. Instrukcja load wczytuje dane z pliku ASCII do tablicy o nazwie takiej jak
nazwa pliku. Poszczególne kolumny pliku tworzą kolumny macierzy. Wydzielenie kolumn
z takiej macierzy wielokolumnowej realizuje instrukcja wskazania zakresu przy
indeksowaniu, jak w poniższym przykładzie.

load abc.dat % Plik abc.dat zawiera trzy kolumny danych w 10 wierszach
a=abc(:, 1); % Wektor a zawiera wszystkie wiersze pierwszej kolumny danych
bc=abc(1:5, 2:3);

% Macierz bc zawiera pierwsze pięć wierszy z kolumn 2 i 3

Do tworzenia wykresów na podstawie danych zawartych w wektorach służy funkcja plot().
Kilka przykładów i pomoc Matlaba na temat tej komendy wyjaśnią szczegóły.

plot(y);

% Rysuje y w funkcji indeksu, łączy poszczególne punkty

plot(x, y);

% Rysuje y w funkcji x (wartości x w osi OX, y w osi OY)

plot(x, y, ‘*r’); % Rysunek czerwony, punkty nie łączone, zaznaczane gwiazdką

Zapisz algorytm LS w pliku algls.m w postaci funkcji:

function par=algls(xx, y)
par=(xx’*xx)\xx’*y;

Wczytaj dane z pliku lsm.dat (load lsm.dat). Rozdziel tablicę lsm na wektory x1, x2
(pierwsza i druga kolumna) i wektor y (trzecia kolumna). Przyjmij zależność liniową
między danymi w postaci y=a*x

1

+b*x

2

. Utwórz macierz xx z wektorów x1, x2. Przetestuj

działanie funkcji algls(). Utwórz rysunek różnic między wartościami y z pliku danych i
wartościami ye wyliczonymi z przyjętej zależności (plot(y-ye, ‘*’)).

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 6

4. Zadanie 3 - przetwarzanie danych

4.1

Wielomiany - szczególna postać funkcji

Wielomian jest funkcją jednoznacznie zdefiniowaną przez współczynniki przy
poszczególnych potęgach zmiennej i tak jest zapisywany w Matlabie. Np. dla wielomianu
x

2

-3x-5 wektor reprezentujący ten wielomian ma postać [1 -3 -5]. Matlab oferuje kilka

funkcji do operowania na wielomianach. Przykładowo wielomian charakterystyczny dla
macierzy można wyznaczyć funkcją poly(), pierwiastki wielomianu oblicza funkcja roots(),
wartość wielomianu funkcja polyval(), pochodną wielomianu funkcja polyder().
W tej chwili interesuje nas najbardziej funkcja dopasowująca wielomian do par wartości X i
Y w sensie najmniejszej sumy kwadratów.

Przeczytaj pomoc na temat funkcji polyfit() (help polyfit). Znajdź współczynniki
wielomianu drugiego rzędu dopasowanego do danych z pliku xy.dat (X-pierwsza kolumna,
Y-druga kolumna). Zilustruj rysunkiem dopasowanie do danych.

4.2

Wyznaczanie wartości charakterystycznych funkcji

Wartości dające informację o przebiegu funkcji to jej miejsca zerowe i ekstrema. Funkcje
Matlaba wyznaczają numeryczne przybliżenia tych wartości wg. określonego algorytmu.
Większość z nich wymaga podania nazwy funkcji, i nie akceptuje zapisu z dodatkowymi
poza punktem wyznaczenia wartości parametrami. Np. dla funkcji wyznaczania miejsc
zerowych niepoprawny będzie zapis fzero(‘polyval(wsp, x)’, x0). Funkcja, której miejsce
zerowe wyznaczamy musi być w takim przypadku zapisana w m-pliku.

Zapisz wielomian z poprzedniego zadania w postaci funkcji w m-pliku zwracającej wartość
w punkcie przekazanym w parametrze. Wyznacz jego miejsca zerowe (fzero()) i punkt
minimalny (fmin()). Zweryfikuj wyznaczone wartości na wykresie i przez porównanie z
pierwiastkami wielomianu (roots()). Oblicz całkę z wielomianu w zakresie wartości x=[-5,
5] (funkcja quad()).

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 7

5. Dla tych, którzy chcą wiedzieć więcej - informacje dodatkowe

5.1

Konstrukcje sterujące

Zestaw instrukcji sterujących Matlaba jest ubogi co bywa niekiedy uciążliwe. Składa się na
niego instrukcja pętli wyliczanej for, pętli z warunkiem while i instrukcji warunkowej if.
Pętla for ma składnię zbliżoną do składni Pascala, ale dającą programiście większe
możliwości. Notacja ma postać:

for ZmiennaSterująca=WektorWartości
...
end;

W szczególnym przypadku WektorWartości może być zadany przez wartość początkową,
przyrost i wartość końcową w postaci WartośćPoczątkowa:Przyrost:WartośćKońcowa, co
przypomina zapis pętli wyliczanej Pascala, a jest standardowym sposobem generowania
wektorów w Matlabie. W ogólnym przypadku WektorWartości może być zadany przez
dowolne wyrażenie. Pętla jest wykonywana tyle razy, ile jest elementów w wektorze
wartości zmiennej sterującej. Pętle mogą być zagnieżdżone.
Pętla warunkowa while jest wykonywana dopóki spełniony jest warunek tej pętli, a
dokładnie wszystkie elementy macierzy, którą tworzy wyrażenie warunku są różne od zera.
Notacja ma postać:

while WarunekLogiczny
...
end;

Instrukcja break przerywa wykonywanie pętli obydwu omówionych rodzajów.
Instrukcja warunkowa if ma ogólną postać:

if Warunek1
...
[elseif Warunek2]
...
[else]
...
end;

Elementy alternatywy z warunkiem i bez warunku są opcjonalne. Podobnie jak przy
warunku pętli, instrukcje warunkowe są wykonywane jeśli wszystkie elementy wektora
warunku są różne od zera.

5.2

Operatory logiczne i funkcje testowania wartości

Matlab oferuje zestaw sześciu operatorów do porównywania macierzy. Są to operatory : <,
<=, >, >=, == (równy), ~= (różny). Operatory te zastosowane do wartości skalarnych dają w
wyniku wartość skalarną 0 lub 1. Zastosowane do macierzy dają macierz wartości 0 i 1. W
tym ostatnim przypadku użyteczne są funkcje testowania wartości w macierzy: any() i all()
zwracają odpowiednio wartość 1 jeśli którykolwiek lub wszystkie elementy wektora są
różne od zera. W przypadku macierzy zwracają wiersz wartości dla każdej kolumny
macierzy osobno. Podwójne zastosowanie funkcji zwraca wartość skalarną (np. all(all(X))
zwróci 1 jeśli wszystkie elementy macierzy X są różne od 0). Funkcja find() zwraca indeksy

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 8

niezerowych elementów w wektorze. W połączeniu z operatorami logicznymi może służyć
do wyszukiwania elementów spełniających określony warunek. Np. ciąg instrukcji:

idxs=find(X==3);
X(idxs)=0;

spowoduje wyzerowanie tych elementów wektora X, które są równe 3.

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 9

6. Dla tych, którzy chcą być najlepsi - zadania dodatkowe

6.1

Zastosowanie algorytmu FFT

Algorytm FFT można stosować również dla sygnałów nieokresowych, przy ograniczeniu
obserwowanego sygnału do określonego przedziału czasowego. W najprostszym przypadku
ograniczenie to można zrealizować przez wyzerowanie sygnału poza oknem obserwacji.
Jest to przypadek okna prostokątnego. Przesuwając okno wzdłuż osi czasu i stosując
algorytm FFT dla sygnału w oknie otrzymamy obraz dynamicznych zmian widma
analizowanego sygnału.

Przeczytaj pomoc Matlaba na temat funkcji wavread(). Wczytaj dowolny plik typu WAV.
Zastosuj funkcję fft() dla całego zapisu WAV. Przedstaw widmo sygnału na rysunku.
Zastosuj okienkowanie sygnału z wybraną długością okna i przedstaw na rysunku przebieg
zmian widma sygnału.

6.2

Filtracja danych

Działanie filtra cyfrowego typu FIR (ang. Finite Impulse Response) polega na mnożeniu
wektora wag filtra przez wektor próbek sygnału wejściowego. Suma iloczynów daje
pojedynczą próbkę sygnału wyjściowego. Rozmiar wektora wag filtra określa jego rząd. W
przypadku tego rodzaju filtra wyjście zależy tylko od historii sygnału wejściowego. Inny
rodzaj filtrów - IIR (ang. Infinite Impulse Response) zawiera sprzężenie zwrotne z wyjścia
na wejście (jest opisany rekurencyjnie).

Zapoznaj się z teorią projektowania filtrów typu FIR [Borodziewicz, Jaszczak]. Zaprojektuj
dolnoprzepustowy filtr typu FIR. Zaimplementuj go w Matlabie i przetestuj jego działanie
dla sygnału poliharmonicznego.

7. Literatura

[1] Matlab User’s Guide; The MathWorks Inc 1993

[2] Mrozek B.: Matlab - uniwersalne środowisko do obliczeń naukowo-technicznych; PLJ,

Warszawa 1996

[3] Stearns S., Ruth D.: Signal processing algorithms in Matlab; Prentice Hall 1996

[4] Borodziewicz W., Jaszczak K.: Cyfrowe przetwarzanie sygnałów; WNT, Warszawa

1987

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Kierunek Elektrotechnika

Ćwiczenie 8.2

Matlab

Narzędzie obliczeń numerycznych

Część II

Prezentacja danych i interfejs użytkownika

Zakład Metrologii AGH

Kraków 1998

Laboratorium Podstaw Informatyki

Strona 2

1. Wprowadzenie

Wyniki obliczeń numerycznych w postaci liczbowej są trudne do interpretacji z powodu
dużej ilości informacji tekstowej. W większości przypadków lepszym wyjściem jest
prezentowanie danych numerycznych w postaci rysunku. W przypadku danych
numerycznych powiązanych zależnością funkcyjną będzie to łatwy do interpretacji wykres
funkcji. W innych przypadkach jakościowe przedstawienie wartości numerycznych np.
kolorem daje szybką orientację w zmienności prezentowanych danych numerycznych.
Środowisko obliczeń numerycznych jest więc skazane do dostarczanie użytkownikowi
odpowiednich narzędzi do graficznej prezentacji danych. Matlab oferuje bogaty zestaw
funkcji graficznych przydatnych w różnych zastosowaniach.
Drugim zadaniem każdego środowiska programowania jest dostarczanie narzędzi do
budowania interfejsu użytkownika tworzonych aplikacji. Zestaw funkcji dostarczanych z
Matlabem zawiera funkcje tworzące większość z obiektów kontrolnych spotykanych w
środowisku MS Windows, z przyciskami, suwakami i opcjami menu. Łączenie tych
obiektów z funkcjami reakcji na wybór użytkownika polega na zadeklarowaniu funkcji
obsługi zdarzenia zawartej w m-pliku lub bezpośrednio w postaci ciągu instrukcji Matlaba.
Instrukcja nie opisuje wszystkich możliwości graficznych środowiska. Wiele dodatkowych
informacji dostarczy User Guide i podręczna pomoc wywoływana poleceniem help.

Zakład Metrologii AGH

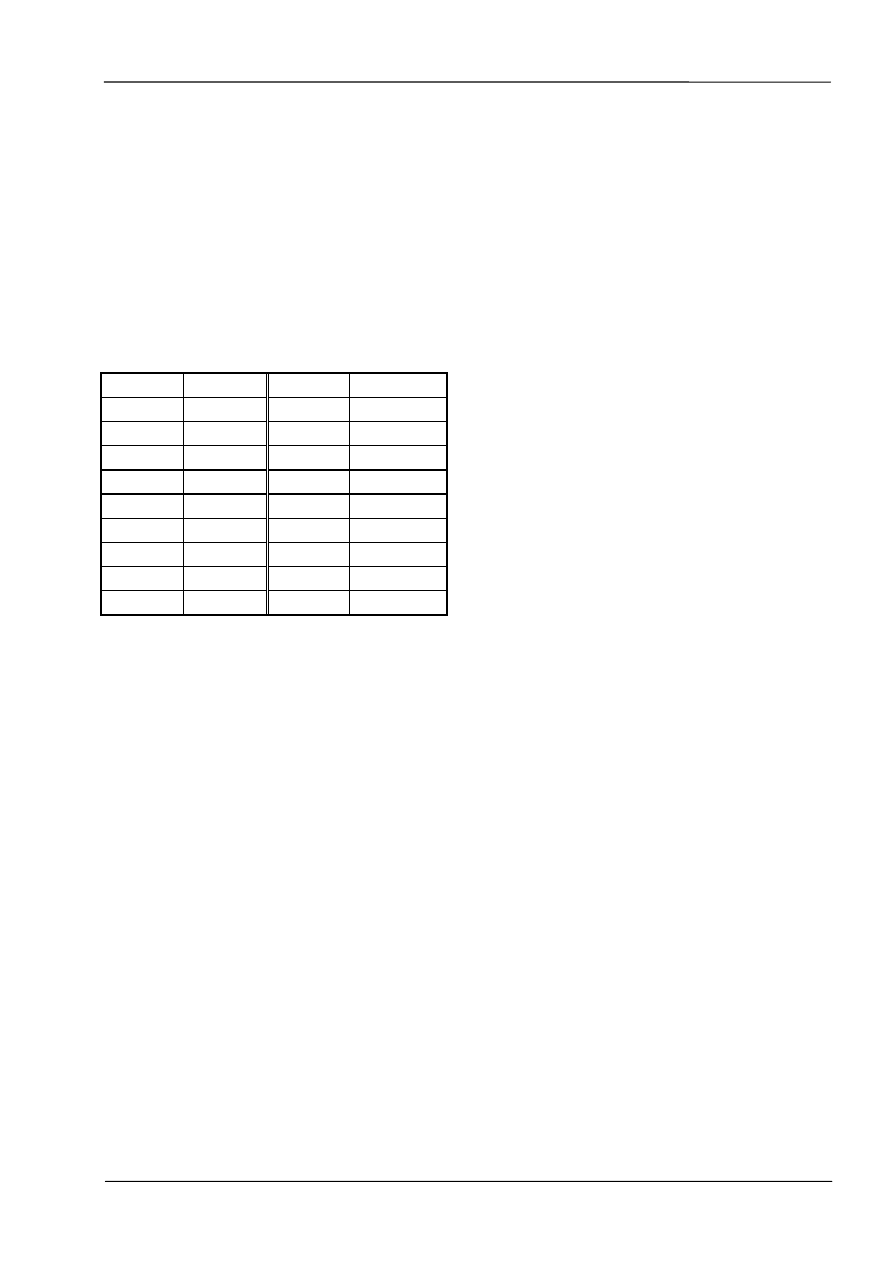
Laboratorium Podstaw Informatyki

Strona 3

2. Zadanie 1 - wykresy dwuwymiarowe

Podstawowym poleceniem graficznego przedstawienia odpowiadających sobie par wartości
z dwu wektorów lub par element wektora i jego indeks jest polecenie plot(). W
szczególnym przypadku, gdy wartości z wektorów wiąże zależność funkcyjna, tworzony
rysunek będzie przybliżonym wykresem funkcji. Przybliżonym, ponieważ Matlab, przy
domyślnym stylu linii tworzy rysunek przez łączenie sąsiadujących w wektorach punktów.
Wygląd linii i punktów rysunku określa kolor i styl linii. Domyślnym stylem linii jest solid,
a kolor jest wybierany kolejno wg. listy kolorów dla każdego wektora wartości w ramach
jednego układu współrzędnych. Kolor i styl może być wybrany przez użytkownika i zadany
parametrem polecenia plot(). Dostępne kolory i style linii zawiera poniższa tabela.

Symbol Color

Symbol Linestyle

y yellow

. point

m magenta

o circle

c cyan

x x-mark

r red

+ plus

g green

* star

b blue

- solid

w white

: dotted

k black

-. dashdot

--

dashed

Przykładowa poniższa sekwencja narysuje przybliżony wykres jednego okresu funkcji sinus
na podstawie wektorów 101 elementowych. Kolor wykresu będzie niebieski, linia będzie
przerywana z wzorkiem ‘- -’.

x=0:2*pi/100:2*pi;
y=sin(x);
plot(x,y,’b--’);

Do opisywania tworzonych rysunków służą polecenia xlabel(), ylabel(), title() opisujące
każdą z osi i cały rysunek. Ich parametrem jest tekst opisu.
Logarytmiczną postać wykresu można otrzymać stosując polecenia semilogx() dla skali
logarytmicznej w osi OX, semilogy() dla otrzymania skali logarytmicznej w osi OY i
loglog() dla skali logarytmicznej w obu osiach.
Do rysowania zależności funkcyjnych jednej zmiennej służy funkcja fplot(), której
parametrem jest nazwa funkcji do narysowania. Zaletą jej stosowania w porównaniu z
ręcznym generowaniem odpowiednich wektorów wartości jest automatyczne dostosowanie
kroku do zmienności funkcji.
Polecenie grid tworzy siatkę rysunku, a polecenie hold powoduje „zamrożenie” rysunku, co
oznacza, że następne polecenie plot() nie utworzy nowego układu współrzędnych a doda
rysunek do bieżącego układu współrzędnych.
Utworzenie wielu wykresów jednocześnie w celu porównania można osiągnąć bądź przez
utworzenie wielu okien rysunku poleceniem figure, bądź przez podzielenie bieżącego okna
na obszary podwykresów poleceniem subplot(). Jego parametrami są ilość podwykresów
określona przez ilość w poziomie i ilość w pionie, oraz numer aktualnego podwykresu.

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 4

Sposób rysowania rysunków przez Matlaba, polegający na łączeniu sąsiednich punktów,
umożliwia rysowanie zależności, które nie są funkcjami np. z powodu przypisania wielu
wartości na osi OY dla jednego punktu na osi OX.

2.1

Ilustracja metody elipsy

Metoda elipsy służy pomiarowi przesunięcia fazowego dwu sygnałów sinusoidalnych o tej
samej częstotliwości z użyciem oscyloskopu. Sygnałami pomiarowymi są najczęściej sygnał
wejściowy i wyjściowy czwórnika, dla którego mierzymy przesunięcie fazowe dla
określonej częstotliwości. Oscyloskop pracuje w czasie pomiaru w trybie XY, czyli z
odchylaniem w osi poziomej przez sygnał z kanału X i odchylaniem w osi pionowej przez
sygnał z kanału Y. Obraz otrzymywany na oscyloskopie ma kształt elipsy o parametrach
zależnych od wzajemnego przesunięcia fazowego sygnałów. Wartość mierzonego
przesunięcia fazowego wyznaczana jest na podstawie charakterystycznych wymiarów
elipsy, nie jest to jednak przedmiotem zadania.
Matematyczny zapis powstającej elipsy ma postać parametryczną. Przy zmiennej
niezależnej t reprezentującej upływający czas, współrzędnych (x,y) opisujących położenie
punktu na płaszczyźnie XY, pulsacji sygnałów

ω i wzajemnego przesunięcia fazowego ϕ,

zależność parametryczna ma postać x=sin(

ωt) i y=sin(ωt+ϕ). Ze względu na okresowość

sygnałów wystarczający do wytworzenia obrazu elipsy jest zakres zmiennej

ωt=2π.

Narysuj w jednym układzie współrzędnych obrazy elips wg. podanych równań dla czterech
przesunięć fazowych (

π/4, π/2, π, 3π/2). Zastosuj różne kolory lub style linii. Dodaj opisy

osi, tytuł rysunku i siatkę wykresu. Narysuj te same elipsy w czterech różnych układach
współrzędnych (w różnych oknach lub w podwykresach) w sposób umożliwiający
porównanie poszczególnych rysunków między sobą.

2.2

Histogram zmiennej losowej o rozkładzie normalnym

Ciągłe zmienne losowe są opisane przez funkcję gęstości rozkładu prawdopodobieństwa.
Przybliżeniem kształtu tej funkcji jest histogram, czyli wykres ilości wartości zmiennej
losowej z próbki N elementowej w kolejnych przedziałach wartości. Wykres taki można
skonstruować poleceniem plot() po przetworzeniu danych z próbki. Jest to jednak wykres
tak często stosowany, że konstruktorzy Matlaba opracowali funkcję hist() tworzącą ten
wykres na podstawie próbki wartości zmiennej losowej.
Zmienna o rozkładzie normalnym z parametrami m (wartość oczekiwana) i

σ (odchylenie

standardowe) w skrócie oznaczany N(m,

σ) jest jednym z najważniejszych rozkładów

teoretycznych. Wiele rozkładów losowych występujących w naturze ma kształt zbliżony do
normalnego. W szczególności są to rozkłady błędów pomiarowych. Funkcja gęstości
prawdopodobieństwa ma dla rozkładu normalnego postać:

(

)

f x

x

m

( )

exp

=

−

−

⎡

⎣

⎢

⎢

⎤

⎦

⎥

⎥

1

2

2

2

2

σ π

σ

Wygeneruj wektor 10000 liczb losowych o rozkładzie normalnym (funkcja randn()
generuje wektor liczb losowych o rozkładzie N(0,1)). Narysuj histogram o wybranej liczbie
przedziałów w określonym zakresie. W tym samym układzie współrzędnych narysuj
przeskalowaną funkcję gęstości prawdopodobieństwa tego rozkładu.

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 5

3. Zadanie 2 - wykresy trójwymiarowe

3.1

Program demonstracyjny Matlaba

Matlab zawiera program demonstracyjny prezentujący między innymi możliwości
prezentacji danych zawartych w macierzach w funkcji danych w wektorach (prostokątny
obszar z regularną siatką określoną przez wektory wartości w osi OX i OY) lub w
macierzach (wartości nad dowolnym dwuwymiarowym obszarem).

Uruchom w Matlabie program demo. Zapoznaj się z możliwościami prezentacji
dwuwymiarowych zależności funkcyjnych.

3.2

Wykres funkcji dwu zmiennych

Zadanie polega na tworzeniu różnego rodzaju wykresów funkcji „sombrero”. Funkcja ta w
biegunowym układzie współrzędnych jest określona wzorem z(r,

ϕ)=sin(r)/r. Poniższa

sekwencja generuje macierz wartości tej funkcji w prostokątnym obszarze kartezjańskiego
układu współrzędnych określonym wektorami x i y.

x=-8:0.5:8;
y=x;
[X,Y]=meshgrid(x,y);
R=sqrt(X.^2+Y.^2)+eps;
Z=sin(R)./R;

Funkcja meshgrid() tworzy prostokątną siatkę wartości X i Y przez powielenie wektorów
przekazanych w parametrach. Odpowiada to wyznaczeniu iloczynu kartezjańskiego
wektorów.
Prezentację powierzchni tej funkcji można wykonać wieloma sposobami realizowanymi
przez różne funkcje Matlaba. Funkcja contour() prezentuje przebieg funkcji za pomocą
izolinii (jak poziomice na mapie), pcolor() za pomocą koloru obrazuje wartość funkcji w
punkcie, funkcje mesh() i surf() rysują powierzchnie trójwymiarowe w rzucie na
dwuwymiarową powierzchnię ekranu, surfc() łączy cechy wykresu konturowego z
powierzchniowym, surfl() wprowadza do rysowanej powierzchni efekt oświetlenia
bocznego.

Przedstaw przebieg funkcji „sombrero” funkcjami contour(), pcolor() z wywołaniem
funkcji shading(‘interp’), mesh() i surf() z wyborem mapy kolorów funkcją colormap(hot),
surfc(), surfl() z colormap(gray) i shading(‘interp’).

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 6

4. Zadanie 3 - interfejs użytkownika w aplikacji

4.1

Menu w oknie aplikacji

Funkcja tworząca dodatkowe opcje użytkownika uimenu() przyjmuje w parametrach nazwy
i wartości wybranych własności tworzonego menu. Najistotniejsze dla nas są własności
‘Label’ i ‘Callback’. Utwórzmy opcję menu poleceniem h=uimenu(‘Label’, ‘Nowa opcja
menu’). Funkcja uimenu() zwraca identyfikator utworzonej opcji. Jeśli zamierzamy
zbudować menu hierarchiczne to dla nowo tworzonej opcji należy podać identyfikator opcji
nadrzędnej h=uimenu(h, ...). Do ustawiania i pobierania wartości własności menu (i
pozostałych obiektów Matlaba) służą funkcje set(h) i get(h). Przykładowo reakcję na wybór
opcji dla utworzonej opcji o identyfikatorze h ustawia polecenie:

set(h, ‘callback’, ‘ustaw(10)’);

Wołana funkcja reakcji może mieć postać:

function ustaw(wartosc)
global Wartosc
Wartosc=wartosc;

Utwórz opcję nowe okno rysunku poleceniem figure. Dodaj opcję menu „Colormap” z
podopcjami „Gray”, „Hot”, „Jet”, „Cool”. Reakcją na wybór powinno być wywołanie
funkcji colormap() z nazwą odpowiedniej mapy kolorów. Szczegółowy opis map kolorów
znajduje się w dodatku do instrukcji.

4.2

Elementy kontrolne

Funkcja tworzenia elementu kontrolnego ma nazwę uicontrol(). Parametrami wywołania są
nazwy własności elementów kontrolnych i ich wartości. Własność Style określa rodzaj
elementu kontrolnego z listy pushbutton, radiobutton, checkbox, edit, text, slider, frame,
popupmenu. Własność Value określa stan elementu. String określa napis (lub napisy)
pojawiający się na elemencie. Jak dla wszystkich obiektów Matlaba funkcje get() i set()
pobierają i ustawiają własności elementów.
Przykładowo utworzenie listy wyboru jednej z wartości z listy wykonuje instrukcja:

h=uicontrol(‘popupmenu’, ‘string’, ‘Opcja1|Opcja2’, ‘callback’, ‘popcall’);

Funkcja reakcji na wybór użytkownika popcall() może mieć postać:

function popcall()
h=gco;
val=get(h, ‘Value’);
strs=get(h, ‘String’);
str=str(val, :);
disp([‘Wybrales opcje: ‘, str]);

Zbuduj w nowym oknie rysunku interfejs do programu odtwarzania plików typu WAVE.
Interfejs powinien zawierać pole edytowalne na nazwę pliku, suwak (ang. slider) do
ustawiania ilości próbek do odtworzenia, przycisk „Wczytaj” i przycisk „Odtwórz”. W
funkcjach reakcji wykorzystaj funkcję odczytu pliku wavread() i funkcję odtwarzania ciągu
próbek sound().

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 7

5. Dla tych, którzy chcą wiedzieć więcej - informacje dodatkowe

5.1

Mapy kolorów

Podstawą odwzorowania wartości funkcji na kolor w funkcjach typu surf(), pcolor() jest
mapa kolorów. Jest to trzykolumnowa macierz o długości odpowiadającej ilości kolorów
używanych przy tworzeniu rysunków i o kolumnach odpowiadających kolorom
podstawowym (RGB: czerwony, zielony, niebieski). Zawartość każdego z kolorów
podstawowych w kolorze opisanym w danym wierszu jest określona przez liczbę z
przedziału (0, 1). Kolor dla określonej wartości jest domyślnie dobierany przez liniowe
odwzorowanie przedziału wartości funkcji na zakres indeksów mapy kolorów. Domyślna
długość mapy kolorów wynosi 64. Najprostszą z map jest mapa gray, utworzona z kolorów
podstawowych w równych proporcjach i liniowo rosnących wartościach. Graficznie mapę
kolorów można przedstawić funkcją plot() (rysuje kolejne składniki RGB kolorami yellow,
magenta i cyan) lub funkcją rgbplot() (rysuje składniki RGB zgodnie z kolorami kolumn).
Mapa gray ma graficzną postać trzech pokrywających się linii od 0 do 1. Mapa hot ma
postać kolejno rosnących linii odpowiadających składnikom podstawowym.
Zmiany domyślnej mapy kolorów dokonuje się instrukcją colormap(), z macierzą mapy
kolorów w parametrze wywołania. Macierze standardowych map kolorów są tworzone
poleceniami zgodnymi z nazwą mapy (hsv, hot, cool, jet, pink, copper, gray). Np. mapę
ośmiu poziomów szarości ustawia dla aktualnego rysunku polecenie colormap(gray(8)).
Domyślny sposób odwzorowania wartości na indeks w mapie kolorów można zmienić przez
podanie innego zakresu wartości do odwzorowania wywołaniem funkcji caxis(). Inny
sposób to podanie wartości do odwzorowania koloru dla każdej wartości rysowanego
wykresu jak w poleceniu surf(Z,C), gdzie macierz Z określa wartość do narysowania, a
macierz C określa kolor do rysowania (wartości skalowane do zakresu indeksów mapy
kolorów).
Przykładem niestandardowej mapy kolorów jest mapa towarzysząca rysunkowi w pliku
clown.mat. Ze względu na rosnący udział składników podstawowych w kolorze, rysunek
ten jest czytelny także z innymi, standardowymi mapami kolorów.

5.2

Obiekty graficzne

Matlab organizuje wszystkie obiekty graficzne pojawiające się na ekranie w hierarchię
zaczynającą się od ekranu komputera. Typy obiektów w hierarchii poniżej obiektu ekranu to
Figure - okna rysunków, jego potomek Axes - układ współrzędnych w części okna rysunku,
potomkowie Axes tworzący rysunki - Line, Patch, Surface, Image, Text. Oddzielne grupy
tworzą obiekty interfejsu użytkownika Uicontrol i Uimenu - potomkowie obiektu Figure.
Funkcje tworzące obiekty poszczególnych typów (np. figure(), axes(), uimenu()) zwracają
identyfikatory obiektu, które służą do jego identyfikacji w funkcjach operujących na
obiektach graficznych. Każdy z obiektów posiada zestaw własności identyfikowanych przez
nazwę i związanych z aktualną wartością. Zestaw dostępnych dla obiektu danego typu
własności można otrzymać wołając funkcję set() z identyfikatorem obiektu. Aktualną
wartość własności można uzyskać wołając funkcję get() z identyfikatorem obiektu i nazwą
własności. Ustawienie wartości własności uzyskuje się przez wywołanie funkcji set() dla
obiektu z podaniem nazwy własności i wartością do ustawienia.

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 8

6. Dla tych, którzy chcą być najlepsi - zadania dodatkowe

6.1

Wyświetlanie sekwencji rysunków

Matlab umożliwia zapamiętanie sekwencji rysunków (wykresów, obrazków, części okna) i
odtworzenie zapamiętanej sekwencji z podaną szybkością zmiany obrazków. Pamiętana
sekwencja zajmuje dużo pamięci. Przygotowaniem pamięci dla sekwencji zajmuje się
funkcja moviein(). Zapamiętanie jednego rysunku sekwencji realizuje funkcja getframe().
Funkcja movie() odtwarza zapamiętaną sekwencję rysunków.

Przygotuj do odtworzenia sekwencję prezentującą kształt funkcji peaks() z różnych
punktów widzenia, np. po obrocie co 10 stopni do 360 stopni. Zapisz przygotowaną
sekwencję do pliku vi_peaks.mat. Przygotuj funkcję wczytującą sekwencję do pamięci i
odtwarzającą ją w oknie. Zadbaj o odtworzenie pierwotnych wymiarów okna.

6.2

Wykresy funkcji zespolonych

Prezentacja w dwu wymiarach zależności funkcyjnej zmiennej zespolonej wymaga
przedstawienia części rzeczywistej i urojonej wartości funkcji nad płaszczyzną zespoloną.
Autorzy Matlaba sugerują możliwość prezentacji tego rodzaju wykresów przez związanie
części rzeczywistej z rysowaną powierzchnią, a części urojonej z jej kolorem w określonym
punkcie. Mała jest, z tego powodu, przydatność takiego wykresu do odczytywania wartości
funkcji zespolonej w punkcie.

Zapoznaj się z opcją programu demo Matlaba „Visualization/Complex”. Przeanalizuj
sposób rysowania wykresów w źródłach funkcji. Zaimplementuj, jeśli masz lepszy niż
autorzy Matlaba pomysł, czytelniejszy sposób prezentacji tego rodzaju zależności
funkcyjnych.

7. Literatura

[1] Matlab User’s Guide; The MathWorks Inc 1993

[2] Mrozek B.: Matlab - uniwersalne środowisko do obliczeń naukowo-technicznych; PLJ,

Warszawa 1996

[3] Drozdowski P.: Wprowadzenie do Matlaba; Politechnika Krakowska 1995

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Kierunek Elektrotechnika

Ćwiczenie 8.3

Matlab

Narzędzie obliczeń numerycznych

Część III

Zastosowania

Zakład Metrologii AGH

Kraków 1998

Laboratorium Podstaw Informatyki

Strona 2

1. Wprowadzenie

Po dwóch ćwiczeniach wprowadzających do programowania w środowisku Matlaba, czas
na zaprogramowanie kompletnej aplikacji numerycznej, z wygodnym interfejsem
użytkownika. W części zadaniowej przygotowano trzy problemy z różnych dziedzin, w
których wykorzystywane są obliczenia numeryczne. Pierwszy z nich dotyczy analizy
sygnałów podstawowym narzędziem DSP (ang. Digital Signal Processing) - algorytmem
szybkiej transformaty Fouriera FFT (ang. Fast Fourier Transform). Drugie zadanie dotyczy
przetwarzania danych graficznych w prostej postaci dwuwymiarowej. Używane są operacje
przesunięcia i rotacji wielokątów, które sprowadzają się do wykonywania mnożenia
macierzowego. W części zadań dodatkowych ćwiczący może rozwinąć ten przypadek na
przestrzeń trójwymiarową, z którą wiąże się problem rzutowania na płaszczyznę
dwuwymiarową ekranu. Ostatnie zadanie to analiza obwodu elektrycznego funkcjami
dostępnymi w dodatkowym pakiecie Matlaba - Control. Jako przykład wybrano obwód
RLC drugiego rzędu.

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 3

2. Zadanie 1 - analiza częstotliwościowa dyskretnego sygnału nieokresowego

Podstawę analizy częstotliwościowej sygnałów stanowi transformata Fouriera. Dla sygnału
spróbkowanego, czyli dyskretnego w czasie, jej odpowiednikiem jest DFT - dyskretna
transformata Fouriera. Opracowanie szybkiego algorytmu FFT tej transformaty, o
złożoności rzędu N*logN dla ciągu N próbek, pozwoliło zastosować praktycznie analizę
częstotliwościową długich sygnałów w zastosowaniach czasu rzeczywistego. Algorytm FFT
operuje na ciągach próbek, dla których N jest potęgą dwójki. Funkcja fft() w Matlabie
zwraca wektor o takiej samej długości jak wektor próbek, zawierający amplitudy
poszczególnych częstotliwości w sygnale. Na pierwszej pozycji jest składowa stała.
Pozostałe widmo jest symetryczne względem elementu o indeksie length(yf)/2+1. Dla
naszych celów interesujące są prążki widma o indeksach od 2 do length(yf)/2+1.
Dla sygnału nieokresowego, nieskończonego teoria wymaga liczenia DFT dla
nieskończonego ciągu próbek, co jest nierealizowalne w skończonym czasie. Praktycznie
można analizować widmo takiego ciągu ograniczonego w danym momencie do skończonej
liczby próbek począwszy od próbki startowej. Przesuwając położenie próbki startowej
można badać zmienność widma ograniczonego sygnału w czasie. Ograniczanie długości
widma jest operacją nakładania okna na sygnał, w opisanym przypadku okna
prostokątnego, nie zmieniającego wartości próbek. Długość okna to ilość próbek w sygnale
ograniczonym oknem.

2.1

Analiza zapisu dźwięku algorytmem FFT z przesuwanym oknem prostokątnym

Zapis sygnału dźwiękowego w formacie WAV jest przykładem długiego sygnału
spróbkowanego w ogólnym przypadku nieokresowego. Można zastosować do niego
opisaną powyżej analizę zmienności widma z przesuwanym oknem. Dla ograniczenia ilości
danych o widmie częstotliwości możemy za każdym razem przesuwać okno o jego długość.
Konstrukcja pętli przesuwającej okno dla wektora próbek Y może być zapisana
następująco:

for i=1 : DlugoscOkna : length(Y)-DlugoscOkna
% Tu należy wołać algorytm FFT dla próbek w oknie i zachować wynik
end;

Prezentacja danych otrzymanych w wyniku działania powyższej pętli może mieć formę
podobną do spotykanej w equalizerach muzycznych, przedstawiającą zależność widma od
czasu w postaci matrycy. Poszczególne działki matrycy kolorem przedstawiają amplitudę
składowej widma o danej częstotliwości. Oś pionowa odpowiada częstotliwości, a pozioma
kolejnym momentom czasu dla próbki startowej. Instrukcja Matlaba image() tworzy taką
matrycę na podstawie macierzy wartości z bezpośrednim odwzorowaniem wartości na
indeks koloru. Dla osiągnięcia czytelnego odwzorowania wartości na kolor konieczne
będzie skalowanie zakresu wartości w prezentowanej macierzy na zakres indeksów w mapie
kolorów (od 1 do length(colormap)).

Przeanalizuj widmo wybranego, krótkiego pliku WAV z katalogu c:\windows. Wykorzystaj
instrukcję wavread() do wczytania zapisu i sound() do odtworzenia dźwięku. Przetestuj
różne długości okna, np. 16, 64 i 512. Wybierz mapę kolorów hot i przeskaluj wartości
modułu widma do długości mapy kolorów przy użyciu funkcji image().

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 4

3. Zadanie 2 - transformacje figur geometrycznych

Przekształcenia figur geometrycznych sprowadzają się do operacji macierzowych na
współrzędnych opisujących figurę. Matlab dostarcza wygodną notację tych operacji, a
jednocześnie umożliwia łatwą do uzyskania prezentację figur geometrycznych. Dzięki temu
możemy się skupić na samych algorytmach przekształceń geometrycznych.
Przesunięcie punktu (x, y) o zadany wektor (tx, ty) do punktu (x’, y’) może być wykonane
jako operacja macierzowa

[

] [

]

x

y

x

y

tx

ty

'

'

*

1

1

1

0

0

0

1

0

1

=

⎡

⎣

⎢

⎢

⎢

⎤

⎦

⎥

⎥

⎥

Współrzędne punktu (x, y) po obrocie o kąt

ϕ względem punktu (x0, y0) można wyznaczyć

z wyrażenia macierzowego:

[

] [

]

x

y

x

y

x

y

x

y

'

'

*

*

cos

sin

sin

cos

*

1

1

1

0

0

0

1

0

0

0 1

0

0

0

0

1

1

0

1

0

1

0

0

0 1

=

−

−

⎡

⎣

⎢

⎢

⎢

⎤

⎦

⎥

⎥

⎥

−

⎡

⎣

⎢

⎢

⎢

⎤

⎦

⎥

⎥

⎥

⎡

⎣

⎢

⎢

⎢

⎤

⎦

⎥

⎥

⎥

ϕ

ϕ

ϕ

ϕ

3.1

Latające czworokąty

Transformowanie pojedynczych wierzchołków figury geometrycznej da efekt w postaci
transformowania całej figury. Jako figurę do transformowania wybierzemy czworokąt,
który można opisać w Matlabie dwukolumnową macierzą z pięcioma wierszami. Wiersze
pierwszy i ostatni powinny być takie same dla uzyskania domknięcia figury. Kolumny
macierzy opisują współrzędne x i y poszczególnych wierzchołków.
Rysowanie tak opisanej figury realizuje instrukcja plot().

Zapisz operacje przesunięcia i rotacji wierzchołków prostokąta w postaci funkcji
zwracających przetransformowane współrzędne. Przetestuj je dla pojedynczego czworokąta
przez rysowanie poruszającej się figury. Utwórz macierz opisującą kilka wielokątów (każde
pięć wierszy macierzy do opisu jednego czworokąta) o losowo wybranych współrzędnych
wierzchołków z zakresu rozmiaru okna rysunku. Utwórz skrypt Matlaba zawierający pętlę
obracającą każdy z czworokątów o różny kąt i przedstawiający zmianę w oknie rysunku.
Dodaj operację przesuwania czworokątów o różne wektory. Po wyjściu całego czworokąta
poza granice rysunku powinien się on pojawić z przeciwnej strony, lub powinien pojawić
się jego następca o takim samym kształcie w środku rysunku.

Zakład Metrologii AGH

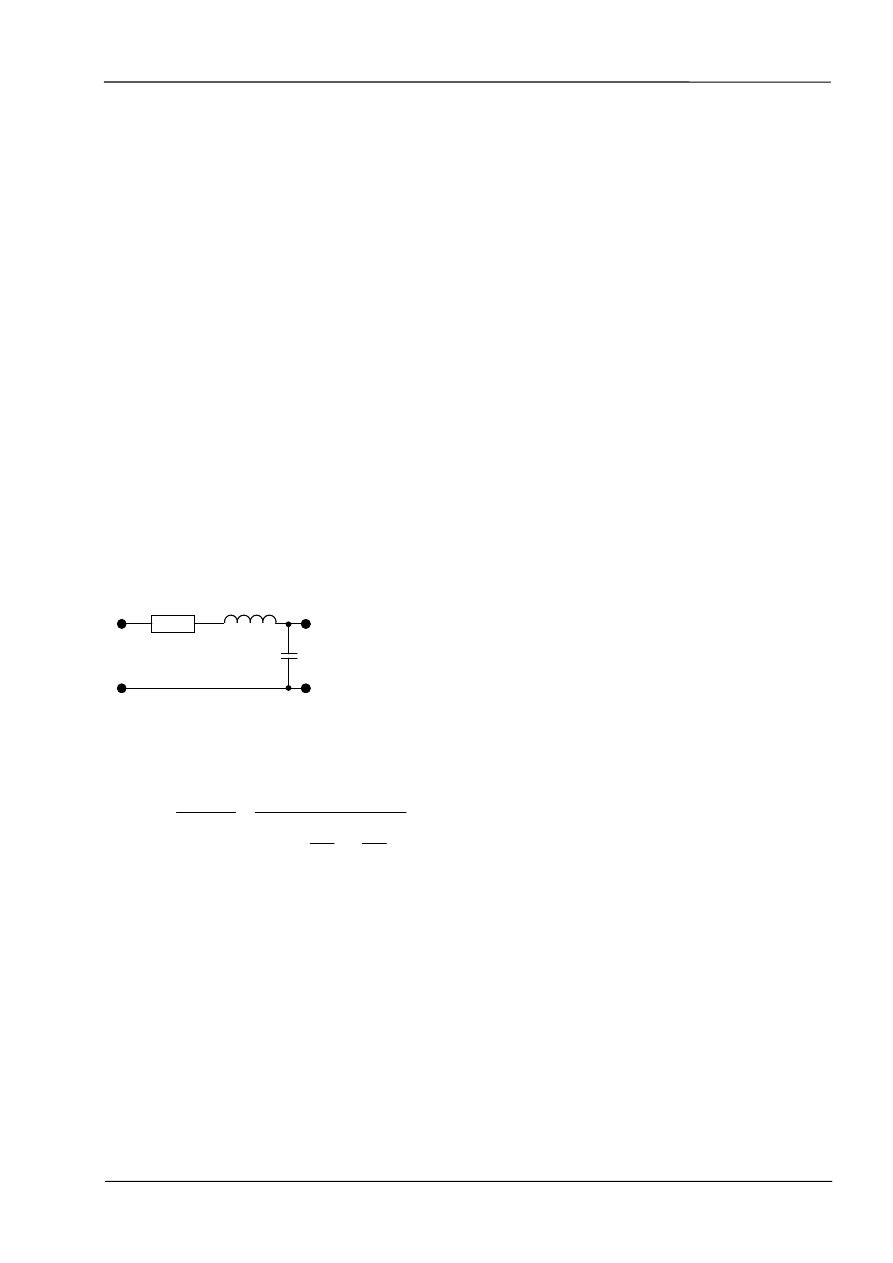
Laboratorium Podstaw Informatyki

Strona 5

4. Zadanie 3 - analiza czasowa i częstotliwościowa obwodu elektrycznego

Na podstawie opisu matematycznego obwodu elektrycznego w postaci równań stanu lub
transmitancji można wyznaczyć jego odpowiedź czasową i charakterystyki
częstotliwościowe.
Odpowiedź czasowa jest wyznaczana dla określonego sygnału wymuszającego na wejściu
obwodu np. metodą splotu z odwrotną transformatą Laplace’a transmitancji. W wyniku tej
operacji otrzymujemy odpowiedź obiektu, czyli przebieg jego sygnału wyjściowego na
sygnał wymuszający. Operowanie równaniami stanu umożliwia dodatkowo uwzględnienie
stanu początkowego obwodu i wielu sygnałów wejściowych.
Charakterystyki częstotliwościowe obiektu określają jego wzmocnienie i wprowadzane
przesunięcie fazowe dla sygnału monoharmonicznego w funkcji częstotliwości. Przedstawia
się je graficznie w postaci dwóch wykresów: wzmocnienia (modułu transmitancji
zespolonej) w funkcji częstotliwości i przesunięcia fazowego (argumentu transmitancji
zespolonej) w funkcji częstotliwości. Wartość odpowiedniej charakterystyki dla wybranej
częstotliwości można wyznaczyć przez podstawienie częstotliwości do wzoru określającego
transmitancję.

4.1

Układ drugiego rzędu

W szczególnym przypadku obwód elektryczny może być układem drugiego rzędu.
Przykładem takiego obwodu jest szeregowo-równoległe połączenie elementów RLC jak na
poniższym rysunku.

R

L

C

U

1

U

2

Transmitancja obiektu drugiego rzędu jest zapisywana z użyciem standardowych
parametrów wzmocnienia statycznego k, pulsacji naturalnej (drgań nietłumionych)

ω

0

i

tłumienia

ζ. W postaci widmowej (po podstawieniu s=jω) ma ona postać wzoru:

K j

U

j

U

j

k

j

(

)

(

)

(

)

ω

ω

ω

ς ω

ω

ω

ω

=

=

+

−

⎛
⎝

⎜

⎞
⎠

⎟

2

1

0

0

2

1

2

Dla powyższego obwodu RLC standardowe parametry mają wartości:

ω

0

=sqrt(1/(LC)),

ζ=R/2*sqrt(C/L), k=1.
Z widmowej postaci transmitancji można

łatwo otrzymać charakterystyki

częstotliwościowe. Matlab dostarcza jednak narzędzi do prezentacji takich charakterystyk
bez konieczności organizacji wyliczania wartości wzmocnienia i przesunięcia fazowego.
Służy do tego funkcja bode(), która wołana bez lewostronnych parametrów tworzy wykresy
pożądanych przez nas charakterystyk.
Analizę odpowiedzi obwodu na standardowe wymuszenia w postaci skoku jednostkowego i
impulsu można przeprowadzić z użyciem funkcji step() i impulse(). Wszystkie wymienione
funkcje należą do pakietu dodatkowego (ang. toolbox) Matlaba o nazwie Control.
Przyjmują opis analizowanego obiektu zarówno w postaci równań stanu jak i transmitancji.

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 6

Opracuj aplikację do prezentacji właściwości przedstawionego na rysunku obwodu RLC.
Prezentowane powinny być charakterystyki częstotliwościowe i odpowiedzi czasowe na
dwa standardowe sygnały wymuszające. Zacznij od funkcji, której parametrami są wartości
R, L i C, rysującej odpowiednie wykresy w nowo tworzonym oknie. Następnie dodaj
interfejs użytkownika do zadawania wartości elementów R, L, C w postaci pól
edytowalnych, połączonych ewentualnie z suwakami. Wołaj funkcję tworzenia wykresów
po naciśnięciu przez użytkownika przycisku lub po każdej zmianie parametru.

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 7

5. Dla tych, którzy chcą wiedzieć więcej - informacje dodatkowe

5.1

FFT w Matlabie

Wyznaczanie widma sygnału w Matlabie realizuje funkcja fft() dyskretnej transformaty
Fouriera wykorzystująca algorytm FFT jeśli długość wektora próbek jest potęgą liczby 2.
Wyniki zwracane przez tę funkcję wymagają krótkiego komentarza.
Widmo sygnału spróbkowanego jest okresowe, powtarzające się z odległością fp na osi X,
gdzie fp jest częstotliwością próbkowania sygnału. Jeden okres widma jest dodatkowo
symetryczny względem środka, czyli punktu n*fp, gdzie n jest numerem okresu. Z
okresowości wynika że widma będzie również symetryczne względem punktu n*fp/2.
Funkcja fft() zwraca jeden okres widma z przedziału częstotliwości od 0 dla indeksu 1 do
fp-fp/N dla indeksu N. Widmo jest symetryczne względem indeksu i=N/2+1 z pominięciem
elementu pierwszego (odpowiadającego składowej stałej sygnału). Prostsze wyrażenia na
indeksy otrzymuje się stosując indeksowanie od 0.
Amplitudy poszczególnych składowych należy przeliczyć przez złożenie symetrycznych
elementów i podzielenie każdej z otrzymanych wartości przez długość wektora próbek.
Ponieważ składowa stała nie ma symetrycznego odpowiednika więc jej amplituda wynosi
A0=yf(1)/length(y), gdzie yf=abs(fft(y)). Pozostałe składowe mają amplitudy
Ai=2*yf(i+1)/length(y).
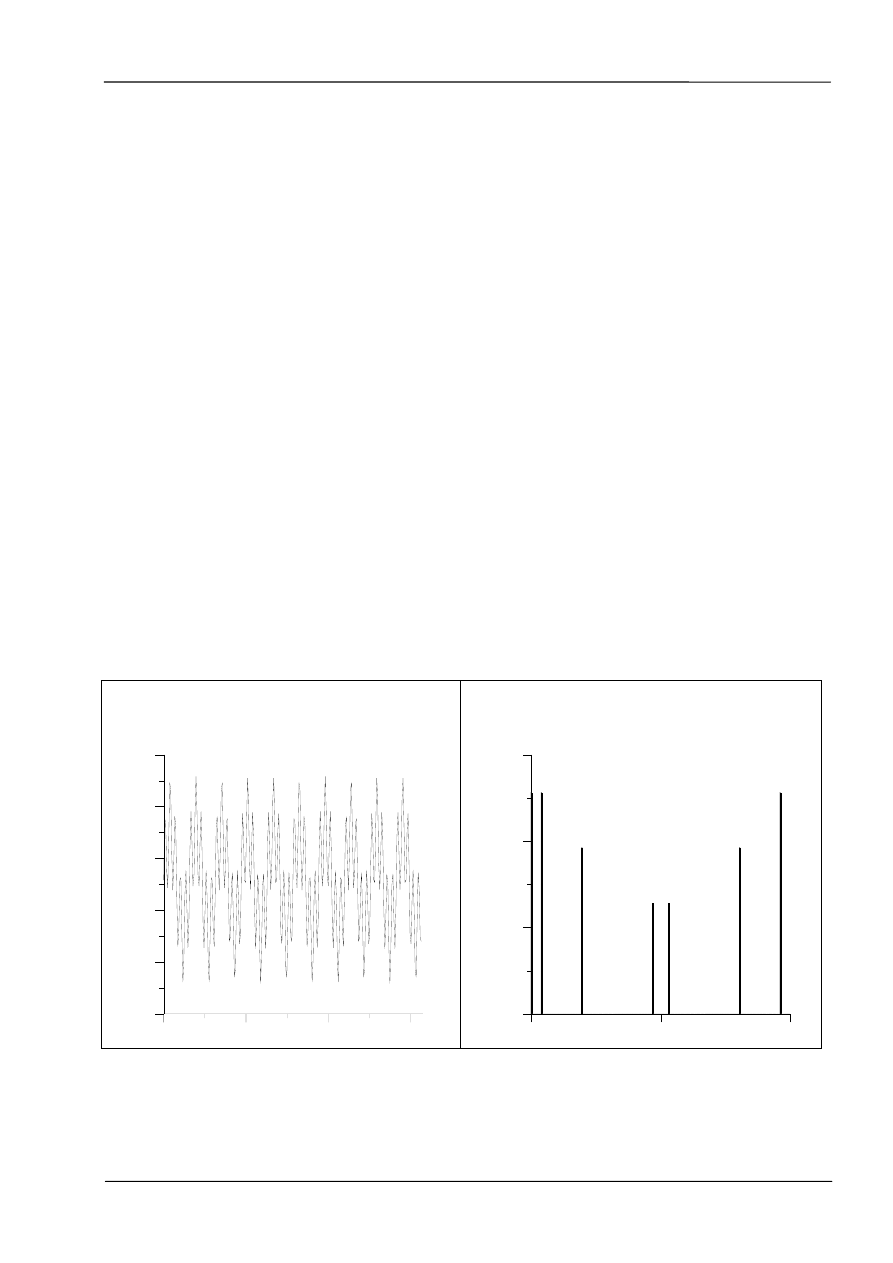
Poniższe rysunki przedstawiają analizę FFT prostego sygnału poliharmonicznego
(złożonego z kilku sygnałów sinusoidalnych). Widoczna jest symetria widma względem
środka. Łatwo w tym przypadku prześledzić odpowiedniość między składowymi
sinusoidalnymi sygnału a prążkami jego widma pod względem amplitudy jak i położenia na
osi częstotliwości (indeksowanie od 0, czyli częstotliwości fp/2 odpowiada indeks N/2).

Sygnał dla t=1:2*pi/256:2*pi-2*pi/256
y=1+2*sin(10*t)+1.5*sin(50*t)+sin(120*t)

0.00

2.00

4.00

6.00

t[s]

-1.00

0.00

1.00

2.00

3.00

4.00

y[V]

Moduł widma sygnału y w funkcji indeksu
od 0 do 255.

0.00

128.00

256.00

i

0.00

100.00

200.00

300.00

ab

s

(ff

t(

y

))

Matlab zawiera również funkcję fftshift() modyfikującą widmo do postaci stosowanej w
literaturze symetrycznej względem 0. Funkcja ifft() wykonuje odwrotną transformatę
Fouriera, czyli zmianę dyskretnego widma sygnału na jego dyskretną postać czasową.

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 8

5.2

Przestrzeń stanów a transmitancja w Matlabie

Opis układów dynamicznych za pomocą równań stanu i za pomocą transmitancji jest
wymienny, ale z ograniczeniami. Opis równaniami stanu jest bardziej ogólny, bo pozwala
na zapis dwoma równaniami macierzowymi dynamiki układów wielowejściowych i
uwzględnia stan początkowy układu. Zapis transmitancyjny jest czytelniejszy. Rzadziej
stosowany jest opis za pomocą zer i biegunów, czyli pierwiastków wielomianów licznika i
mianownika transmitancji.
Matlab pozwala na używanie wszystkich powyższych sposobów opisu układów. Większość
funkcji przyjmuje opis w dwu postaciach transmitancji i równań stanu (step(), bode(), itp.).
Dostępne są również funkcje zmieniające opis układu z przestrzeni stanów na transmitancję
(funkcja ss2tf()) i odwrotnie (funkcja tf2ss()) i z opisu zera-bieguny na pozostałe opisy
(zp2tf(), zp2ss(), ss2zp(), tf2zp()).

Zakład Metrologii AGH

Laboratorium Podstaw Informatyki

Strona 9

6. Dla tych, którzy chcą być najlepsi - zadania dodatkowe

6.1

Transformacje figur geometrycznych w przestrzeni

Analogicznie do transformacji figur na płaszczyźnie, transformacje w przestrzeni również
można opisać wyrażeniami macierzowymi. Dochodzi jednak w tym przypadku problem
rzutowania figury na dwuwymiarową płaszczyznę ekranu.

Zapoznaj się z teorią przekształceń geometrycznych w przestrzeni [Jankowski]. Zbuduj w
Matlabie aplikację prezentującą przesuwający się i kręcący sześcian.

6.2

Filtracja sygnałów dyskretnych

Programowa filtracja sygnałów dyskretnych sprowadza się do wykonywania operacji
mnożenia i dodawania. Rozróżnia się przy tym filtry typu FIR o skończonej odpowiedzi
impulsowej (sygnał wyjściowy zależy od próbek sygnału wejściowego) i filtry IIR o
nieskończonej odpowiedzi impulsowej (o wyjściu zależnym także od poprzednich stanów
wyjścia).

Zapoznaj się z teorią filtracji cyfrowej [Borodziewicz]. Zaimplementuj w Matlabie filtr typu
FIR i zastosuj go do filtracji dźwięków zapisanych w plikach typu WAV.

7. Literatura

[1] Matlab User’s Guide; The MathWorks Inc 1993

[2] Mrozek B.: Matlab - uniwersalne środowisko do obliczeń naukowo-technicznych; PLJ,

Warszawa 1996

[3] Drozdowski P.: Wprowadzenie do Matlaba; Politechnika Krakowska 1995

[4] Borodziewicz W., Jaszczak L.: Cyfrowe przetwarzanie sygnałów; WNT, Warszawa1987

[5] Jankowski M.: Elementy grafiki komputerowej; WNT, Warszawa 1990

Zakład Metrologii AGH