1

Rynek pracy

1. Prosty model alokacji czasu i podaży pracy
2. Zmieniające się nachylenie krzywej podaży pracy
3. Płaca za nadgodziny
4. Teoria gospodarstwa domowego alokacji czasu - Becker
5. Równowaga na rynku doskonale konkurencyjnym
6. Rynek pracy niedoskonale konkurencyjny - monopson
7. Renta ekonomiczna i skutki monopsonu po stronie

dobrobytu

8. Związki zawodowe

2

Prosty model alokacji czasu i podaży pracy

Czas wolny (relaks) traktowany jest jako dobro
konsumpcyjne, które nabywane jest za czas nie spędzony w
pracy. Pracownik rezygnuje z płacy w celu konsumpcji czasu
wolnego, a kosztem tej konsumpcji jest nie otrzymana płaca.
Przy istniejącym ograniczeniu czasowy wynoszącym 24
godziny na dobę, płacach rynkowych, dochodzie nie z pracy
konsumenta, można skonstruować ograniczenie budżetowe
definiujące osiągalną przez konsumenta kombinację dóbr
konsumpcyjnych i czasu wolnego.

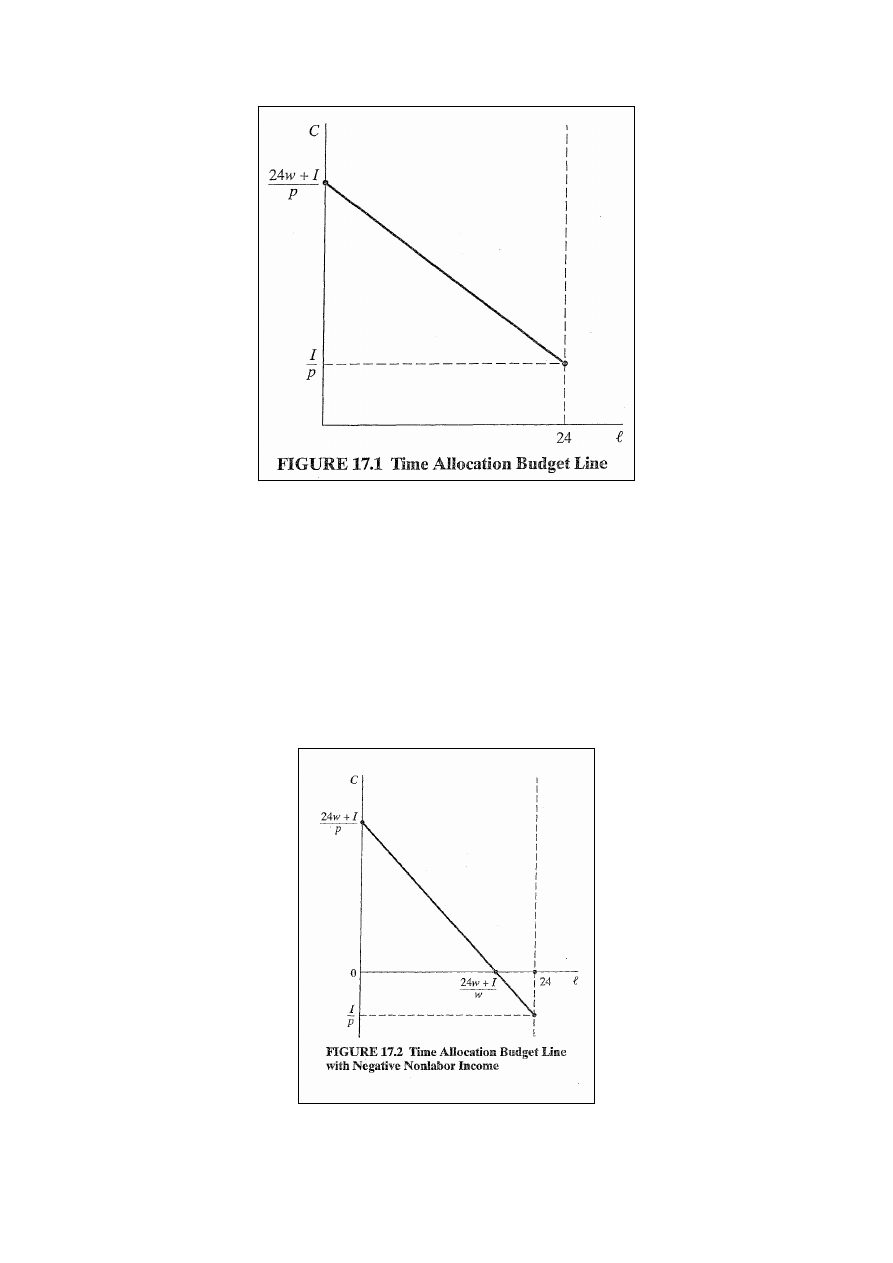
Ograniczenie budżetowe alokacji czasu
Wszystkie dobra konsumpcyjne agregujemy w jeden koszyk
nabywany po cenie p będącej indeksem cenowym.
Mamy następujące zmienne i parametry:

C : nabywane dobra konsumpcyjne
P : indeks cenowy dóbr konsumpcyjnych
l : czas wolny
w : rynkowa stawka płac
I : dochód nie z pracy
L = 24 – l : czas pracy.

Z ograniczenia budżetowego wynika, że wydatki na dobra
konsumpcyjne nie mogą przewyższać dochodu z pracy i spoza
pracy: pC ≤ I + w(24 - l). (rys. 17.1 - uwaga1: nachylenie linii
ograniczenia budżetowego = w/p).

3

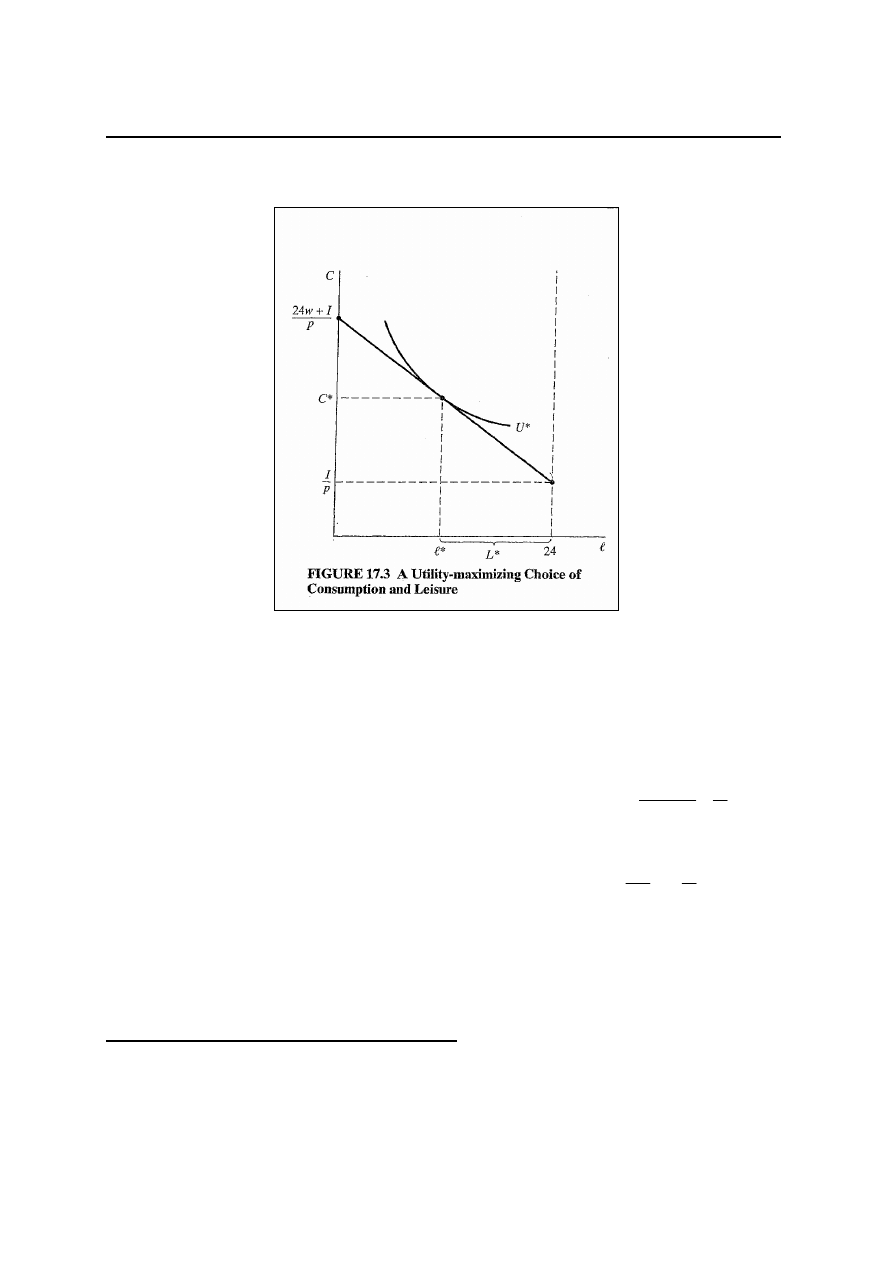
I/p nie musi być dodatnie np. gdy jednostka ma większe długi
niż oszczędności. Odsetki od długów stanowią stały koszt
ponoszony przed zakupem dóbr konsumpcyjnych. Alimenty są
następnym przykładem. Jeżeli ograniczenie budżetowe jest
spełnione w postaci równania przy zerowej konsumpcji, to
czas wolny może wynieść wyłącznie: l = (24w + I)/w. Większa
konsumpcja jest nieosiągalna ze względu na zobowiązania
finansowe. (rys. 17.2)

4

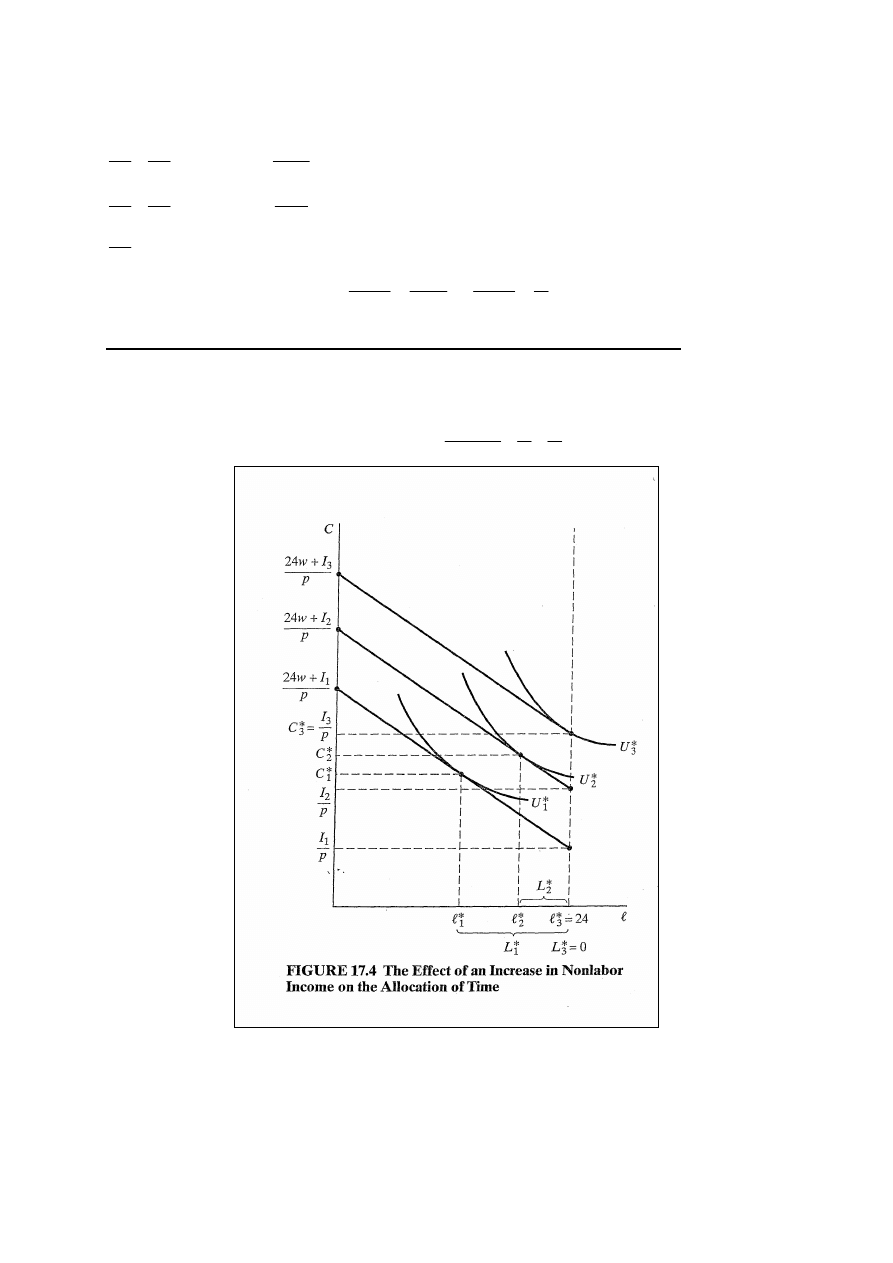
Wybór wielkości konsumpcji dóbr i czasu wolnego przy maxU
Zał.: preferencje jednostki spełniają warunki teorii
preferencji konsumenta.

Rys. 17.3: konsument wybiera punkt (C*, l*) z najwyższej
osiągalnej krzywej obojętności (U*), w którym nachylenie
linii ograniczenia budżetowego równa się nachyleniu krzywej
obojętności. Optymalna ilość godzin przepracowanych (L*)
jest różnicą maksymalnego czasu (24) i l*, czyli: L* = 24 – l*.
Równanie linii ograniczenia budżetowego:

l

p

w

p

I

w

C

−

+

=

24

. Po

zróżniczkowaniu tego równania względem l określamy
nachylenie linii ograniczenia budżetowego:

p

w

dl

dC

−

=

, które

równa się płacy realnej stanowiącej siłę nabywczą godziny
pracy. Warunek styczności: MRS

Cl

= w/p.

Wyprowadzenie matematyczne:
Max U(C, l)
p.w.: pC = w(24 - l) + I
Lagrangian:

]

)

24

(

[

)

,

(

pC

I

l

w

l

C

U

−

+

−

+

=

Ψ

λ

5

Warunki pierwszego rzędu:

p

MU

p

C

U

C

C

=

⇒

=

−

∂

∂

=

∂

Ψ

∂

λ

λ

0

w

MU

w

l

U

l

l

=

⇒

=

−

∂

∂

=

∂

Ψ

∂

λ

λ

0

pC

I

l

w

−

+

−

=

∂

Ψ

∂

)

24

(

λ

.

Rozwiązując dla λ:

p

w

MU

MU

w

MU

p

MU

l

C

l

C

=

⇒

=

=

λ

.

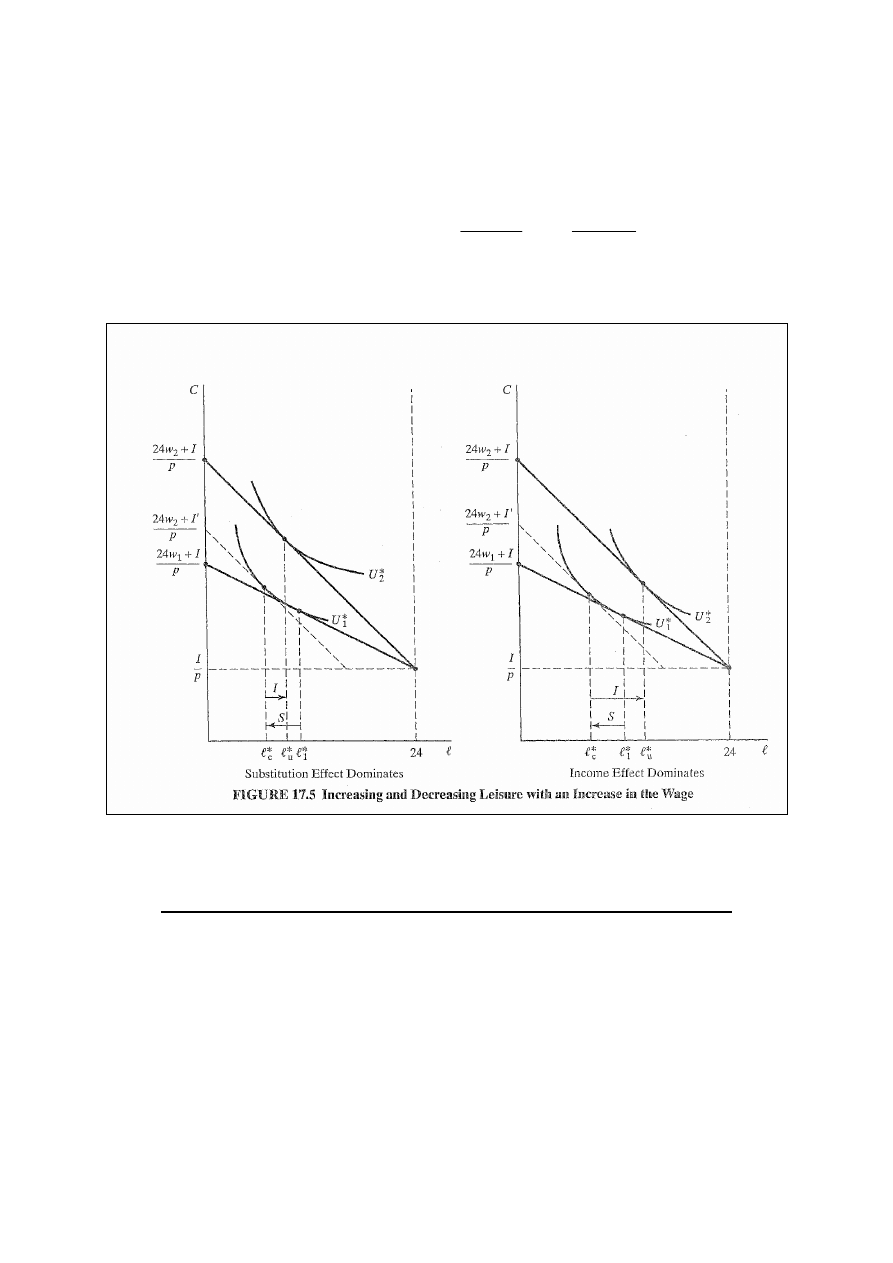
Statyka porównawcza wzrostu dochodu spoza pracy
Zmiana dochodu spoza pracy działa jak czysty efekt
dochodowy, czyli prowadzi do przesunięcia równoległego linii
ograniczenia budżetowego:

l

p

w

p

I

p

I

w

C

−

+

+

=

24

. (rys. 17.4)

Jeżeli dobra konsumpcyjna i czas wolny są dobrami
normalnymi, to równoległe przesunięcie linii prowadzi do

6

wzrostu zarówno konsumpcji dóbr, jak i czasu wolnego, czyli
do ograniczenia liczby przepracowanych godzin.

Zmiany stawki płac: efekt dochodowy i substytucyjny
Problem: pokusa zrównania wzrostu płac ze wzrostem
dochodu w standardowym modelu konsumenta.
Odpowiednikiem dochodu z tego modelu (M) jest teraz I.
Stawka płac jest ceną w obecnym modelu – ceną czasu
wolnego wyrażoną za pomocą nie zarobionych płac. Tak więc
zmiana stawki płac prowadzi do zmiany nachylenia linii
ograniczenia budżetowego. Działa więc efekt substytucyjny i
dochodowy zmiany stawki płac.

W przeciwieństwie do standardowego modelu efekty działają
w przeciwnych kierunkach, gdy dobra konsumpcyjne i czas
wolny są dobrami normalnymi. Dzieje się tak dlatego, że
wzrost płac podnosi cenę czasu wolnego i jednocześnie
zwiększa dostępny zbiór konsumpcyjny. (W modelu
równowagi konsumenta efekty działają w tym samym
kierunku, gdyż wzrost ceny dobra oznacza zmniejszenie
dostępnego zbioru konsumpcyjnego.)

Jeżeli czas wolny jest dobrem normalnym, to wzrost stawki
płac:

-

zmniejsza optymalny wybór czasu wolnego na skutek
działania ES (zmniejsza się konsumpcja dobra, którego
cena zwiększyła się),

-

zwiększa optymalny wybór czasu wolnego na skutek
działania ED.

7

Efekt netto zależy od względnej siły obu efektów. Wzrost
płac może doprowadzić do zwiększenia lub zmniejszenia
wielkości podaży pracy.
Rys. 17.5: wzrost stawki płac z

p

I

w

+

1

24

do

p

I

w

+

2

24

, co prowadzi

do obrotu linii ograniczenia budżetowego.

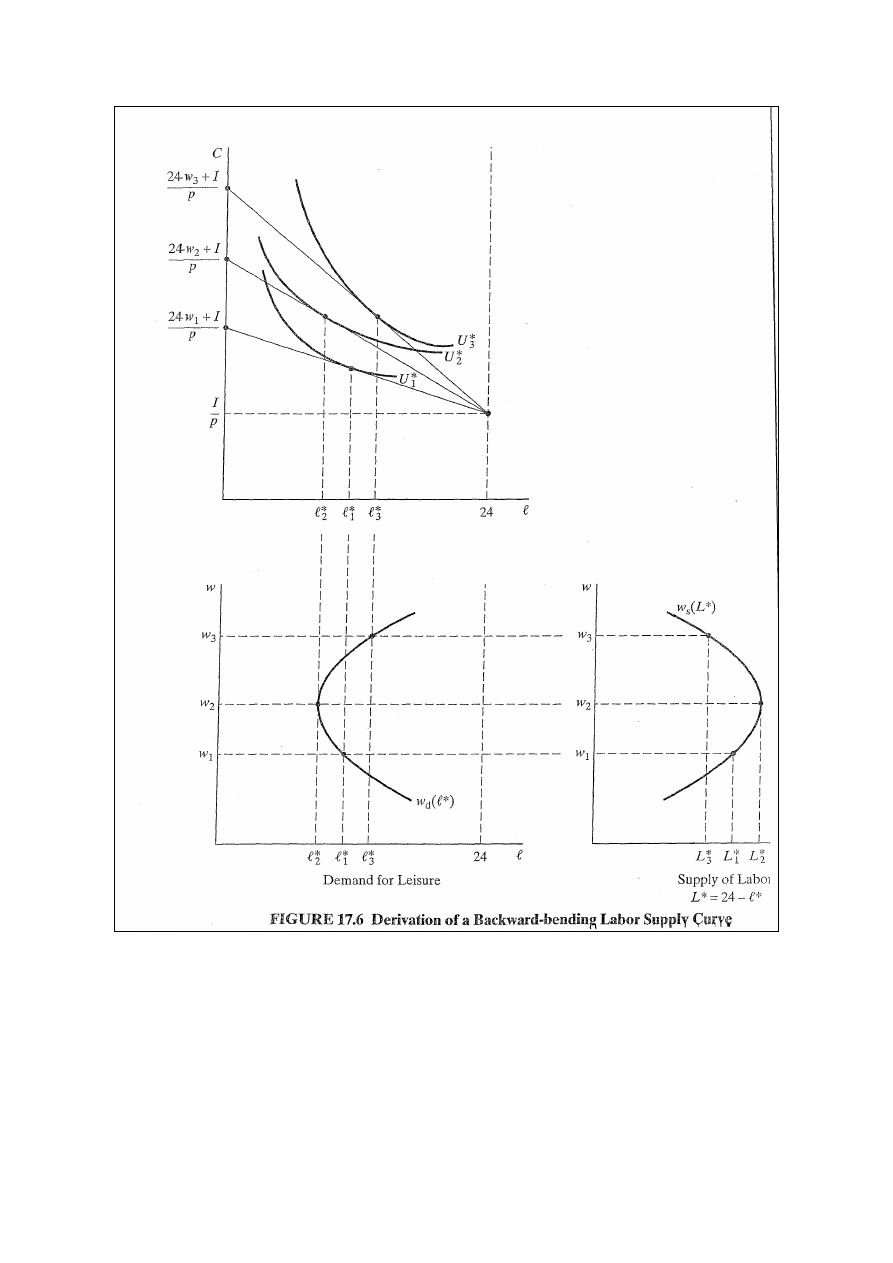
Zmieniające się nachylenie krzywej podaży pracy

Rys. 17.6 (empiryczne potwierdzenie takiego kształtu
krzywej podaży pracy)

8

9

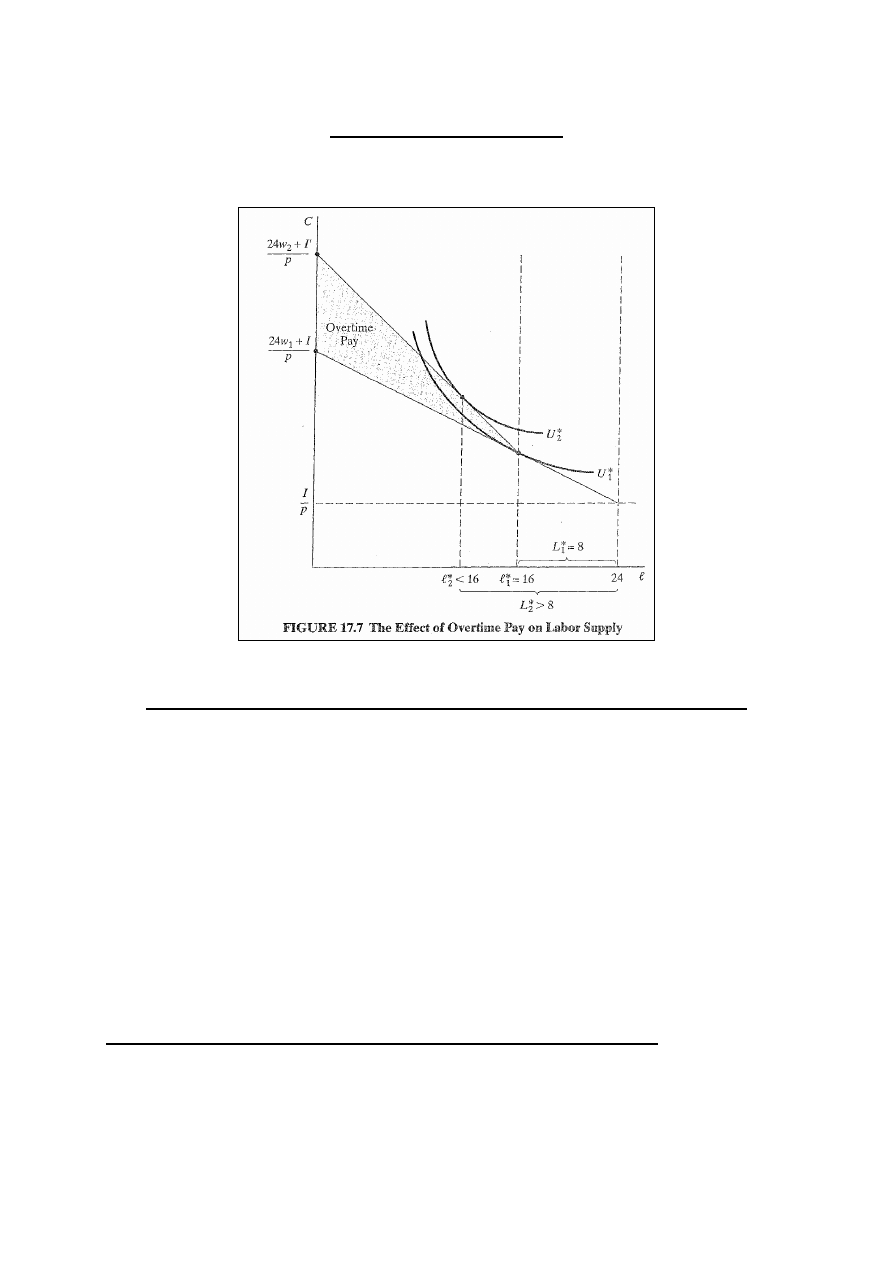
Płaca za nadgodziny

Rys. 17.7: zachęta pracodawców dla doświadczonych
pracowników aby pracować więcej – działa tylko ES.

Teoria gospodarstwa domowego alokacji czasu

Becker (

Economic Approach to Human Behavior

) stworzył

alternatywny model zachowania konsumenta jako
rozszerzenie przedstawionego prostego modelu podaży
pracy. Uważa on, że rozróżnienie między czasem wolnym i
konsumpcją dóbr jest sztuczne, gdyż ogromna część
populacji nie pracuje w celu uzyskania rynkowej płacy, ale
pracuje w domu. Co więcej każda konsumpcja wymaga pewnej
kombinacji dóbr kupionych i wytworzonych w domu oraz
czasu wolnego.
Wybór między produkcją w domu i pracą na rynku
Każdy konsument napotyka krzywą możliwości produkcji w
domu i linię ograniczenia budżetowego płacy rynkowej.

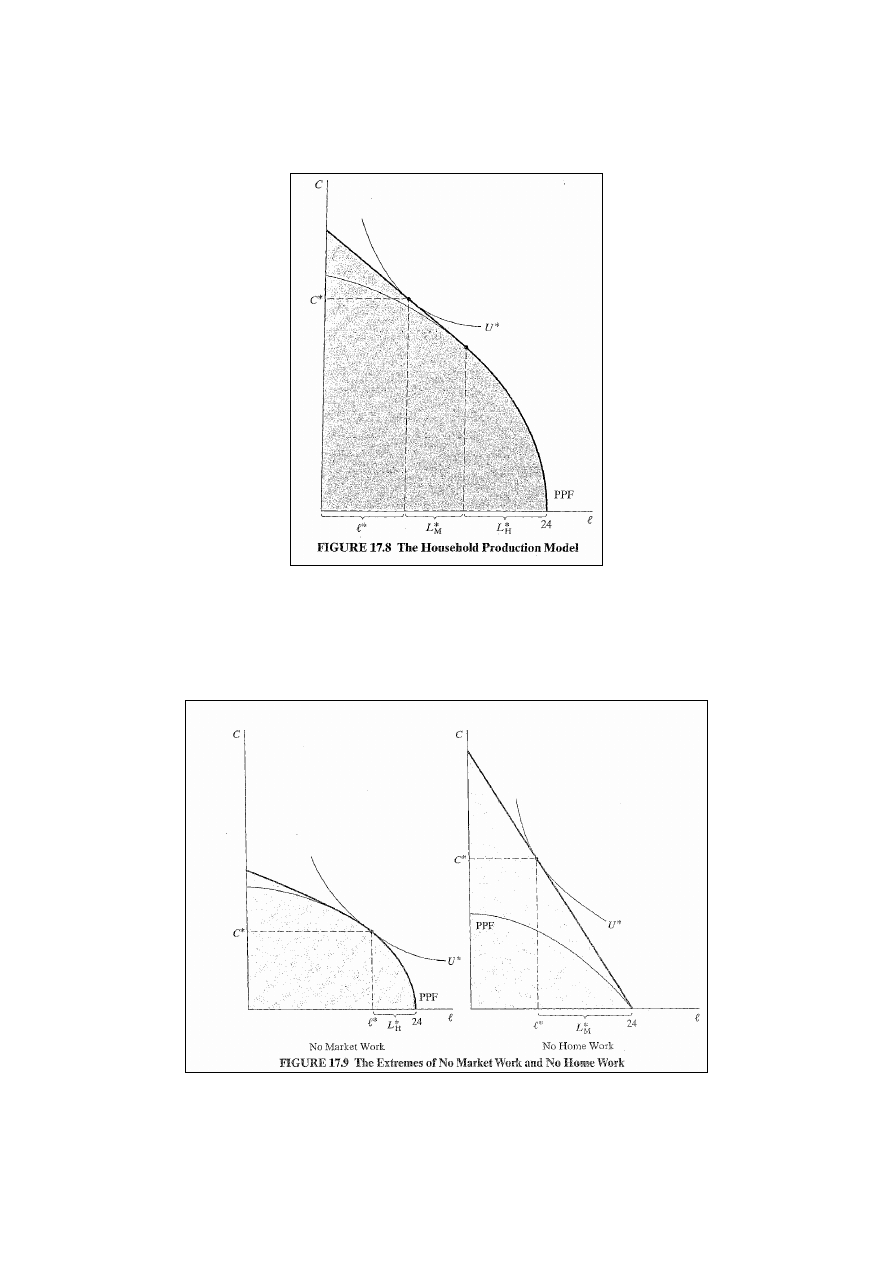
10

Rys. 17.8: zał.: indeks cenowy = 1 i nie ma dochodu spoza
pracy.

Jednostka będzie pracować w domu tak długo, jak MP

H

> MP

M

(w). Jeśli MP

H

< w, to jednostka podejmie pracę na rynku.

W tym modelu jednostka może nie pracować w domu lub na
rynku (rys. 17.9).

11

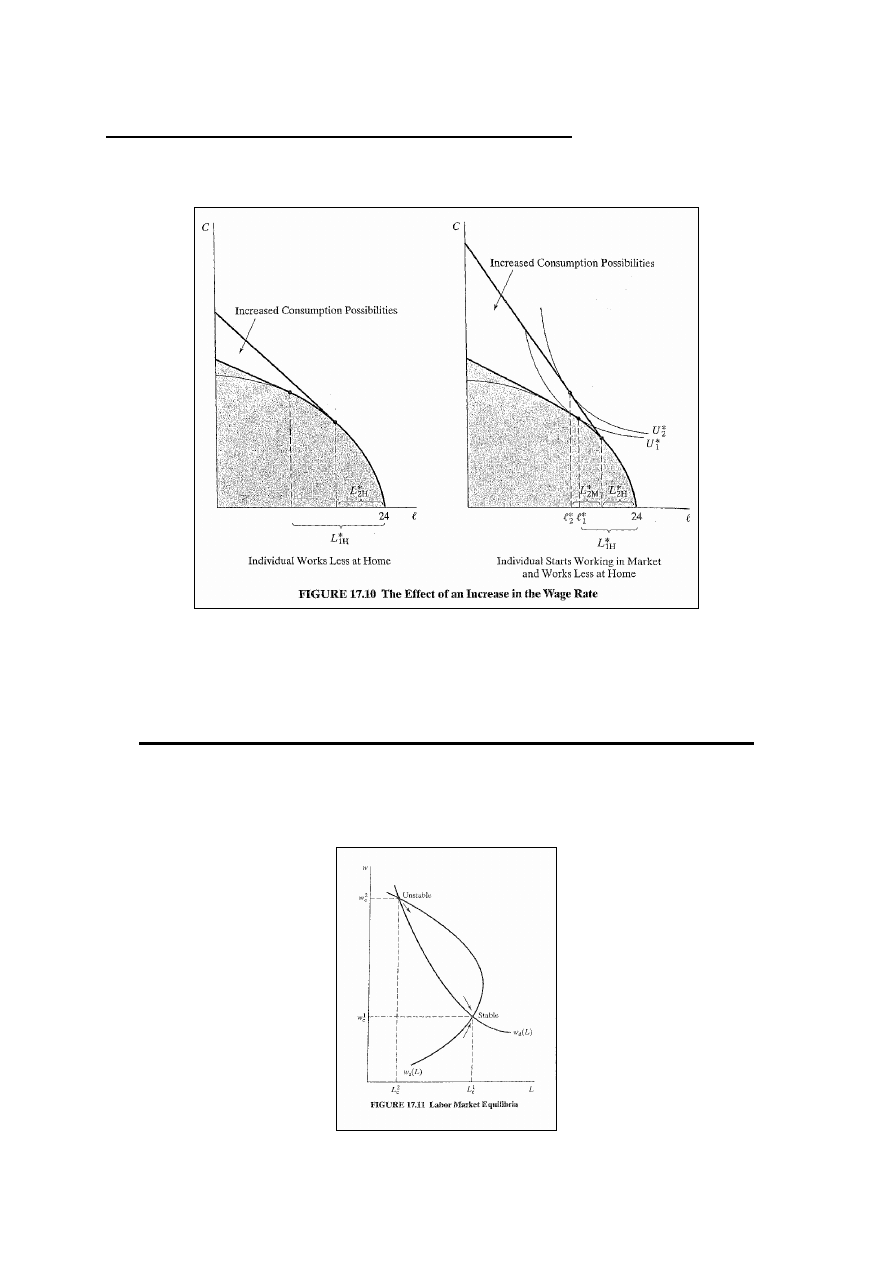
Statyka porównawcza wzrostu stawki płac
Rys. 17.10: wzrost w prowadzi do wejścia na rynek pracy i do
zmniejszenia czasu pracy w domu.

(Becker wykorzystywał model do pokazania zmian związanych
z wchodzeniem przez kobiety na rynek pracy.)

Równowaga na rynku doskonale konkurencyjnym

Wracamy do funkcji indywidualnej podaży pracy i łączymy ją
z popytem firmy na pracę (część MRP

L

) aby skonstruować

rynkowe funkcje podaży pracy i popytu na pracę. Rys. 17.11.

12

Rynki pracy niedoskonale konkurencyjne - monopson

Nie wszystkie rynki pracy są doskonale konkurencyjne.
Szczególnie interesującym przykładem niedoskonałej
konkurencji jest monopson – jedyny nabywca pracy na danym
rynku. Podobnie jak monopolista traktuje rynkową krzywą
popytu jako swą własną, indywidualną krzywą popytu, tak
monopsonista na rynku pracy traktuje rynkową krzywą
podaży pracy, jako swą własną podaż. Na rynku doskonale
konkurencyjnym koszt krańcowy zatrudnienia dodatkowej
jednostki pracy równa się płacy, a dla monopsonu koszt
krańcowy zatrudnienia dodatkowej jednostki pracy równa się
płacy dla tej jednostki plus kosztowi podwyżki płac dla
wszystkich już zatrudnionych, przy dodatnio nachylonej
krzywej podaży pracy. Całkowity koszt pracy wynosi

w

(

L

)

L

,

gdzie

w

(

L

) jest krzywą podaży pracy. Możemy więc

wyprowadzić koszt krańcowy zatrudnienia dodatkowej
jednostki pracy:

( )

[

]

w

dL

dw

L

w

L

L

w

dL

d

TC

dL

d

MC

L

L

>

+

=

=

=

dla

0

>

dL

dw

czyli dodatnio

nachylonej krzywej podaży pracy.
Z powyższego równania wynika, że krzywa kosztu
krańcowego pracy leży powyżej krzywej podaży pracy. Jeżeli
krzywa podaży byłaby liniowa, to funkcję można by zapisać
wzorem:

w = a + bL

.

Różniczkując tę funkcję względem

L

:

b

dL

dw =

.

Wstawiając dwa ostatnie równania do wzoru na MC

L

:

bL

a

bL

bL

a

MC

L

2

+

=

+

+

=

.

Z powyższego równania wynika, że punkt przecięcia z osią
pionową krzywa MC

L

ma taki sam, jak krzywa podaży pracy,

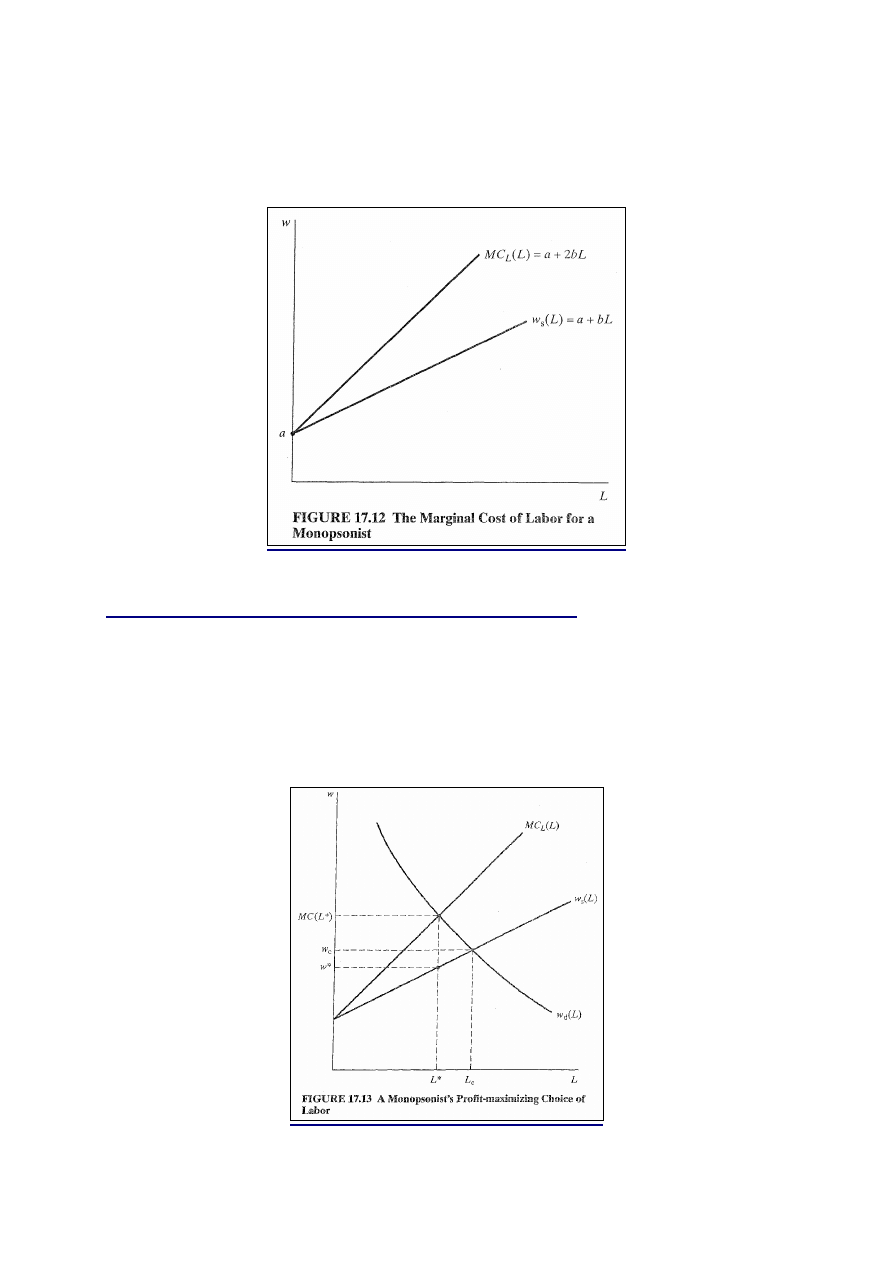
13

ale ma nacylenie dwukrotnie większe od krzywej podaży
pracy. (rys. 17.12)

Maksymalizacja zysku przez monopsonistę
Zasada maksymalizacji zysku przez monopson jest taka
sama, jak firmy działającej na doskonale konkurencyjnym
rynku pracy. Należy zatrudniać pracę aż do przychód
krańcowy z pracy zrówna się z kosztem krańcowym pracy –
rys. 17.13.

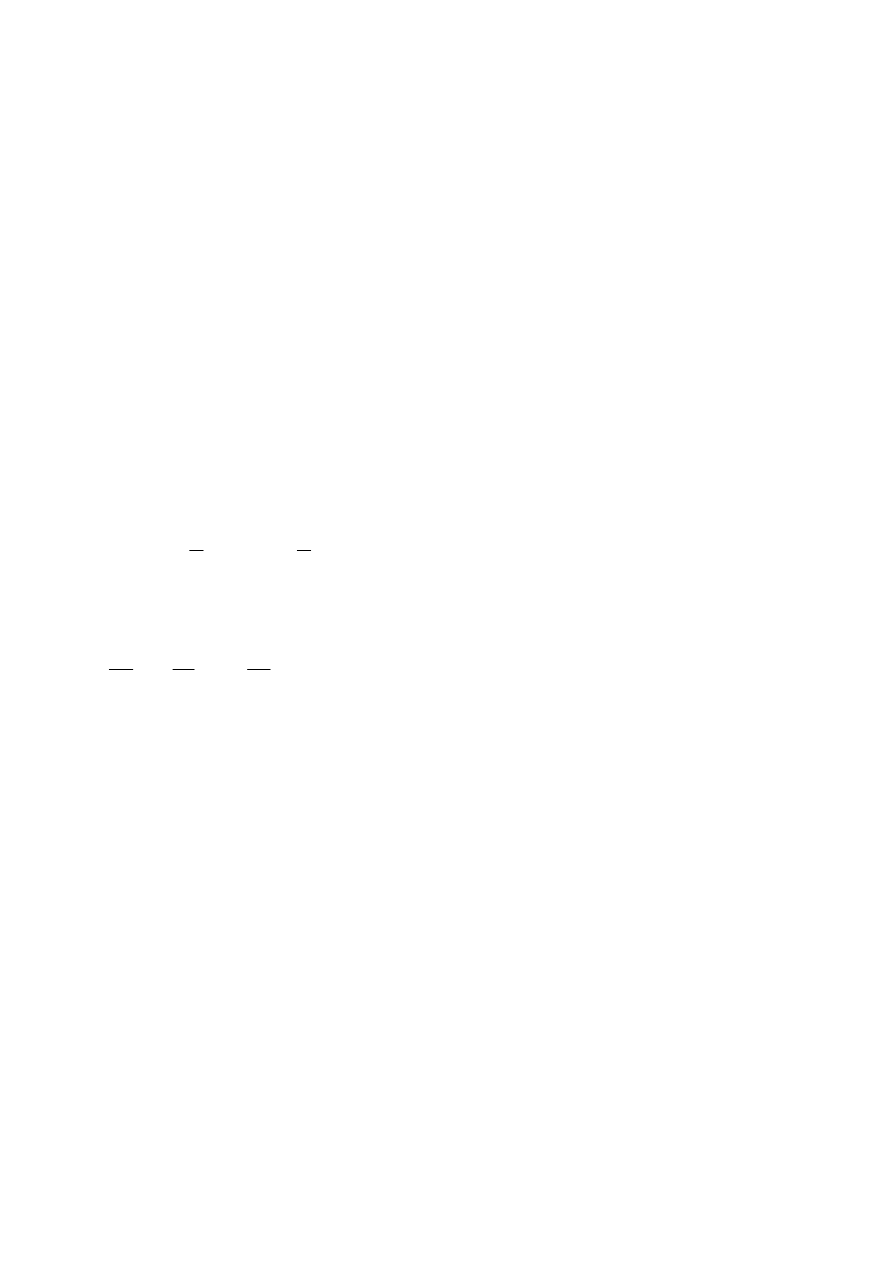
14

Wielkość pracy maksymalizująca zysk (L*) znajduje się w
punkcie przecięcia krzywej kosztu krańcowego z krzywą
popytu na pracę, czyli krzywą przychodu krańcowego z pracy.
Przy dodatnio nachylonej krzywej podaży pracy i ujemnie
nachylonej krzywej popytu na pracę ta wielkość jest zawsze
mniejsza od wielkości, jaka zostałaby wybrana w warunkach
doskonałej konkurencji (L

C

). Firma wypłaca płacę w* przy L*.

Płaca ta jest zawsze niższa od płacy doskonale
konkurencyjnej (w

C

) i od kosztu krańcowego zatrudnienia

ostatniej jednostki pracy MC(L*).
Matematycznie możemy to zapisać przedstawiając funkcję
zysku firmy w SR zapisaną od wielkości zatrudnienia pracy
przy stałym zatrudnieniu kapitału:

K

r

L

L

w

K

L

x

p

x

−

−

=

)

(

)

,

(

π

.

Przyjmując założenie, że cena jest parametrem warunek
konieczny przyjmuje postać:

L

L

x

MC

MRP

l

dL

dw

w

dL

dx

p

dL

d

=

⇒

=











 +

−

=

0

π

.

15

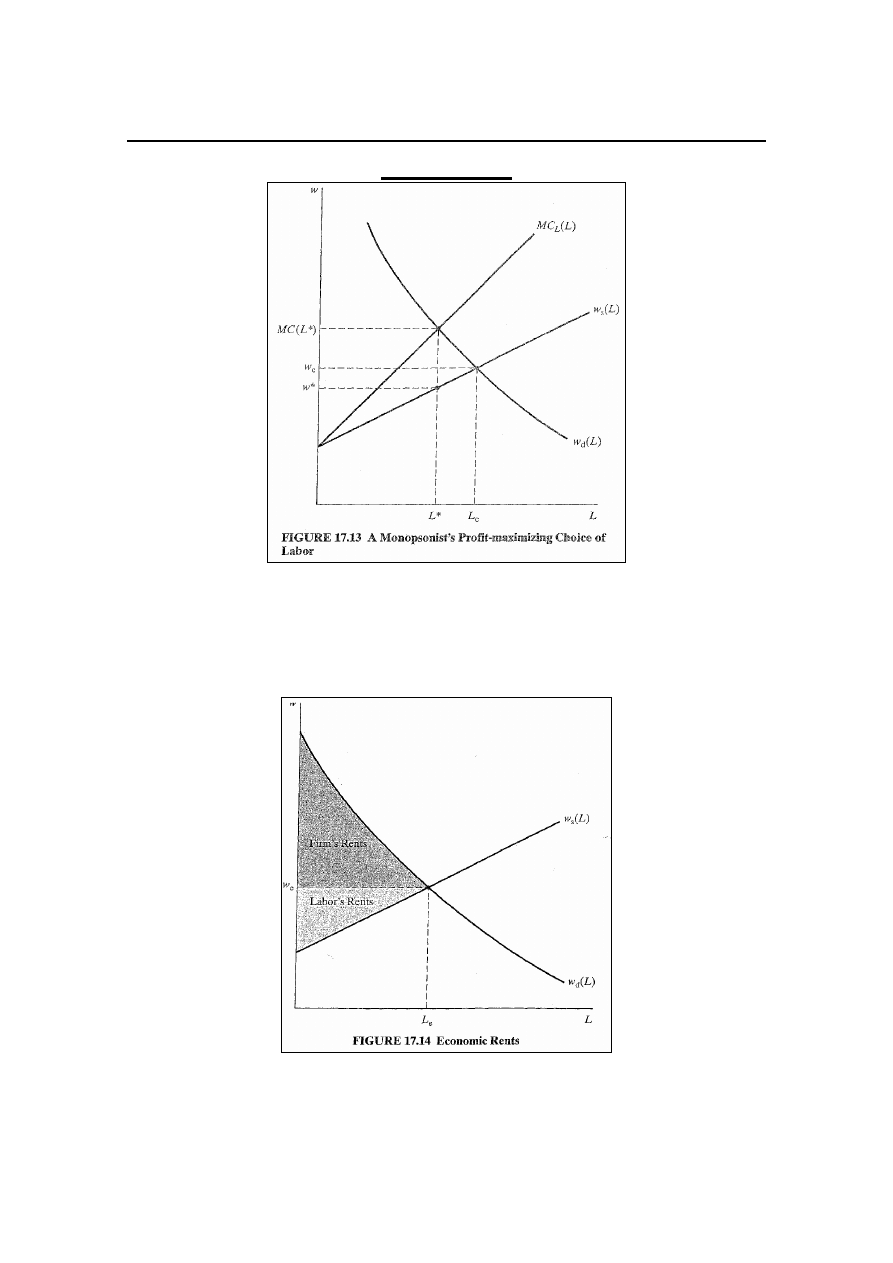
Renta ekonomiczna i skutki monopsonu po stronie

dobrobytu

Rys. 17.13 – rynek pracy – monopson, rynek produktu – d.k.
Na rynku czynników pojęciem analogicznym do nadwyżki
konsumenta i producenta jest renta ekonomiczna – rys.
17.14.

16

Deadweight loss
Rys. 17.15. W przypadku monopsonu czynniki nie odpływają do
rynkowej produkcji innych dóbr, gdyż monopson jest
jedynym pracodawcą dla danego rodzaju pracy. Praca nie
zatrudniona przez monopson przechodzi do produkcji w
domu, ale gospodarka nie może osiągnąć swej krzywej
możliwości produkcyjnych, gdyż monopson nie spełnia
warunku efektywności: MP

L

/MP

K

≠ MC

L

/MC

K

.

Doskonała dyskryminacja płac
Rozwiązaniem analogicznym do doskonałej dyskryminacji cen
przez monopol dla monopsonu jest doskonała dyskryminacja
płac. Jeżeli monopson płaciłby różnym pracownikom różne
płace lub różne płace takim samym pracownikom, ale za różną
liczbę przepracowanych godzin, to zwiększałby zatrudnienie
do MC = w. Płaca zapłacona za ostatnią godzinę pracy byłaby
płacą doskonale konkurencyjną i wielkość zatrudnienia byłaby
taka, jak w konkurencji doskonałej. Kosztem takiego zabiegu
jest przejęcie przez monopson rent ekonomicznych
czynników. Gospodarka znajduje się na krzywej

17

transformacji, ale w innym punkcie niż przy konkurencji
doskonałej.

Związki zawodowe

Pracownicy mogą zrzeszać się w związki zawodowe w celu
występowania w charakterze monopolu. Ponieważ związki są
kartelem, to napotykają te same trudności, co kartele
zawiązywane ze względu na produkt. Trudna do określenia
jest funkcja celu, a maksymalizacja całkowitych płac wymaga
innej strategii niż maksymalizacja zatrudnienia.

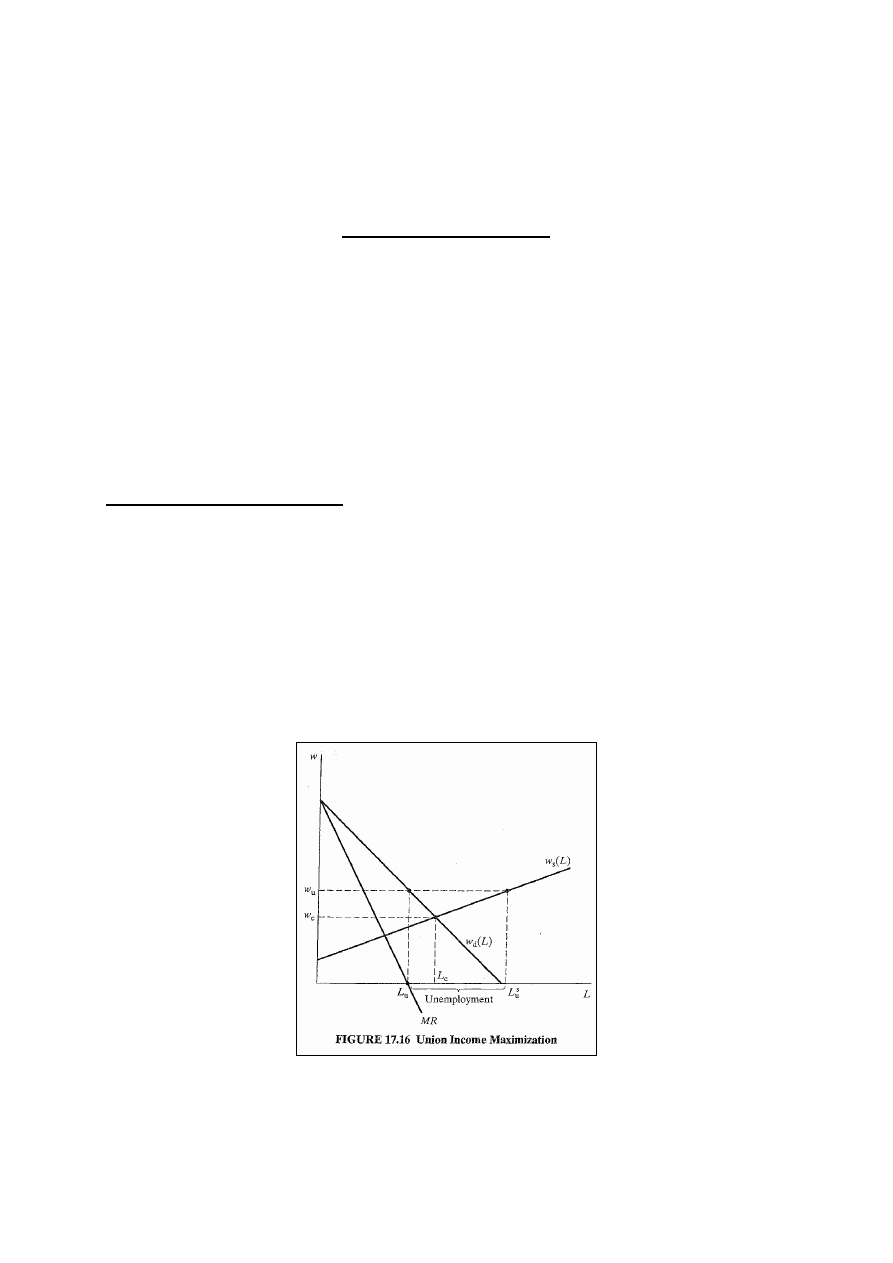
Maksymalizacja płacy
Zał.: związki dążą do maksymalizacji płac całkowitych, a więc
całkowita wielkość przeznaczona na dystrybucję jest
maksymalizowana. Problem: jak podzielić wypłaty. Sytuacja
trudniejsza, gdyż część pracowników straci pracę i część
będzie musiała ograniczyć liczbę przepracowanych godzin na
skutek podwyżki płac – konieczność kompensacji ze składek
pracujących członków.

Rys. 17.16. Na początku rynek pracy jest doskonale
konkurencyjny: w

c

i L

c

. Powstają ZZ i dążą do maksymalizacji

płac. Ponieważ wypłaty na rynku pracy równoważne

18

przychodom całkowitym na rynku produktów, to ZZ
wybierają płacę i wielkość pracy tak aby elastyczność popytu
na pracę wynosiła –1. (max TR) Maksymalizacja wypłat: w

u

i

L

u

. Problem ZZ: w punkcie: w

u

i L

u

s

wszyscy chcą pracować.

Zanim ZZ wypracują odpowiedni schemat i kompensacje,
część tych bezrobotnych (L

u

s

- L

u

) podejmie pracę za niższe

wynagrodzenie.
Negocjacje ZZ z monopsonem
Argument: pracownicy muszą zrzeszać się, gdyż monopson
płaci im mniej niż wynosi ich MRP. W takiej sytuacji
negocjacje mogą poprawić dobrobyt, jeśli osiągnięte będzie
wspólne maksimum.

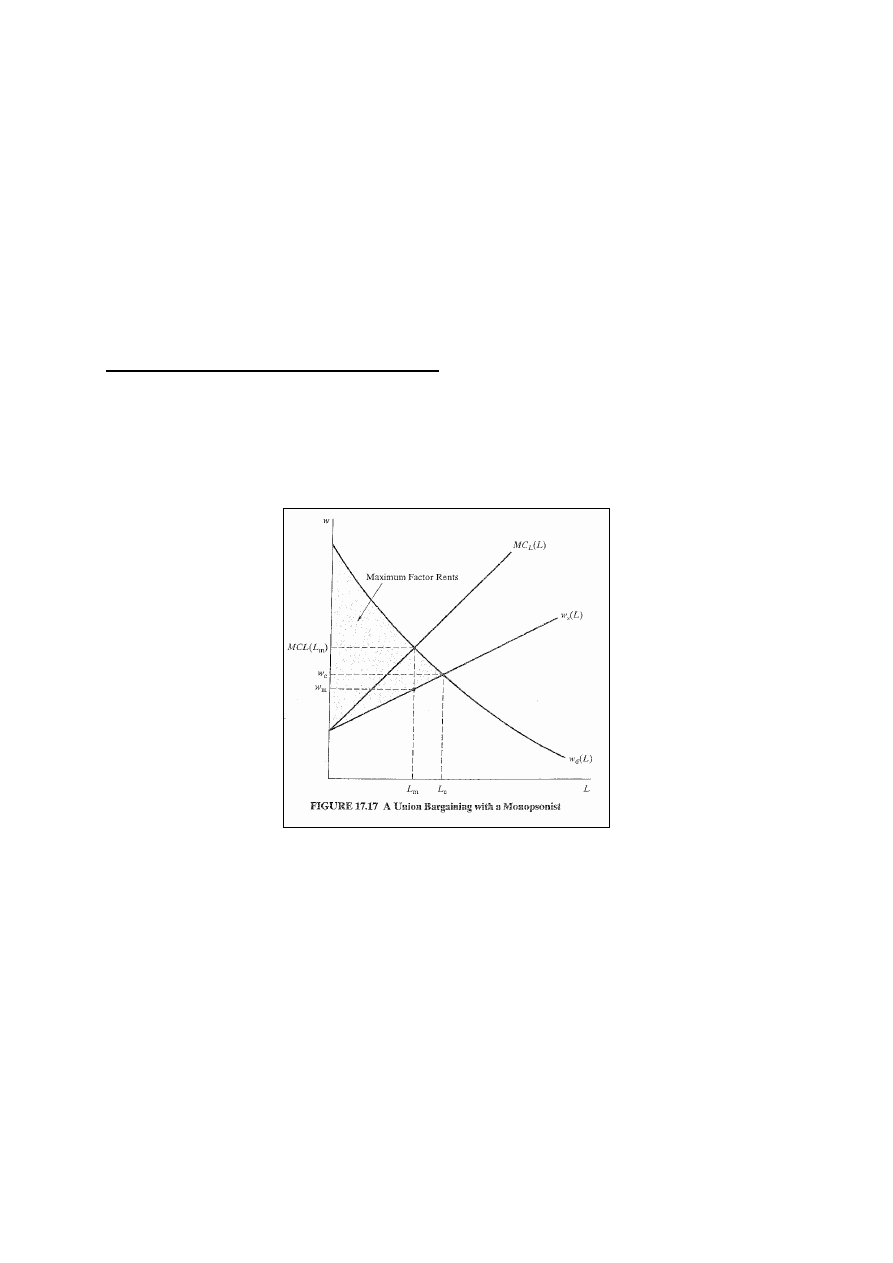
Rys. 17.17: wspólne maksimum znajduje się w punkcie, w
którym renty czynników są maksymalne (przy zatrudnieniu
odpowiadającym warunkom doskonałej konkurencji).
Monopson płaci w

m

i zatrudnia L

m

. Nawet jeśli ZZ wymuszą

podwyżkę płac, to więcej pracowników znajdzie zatrudnienie,
a nie mniej. (Cel: L

c

) Problem: nie wiemy, jak będzie

podzielona renta między ZZ i firmę. Efektywne rozwiązanie:
płaca dla pracowników = w

c

i dać im udział w zyskach firmy.

Udział w zyskach jest częstym wynikiem negocjacji ZZ.