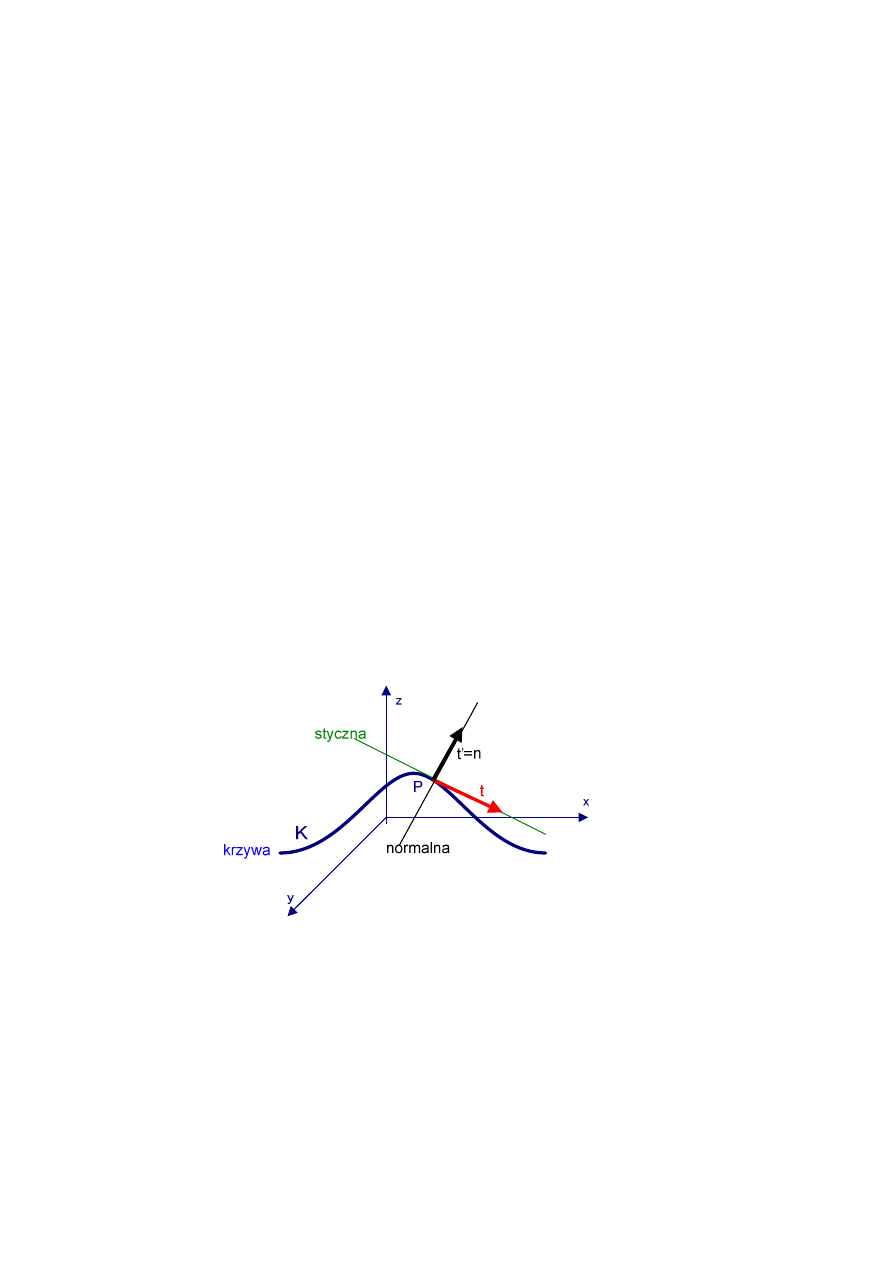
G. 5. Trójścian Freneta
Rozważmy krzywą K daną równaniem w parametryzacji naturalnej
→
r
= r(s) = a
x
(s) i + a
y
(s) j + a
z
(s) k ,
gdzie i, j, k są wersorami osi Ox, Oy, Oz układu współrzędnych Oxyz.
Rozważamy punkt P(s
0
) tej krzywej odpowiadający wartości s
0
parametru, czyli
P(s
0
) = ( a
x
(s
0
) ; a
y
(s
0
) ; a
z
(s
0
) ).
Na poniższym rysunku krzywą K zaznaczono kolorem niebieskim.
Styczna
Niech wektor
→
t
= r’(s
0
) = a’
x
(s
0
) i + a’
y
(s
0
)j + a’
z
(s
0
)k będzie wektorem stycznym do
tej krzywej w punkcie P(s
0
) = ( a
x
(s
0
) ; a
y
(s
0
) ; a
z
(s
0
) ). Wektor ten na rysunku zaznaczano
kolorem czerwonym.
Wektor
→
t
= r’(s
0
) wyznacza prostą styczną m w punkcie P(s
0
) tej krzywej (na
rysunku prosta zaznaczona kolorem zielonym). Styczna ta w układzie współrzędnych Oxyz
ma następujące równanie parametryczne:
x = a
x
(s
0
) + a’
x
(s
0
)
λλλλ
; y = a
y
(s
0
) + a’
y
(s
0
)
λλλλ
; z = a
z
(s
0
) + a’
z
(s
0
)
λλλλ
dla
λλλλ
∈
R.
Normalna główna
Oznaczmy symbolem
→
t
wersor stycznej
→
)
(
,
s
r
, czyli zakładamy, że
→
t
=
→
)
(
,
s
r
oraz
długość wektora
→
t
wynosi 1.
Wyznaczamy wektor
→
,
t
będący drugą pochodną wektora
→
)
(
,
,
s
r
. Jest on wektorem

prostopadłym (ortogonalnym) do wektora
→
t
. Na rysunku zaznaczono kolorem czarnym.
Oznaczmy przez
→
n
wersor wektora niezerowego
→
)
(
,
,
s
r
, tzn.
→
n
=
→
→
|
)
(
|
)
(
,
,
,
,
s
r
s
r
, gdzie |
→
)
(
,
,
s
r
| jest długością wektora
→
)
(
,
,
s
r
.
Wersor
→
n
nazywamy wersorem normalnym głównym; wyznacza on prostą
nazywaną prostą normalną główną w punkcie P(s
0
) = ( a
x
(s
0
) ; a
y
(s
0
) ; a
z
(s
0
) ) tej krzywej.
(na rysunku prosta zaznaczona kolorem czarnym). Prosta normalna główna w układzie
współrzędnych Oxyz ma następujące równanie parametryczne:
x = a
x
(s
0
) + a’’
x
(s
0
)
λλλλ
; y = a
y
(s
0
) + a’’
y
(s
0
)
λλλλ
; z = a
z
(s
0
) + a’’
z
(s
0
)
λλλλ
dla
λλλλ
∈
R.
Binormalna
Wektory
→
t
,
→
n
są wersorami wzajemnie prostopadłymi; mówimy, że tworzą one parę
wektorów ortonormalnych.
Dobieramy do nich wektor jednostkowy
→
b
taki, że trójka wersorów
→
t
,
→
n
,
→
b
tworzy
pary wektorów wzajemnie prostopadłych (łącznie tworzą układ ortonormalny) oraz są tak
zorientowane jak układ wersorów osi i, j, k.
Jako
→
b
wystarczy przyjąć
→
b
=
→
t
××××
→
n
. Nazywamy go wersorem binormalnym
krzywej.
Wersor
→
b
wyznacza prostą nazywaną binormalną w punkcie
P(s
0
) = ( a
x
(s
0
) ; a
y
(s
0
) ; a
z
(s
0
) ) tej krzywej.
Prosta binormalna w układzie współrzędnych Oxyz ma następujące równanie
parametryczne:
x = a
x
(s
0
) + [a’
y
(s
0
) a’’
z
(s
0
)
−
a’
z
(s
0
) a’’
y
(s
0
) ]
λλλλ
;
y = a
y
(s
0
) + [ a’
x
(s
0
) a’’
z
(s
0
)
−
a’’
x
(s
0
) a’
z
(s
0
)]
λλλλ
;
z = a
z
(s
0
) + [ a’
x
(s
0
) a’’
y
(s
0
)
−
a’
y
(s
0
) a’’
x
(s
0
)]
λλλλ
dla
λλλλ
∈
R.
Zachodzą zatem zależności:
→
b
=
→
t
××××
→
n
,
→
t
=
→
n
××××
→
b
,
→
n
=
→
b
××××
→
t
.
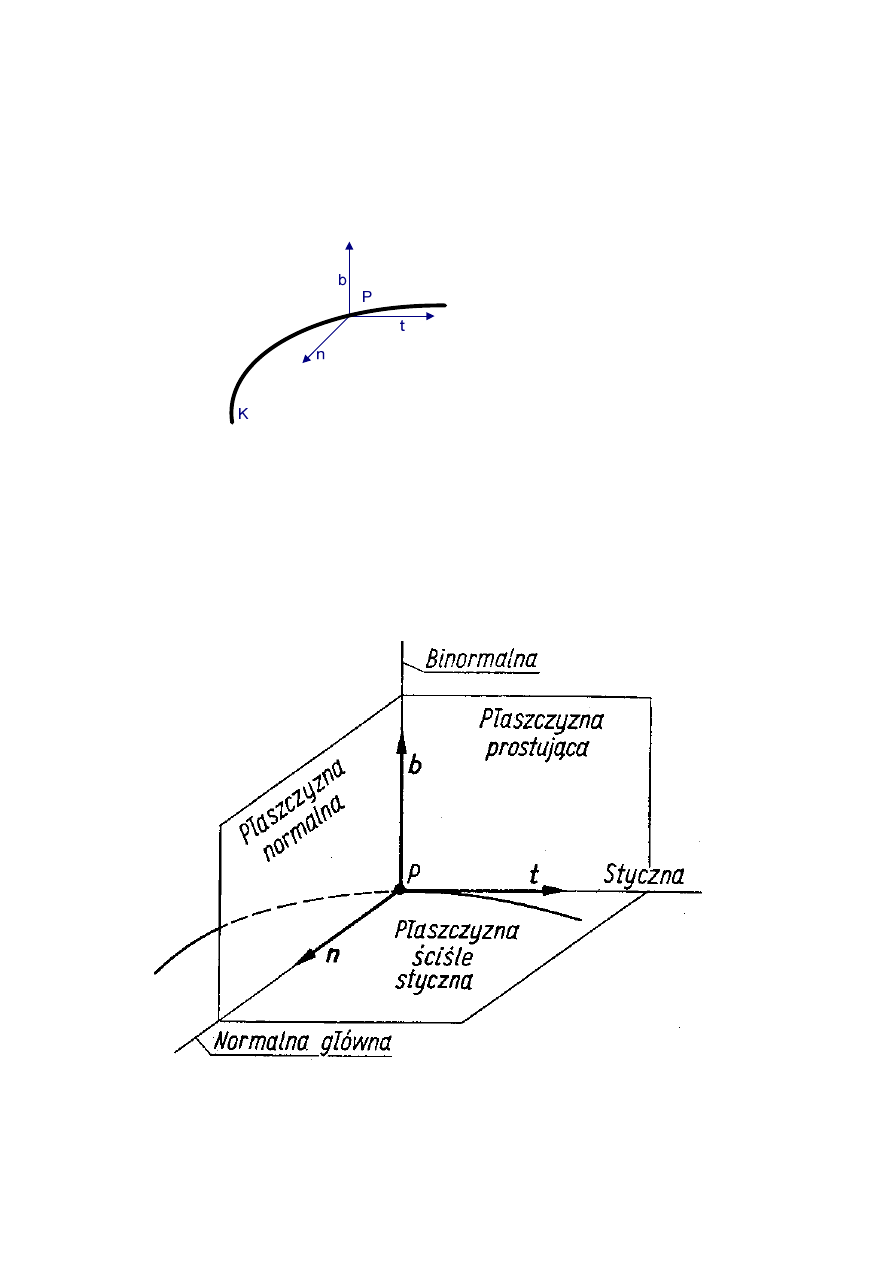
Trójścian Freneta
Każdemu punktowi P krzywej K można przyporządkować układ trzech wektorów:
→
t
- wersor styczny,
→
n
- wersor normalny główny,
→
b
- wersor binormalny.
Wersory
→
t
,
→
n
,
→
b
wyznaczają trzy płaszczyzny wzajemnie prostopadłe: wektory
→
t
,
→
n
- płaszczyznę ścisle styczną, wektory
→
n
,
→
b
- płaszczyznę normalną, wektory
→
b
,
→
t
-
płaszczyznę prostującą (rektyfikacyjną) do krzywej K w punkcie P.
Układ tych trzech płaszczyzn tworzy tzw. trójścian Freneta.
Niech
→
R
= [x, y, z] ,
→
r
= [ a
x
(s
0
); a
y
(s
0
); a
z
(s
0
)] , zaś
°
oznacza iloczyn skalarny wektorów.
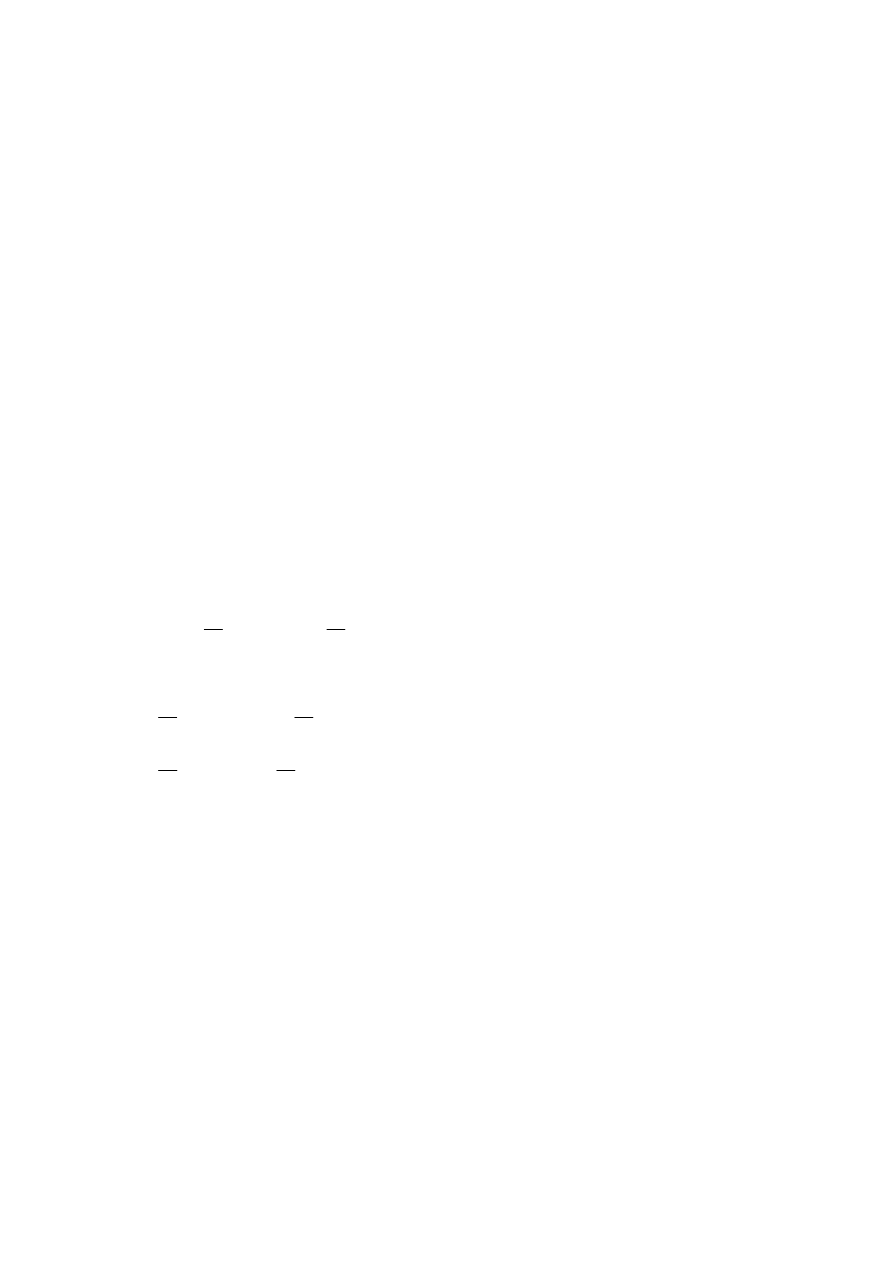
Równania wektorowe tych płaszczyzn przechodzących przez punkt
P
0
= ( a
x
(s
0
); a
y
(s
0
); a
z
(s
0
) ) są następujące:
a) płaszczyzny ściśle stycznej: (
→
R
-
→
r
)
°°°°
→
b
= 0 ,
b) płaszczyzny normalnej: (
→
R
-
→
r
)
°°°°
→
t
= 0 ,
c) płaszczyzny prostującej: (
→
R
-
→
r
)
°°°°
→
n
= 0.
Jeśli dany łuk jest płaski, wówczas płaszczyzna ściśle styczna jest płaszczyzną, w
której ten łuk leży.
Przykład 1.
Wyznacz płaszczyznę styczną do powierzchni danej równaniem z = 8x
2
– 6xy
3
w punkcie
P = (-1, 2, 56) . Wyznacz wektor normalny do tej płaszczyzny w punkcie P.
Rozwiązanie
Równanie płaszczyzny stycznej do powierzchni o równaniu z = f(x, y) w punkcie
P
0
= (x
0
, y
0
, z
0
) jest następujące:
z – z
0
=
)
(P
x
f
∂
∂
(x – x
0
) +
)
(P
y
f
∂
∂
(y – y
0
)
W naszym wypadku mamy: P = (-1, 2, 56) , x
0
= -1, y
0
= 2, z
0
= 56.
x
f
∂
∂
= 16x – 18y
3
,
)
2
,
1
(
−
∂
∂
x
f
= - 160,
y
f
∂
∂
= – 18xy
2
,
)
2
,
1
(
−
∂
∂
y
f
= 72.
Równanie płaszczyzny stycznej jest następujące:
z – 56 = – 160 (x + 1) + 72(y – 2), czyli: – 160 x + 72 y – z – 248 = 0.
Wektor
→
n
normalny do tej płaszczyzny
→
n
= [– 160, 72, – 1].
Zatem prosta normalna ma równania parametryczne:
x = – 1 – 160 t, y = 2 + 72 t, z = 56 – t dla t
∈
R.
Zadania do samodzielnego rozwiązania
Zadanie 1.
Krzywą K zadano równaniem wektorowym
→
r
= u i + u
2
j
+
u
3
k , u
∈
[0, 6].
a) Wyznacz wektor stycznej do krzywej K w punkcie M = (2, 4, 8).
b) Napisz równanie: (b1) prostej stycznej, (b2) płaszczyzny normalnej, (b3)
płaszczyzny
ściśle stycznej do krzywej K w punkcie M = (2, 4, 8).
Zadanie 2.
Wyznacz płaszczyznę styczną do powierzchni danej równaniem x
2
+ y
2
+ z
2
= 100
w punkcie P = (6, 4
3
, 4) .
Odpowiedzi
Zad. 1. Zauważ, że punkt M odpowiada wartości u = 2 parametru.
a) Wektor stycznej
→
t
= i + 2u j + 3 u
2
k ; w punkcie M wektor ten jest równy
→
t
= i + 4 j + 12
k.
(b1) Równanie stycznej: x = 2 +
λ
; y = 4 + 4
λ
, z = 8 + 12
λ
dla
λ
∈
R.
(b2) Równanie płaszczyzny normalnej: x + 4 y + 12 z – 114 = 0.
(b3) Równanie płaszczyzny ścisle stycznej: 12x – 6y + x – 8 = 0.
Zad. 2. 1,5x +
3
y – z – 17 = 0.
Wyszukiwarka
Podobne podstrony:
Krzywizna, dlugosc krzywej, trojscian Freneta, elementy teori pola
ABZ boxes wazon trojscienny
am2cz17 frenet
więcej podobnych podstron