
http://www.if.pwr.wroc.pl/~wozniak/
fizyka1.html
Dr hab. inż. Władysław Artur Woźniak
Instytut Fizyki Politechniki Wrocławskiej
Dr hab. inż. Władysław Artur Woźniak
Wykład FIZYKA I
2. Kinematyka punktu materialnego

KINEMATYKA PUNKTU MATERIALNEGO
Kinematyka
zajmuje się związkami między położeniem,
prędkością i przyspieszeniem badanej cząstki – nie obchodzi
nas, skąd bierze się przyspieszenie czy przyczyna, która
ruch powoduje (SIŁA).
Dr hab. inż. Władysław Artur Woźniak
Pojęcia wstępne
Ruch mechaniczny – zmiana wzajemnego położenia ciał w przestrzeni (lub
jednych ich części względem drugich) pod wpływem czasu.
Punkt materialny – ciało, którego rozmiary i kształty możemy w danym
zagadnieniu pominąć.
Układ odniesienia – ciało, jego część lub grupa ciał względem siebie
nieruchomych, względem których podajemy położenie danego ciała w przestrzeni.
Równania ruchu – opisują zmiany położenia ciała w przestrzeni w funkcji czasu.
Trajektoria ruchu – krzywa w przestrzeni, opisująca zmianę położenia ciała.
KINEMATYKA PUNKTU MATERIALNEGO
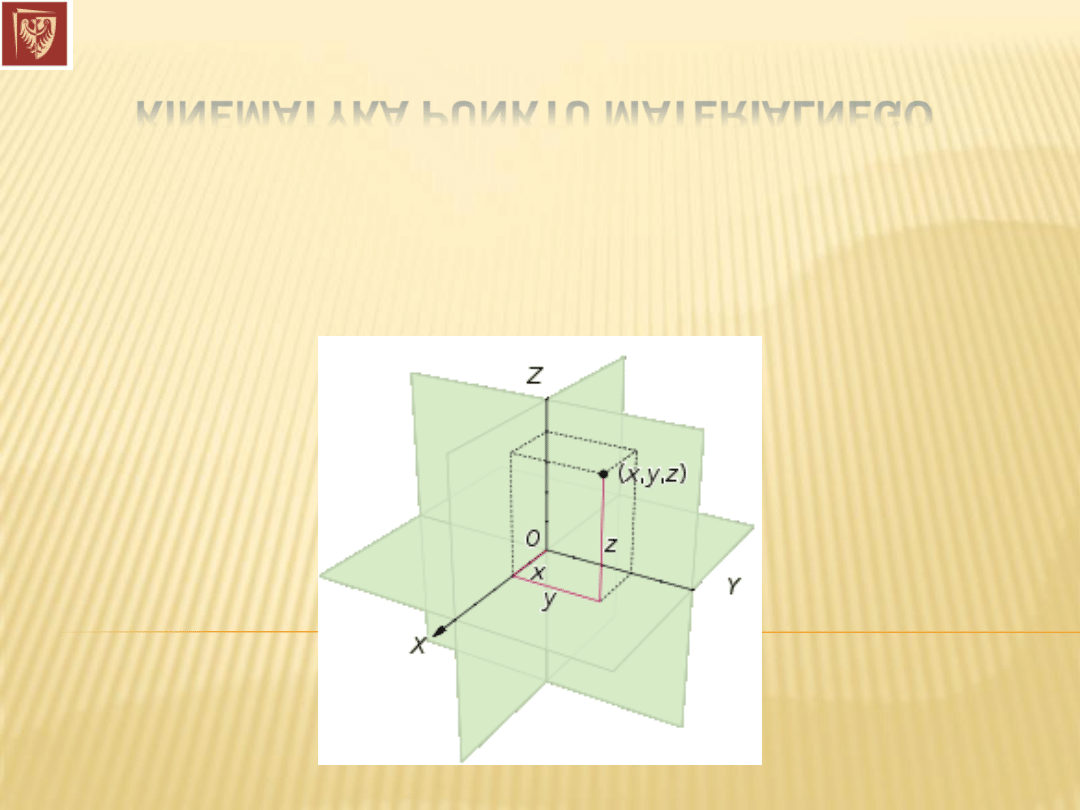
Układy współrzędnych
(3-D) Kartezjański układ współrzędnych (2-D prostokątny):
Dr hab. inż. Władysław Artur Woźniak
KINEMATYKA PUNKTU MATERIALNEGO
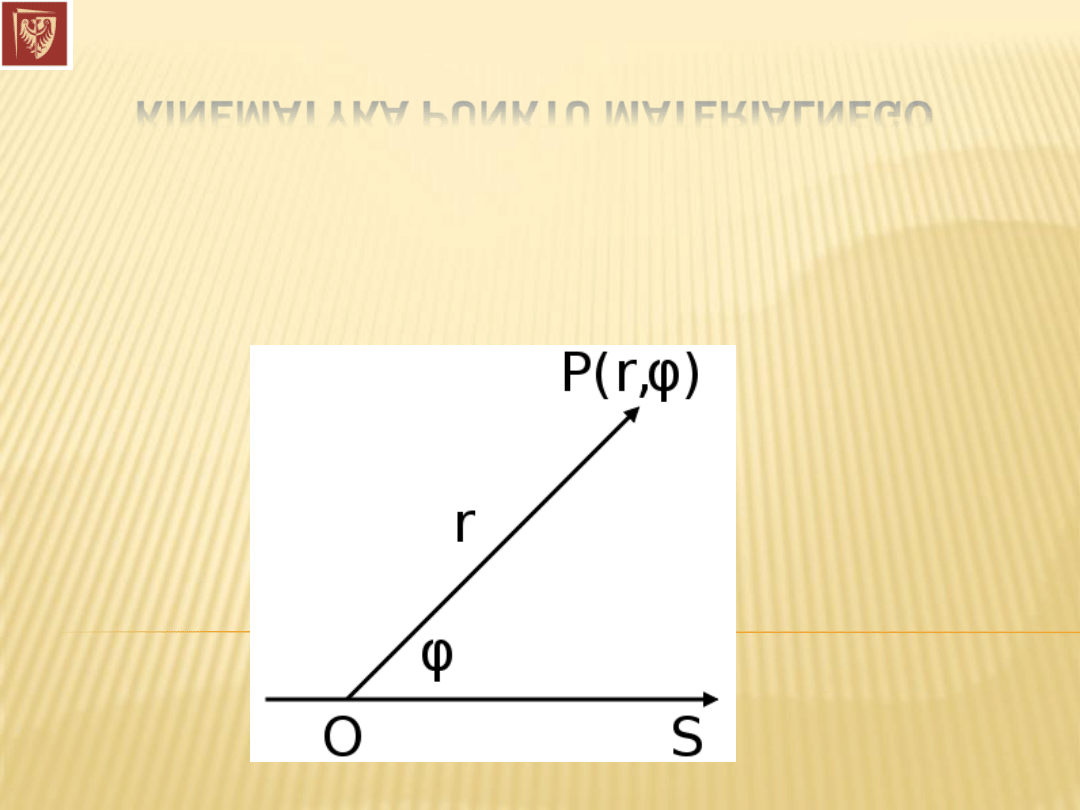
Układy współrzędnych
(2-
D) Układ współrzędnych biegunowych:
Dr hab. inż. Władysław Artur Woźniak
KINEMATYKA PUNKTU MATERIALNEGO
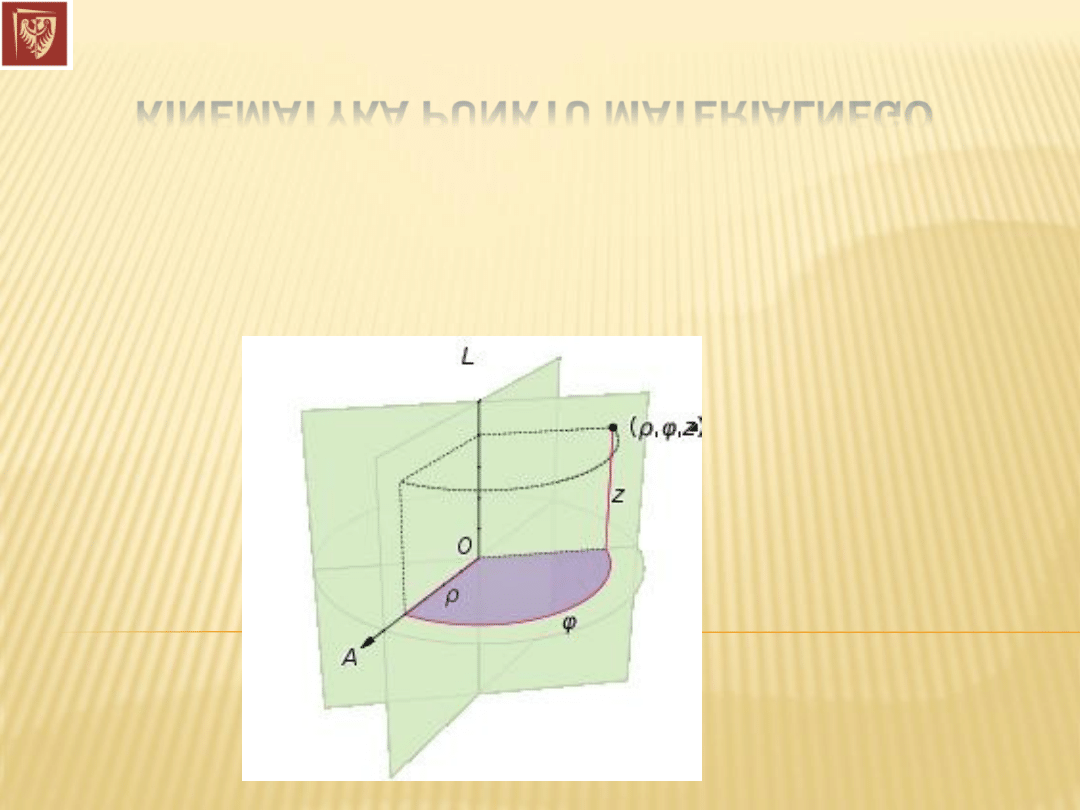
Układy współrzędnych
(3-
D) Układ współrzędnych cylindrycznych:
Dr hab. inż. Władysław Artur Woźniak
KINEMATYKA PUNKTU MATERIALNEGO
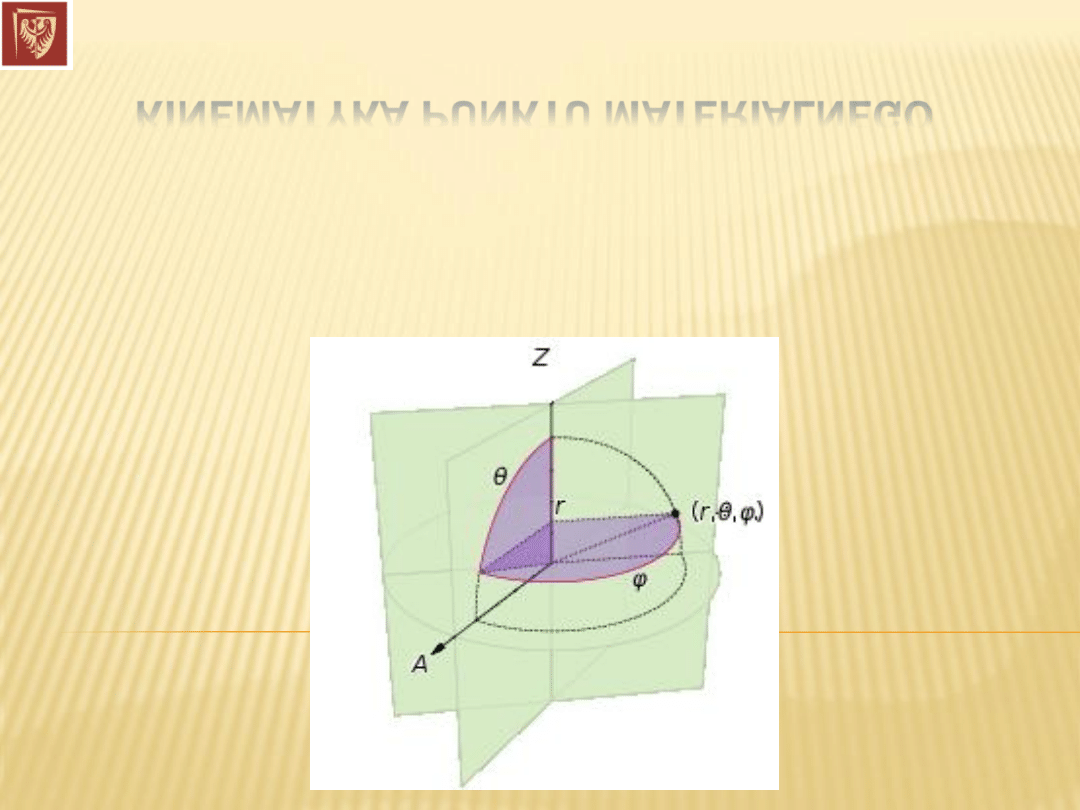
Układy współrzędnych
(3-
D) Układ współrzędnych sferycznych:
Dr hab. inż. Władysław Artur Woźniak

KINEMATYKA PUNKTU MATERIALNEGO
Podstawowe zasady:
Względność ruchu – każdy ruch mechaniczny jest względny, bo
polega na wzajemnym przemieszczaniu się ciał; charakter ruchu
ciała jest różny w zależności od układu odniesienia.
Zasada niezależności ruchów (superpozycji) – jeśli jakiś punkt
bierze udział jednocześnie w kilku ruchach, to wypadkowe
przesunięcie punktu równe jest sumie wektorowej przesunięć
wykonanych przez ten punkt w tym samym czasie w każdym z
tych ruchów oddzielnie.
Dr hab. inż. Władysław Artur Woźniak

NIEZWYKLE WAŻNE
2
2=4
Dr hab. inż. Władysław Artur Woźniak

KINEMATYKA PUNKTU MATERIALNEGO
Prędkość
Wielkość wektorowa, która określa zarówno szybkość ruchu, jak i jego
kierunek w danej chwili.
Prędkość chwilowa:
Jednostką jest metr na sekundę.
Dr hab. inż. Władysław Artur Woźniak
dt
r
d
t
t
t
r
t
r
v
t
t
0
0
0
lim
2
2
0
0
0
lim
dt
r
d
dt
v
d
t
t
t
v
t
v
a
t
t
Definicje podstawowych
wielkości
Przyspieszenie
Wielkość wektorowa, która określa zmiany wektora prędkości w czasie
(zarówno wartości, jak i kierunku).
Przyspieszenie chwilowe:
Jednostka: metr na
sekundę na sekundę.

KINEMATYKA PUNKTU MATERIALNEGO
Klasyfikacja ruchów
Ze względu na tor (trajektorię) ruchu:
- prostoliniowe
(postępowe);
- krzywoliniowe (w tym:
po okręgu, rzut ukośny);
Ze względu na zależność położenia od czasu:
- jednostajne;
- jednostajnie zmienne
(przyspieszone, opóźnione);
-
pozostałe...;
Dr hab. inż. Władysław Artur Woźniak

KINEMATYKA PUNKTU MATERIALNEGO
Ruchy prostoliniowe (postępowe)
Ruch jednostajny
„Jednostajność” oznacza liniową zależność położenia od czasu i stałość prędkości:
– to wektor położenia początkowego (związany z wyborem układu
współrzędnych);
– to wektor prędkości początkowej (w tym wypadku jest ona stała w
czasie całego ruchu);
Dr hab. inż. Władysław Artur Woźniak
0
0
r
r
0
0
v
v
t
v
r
t
r
0
0
t
const
v
t
v
0

KINEMATYKA PUNKTU MATERIALNEGO
Ruchy prostoliniowe (postępowe)
Ruch jednostajnie przyspieszony
Tu „jednostajne przyspieszenie” oznacza stałość przyspieszenia od czasu.
(oznaczenia jak w p.1)
Ruch jednostajnie opóźniony:
skierowany przeciwnie do
Dr hab. inż. Władysław Artur Woźniak
2
2
0
0
t
a
t
v
r
t
r
t
a
v
t
v
0
t
const
t
a
a
0
v
KINEMATYKA PUNKTU MATERIALNEGO
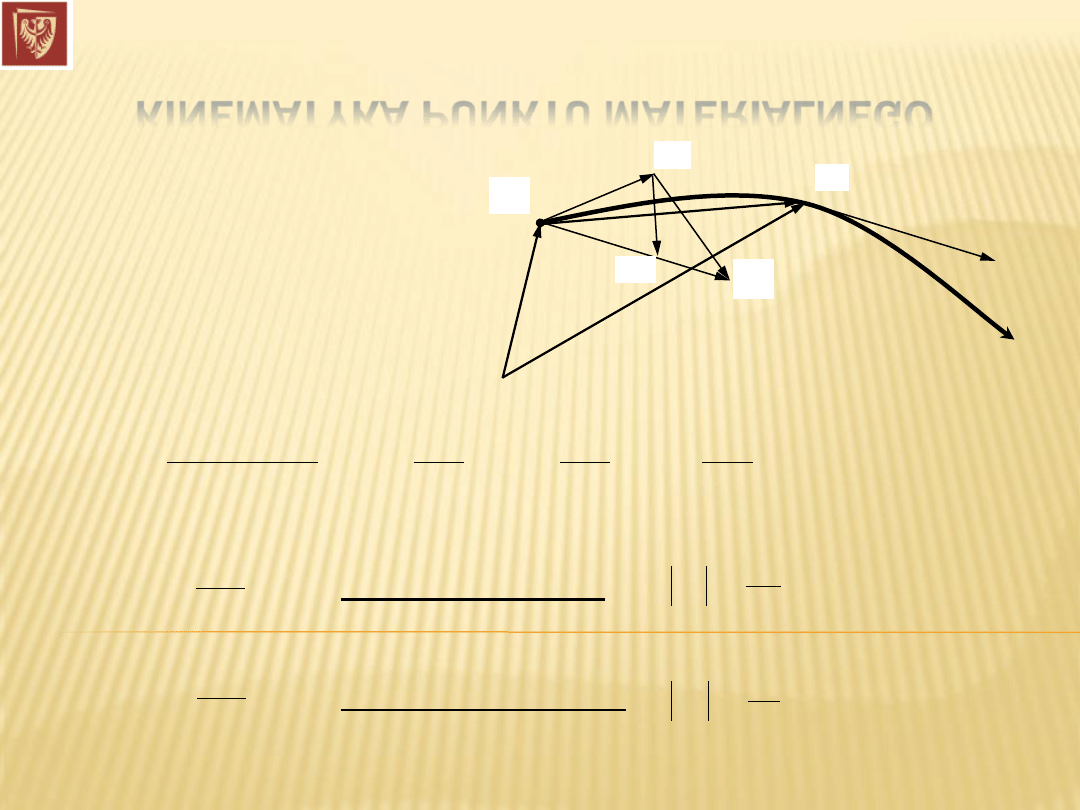
Ruchy krzywoliniowe
Dr hab. inż. Władysław Artur Woźniak
M
N
B
D
C
t
CD
t
BC
t
BD
t
t
t
v
t
v
a
t
t
t
t
t
0
0
0
0
0
lim
lim
lim
lim
0
t
CD
a
t
s
0
lim
– to przyspieszenie styczne:
dt
dv
a
s
t
BC
a
t
n
0
lim
– to przyspieszenie normalne:
R
v
a
n
2
gdzie: R jest promieniem krzywizny toru.

KINEMATYKA PUNKTU MATERIALNEGO
Dr hab. inż. Władysław Artur Woźniak
dt
dv
a
s
0
s
a
0
const
a
s
R
v
a
n
2
0
n
a
R
s
R
1
s
n
a
a
a
2
2
s
n
a
a
a
przyspieszenie styczne:
– charakteryzuje szybkość zmiany liczbowej
wartości prędkości ruchu;
gdy
to ruch nazywamy jednostajnym;
gdy
to jest to ruch jednostajnie zmienny;
– charakteryzuje szybkość zmiany kierunku
prędkości ruchu;
promień krzywizny
definiowany jest poprzez:
przyspieszenie całkowite:
przyspieszenie normalne:
w ruchu prostoliniowym:
Ruchy krzywoliniowe

KINEMATYKA PUNKTU MATERIALNEGO
Ruch po
okręgu
Dr hab. inż. Władysław Artur Woźniak
n
a
d
a
d
s
a
a
0
s
a
R
v
a
d
2
W ruchu po
okręgu:
•
zawsze jest spełniony warunek:
Ruchem jednostajnym po okręgu
nazywamy ruch, w którym:
i
• przyspieszenie normalne
nazywamy dośrodkowym
R
d
a
s
a

KINEMATYKA PUNKTU MATERIALNEGO
Ruch po okręgu
Dr hab. inż. Władysław Artur Woźniak
„Kątowe” wielkości kinematyczne w ruchu po okręgu:
- prędkość kątowa:
(pseudowektor)
-
przyspieszenie kątowe:
(pseudowektor)
Parametry ruchu po okręgu:
- okres ruchu:
- częstotliwość obiegu:
Związki między wielkościami kątowymi i liniowymi w ruchu po okręgu
dt
d
2
2
dt
d
dt
d
2
T
2
1
T
f
R
v
R
a
s
(to NIE jest definicja OKRESU!)
KINEMATYKA PUNKTU MATERIALNEGO
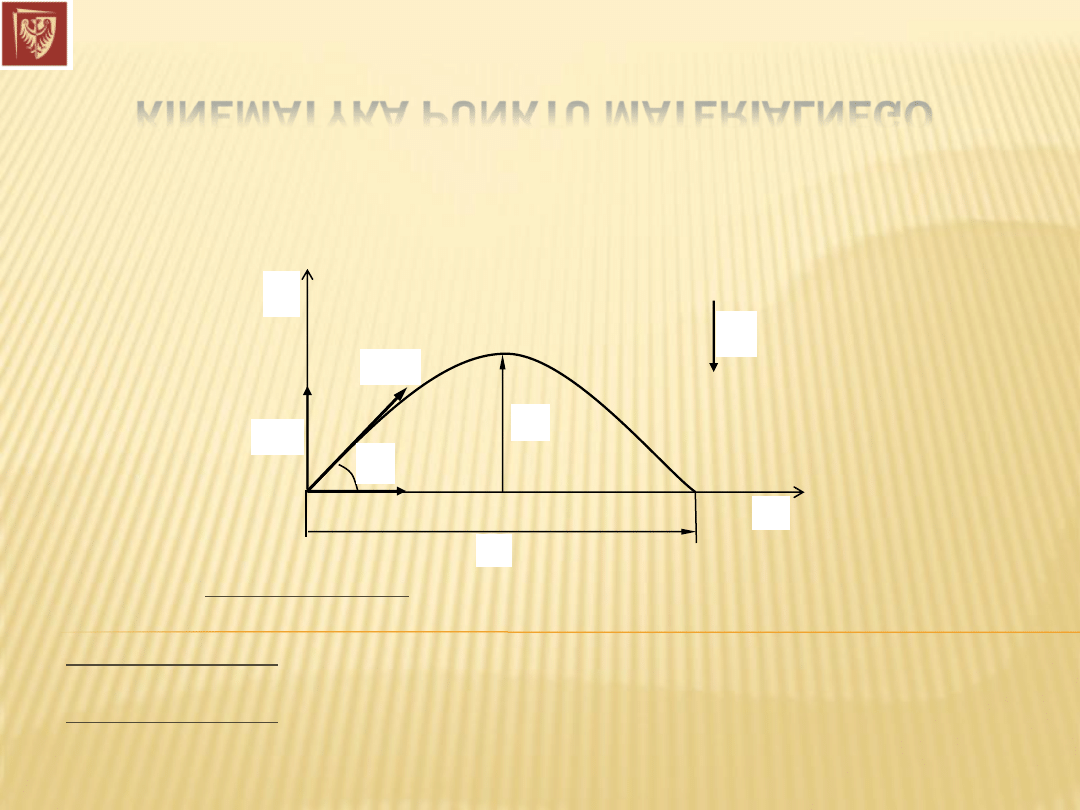
Ruch dwuwymiarowy
– rzut ukośny
Dr hab. inż. Władysław Artur Woźniak
x
y
L
H
v
0
v
0y
g
Korzystając z zasady superpozycji:
Ruch w kierunku „x”: jednostajny z prędkością
Ruch w kierunku „y”: jednostajnie opóźniony z prędkością początkową i przyspieszeniem
cos
0
v
v
ox
sin
0
v
v
oy
g
g
KINEMATYKA PUNKTU MATERIALNEGO
Ruch dwuwymiarowy
– rzut ukośny
Dr hab. inż. Władysław Artur Woźniak
Równania ruchu:
Składowe prędkości:
Trajektoria ruchu:
(jak ją otrzymać?)
Parametry toru
(jak je wyznaczyć z równań ruchu?):
- zasięg:
- maksymalna wysokość wzniesienia:
t
v
t
x
x
0
2
2
0
gt
t
v
t
y
y
x
x
v
t
v
0
gt
v
t
v
y
y
0
2
2
cos
2
x
v
g
x
tg
x
y
o
g
v
L
2
sin
2
0
g
v
H
2
sin
2
2
0

KINEMATYKA PUNKTU MATERIALNEGO
Wartości średnie na przykładzie prędkości
Dr hab. inż. Władysław Artur Woźniak
Ruch jednostajny:
Ruch ze zmienną prędkością:
Przy ciągłej zmianie prędkości:
0
0
t
t
t
x
t
x
v
n
i
n
n
i
n
n
n
i
n
n
i
n
t
t
v
t
s
v
1
1
1
1
a
b
b
a
t
t
dt
t
v
v
Wyszukiwarka
Podobne podstrony:
zestaw 5 dynamika punktu materi Nieznany
fizyka 2 KINEMATYKA PUNKTU MATERIALNEGO
3 Dynamika punktu materialnego Nieznany (2)
04 Dynamika punktu materialneg Nieznany (2)
3 Kinematyka punktu materialnego, FIZYKA
3 Kinematyka punktu materialnego, AiR, semestr I, Mechanika Techniczna
fiza, rozdz.3-Kinematyka punktu materialnego, 3
zestaw 5 dynamika punktu materi Nieznany
fizyka 2 KINEMATYKA PUNKTU MATERIALNEGO
2 Kinematyka punktu materialnego[2]
CI GA, FIZYKA PYTANIA, 1-Kinematyka ruchu punktu materialnego po okręgu
kinematyka i dynamika punktu materialnego, Studia 1, I rok, mechanika
Kinemat punktu id 234923 Nieznany
CI GA, FIZYKA PYTANIA 2, 1-Kinematyka ruchu punktu materialnego po okręgu
instrukcja bhp dla materialow w Nieznany
Bezpieczenstwo zakres materialu Nieznany
więcej podobnych podstron