Cz

ęść

1:

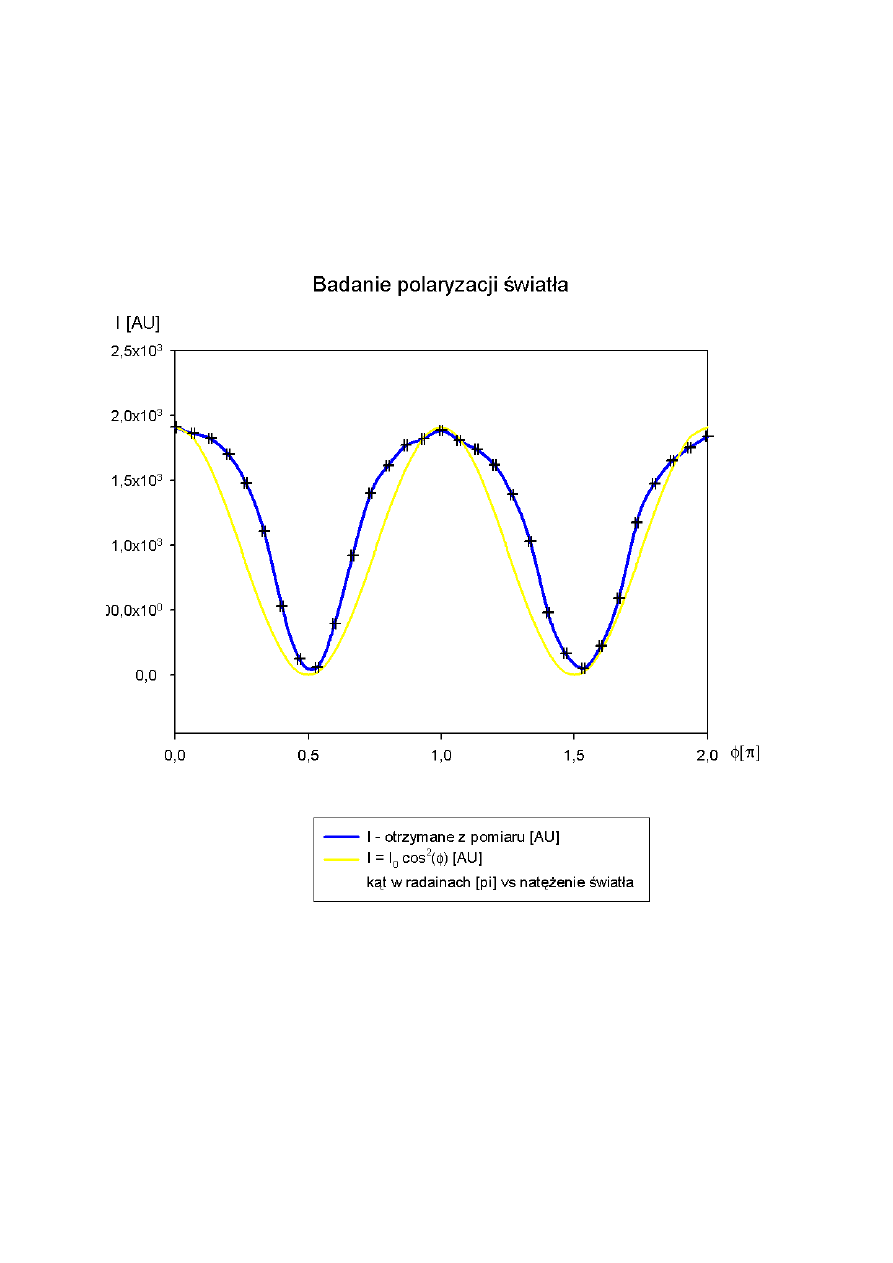
Postępując zgodnie z poleceniami zaobserwowaliśmy, że zmiany natężenia światła zmieniają
się periodycznie, wartości równorzędne powtarzają się co π rad.

Przystąpiliśmy zatem do analizy zmian natężenia względem zmiany kąta na Analizatorze.
(Wartości odczytane z aparatury znajdują się na oddzielnym arkuszu, opatrzonym podpisem
adiunkta)

Aby przedstawić wynik wzorcowy za

0

I przyjąłem największą wartość otrzymaną przy

pierwszym pomiarze.

Na wykresie można odczytać zbieżność otrzymanych wyników z Prawem Malusa tzn.:

AU

I

I

I

1911

)

cos(

0

0

=

=

ϕ

Analiza błędów pomiaru

Błędy pomiaru wynikały głównie z niedokładności aparatury oraz z faktu, że sala nie była
idealnie zaciemniona.

AU

I

I

5

0

=

∆

=

∆

z tego wynika:

0

2

0

0

0

1

I

I

I

I

I

I

I

∆

⋅

+

∆

⋅

=

∆

Cz

ęść

2:

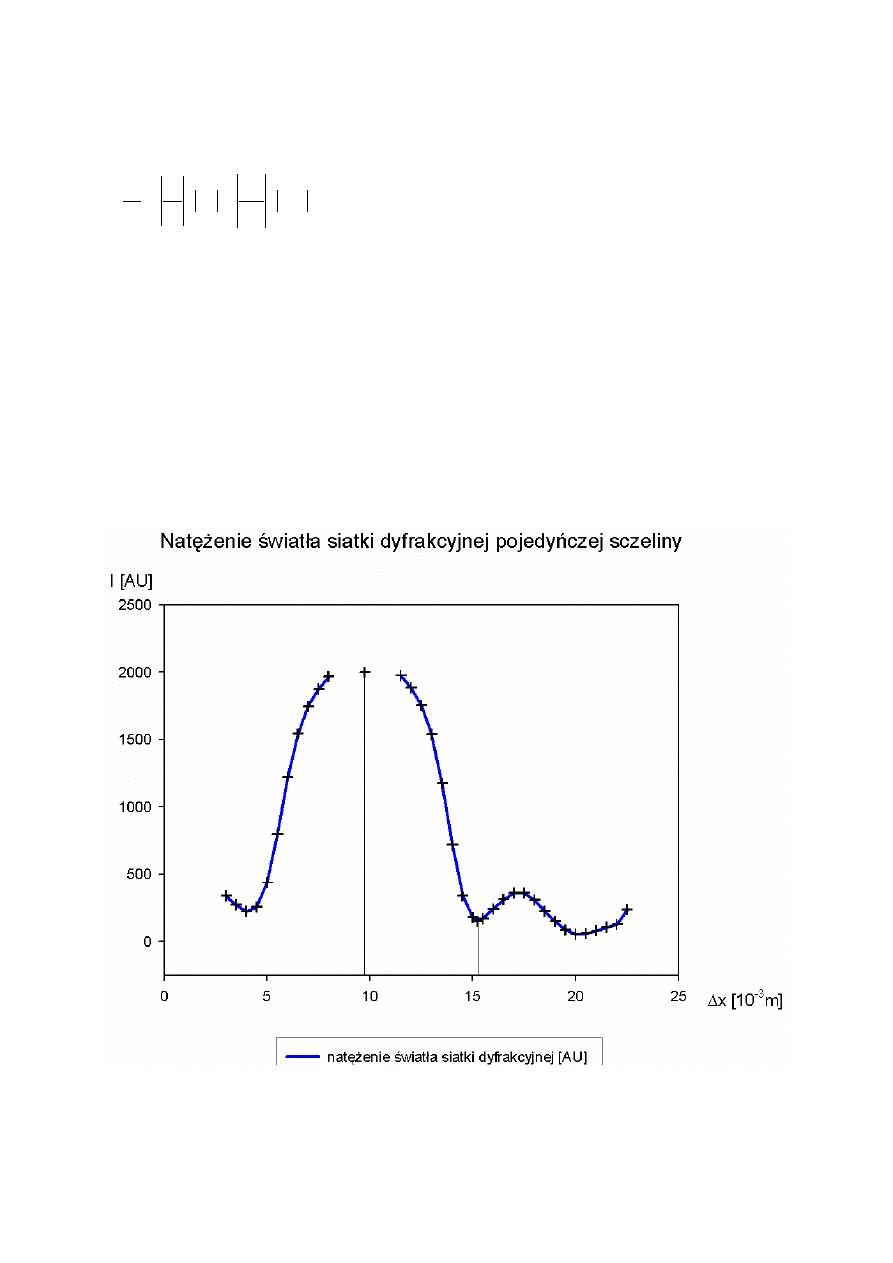
Zależność odległości pomiędzy sąsiednim maksimum i minimum od szerokości wynika z
faktu, że im szersza jest szczelina, tym większa różnica długości drogi przebytej przez fale po
zajściu procesu dyfrakcji na szczelinie.
Odległość ta jest różna dla fal mających swój początek w różnych fragmentach szczeliny.

Za krok pomiaru obraliśmy 0,5 mm

Ekran ustawiliśmy w odległości

mm

d

785

=

Do badania zjawiska został nam udostępniony laser He-Ne tworzącego falę o dł.

λ

= 632,8 nm.

Otrzymane dane znajdują się na dodatkowym arkuszu opatrzonym podpisem adiunkta.

Różnica pomiędzy maksimum i sąsiednim mu minimum:

]

[

5

,

5

75

,

9

25

,

15

mm

x

=

−

=

∆

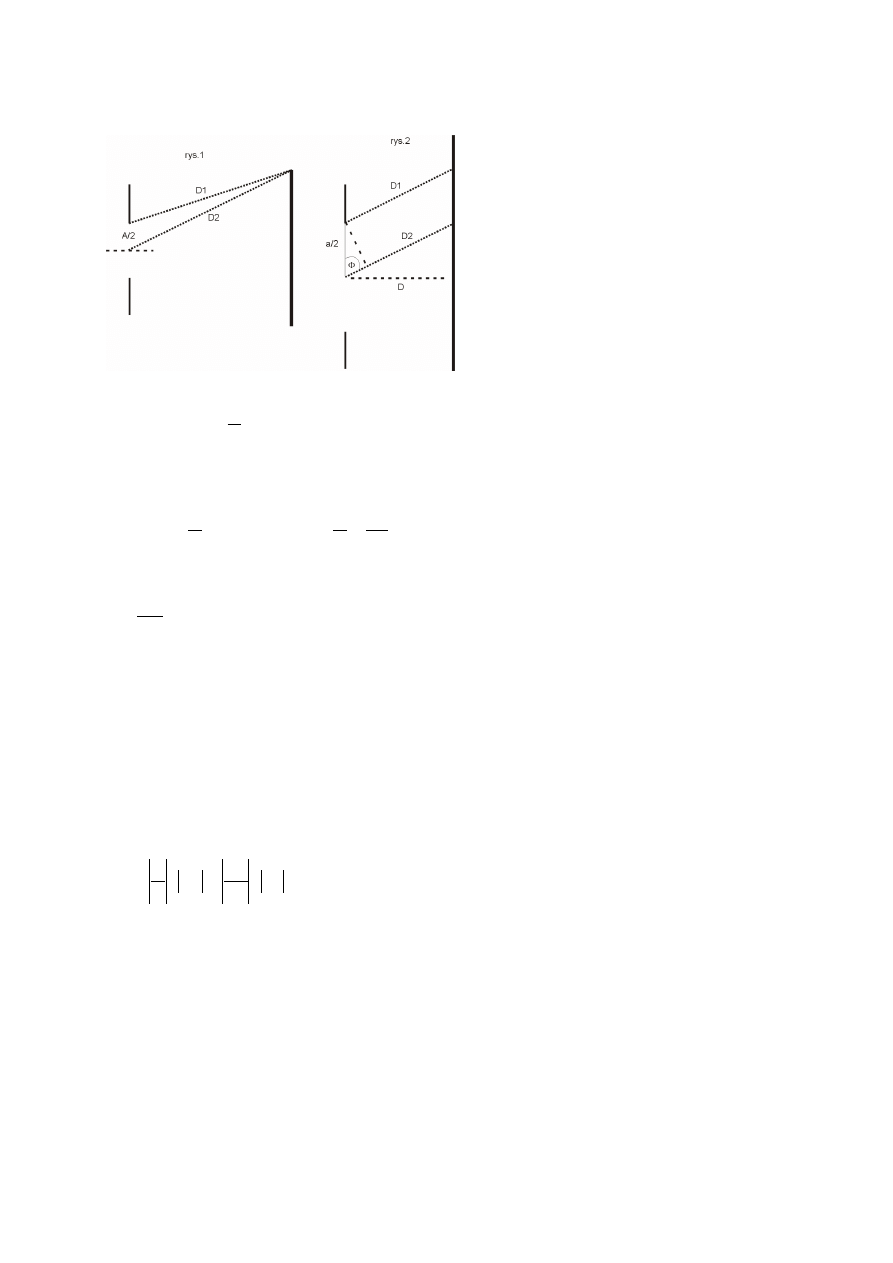
Aby wystąpiło wygaszenie fali musi ona interferować z falą, różnica długości fal (D1 i D2)

musi być równa

2

λ

(rys.1)

Ponieważ

odległość fali od ekrany jest znacznie wieksza od szeorkości szczeliny (

a

d

>>

),

możemy traktować fale jako równoległe, oraz

D

D

≈

2

W wyniku tego zauważamy:

2

2

1

λ

=

−

D

D

D

x

a

∆

=

=

λ

φ

)

cos(

z tego otrzymujemy:

x

D

a

∆

=

λ

co w naszym przypadku daje:

m

a

5

10

03

,

9

−

⋅

=

m

6

10

74

,

0

−

⋅

±

Analiza błędów pomiaru:

Błąd pomiaru śruby milimetrowej

m

x

5

10

1

−

⋅

=

∆

Błąd pomiaru odległości ekranu

m

d

005

,

0

=

∆

m

x

x

d

d

x

a

6

2

10

74

,

0

−

⋅

=

∆

⋅

+

∆

⋅

=

∆

λ

λ