1

Fale materii

FALE MATERII

W 1924 r. de Broglie zapostulował,

ż

e skoro

ś

wiatło ma

dwoist

ą

, falowo-cz

ą

stkow

ą

, natur

ę

, to tak

ż

e materia mo

ż

e

mie

ć

tak

ą

natur

ę

.

Klasyczna teoria elektromagnetyzmu

ś

wiatło o energii

E

ma p

ę

d

p = E/c

f

h

p

λ

=

Hipoteza

długo

ść

przewidywanych fal materii jest okre

ś

lona tym samym zwi

ą

zkiem, który

stosuje si

ę

do

ś

wiatła

p

h

=

λ

Wyra

ż

enie to wi

ąż

e p

ę

d cz

ą

stki materialnej z długo

ś

ci

ą

przewidywanych fal materii

Hipoteza de Broglie’a (1924, Nagroda Nobla w 1929)

2

Przykład: Jaka długo

ść

fal materii odpowiada

„masywnym”

obiektom np. piłce, o masie

1 kg, poruszaj

ą

cej si

ę

z pr

ę

dko

ś

ci

ą

10 m/s, a jaka

„lekkim”

elektronom przyspieszonych

napi

ę

ciem 100 V?

Dla

piłki

p = mv = 1 kg·10 m/s = 10 kg m/s

m

10

6

.

6

kgm/s

10

Js

10

6

.

6

35

34

−

−

⋅

=

⋅

=

=

p

h

λ

λ ≅

0 (w porównaniu z rozmiarami obiektu)

do

ś

wiadczenia prowadzone na takim obiekcie

nie pozwalaj

ą

na rozstrzygni

ę

cie czy materia wykazuje własno

ś

ci falowe.

Elektrony

przyspieszone napi

ę

ciem

100 V uzyskuj

ą

energi

ę

kinetyczn

ą

E

k

= eU = 100 eV = 1.6·10

-17

J

s

m

.

kg

.

J

.

6

31

17

10

9

5

10

1

9

10

6

1

2

2

⋅

=

⋅

⋅

⋅

=

=

−

−

m

E

k

v

nm

12

.

0

m

10

2

.

1

s

m

kg

10

9

.

5

10

1

.

9

Js

10

6

.

6

v

10

6

31

34

=

⋅

=

⋅

⋅

⋅

⋅

=

=

=

−

−

−

m

h

p

h

λ

Jest to wielko

ść

rz

ę

du odległo

ś

ci mi

ę

dzyatomowych w ciałach stałych.

Jak zbada

ć

falow

ą

natur

ę

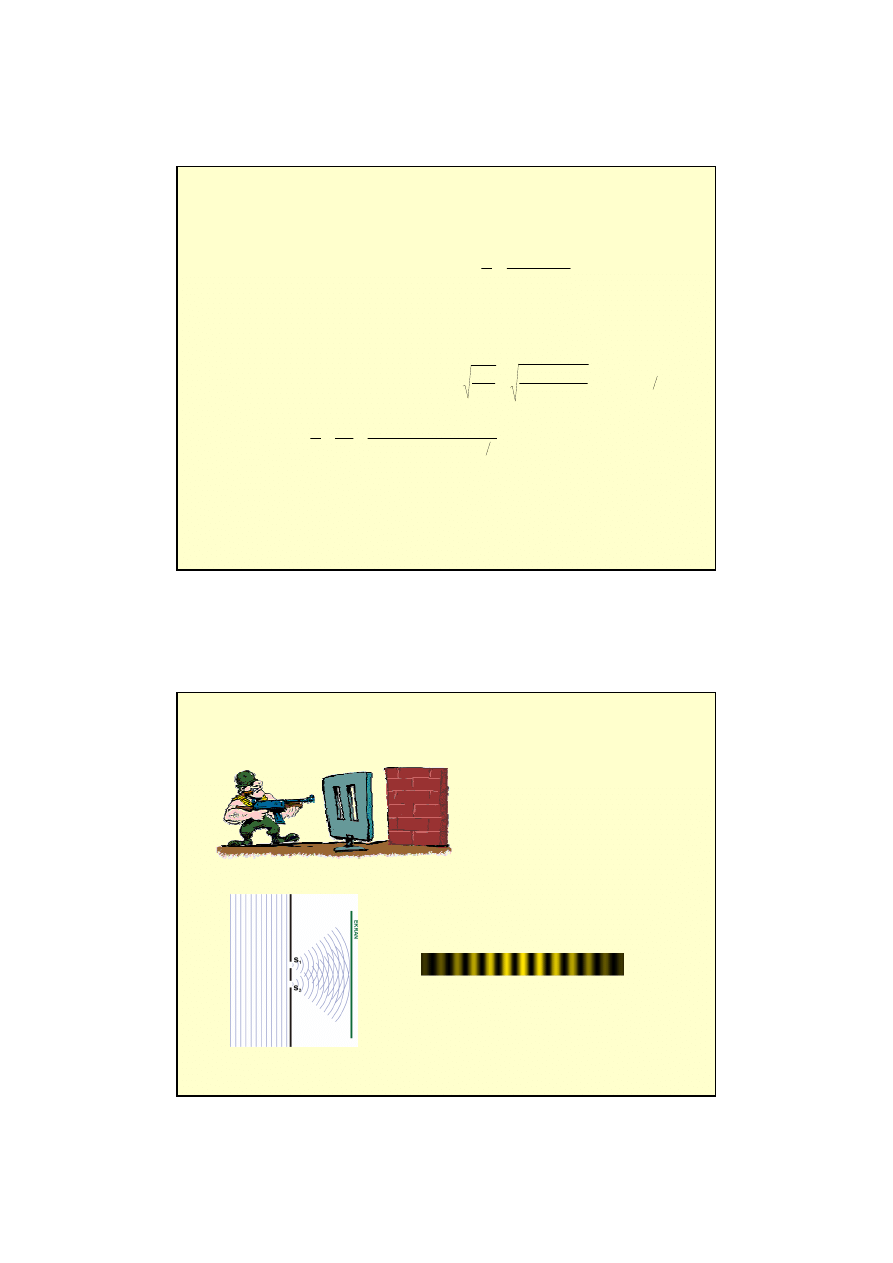
materii? Mo

ż

e zbada

ć

obraz po przej

ś

ciu przez szczeliny ?

obraz dla cz

ą

stek

obraz dla fal

3

5

PRZYPOMNIENIE:
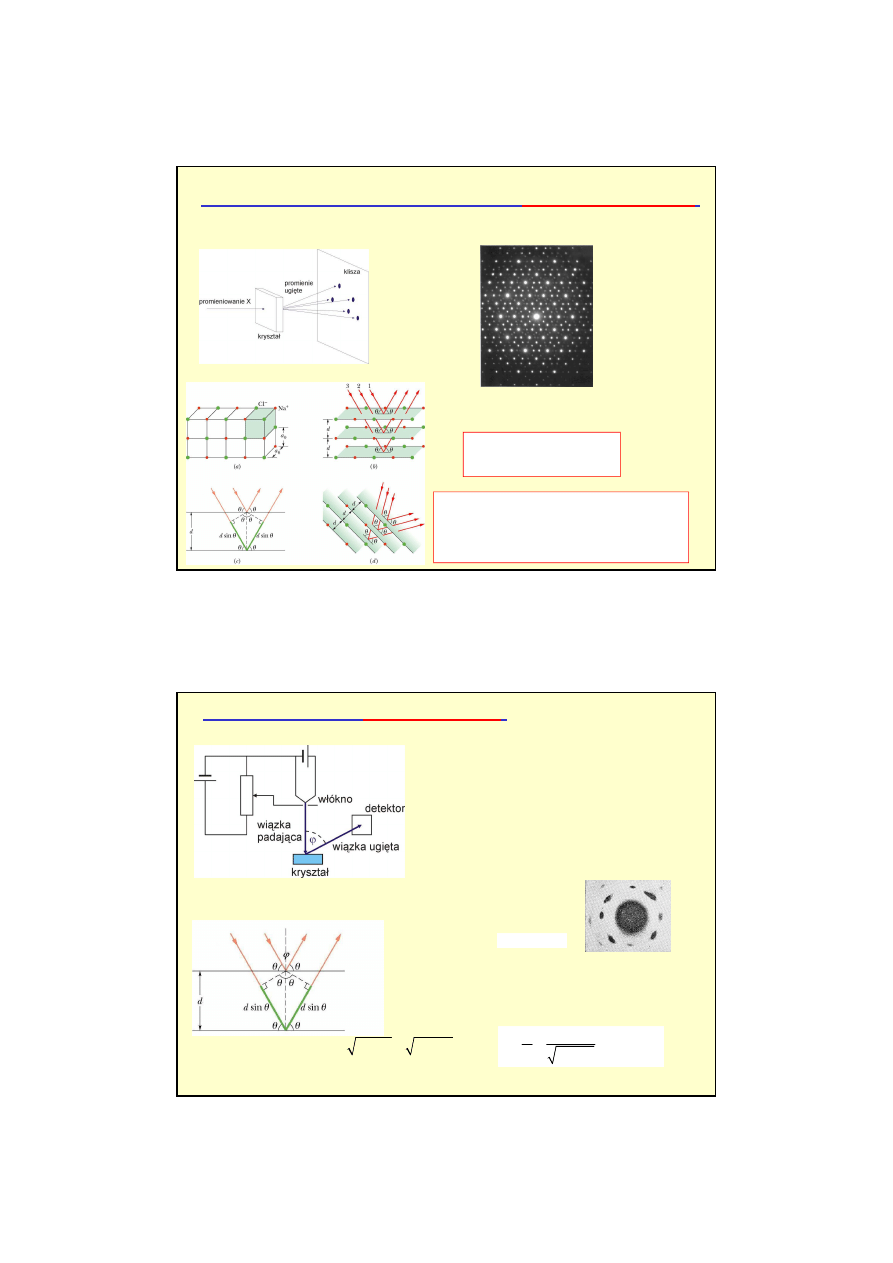
Dyfrakcja promieni Roentgena (promienie X-

fale elektromagnetyczne

)

Kryształ – „naturalna siatka dyfrakcyjna”

Dyfrakcja Lauego

2 sin

,

1, 2, 3,.....(maksima)

d

m

m

θ

λ

=

=

prawo Bragga

Pomiar dyfrakcja promieni X jest
do

ś

wiadczaln

ą

metod

ą

badania

rozmieszczenia atomów w
kryształach.

Do

ś

wiadczenie Davissona i Germera (1927)

Elektrony przyspieszane s

ą

napi

ę

ciem U

Wi

ą

zka pada na kryształ niklu, a detektor

jest ustawiony pod zmiennym k

ą

tem

ϕ

Rejestrowane jest nat

ęż

enie wi

ą

zki

ugi

ę

tej na krysztale dla ró

ż

nego U.

Maksimum dyfrakcyjne rejestrowane jest dla

ϕ

= 50° przy

U

= 54 V.

θ

= 90°

−

ϕ

/2 = 65 °

λ

θ

=

sin

2d

dla niklu (d = 0.091 nm)

λ

= 0.165 nm

0.165 nm

2

e

h

h

p

eUm

λ

= =

=

2

2

e

k

e

m E

m eU

=

=

p

długo

ść

fali de Broglie’a

Dyfrakcja elektronów (

elektrony to cz

ą

stki

)

4

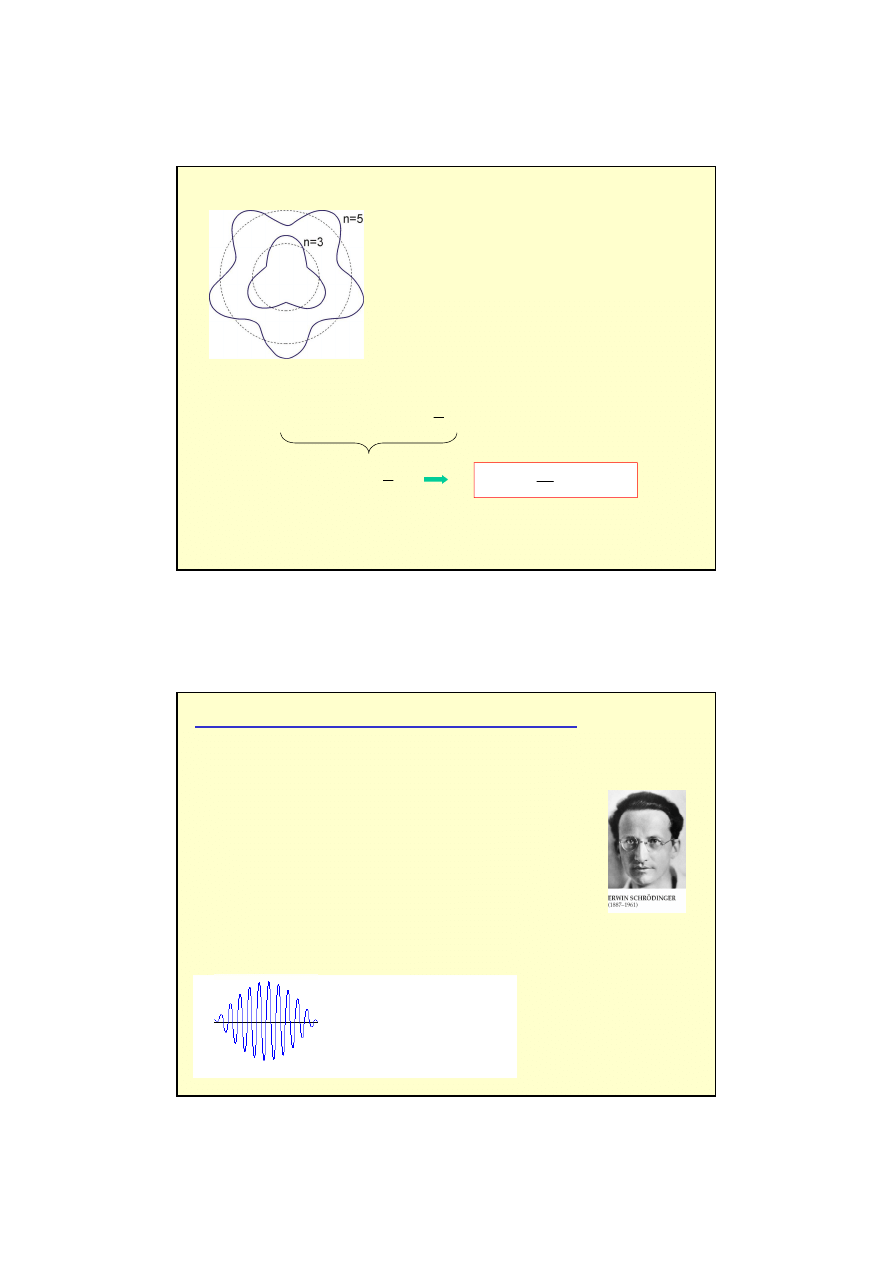
Orbita musi na swym obwodzie mie

ś

ci

ć

całkowit

ą

liczb

ę

długo

ś

ci fal de Broglie'a

λ

π

n

r

=

2

p

h

n

r

=

π

2

p

h

=

λ

,.....

2

,

1

2

=

=

=

n

h

n

pr

L

π

Struktura atomu i fale materii

Ruch fal jest ograniczony przez nało

ż

enie warunków

fizycznych, analogicznie jak dla drga

ń

struny zamocowanej

na obu ko

ń

cach.

Mamy wtedy do czynienia z fal

ę

stoj

ą

c

ą

(a nie bie

żą

c

ą

)

w strunie mog

ą

wyst

ę

powa

ć

tylko pewne długo

ś

ci fal.

Mamy do czynienia z kwantyzacj

ą

długo

ś

ci fal wynikaj

ą

c

ą

z

ogranicze

ń

nało

ż

onych na fal

ę

.

Warunek Bohra kwantyzacji momentu p

ę

du jest konsekwencj

ą

przyj

ę

cia zało

ż

enia,

ż

e elektron jest reprezentowany przez fal

ę

materii.

Postulat de Broglie'a wi

ąż

e elektron ze stoj

ą

ca fal

ą

materii.

ELEMENTY MECHANIKI KWANTOWEJ

Postulat de Broglie'a wi

ąż

e elektron ze stoj

ą

ca fal

ą

materii ale....

• nie daje informacji o sposobie rozchodzenia si

ę

fal materii,

• nie odpowiadał na pytanie jak

ą

posta

ć

mo

ż

e mie

ć

funkcja opisuj

ą

ca fale materii, jak j

ą

wyznaczy

ć

oraz jaka jest jej interpretacja.

W 1926 roku E. Schrödinger sformułował mechanik

ę

falow

ą

(jedno ze sformułowa

ń

fizyki kwantowej) zajmuj

ą

c

ą

si

ę

opisem

falowych

własno

ś

ci

materii

–

uogólnienie

postulatu

de

Broglie'a.

E. Schrödinger (Nagroda Nobla 1933)

pakiet falowy

interferencja

wielu fal o ró

ż

nych p

ę

dach

(analogia do dudnie

ń

)

5

•Fale mechaniczne np. w strunie s

ą

opisywane przez

równania mechaniki Newtona (równanie falowe
d'Alamberta):

•Fale EM s

ą

opisywane przez równania Maxwella

(równanie falowe d'Alamberta):

•Fale materii s

ą

opisywane przez równanie Schrödingera:

Równanie Schrödingera (1926)

2

2

2

2

2

1

t

y

x

y

∂

∂

∂

∂

v

=

2

2

2

2

2

1

t

c

x

∂

∂

∂

∂

B

B

=

2

2

2

2

2

1

t

c

x

∂

∂

∂

∂

E

E

=

i

równanie w jednym wymiarze:

t

t

x

i

t

x

x

U

x

t

x

m

∂

∂

=

+

∂

∂

−

)

,

(

)

,

(

)

(

)

,

(

2

2

2

2

Ψ

Ψ

Ψ

ℏ

ℏ

π

2

h

=

ℏ

dla stanu stacjonarnego U (x) jej energią potencjalną zależną tylko od jej położenia

(dla uproszczenia rozważamy równanie jednowymiarowe, zależne od x)

t

i

e

x

t

x

ω

ψ

Ψ

−

⋅

=

)

(

)

,

(

modulacja

przestrzenna

zmienność

w czasie

rozwi

ą

zanie - fala materii:

ℏ

E

=

ω

(

)

(

)

0

0

:

e

,

e

;

/

i kx

t

i kx

t

y

y

z

z

rozwiazania E

E

B

B

c

k

ω

ω

ω

−

−

=

=

=

(

)

0

:

e

v

/

i kx

t

rozwiązanie

y

y

k

ω

ω

−

=

=

E

jest energi

ą

całkowit

ą

cz

ą

stki,

U (x)

jej energi

ą

potencjaln

ą

zale

ż

n

ą

od jej poło

ż

enia

Rozwi

ą

zanie równania Schrödingera polega na znalezieniu

funkcji falowej

ψ(

x)

i warto

ś

ci

energii cz

ą

stki

E

przy znanej działaj

ą

cej na cz

ą

stk

ę

sile zadanej poprzez energi

ę

potencjaln

ą

U (x)

.

Równanie Schrödingera (1926)

t

t

x

i

t

x

x

U

x

t

x

m

∂

∂

=

+

∂

∂

−

)

,

(

)

,

(

)

(

)

,

(

2

2

2

2

Ψ

Ψ

Ψ

ℏ

ℏ

Rozwi

ą

zanie (podobnie jak dla linii długiej):

równanie w jednym wymiarze:

)

(

)

(

)

(

)

(

2

2

2

2

x

E

x

x

U

x

x

m

ψ

ψ

ψ

=

+

∂

∂

−

ℏ

?

)

(

=

x

ψ

t

i

e

x

t

x

ω

ψ

Ψ

−

⋅

=

)

(

)

,

(

ostateczne rozwi

ą

zanie:

ℏ

E

gdzie

e

x

t

x

t

i

=

⋅

=

−

ω

ψ

Ψ

ω

:

)

(

)

,

(

6

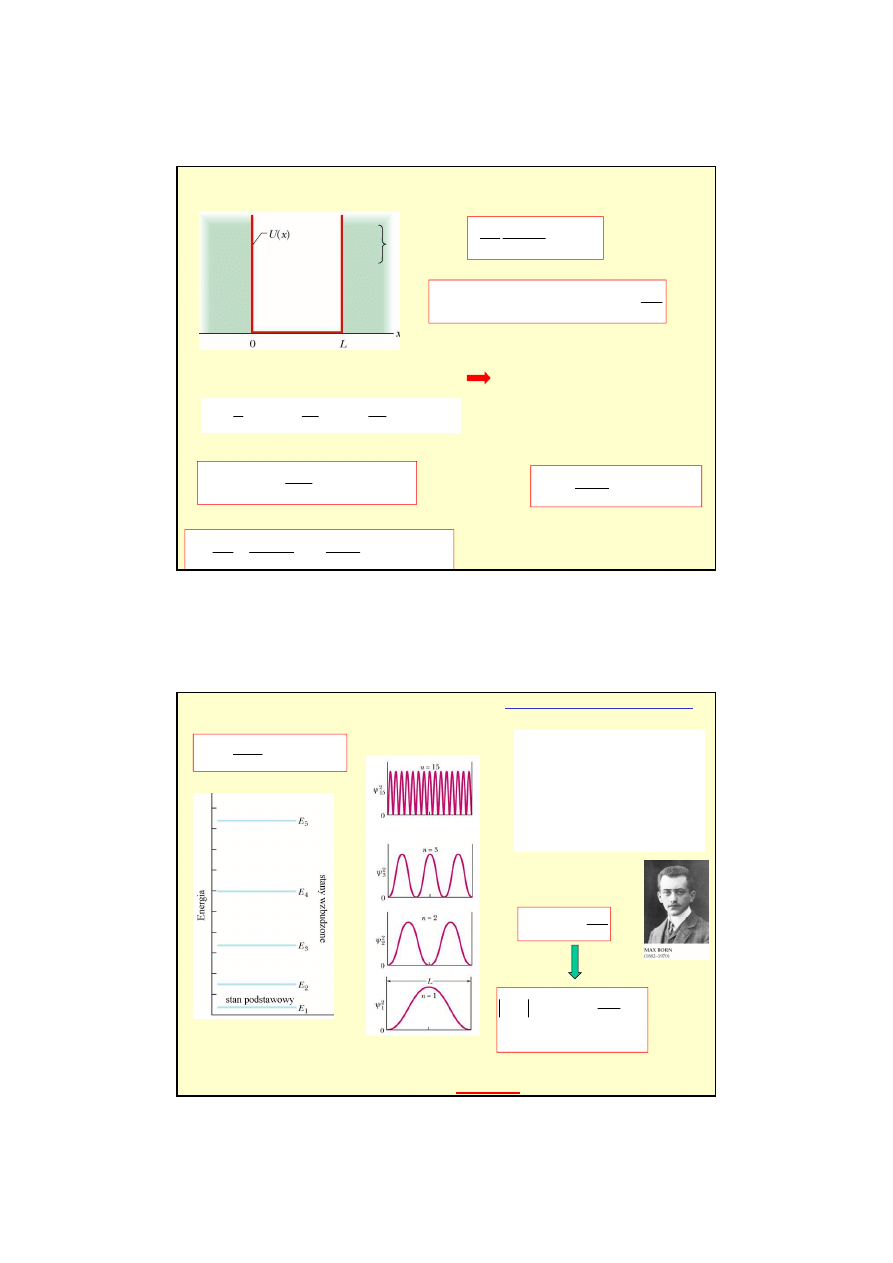
Przykład 1

:

elektron w

∞

studni potencjału spełnia

równanie Schrödingera dla U=0:

x < 0
x > L

U (x)

∞

Poza studni

ą

prawdopodobie

ń

stwo znalezienia

cz

ą

stki = 0

ψ

(0) = 0

i

ψ

(L) = 0

Analogia do struny umocowanej
na obu ko

ń

cach.

...

,

2

,

1

;

lub

2

2

=

=

=

⇒

=

n

L

n

k

n

L

n

L

π

λ

λ

długo

ść

fali jest skwantowana

......

,

2

,

1

,

sin

)

(

=

=

n

L

x

n

A

x

π

ψ

równanie fali stoj

ą

cej:

Dla cz

ą

stki zwi

ą

zanej wyst

ę

puje

kwantyzacja energii !!

......

,

2

,

1

,

2

2

)

/

(

2

2

2

2

2

2

2

=

=

=

=

n

mL

n

m

h

m

p

E

ℏ

π

λ

lub inaczej z relacji de Broglie’a:

0

≤

x

≤

L

U (x) = 0

)

(

)

(

2

2

2

2

x

E

x

x

m

ψ

ψ

=

∂

∂

−

ℏ

λ

π

ψ

2

:

)

sin(

)

(

=

=

k

gdzie

kx

A

x

......

,

2

,

1

,

2

2

2

2

2

=

=

n

mL

n

E

ℏ

π

spełnia równanie
Schrödingera
dla energii:

rozwi

ą

zanie równania Schrödingera to funkcja falowa fali stojacej – cz

ą

stka jest zwi

ą

zana

(uwi

ę

ziona) w studni potencjału ! :

UWAGA: Opisuj

ą

c zachowanie cz

ą

stki funkcj

ą

falow

ą

(spełniaj

ą

c

ą

równania Schrödingera) wyja

ś

nili

ś

my przyczyn

ę

kwantyzacji energii !!

......

,

2

,

1

,

8

2

2

2

=

=

n

mL

h

n

E

......

,

2

,

1

,

sin

)

(

2

2

2

=













=

n

L

x

n

A

x

π

ψ

L

x

n

A

x

π

ψ

sin

)

(

=

Interpretacja M. Borna: wielko

ść

I

ψ

I

2

w dowolnym punkcie

przedstawia tzw. g

ę

sto

ść

prawdopodobie

ń

stwa,

ż

e cz

ą

stka

znajdzie si

ę

w pobli

ż

u tego

punktu. Prawdopodobie

ń

stwo,

ż

e

znajdziemy cz

ą

stk

ę

w przedziale

[x, x+dx] wynosi I

ψ

(x)I

2

dx.

Nagroda Nobla 1954

7

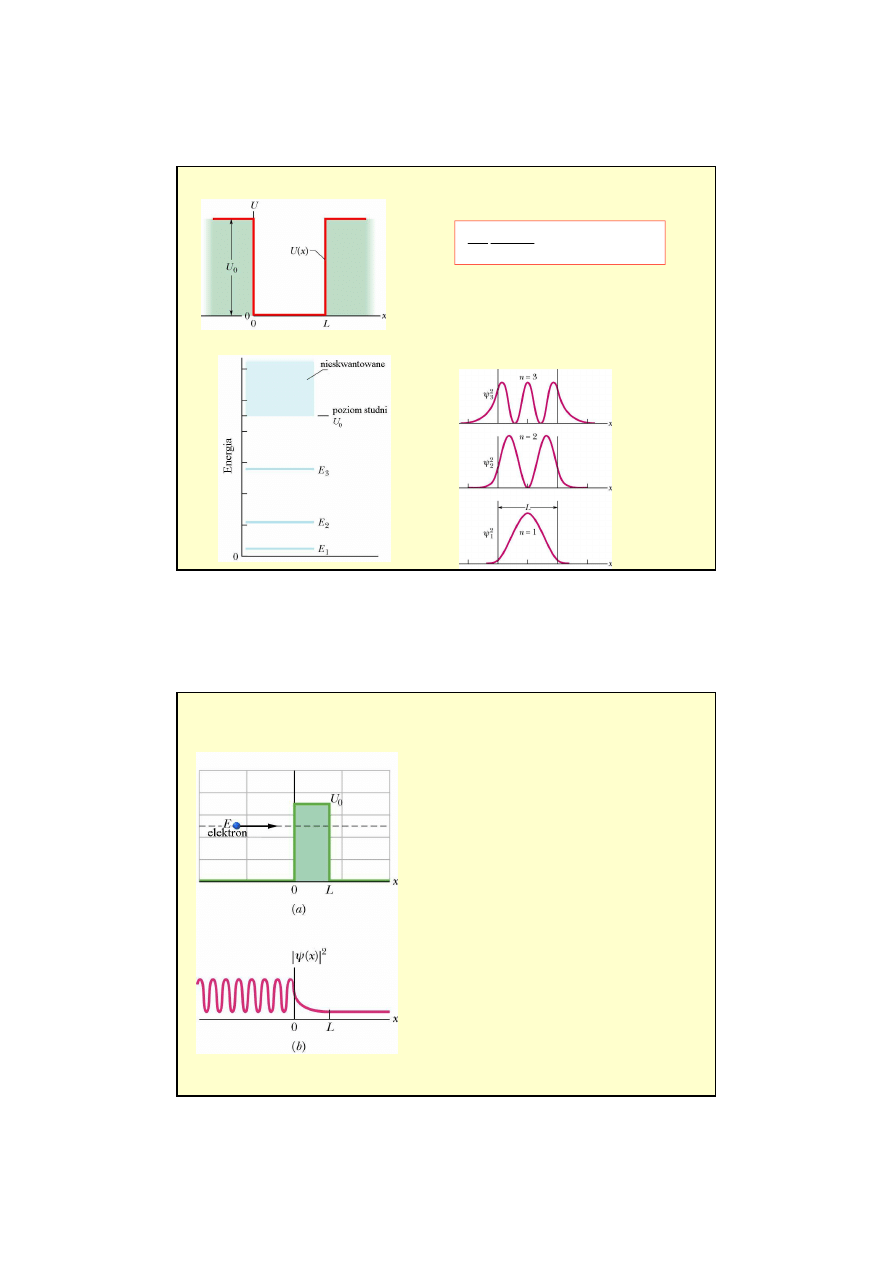
Przykład 2

: elektron w sko

ń

czonej studni potencjału

Elektronowe fale materii

przenikaj

ą

do obszaru o U (x) = U

0

niedost

ę

pnego według klasycznej

mechaniki Newtona

)

(

)

(

)

(

)

(

2

2

2

2

x

E

x

x

U

x

x

m

ψ

ψ

ψ

=

+

∂

∂

−

ℏ

Przykład 3

: tunelowanie elektronu przez barier

ę

potencjału

E < U

0

!!!

klasycznie

elektron

odbije si

ę

od bariery

kwantowo

istnieje prawdopodobie

ń

stwo,

ż

e elektron przeniknie (przetuneluje) przez

barier

ę

dla x < 0 obserwujemy fal

ę

stoj

ą

c

ą

powstał

ą

w wyniku nało

ż

enia si

ę

elektronowej fali

padaj

ą

cej i odbitej od bariery

Elektron mo

ż

e przej

ść

przez „

ś

cian

ę

” mimo,

ż

e

jego energia, z pozoru, na to nie pozwala

8

Atomy - równanie Schrödingera

Orbitale mo

ż

na traktowa

ć

jako rozkłady ładunku elektronu wokół j

ą

dra.

n=1, l=0, m=0

n=2, l=1, m=0

n=2, l=1, m=1

n=3, l=2, m=1

n=3, l=2, m=2

n=4, l=2, m=2

n=2, l=1, m=0

n=1, l=0, m=0 n=2, l=0, m=0

Rozwiązanie równania Schrödingera dla atomu wodoru

Szukamy funkcji falowych spełniaj

ą

cych równanie Schrödingera dla elektronu zwi

ą

zanego w polu

elektrycznym j

ą

dra. Energia potencjalna dla takiego elekronu dana jest wzorem:

r

e

r

U

0

2

4

)

(

πε

−

=

9

Rozwi

ą

zanie równania Schrödingera dla atomu wodoru dostarcza oprócz funkcji

falowych równie

ż

warto

ś

ci

energii elektronu

zwi

ą

zanego w atomie.

,.....

2

,

1

8

2

1

2

2

2

0

4

=

=

−

=

n

n

E

n

h

me

E

n

ε

Warto

ś

ci zgodne z do

ś

wiadczalniem

weryfikacja teorii Schrödingera.

Teoria Schrödingera atomu jednoelektronowego

obraz struktury atomu

podstawy kwantowego

opisu atomów wieloelektronowych, cz

ą

steczek oraz

j

ą

der atomowych.

Opis falowy mikro

ś

wiata jest ju

ż

dzisiaj dobrze

ugruntowan

ą

teori

ą

.

Energia elektronu

Sens fizyczny liczb kwantowych

n – główna liczba kwantowa

Orbitalny moment p

ę

du

Mechanika klasyczna

p

r

v

r

L

×

=

×

=

e

m

•

Dla elektronu kr

ążą

cego wokół j

ą

dra mo

ż

na dokładnie

wyznaczy

ć

długo

ść

L oraz warto

ść

jednej jego składowej

np. L

z

.

•

Pozostałe składowe L

x

i L

y

maj

ą

warto

ś

ci nieokre

ś

lone.

•

Warto

ś

ci L oraz L

z

s

ą

skwantowane

l

z

m

L

l

l

L

ℏ

ℏ

=

+

=

,

)

1

(

l = 0, 1, 2, ..(n-1);

m

l

= 0, ±1, ±2, ±3, ...., ± l

Warto

ść

orbitalnego momentu p

ę

du elektronu w atomie i jego rzut na o

ś

z przyjmuj

ą

ś

ci

ś

le okre

ś

lone warto

ś

ci zale

ż

ne od liczb kwantowych:

l (pobocznej liczby kwantowej) i m

l

(magnetycznej liczby kwantowej).

10

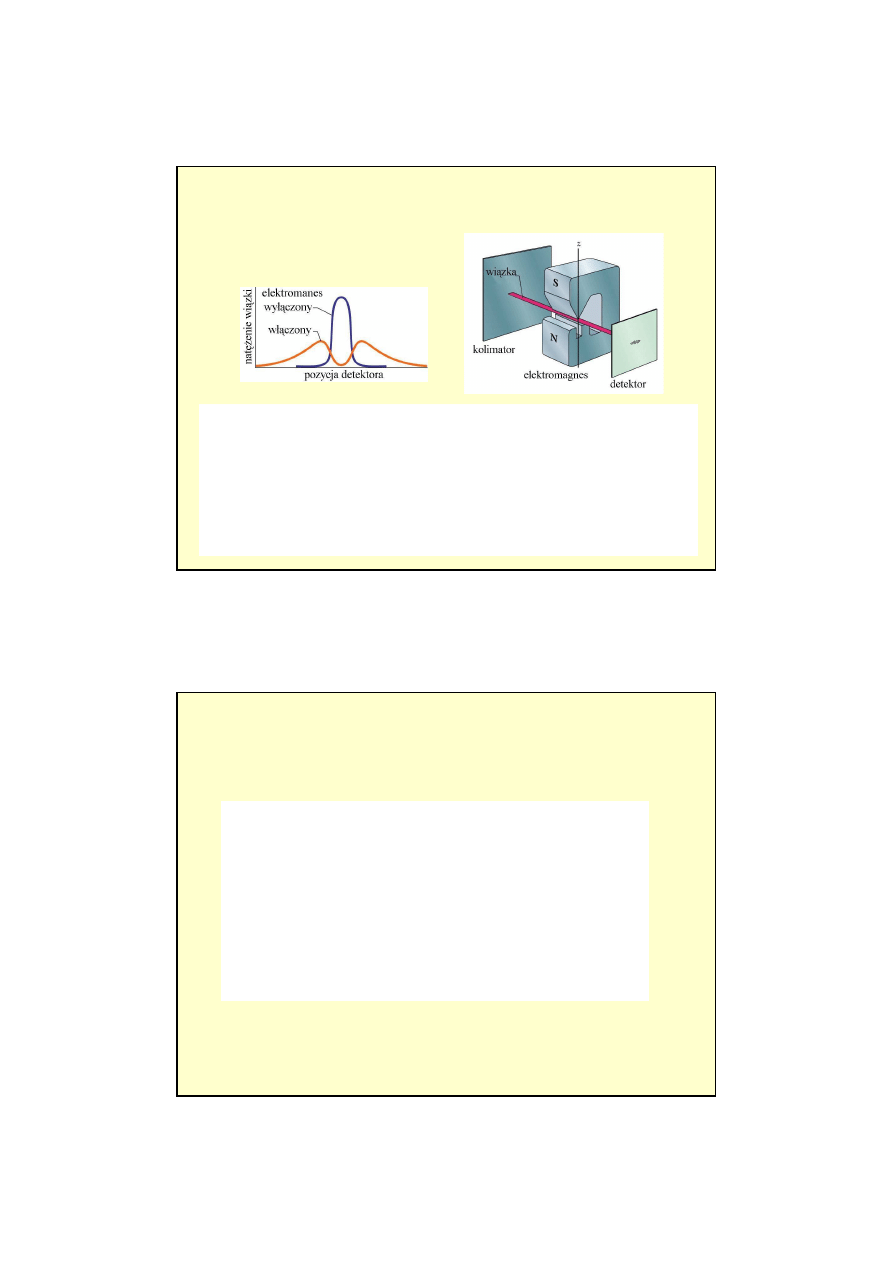
Spin elektronu

Do

ś

wiadczenie Sterna-Gerlacha

Elektrony posiadaj

ą

wewn

ę

trzny moment p

ę

du

spinowy moment p

ę

du (spin).

Spin jest skwantowany przestrzennie

dla danego stanu orbitalnego s

ą

mo

ż

liwe

dwa kierunki spinu

rzut wektora spinu na o

ś

z mo

ż

e przyjmowa

ć

tylko dwie

warto

ś

ci

magnetyczna spinowa liczba kwantowa m

s

, która mo

ż

e przyjmowa

ć

dwie warto

ś

ci m

s

= ± ½.

Moment p

ę

du atomu jest sum

ą

momentów p

ę

dów orbitalnych i spinów

wszystkich elektronów w atomie i jest te

ż

skwantowany przestrzennie.

W atomie srebra na zewnętrznej powłoce znajduje
się pojedynczy elektron, którego spin nie jest
"równoważony" przez elektron ze spinem
przeciwnym.

Sens fizyczny liczb kwantowych - podsumowanie

•

Funkcja falowa elektronu zale

ż

y od trzech liczb kwantowych n, l,

m

l

otrzymanych z równania Schroedingera oraz liczby m

s

wynikaj

ą

cej z efektów relatywistycznych.

•

Główna liczba kwantow

ą

n jest zwi

ą

zana z kwantowaniem energii

całkowitej elektronu w atomie wodoru.

•

Liczby kwantowe l, m

l

opisuj

ą

warto

ść

i rzut wektora momentu

p

ę

du elektronu (obie wielko

ś

ci s

ą

skwantowane) .

•

Spinowa liczba kwantowa m

s

, która mo

ż

e przyjmowa

ć

dwie

warto

ś

ci m

s

= ± ½ opisuje rzut wektora spinu na o

ś

z.

11

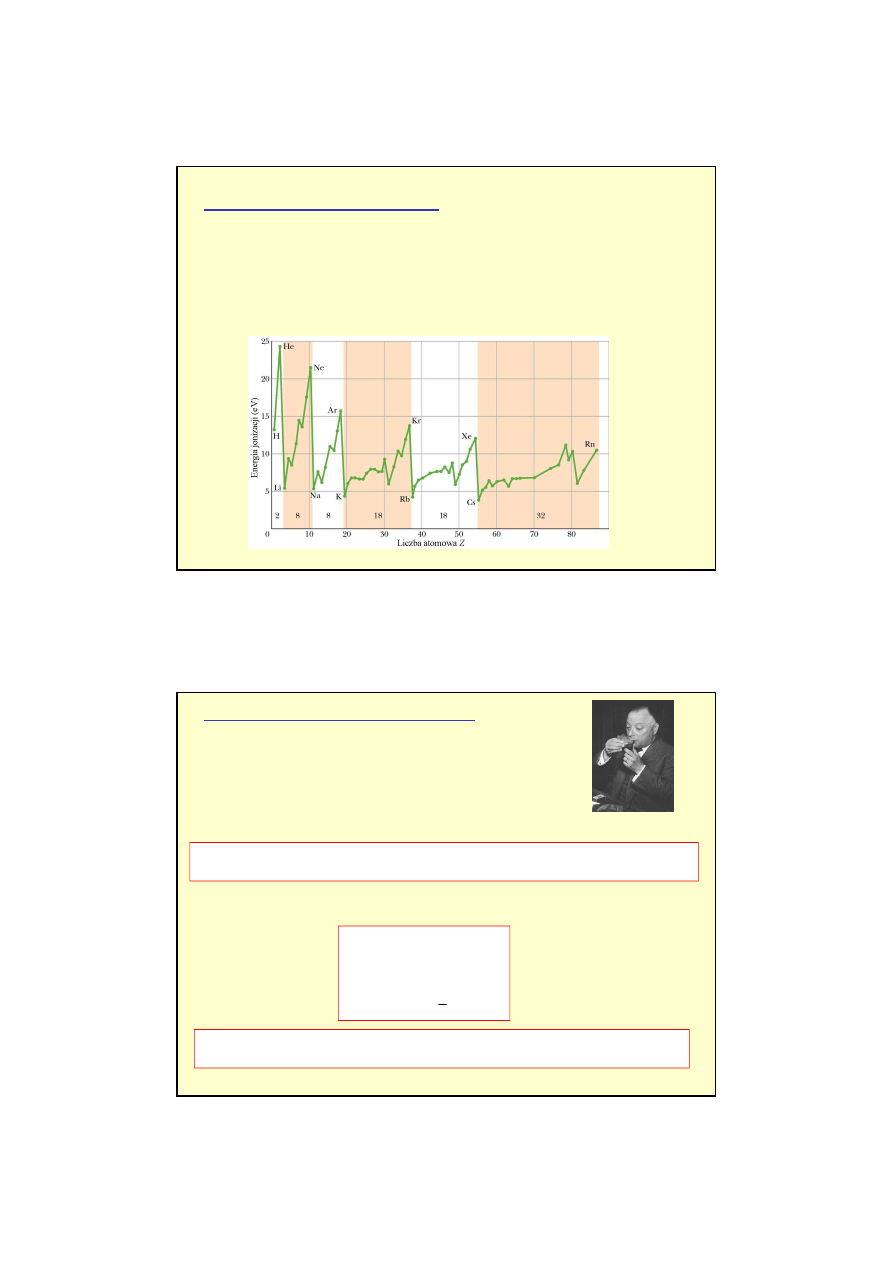
Mendelejew (1869 r.)

wi

ę

kszo

ść

własno

ś

ci pierwiastków chemicznych jest

okresow

ą

funkcj

ą

liczby atomowej Z (liczba elektronów w atomie)

układ

okresowy pierwiastków.

Wła

ś

ciwo

ś

ci chemiczne i fizyczne pierwiastków powtarzaj

ą

si

ę

je

ż

eli zebra

ć

je w

grupy zawieraj

ą

ce 2, 8, 8, 18, 18, 32 elementów.

Atom wieloelektronowy

W 1925 r. Pauli podał zasad

ę

(nazywan

ą

zakazem

Pauliego), dzi

ę

ki której automatycznie s

ą

generowane

grupy o liczebno

ś

ci 2, 8, 18, 32.

Stan kwantowy charakteryzuje zespół czterech liczb kwantowych:

2

1

),

1

(

,

.....

,

2

,

1

,

0

1

,

......

,

2

,

1

,

0

.....

,

3

,

2

,

1

±

=

±

−

±

±

±

=

−

=

=

s

l

m

l

l

m

n

l

n

Zasada Pauliego - nagroda Nobla 1945

W atomie wieloelektronowym elektrony musz

ą

si

ę

ró

ż

ni

ć

przynajmniej jedn

ą

liczb

ą

kwantow

ą

.

W atomie wieloelektronowym w tym samym stanie kwantowym, mo

ż

e znajdowa

ć

si

ę

co najwy

ż

ej jeden elektron.

Wolfgang Pauli

12

Przykład:

Na orbicie pierwszej n = 1 mog

ą

znajdowa

ć

si

ę

tylko dwa elektrony bo

dla n = 1 odpowiednie liczby kwantowe wynosz

ą

(n, l, m

l

, m

s

) = (1,0,0,± ½)

dla n = 2

(n, l, m

l

, m

s

) = (2,0,0,± ½)

(2,1,1,± ½), (2,1,0,± ½), (2,1,-1,± ½)

w stanie n = 2 mo

ż

e by

ć

8 elektronów

(n, l, m

l

, m

s

)= (3,0,0,± ½)

(3,1,1,± ½), (3,1,0,± ½), (3,1,-1,± ½)

(3,2,2,± ½), (3,2,1,± ½), (3,2,0,± ½), (3,2,-1,± ½), (3,2,-2,± ½)

dla n = 3

w stanie n = 3 mo

ż

e by

ć

18 elektronów

Zasada (zakaz) Pauliego obowi

ą

zuje dla ka

ż

dego układu zawieraj

ą

cego elektrony,

nie tylko dla elektronów w atomach.

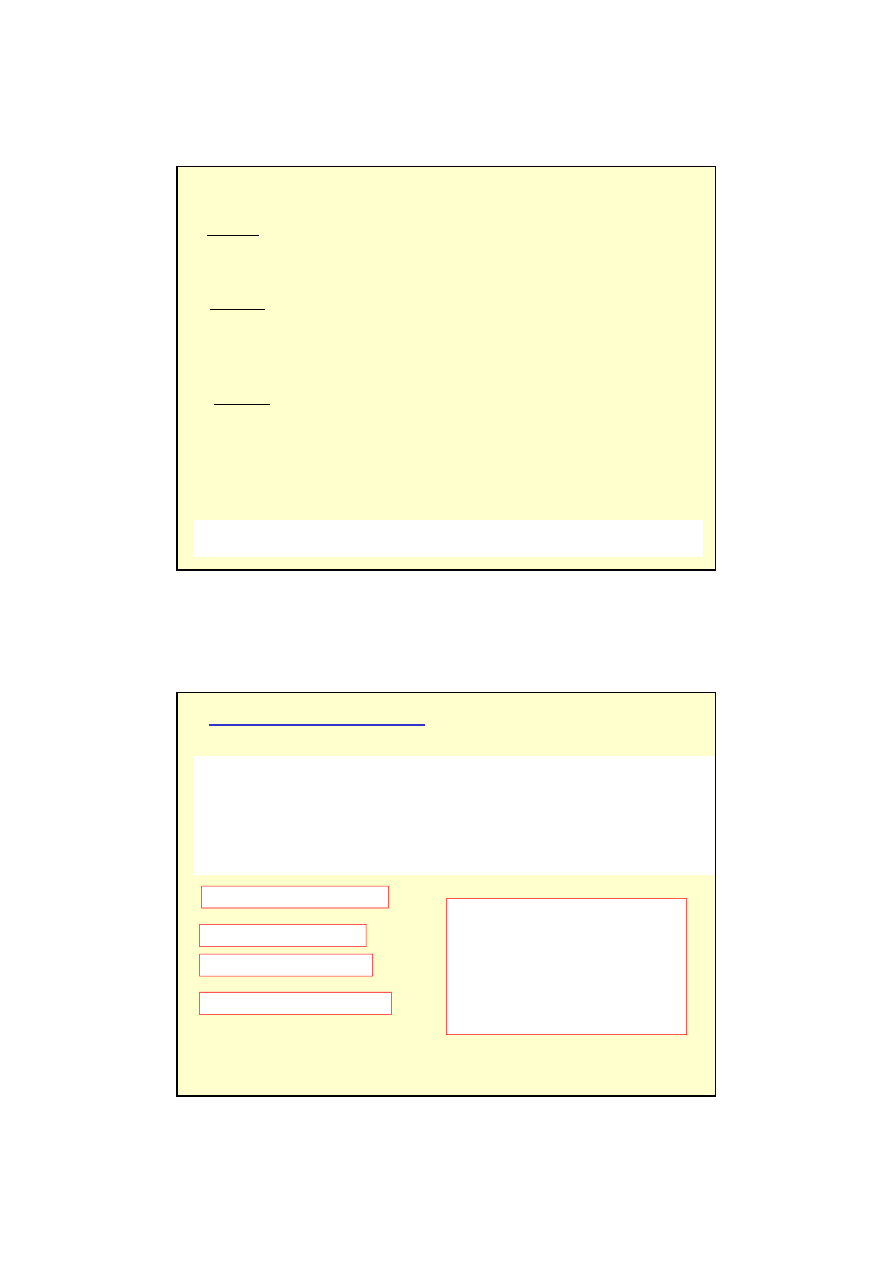
Układ okresowy pierwiastków

•

Korzystamy z zasady Pauliego

•

Konwencja: numer powłoki (n) piszemy cyfr

ą

, natomiast podpowłoki (orbitale):

l = 0, 1, 2, 3, oznaczmy literami s, p, d, f itd.

•

Wska

ź

nik górny przy symbolu podpowłoki

liczba znajduj

ą

cych si

ę

w niej

elektronów, wska

ź

nik dolny przy symbolu chemicznym pierwiastka

warto

ść

Z.

Wodór (Z = 1)

→

1

H : 1s

1

Lit (Z = 3)

→

3

Li : 1s

2

2s

1

Beryl (Z = 4)

→

4

Be : 1s

2

2s

2

Od boru (Z = 5) do neonu (Z = 10)

bor (Z = 5)

→

5

B :

1s

2

2s

2

2p

1

w

ę

giel (Z = 6)

→

6

C :

1s

2

2s

2

2p

2

azot (Z = 7)

→

7

N :

1s

2

2s

2

2p

3

tlen (Z = 8)

→

8

O :

1s

2

2s

2

2p

4

fluor (Z = 9)

→

9

F :

1s

2

2s

2

2p

5

neon (Z = 10)

→

10

Ne :

1s

2

2s

2

2p

6

Hel (Z = 2)

→

2

He : 1s

2

13

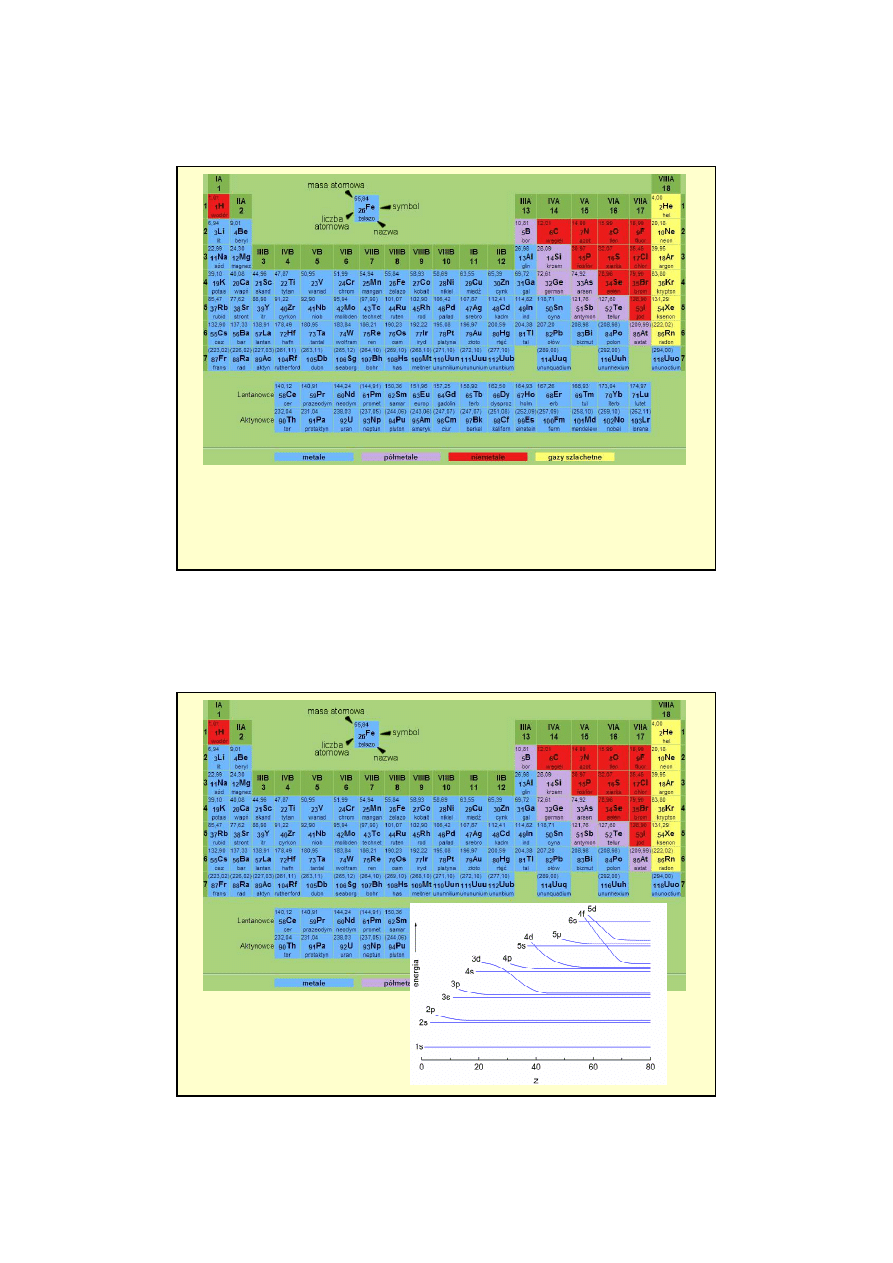
• W obrębie jednego

okresu

powłoka walencyjna jest zajmowana przez kolejne elektrony. Po zapełnieniu

całej powłoki następuje przejście do nowego okresu i powstanie kolejnej powłoki elektronowej.

• Można więc powiedzieć, że atomy występujące w tych samych okresach mają taką samą liczbę powłok
elektronowych, a występujące w tych samych grupach mają taką samą liczbę elektronów na powłokach
walencyjnych (tzn. zewnętrznych).

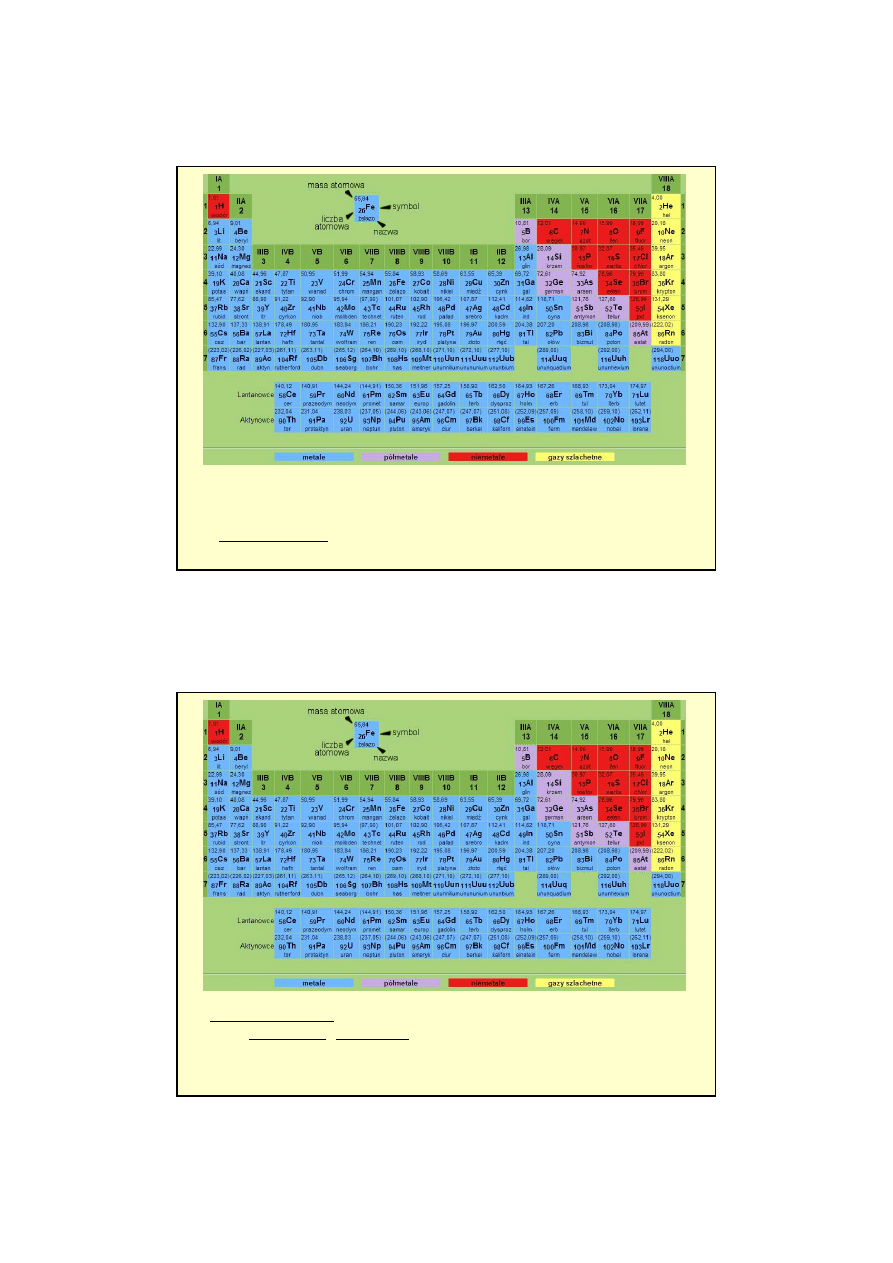
Ró

ż

nice energii pomi

ę

dzy

niektórymi podpowłokami s

ą

tak

małe,

ż

e mo

ż

e zosta

ć

odwrócona kolejno

ść

ich

zapełniania.

14

Grupy

zazwyczaj wypisuje się w kolumnach, a

okresy

w rzędach. Grupy dzieli się

na grupy główne i grupy poboczne.

W grupach głównych (A) elektrony z powłoki walencyjnej zajmują orbitale s i p (na
powłokach tego typu mieści się dokładnie 8 elektronów)

W grupach pobocznych (B) elektrony z powłoki walencyjnej zajmują orbitale s i d, a
w grupie lantanowców i aktynowców orbitale: s, d i f.

Układ okresowy dzielimy na bloki: s i p (grupy główne), d (grupy poboczne) oraz f
(lantanowce i aktynowce).

15

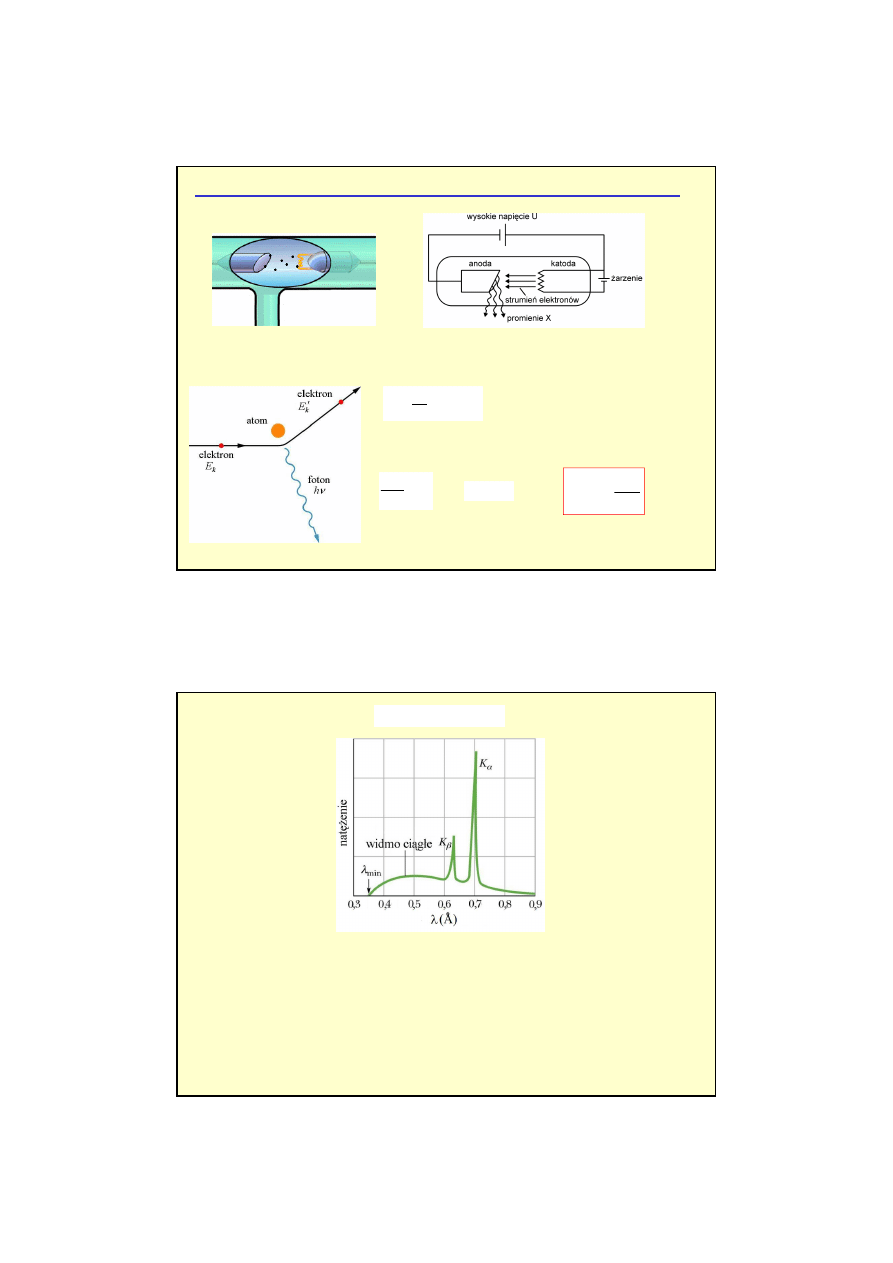
1) Promienie X

Elektrony przyspieszane przez wysokie napięcie rzędu 10

4

V uderzają w anodę (tarczę).

W anodzie elektrony są hamowane aż do ich całkowitego zatrzymania. Zgodnie z fizyką
klasyczną, występuje emisja promieniowania elektromagnetycznego o

widmie ciągłym

.

Promieniowanie atomów wieloelektronowych - przykłady

'
k

k

E

E

hc

hv

−

=

=

λ

Gdy elektron traci całą energię w jednym procesie zderzenia

E

k

' = 0

k

E

hc

=

min

λ

eU

E

k

=

eU

hc

min

=

λ

λλλλ

min

zależy jedynie od napięcia U, a nie zależy np. od materiału z jakiego zrobiono tarczę.

•

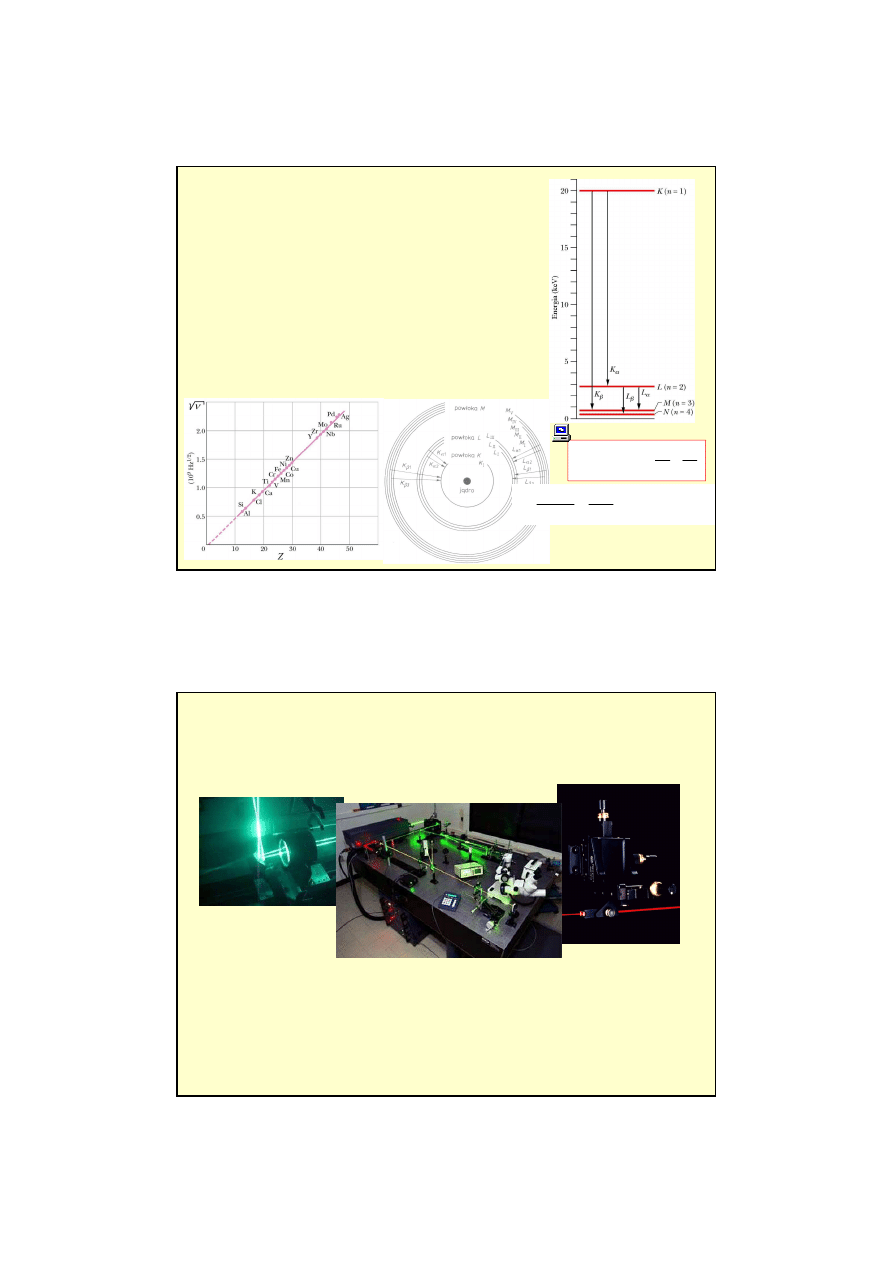
Istnieje dobrze okre

ś

lona

minimalna długo

ś

ci fali

λ

min

widma ci

ą

głego

.

•

Warto

ść

λ

min

zale

ż

y jedynie od napi

ę

cia U

i jest taka sama dla wszystkich

materiałów, z jakich wykonana jest anoda.

•

Obserwuje si

ę

charakterystyczne linie widmowe

(maksima nat

ęż

enia)

wyst

ę

puj

ą

ce dla

ś

ci

ś

le okre

ś

lonych długo

ś

ci fal.

•

Zaobserwowano,

ż

e

widmo liniowe zale

ż

y od materiału

(pierwiastka) anody.

Widmo rentgenowskie

16

Na gruncie

fizyki kwantowej

można wyjaśnić powstawanie

widma liniowego (charakterystycznego).

•

Elektron przelatuj

ą

c przez atom anody mo

ż

e

wybi

ć

elektrony z ró

ż

nych powłok atomowych

.

•

Na opró

ż

nione miejsce (po wybitym elektronie) mo

ż

e

przej

ść

elektron z wy

ż

szych powłok

emisja fotonu o

ś

ci

ś

le okre

ś

lonej energii.

•

Zazwyczaj proces powrotu atomu do stanu
podstawowego składa si

ę

z kilku kroków przy czym

ka

ż

demu towarzyszy emisja fotonu.

W ten sposób powstaje

widmo liniowe

- charakterystyczne

dla atomów pierwiastka anody.













−

−

=

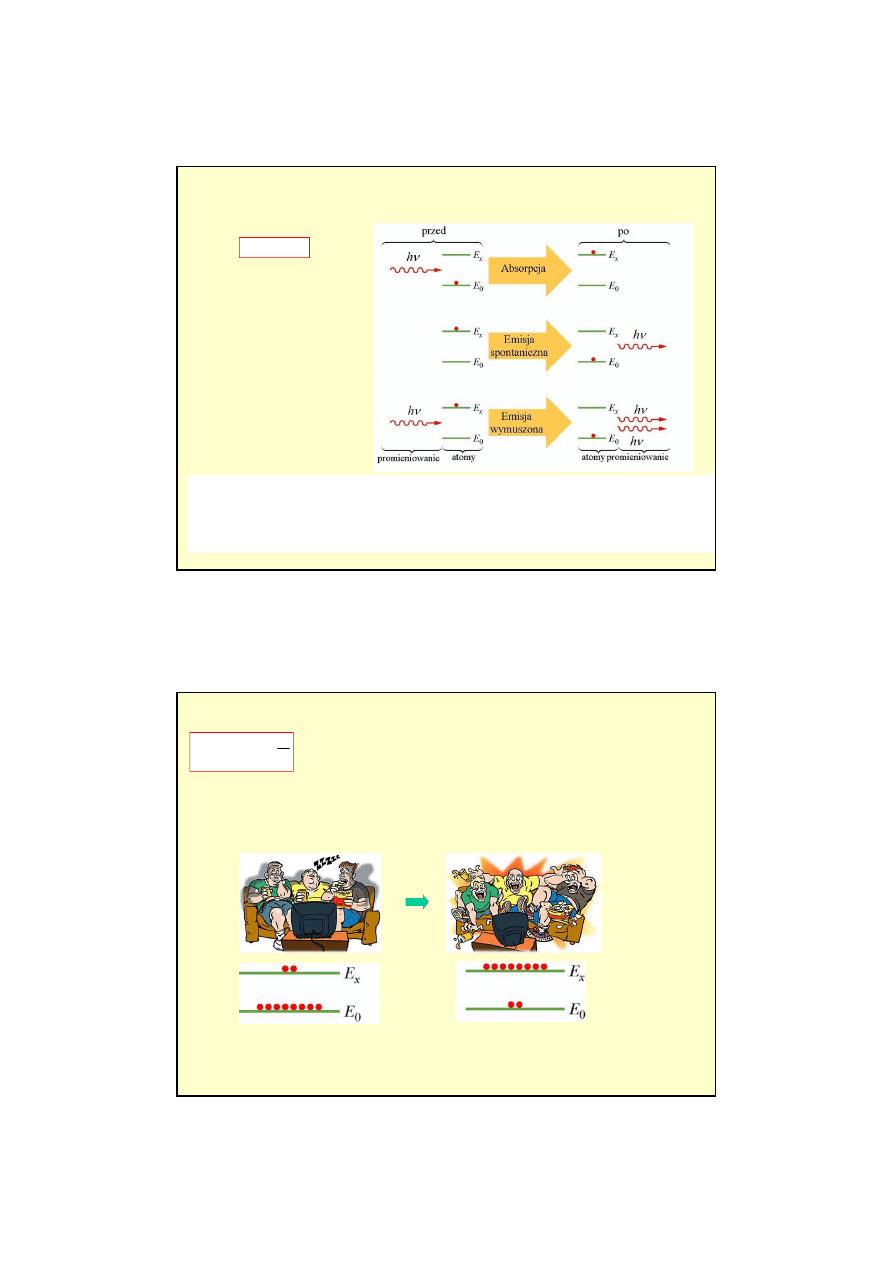
2

2

2

1

1

j

k

Rc

a

Z

)

(

v

Prawo Moseleya

eV

E

h

E

c

h

me

R

6

.

13

|

|

|

|

8

0

0

3

2

0

4

=

=

=

ε

a

- stała ekranowania

(zale

ż

y od serii tj. K, L, M...)

- stała Rydberga

Wykorzystanie zjawisk kwantowych w praktyce:

kwantowy generator

ś

wiatła

- laser.

Laser - Light Amplification by Stimulated Emission of Radiation

Ś

wiatło laserowe

•

monochromatyczno

ść

i mała szeroko

ść

linii emisyjnej

du

ż

a moc w wybranym

obszarze widma,

•

spolaryzowanie wi

ą

zki

ś

wiatła,

•

spójno

ść

wi

ą

zki w czasie i przestrzeni,

•

bardzo mał

ą

rozbie

ż

no

ść

2) Lasery

17

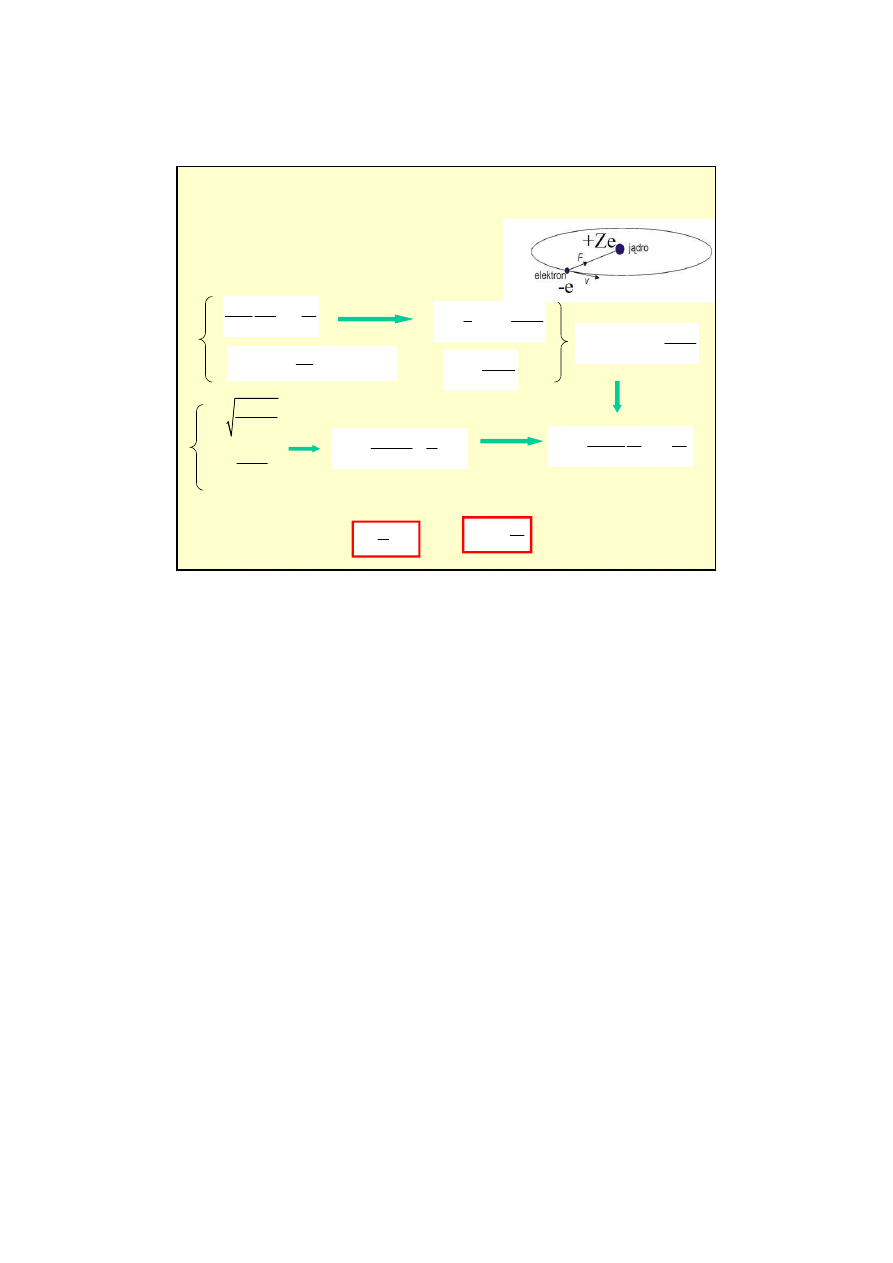
0

x

hv

E

E

=

−

W

emisji spontanicznej

mamy do czynienia z fotonami, których fazy

i kierunki s

ą

rozło

ż

one przypadkowo. Natomiast foton wysyłany w

procesie

emisji wymuszonej

ma tak

ą

sam

ą

faz

ę

oraz taki sam kierunek

ruchu jak foton wymuszaj

ą

cy.

Emisja spontaniczna i wymuszona

emisja wymuszona

przyspieszenie emisji energii
przez o

ś

wietlenie atomów

wzbudzonych odpowiednim
promieniowaniem.

okre

ś

la ile atomów jest w

stanie podstawowym

(stanie o

najni

ż

szej energii), a ile w

stanach wzbudzonych

(o wy

ż

szych

energiach) w danej temperaturze

Rozkład Boltzmana

kT

E

Ae

E

N

−

=

)

(

W danej temperaturze

liczba atomów w stanie podstawowym jest wi

ę

ksza ni

ż

liczba atomów w stanach o wy

ż

szej energii

.

W takim układzie atomów (cz

ą

steczek)

obserwujemy

absorpcj

ę

promieniowania

,

emisja wymuszona jest znikoma

.

Ż

eby w układzie

przewa

ż

ała emisja wymuszona

,

to w wy

ż

szym stanie

energetycznym powinno znajdowa

ć

si

ę

wi

ę

cej atomów (cz

ą

steczek) ni

ż

w stanie

ni

ż

szym. Mówimy,

ż

e rozkład musi nast

ą

pi

ć

inwersja obsadze

ń

.

18

Inwersj

ę

obsadze

ń

mozna wywoła

ć

na kilka sposobów min. za pomoc

ą

zderze

ń

z innymi atomami

lub za pomoc

ą

tzw.

pompowania optycznego

czyli

wzbudzania atomów na wy

ż

sze poziomy energetyczne przez ich o

ś

wietlanie.

Przepływ pr

ą

du przez

mieszanin

ę

He – Ne

zderzenia elektronów

z atomami He

wzbudzenia He

do stanu E

3

Zderzenia He (E

3

) – Ne

wzbudzenia

Ne do stanu E

2

Inwersja obsadze

ń

stan E

2

obsadzony liczniej ni

ż

stan E

1

Przej

ś

cie na poziom E

1

zachodzi

wskutek emisji wymuszonej

Inny sposób „odwrócenia” rozkładu boltzmanowskiego jest wykorzystany w

laserze rubinowym.

Rubin

Laser zbudowany na ciele
stałym składa si

ę

z pr

ę

ta

wykonanego
z kryształu Al

2

O

3

, w którym

jonami czynnymi s

ą

atomy

domieszki np. atomy chromu.

Promieniowanie "pompuj

ą

ce" jest wytwarzane przez lamp

ę

błyskow

ą

umieszczon

ą

wokół kryształu. Absorbuj

ą

c

ś

wiatło z lampy błyskowej atomy chromu przechodz

ą

do stanu wzbudzonego.

Obecnie działaj

ą

zarówno lasery impulsowe jak i lasery o pracy ci

ą

głej.

O

ś

rodkami czynnymi w laserach s

ą

gazy, ciała stałe i ciecze, a zakres długo

ś

ci fal

jest bardzo szeroki; od podczerwieni przez obszar widzialny a

ż

do nadfioletu.

19

2

p

0

4

Ze

E

r

πε

= −

2

2

k

0

1

2

8

Ze

E

m

r

πε

=

=

v

2

2

2

0

1

v

4

Ze

m

r

r

πε

=

,.....

2

,

1

,

2

v

=

=

=

n

h

n

r

m

L

π

energia
całkowita < 0

2

0

8

k

p

Ze

E

E

E

r

πε

=

+

= −

Pojedynczy elektron porusza si

ę

po orbitach

kołowych o promieniu r pod wpływem siły
Coulomba. W j

ą

drze jest Z protonów.

2

0

v

4

Ze

mr

πε

=

mr

h

n

π

2

v

=

2

2

2

0

1

2

1

n

h

r

n

n r

Z me

Z

ε

π

=

=

,....

2

,

1

=

n

2

4

2

1

2

2

2

2

0

1

8

n

E

Z me

E

Z

h n

n

ε

= −

=

,....

2

,

1

=

n

E

1

= −13.6 eV

wartości energii dozwolonych stanów
stacjonarnych

DODATEK: Jon wodoropodobny

2

1

1

n

r

n r

Z

=

2

1

2

n

E

E

Z

n

=