Identyfikacja procesów

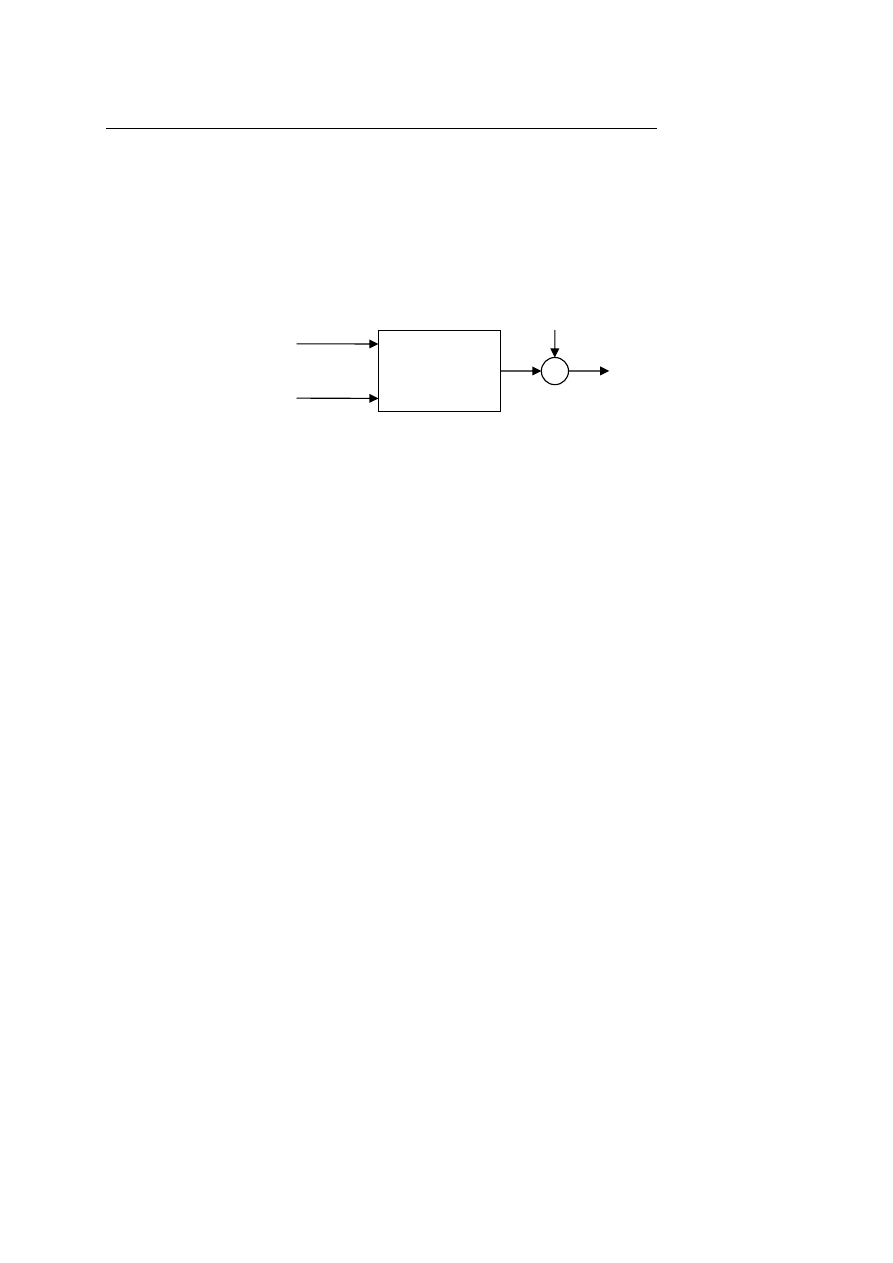
ROZDZIAŁ I – ogólne pojęcia, modele fizyczne i instrumentalne

Wyrażenie „identyfikacja procesów” możemy skojarzyć z problemem identyfikacji,

zarówno sygnałów jak i obiektów. Zaczniemy od omówienia kilku podstawowych zagadnień.

Identyfikacja obiektów dynamicznych odbywa się w układzie pokazanym na rys.1. Na

wejście obiektu, którego parametry będziemy identyfikować podawany jest sygnał wejściowy
u(t), który jest sygnałem mierzalnym, oraz sygnał n(t), który jest niemierzalnym szumem.
Sygnałem wyjściowym badanego obiektu jest sygnał y(t). Czasami może występować w
sygnale wyjściowym addytywne zakłócenie.

u(t)

n(t)

y(t)

z(t)

?

Rys.1. Obiekt wraz z dotyczącymi go sygnałami.

W procesie identyfikacji szukamy wartości parametrów opisujących badany obiekt w

oparciu o jego model, czyli przybliżony matematyczny opis działania obiektu. Każdy model
opisany jest poprzez równania dynamiki s oraz wektor

Θ

parametrów występujących w tych

równaniach. Możemy to symbolicznie zapisać w postaci

( )

Θ

= ,

s

M

.

Omawiając pojęcie modelu należy również wspomnieć o pojęciu modelu prawdziwego. Jest
to model w idealny sposób odzwierciedlający obiekt rzeczywisty. W procesie tworzenia
modelu oraz jego identyfikacji dążymy właśnie do postaci modelu prawdziwego, której ze
względu na jej idealność nigdy oczywiście nie osiągniemy. Symboliczny zapis modelu
prawdziwego:

(

)

0

0

,

Θ

= s

S

.

Modele

możemy podzielić na modele fizyczne i instrumentalne. Modele fizyczne

powstają w oparciu o równania czasu ciągłego, otrzymane z zapisania różnych praw fizyki
rządzących modelowanym obiektem np: prawa zachowania masy i energii, równania
równowagi sił i momentów itp. Otrzymane równania czasu ciągłego możemy następnie
przedstawić w postaci równań stanu danego obiektu:

(

)

(

)

⎪⎩

⎪

⎨

⎧

Θ

=

Θ

=

•

,

,

,

,

,

,

z

u

x

g

y

n

u

x

f

x

Modele fizyczne są, a przynajmniej staramy się by były, modelami „dokładnymi” czyli
takimi, które jak najlepiej odzwierciedlają rzeczywistość.
Niestety modele fizyczne są często bardzo złożone, opisane skomplikowanymi zależnościami
matematycznymi, co powoduje iż ciężko się je interpretuje i równie ciężko sterować
obiektami opisanymi w taki sposób.

Na szczęście istnieje pewne rozwiązanie powyższego problemu. Jeśli dokonamy

dyskretyzacji oraz linearyzacji modelu opisanego równaniami stanu wokół określonego
punktu pracy to zazwyczaj będziemy mogli sprowadzić opis fizyczny do równania
dyskretnego liniowego:

( )

( )

( ) (

∑

∑

=

=

+

−

+

−

=

r

i

p

i

i

i

t

n

i

t

u

b

i

t

y

a

t

y

1

1

)

W tym opisie wyjście w danej chwili czasu jest sumą liniowej kombinacji poprzednich wyjść,
liniowej kombinacji poprzednich wejść oraz szumu w tej chwili czasu. Występujący w tym
równaniu niemierzalny szum mówi nam iż otrzymany przebieg y(t)jest tylko przybliżeniem
przebiegu rzeczywistego. Czas t w tym równaniu przyjmuje wartości całkowite jako, że jest to

czas dyskretny, bezwymiarowy. Parametrami takiego modelu są wartości a

1

,…,a

r

oraz

b

1

,…,b

p

, natomiast wartości r i p określają strukturę modelu, inaczej mówiąc decydują o jego

rzędzie. Należy pamiętać, że zerowe wartości współczynników a

i

oraz b

i

redukują rząd.

Na sygnał szumu n(t) składają się zakłócenia, zmiany punktu pracy oraz błędy modelowania.
Złożenie tych trzech czynników powoduje iż sygnał n(t) jest niemierzalnym szumem białym
czyli ciągiem nieskorelowanych zmiennych losowych.

W procesie identyfikacji wykorzystujemy szereg informacji. Między innymi

dysponujemy pewnymi mierzalnymi danymi o badanym obiekcie:

o

obserwujemy obiekt przez N chwil czasu (od chwili 1 do N)

N

t

,...,

1

=

o

zbiór danych wyjściowych

( ) {

)

(

),...,

1

(

N

y

y

N

Y

=

}

}

o

zbiór danych wejściowych

( ) {

)

(

),...,

1

(

N

u

u

N

U

=

o

zbiór wszystkich danych zmierzonych

( ) {

}

)

(

),

(

N

Y

N

U

N

=

Ξ

Przed przystąpieniem do procesu identyfikacji dysponujemy również pewnymi informacjami
wstępnymi (a priori):

o

możemy znać rząd obiektu, bądź konkretnie np.:

4

=

p

, bądź też mniej konkretnie

np.:

. Wiedze taką możemy posiadać z własnych doświadczeń wyniesionych z

badania wielu podobnych obiektów do analizowanego obecnie bądź też z wiedzy
innych zespołów.

10

<

r

o

możemy znać wartość konkretnego parametru np.:

5

.

0

1

=

a

o

możemy znać zależność danego parametru od jakiejś innej wielkości np.:

(zależność od kwadratu prędkości, tu: dla modelu statku)

2

2

01

.

0

v

a

=

o

możemy znać zakres współczynnika np.:

]

5

.

1

,

0

.

1

[

1

=

b

o

możemy znać rozkład prawdopodobieństwa z jakim współczynnik przyjmuje dane
wartości np.:

( )

(

)

05

.

0

,

2

.

0

2

N

b

p

=

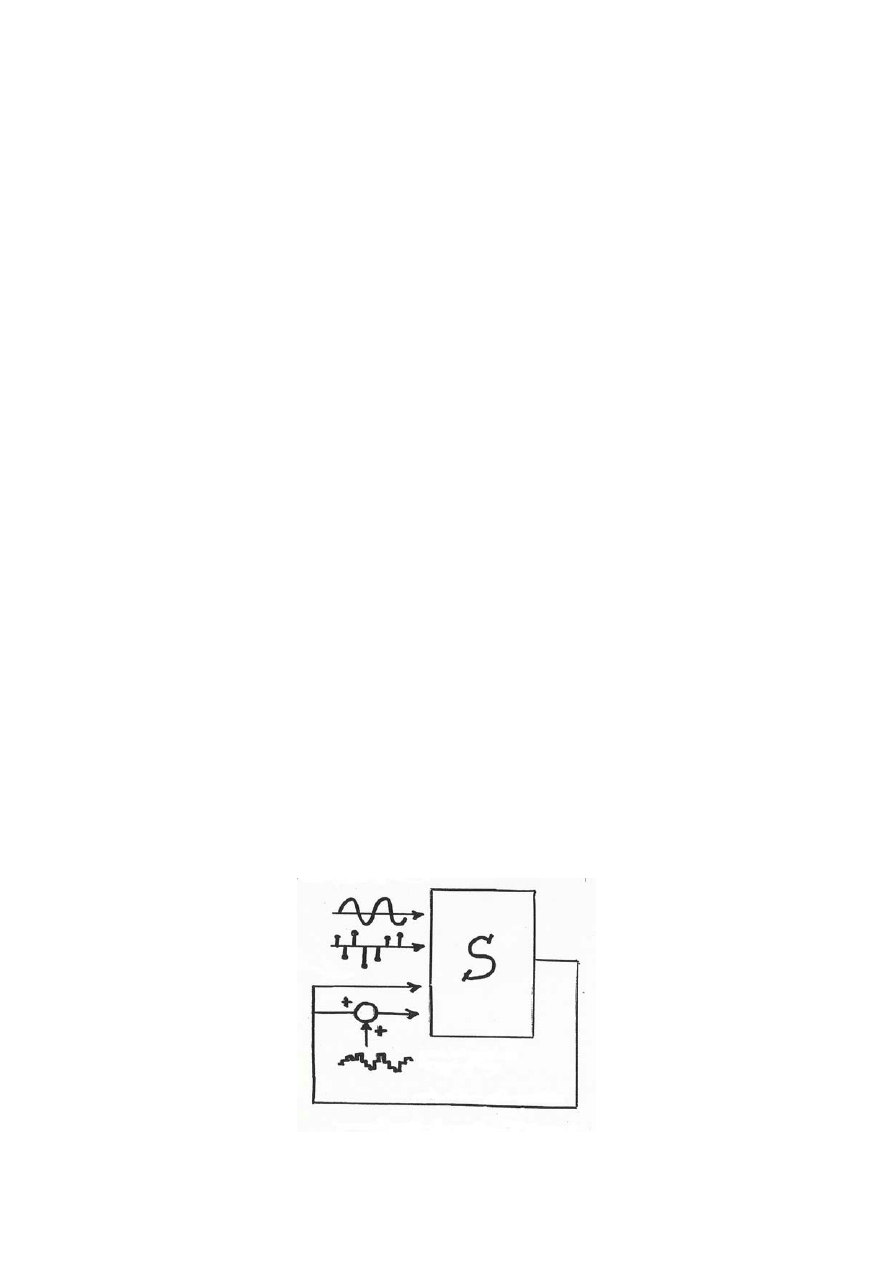
Kolejną kwestią w procesie identyfikacji jest uwarunkowanie eksperymentu (Rys.2). Na tym
etapie musimy zastanowić się nad odpowiednim doborem sygnałów pobudzających, gdyż
przy złym pobudzeniu możemy w ogóle nie uzyskać danych bądź też uzyskane wielkości
będą zupełnie bezużyteczne. Należy również zadać sobie pytanie czy badamy obiekt w
warunkach pętli sprzężenia zwrotnego i jeśli tak to należy się zastanowić nad wprowadzeniem
w pętli sprzężenia addytywnego zakłócenia, gdyż niektóre sygnały mogą być bez jego
wprowadzenia wręcz destruktywne dla naszego obiektu. Tak więc uwarunkowanie
eksperymentu możemy zapisać w postaci sygnału

( )

( ) ( ) ( )

(

)

t

v

t

u

t

y

t

f

t

u

,

1

,

,

−

=

, gdzie v(t) jest

sygnałem zewnętrznym.

Rys. 2. Uwarunkowanie eksperymentu.

Na podstawie dotychczasowej wiedzy jesteśmy w stanie określić pewien uproszczony
schemat postępowania, mianowicie:

(informacja wstępna) + (dane o obiekcie)

(przybliżony model matematyczny)

⎯

⎯

⎯

⎯

⎯

procesu

obiektu

cja

identyfika

/

→

Możemy również opisać procedurę/fazy identyfikacji:

1. Planowanie eksperymentu (wybór okresu próbkowania, filtracja sygnałów, dobór

sygnałów wejściowych)

2. Wybór struktury modelu (identyfikacja strukturalna, wybór rzędu modelu, określenie

ile współczynników będziemy estymować)

3. Estymacja parametrów (identyfikacja parametryczna)
4. Weryfikacja modelu (odpowiadamy na pytanie czy otrzymany model nas zadawala,

jeśli nie to wracamy do pkt.1.)

Na koniec podamy podstawowe cele modelowania:
1. modele fizyczne:

a) symulacja (z reguły nie możemy eksperymentować na obiektach rzeczywistych bez
przeprowadzenia wcześniejszych symulacji.
b) zastępowanie obiektów (np.: modele starych instrumentów muzycznych)

2. modele instrumentalne:

a) prognozowanie (predykcja)
b) predykcyjne kodowanie sygnałów
c) estymacja widma
d) korekcja kanałów telekomunikacyjnych
e) eliminacja zakłóceń impulsowych
f) aktywne tłumienie hałasu
g) sterowanie adaptacyjne

ROZDZIAŁ II – przypomnienie podstaw procesów losowych

Przy próbkowaniu sygnałów ciągłych, z którym w oczywisty sposób będziemy mieli

do czynienia w procesie dyskretyzacji sygnału dla celów identyfikacji, należy pamiętać o
zasadach próbkowaniem rządzących. Definiujemy częstotliwość próbkowania jako

odwrotność okresu próbkowania

p

p

T

f

1

=

, aby móc odtworzyć sygnał analogowy z sygnału

spróbkowanego musimy pamiętać o twierdzeniu o próbkowaniu, z którego wynika zależność:

B

p

f

f

2

≥

gdzie

oznacza pasmo sygnału analogowego (tj. częstotliwość graniczną widma sygnału).

B

f

Istotne oznaczenia, które będą się przewijały w kontekście prezentowanych problemów to
czas unormowany

,...

1

,

0

,

1

...,

−

=

t

gdzie t oznacza wielokrotność okresu próbkowania

;

częstotliwość unormowana definiowana zależności:

p

T

[

5

.

0

,

0

0

∈

=

p

f

f

f

]

]

oraz pulsacja

unormowana

[

π

π

ω

,

0

2

∈

=

f

, obie te wielkości, zarówno częstotliwość unormowana jak i

pulsacja są wielkościami bezwymiarowymi, natomiast f

0

oznacza prawdziwą częstotliwość

wyrażoną w Hertzach.
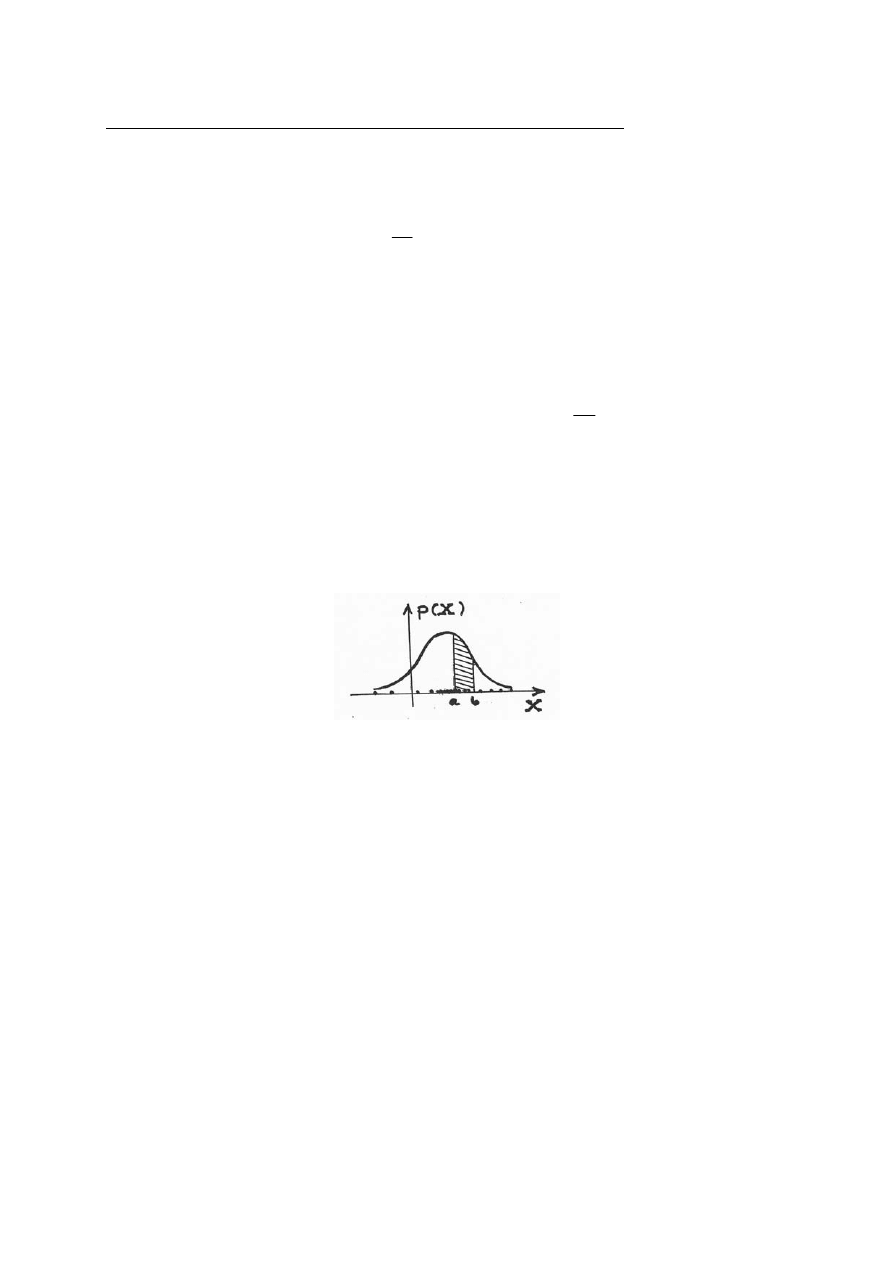
Kolejne pojęcie jakie należy sobie przypomnieć to pojęcie skalarnej zmiennej losowej, czyli
pewnej funkcji X(e), gdzie e oznacza elementarne zdarzenie losowe oraz pojęcie rozkładu
prawdopodobieństwa zmiennej losowej. Funkcję gęstości rozkładu prawdopodobieństwa
określa Rys.3.

Rys.3. Funkcja gęstości rozkładu prawdopodobieństwa

p(X) zmiennej losowej X

Należy również pamiętać, że prawdopodobieństwo znalezienia się zmiennej losowej w
przedziale [a,b] rozkładu prawdopodobieństwa równe jest całce z funkcji gęstości tego
rozkładu w przedziale [a,b]:

[ ]

{

}

( )

( )

∫

∫

∞

∞

−

=

=

∈

1

,

dX

X

p

dX

X

p

b

a

X

P

b

a

Możliwa jest sytuacja, w której

. W tym celu wystarczy, aby przedział [a,b] był

bardzo wąski. Nie należy bowiem utożsamiać gęstości rozkładu prawdopodobieństwa z
samym prawdopodobieństwem. Kolejnym ważnym elementem jest wartość oczekiwana
zmiennej losowej:

( )

1

>

X

p

[ ]

( )

∫

=

=

dX

X

Xp

X

E

m

X

Możemy powiedzieć, że stanowi ona „środek ciężkości” rozkładu prawdopodobieństwa.
Wartość oczekiwana posiada własność liniowości:

[

]

[ ]

[ ]

2

2

1

1

2

2

1

1

X

E

k

X

E

k

X

k

X

k

E

+

=

+

Inną wielkością związaną ze zmienną losową jest jej wariancja, określana również jako średni
kwadrat rozrzutu. Określa ona rozrzut zmiennej losowej wokół jej wartości średniej:

[ ]

(

)

[

]

(

) ( )

∫

−

=

−

=

=

dX

X

p

m

X

m

X

E

X

X

X

X

2

2

2

var

δ

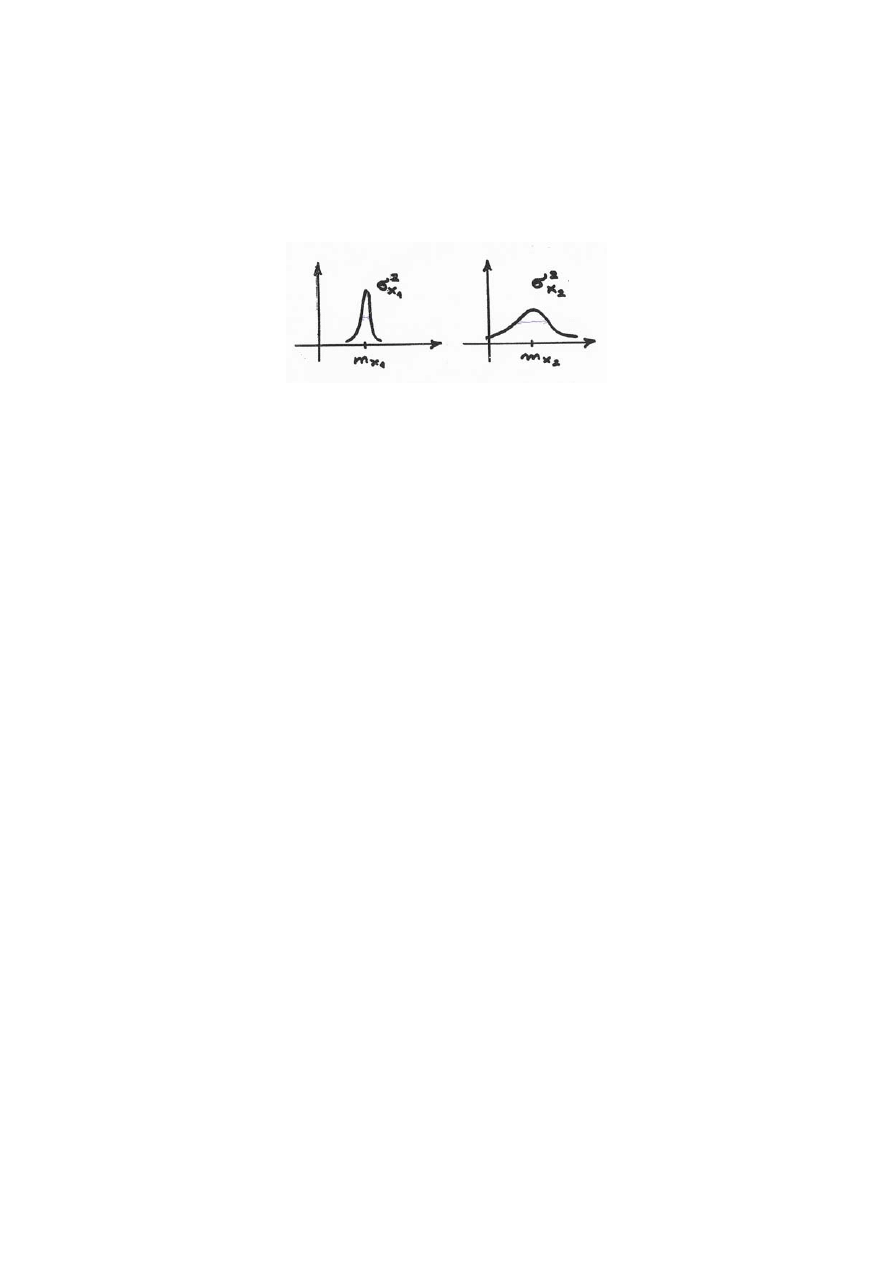
Im mniej skupiony jest rozkład prawdopodobieństwa wokół swej wartości średniej tym
wariancja jest mniejsza (Rys.4.).

Rys.4. Porównanie dwóch różnych wariancji zmiennych losowych.

Pierwsza zmienna ma mniejszą wariancję.

Pojęcie zmiennej losowej jednowymiarowej możemy rozszerzyć do przestrzeni
wielowymiarowej, wprowadzając pojęcie wektorowej zmiennej losowej, dla którego również
możemy zdefiniować pojęcie wartości oczekiwanej, jako wektora wartości oczekiwanych
poszczególnych zmiennych losowych.

( )

( )

( )

⎥

⎥

⎥

⎦

⎤

⎢

⎢

⎢

⎣

⎡

=

e

X

e

X

e

X

n

...

1

[ ]

1

,...,

1

nx

i

X

n

i

X

E

m

⎥

⎦

⎤

⎢

⎣

⎡

=

=

Miarą rozproszenia realizacji wektorowej zmiennej losowej wokół jej wartości średniej jest
macierz kowariancji:

[ ]

(

)(

)

[

]

(

)

(

)

[

]

nxn

Xj

j

Xi

i

T

X

X

X

n

j

i

m

X

m

X

E

m

X

m

X

E

X

⎥

⎦

⎤

⎢

⎣

⎡

=

−

−

=

−

−

=

=

∑

,...,

1

,

cov

Na głównej przekątnej macierzy kowariancji znajdą się wariancję poszczególnych
zmiennych, natomiast pozostałe elementy macierzy to współczynniki korelacji pomiędzy
zmiennymi, dla nieskorelowanych zmiennych będą one zerowe. Macierz kowariancji jest
macierzą nieujemnie określoną, czyli spełniony jest warunek:

y

∀

∑

≥ 0

y

y

X

T

Przy czym wyrażenie przed znakiem nierówności jest skalarem i gdy ten warunek nie jest
spełniony dal danej macierzy to nie jest to macierz kowariancji.
Dowód na nieujemną określoność macierzy kowariancji:

(

)(

)

[

]

∑

−

−

=

T

X

X

X

m

X

m

X

E

(

)(

)

[

]

(

)(

)

[

]

[ ]

0

2

≥

=

−

−

=

−

−

=

∑

z

E

y

m

X

m

X

y

E

y

m

X

m

X

E

y

y

y

T

X

X

T

T

X

X

T

X

T

Zastanówmy się teraz na problemem porównywania macierzy kowariancji. Otóż właściwie
nie da się porównać dwóch macierzy tak aby otrzymać jednoznaczną odpowiedź, że np.:
macierz pierwsza jest większa; aczkolwiek możliwa jest pewna ograniczona ocena dwóch
macierzy. O tym jak wygląda skupienie rozkładów informują nas równania elipsoid
koncentracji:

1

1

=

∑

−

X

T

y

y

Równanie to pozwala na wykreślenie elipsoid, obrazujących koncentrację zmiennych wokół
wartości średniej, na tej podstawie możliwe jest porównanie dwóch macierzy kowariancji,

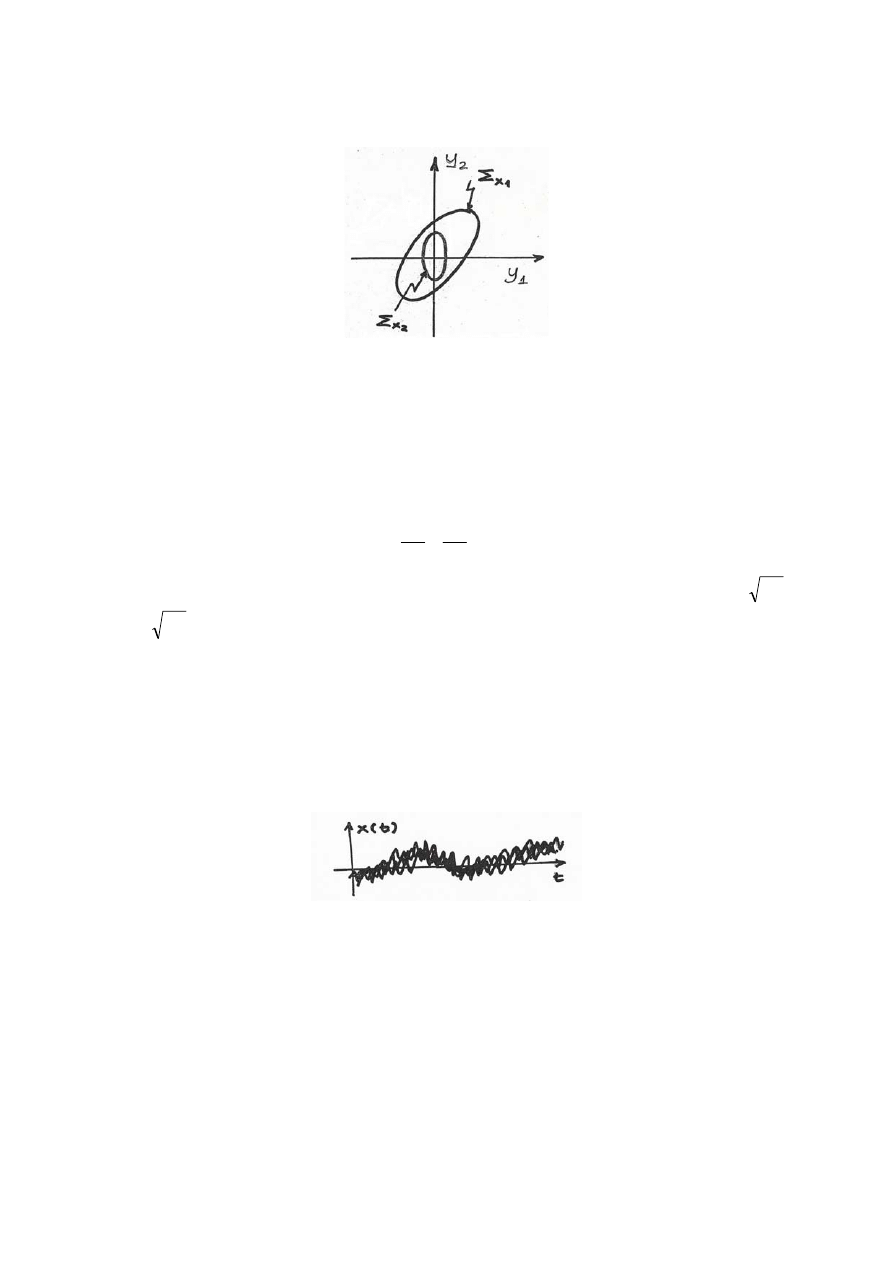
poprzez określenie, że np.: elementy macierzy pierwszej są bardziej skupione wokół wartości
średniej itp.

Rys.5. Przykładowe elipsoidy koncentracji dla dwóch,

dwuwymiarowych macierzy kowariancji.

Dla macierzy kowariancji dwuwymiarowych (2x2) elipsoidy sprowadzają się do elips.
Przykładowo, jeśli mamy prostą macierz kowariancji, w której elementy skośne równe są 0:

∑

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

=

2

2

0

0

y

x

X

σ

σ

⎥

⎦

⎤

⎢

⎣

⎡

=

2

1

y

y

y

równanie elipsy będzie dla tego przykładu następujące:

1

2

2

2

2

2

1

=

+

y

x

y

y

σ

σ

W tym przypadku osie elipsy pokrywają się z osiami układu współrzędnych, przy czym

2

x

σ

oraz

2
y

σ

są długościami odpowiednich półosi elipsy. Jeżeli elementy poza główną

przekątną byłyby niezerowe to elipsa byłaby obrócona.

Warto również przypomnieć sobie pojęcia i wielkości związane z procesami stochastycznymi.
Zaczniemy od zapisania zdarzenia elementarnego:

( )

e

t

x ,

oraz przypomnienia, że dyskretny

proces stochastyczny to ciąg zmiennych losowych lub też zbiór realizacji zmiennej losowej.
Warto pamiętać, iż pojedyncza realizacja nie ma w sobie nic losowego. Losowość ujawnia się
gdy na jednym wykresie pokażemy wiele realizacji zmiennej losowej.

Rys.6. Przykładowy zbiór realizacji zmiennej losowej x(t)

Omówimy teraz własności zbioru realizacji zmiennej losowej. Wartość oczekiwana procesu
stochastycznego jest ciągiem wartości oczekiwanych poszczególnych zmiennych. i możemy
przedstawić ją zależnością:

( )

( )

[ ]

t

x

E

t

m

x

=

Jeśli mielibyśmy przedstawić graficzną interpretację wartości oczekiwanej to byłaby to
krzywa przechodząca mniej więcej przez środek naszego pęku realizacji (patrz Rys.6).
Kolejne własności procesu stochastycznego prezentują funkcje autokorelacji i
autokowariancji. W uproszczeniu możemy powiedzieć, iż określają one w jakim stopniu
wartość zmiennej losowej w danej chwili czasu t

2

zależy od wartości tej zmiennej w chwili t

1

.

Funkcje autokorelacji i autokowariancji (inaczej określaną również jako korekcje zmiennych
scentralizowanych) możemy zapisać w poniższej notacji:

(

)

( ) ( )

[

]

2

1

2

1

,

t

x

t

x

E

t

t

R

x

=

(

)

( ) ( )

⎥⎦

⎤

⎢⎣

⎡

=

2

1

2

1

,

t

x

t

x

E

t

t

C

o

o

x

gdzie:

- zmienna scentralizowana, proces o zerowej wartości oczekiwanej

( ) ( )

( )

t

m

t

x

t

x

x

o

−

=

Procesy, dla których wartość oczekiwana jest stała, czyli nie zależy od czasu, natomiast
wartości funkcji autokorelacji i autokowariancji zależą tylko od różnicy czasów t

1

oraz

t

2

nazywamy procesami stacjonarnymi w szerokim sensie. Zapisując powyższe warunki
symbolicznie:

( )

(

)

(

(

)

(

τ

τ

x

x

x

x

x

x

C

t

t

C

R

t

t

R

m

t

m

=

=

)

)

=

2

1

2

1

,

,

gdzie:

2

1

t

t

−

=

τ

Dla procesów stacjonarnych możemy określić widmową gęstość mocy. Dla takiego procesu w
całym przedziale czasu średnia wartość wydzielanej energii (moc) jest stała. Dla sygnałów
dyskretnych o skończonej gęstości mocy wyznaczamy transformatę Fouriera:

( )

( )

[

]

( )

∑

∞

−∞

=

−

=

=

τ

ω

τ

τ

ω

t

j

x

x

x

e

R

R

F

S

π

ω

π

<

<

−

Znajomość charakterystyki widma pozwala nam na znalezienie funkcji autokorelacji i
odwrotnie. Zależność odwrotną do powyższej możemy zapisać:

( )

( )

∫

−

=

π

π

ω

ω

ω

π

τ

d

e

S

R

t

j

x

x

2

1

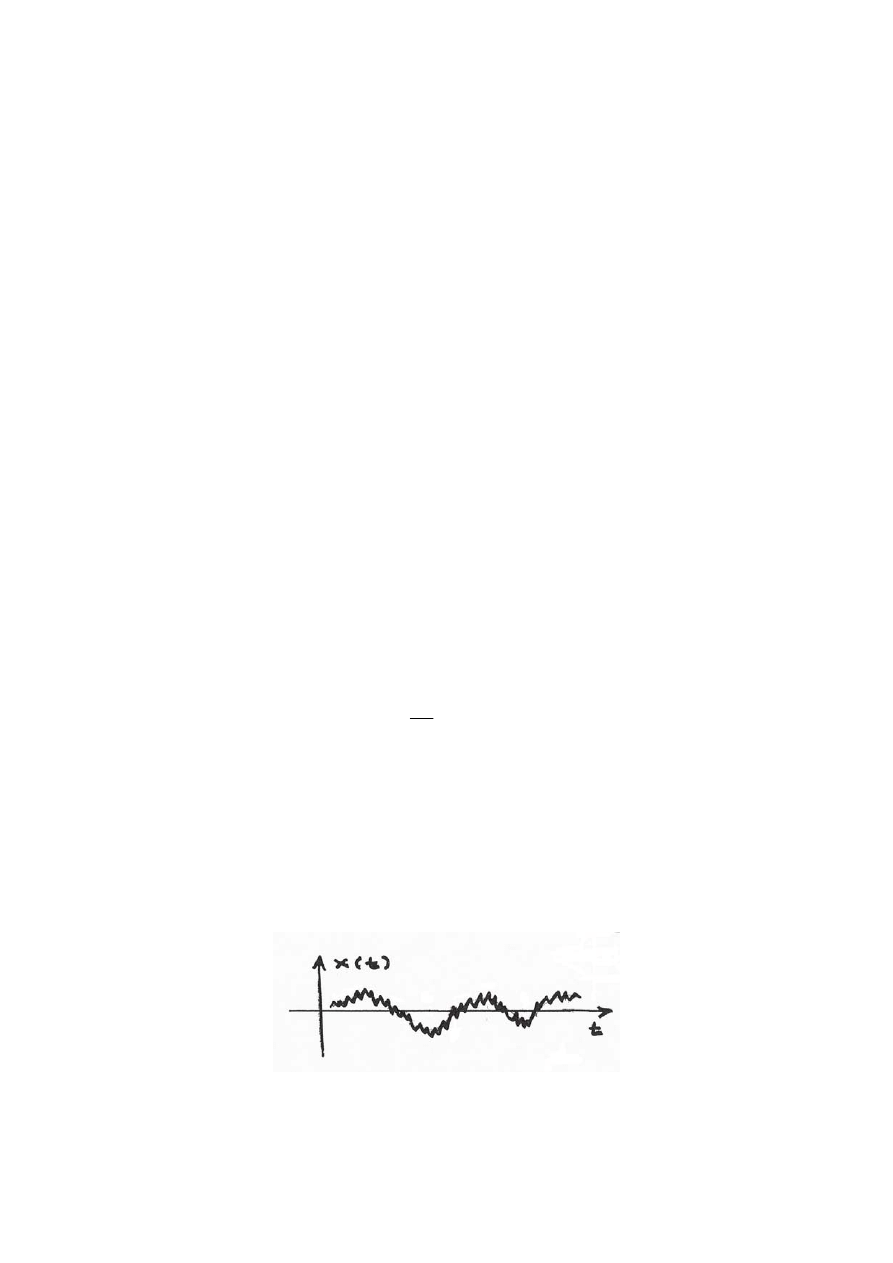
Przykład. Zadaniem jest znalezienie widma sygnału przedstawionego na

Rys.7 bez

dokonywania żmudnych obliczeń. Należy zauważyć, iż poniższy sygnał jest złożeniem dwóch
sygnałów: sinusoidy oraz sygnału, będącego na kształt szumu, przy czym większy wpływ na
sygnał wynikowy ma sinusoida. Przyjmijmy, że okres sygnału T równy jest 1s, natomiast
liczba „górek” w jednym okresie wynosi 20. W ten sposób wiemy, iż widmo będzie miało 2
szczyty rezonansowe w częstotliwościach 1Hz oraz 20Hz. Teraz możemy odręcznie
naszkicować widmo z dwoma szczytami.

Rys.7. Przebieg sygnału do przykładu.

Przeanalizujmy teraz jak zachowują się procesy stochastyczne przy przechodzeniu przez
układy liniowe. Na początek przyjmiemy założenie, że proces

jest procesem

stacjonarnym w szerokim sensie o wartości oczekiwanej

, funkcji autokorelacji

( )

t

x

x

m

( )

τ

x

R

oraz

widmie

( )

ω

x

S

. Naszym zadaniem będzie określenie własności procesu

, jaki pojawi się

na wyjściu układu liniowego opisanego funkcją

( )

t

y

( )

t

k

pobudzonego sygnałem

(

Rys.8.).

( )

t

x

( )

t

k

( )

t

x

( )

t

y

Rys.8. Przechodzenie sygnału stochastycznego przez układ liniowy

Jak łatwo stwierdzić sygnał

będzie dany zależnością:

( )

t

y

( )

( ) (

)

∑

∞

=

−

=

0

n

n

t

x

n

k

t

y

Obliczmy wartość oczekiwaną procesu

( )

t

y

:

( )

( ) (

)

( ) (

)

[

]

( )

∑

∑

∑

∞

=

∞

=

∞

=

=

=

−

=

⎥

⎦

⎤

⎢

⎣

⎡

−

=

0

0

0

n

y

x

n

n

y

m

m

n

k

n

t

x

E

n

k

n

t

x

n

k

E

t

m

Otrzymany wynik możemy zinterpretować następująco: jeżeli na wejście układu liniowego
podamy proces o stałej wartości oczekiwanej to na wyjściu również otrzymamy proces o
stałej wartości oczekiwanej.
Wyznaczmy teraz funkcję autokorelacji:

(

)

( ) ( )

[

]

( ) ( )

(

)

(

)

( ) ( )

(

)

(

)

[

]

( ) ( ) (

)

( )

∑∑

∑∑

∑∑

∞

=

∞

=

∞

=

∞

=

∞

=

∞

=

=

+

−

−

=

=

−

−

=

=

⎥

⎦

⎤

⎢

⎣

⎡

−

−

=

=

0

0

2

1

0

0

2

0

0

2

2

1

2

1

1

1

,

n

m

y

x

n

m

n

m

y

R

m

n

t

t

R

m

k

n

k

m

t

x

n

t

x

E

m

k

n

k

m

t

x

n

t

x

m

k

n

k

E

t

y

t

y

E

t

t

R

τ

Jak widać funkcja autokorelacji sygnału

( )

t

y

nie zależy od czasu a tylko od różnicy czasów

2

1

t

t

−

=

τ

. Stąd wniosek: jeżeli sygnał podawany na wejście stabilnego układu liniowego

niezmiennego w czasie jest stacjonarny w szerokim sensie to sygnał obserwowany na jego
wyjściu (w stanie ustalonym) jest również stacjonarny w szerokim sensie.
Skoro sygnał wyjściowy jest stacjonarny w szerokim sensie to możemy wyznaczyć jego
widmową gęstość mocy:

( )

( )

( ) ( ) (

)

( )

( )

(

)

(

)

( ) ( )

( )

( )

( )

ω

ω

τ

τ

τ

ω

ω

ω

ω

τ

τ

ω

ω

ω

τ

τ

ωτ

ωτ

x

j

x

j

j

m

n

j

x

m

m

j

n

n

j

n

m

j

x

j

y

y

S

e

K

S

e

K

e

K

e

m

n

R

e

m

k

e

n

k

e

m

n

R

m

k

n

k

e

R

S

2

*

0

0

0

0

=

=

=

+

−

=

=

+

−

=

=

−

∞

−∞

=

+

−

−

∞

=

−

∞

=

−

∞

−∞

=

∞

−∞

=

∞

=

∞

=

−

−

∑

∑

∑

∑

∑∑∑

gdzie

oznacza transmitancję widmową układu liniowego.

( )

( )

∑

∞

=

−

=

0

n

n

j

j

e

n

k

e

K

ω

ω

ROZDZIAŁ III – modele szeregów czasowych – model autoregresyjny (AR)

Model autoregresyjny (AR, autoregressive) to model szeregu czasowego, w którym przebieg
sygnału

na wyjściu układu liniowego tłumaczymy jego wcześniejszym przebiegiem.

Model AR(r) – model rzędu r opisujemy równaniem autoregresyjnym:

( )

t

y

( )

( ) ( )

∑

=

+

−

=

r

i

i

t

n

i

t

y

a

t

y

1

gdzie to współczynniki autregresji, natomiast

i

a

( )

t

n

jest gaussowskim szumem białym, czyli

ciągiem niezależnych zmiennych losowych o zerowej wartości oczekiwanej

oraz

o stałej wariancji

( )

[ ]

0

=

t

n

E

( )

[ ]

ρ

=

t

n

var

. Szum biały ma płaskie widmo częstotliwościowe, jako że

stanowi on złożenie wszystkich częstotliwości w paśmie (podobnie jak światło widzialne jest
złożeniem wszystkich fal z zakresu – stąd nazwa „szum biały”). To właśnie szum

( )

t

n

w

równaniu autoregresyjnym odpowiada za losowy charakter przebiegu

( )

t

y

.

Wprowadzając operator jednokrokowego opóźnienia

1

−

q

( ) ( )

(

)

1

1

−

=

−

t

y

t

y

q

możemy

przepisać równanie autoregresyjne w sposób następujący:

( )

( ) ( )

t

n

t

y

q

A

=

−1

gdzie

( )

∑

=

−

−

−

=

r

i

i

i

q

a

q

A

1

1

1

czyli:

( )

( ) ( )

( )

(

)

(

) (

t

n

r

t

y

a

t

y

a

t

y

a

t

y

t

y

q

A

r

=

−

−

−

−

−

−

−

=

−

...

2

1

2

1

1

)

( )

1

1

−

q

A

( )

t

n

( )

t

y

Rys.9. Schemat modelu autoregresyjnego

Stosowany w modelu AR układ to filtr formujący, wielobiegunowy o r biegunach. Im węższe
jest widmo tego filtru tym sygnał na wyjściu będzie bardziej zbliżony do sinusoidalnego. Na
uwagę zasługuje fakt iż w tym modelu, podając na wejście sygnał, będący kwintesencja
losowości – szum biały na wyjściu otrzymujemy sygnał sinusoidalny. Ten model służy
właśnie do modelowania przebiegów pseudookresowych.
Należy jednak pamiętać iż spełniony musi być bardzo ważny warunek. Filtr musi być
asymptotycznie stabilny, czyli wszystkie pierwiastki wielomianu charakterystycznego

( )

1

−

q

A

muszą mieć moduły mniejsze od 1, czyli muszą leżeć wewnątrz okręgu jednostkowego na
płaszczyźnie zespolonej.
W celu określenia dopuszczalnego zakresu, w jakim muszą się znajdować współczynniki
autoregresji można się pokusić o wykreślenie obszarów dopuszczalnych. Dla modeli rzędu
pierwszego będzie to obszar na osi liczbowej w zakresie <-1;1>, dla modelu rzędu drugiego
będzie to już dużo bardziej skomplikowany obszar trójkątny, natomiast okazuje się, że dla
modeli wyższych rzędów wykreślenie obszarów dopuszczalnych wartości współczynników
autoregresji staje się bardzo trudne, gdyż są to bardzo skomplikowane figury. Dlatego też
właściwie nie istnieją testy na stabilność modelu AR.