Politechnika Rzeszowska 

im. Ignacego Łukasiewicza

 

 

Katedra Informatyki 

i Automatyki

 

 

Projekt z przedmiotu:  

Sztuczna Inteligencja 

 
 
 

Temat:  

Zrealizować sieć  neuronową uczoną algorytmem wstecznej 

 

 

propagacji błędu ( learnbp ) uczącą się rozpoznawania  

 

 

zwierząt.

  

 
 
 
 
 
 
 
 
 
 

Autor: 

 Sebastian Twardzik 

Rok:   

 

        II EF-DI 

Grupa: 

 

                P15 

Data:   

 

 24.05.2011r. 

 
 
 

 

2 

Spis treści: 

1. Opis problemu...........................................................................................................................3 

2. Dane do projektu.......................................................................................................................3 

 

2.1 Opis danych.................................................................................................................3 

 

2.2 Normalizacja danych...................................................................................................3 

 

2.3 Wczytanie danych.......................................................................................................4 

3. Opis algorytmu..........................................................................................................................4 

 

3.1 Czym jest sieć neuronowa?.........................................................................................4 

 

3.2 Koncepcja budowy sieci neuronowej..........................................................................4 

 

3.3 Opis algorytmu............................................................................................................5 

 

3.4 Skrypt realizujący sieć neuronową..............................................................................6 

4. Eksperymenty............................................................................................................................8 

5. Podsumowanie i wnioski........................................................................................................13 
6. Bibliografia.............................................................................................................................13 

 
Zawartość płyty CD: 

- kod 
- wykresy 
- wyniki oraz skrypt rysujący wykresy 
- projekt 
- info.txt 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 

3 

1. Opis problemu. 

Celem projektu jest stworzenie sieci neuronowej, która będzie przyporządkowywać zwierzę do jednej z 
następujących grup: 
- (1) ssaki 
- (2) ptaki 
- (3) gady 
- (4) ryby 
- (5) płazy 
- (6) owady 
- (7) bezkręgowce. 
Przeanalizowanych zostało 101 gatunków zwierząt na podstawie siedemnastu ich cech. Ostatnią wartością w 
tabeli jest numer klasy do jakiej należy dany gatunek.  
 
Dane do projektu zostały pobrane z repozytorium Uniwersytetu Kalifornijskiego w Irvine  
(http://archive.ics.uci.edu/ml/datasets/zoo) stworzonego przez Richarda Forsytha. 
 

2. Dane do projektu. 
2.1 Opis danych. 

Tablica z danymi składa się z 18 wierszy z cechami zwierząt: 

1. Nazwa zwierzęcia  
2. włosy: Boolean  
3. pióra: Boolean  
4. jaja: Boolean  
5. mleko: Boolean  
6. powietrzne: Boolean  
7. wodne: Boolean  
8. drapieżnik: Boolean  
9. zębate: Boolean  
10. kręgowiec: Boolean  
11. oddycha: Boolean  
12. jadowite: Boolean  
13. płetwy: Boolean  
14. nogi: liczbowe (wartości: {0,2,4,5,6,8})  
15. ogon: Boolean  
16. domowe: Boolean  
17.rozmiaru kota (catsize): Boolean  
18. typ: liczbowe (liczby całkowite w przedziale [1,7])  

Oraz 101 kolumn z gatunkami zwierząt. Tabela poniżej opisuje układ kolumn. 
 

Numer 

kolumny 

Typ zwierzęcia 

1 - 41 

ssaki 

42 - 61 

ptaki 

62- 66 

gady 

67 - 79 

ryby 

80 - 83 

płazy 

84 - 91 

owady 

92 - 101 

bezkręgowce 

 

2.2 Normalizacja danych. 

Do dalszej części projektu dane należy odpowiednio przekształcić. W tym celu usuwamy pierwszy wiersz tablicy( 
ten zawierający nazwy zwierząt). Ostatni wiersz również należy usunąć i stworzyć z niego osobny wektor. Cechy 
które nie są opisane wartościami Boolowskimi należy znormalizować, tzn. wielkości te mają się mieścić w 
przedziale od 0 do 1. Po takich przekształceniach otrzymujemy dwie tablice: 
P<16 x 101> zawierającą cechy zwierząt oraz  
T<1 x 101> zawierającą gatunki zwierząt.  
Całość zapisujemy pod nazwą Zoo2.mat. 

 
 

 

4 

2.3 Wczytanie danych. 

Przed wczytaniem danych należy wyczyścić przestrzeń roboczą oraz ustawić pewne parametry środowiska. 
Aby to zrobić należy zacząć program w ten sposób: 
 

clear 

all

   

% czyszczenie wszystkich zmiennych

 

nntwarn 

off

 

% wył

ą

czenie ostrze

ż

e

ń

 NNT

 

format 

long

 

% 15 cyfr double i 7 single

 

format 

compact

  

% format danych wyj

ś

ciowych brak enter przed ans=

 

 

 

load 

zoo2

;      

% załadowanie danych do przestrzeni roboczej

 

 
 

3. Opis algorytmu 
 
3.1 Czym jest sieć neuronowa? 

Sieć neuronowa jest to model matematyczny realizujący obliczenia lub przetwarzanie sygnałów. Składa się ona z 
sieci węzłów obliczeniowych zwanych neuronami oraz z ich połączeń.. Została ona zaprojektowana na wzór  
ludzkiego mózgu. Jednak w przypadku mózgu każdy neuron jest połączony z około 10 000 innych. Natomiast w 
przypadku sztucznej sieci łączy się on jedynie z sąsiadem. Wszystkie one działają kolejno a nie tak jak w mózgu: 
jednocześnie.  
 
Podstawowe właściwości sieci neuronowych mające swoje odzwierciedlenie w biologicznym układzie 
nerwowym, to:  

•

 

zdolność do uogólniania danych. 

•

 

interpolacja i przewidywanie. 

•

 

mała wrażliwość na szumy w zbiorze danych. 

•

 

zdolność do efektywnej pracy nawet po usunięciu kilku neuronów lub połączeń między nimi. 

•

 

przetwarzanie równoległe i rozproszone.  

Najpopularniejsze obecnie zastosowanie sieci neuronowych: 

•

 

w programach do rozpoznawania pisma (OCR) 

•

 

na lotniskach do sprawdzania, czy prześwietlony bagaż zawiera niebezpieczne ładunki 

•

 

do syntezy mowy. 

 

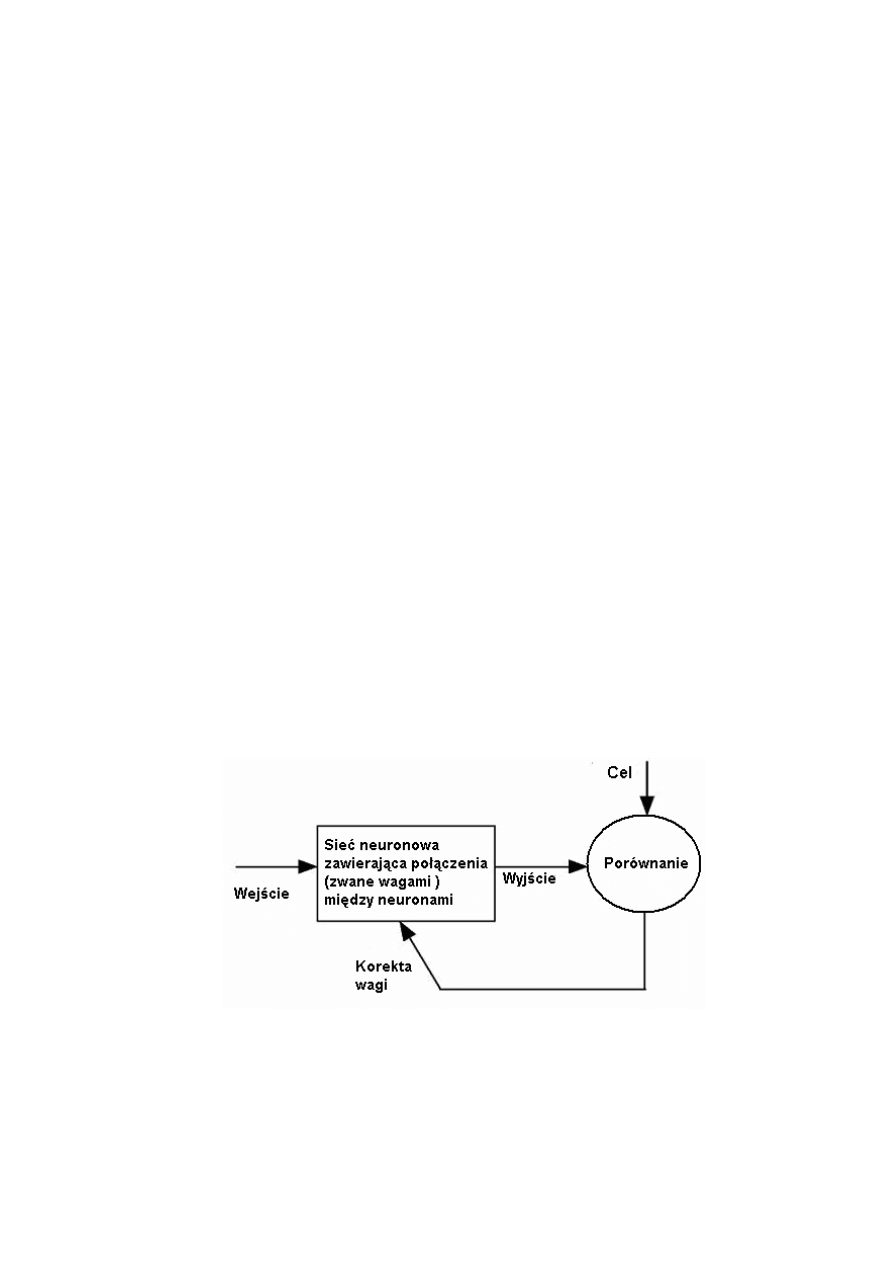
3.2 Koncepcja budowy sieci neuronowej. 

 

 

 

 

 

5 

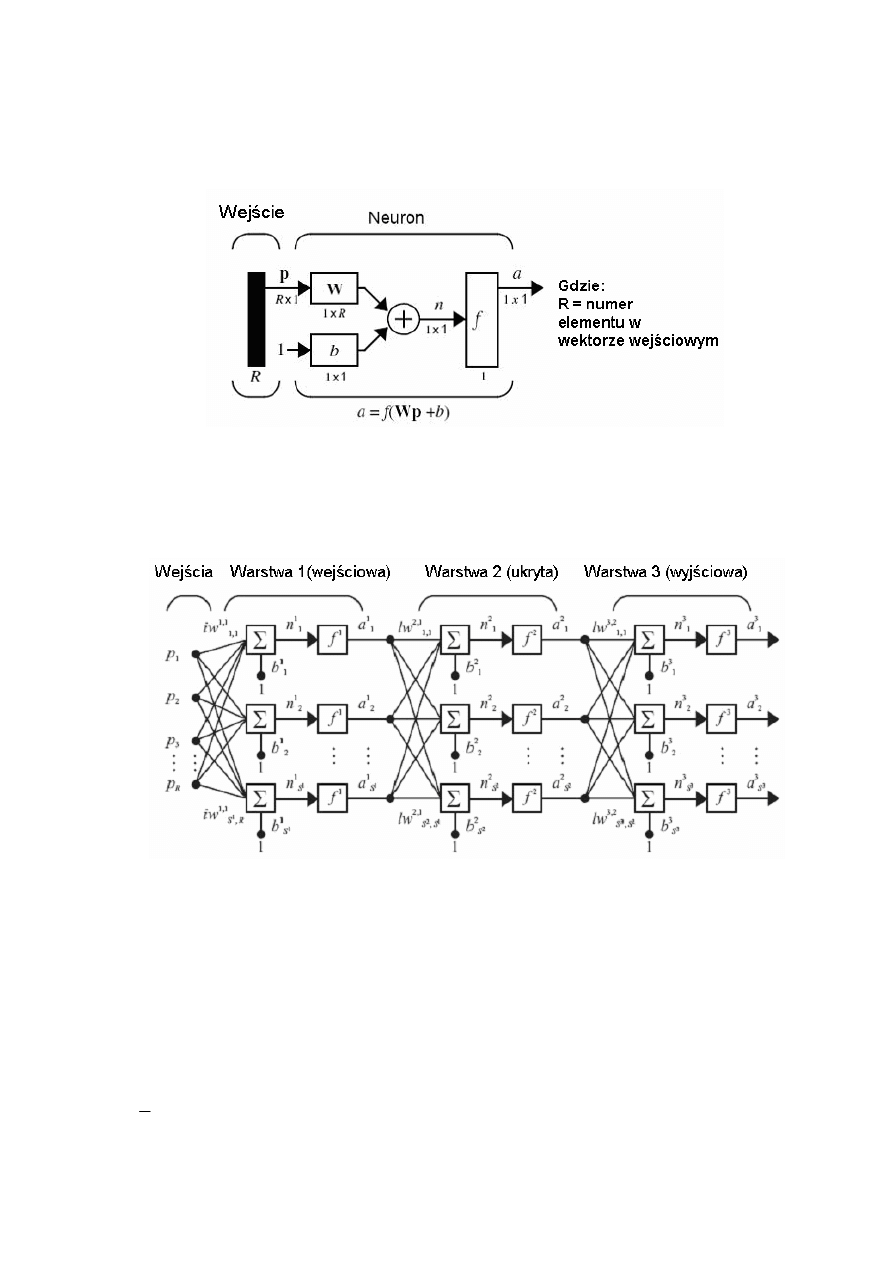
Matematyczny model neuronu oraz sieci 3 warstwowej: 

 

 

gdzie:    a jest wyjściem sieci 
 

W jest prostokątną macierzą wag 

 

p są to sygnały wejściowe 

 

b jest wektorem przesunięć 

 

Budowa neuronu. 

 

 

Budowa sieci neuronowej 3 warstwowej – model. 

 
3.3 Opis algorytmu. 

W projekcie zastosowany został algorytm uczenia pod nadzorem ze wsteczną propagacją błędu (learnbp). 
 
Algorytm wstecznej propagacji błędu określa sposób doboru wag w sieci wielowarstwowej przy użyciu 
gradientowych metod optymalizacji. Uczenie polega na odpowiednim doborze wag neuronów tak aby błąd 
ś

redniokwadratowy sieci ( SSE) był mniejszy niż zadany.  

Wartość błędu dla pojedynczego neuronu może być dodatnia lub ujemna a więc dla dwóch źle nauczonych 
neuronów może wynieść zero. Aby temu zapobiec e

j

 jest podniesione do kwadratu, a więc : 

 

∑

=

=

K

j

j

e

E

1

2

2

1

 

 

 

6 

Nazwa algorytmu pochodzi od metody obliczania błędów w poszczególnych warstwach sieci. 
W pierwszym kroku na podstawie danych wejściowych i wyjściowych wykonywane są ich obliczenia w ostatniej 
warstwie. 
Kolejno obliczany jest błąd dla neuronów poprzedniej warstwy itd. W ten sposób sygnał błędu rozprzestrzenia się 
od warstwy wyjściowej wstecz.  
Korekcja błędu sieci jest oparta na minimalizacji funkcji miary błędu, będącej sumą kwadratów błędów na 
wyjściach sieci. Wektor wag neuronu jest przesuwany w kierunku ujemnego gradientu. Dodatkowo wektor ten jest 
przemnażany przez współczynnik 

η

, który nazywany jest współczynnikiem szybkości uczenia. Zatem zmiana 

wagi w każdej iteracji jest równa:

 

 

 
 
Wykorzystując oprogramowanie MatLab opisaną wyżej funkcje wywołujemy w następujący sposób: 

           
[dW1,dB1] = learnbp(P,D1,lr);  

Gdzie:  
                     P- Macierz wektorów wejściowych  
                     D1- Macierz wektorów błędów [S,Q] 
                     lr - Współczynnik uczenia 
                    dW1- macierz zmian wagi  
                    dB1- wektor zmian biasów 
 

3.4 Skrypt realizujący sieć neuronową. 

Do skryptu zostały dodane pętle zmieniające różne parametry sieci. Efekty pracy zapisywane są w pliku 
tekstowym "wyniczek.txt". 

 

clear 

all

   

% czyszczenie wszystkich zmiennych

 

nntwarn 

off

 

% wył

ą

czenie ostrze

ż

e

ń

 NNT

 

format 

long

 

% 15 cyfr double i 7 single

 

format 

compact

  

% format danych wyj

ś

ciowych brak enter przed ans=

 

 
 

 

load 

zoo2

; 

wiersz = 1; 
[R,Q] = size(P); 

%zwraca wymiar macierzy [R -kol, Q- wier]

 

 

 

for

 eksperyment = 1 : 1 : 10, 

     
    lr = 1e-2;  
    

for

 licznik = 0: 1 : 2, 

        lr = lr / 10; 
         
        

for

 S1 = 1: 10 : 101,  

            

for

 S2 = 1: 10 : S1, 

                [S3,Q] = size(T); 
                

%S1 - liczba neuronów warstwy 1

 

                

%S2 - liczba neuronów warstwy 2

 

 

 

                [W1,B1] = nwtan(S1,R);   

% generator losowy Nguyn- Widrow dla  

 

 

 

 

 

 

  % neuronów TANSIG

 

                

% otrzymujemy macierz W1 o wymiarach S1xR i wektor B1 o wymiarze S1 

 

                [W2,B2] = nwtan(S2,S1);  

% W1, W2, W3- macierze wag

 

                [W3,B3] = rands(S3,S2);  

% generowanie macierzy wag i wektora biasu 

 

 

 

 

 

 

  % o warto

ś

ciach statystycznych o 

 

                

% jednorodnym rozkładzie z zakresu [-1,1] 

 

                

% B1, B2, B3- wektory bias 

 

                

% otrzymujemy macierz W1 o wymiarach S3xS2 i wektor B3 o wymiarze S3 

 

 

 

                disp_freq=100;  

%cz

ę

stotliwo

ść

 wy

ś

wietlania     

 

                max_epoch=20000;  

%maksymalna liczba kroków 

 

                err_goal=.25;    

% bł

ą

d docelowy- warto

ść

 kra

ń

cowa  

 

               

 

7 

                error = [];         
  
                A1 = tansig(W1*P,B1); 

% kalkuluje wyj

ś

cia warstwy na podstawie wej

ść

 

                A2 = tansig(W2*A1,B2); 

% parametry W1*P- wej

ś

cia warstwy* odpowiednie 

 

 

 

 

 

 

 % wagi

 

                A3 = purelin(W3*A2,B3); 

% zwraca macierz ( A3 E <-1,1>)

 

                E = T -A3;     

 

 

% A- wyj

ś

cie warstwy

 

                SSE = sumsqr(E); 
                

for

 epoch=1:max_epoch, 

                    

if

 SSE < err_goal,   

% je

ż

eli suma kwadratów bł

ę

dów mniejsza od 

 

 

 

 

 

 

  % bł

ę

du minimalnego 

 

                        epoch = epoch - 1; 
                    

break

, 

                    

end

, 

                    D3 = deltalin(A3,E);    

% funkcja delty dla neuronów purelin  

 

 

 

 

 

 

     % E- macierz bł

ę

dów

 

                    

%( ró

ż

nica warto

ś

ci faktycznych i przewidzianych przez sie

ć

 

 

 

 

% neuronow

ą

 w poprzednim kroku)

 

                    

% zwraca pochodn

ą

 bł

ę

dów dla ukrytej warstwy

 

                    D2 = deltatan(A2,D3,W3); 

% % funkcja delty dla neuronów tansig  

 

 

 

 

 

 

% W - macierz wag pomi

ę

dzy warstwami[S1, S2]

 

                    D1 = deltatan(A1,D2,W2);    
  
                    [dW1,dB1] = learnbp(P,D1,lr);  
                    

% P- Macierz wektorów wej

ś

ciowych 

 

                    

% D1- Macierz wektorów bł

ę

dów [S,Q]

 

                    

% lr- Współczynnik uczenia

 

                    

% dW1- macierz zmian wagi

 

                    

% dB1- wektor zmian biasu

 

                    

% zwraca dW1 i dB1

 

                       
                    [dW2,dB2] = learnbp(A1,D2,lr);   
                    [dW3,dB3] = learnbp(A2,D3,lr); 
                        
                    W1 = W1 + dW1; 
                    B1 = B1 + dB1; 
                         
                    W2 = W2 + dW2; 
                    B2 = B2 + dB2; 
                         
                    W3 = W3 + dW3; 
                    B3 = B3 + dB3; 
                         
                    A1 = tansig(W1*P,B1); 

% kalkuluje wyj

ś

cia warstwy na podstawie 

 

 

 

 

 

 

   % wej

ść

 

                    A2 = tansig(W2*A1,B2); 

% parametry W1*P- wej

ś

cia warstwy*  

 

 

 

 

 

 

    %odpowiednie wagi

 

                    A3 = purelin(W3*A2,B3); 

% zwraca macierz ( A3 E <-1,1>) 

 

                         
                    E = T - A3;     

% A- wyj

ś

cie warstwy

 

 

 

                    SSE = sumsqr(E); 

% sumuje spot

ę

gowane elementy macierzy

 

                    error = [error SSE]; 

% składa 2 macierze w jedn

ą

 

                    

if

(rem(epoch,disp_freq) == 0)  

% rem- reszta z dzielenia. co ile 

 

 

 

 

 

 

 

     % epok ma wy

ś

wietla

ć

 numer epoki

 

                        epoch 
                        SSE 
                        eksperyment 
                        S1 
                        S2 
                        lr 
                        pause(1e-100) 
                    

end

  

                

end

 

                

% tu zapis wyników do tablicy

 

                wynik( wiersz , 1) = eksperyment;  
                wynik( wiersz , 2) = S1;  
                wynik( wiersz , 3) = S2;  

 

8 

                wynik( wiersz , 4) = lr;  
                wynik( wiersz , 5) = 100*(1-sum((abs(T-A3)>.5)')/length(T));  
                wynik( wiersz , 6) = SSE;  
                wynik( wiersz , 7) = epoch;  
                    
                wiersz = wiersz + 1; 
  
                epoch 
                SSE 
                [T' A3' (T-A3)' (abs(T-A3)>.5)']   
                100*(1-sum((abs(T-A3)>.5)')/length(T)) 
            

end

 

        

end

 

    

end

 

end

 

save 

wyniczek4.txt

 

wynik

 

-ascii

;  

 
4. Eksperymenty 

Eksperymenty wykonane w ramach projektu opierały się na zmianie ilości neuronów w pierwszej oraz drugiej 
warstwie, oraz zmianie współczynnika uczenia( lr). Zostało wykonanych 10 takich eksperymentów.  
Dane uczące zostały zapisane w tablicy <16 x 101>. 
Dla każdego eksperymentu zostało wykonane 9 wykresów trójwymiarowych. 
 
Najlepszą miarą tego ja szybko sieć się uczy jest liczba epok po której błąd minimalny został osiągnięty. 
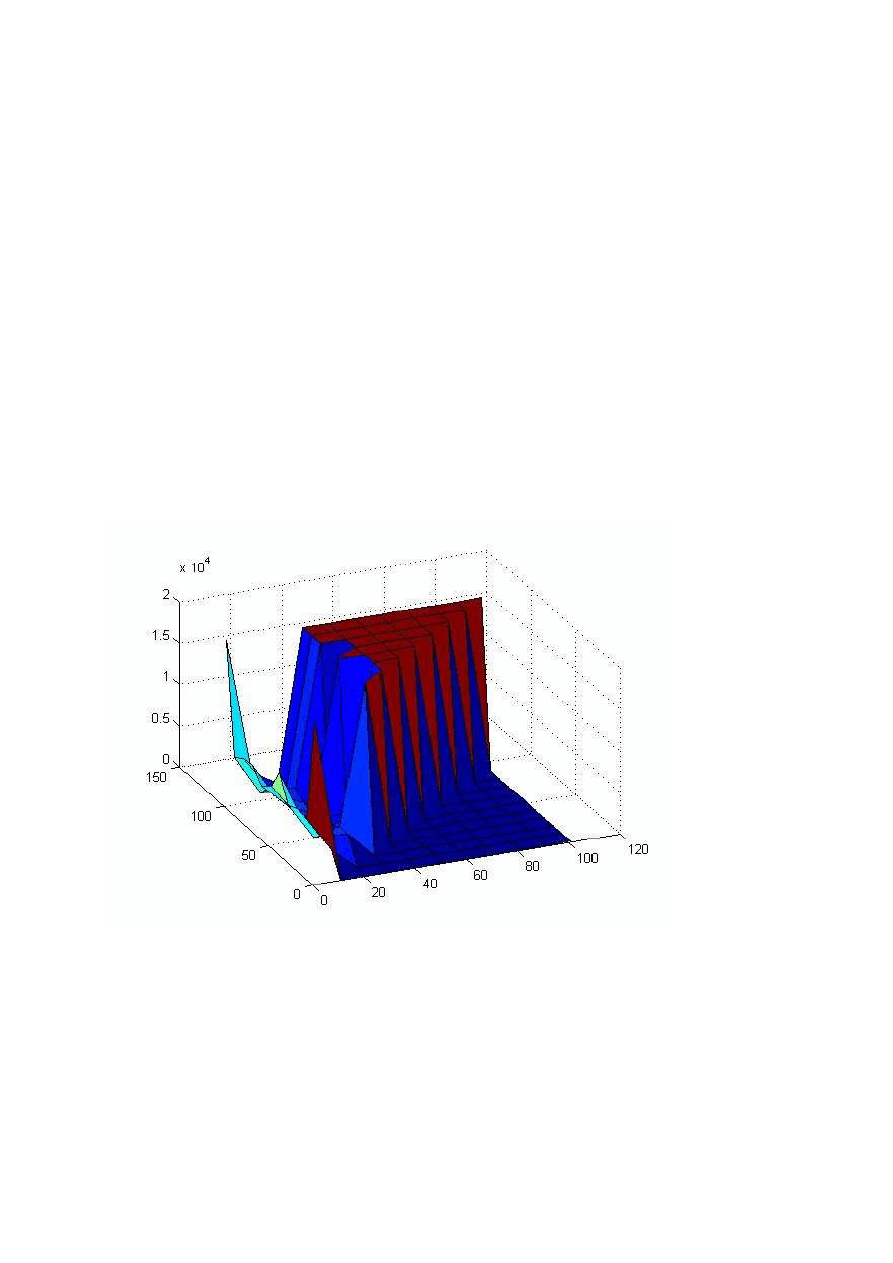
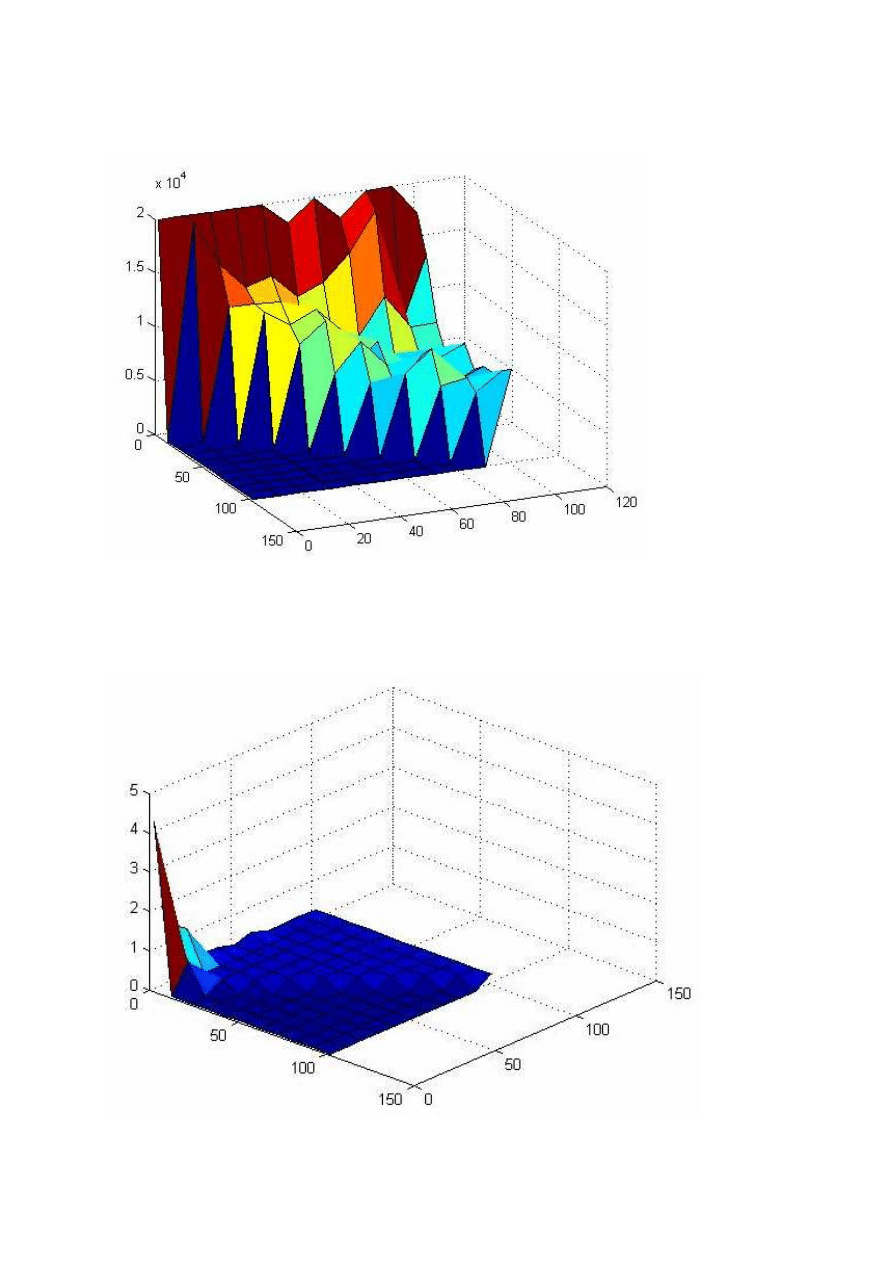
Dla współczynnika uczenia lr = 0.001 wykres wygląda tak: 

  

Jak widać sieć uczy się tylko dla małej liczby (mniej niż 30) neuronów w drugiej warstwie. 
 
 
 
 
 
 
 
 
 
 
 
 

 

9 

 
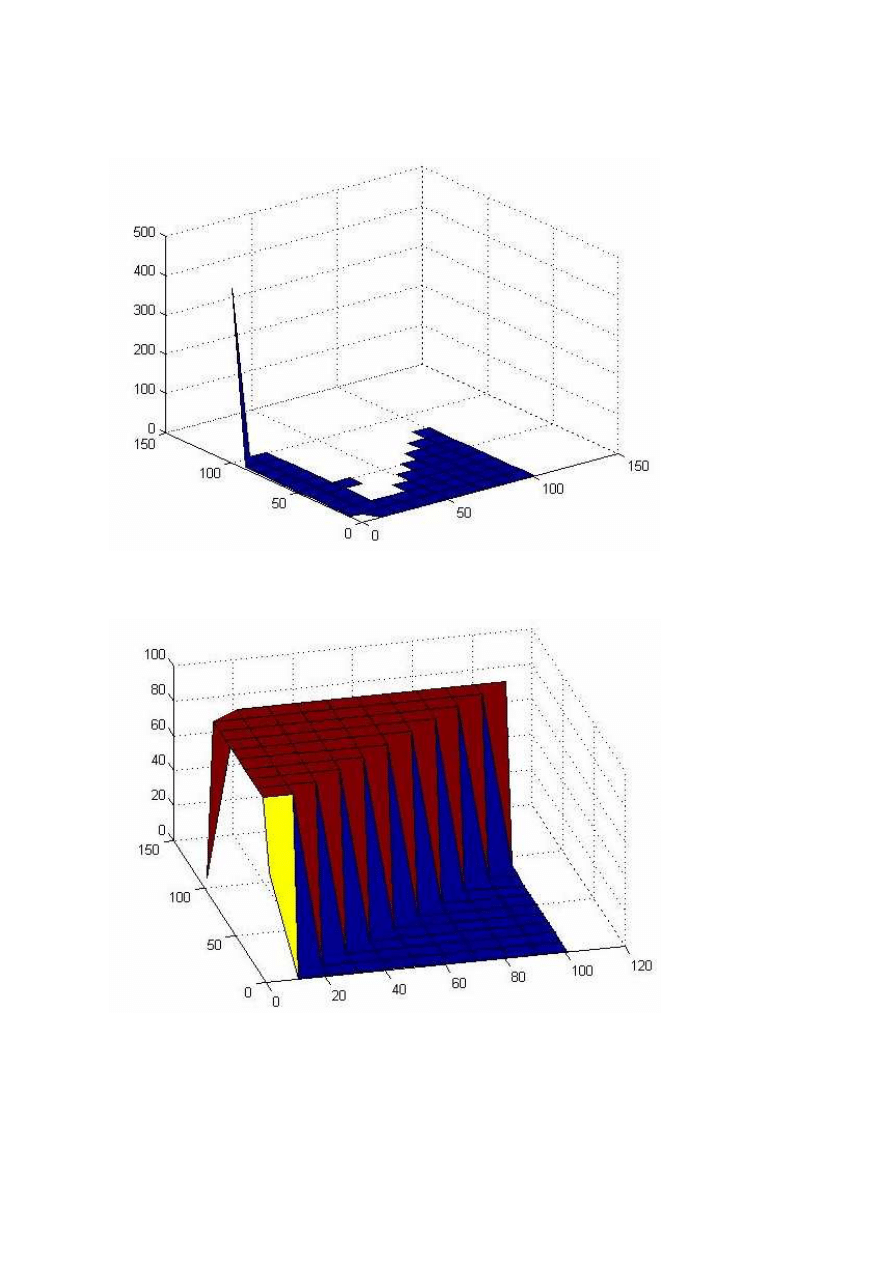
Błąd SSE dla współczynnika lr = 0.001 obrazuje wykres: 
 

 

 

Tam gdzie funkcja nie przyjmuje żadnych wartości błąd jest bardzo duży( wartość Nan). 
 
A oto wykres pokazujący w ilu procentach sieć się nauczyła. Wartość ta wynosi 100% również tam gdzie błąd 
SSE ma wartość Nan a więc wykres nie zupełnie pokazuje prawdę. 

 

 

 
 
 
 
 
 
 

 

10 

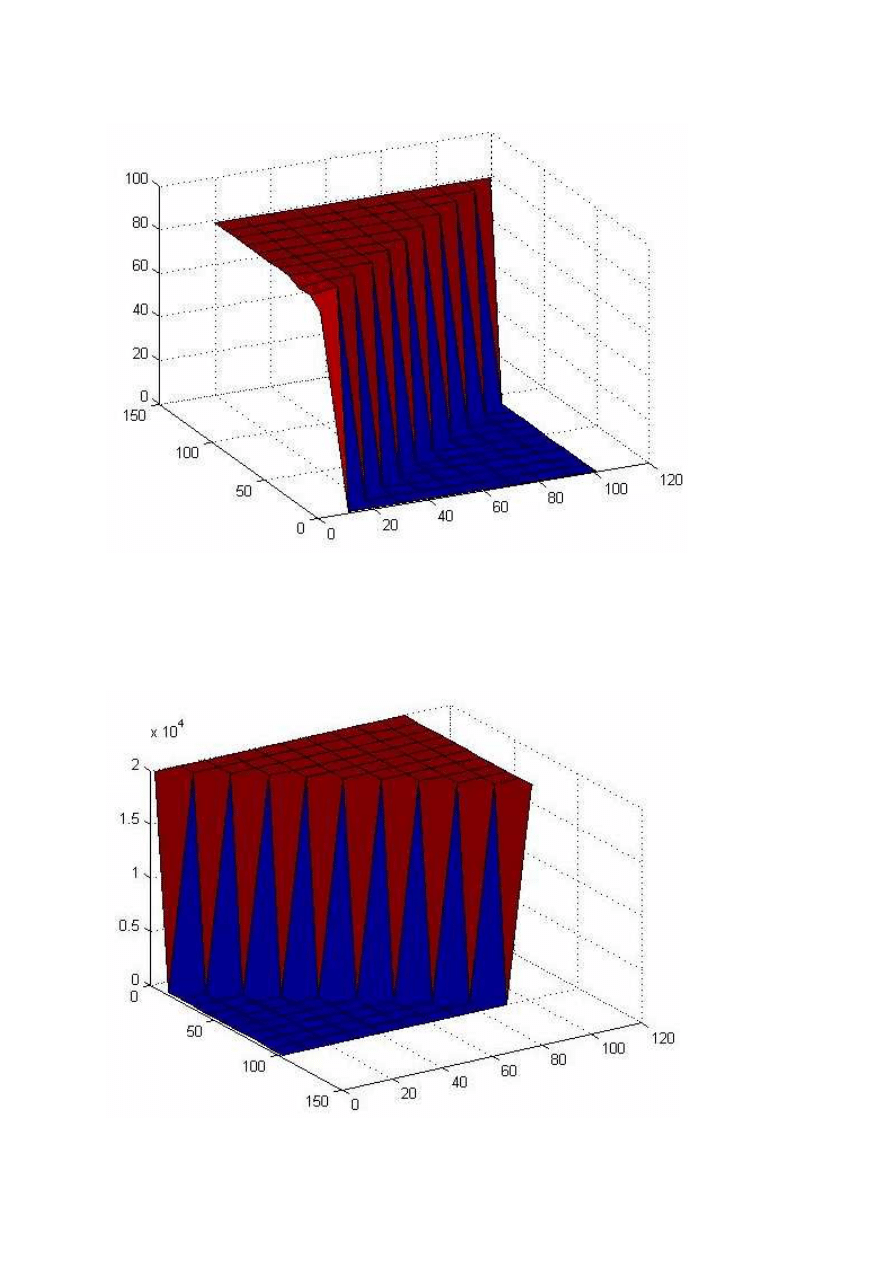
Następnie zmieniony został współczynnik uczenia na lr = 0.0001. Dla tej wartości wykresy wyglądają 
następująco: 
f(S1, S2) = epoch 

  

Jak widać sieć jest w stanie nauczyć się niezależnie od ilości neuronów w warstwach. Ich ilość wpływa na tempo 
uczenia. Im więcej neuronów tym szybciej sieć się uczy.   
 
 
 
A oto pozostałe wykresy: 
f(S1, S2) = SSE 

 

 
 

 

11 

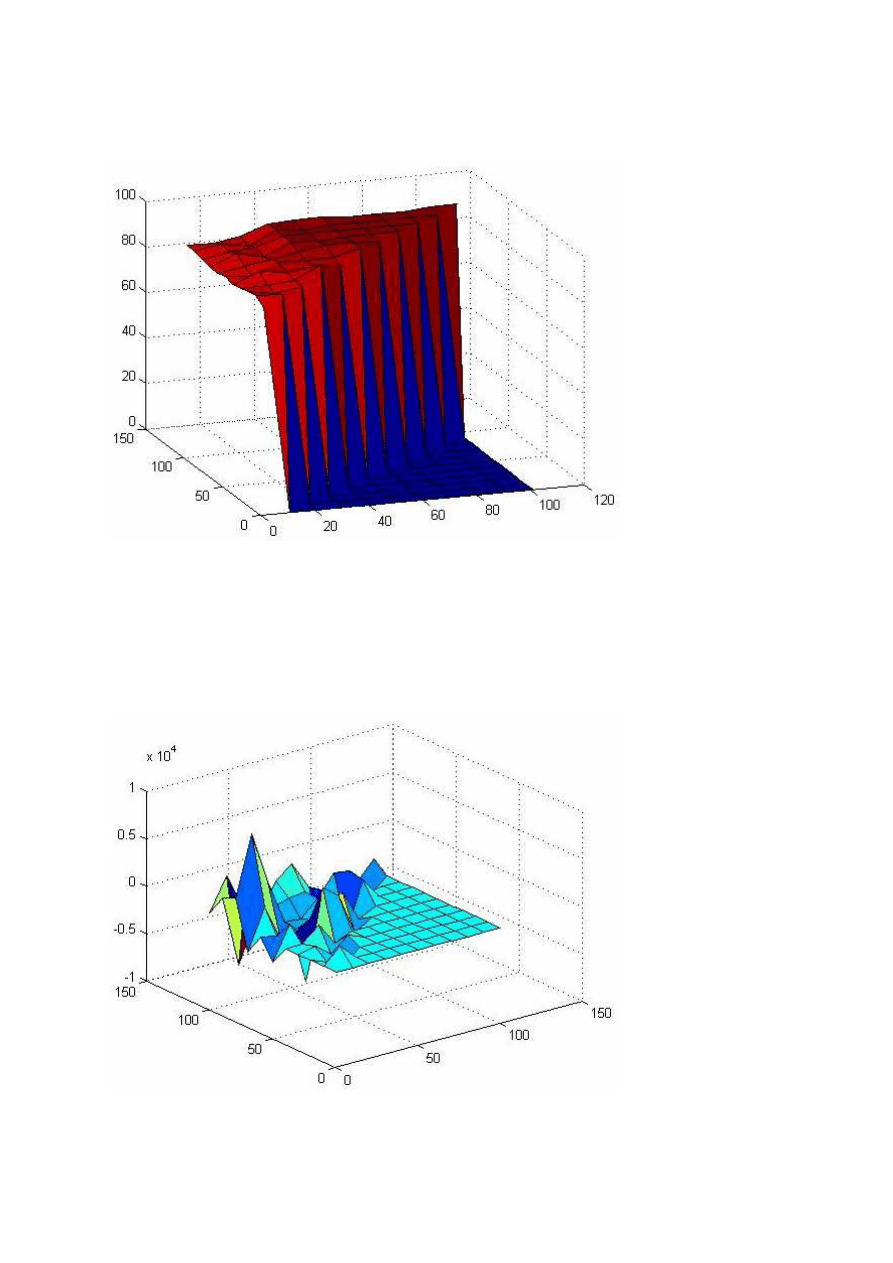
f(S1, S2) =  % 

 

W tym przypadku współczynnik uczenia jest dobrze dobrany. 
  
 
 
 
 
Ostatnia wartość współczynnika lr wynosiła 0.00001. Dla tej wartości wykresy wyglądają następująco: 
f(S1, S2) = epoch 

 

 

 

12 

Sieć nie jest w stanie się nauczyć liczbie epok równej 20 000. A w ilu procentach była w stanie się nauczyć 
pokazuje poniższy wykres: 
f(S1, S2) = % 

 

Wyniki są zbliżone do 100%. Wykres zależności SSE od ilości neuronów w warstwach jest tu zbędny. 
Prawdopodobnie przy większej liczbie epok sieć by się nauczyła.  
 
Wykonane wykresy pokazują że współczynnik uczenia lr = 0.0001 jest optymalną wielkością dla tych danych 
wejściowych.  
Dla kolejnych eksperymentów wyniki nie były identyczne. Najlepiej będzie to odzwierciedlał wykres  
f(S1, S2) = epoch  przy współczynniku uczenia lr = 0.0001. 
 
Poniższe wykresy pokazują różnicę pomiędzy eksperymentem: 

•

 

pierwszym i trzecim 

 

 
 
 

 

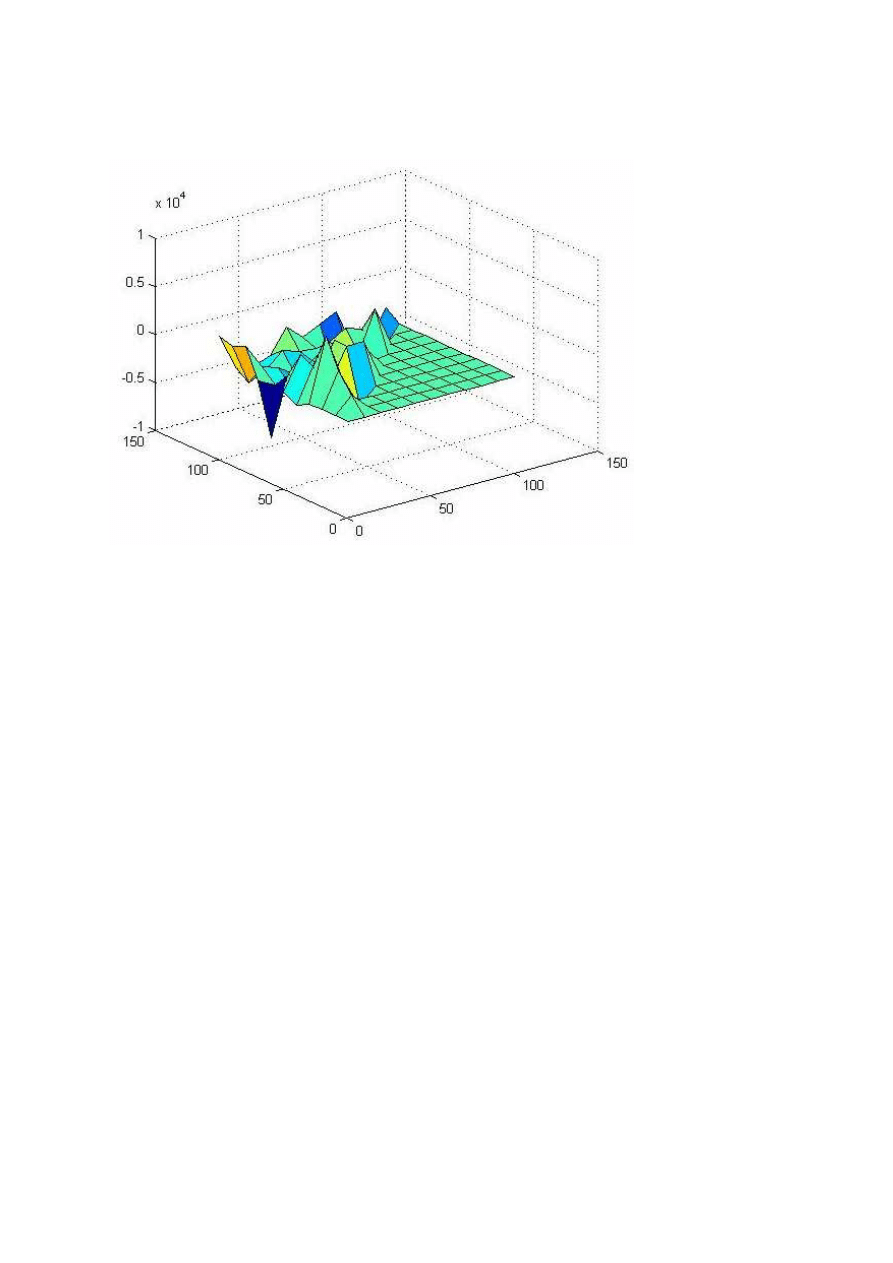
13 

 
 

•

 

czwartym i siódmym 

 

 

5. Podsumowanie i wnioski. 

Celem projektu było zbadanie działania wielowarstwowej, sztucznej sieci neuronowej. Do tego celu została 
wykorzystana funkcja  learnbp z pakietu MatLab która realizuje algorytm uczenia ze wsteczną propagacją błędu. 
Zadaniem sieci było przyporządkowywanie zwierząt do jednej z grup na podstawie ich cech. Dane uczące zostały 
pobrane z repozytorium uniwersytetu Kalifornijskiego w Irvine. 
 
Do realizacji projektu dane musiały zostać odpowiednio znormalizowane. Podczas badań zmieniane były 
następujące parametry sieci: Liczba neuronów w pierwszej warstwie, liczba neuronów w drugiej warstwie ( nigdy 
nie przekraczała liczby neuronów w pierwszej ) oraz współczynnik uczenia. Wykonanych zostało 10 
eksperymentów. Pokazały one że dla tych samych parametrów szybkość uczenia może się nieznacznie różnić a 
więc wyniki nie są powtarzalne.  
Dla współczynnika uczenia lr = 0.001 sieć uczyła się najszybciej ( najmniejsza potrzebna liczba epok to około 
1180 ) przy odpowiednio dobranej liczbie neuronów, ale nie uczyła się wcale gdy ich liczba była źle dobrana. 
Natomiast dla współczynnika lr = 0.0001 uczyła się zawsze. A więc jeśli jest on mniejszy mamy gwarancję że 
sieć będzie się uczyć ale proces ten będzie potrzebował więcej epok aby osiągnąć minimalny błąd.  
 
Współcześnie sztuczne sieci neuronowe znajdują coraz więcej zastosowań. Problem rozpoznawania zwierząt to 
tylko mała część ich możliwości. Wykorzystywane są również do rozpoznawania obrazów, mowy, diagnostyki 
medycznej czy teorii sterowania. Swoją rosnącą popularność sieci neuronowe zawdzięczają min. zdolności do 
uczenia się i uogólniania nabytej wiedzy oraz równoległemu przetwarzaniu informacji.    
 

6. Bibliografia 

1. 

http://ssn.elektrotechnika.ip.pwsz.edu.pl/nnt/nnt1.php 

2. 

http://pbryzi.fm.interia.pl/W/SN.htm 

3. 

http://www.neuron.kylos.pl/pliki/jednokier/jednokier4.html 

4.  

http://galaxy.agh.edu.pl/~vlsi/AI/backp_t/backprop.html