Laboratorium Modelowania Biosystemów Modele stochastyczne

Prowadzący: dr inż. Zbigniew Starosolski

1. WPROWADZENIE
1) Model w wykładniczym czasem podziału

W tym modelu przyjmujemy, w odróżnieniu od deterministycznego modelu wzrostu malthusiańskiego, iż
czas podziału nie jest stały, lecz fluktuuje wokół pewnej wartości średniej. W związku z tym do opisu modelu
niezbędne jest określenie rozkładu czasów podziału. Jedną z możliwości jest np. rozkład wykładniczy, którego
funkcja gęstości opisana jest wzorem :

f(t) = λe

-λt

dla t≥0 przy czym λ = 1/T

c

gdzie T

c

jest średnią wartością czasu podziału

Zmianę liczebności populacji możemy opisać jako różnicę strumieni dopływającego (+) oraz odpływającego (-) :

dN = ( X

+

- X

-

)dt

przy czym

X

-

= aN (gdzie a = λ)

oraz przyjmujemy podział na 2 komórki potomne:

X+ = 2X

otrzymujemy więc :

dN/dt = aN

gdzie N jest średnią liczebnością populacji


2) Modele kompartmentalne – stochastyczne


Mamy układ składający się z k równań różniczkowych zapisanych w postaci:

k

i

t

N

t

N

N

i

i

i

i

i





1

),

(

)

(

1

1















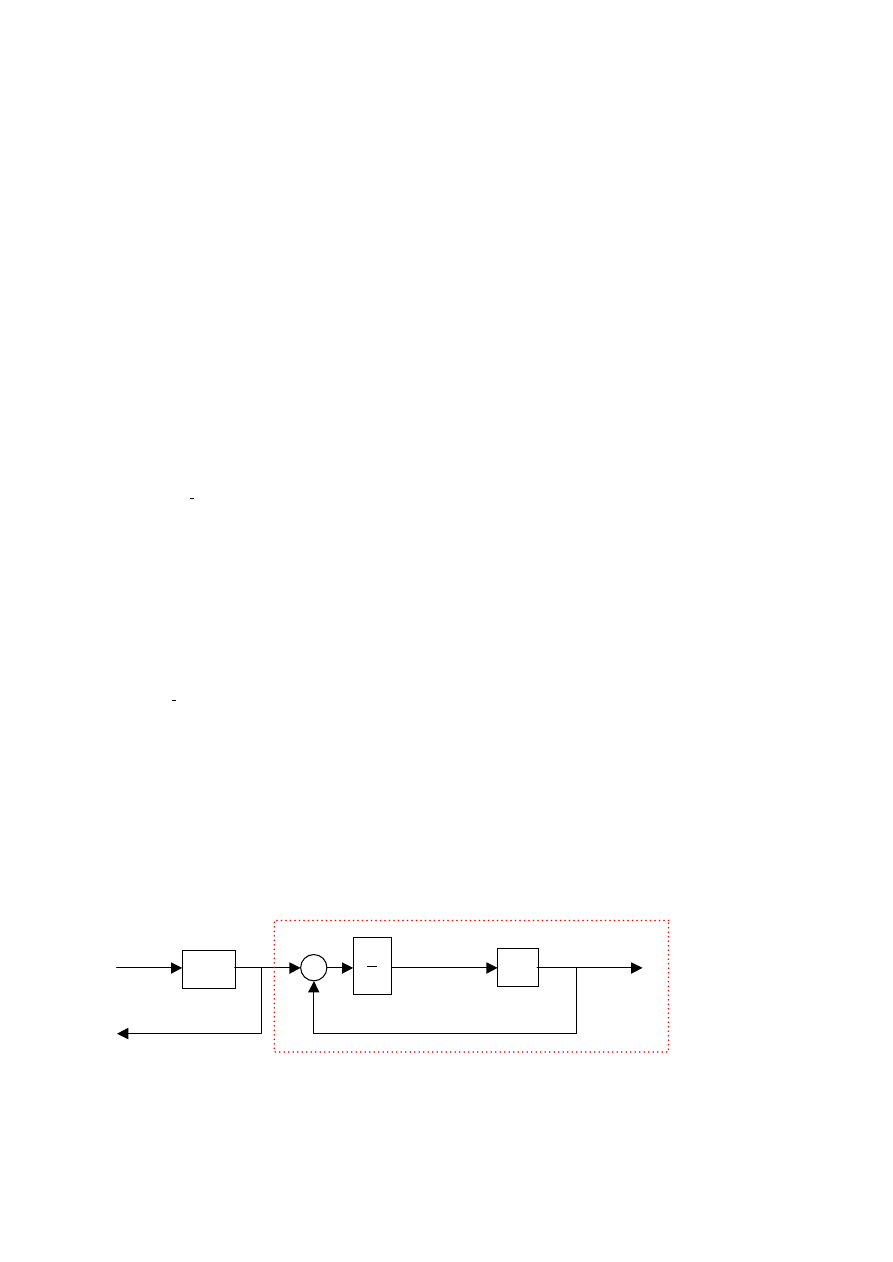
każde i-te równanie możemy zamodelować wykorzystując rachunek operatorowy jako:

1



i



i



s

1



i

X



i

X

i

N

i

N

1



i

N

+

-

po przekształceniu (części schematu zaznaczoną czerwoną linią punktową) możemy uprościć do bloku postaci

(inercja I rzędu, o stałej czasowej

i

i





1



)

Układ równań różniczkowych wraz z równaniem granicznym wiążącym populacje można zapisać następująco jako:

























k

i

t

N

t

N

N

t

N

t

N

N

i

i

i

i

i

k

k







2

),

(

)

(

)

(

)

(

2

1

1

1

1

1









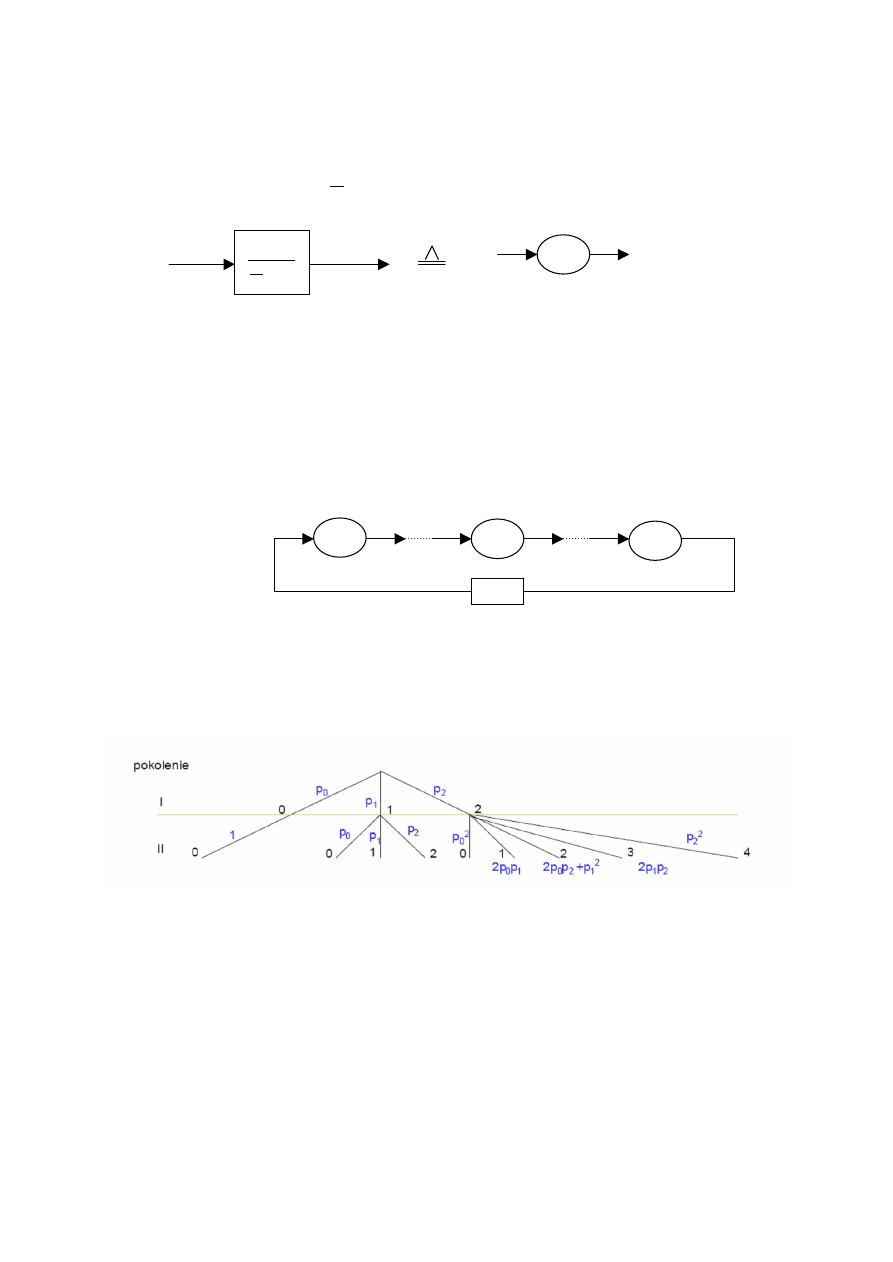
co można zapisać za pomocą schematu, którego analizowanie opiera się na obserwacji przepływów i stanów
kompartmentów:










3) Proces gałązkowy
Model ten jest przydatny do badania populacji komórek, w sytuacji, gdy komórka ma różną ilość potomków lub gdy
podział nie oznacza śmierci komórki macierzystej. Załóżmy, iż komórka może mieć 0, 1 lub 2 potomków, jako p0,
p1 i p2 oznaczmy prawdopodobieństwa tych zdarzeń (p

0

+p

1

+p

2

=1). Poniższy rysunek prezentuje tzw. „drzewo”

procesu dla dwóch pokoleń:










zatem w prosty sposób można zapisać prawdopodobieństwa ilości osobników w danej generacji p(X

k

):

X

k

– liczba osobników k-tej generacji

p(X0=1)= 1
p(X1=0)= p

0

p(X1=1)= p

1

p(X1=2)= p

2

p(X2=0)= p

0

+ p

0

p

1

+ p

2

p

02

p(X2=1)= p

0

+ 2p

2

p

0

p

1

p(X2=2)= p

1

p

2

+ p

2

(2p

0

p

2

+ p

12

)

p(X2=3)= 2p

22

p

1

p(X2=4)= p

23

Jeśli potraktujemy X

k

jako zmienną losową możemy wyznaczyć jej wartość oczekiwaną ( E(X

1

)=µ ).

1

1

1



s

i





i

X



i

X

i



i

X



i

X

1

i

k

2



i

X



i

X

2. PROGRAM ĆWICZENIA
Zadanie 1:
Dla modelu z wykładniczym czasem podziału, mając daną wielkość początkową populacji N0, określić średnią
wielkość populacji po zadanym czasie. Czasy podziału wygenerować generatorem o rozkładzie wykładniczym.

Zadanie 2:

Dla populacji komórkowej k=10 zbadaj zależność zachowania się modelu kompartmentalnego od przebiegu funkcji
czasów podziałów. Dla wybranego przez prowadzącego typu przebiegu funkcji czasów podziału dla k=2 zbadaj
stabilność układu. Wykreśl przykładowe przebiegi.

Zadanie 3:
Stosując proces gałązkowy, mając daną wielkość początkową populacji N0, wyznaczyć wartość oczekiwaną
populacji w zadanym pokoleniu. Wyjaśnić jaki los czeka populacje w zależności od wielkości wartości oczekiwanej
w jednym pokoleniu (µ).

3 PYTANIA SPRAWDZAJĄCE
Podaj definicje i własności : proces stochastyczny, proces deterministyczny, zmienna losowa, bilans masy, rozkład
normalny, rozkład wykładniczy, wartość średnia, funkcja tworząca, funkcja prawdopodobieństwa, gęstość funkcji
prawdopodobieństwa, wartość własna macierzy, wyznacznik macierzy, warunki konieczne i wystarczające
stabilności asymptotycznej układu