1

DECYBELE

W elektronice, a zwłaszcza w telekomunikacji cz

ę

sto wyst

ę

puje potrzeba

porównania ze sob

ą

takich samych wielko

ś

ci fizycznych, których warto

ś

ci

mog

ą

si

ę

ró

ż

ni

ć

od siebie o kilka lub nawet o kilkana

ś

cie rz

ę

dów. Aby unikn

ąć

kłopotliwego operowania liczbami rz

ę

du milionów czy miliardów, wygodne jest

a czasami konieczne u

ż

ycie zamiast ilorazu danej wielko

ś

ci (czyli tzw.

stosunku bezwymiarowego) - jego logarytmu.

Zastosowanie miary logarytmicznej ułatwia równie

ż

graficzn

ą

prezentacj

ę

wielko

ś

ci fizycznych zmieniaj

ą

cych si

ę

w bardzo szerokich granicach.

Miary logarytmiczne stosuje si

ę

najcz

ęś

ciej do okre

ś

lenia stosunku

mocy, napi

ęć

lub pr

ą

dów w dwóch punktach układu, urz

ą

dzenia lub

systemu.

Powszechnie stosowan

ą

jednostk

ą

logarytmicznej miary stosunku

dwóch wielko

ś

ci jest decybel (w skrócie dB), równy 1/10 bela - jednostki

nie stosowanej w praktyce.

Decybele nie tylko umo

ż

liwiaj

ą

skrócony zapis bardzo du

ż

ych lub bardzo

małych liczb, ale te

ż

upraszczaj

ą

procedur

ę

obliczeniow

ą

, gdy

ż

zast

ę

puj

ą

mno

ż

enie i dzielenie liczb wielocyfrowych dodawaniem lub odejmowaniem ich

decybelowych równowa

ż

ników.

2

Stosunek A (w dB) dwóch mocy P

1

i P

2

w mierze logarytmicznej jest równy:

1

2

)

(

log

10

P

P

K

dB

P

=

(1)

gdzie:

P

1

- warto

ść

mocy na wej

ś

ciu układu (tzw. mocy odniesienia),

P

2

- warto

ść

mocy na jego wyj

ś

ciu,

przy czym obie wielko

ś

ci s

ą

wyra

ż

one w watach (W) lub woltamperach (VA).

Je

ś

li: P

2

> P

1

, to nast

ę

puje wzmocnienie mocy sygnału w układzie,

je

ś

li P

2

< P

1

to układ tłumi sygnał.

Przy P

1

= P

2

warto

ść

A jest równa 0 dB.

Zale

ż

no

ść

(1) jest cz

ę

sto wykorzystywana do okre

ś

lenia stosunku

sygnału (jest nim zwykle sygnał sinusoidalny) do szumu. W takim przypadku

jest konieczne podanie szeroko

ś

ci pasma cz

ę

stotliwo

ś

ci, przy jakim okre

ś

la

si

ę

ten stosunek. Dlatego przy okre

ś

laniu stosunku sygnału do szumu s

ą

stosowane ró

ż

nego rodzaju filtry cz

ę

stotliwo

ś

ciowe, których charakterystyki s

ą

oznaczane literami A, B lub C. Na przykład w technice audio s

ą

stosowane

filtry typu A o charakterystyce zbli

ż

onej do charakterystyki cz

ę

stotliwo

ś

ciowej

ucha ludzkiego.

3

Miary logarytmiczne stosuje si

ę

równie

ż

do wyra

ż

ania stosunków napi

ęć

lub pr

ą

dów. Porównywane moce mo

ż

na wyrazi

ć

jako iloczyny odpowiednich

napi

ęć

(U

1

, U

2

) i pr

ą

dów (I

1

, I

2

). Je

ś

li te napi

ę

cia lub pr

ą

dy maj

ą

taki sam

kształt, np. s

ą

przebiegami sinusoidalnymi, to zale

ż

no

ść

(1) przyjmuje posta

ć

:

1

1

2

2

)

(

log

10

I

U

I

U

K

dB

P

=

(2)

Poniewa

ż

moc w układzie wydziela si

ę

na okre

ś

lonej impedancji (Z

1

, Z

2

), tzn.:

P

U

I

U

Z

P

U

I

U

Z

oraz

x

x

1

1

1

1

2

2

2

2

2

2

2

2

=

⋅ =

=

⋅ =

=

,

log

log

wi

ę

c zale

ż

no

ść

(2) w przypadku, gdy moduły tych impedancji s

ą

sobie równe,

mo

ż

e by

ć

przedstawiona w postaci stosunku napi

ęć

lub pr

ą

dów:

)

4

(

log

20

)

3

(

log

20

1

2

)

(

1

2

)

(

I

I

K

U

U

K

dB

I

dB

U

=

=

4

Nale

ż

y przy tym podkre

ś

li

ć

,

ż

e dopóki obydwa sygnały maj

ą

taki sam

kształt przebiegu (sinusoidalny), dopóty równania (1) oraz (3) i (4) daj

ą

taki

sam wynik. Je

ś

li odnoszone wzgl

ę

dem siebie sygnały ró

ż

ni

ą

si

ę

kształtem, to

wtedy albo trzeba zastosowa

ć

równanie (1), albo te

ż

mo

ż

na zastosowa

ć

równania (3) i (4), zast

ę

puj

ą

c amplitudy napi

ęć

lub pr

ą

dów warto

ś

ciami

skutecznymi.

W przypadku gdy stosunek porównywanych wielko

ś

ci w mierze liniowej

jest mniejszy od jedno

ś

ci, to wówczas wyra

ż

ony w mierze logarytmicznej jest

ujemny. Na przykład, gdy U

2

/U

1

= 0,5, to A = - 6 dB.

W tablicy 1 (zał

ą

cznik) zebrano kilka typowych warto

ś

ci stosunków mocy

P

2

/P

1

, stosunków napi

ęć

wyra

ż

onych stosunkiem amplitud U

2

/U

1

, oraz ich

ekwiwalenty decybelowe.

Chocia

ż

decybeli u

ż

ywa si

ę

zazwyczaj do okre

ś

lania stosunku poziomów

mocy lub amplitud sygnałów, czasami stosuje si

ę

je jako miary bezwzgl

ę

dne

tych wielko

ś

ci. W takich przypadkach zakłada si

ę

,

ż

e wielko

ś

ci P

1

,U

1

lub I

1

reprezentuj

ą

pewne warto

ś

ci odniesienia i wtedy stosuje si

ę

dodatkowe

wyznaczniki literowe oznaczaj

ą

ce przyj

ę

cie tych warto

ś

ci.

I tak:

dBW - oznacza stosunek mocy odniesiony do 1 W (0 dBW = 1 W, 10 dBW =

10 W, 20 dBW = 100 W);

dBm - oznacza stosunek mocy odniesiony do 1 mW (0 dBm = 1 mW), co

odpowiada warto

ś

ci skutecznej napi

ę

cia odniesienia ok. 0,775 V lub pr

ą

du

5

odniesienia ok. 1,29 mA przy typowej impedancji 600

Ω

(30 dBm = 1 W,

50dBm = l00W). Dla impedancji równej 50

Ω

warto

ść

skuteczna napi

ę

cia

odniesienia wynosi ok. 0,224 mV;

dBU - oznacza stosunek napi

ęć

odniesiony do 1 V (0 dBV = 1 V,10 dBV = 20

V);

dBu - oznacza stosunek napi

ęć

odniesiony do ok. 0,775 V;

dBmU - oznacza stosunek napi

ęć

odniesiony do 1 mV;

dB

µµµµ

U - oznacza stosunek napi

ęć

odniesiony do 1

µ

V;

dBl - oznacza stosunek pr

ą

dów odniesiony do 1 A;

dBf - oznacza stosunek mocy sygnału odniesiony do mocy sygnału

odniesienia równej 1 fW (0 dBf = 1 fW = 10

-15

W). W jednostkach dBf okre

ś

la

si

ę

czuło

ść

odbiorników radiofonicznych, zwłaszcza na zakresie UKF. Np. je

ś

li

w warunkach dopasowania w antenie o impedancji 300

Ω

indukuje si

ę

SEM =

1,1

µ

V, to sygnał przekazywany do odbiornika wynosi

P

U

Z

W

fW

=











=

⋅

⋅

=

⋅

≈

−

−

2

1 1 10

300 4

1 008 10

1

2

6

2

15

( ,

)

.

czyli 0 dBf.

6

Oprócz bezwzgl

ę

dnych poziomów odniesienia stosuje si

ę

poziomy

wzgl

ę

dne i na ogół dotycz

ą

one poziomów mocy.

Na przykład je

ś

li wzgl

ę

dny poziom mocy jest równy -36 dBr, to oznacza,

ż

e

poziom mocy w tym punkcie jest o 36 dB mniejszy od poziomu w punkcie

odniesienia, tzn. w punkcie, w którym poziom wzgl

ę

dny jest równy 0 dBr

(indeks r oznacza "relative", czyli wzgl

ę

dny).

Inny przykład: dBrnC oznacza poziom sygnału wzgl

ę

dem szumowego

sygnału odniesienia wa

ż

onego cz

ę

stotliwo

ś

ciowo według charakterystyki typu

C (indeks n oznacza "noise", czyli szum).

Przykłady obliczeniowe

Przykład 1. Je

ż

eli na wej

ś

cie wzmacniacza napi

ę

ciowego o wzmocnieniu

bezwzgl

ę

dnym równym:

K

U

100

V

V

=

podamy sygnał sinusoidalny o

amplitudzie 1mV, to na wyj

ś

ciu tego wzmacniacza uzyskamy napi

ę

cie i

amplitudzie 100mV. Aby poda

ć

ten stosunek napi

ęć

w decybelach, musimy

skorzysta

ć

z wzoru (3):

.

że

wiemy,

Ponieważ

40

2

20

20log100

a

100,

2

10

bo

2,

log100

zatem

a,

10

log

oznacza

a

log

symbol

a

b,

c

a

log

c,

b

a

20log100

1

100

20log

1

U

2

U

20log

K[dB]

=

⋅

=

=

=

=

=

=

=

=

to

7

A wi

ę

c wzmocnienie wzgl

ę

dne w decybelach b

ę

dzie wynosi

ć

:

K

U

[dB] = 20log100 = 40dB.

Przykład 2.

Z kolei je

ż

eli mamy informacj

ę

,

ż

e wzmocnienie wzgl

ę

dne

wzmacniacza mocy przy sygnale wej

ś

ciowym 1mW wynosi 30dB, to oznacza,

ż

e:

1W

1000P

P

że

oznacza

co

,

10

P

P

zatem

,

3

P

P

log

:

mamy

i

10

przez

Skracamy

.

30dB

P

P

10log

K

1

2

3

1

2

1

2

1

2

P

=

=

=

=

=

=

Zatem moc wyj

ś

ciowa wynosi 1W.

Przykład 3.

Je

ż

eli mamy urz

ą

dzenie, które tłumi sygnał, czyli napi

ę

cie

wyj

ś

ciowe b

ę

dzie mniejsze od wej

ś

ciowego, np.:

dB

20

)

1

(

20

log0,1

20

K

zatem

0,1

10

gdy ż

,

1

log0,1

:

Dalej

20log0,1

K

to

,

V

V

0,1

U

U

U(dB)

1

-

U(dB)

1

2

−

=

−

•

=

•

=

=

−

=

=

=

Jak widzimy, dla wzmocnienia <1 (tłumienie) warto

ść

wzmocnienia

wzgl

ę

dnego wyra

ż

onego w decybelach b

ę

dzie ujemna.

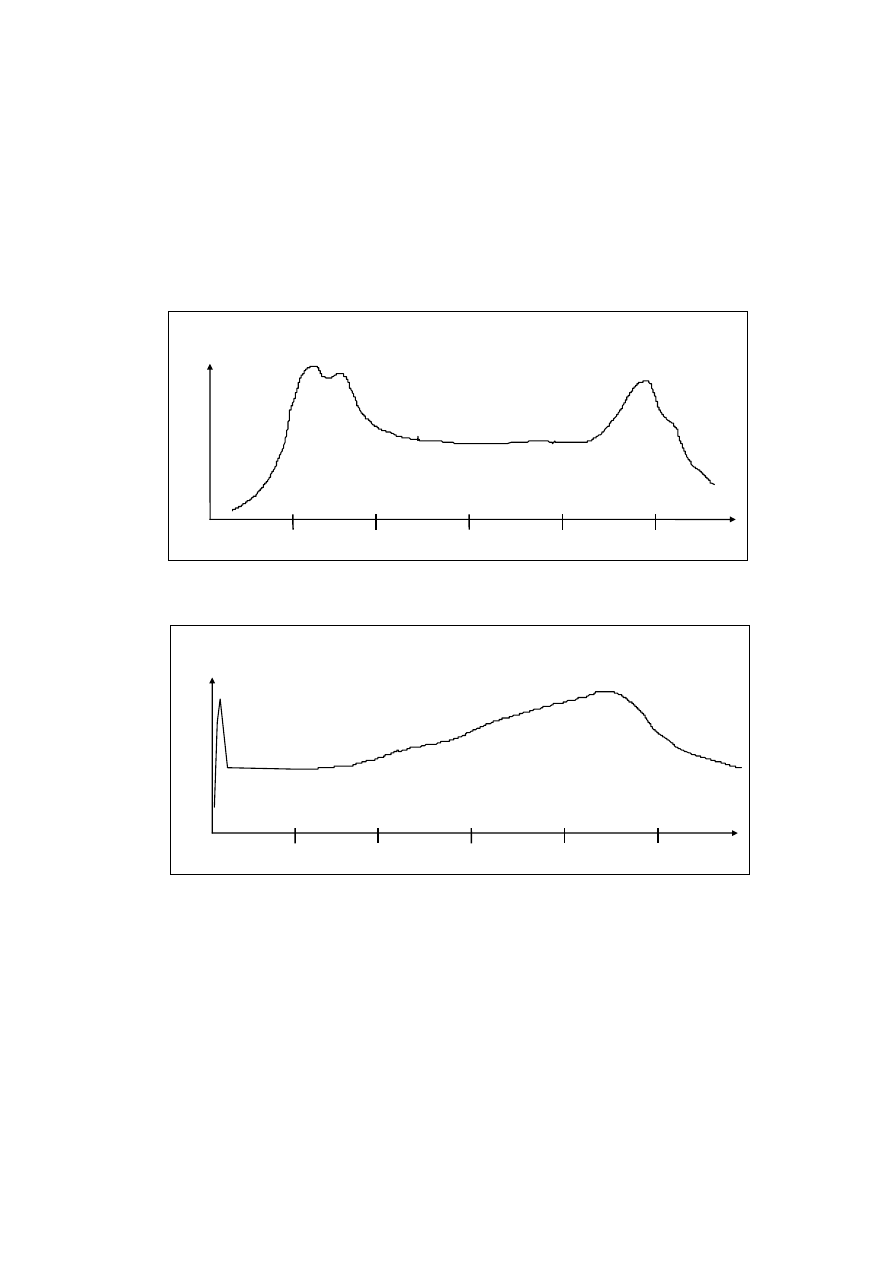
Przy graficznym przedstawianiu niektórych funkcji miara logarytmiczna nie

tylko ułatwia, ale w niektórych przypadkach jest jedyn

ą

mo

ż

liwo

ś

ci

ą

obejrzenia

wykresu w rozs

ą

dnym wymiarze rysunku. Na przykład we

ź

my przebieg

charakterystyki cz

ę

stotliwo

ś

ciowej jakiego

ś

wzmacniacza. Na wykresie ze

skal

ą

logarytmiczn

ą

b

ę

dzie on wygl

ą

dał tak:

8

0 10 100 1000 10000 100000 Hz

K

U

K

U

0 20.000 40.000 60.000 80.000 100.000 Hz

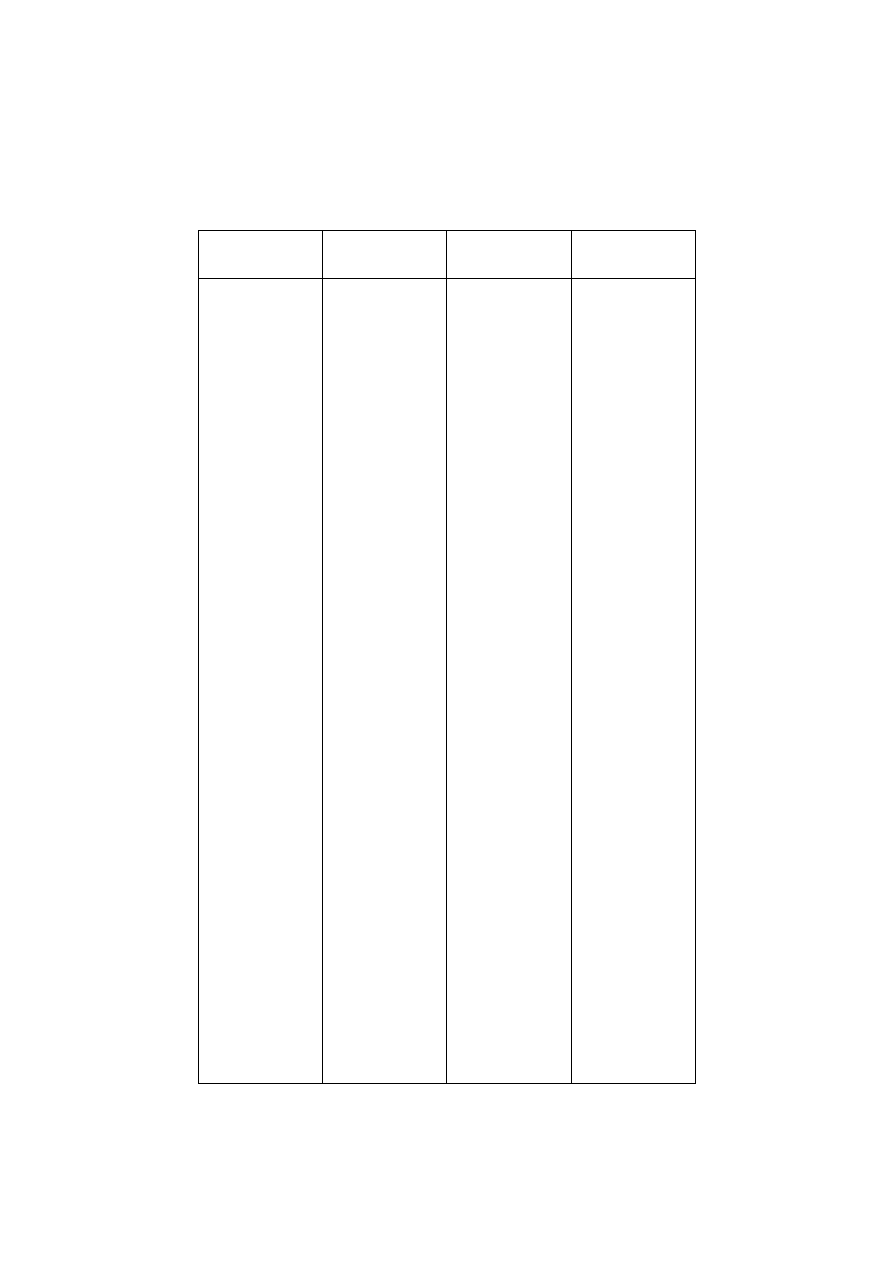
9

Stosunek napi

ęć

i mocy podany w decybelach

dla napi

ęć

= 20log(U2/U1), dla mocy = 10log(P2/P1)

U2/U1

U2/U1 w dB

P2/P1

P2/P1 w dB

0,000001
0,00001
0,0001
0,001
0,01
0,05
0,1
0,2
0,3
0,5
0,8
0,9
1
1,5
2
3
4
6
8
10
16
20
30
40
50
60
70
80
90
100
1000
10000
100000
1000000

-120
-100
-80
-60
-40
-26
-20
-14
-10
-6
-2
-1
0
4
6
10
12
16
18
20
24
26
30
32
34
36
37
38
39
40
60
80
100
120

0,000001
0,00001
0,0001
0,001
0,01
0,05
0,1
0,2
0,3
0,5
0,8
0,9
1
1,5
2
3
4
6
8
10
16
20
30
40
50
60
70
80
90
100
1000
10000
100000
1000000

-60
-50
-40
-30
-20
-13
-10
-7
-5
-3
-1
0
0
2
3
5
6
8
9
10
12
13
15
16
17
18
18
19
20
20
30
40
50
60