Prace Naukowe Instytutu Maszyn i Napędów Elektrycznych

Nr 44 Politechniki Wrocławskiej Nr 44

————————————————————————————————————————————

Studia i Materiały Nr 19 1996

__________________

*Instytut Maszyn i Napędów Elektrycznych Politechniki Wrocławskiej, Wybrzeże Wyspiańskiego 27, 50–370 Wrocław

elektrotechnika, maszyny elektryczne,

synchroniczne, uzwojenie, reaktancja

Ludwik ANTAL*

PARAMETRY BEZŻŁOBKOWEGO UZWOJENIA TWORNIKA

MASZYNY SYNCHRONICZNEJ

Przedstawiono wyniki pomiarów i obliczeń parametrów indukcyjnych maszyny synchronicznej bez żelaza
o bezżłobkowym uzwojeniu twornika i ekranowanym wirniku. Pomiary wykonano na modelu maszyny
o średnicy wewnętrznej uzwojenia twornika 0,304 m i długości 0,757 m, z ekranem miedzianym o długości
1,008 m. Wyniki pomiarów porównano z wynikami obliczeń.

1. WSTĘP

Poprawne zaprojektowanie maszyny elektrycznej wymaga umiejętności obliczenia jej

parametrów indukcyjnych. Parametry te decydują o mocy maszyny, jej stabilności,
obciążeniach statycznych i dynamicznych itp. W maszynie bezżłobkowej,
charakteryzującej się brakiem elementów stalowych lub posiadającej jedynie zewnętrzny
ekran magnetyczny, obliczenie parametrów wydaje się być łatwiejsze niż w maszynach o
budowie klasycznej. Uwzględniając jednak powód rozpatrywania takich konstrukcji, tzn.
znaczne zwiększenie obciążeń elektromagnetycznych uzwojeń (okładu prądowego i
indukcji), można zauważyć, że konsekwencje niedokładnych obliczeń mogą być poważne.
Znane są z literatury technicznej przypadki budowy modeli maszyn, które nie mogły być
obciążone ze względu na zbyt elastyczne mocowania uzwojenia twornika lub nie mogły być
synchronizowane z powodu swej niestabilności.

Dwuwymiarowe rozwiązanie pola magnetycznego maszyny bezżłobkowej (przy

założeniu nieskończonej długości maszyny), a na tej podstawie indukcyjności uzwojeń, nie
stanowi większego problemu. Rozwiązania takie z różnym stopniem uproszczeń można
znaleźć w wielu publikacjach. Rozwiązania trójwymiarowe dotyczą konkretnych rozwiązań
konstrukcyjnych, a ich wyniki nie mogą być użyte bezpośrednio do określenia
podstawowych wymiarów maszyny i relacji wymiarowych jej elementów. W tej sytuacji

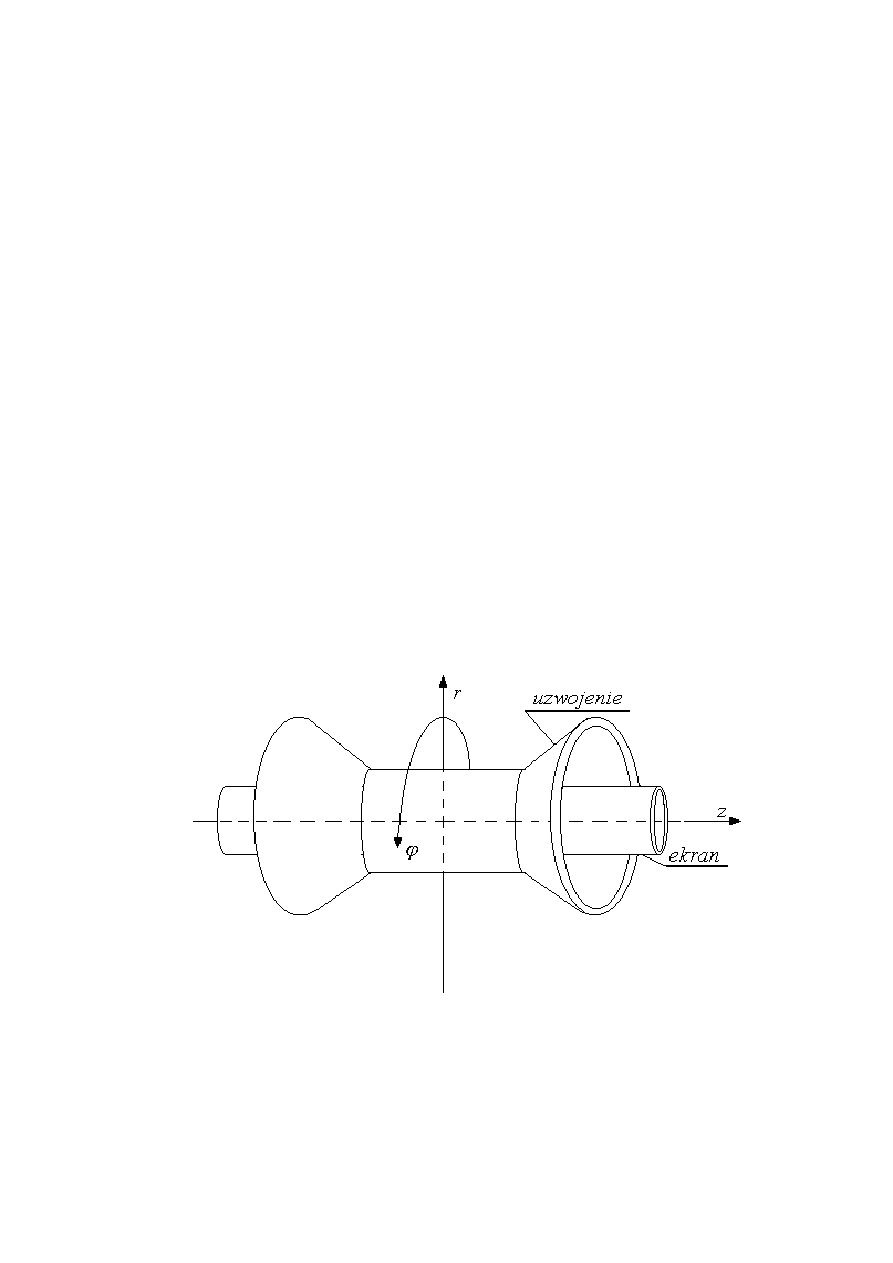
4

korzystne byłoby uzupełnienie rozwiązań dwuwymiarowych odpowiednimi współ-
czynnikami empirycznymi, prowadzącymi do równoważności rozwiązań dwuwymiarowych
z trójwymiarowymi. Taki współczynnik korygujący, uwzględniający wpływ strefy połączeń
czołowych uzwojeń i krańców ekranów elektromagnetycznych, może być użyty do
określenia długości obliczeniowej maszyny. Długość ta powinna mieć różne wartości
podczas obliczania reaktancji synchronicznej i reaktancji przejściowych. W niniejszej pracy
podjęto próbę określenia na podstawie pomiarów takich długości obliczeniowych dla
wyznaczenia reaktancji synchronicznej i podprzejściowej maszyny bezżłobkowej bez
żelaza.

2. OPIS MODELU I BADAŃ

Zasadniczym elementem badanego modelu maszyny jest uzwojenie bezżłobkowe,

trójfazowe, dwuwarstwowe o średnicy wewnętrznej 0,304 m i długości 0,757 m, służące do
wytwarzania pól wirujących o różnej prędkości kątowej [1]. Pręty tego dwuwarstwowego
uzwojenia wykonane są z linki miedzianej składającej się z 72 skręconych drutów o
średnicy 0,82 mm. Taka konstrukcja prętów gwarantuje małe straty wiroprądowe w
uzwojeniu, w szerokim przedziale zmian częstotliwości, a więc praktycznie stałe straty
mocy w uzwojeniu, dla stałej wartości prądu i stałej temperatury. Uzwojenie zasilane jest z
elektromaszynowego układu przetwarzania częstotliwości [2], umożliwiającego płynną
regulację napięcia i regulację częstotliwości w przedziale 10–120 Hz, przy prądzie do
250 A.

Rys. 1. Schemat stanowiska pomiarowego.

Fig. 1. Scheme of measuring stand

Do wnętrza uzwojenia wprowadza się ekran elektromagnetyczny. Konstrukcja nośna

uzwojenia oraz konstrukcja mocująca ekran wykonane są z materiałów izolacyjnych

5

(tekstolit, włókno szklane) i nie zawierają elementów metalicznych. Badany model
schematycznie przedstawiono na rysunku 1. Stanowisko wyposażone jest w aparaturę
pomiarową umożliwiającą pomiar mocy, częstotliwości, prądów i napięć oraz rejestrację
pola magnetycznego i temperatury.

Reaktancje i rezystancje uzwojenia twornika wyznaczono z pomiarów mocy, prądu

i napięcia przy stałym prądzie i temperaturze dla różnych częstotliwości napięcia
zasilającego uzwojenie.

Dane geometryczne uzwojenia i ekranu zestawiono w tabeli 1.

Tabela 1

Wymiary uzwojenia bezżłobkowego

Wymiar Oznaczenie Jednostka. Wartość

Długość całkowita

l

c

mm 757,00

Długość części prostoliniowej

l

p

mm 308,00

Długość połączeń czołowych

l

cz

mm 224,50

Długość ekranu

l

e

mm 1008,00

Średnica dolna Cu

D

i

mm 313,40

Średnica górna warstwy dolnej

D

ig

mm 330,80

Średnica średnia Cu

D

sr

mm 333,80

Średnica dolna warstwy górnej

D

od

mm 335,60

Średnica górna Cu

D

o

mm 353,00

Średnica zewnętrzna ekranu

D

s

mm 296,00

Grubość ekranu

h

e

mm 8,00

Wysokość pręta w izolacji

h

iz

mm 9,00

Wysokość pręta

h

p

mm 8,40

Szerokość pręta w izolacji

b

iz

mm 8,40

Szerokość pręta

b

p

mm 7,40

Izolacja międzywarstwowa

h

w

mm 2,40

Powierzchnia Cu

S

cu

mm 18213,95

Powierzchnia pręta

S

pr

mm 75,60

Powierzchnia czynna pręta z linki

S

prcz

mm 38,02

Liczba prętów 2Ż

- 144

Liczba quasi żłobków

Ż

- 66

Liczba szeregowych zwojów

w

a

- 22

Poskok

y

- 27

Skrót

b

- 0,818

3. WYNIKI POMIARÓW I OBLICZEŃ

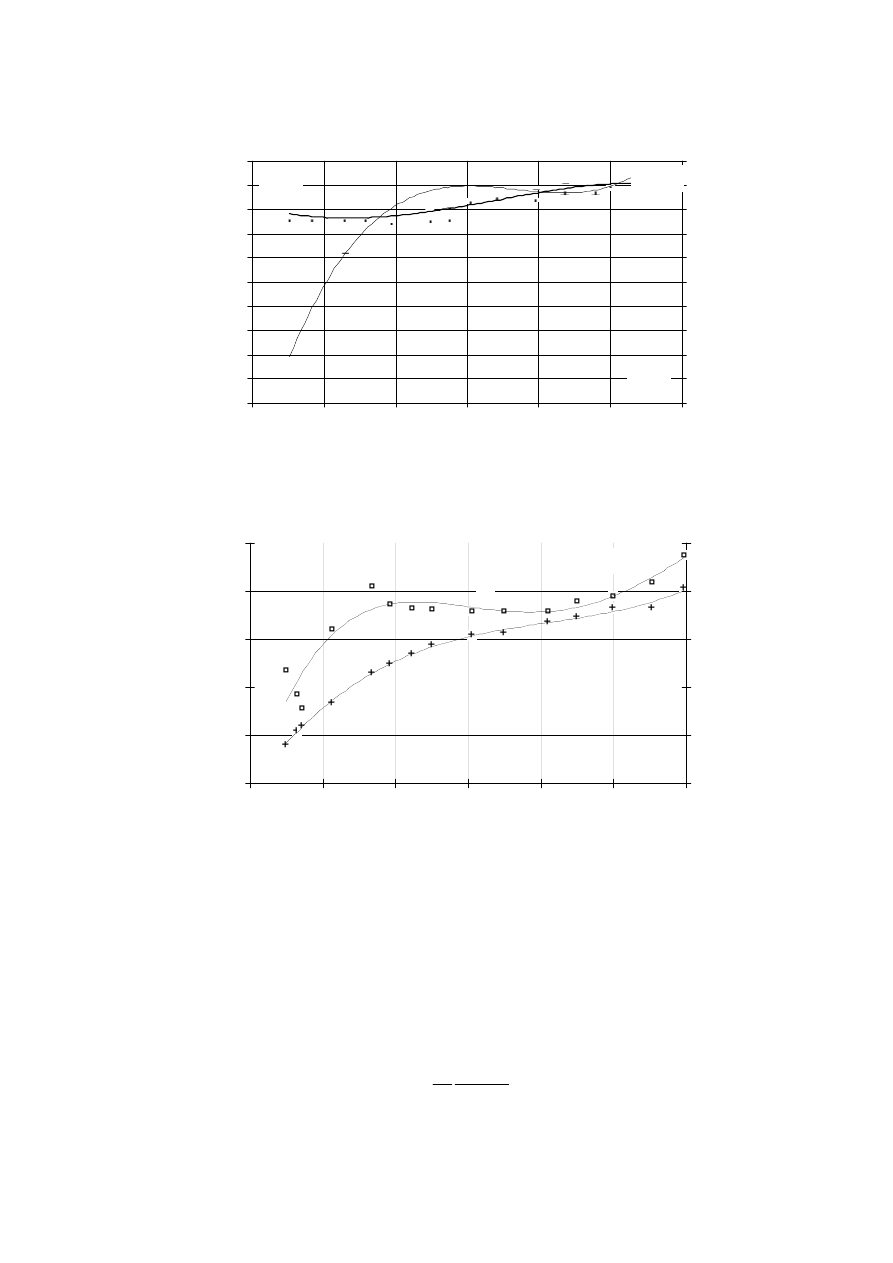
Na rysunkach 2 i 3 przedstawiono obliczone z wyników pomiarów wartości rezystancji

i indukcyjności na zaciskach uzwojenia twornika dla modelu bez ekranu i z długim ekranem
miedzianym jako funkcje częstotliwości napięcia zasilającego.

6

0.017

0.018

0.019

0.020

0.021

0.022

0.023

0.024

0.025

0.026

0.027

0.0

20.0

40.0

60.0

80.0

100.0

120.0

0.22

0.23

0.24

0.25

0.26

0.27

0.28

0.29

0.30

0.31

0.32

R

L

f [Hz]

R [Ω]

L [mH]

Rys. 2. Parametry uzwojenia bezżłobkowego

Fig. 2. Parameters of a slotless winding

0.025

0.027

0.029

0.031

0.033

0.035

0

20

40

60

80

100

120

0.10

0.11

0.12

0.13

0.14

0.15

R

L

f [Hz]

R

[Ω]

L [mH]

Rys. 3. Parametry uzwojenia bezżłobkowego z długim ekranem miedzianym h = 8 mm

Fig. 3. Parameters of a slotless winding with long copper shield h = 8 mm

Obliczenia reaktancji ograniczono do pierwszej harmonicznej ze względu na znikomo

małe wartości wyższych harmonicznych w rozkładzie przestrzennym pola badanego
uzwojenia [1]. Reaktancję synchroniczną dla pierwszej harmonicznej X

d1

obliczono z

zależności (1) uwzględniającej wymiary poprzecznego przekroju uzwojenia [5]:

X

w l

d

a

1

0

2

1

=

ωµ

λ

o a

,

(1)

przy czym

λ

π

α

α

a

a

a

a

k C

1

2

2

1

2

1

12

=

sin

,

(2)

7

a

C

r

r

r

a

a

1

4

3

2 2

1 3

4

6 1

=

+

−

−

(

)

a

o a

"

.

(3)

Reaktancję podprzejściową X

d

”

obliczono ze wzoru (4):

X

w l

d

a

"

=

ωµ

λ

0

2

1

, (4)

w którym

λ

λ

π

a

a

si

a

r

r

1

1

3

2

2

108

1

"

(

)

=

−

+

. (5)

W podanych wzorach:

ω

– prędkość kątowa,

µ

0

– przenikalność magnetyczna powietrza,

r

a

=D

i

/D

o

– stosunek skrajnych średnic miedzi uzwojenia,

r

si

=(D

s

–2h

e

)/D

o

– stosunek wewnętrznej średnicy ekranu do zewnętrznej

średnicy uzwojenia,

k

a1

– współczynnik uzwojenia dla pierwszej harmonicznej,

α

a

– kątowa rozpiętość pręta uzwojenia,

l

o

= 1,2(l

p

+l

cz

) – obliczeniowa długość maszyny,

λ

– względna przewodność magnetyczna.

W celu oceny wpływu stopnia uproszczeń rozwiązań dwuwymiarowych na rezultaty

obliczono również reaktancje z zależności maksymalnie uproszczonych uwzględniających
jedynie rozkład prętów uzwojenia i średnie wymiary uzwojenia i ekranu. Dla maszyny
trójfazowej, dwubiegunowej reaktancje synchroniczną i podprzejściową na jednostkę
długości wg [6] opisują zależności:

X

w k

d

a a

=

⎛
⎝⎜

⎞
⎠⎟

3

0

2

ωµ π

π

,

(7)

X

w k

R

R

d

a a

s

a

"

=

⎛
⎝⎜

⎞
⎠⎟

−

⎛
⎝

⎜

⎞
⎠

⎟

⎡

⎣

⎢

⎢

⎤

⎦

⎥

⎥

3

1

0

2

2

ωµ π

π

,

(8)

gdzie: R

a

– średni promień uzwojenia twornika,

R

s

– średni promień ekranu wirnika.

Wyniki pomiarów i obliczeń zestawiono w tabeli 2. W obu metodach obliczeń użyto

długości obliczeniowej l

o

stanowiącej 1,2 średniej długości uzwojenia twornika (długość

części prostoliniowej uzwojenia i jednego połączenia czołowego) zarówno podczas
obliczania reaktancji synchronicznej, jak i podprzejściowej. Uzasadnieniem dla tak
określonej długości obliczeniowej jest rozkład pola magnetycznego wzdłuż osi podłużnej
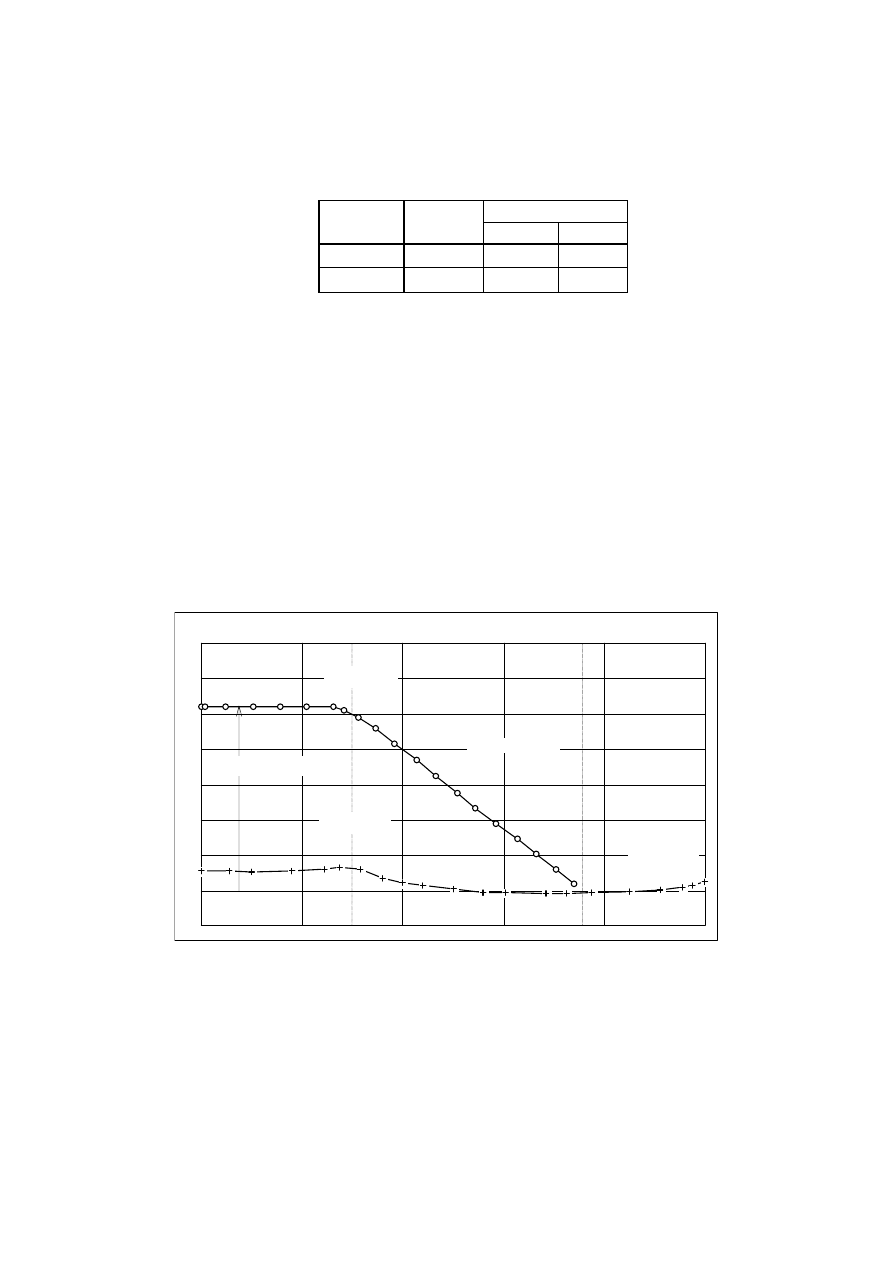
uzwojenia (rys.4). Niemal liniowa zależność składowej promieniowej indukcji od długości
połączeń czołowych pozwala zastąpić rzeczywisty rozkład indukcji prostokątem o bokach
odpowiednio B

∞

(B

r

w części prostoliniowej maszyny) i l

o

.

8

Tabela 2

Wyniki pomiarów i obliczeń

Reaktancja

Pomiar Obliczenia

wg (1–6) wg (7–8)

X

d

[W]

0,0937

0,0941

0,0979

X

d

"[W] 0,0432 0,0250 0,0250

Nie jest to jednak uzasadnione, jak widać z rysunku 4, w przypadku obliczania reaktancji
podprzejściowej. Dlatego też w tabeli 2 wartości obliczone tej reaktancji są niemal
dwukrotnie mniejsze niż uzyskane z pomiarów. Obliczone wartości reaktancji
synchronicznej są natomiast zbliżone do wartości uzyskanej z pomiarów. Rozkład indukcji
nad ekranem długim (rys.4) wskazuje na istnienie dodatkowego obwodu prądów wirowych
w części końcowej ekranu (dwukrotna zmiana znaku składowej promieniowej indukcji).
Można więc oczekiwać, że wpływ stref końcowych ekranu na wartość reaktancji
podprzejściowej jest istotny. Wynik obliczeń byłby zbliżony do wyniku pomiarów, gdyby
za długość obliczeniową do obliczania reaktancji podprzejściowej przyjąć całkowitą
długość ekranu. Zrównanie się tych dwu wartości w tym konkretnym przypadku następuje,
gdy l

o

=1,1l

e

.

-2

0

2

4

6

8

10

12

14

0

0.1

0.2

0.3

0.4

0.5

B [10

-3

T]

z [m]

B

r

- bez ekranu

Prostoliniowa część uzwojenia

B

r

- z ekranem

Koniec ekranu

Połączenia czołowe

B

∞

Rys. 4. Rozkład składowej promieniowej indukcji wzdłuż osi podłużnej uzwojenia bez ekranu i z długim

ekranem miedzianym

Fig. 4. Distribution of radial component of flux density along z–axis of winding with and without long copper

shield

Formuły obliczeniowe zbudowane na podstawie płaskiego rozkładu pola nie

uwzględniają udziału w sprzężeniu magnetycznym uzwojenia twornika składowej osiowej

9

pola w strefie czołowej. Próbą szacunkowego uwzględnienia tego wpływu jest korygujący
współczynnik liczbowy w l

o

.

4. WNIOSKI

Przedstawione wyniki pomiarów i obliczeń wskazują na możliwość budowy prostych

formuł dla obliczania reaktancji maszyn bezżłobkowych, które będą przydatne do
opracowania algorytmu projektowania takich maszyn. Wpływ składowych promieniowej
i osiowej indukcji w strefie końcowej maszyny może być uwzględniony odpowiednio
dobraną dla poszczególnych reaktancji, długością obliczeniową. Długość obliczeniowa dla
reaktancji synchronicznej maszyny bezżłobkowej, wyznaczona z pomiarów, jest zbliżona
do obliczonej w układzie trójwymiarowym dla cewek siodłowych [6].

LITERATURA

[1] Antal L., Wykonanie i badanie modelu wirnika generatora synchronicznego, Cz. I. Raport IUE PWr. SPR 19/83,

1983.

[2] Antal L., Wykonanie i badanie modelu wirnika generatora synchronicznego, Cz. II. Raport IUE PWr. SPR 19/84,

1984.

[3] Antal L., Rozkład pola magnetycznego nad powierzchnią ekranu elektromagnetycznego, cylindrycznego, Pr. Nauk.

Inst. Układów Elektromaszynowych PWr. nr 43, Studia i Materiały nr 18,1993,

[4] Antal L., Badanie cylindrycznych ekranów elektromagnetycznych, bezżłobkowej maszyny synchronicznej, Pr. Nauk.

Inst. Układów Elektromaszynowych PWr. nr 43, Studia i Materiały nr 18,1993,

[5] Antal L., Parametry indukcyjne bezżłobkowej maszyny synchronicznej, Archiwum Elektrotechniki,1980, XXIX, z.3,
[6] Antal L., Długość obliczeniowa synchronicznej maszyny bezżłobkowej, Archiwum Elektrotechniki, 1980, XXIX,

z.3,

[7] Bumby J.R.., Superconducting rotating electrical machines, Clarendon Press, Oxford, 1983,

PARAMETERS OF A SLOTLESS WINDING OF SYNCHRONOUS MACHINE

ARMATURE

Experimental as well as calculated data of induction parameters of air–cored

synchronous machine with slotless winding armature and shielded rotor have been
presented. Measurement have been done on a machine model with stator internal diameter
of 0.304 m and length 0.757 m. The copper shield of 1.008 m length was used.
Experimental and calculated data were compared.