www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
P
RZYKŁADOWE ZADANIA
MATURALNE
M
ATURA
2010
POZIOM PODSTAWOWY
I
NFORMATOR
CKE
1. Wykorzystanie i tworzenie informacji
Z
ADANIE
1
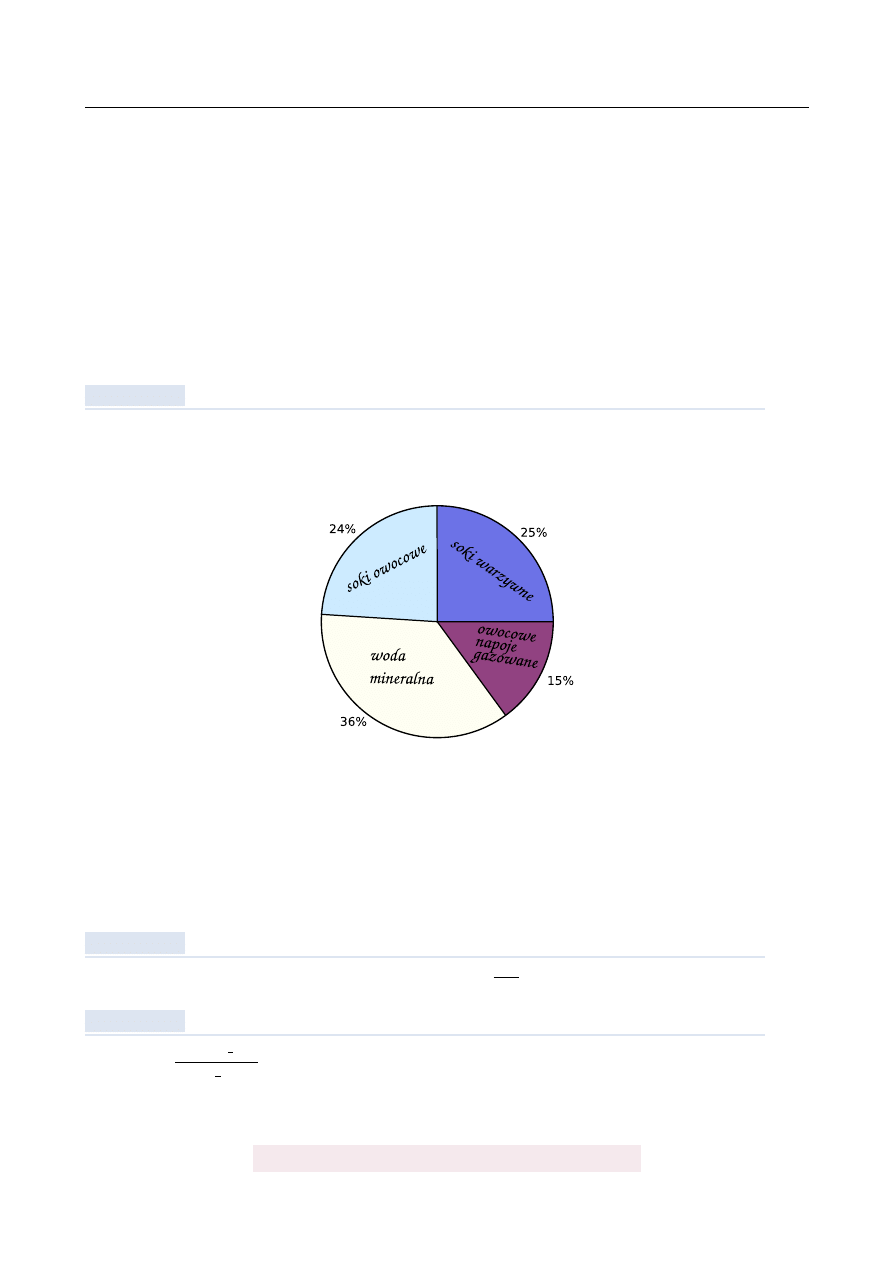
Diagram przedstawia wyniki ankiety, w której ankietowani odpowiedzieli na pytanie, ja-
kie napoje pij ˛
a mi˛edzy posiłkami. Ankietowani wybierali tylko jeden z czterech rodzajów
napojów.
Na podstawie informacji przedstawionych na diagramie oblicz:
a) ile procent badanych osób pije soki owocowe lub wod˛e mineraln ˛
a,
b) ile procent badanych osób nie pije owocowych napojów gazowanych,
c) ile procent badanych osób nie pije soków warzywnych i nie pije wody mineralnej.
Z
ADANIE
2
Dany jest ci ˛
ag
(
a
n
)
okre´slony wzorem a
n
= (−
1
)
n
·
2
−
n
n
2
dla n
>
1. Oblicz a
2
, a
4
i a
5
.
Z
ADANIE
3
Przedstaw
4
−1
−
3
·
(
2
3
)
−2
5
−
(
1
2
)
−1
w postaci nieskracalnego ułamka zwykłego.
Materiał pobrany z serwisu
1

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
4
Podaj miejsca zerowe funkcji okre´slonych dla wszystkich liczb rzeczywistych x:
a) f
(
x
) =
x
(
x
+
2
)
,
b) g
(
x
) = (
x
−
5
)(
x
+
2
)
,
c) h
(
x
) = (
5
−
2x
)(
2x
+
1
)
.
Z
ADANIE
5
Oblicz a
−
b, gdy a
=
sin
4
α
−
cos
4
α
, b
=
1
−
4 sin
2
α
cos
2
α
dla α
=
60
◦
.
Z
ADANIE
6
Wska ˙z równanie okr˛egu o ´srodku w punkcie S
= (−
1, 2
)
i promieniu r
=
√
2.
A)
(
x
+
1
)
2
+ (
y
−
2
)
2
=
2
B)
(
x
+
1
)
2
+ (
y
−
2
)
2
=
√
2
C)
(
x
−
1
)
2
+ (
y
+
2
)
2
=
2
D)
(
x
+
1
)
2
− (
y
−
2
)
2
=
√
2
2. Wykorzystanie i interpretowanie reprezentacji
Z
ADANIE
7
Na osi liczbowej zaznaczono przedział A zło ˙zony z tych liczb rzeczywistych, których odle-
gło´s´c od punktu 1 jest niewi˛eksza od 4,5. Przedział A przesuni˛eto wzdłu ˙z osi o 2 jednostki
w kierunku dodatnim, otrzymuj ˛
ac przedział B. Wyznacz wszystkie liczby całkowite, które
nale ˙z ˛
a jednocze´snie do A i do B.
Z
ADANIE
8
Rozwi ˛
a ˙z równanie x
+
x
3
=
1
+
x
2
.
Z
ADANIE
9
Oblicz najwi˛eksz ˛
a i najmniejsz ˛
a warto´s´c funkcji f
(
x
) =
2x
2
−
4x
+
11 w przedziale A
=
h
0, 4
i
.
Z
ADANIE
10
Pan Kowalski planuj ˛
ac wyjazd na wakacje letnie w nast˛epnym roku postanowił zało ˙zy´c lo-
kat˛e, wpłacaj ˛
ac do banku 2000 zł na okres jednego roku. Ma do wyboru trzy rodzaje lokat:
lokata A
– oprocentowanie w stosunku rocznym 5%, kapitalizacja odsetek po roku;
lokata B
– oprocentowanie w stosunku rocznym 4,8%, kapitalizacja odsetek co pół roku;
lokata C
– oprocentowanie w stosunku rocznym 4,6%, kapitalizacja odsetek co kwartał.
Oce ´n, wykonuj ˛
ac odpowiednie obliczenia, która lokata jest najkorzystniejsza dla Pana Ko-
walskiego.
Materiał pobrany z serwisu
2
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
11
W trójk ˛
acie równoramiennym ABC, w którym
|
AC
| = |
BC
| =
10 cm, wysoko´s´c poprowa-
dzona z wierzchołka C jest równa 5 cm. Oblicz miary k ˛
atów tego trójk ˛
ata. Odpowied´z podaj
w stopniach.
Z
ADANIE
12
Ostrok ˛
atny trójk ˛
at równoramienny ABC o podstawie AB jest wpisany w okr ˛
ag o ´srodku S,
przy czym k ˛
at SAB ma miar˛e 40
◦
. Oblicz miar˛e k ˛
ata CAB.
Z
ADANIE
13
Oblicz odległo´s´c punktu A od ´srodka odcinka BC, gdzie A
= (
1, 3
)
, B
= (
4, 7
)
, C
=
(−
2,
−
3
)
.
Z
ADANIE
14
W graniastosłupie czworok ˛
atnym prawidłowym przek ˛
atna o długo´sci m jest nachylona do
płaszczyzny podstawy pod k ˛
atem α. Wiadomo, ˙ze sin α
=
0, 2. Wyznacz obj˛eto´s´c tego gra-
niastosłupa.
Z
ADANIE
15
O zdarzeniach losowych A i B wiemy, ˙ze: P
(
A
) =
1
2
, P
(
B
) =
2
3
, P
(
A
∪
B
) =
4
5
. Oblicz:
a) P
(
A
∩
B
)
b) P
(
A
\
B
)
Z
ADANIE
16
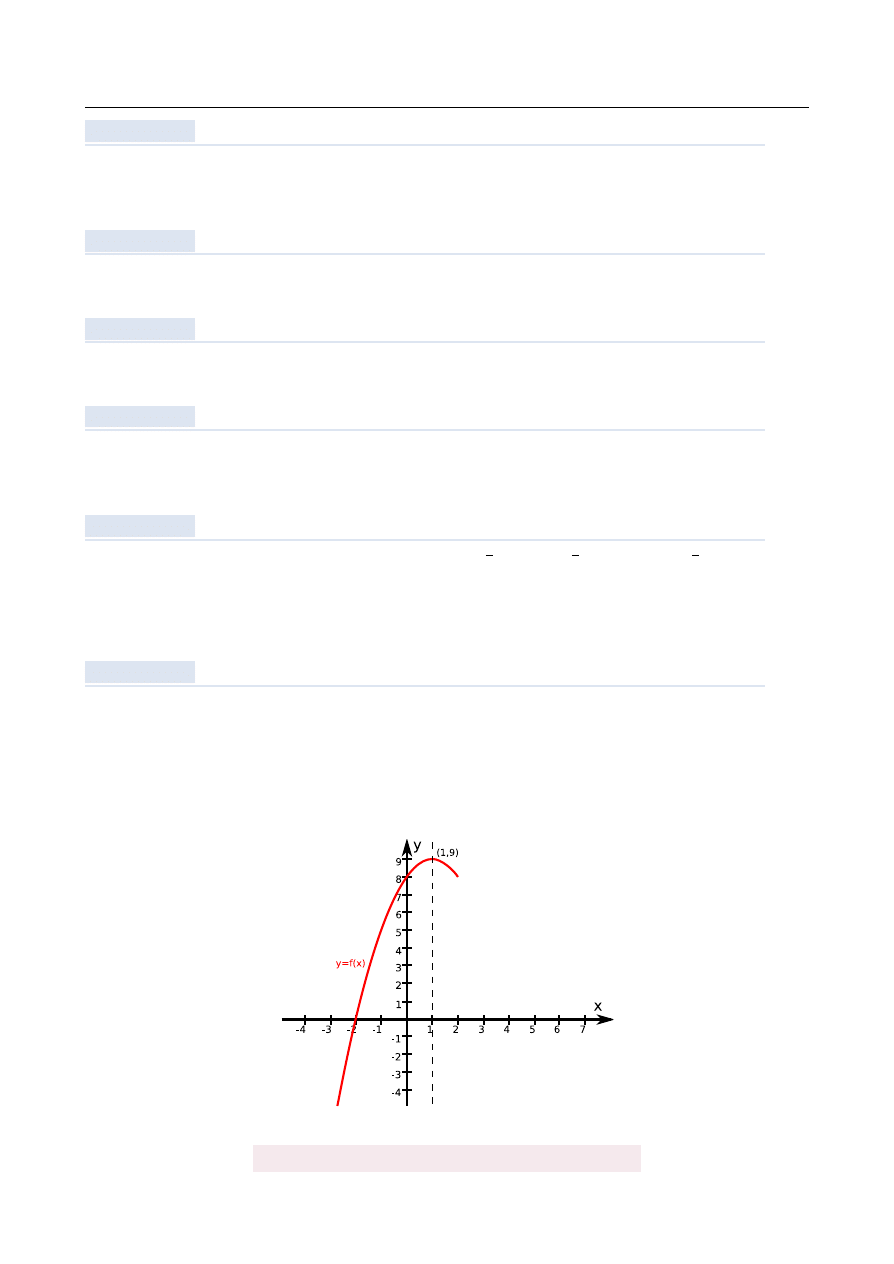
Na podstawie fragmentu wykresu funkcji kwadratowej y
=
f
(
x
)
wska ˙z, które zdanie jest
prawdziwe.
A) Miejscami zerowymi funkcji s ˛
a liczby: -2 oraz 4.
B) Funkcja jest rosn ˛
aca w przedziale
(−
2, 4
)
.
C) Funkcja przyjmuje warto´sci wi˛eksze od zera dla x
<
1.
D) Zbiorem warto´sci funkcji jest przedział
(−
∞, 9
)
.
Materiał pobrany z serwisu
3
www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
Z
ADANIE
17
W kolejce do kasy biletowej ustawiły si˛e cztery dziewczynki i pi˛eciu chłopców. Liczba wszyst-
kich mo ˙zliwych ustawie ´n osób w tej kolejce wynosi
A) 4!+5!
B) 9!
C) 4
·
5
D) 4!
·
5!
3. Modelowanie matematyczne
Z
ADANIE
18
Dany jest prostok ˛
at o bokach a i b. Zmniejszamy długo´s´c boku a o 10% oraz zwi˛ekszamy
długo´s´c boku b o 20%.
a) O ile procent zwi˛ekszy si˛e pole tego prostok ˛
ata?
b) Wyznacz długo´s´c boku b, dla której nowy prostok ˛
at b˛edzie miał taki sam obwód jak
prostok ˛
at wyj´sciowy, je´sli wiadomo, ˙ze bok a ma długo´s´c 30 cm.
Z
ADANIE
19
Liczb˛e 42 przedstaw w postaci sumy dwóch składników tak, by ró ˙znica ich kwadratów była
równa 168.
Z
ADANIE
20
Dla ka ˙zdej liczby rzeczywistej b równanie y
=
1
2
x
2
−
bx
+
2 opisuje pewn ˛
a parabol˛e. Wy-
znacz wszystkie warto´sci parametru b, dla których wierzchołek paraboli le ˙zy nad osi ˛
a Ox.
Z
ADANIE
21
Punkt B
= (−
1, 9
)
nale ˙zy do okr˛egu stycznego do osi Ox w punkcie A
= (
2, 0
)
. Wyznacz
równanie tego okr˛egu.
Z
ADANIE
22
Strzelaj ˛
ac do tarczy pewien strzelec uzyskuje co najmniej 9 punktów z prawdopodobie ´n-
stwem 0,5, a co najwy ˙zej 9 punktów z prawdopodobie ´nstwem 0,7. Oblicz prawdopodobie ´n-
stwo, ˙ze ten strzelec uzyska dokładnie 9 punktów.
Z
ADANIE
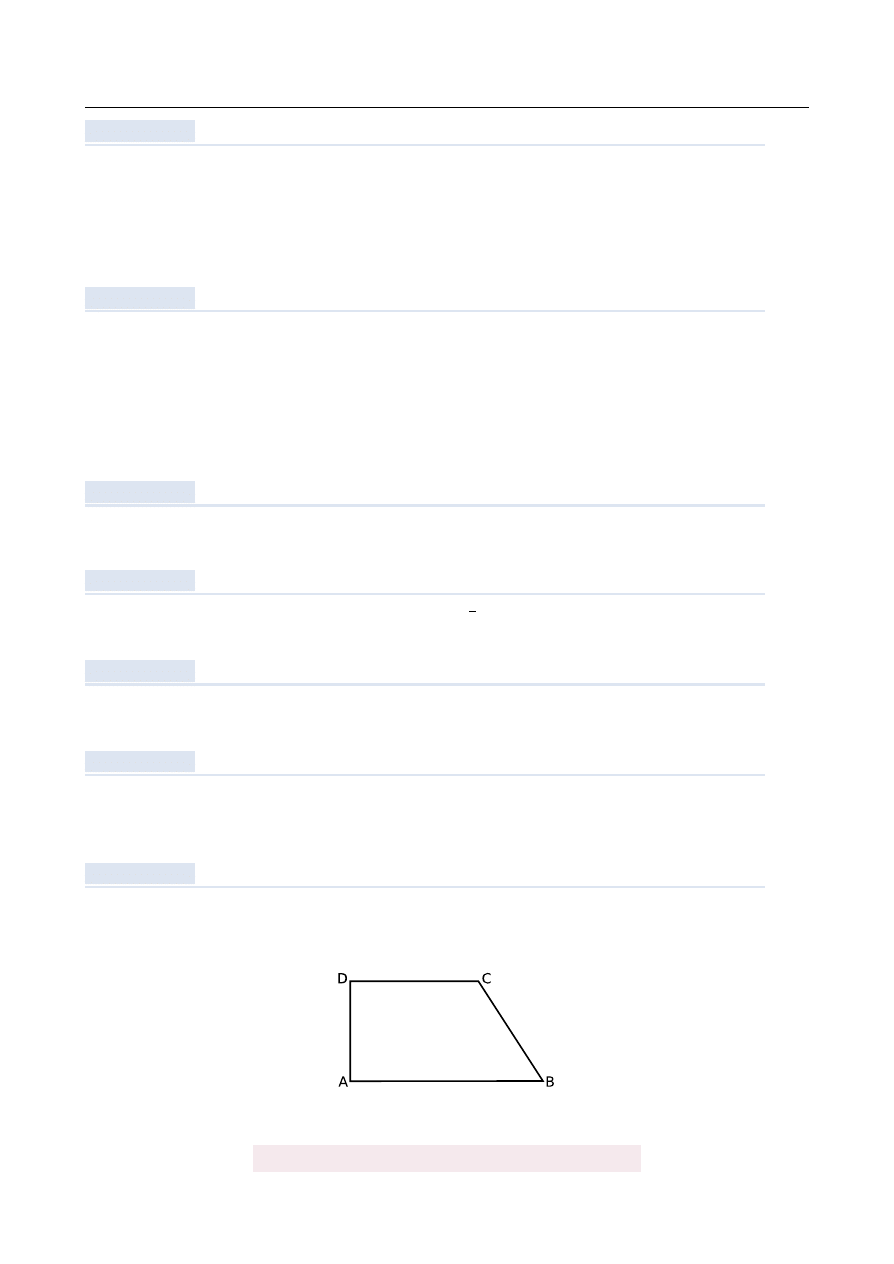
23
Długo´s´c ramienia BC trapezu prostok ˛
atnego jest dwa razy wi˛eksza od ró ˙znicy długo´sci jego
podstaw. K ˛
at ABC ma miar˛e
A) 30
◦
B) 45
◦
C) 60
◦
D) 75
◦
Materiał pobrany z serwisu
4

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
4. U˙zycie i tworzenie strategii
Z
ADANIE
24
Podaj przykład liczb całkowitych dodatnich a i b, spełniaj ˛
acych nierówno´s´c
5
7
<
a
b
<
6
7
.
Z
ADANIE
25
Stosuj ˛
ac wzory skróconego mno ˙zenia rozłó ˙z na czynniki wyra ˙zenie 1
−
a
2
+
2ab
−
b
2
.
Z
ADANIE
26
W ci ˛
agu arytmetycznym
(
a
n
)
dane s ˛
a wyrazy: a
3
=
4, a
6
=
19. Wyznacz wszystkie warto´sci
n, dla których wyrazy ci ˛
agu
(
a
n
)
s ˛
a mniejsze od 200.
Z
ADANIE
27
Liczby dodatnie a, b, c spełniaj ˛
a warunek: log
4
c
=
log
3
b
=
log
2
a
=
2. Oblicz
√
abc.
Z
ADANIE
28
Ile punktów wspólnych ma okr ˛
ag o równaniu x
2
+ (
y
−
3
)
2
=
6 z prost ˛
a o równaniu 3x
+
y
−
15
=
0?
Z
ADANIE
29
Zbiorem warto´sci funkcji kwadratowej g jest przedział
(−
∞, 5
i
, a zbiorem rozwi ˛
aza ´n nie-
równo´sci g
(
x
) >
0 jest przedział
(
2, 8
)
. Wyznacz wzór funkcji g.
Z
ADANIE
30
Rozwi ˛
a ˙z równanie
(
2x
+
1
) + (
2x
+
4
) + (
2x
+
7
) +
. . .
+ (
2x
+
28
) =
155, je´sli wiadomo, ˙ze
składniki po lewej stronie s ˛
a kolejnymi wyrazami pewnego ci ˛
agu arytmetycznego.
Z
ADANIE
31
Wiedz ˛
ac, ˙ze α jest k ˛
atem ostrym i tg α
=
2, oblicz warto´s´c wyra ˙zenia
4 cos α
−
3 sin α
3 cos α
+
5 sin α
.
Z
ADANIE
32
Dany jest trójk ˛
at prostok ˛
atny ABC o przeciwprostok ˛
atnej AB, taki ˙ze sin
]
BAC
=
0, 3 i
|
AC
| =
7. Oblicz pole koła opisanego na tym trójk ˛
acie.
Z
ADANIE
33
W układzie współrz˛ednych na płaszczy´znie zaznaczono punkty A
= (
2, 0
)
i B
= (
4, 0
)
.
Wyznacz wszystkie mo ˙zliwe poło ˙zenia punktu C, dla których ABC jest trójk ˛
atem równora-
miennym o podstawie AB i polu równym 3.
Z
ADANIE
34
Rzucamy trzy razy symetryczn ˛
a sze´scienn ˛
a kostk ˛
a do gry. Opisz zbiór wszystkich zdarze ´n
elementarnych, a nast˛epnie oblicz prawdopodobie ´nstwo, ˙ze w ka ˙zdym rzucie liczba oczek
b˛edzie wi˛eksza od numeru rzutu.
Materiał pobrany z serwisu
5

www.zadania.info – N
AJWI ˛
EKSZY
I
NTERNETOWY
Z
BIÓR
Z
ADA ´
N Z
M
ATEMATYKI
5. Rozumowanie i argumentacja
Z
ADANIE
35
Wiadomo, ˙ze 1,5849 jest przybli ˙zeniem liczby 10
0,2
z zaokr ˛
agleniem do 4 miejsc po prze-
cinku. Wyznacz przybli ˙zenie liczby 10
−
4
5
z zaokr ˛
agleniem do 3 miejsc po przecinku oraz
przybli ˙zenie liczby 10
11
5
z zaokr ˛
agleniem do 1 miejsca po przecinku.
Z
ADANIE
36
Wyka ˙z, ˙ze dla m
=
3 nierówno´s´c x
2
+ (
2m
−
3
)
x
+
2m
+
5
>
0 jest spełniona przez wszystkie
liczby rzeczywiste x.
Z
ADANIE
37
Jednym z miejsc zerowych funkcji kwadratowej f jest liczba 5, maksymalny przedział, w
którym ta funkcja jest malej ˛
aca to
h
2,
+
∞
)
. Najwi˛eksza warto´s´c funkcji f w przedziale
h−
8,
−
7
i
jest równa
(−
24
)
. Wyznacz wzór funkcji f i narysuj jej wykres.
Z
ADANIE
38
W pewnym trójk ˛
acie prostok ˛
atnym suma cosinusów k ˛
atów ostrych jest równa
2
√
3
3
. Oblicz
iloczyn sinusów tych k ˛
atów.
Z
ADANIE
39
Dany jest trapez ABCD o podstawach AB i CD. Przek ˛
atne tego trapezu przecinaj ˛
a si˛e w
punkcie S. Wyka ˙z, ˙ze
|
SA
| · |
SD
| = |
SB
| · |
SC
|
.
Z
ADANIE
40
Prostok ˛
at ABCD obracaj ˛
ac si˛e wokół boku AB, zakre´slił walec w
1
. Ten sam prostok ˛
at obraca-
j ˛
ac si˛e wokół boku AD, zakre´slił walec w
2
. Otrzymane walce maj ˛
a równe pola powierzchni
całkowitych. Wyka ˙z, ˙ze prostok ˛
at ABCD jest kwadratem.
Materiał pobrany z serwisu
6
Wyszukiwarka
Podobne podstrony:
2010 INF CKE PP zad otwarte ARKUSZ Z INF
Przykl Zad Koll 3-cie sem3 HD CD 2010, Technologia chemiczna, Chemia fizyczna, Ćwiczenia, Kolokwium
1 niemiecki 2010 zad pp
1 matematyka 2010 zad pp
1 angielski 2010 zad pp
Odpowiedzi Przykladowy arkusz PP Fizyka (2)
Odpowiedzi Przykladowy arkusz PP Biologia
BO2 - PRZYKL ZAD EGZ, Badania Operacyjne
Przykladowe zad do 2 kola, wzr UG, Statystyka, testy
Odpowiedzi Przykladowy arkusz PP Polski
chemia przykladowe zad id 11281 Nieznany
MATURA 10 polski CKE przykładowe rozwiązania do arkusza
2010 - Egzamin ADWOKACKI, 100729 zad adm egz adw, K A Z U S testament
więcej podobnych podstron