Kryteria stopu algorytmu grupowania reguł

a efektywność systemu wspomagania decyzji

Agnieszka Nowak

Alicja Wakulicz-Deja

Zakład Systemów Informatycznych

Instytut Informatyki Uniwersytetu Śląskiego

Sosnowiec, ul. Będzińska 39, [phone]

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

1 / 34

Plan referatu

1

Efektywność wnioskowania w klasycznych systemach wspomagania decyzji.

2

Motywacja tworzenia hierarchicznej bazy wiedzy.

3

Prawda o aglomeracyjnym algorytmie grupowania.

4

Efektywność osiągana różnymi drogami ?.

5

Podsumowanie.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

2 / 34

Zagadnienia...

Referat powinien udzielić satysfakcjonujących odpowiedzi na pytania:

1

Dlaczego potrzebna jest zmiana struktury bazy wiedzy ?

2

Dlaczego proponujemy hierarchię ?

3

Dlaczego jako algorytm grupowania wybieramy akurat AHC ?

4

Jak zamierzamy zmodyfikować klasyczne podejścia ?

5

W jakim celu wprowadzamy swoje zmiany ?

6

Jak będziemy sprawdzać efektywność (jakość) zbudowanego systemu ?

7

Podsumowanie - odpowiedź na pytanie: Jaka jest efektywność
proponowanego rozwiązania?

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

3 / 34

Dlaczego potrzebna jest zmiana struktury bazy wiedzy ?

Efektywność wnioskowania w klasycznych systemach wspomagania decyzji takich
jak np MYCIN, EMYCIN etc. zależy od kilku czynników:

wybranej metody wnioskowania,

posiadanej w systemie wiedzy (liczby reguł w bazie wiedzy),

liczby obserwacji,

wybranej strategii sterowania wnioskowaniem.

Konkluzje:

trudna ocena takiego systemu,

wymagana kompletność bazy wiedzy,

czas wnioskowania rośnie gdy zwiększa się liczba reguł w bazie wiedzy,

optymalny system wspomagania decyzji, to taki system, który

dostarcza decyzji w jak najkrótszym czasie, angażując użytkownika
tylko w pewnym minimalnym zakresie.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

4 / 34

Dlaczego proponujemy hierarchię ?

Wiedza każdego systemu może być reprezentowana na wiele różnych sposobów,
np. za pomocą rozkładów prawdopodobieństwa, współczynników pewnych funkcji,
struktur symbolicznych gramatyk formalnych, czy hierarchii podziałów. Poprzez
analizowanie przykładów, system ma odkryć nieznany podział (lub hierarchię
podziałów) dostarczonego mu zbioru, czyli dokonać grupowania tego zbioru.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

5 / 34

Motywacja tworzenia hierarchicznej bazy wiedzy

Optymalizacja czasu pracy systemu, jak i metody wnioskowania jest
skomplikowana.

Zadaniem interpretera reguł jest znalezienie i uaktywnienie reguł
odpowiednich do zaobserwowanych faktów. Oczywiste jest, że jeżeli rozmiar
bazy reguł wzrasta, to i czas szukania reguł przez interpreter się zwiększa.

Aby temu zapobiec proponujemy grupowanie reguł (aglomerację) w
bazach wiedzy i wnioskowanie na grupach (skupieniach) reguł.

Cel: Analiza skupień ma skrócić w sposób istotny czas wnioskowania.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

6 / 34

Dlaczego spośród wszystkich algorytmów grupowania wybieramy
akurat AHC ?

Liczba Stirlinga II-go rzędu
Moc (liczba możliwych kombinacji) grupowania metodą k-optymalizacyjną n
elementów na k grup (skupień) da się wyznaczyć z następującego wyrażenia:

M = (

1

k!

)[

n

X

i =1

(

k
i

)(−1)

k−i

∗ i

n

]]

Wówczas mając zaledwie do pogrupowania 6 (n = 6) obiektów do 3 (k = 3) grup,
liczba możliwych kombinacji wynosi:

M = (

1

3!

)[(

3
1

)(−1)

2

∗ 1

6

+ (

3
2

)(−1) ∗ 2

6

+ (

3
3

)(−1)

0

∗ 3

6

] = 90

Algorytm hierarchicznego łączenia obiektów - rozwiązuje ten problem
poprzez samą ideę algorytmu, która zawsze nakazuje w każdym kroku
połączyć dwa najbardziej podobne obiekty.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

7 / 34

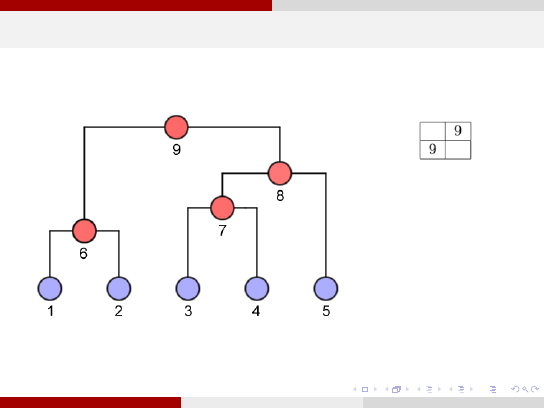
Klasyczne grupowanie hierarchiczne

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

8 / 34

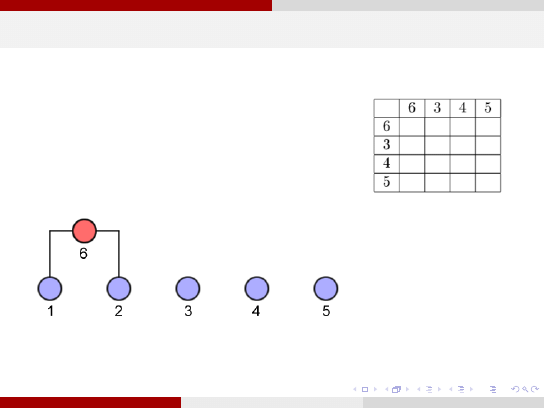
Klasyczne grupowanie hierarchiczne

krok 1: połączenie w grupę obiektów 1 i 2

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

9 / 34

Klasyczne grupowanie hierarchiczne

krok 2: połączenie w grupę obiektów 3 i 4

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

10 / 34

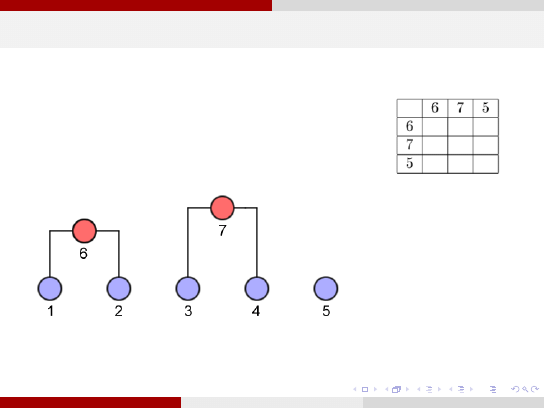
Klasyczne grupowanie hierarchiczne

krok 3: połączenie w grupę obiektów 7 i 5

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

11 / 34

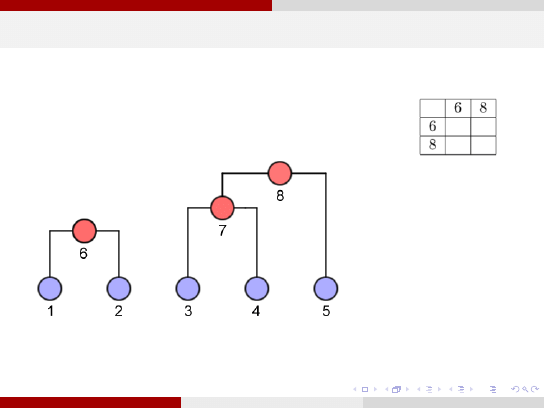
Klasyczne grupowanie hierarchiczne

krok 4: połączenie w grupę obiektów 6 i 8

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

12 / 34

Macierzowy algorytm aglomeracyjny - algorytm Johnson’a

1

t=0 /*nr poziomu w hierarchii*/

2

utworzenie początkowego podziału

Podz

N

0

(N) = {G

i

= {x

i

}|i = 1, . . . , N}

3

utworzenie początkowej N × N macierzy niepodobieństwa P(t) :

P(i , j )(t) = D(G

i

, G

j

)i , j = 1, . . . , N

4

repeat a) − e):

a) wybranie spośród wszystkich par grup (G

i

, G

j

) w podziale t najbliższej pary

(G

i

, G

j

):

D(G

i

, G

j

) =

min

r ,s

D(G

i

, G

j

)

b) t = t + 1
c) utworzenie nowej grupy G

q

= G

i

∪ G

j

d) utworzenie nowego podziału:

Podz

N−1

t

(N) = {Podz

N−t+1

t−1

(N) − {G

i

, G

j

}} ∪ {G

q

}

e) aktualizacja macierzy niepodobieństwa P(t) dla kroku t na podstawie P(t − 1)
(kroki 1-2):
1.Usunięcie dwóch rzędów i dwóch kolumn z macierzy P(t − 1), które odpowiadają
łączonym grupom.
2.Dodanie nowego rzędu i nowej kolumny dla nowo utworzonej grupy, które
zawierają obliczone odległości pomiędzy nowo utworzoną grupą i wszystkimi
grupami z kroku (t − 1), które nie zostały w tym kroku zmienione.

5

until (wszystkie wektory są w jednej grupie).

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

13 / 34

Sposoby aktualizacji macierzy - obliczania nowych odległości w
każdym kroku

Wg Jain i Dubes’a:

1

Algorytm pojedynczego łączenia

(ang. single linkage algorithm)

D(C

q

, C

s

) = min{D(C

i

, C

s

), D(C

j

, C

s

)}

2

Algorytm pełnego łączenia

(ang. complete linkage algorithm)

D(C

q

, C

s

) = max {D(C

i

, C

s

), D(C

j

, C

s

)}

3

Algorytm uśredniania par

(ang. weighted average linkage)

D(C

q

, C

s

) =

1

2

(D(C

i

, C

s

) + D(C

j

, C

s

))

Ponadto:

4

Average Linkage (UPGMA),Centroid (UPGMC), Median (WPGMC),

5

Algorytm Warda (ang. Increase in Sum of Squares).

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

14 / 34

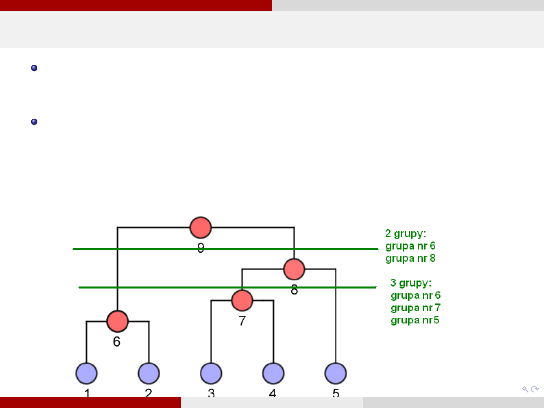
Ważne aspekty grupowania hierarchicznego

Złożoność czasowa macierzowych algorytmów aglomeracyjnych wynosi
O(N

2

lg N) natomiast pamięciowa O(N

2

).

Ta ostatnia wynika z konieczności

pamiętania macierzy niepodobieństwa o wymiarach N × N.

Wynik algorytmu grupowania hierarchicznego można przedstawić w postaci
tzw. dendrogramu niepodobieństwa, w którym występuje oś skojarzona z
używaną miarą niepodobieństwa. Przecięcie poziome dendrogramu daje jeden
z możliwych podziałów.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

15 / 34

Jak będziemy sprawdzać efektywność (jakość) zbudowanego systemu ?

[Jain A.K., Dubes R.C., ”Algorithms for clustering data”, Prentice Hall, 1998]

Procedura grupowania to nie tylko samo grupowanie ? Procedurę grupowania tworzą
następujące zadania składowe:

1

utworzenie reprezentacji,

2

wybór miary podobieństwa,

3

ustalenie tendencji grupującej,

4

grupowanie,

5

walidacja wyniku,

6

abstrakcja cech.

W zależności od użytej miary podobieństwa, rodzaju algorytmu grupowania oraz różnych

wartości jego parametrów, uzyskuje się różne wynikowe podziały danego zbioru obiektów.

Z tego względu konieczne jest stosowanie weryfikacji uzyskanego podziału zwanej

potocznie walidacją, która stanowi procedurę sprawdzającą ”poprawność” uzyskanego

podziału. Walidacji tej dokonuje się za pomocą weryfikacji hipotez statystycznych lub

odpowiednio skonstruowanych wskaźników (indeksów) walidacyjnych: np. indeks Dunn

0

a

czy Xie − Beni .

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

16 / 34

Zdefiniowanie kryterium jakości

[K.Stąpor,”Automatyczna klasyfikacja obiektów”, EXIT, W-wa 2005]

W algorytmach iteracyjnej optymalizacji tj. k-means, k-medoids, najlepszy
podział zbioru jest wyznaczany przez iteracyjne polepszanie pewnych wskaźników
jakości, startując z początkowego podziału, najczęściej losowego. Wskaźniki
jakości definiuje się w postaci funkcji kryterialnej, która jest zależna od zbioru
uczącego oraz wektora nieznanych parametrów określających daną grupę.
Funkcja kryterialna najczęściej jest konstruowana w postaci sumy kwadratów
odległości wektorów w grupach od prototypów tych grup. Stanowi więc miarę
rozproszenia wektorów w poszczególnych grupach.
Ocenie może podlegać:

uzyskany pojedynczy podział,

hierarchia podziałów,

pojedyncza grupa.

Spośród wszystkich możliwych podziałów uzyskanych jako wynik
działania danego algorytmu grupowania z różnymi wartościami
parametrów należy wybrać ten, który najlepiej opisuje strukturę zbioru.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

17 / 34

Jak oceniać rezultaty k-means, k-medoids ?

Jeśli x

c

- centroid, średnia wartość z wszystkich obiektów nalezących do danej

grupy C . wówczas, można zdefiniować miarę dopasowania skupienia c:

TD(C ) =

X

p∈C

dist(p, x

c

)

2

Dalej, całkowity koszt grupowania w danej iteracji mozna wyznaczyć jako:

TD =

k

X

i =1

TD(C

i

)

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

18 / 34

Jak oceniać rezultaty grupowania hierarchicznego ?

Problem wyboru optymalnego podziału rozwiązuje sama idea algorytmu. Jedynie,
w zależności od wybranej metody tworzenia centroidu (single linkage, complete
linkage, Ward, etc.), dwa najbardziej podobne obiekty mogą zostać łączone w
grupę w innym czasie (w innym kroku algorytmu, raz wcześniej, raz później).
Zatem, stosując techniki hierarchiczne, zwiększamy co prawda czas działania
algorytmu, ale usuwamy problem oceny otrzymanego rozwiązania.
Efektywność wnioskowania po grupowaniu reguł metodą analizy skupień
Kryteria oceny systemów wnioskujących można podzielić na dwie grupy:

kryteria związane ze złożonością obliczeniową algorytmu,

kryteria związane z jakością otrzymanego podziału,

kryteria związane z jakością generowanych wyników, np. trafność
rozpoznawania, dokładność lokalizacji obiektu, etc.[kompletność, dokładność].

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

19 / 34

Jak zamierzamy zmodyfikować klasyczne podejścia ?

Pożądane własności dobrego podziału:

możliwie najmniejsza liczba parametrów koniecznych do specyfikowania,
możliwie najmniejsza krotność analizy elementów zbioru U,
możliwość wykrywania grup o dowolnym kształcie, wielkości, gęstości,
niewrażliwość na obecność szumu (wektorów odstających) w zbiorze,
możliwość przetwarzania danych różnych typów (ciągłe, dyskretne), w szczególności ich
kombinacji,
niezależność wyniku od kolejności analizy obiektów zbioru U,
możliwie największe podobieństwo obiektów wewnątrz danej grupy oraz możliwie
najmniejsze podobieństwo grup do siebie.

Rzeczywistość jest inna - niepożądane własności podziału:

podobieństwo między obiektami w danej grupie spada poniżej pewnego ustalonego
poziomu minimum.

Różne są sposoby ustalania tego minimalnego współczynnika podobieństwa. W rozważaniach
podejmowanych przez nas wcześniej brane były pod uwagę dwie metody:

średnia z minimum i maksimum,

T =

min(s(x , y )) + max(s(x , y ))

2

,

średnia ważona.

T = s

0

(x , y ).

gdzie:

s(x , y )- to pewna miara podobieństwa między obiektami x oraz y (np. miara Gowera).

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

20 / 34

Kryteria oceny jakości podziału

Jakość grupowania zależy od tego jak różnie obiekty są rozrzucone w węzłach
drzewa a to z kolei zależy od algorytmu jakim były łączone i od tego jakich
metryk używano do ich łączenia.
Są 2 standardowe miary:

miara oceny (ang. FScore),

FScore =

2RP

R + P

gdzie:

R - kompletność (ang. Recall ), P - dokładność (ang. Precision).

miara rozkładu - entropii (ang.Entropy ).

Entropy (S

r

) = −

1

lg q

q

X

i =1

n

i

r

n

r

lg

n

i

r

n

r

gdzie:

q - liczba klas, n

i

r

- liczba obiektów w i -tej klasie.

Entropia całego drzewa T wynosi:

Entropy (T ) =

t

X

r =1

1

t

X

(S

r

)

t - liczba węzłów w drzewie T .

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

21 / 34

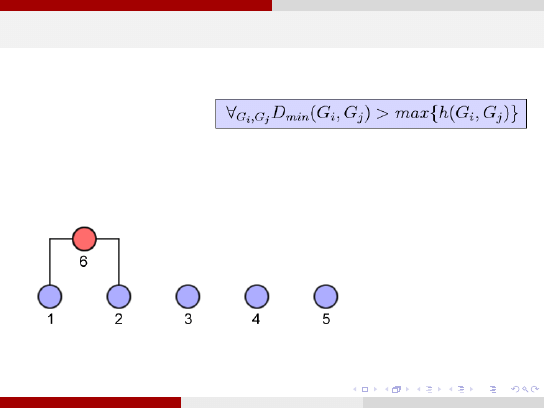
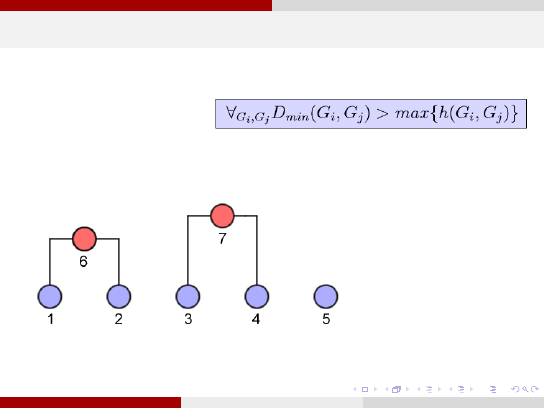
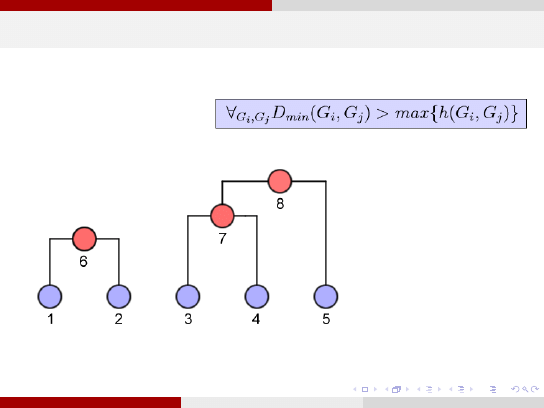
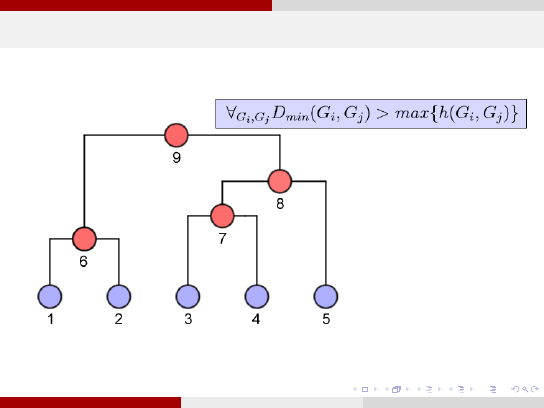
Miara Theodoridis i Koutroumbas,1999

[S. Theodoridis, K. Koutroumbas, ”Patern Recognition”, Academic Press, 1999]

Odpowiedni

poziom odcięcia to ten, dla którego spełniony jest warunek:

∀

G

i

,G

j

D

min

(G

i

, G

j

) > max {h(G

i

, G

j

)}

gdzie:

h(G

i

) jest miarą samopodobieństwa grupy, tj. podobieństwa pomiędzy wektorami z danej grupy.

Miarę samopodobieństwa można zdefiniować np. jako maksymalną odległość wektorów w grupie:

h(G ) = max {d (x , y )|

x ,y ∈G

}

lub też jako średnią wartość odległości między wektorami w grupie:

h(G ) =

1

2N

G

X

x ∈G

X

y ∈G

d (x , y )

gdzie:

d (x , y ) oznacza którąkolwiek z miar niepodobieństwa wektorów. Innymi słowy, w końcowym

podziale niepodobieństwo pomiędzy dowolną parą grup musi być większe niż samopodobieństwo

każdej z grup.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

22 / 34

mAHC

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

23 / 34

mAHC

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

24 / 34

mAHC

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

25 / 34

mAHC

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

26 / 34

mAHC

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

27 / 34

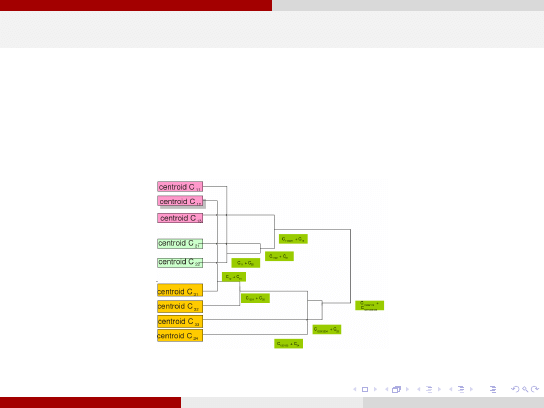
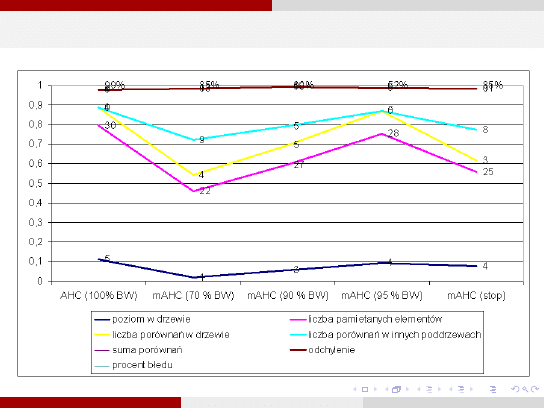
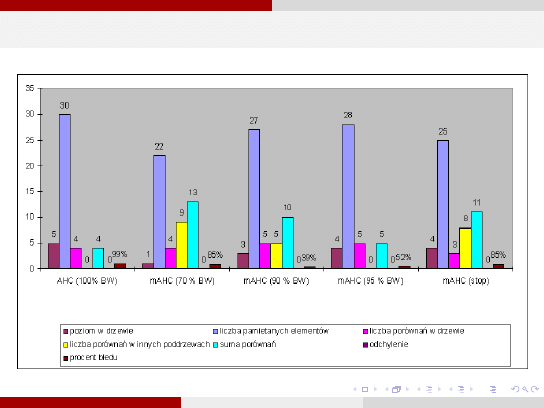
AHC kontra mAHC

a

b

c

d

e

f

g

AHC [100]

5

30

4

0

4

0.09

99

mAHC [70]

1

22

4

9

13

0.13

85

mAHC [90]

3

27

5

5

10

0.03

39

mAHC [95]

4

28

5

0

5

0.04

52

mAHC - inne

4

25

3

8

11

0.13

85

a - poziom w drzewie
b - liczba pamietanych elementow
c - liczba porównań w drzewie
d - liczba porównań w innych drzewach
e - suma porównań
f - odchylenie
g - procent błędu

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

28 / 34

mAHC kontra AHC

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

29 / 34

mAHC kontra AHC

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

30 / 34

Miara efektywności van Rijsbergen’a, 1979

Miara ta umożliwia ocenę obydwu parametrów: kompletności oraz dokładności
jednocześnie.

E

HC

= 1 −

1 + b

2

b

2

R

+

1

P

gdzie odpowiednio:

b to współczynnik skalujący ∈ [0..1],

R to to kompletność (ang. recall ),

P to dokładność (ang. precision).

Idealna sytuacja
R

HC

= 1.0, P

HC

= 1.0

jeśli b =

1
2

wówczas: E

HC

= 1 −

5
4

1
4

+1

= 1 −

5/4
5/4

= 1 − 1 = 0

Zależność jest taka, że im wartość E

HC

jest bliższa 0 tym większa jest efektywność

systemu, i odwrotnie.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

31 / 34

Eksperymenty

Wyniki eksperymentów

a

b

c

d

e

f

baza nr 1

16

31

5

16

10

62

baza nr 2

199

397

23

199

34

17

baza nr 3

480

959

27

480

36

7

baza nr 4

702

1403

30

702

38

5, 4

gdzie:

a - liczba reguł, b - liczba grup,c - liczba poziomow w drzewie (wysokość drzewa),

d - liczba porownań przy PZ, e - liczba porownań w AHC, f - procent BD

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

32 / 34

Podsumowanie - Wnioski

1

Hierarchiczne grupowanie reguł w bazach wiedzy przyspieszy procesy
wnioskowania poprzez kryterium podobieństwa - relewantności elementów
drzewa względem podanej nowej wiedzy.

2

Niekwestionowaną zaletą, drugą obok krótkiego czasu jest także fakt, iż
wnioskując w ten sposób system będzie generował tylko niezbędne nowe
fakty, nie obciążając w ten sposób systemu czy użytkownika nową wiedzą.

3

Dodatkowo - możemy zwiększyć jakość uzyskanego podziału poprzez
grupowanie obiektów z kontrolą bliskości - kryterium stopu algorytmu.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

33 / 34

Literatura

1

Anderberg M.R., "Cluster analysis for applications", New York, Academic
Press, 1973.

2

Dubes R.C., Jain A.K., "Algorithms for clustering data", Prentice Hall,
1998.

3

Everitt B.S., "Cluster Analysis (3rd edition)", Edward Arnold / Halsted
Press, London, 1993.

4

Hand D., Mannila H., Smyth P., "Eksploracja danych", Wydawnictwa
Naukowo-Techniczne, Warszawa, 2005.

5

Kaufman L., Rousseeuw P.J., "Finding Groups in Data: An Introduction to
Cluster Analysis", John Wiley Sons, New York, 1990.

6

Nowak A., Wakulicz-Deja A. Bachliński S., "Optimization of Speech
Recognition by Clustering of Phones", Concurrency, Specification and
Concurrency 2005 - Ruciane-Nida, Poland, September 28-30, 2005

7

Nowak A., Wakulicz-Deja A. , "The concept of the hierarchical clustering
algorithms for rules based systems", Intelligent Information Systems 2005 -
New Trends in Intelligent Information Processing and Web Mining, Gdańsk,
Poland, June 13-16, 2005

8

Nowak A., Wakulicz-Deja A., "Aglomeracyjne metody tworzenia skupień reguł
dla optymalizacji procesów wnioskowania", Systemy Wspomagania Decyzji 2004,
Zakopane, Poland, Grudzień 7-9, 2004.

9

Stąpor K., "Automatyczna klasyfikacja obiektów", Akademicka Oficyna
Wydawnicza EXIT, Warszawa 2005.

10

Theodoridis S., Koutroumbas K., "Patern Recognition", Academic Press, 1999.

Agnieszka Nowak, Alicja Wakulicz-Deja (Zakład Systemów Informatycznych Instytut Informatyki Uniwersytetu Śląskiego Sosnowiec, ul. Będzińska 39, [phone])

Kryteria stopu algorytmu grupowania reguł a efektywność systemu wspomagania decyzji

34 / 34