1. Czym zajmuje si

ę

statyka?

Statyka to dział mechaniki zajmuj

ą

cy si

ę

równowag

ą

układów sił. Statyka jako dział mechaniki

ogólnej wykorzystuje nast

ę

puj

ą

ce zasady (aksjomaty), których si

ę

nie udowadnia, a przyjmuje

jako pewniki.

2. Co nazywamy układem sił?

Zbiór dowolnej liczby sił jednocze

ś

nie działaj

ą

cych na ciało nazywamy układem sił.

3. Dokona

ć

podziału sił i ich układów.

Siły mechaniczne

Zewn

ę

trzne

Wewn

ę

trzne

Czynne

Reakcje

Mi

ę

dzycz

ą

steczkowe

Napi

ę

cia

(bierne)

a) Układ płaski - odznacza si

ę

tym,

ż

e wszystkie siły tworz

ą

ce ten układ le

żą

w jednej

płaszczy

ź

nie. Układy te mo

ż

emy podzieli

ć

na:

- układ płaski zbie

ż

ny – jest zbiorem ( w jednej płaszczy

ź

nie) sił, których lini

ę

działania przecinaj

ą

si

ę

w jednym punkcie.

- układ płaski równoległy – jest zbiorem ( w jednej płaszczy

ź

nie) sił, których linie działania s

ą

do

siebie równoległe. Szczególnym przypadkiem takiego układu s

ą

siły działaj

ą

ce wzdłu

ż

wspólnej

prostej.

- układ płaski dowolny - jest zbiorem (w jednej płaszczy

ź

nie) sił o ró

ż

nych kierunkach działania.

b) Układ przestrzenny


4. Poda

ć

brzmienie trzeciego prawa Newtona (dla dwóch brył)?

Je

ż

eli ciało A działa na ciało b pewn

ą

sił

ą

F to ciało B działa na ciało A sił

ą

F o tym samej warto

ś

ci

i kierunku ale o przeciwnym zwrocie.

5. Na jakie grupy dzielimy wi

ę

zy ograniczaj

ą

ce swobod

ę

ruchu ciała?

Podpory ruchoma - Reakcja podpory ruchomej jest zaczepiona w punkcie styczno

ś

ci ciała z

podpor

ą

i ma zawsze kierunek prostopadły do powierzchni podpieranej (niezale

ż

nie od

kierunków sił działaj

ą

cych na ciało podpierane).

Podpora stała - Tego rodzaju wi

ę

zy uniemo

ż

liwiaj

ą

przesuni

ę

cie ciała, lecz umo

ż

liwiaj

ą

obrót

wokół punktu podparcia. Kierunek reakcji nie znany, rzutujemy na os x i y.

Wi

ę

zy wiotkie - Zaliczamy tu sznury, liny, ła

ń

cuchy itp. Siła w takich wi

ę

zach jest zawsze

skierowana wzdłu

ż

osi tych wi

ę

zów.

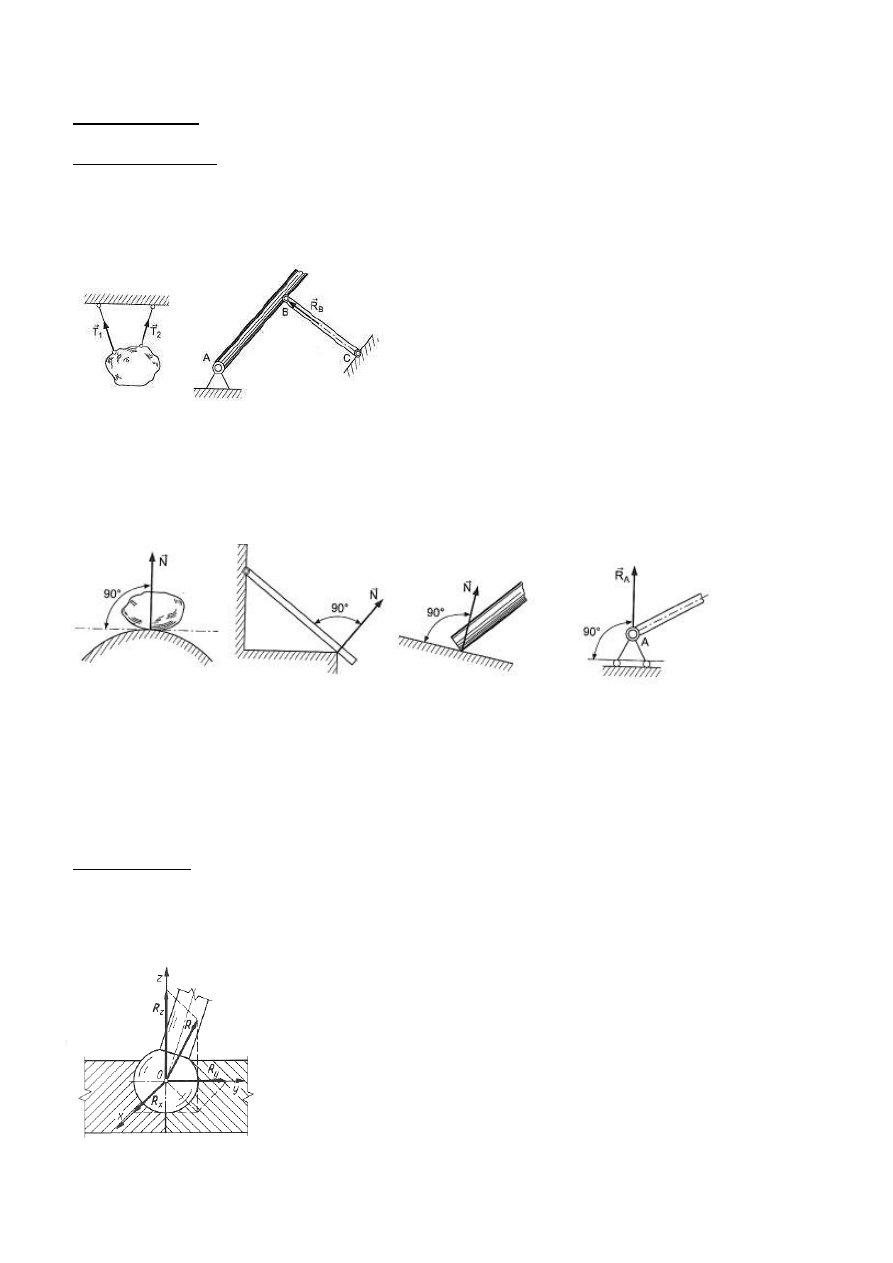
Przegub kulisty

Przegub walcowy

6. Jak działaj

ą

reakcje w ci

ę

gnach? Zilustrowa

ć

przykładami.

Reakcja w ci

ę

gnach jest jak w wi

ę

zach wiotkich czyli skierowana wzdłu

ż

ci

ę

gna a jej zwrot jest

skierowany w gór

ę

.

7. Jak działaj

ą

reakcje w podporach gładkich-przesuwnych? Zilustrowa

ć

przykładami.

Reakcja podpory ruchomej jest zaczepiona w punkcie styczno

ś

ci ciała z podpor

ą

i ma zawsze

kierunek prostopadły do powierzchni podpieranej (niezale

ż

nie od kierunków sił działaj

ą

cych na

ciało podpierane). Podpor

ę

ruchom

ą

oznaczamy schematycznie za pom

ą

c

ą

trójk

ą

ta

równobocznego dodatkowo podkre

ś

lonego lini

ą

, która przedstawia powierzchni

ę

podpieraj

ą

ca.

8. Jak działaj

ą

reakcje w podporach chropowatych-nieprzesuwnych? Zilustrowa

ć

przykładami.

Reakcja zaczepiona jest w punkcie styczno

ś

ci ciała z podpor

ą

i ma na ogół kierunek nie

prostopadły do płaszczyzny. Kierunek reakcji nie znany, rzutujemy na os x i y.

9. Jak działaj

ą

reakcje w przegubach walcowych i kulistych? Zilustrowa

ć

przykładami.

Przegub kulisty składa si

ę

z pr

ę

ta o zako

ń

czeniu w kształcie kuli, która jest osadzona w kulistym

ło

ż

ysku (rys. 3.5a). Podpora taka unieruchamia koniec pr

ę

ta, ale umo

ż

liwia jego obrót wokół

dowolnej osi. Kierunek reakcji R powstaj

ą

cej w przegubie kulistym jest nieznany, jednak przy

braku tarcia b

ę

dzie ona przechodzi

ć

przez

ś

rodek kuli. Zatem do jej okre

ś

lenia w przestrzeni

nale

ż

y zna

ć

trzy współrz

ę

dne: R

x

, R

y

i R

z

Przegub walcowy jest wykonany w postaci poł

ą

czenia sworzniowego. Koniec pr

ę

ta jest osadzony

na walcowym sworzniu przechodz

ą

cym przez kołowy otwór wykonany w tym pr

ę

cie (rys. 3.5b). W

przypadku braku tarcia reakcja sworznia R na pr

ę

t b

ę

dzie miała kierunek prostopadły do

powierzchni styku, czyli jej kierunek przejdzie przez o

ś

sworznia. Reakcja ta b

ę

dzie le

ż

e

ć

w

płaszczy

ź

nie prostopadłej do osi sworznia.

Do jej wyznaczenia s

ą

potrzebne dwie niewiadome: R

x

i R

y

.

10. Jak działaj

ą

reakcje w utwierdzeniach-zamocowaniach? Zilustrowa

ć

przykładem.

Utwierdzenie polega na całkowitym unieruchomieniu np. belki przez wmurowanie jej ko

ń

ca w

ś

cian

ę

, przyspawanie lub przykr

ę

cenie do

ś

ciany. Podpora taka uniemo

ż

liwia przemieszczanie

si

ę

utwierdzonego ko

ń

ca w dwóch kierunkach i obrót wokół tego ko

ń

ca. W miejscu utwierdzenia

A wyst

ą

pi reakcja utwierdzenia R

A

i moment utwierdzenia M

A

. Taka podpora wprowadza do

zadania trzy niewiadome: R

ax

, R

ay

i M

A

.

11. Poda

ć

definicj

ę

twierdzenia o trzech siłach.

Je

ż

eli ciało sztywne jest w równowadze pod działaniem trzech nierównoległych sił le

żą

cych w

jednej płaszczy

ź

nie, to linie działania tych sił musz

ą

przecina

ć

si

ę

w jednym punkcie, a siły

tworzy

ć

trójk

ą

t zamkni

ę

ty.

12. Poda

ć

warunki równowagi płaskiego

ś

rodkowego układu sił (definicja, zapis).

Aby płaski układ sił zbie

ż

nych był w równowadze, warunkiem koniecznym i wystarczaj

ą

cym jest,

by sumy rzutów tych sił na dwie osie układu współrz

ę

dnych były równe zeru.

13. Poda

ć

warunki równowagi przestrzennego

ś

rodkowego układu sił (definicja, zapis).

Aby przestrzenny układ sił zbie

ż

nych był w równowadze,

warunkiem koniecznym i wystarczaj

ą

cym jest, by suma

rzutów tych sił na ka

ż

d

ą

o

ś

układu współrz

ę

dnych była

równa zeru.

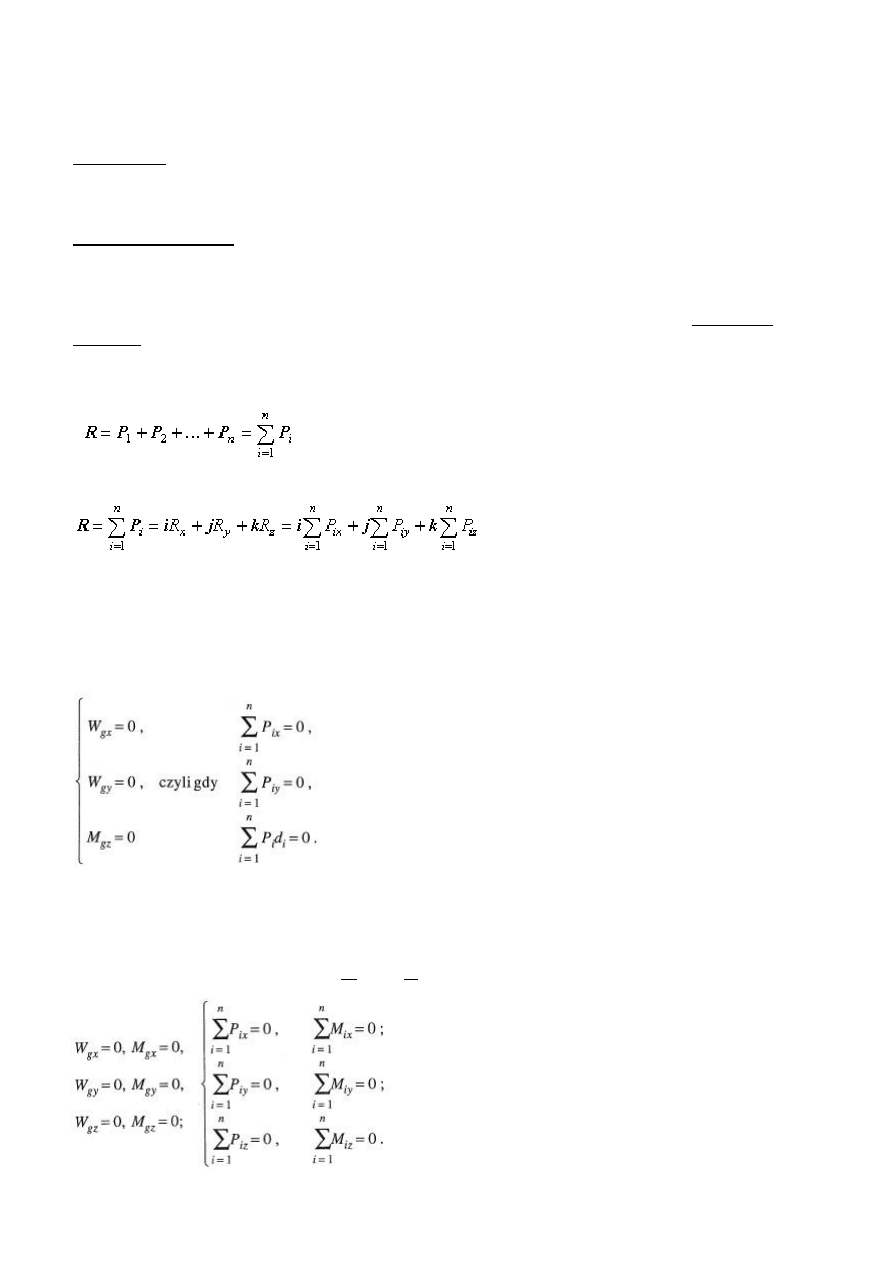
14. Poda

ć

definicj

ę

momentu siły wzgl

ę

dem punktu (bieguna).

Moment siły wzgl

ę

dem punktu jest to iloczyn warto

ś

ci siły i jej ramienia.

15. Poda

ć

definicj

ę

wektora głównego i momentu głównego (dla układu płaskiego sił).

Momentem głównym dowolnego układu sił na płaszczy

ź

nie wzgl

ę

dem przyj

ę

tego bieguna O

nazywamy sum

ę

algebraiczn

ą

momentów poszczególnych sił tego układu wzgl

ę

dem tego

samego bieguna O.

Dowolny przestrzenny układ sił działaj

ą

cych na ciało sztywne mo

ż

emy zast

ą

pi

ć

wektorem

głównym R, przyło

ż

onym do dowolnie wybranego

ś

rodka redukcji O, równym sumie

geometrycznej wszystkich sił układu oraz momentem głównym Mo, równym sumie
geometrycznej momentów tych sił wzgl

ę

dem

ś

rodka redukcji.

Wektor główny obliczamy ze wzoru:

lub je

ż

eli znane s

ą

składowe sił w prostok

ą

tnym układzie współrz

ę

dnych, wektor główny

obliczamy ze wzoru:

16. Poda

ć

warunki równowagi płaskiego dowolnego układu sił (definicja, zapis).

Warunkiem koniecznym i wystarczaj

ą

cym równowadze płaskiego dowolnego układu sił jest, aby

sumy algebraiczne rzutów sił na ka

ż

d

ą

z dwóch nierównoległych osi równały si

ę

zeru oraz suma

momentów sił wzgl

ę

dem dowolnie obranego bieguna na płaszczy

ź

nie działania tych sił była

równa zeru.









17. Poda

ć

warunki równowagi przestrzennego dowolnego układu sił:

Warunkiem równowagi przestrzennego dowolnego układu sił jest aby algebraiczne sumy rzutów
wszystkich sił na 3 osie prostok

ą

tnego układu współrz

ę

dnych były równe 0 oraz aby algebraiczne

sumy rzutów momentów wszystkich sił wzgl

ę

dem tych 3 osi były równe 0.

Przestrzenny dowolny

układ pozostaje w równowadze, gdy:

ܹ

g

= 0 i

ܯ

g

= 0

18. Poda

ć

wzory na okre

ś

lenie współrz

ę

dnych

ś

rodka ci

ęż

ko

ś

ci figury płaskiej.

F - pole figury płaskiej

19. Zdefiniowa

ć

momenty statyczne figury płaskiej wzgl

ę

dem osi.

Momentem statycznym figury płaskiej wzgl

ę

dem dowolnej osi nazywamy iloczyn pola tej figury i

współrz

ę

dnej

ś

rodka ci

ęż

ko

ś

ci tej figury wzgl

ę

dem tej samej osi.

20. Czym zajmuje si

ę

wytrzymało

ść

materiałów.

Wytrzymało

ść

materiałów zajmuje si

ę

badaniem zjawisk wyst

ę

puj

ą

cych w ciałach rzeczywistych,

to jest w ciałach odkształconych pod wpływem przyło

ż

onych do nich obci

ąż

e

ń

.

21. Jakie 4 warunki nale

ż

y spełni

ć

aby poprawnie zaprojektowa

ć

element konstrukcyjny z

punktu widzenia wytrzymało

ś

ci:

1. Warunek bezpiecze

ń

stwa - pozwala na ustalenie czy pod wpływem zało

ż

onego obliczenia

obci

ąż

enia element nie ulegnie zniszczeniu.

2. Warunek sztywno

ś

ci - umo

ż

liwia ograniczenie odkształce

ń

elementu tak, aby nie utrudniały

one b

ą

d

ź

wr

ę

cz nie uniemo

ż

liwiały nale

ż

ytego jego funkcjonowania.

3. Warunek stateczno

ś

ci - zabezpiecza niektóre elementy konstrukcyjne przed znacznymi

odkształceniami spowodowanymi obci

ąż

eniem,

ż

e powoduj

ą

zmian

ę

ich pierwotnej postaci , a

zatem zmian

ę

charakteru pracy tych elementów.

4. Warunek ekonomiczno

ś

ci konstrukcji - zapewnia wykonanie elementu z materiału najbardziej

odpowiedniego ze wzgl

ę

du na dany rodzaj obci

ąż

enia z równoczesnym pełnym wykorzystaniem

własno

ś

ci wytrzymało

ś

ciowych tworzywa.

22. Co rozumiemy pod poj

ę

ciem sił zewn

ę

trznych w wytrzymało

ś

ci materiałów?

Pod poj

ę

ciem sił zewn

ę

trznych rozumiemy siły czynne czyli obci

ąż

enia oraz siły bierne czyli

reakcje. Zarówno obci

ąż

enia i reakcje działaj

ą

na dane ciało z zewn

ą

trz.

23. Co rozumiemy pod poj

ę

ciem sił wewn

ę

trznych w wytrzymało

ś

ci materiałów?

Siły wewn

ę

trzne s

ą

to siły z jakimi oddziaływaj

ą

na siebie cz

ą

stki wewn

ą

trz ciała przeciwdziałaj

ą

c

ka

ż

dej zmianie odległo

ś

ci poszczególnych jego punktów.

24 Poda

ć

3 zasadnicze rodzaje obci

ąż

enia konstrukcji.

- rozci

ą

ganie ,

ś

ciskanie

- skr

ę

canie ,

ś

cinanie

- zginanie

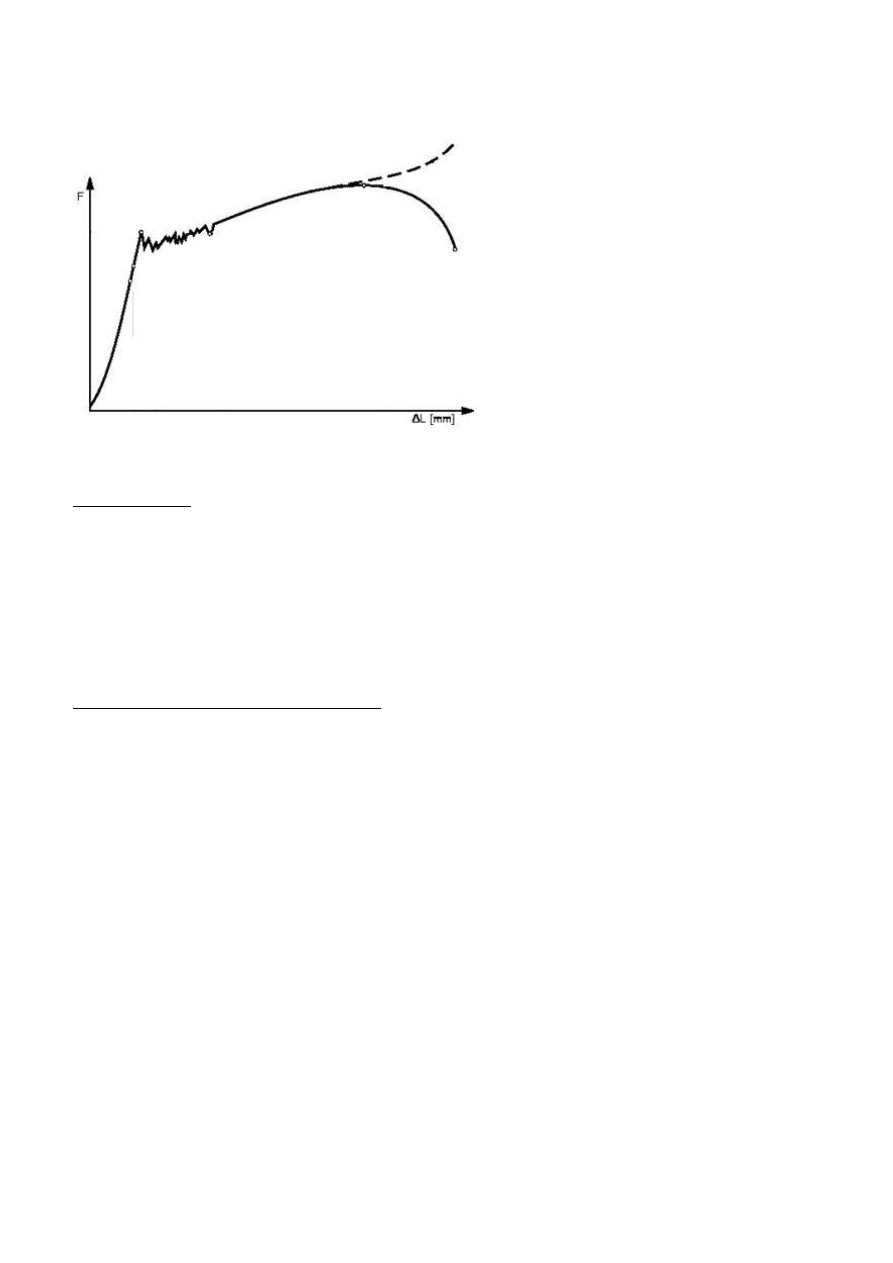
25. Wykres rozci

ą

gania dla stali mi

ę

kkiej.

26. Poda

ć

prawo Hooke'a dla rozci

ą

gania, co to jest sztywno

ść

pr

ę

ta na rozci

ą

ganie?

Prawo Hooke'a – prawo mechaniki okre

ś

laj

ą

ce zale

ż

no

ść

odkształcenia od napr

ęż

enia. Głosi

ono,

ż

e odkształcenie ciała pod wpływem działaj

ą

cej na

ń

siły jest wprost proporcjonalne do tej

siły. Ta prawidłowo

ść

pozostaje prawdziwa tylko dla niezbyt wielkich odkształce

ń

, nie

przekraczaj

ą

cych tzw. granicy Hooke'a (zwanej te

ż

granic

ą

proporcjonalno

ś

ci), i tylko dla

niektórych materiałów. Odkształcenie tego rodzaju znika, gdy przyło

ż

ona siła przestaje działa

ć

.

Współczynnik mi

ę

dzy sił

ą

a odkształceniem jest cz

ę

sto nazywany współczynnikiem (modułem)

spr

ęż

ysto

ś

ci.

27. Poda

ć

definicj

ę

momentu bezwładno

ś

ci figury płaskiej.

Momentem bezwładno

ś

ci figury płaskiej o polu F wzgl

ę

dem dowolnej osi le

żą

cej w płaszczy

ź

nie

figury nazywamy sum

ę

iloczynów elementarnej powierzchni dF figury i kwadratów ich odległo

ś

ci

od bieguna.

28. Poda

ć

wzór Steinera.

Moment bezwładno

ś

ci wzgl

ę

dem osi jest równy sumie momentu bezwładno

ś

ci wzgl

ę

dem

równoległej osi centralnej oraz iloczynu pola F figury i kwadratu odległo

ś

ci miedzy nimi.

29. Poda

ć

warunek wytrzymało

ś

ci elementu rozci

ą

ganego.

Gr < kr

Gr = P / F < kr

kr - wytrzymało

ść

na rozci

ą

ganie

30. Poda

ć

warunek wytrzymało

ś

ci elementu

ś

cinanego.

Tt < kt Tt = F / S < kt

kt - wytrzymało

ść

na

ś

cinanie

F - siła zewn

ę

trzna tn

ą

ca

S - pole przekroju poprzecznego

31. Poda

ć

warunek wytrzymało

ś

ci elementu skr

ę

canego.

Ts = Ms / Ws < ks

ks - wytrzymało

ść

na skr

ę

canie

Ms - moment skr

ę

caj

ą

cy

Ws - wska

ź

nik wytrzymało

ś

ci na skr

ę

canie

32. Poda

ć

warunek wytrzymało

ś

ci elementu zginanego.

Gg < kg

Gg = Mg max / Wg < kg

kg - wytrzymało

ść

na zginanie

Mg max - maksymalny moment gn

ą

cy

Wg - wska

ź

nik wytrzymało

ś

ci na zginanie Wg = Iz/ h max

33. Poda

ć

wzór na całkowity k

ą

t skr

ę

cania pr

ę

ta, co to jest sztywno

ść

pr

ę

ta na skr

ę

canie?

Sztywno

ść

pr

ę

ta na skr

ę

canie to iloczyn modułu Kirchhoffa i momentu bezwładno

ś

ci na

skr

ę

canie.

34. Poda

ć

wzór opisuj

ą

cy krzywizn

ę

zgi

ę

tej belki, co to jest sztywno

ść

zginania?

Sztywno

ść

zginania to iloczyn modułu Younga i głównego centralnego momentu bezwładno

ś

ci

przekroju.

35. Poda

ć

definicj

ę

wska

ź

nika wytrzymało

ś

ci przy zginaniu oraz co ten wska

ź

nik

charakteryzuje?

Wska

ź

nik wytrzymało

ś

ci na zginanie (wska

ź

nik zginania) to iloraz (głównego centralnego)

momentu bezwładno

ś

ci przez maksymaln

ą

odległo

ść

skrajnych włókien.

36. Co to jest warstwa oboj

ę

tna belki?

Warstwa oboj

ę

tna belki jest to warstwa wewn

ą

trz materiału, która nie jest ani rozci

ą

gana ani

ś

ciskana. W prostych belkach warstwa oboj

ę

tna przechodzi przez

ś

rodki ci

ęż

ko

ś

ci przekrojów.

37. Poda

ć

posta

ć

uproszczonego równania ró

ż

niczkowego linii ugi

ę

cia belki.

Ely'' = - Mg = - Py

El - najmniejsza sztywno

ść

na zginanie

Mg, Py - moment zginaj

ą

cy

38. Co nazywamy wyboczeniem? Poda

ć

stany równowagi pr

ę

ta

ś

ciskanego.

Pr

ę

ty charakteryzuj

ą

ce si

ę

znaczn

ą

długo

ś

ci

ą

i małymi wymiarami poprzecznymi przy pewnej

warto

ś

ci siły

ś

ciskaj

ą

cej P trac

ą

stateczno

ść

, to znaczy wychylaj

ą

si

ę

z poło

ż

enia równowagi ,

zjawisko takie charakteryzuj

ą

ce si

ę

wygi

ę

ciem osi pr

ę

ta nosi nazw

ę

wyboczenia.

39. Podaj wzór na warto

ść

siły krytycznej Eulera oraz poda

ć

jej definicj

ę

.

Siła krytyczna Eulera - siła krytyczna w zakresie liniowo spr

ęż

ystym.

40. Poda

ć

posta

ć

ogólnego wzoru Eulera.

41. Poda

ć

warunek ograniczaj

ą

cy stosowanie wzoru Eulera.

Obliczenia za pomoc

ą

wzoru Eulera mo

ż

emy przeprowadzi

ć

tylko wtedy, gdy smukło

ść

pr

ę

ta jest

wi

ę

ksza od smukło

ś

ci granicznej.

42. Jak

ą

warto

ś

ci

ą

mierzone jest wyt

ęż

enie materiału? Co to jest napr

ęż

enie zredukowane?

Wyt

ęż

enie materiału to w wytrzymało

ś

ci materiałów stan materiału obci

ąż

onego siłami

zewn

ę

trznymi, w którym istnieje niebezpiecze

ń

stwo przej

ś

cia w stan plastyczny (przekroczenie

granicy spr

ęż

ysto

ś

ci). Wyt

ęż

enie materiału okre

ś

la si

ę

przez redukcj

ę

zło

ż

onego stanu

napr

ęż

enia do jednego napr

ęż

enia zredukowanego lub zast

ę

pczego. To napr

ęż

enie mo

ż

e by

ć

porównane z podstawowymi wytrzymało

ś

ciowymi stałymi materiałowymi wytrzymało

ś

ci

ą

na

rozci

ą

ganie Rm lub napr

ęż

eniem rozrywaj

ą

cym Ru, które uzyskuje si

ę

w czasie statycznej próby

rozci

ą

gania.

Napr

ęż

enie zredukowane to wyznaczane na podstawie hipotez wytrzymało

ś

ciowych napr

ęż

enie

zast

ę

puj

ą

ce działanie wszystkich napr

ęż

e

ń

składowych w obci

ąż

onym ciele.

43. Poda

ć

zale

ż

no

ść

na napr

ęż

enia zredukowane według hipotezy Hubera.

44. Omów hipotez

ę

Hubera.

Hipoteza głosz

ą

ca,

ż

e miar

ą

wyt

ęż

enia materiału w dowolnym punkcie obci

ąż

onego (siłami) ciała

spr

ęż

ystego jest ta cz

ęść

energii spr

ęż

ystej materiału, która jest zwi

ą

zana z odkształceniem

postaciowym - tylko ten rodzaj odkształcenia ma wpływ na osi

ą

gniecie stanu krytycznego, który w

przypadku materiałów ci

ą

gliwych objawia si

ę

powstaniem trwałych odkształce

ń

plastycznych,

natomiast w przypadku materiałów kruchych powoduje p

ę

kni

ę

cia. Pozostała cz

ęść

energii

spr

ęż

ystej zwi

ą

zana ze zmian

ą

obj

ę

to

ś

ci ciała nie ma wpływu na wyt

ęż

enie, gdy

ż

odkształcenie

czysto obj

ę

to

ś

ciowe jest praktycznie zupełnie spr

ęż

yste (nie narusza spójno

ś

ci materiałów).

Według hipotezy Hubera mo

ż

na obliczy

ć

napr

ęż

enie zredukowane dla dowolnego

trójwymiarowego stanu napr

ęż

enia.

45. Wymieni

ć

podstawowe przypadki wytrzymało

ś

ci zło

ż

onej.

- zginanie uko

ś

ne

- zginanie poł

ą

czone z rozci

ą

ganiem lub

ś

ciskaniem

- zginanie poł

ą

czone ze skr

ę

cananiem

- ogólny przypadek wytrzymało

ś

ci zło

ż

onej czyli poł

ą

czenie roci

ą

gania, zginania i skr

ę

cania

46. Poda

ć

wzory na moment zredukowany przy zginaniu ze skr

ę

caniem

a) wg hipotezy Hubera
b) wg hipotezy najwi

ę

kszych napr

ęż

e

ń

stycznych

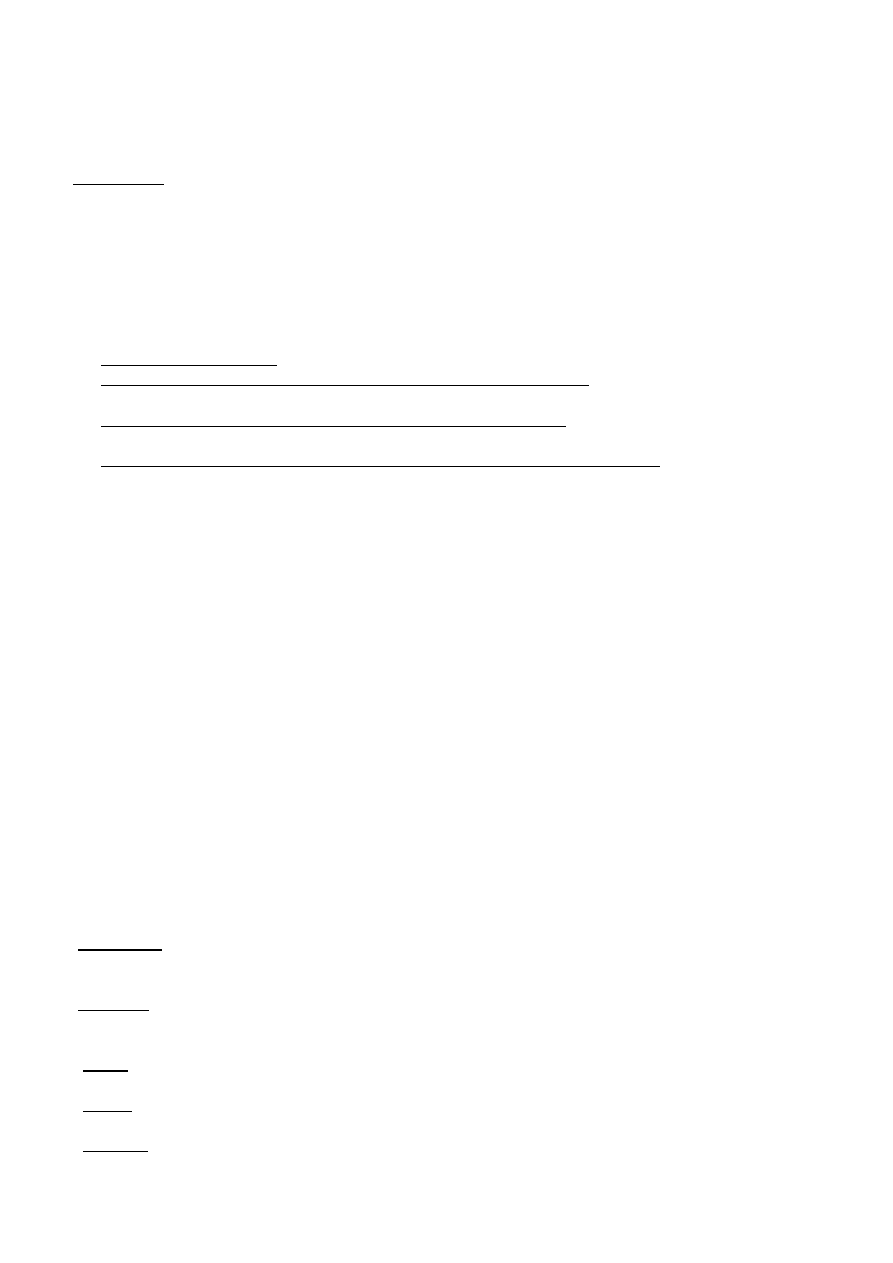
47. Czym si

ę

zajmuje kinematyka? Podział kinematyki.

Kinematyka jest działem mechaniki zajmuj

ą

cym si

ę

badaniem ruchu ciał bez uwzgl

ę

dnienia sił

powoduj

ą

cych ten ruch.

Dzielimy j

ą

na :

- kinematyk

ę

punktu

- kinematyk

ę

ciała stałego

48.Wymieni

ć

sposoby opisania ruchu punktu.

1) przez podanie wektora - promienia wodz

ą

cego punkt ruchomy w funkcji czasu,

2) przez podanie współrz

ę

dnych kartezja

ń

skich jako funkcji czasu, czyli tak zwanych równa

ń

sko

ń

czonych ruchu,

3) przez podanie toru i współrz

ę

dnej krzywoliniowej wzdłu

ż

toru, okre

ś

laj

ą

cej sposób poruszania

si

ę

po torze,

4) przez podanie innych współrz

ę

dnych krzywoliniowych jako funkcji czasu np: biegunowych,

walcowych, sferycznych.

49. Przyspieszenie punktu w ruchu krzywoliniowym.

Ruch odbywaj

ą

cy si

ę

ze stał

ą

warto

ś

ci

ą

pr

ę

dko

ś

ci liniowej po dowolnej krzywej. Szczególnym

przypadkiem ruchu jednostajnego krzywoliniowego jest ruch jednostajny po okr

ę

gu.

50. Poda

ć

klasyfikacj

ę

ruchu punktu ze wzgl

ę

du na tor.

1. Ruchy prostoliniowe
2. Ruchy krzywoliniowe
- ruchy płaskie (na płaszczy

ź

nie)

- ruchy przestrzenne

51. Poda

ć

klasyfikacj

ę

ruchu punktu ze wzgl

ę

du na sposób poruszania si

ę

po torze.

- jednostajny
- jednostajnie zmienny
- ruch zmienny
- ruch okresowy

52. Poda

ć

klasyfikacj

ę

ruchów brył.

-post

ę

powy - dowolna prosta przeprowadzona przez brył

ę

sztywn

ą

przesuwa si

ę

równolegle do

samej siebie, wektory pr

ę

dko

ś

ci wszystkich punktów bryły sztywnej s

ą

w danej chwili jednakowe

-obrotowy - wszystkie punkty bryły sztywnej poruszaj

ą

si

ę

po okr

ę

gach, których

ś

rodki le

żą

na

jednej wspólnej prostej zwanej chwilow

ą

osi

ą

obrotu

- płaski

- kulisty

- dowolny

53. Zapisa

ć

zwi

ą

zek mi

ę

dzy pr

ę

dko

ś

ci

ą

obrotow

ą

, a pr

ę

dko

ś

ci

ą

k

ą

tow

ą

.

Dla n-tego punktu o wektorze wodz

ą

cym , relacja mi

ę

dzy pr

ę

dko

ś

ci

ą

liniow

ą

oraz

pr

ę

dko

ś

ci

ą

k

ą

tow

ą

(obrotow

ą

) jest opisana zwi

ą

zkiem:

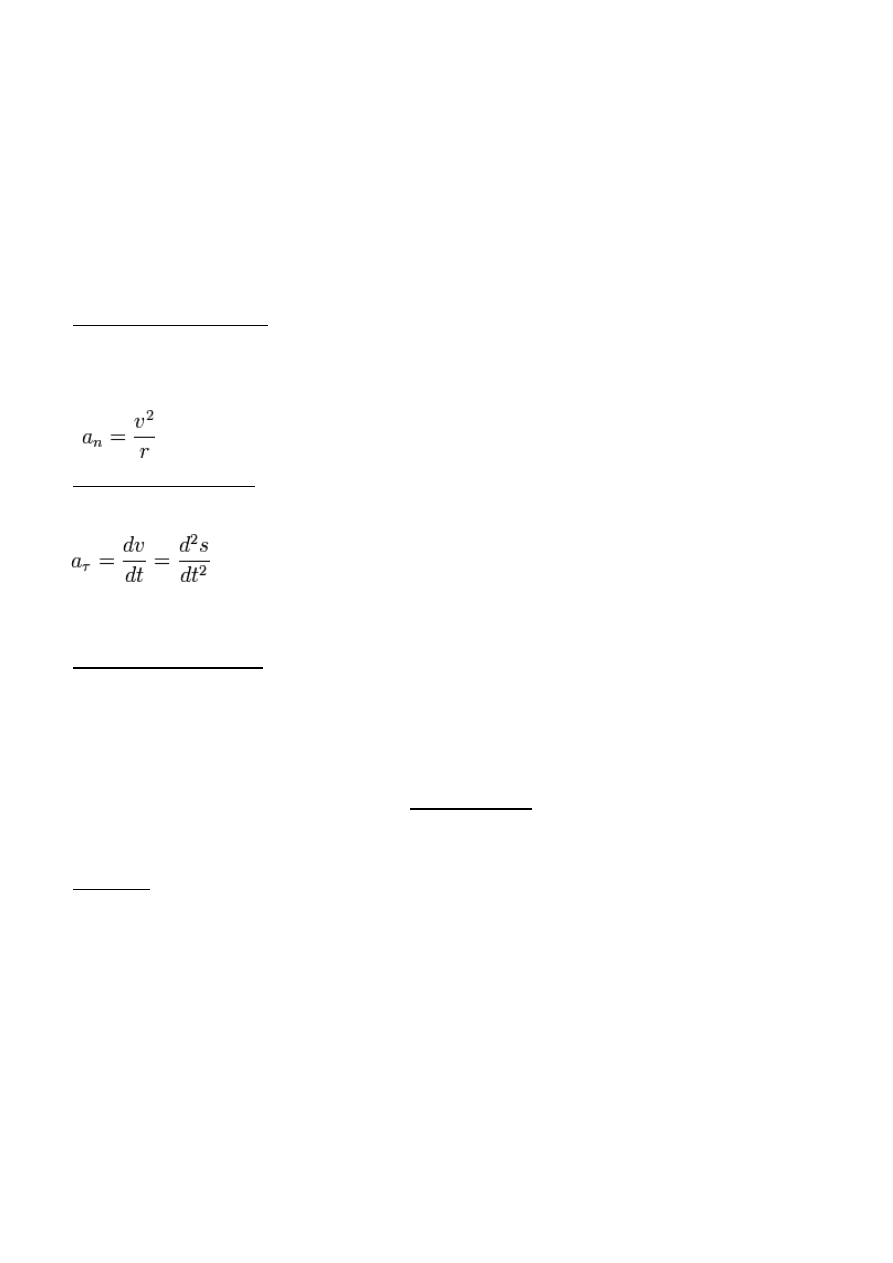
54. Jak wyznaczamy przyspieszenie styczne i normalne punktów w ruchu obrotowym?

Przyspieszenie normalne (do

ś

rodkowe) to składowa przyspieszenia prostopadła do toru ruchu.

Reprezentuje t

ę

cz

ęść

przyspieszenia, która wpływa na kierunek pr

ę

dko

ś

ci, a zatem na kształt

toru. Je

ż

eli pr

ę

dko

ść

chwilowa oznaczona jest jako v, a promie

ń

chwilowego zakrzywienia toru

(promie

ń

okr

ę

gu stycznego do toru) ruchu wynosi r, to warto

ść

an przyspieszenia do

ś

rodkowego

ciała jest równa:



Przyspieszenie styczne to składowa przyspieszenia styczna do toru ruchu, wpływaj

ą

ca na

warto

ść

pr

ę

dko

ś

ci. Stosuj

ą

c oznaczenie v dla warto

ś

ci pr

ę

dko

ś

ci chwilowej i oznaczenie s dla

drogi pokonanej przez ciało, przyspieszenie styczne okre

ś

laj

ą

wzory:

55. Omówi

ć

własno

ś

ci przyspieszenia Coriolisa.

Przyspieszenie Coriolisa jest podwójnym iloczynem wektorowym pr

ę

dko

ś

ci k

ą

towej i pr

ę

dko

ś

ci

wzgl

ę

dnej. To przyspieszenie wyst

ę

puje w geometrycznej sumie przyspieszenia bezwzgl

ę

dnego

punktu.

56. Poda

ć

definicj

ę

ruchu płaskiego bryły.

Je

ż

eli wszystkie punktu bryły poruszaj

ą

si

ę

w płaszczyznach równoległych do pewnej

płaszczyzny nieruchomej, to ruch bryły jest ruchem płaskim.

57. Czym zajmuje si

ę

dynamika?

Dynamika jest działem mechaniki zajmuj

ą

ca si

ę

badaniem ruchu ciał pod wpływem działa sił.

Zajmuje si

ę

przyczynami i skutkami ruchów oraz ustala zale

ż

no

ść

mi

ę

dzy ruchem ciał a siłami

oddziałuj

ą

cymi na nie.

58. Poda

ć

definicj

ę

drugiego prawa Newtona.

Je

ś

li siły działaj

ą

ce na ciało nie równowa

żą

si

ę

(czyli siła wypadkowa jest ró

ż

na od zera), to ciało

porusza si

ę

z przyspieszeniem wprost proporcjonalnym do siły wypadkowej, a odwrotnie

proporcjonalnym do masy ciała.

n

r

r

n

v

r

ω

r

n

n

v

r

ω

= ×

r

r

r

59. Wymieni

ć

dwa podstawowe zadania dynamiki punktu (na czym polega rozwi

ą

zywanie

obu zada

ń

).

Zadania proste (pierwsze) - polega na wyznaczeniu sił działaj

ą

cych na punkt materialny, którego

ruch jest znany.

Zadania odwrotne (drugie) - polega na okre

ś

leniu ruchu punktu materialnego gdy znamy siły

działaj

ą

ce.

60. Zdefiniowa

ć

prac

ę

stałej siły na przesuni

ę

ciu prostoliniowym. Poda

ć

jednostk

ę

pracy.

Praca stała co do warto

ś

ci siły na przesuni

ę

ciu prostoliniowym jest to iloczyn skalarny wektora

siły i wektora przesuni

ę

cia punktu jej przyło

ż

enia. Jednostka pracy jest wat.

61. Poda

ć

definicj

ę

sprawno

ś

ci mechanicznej.

Sprawno

ść

mechaniczna (moc siły)

to praca odniesiona do jednostki czasu.

62. Poda

ć

wzór na energi

ę

kinetyczn

ą

ciała w ruchu post

ę

powym.

63. Poda

ć

wzór na energi

ę

kinetyczn

ą

ciała w ruchu obrotowym.

64. Co nazywamy energi

ą

mechaniczn

ą

. Jak brzmi zasada zachowania energii

mechanicznej.

Energi

ą

mechaniczn

ą

nazywamy geometryczn

ą

sum

ę

energii kinetycznej i potencjalnej.

Zasada zachowania energii mówi,

ż

e suma energii kinetycznej i potencjalnej w polu potencjalnym

jest wielko

ś

ci

ą

stał

ą

.