Maszyna hydrauliczna (przepływowa)
Urządzenie, w którym zmienia się energia całkowita przepływającego płynu (cieczy) wskutek wykonania przez płyn pracy mechanicznej lub wskutek pobrania przez płyn energii mechanicznej.
Chodzi tu o bezpośrednie przekazywanie energii do płynu (maszyny robocze, wentylatory, sprężarki, pompy) lub od płynu (turbiny wodne, parowe lub gazowe). Płyn styka się bezpośrednio z elementami maszyn, wywierając na elementy maszyny odpowiednie siły i momenty
Najprostsza maszyna przepływowa
Teoria maszyny przepływowej - zespół równań (związków) wyrażających oddaną przez maszynę lub dostarczoną do maszyny energię mechaniczną w funkcji parametrów geometrycznych i kinematycznych maszyny oraz parametrów płynu na wlocie do maszyny a więc w funkcji kształtu, wymiarów, liczby obrotów oraz ciśnienia na wlocie prędkości.
Silniki przepływowe - turbiny wodne, parowe, gazowe, (koło wodne)
Maszyny robocze - - pompy tłokowe
pompy wirowe
wentylatory (osiowe, promieniowe itp.)
sprężarki
dmuchawy
Turbiny wodne -
natryskowa tzw. turbina Peltona
naporowa, tzw. turbina Francisa (promieniowa)
turbina Kaplana (osiowa
Turbina Peltona
Turbina Francisa
Turbina Kaplana
Pompy tłokowe
Zasada działania pompy tłokowej- okresowe przenoszenie ściśle określonych objętości cieczy z tzw. Obszaru ssania do tzw. Obszaru tłoczenia. Przemieszczenie cieczy wywołane jest odpowiednim ruchem organu czynnego pompy tj. tłokiem. W pompach tłokowych dostarczona tłokowi energia mechaniczna zamieniana jest bezpośrednio na energię potencjalną cieczy, w szczególności idzie ona na przyrost ciśnienia statycznego
Pompy wirowe
Składają się z trzech zasadniczych części: wirnika, kierownicy i korpusu. Kierownica nie zawsze występuje, a jej role odgrywa odpowiednio ukształtowany korpus tzw. Spirala wylotowa.
Zasada działania: polega na zwiększeniu energii kinetycznej cieczy przepływającej przez pompę, a nastepnie przekształceniu energii kinetycznej na ciśnienie w kierownicy lub w spirali wylotowej
![]()
Napiszmy na bazie równania Bernoulliegobilans energii cieczy przez wirnik:
Gdzie ρghL wartość energii mechanicznej jaką oddaje lub pobiera 1 kg płynu w jednostce czasu przepływając przez wirnik. Przy czym energia oddana przez płyn ma znak dodatki (silniki), zaś pobrana przez płyn ujemny (pompy, wentylatory).
Obliczmy zatem następnie przyrost ciśnienia p1-p2 podczas przepływu przez wirnik.
Napiszmy równanie Bernoulliego w układzie związanym z wirnikiem, w tym układzie ruch może być traktowany jako ustalony
![]()
potencjał sił odśrodkowych i masowych
![]()
Pierwsza postać równania teorii maszyn hydraulicznych
![]()
Po podstawieniu otrzymamy
Skąd po przekształceniach otrzymamy
![]()
Po wykorzystaniu równania (1) otrzymamy
![]()
![]()
Równanie teorii maszyn wirnikowych
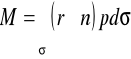
Moment działający na wirnik
Zgodnie ze wzorem na moment ၳ - pole powierzchni łopatek
Zastosujemy go do przestrzeni międzyłopatkowej.
![]()
Całki po powierzchniach
![]()
![]()
![]()
![]()
Drugie równanie maszyn przepływowych
Pozostanie nam zatem:
![]()
![]()
Jest to tzw. Druga postać podstawowego równania maszyn przepływowych.
Sprawność
![]()
Rozporządzalna wysokość cieczy H tylko częściowo można wykorzystać na wytworzenia w silniku energii mechanicznej użytecznej, część naporu e idzie na pokonanie opoow ruchu wywołanych lepkością płynu, pozostała część wysokości H na wytworzenie nergii kinetycznej v2/2g, z jaką płyn opuszcza rurę ssąca. Zatem dla silników można napisać
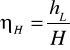
Sprawność ၨH energii mechanicznej wytworzonej w urządzeniu do rozporządzalnej wysokości H
Wtedy równanie podstawowe silników hydraulicznych będzie
![]()
Sprawność hydrauliczna wynosi ၨH = 0,8 Ⴘ 0,93 energii rozporządzalnej
Podobieństwo przepływu przez maszyny przepływowe
![]()
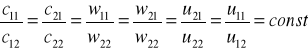
![]()
![]()
Ale
![]()
zatem
Ponieważ wydatek dany jest wzorem Q1 = 2ၰ r1 b1 c1 sinၡ1 = 2ၰ r2 b2 c2 sinၡ2
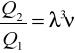
Skąd stosunek wydatków
Zakładając równe sprawności obu maszyn obliczymy stosunek sprężów
![]()
![]()
Podobnie stosunek mocy
![]()
![]()
Wyróżnik szybkobieżności - podstawowy parametr podobieństwa maszyn przepływowych, nazywamy liczbe obrotów wzorcowej maszyny przepływowej podobnej geometrycznie do konkretnej rozpatrywanej maszyny i rozwijającej jednostkowa moc przy jednostkowej spiętrzeniu (wysokości, naporze). W tym celu rugujemy l ze wzorów na podobieństwo (spiętrzenie i moc) i otrzymamy wtedy:
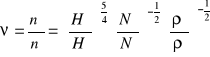
![]()
![]()
RUCH TURBULENTY
Ruchem turbulentnym nazywamy zatem ruch cieczy odpowiadający brakowi stateczności rozwiązań stacjonarnych a odznaczającymi się nieregularnymi i szybko zmieniającymi się w czasie liniami prądu.
Te trudności w rozwiązaniu niestacjonarnego układu równań zrodziły koncepcję opisu ruchu turbulentnego w oparciu o uśrednienie parametrów przepływu. Doprowadziło to w konsekwencji do równań Reynoldsa.
Teoria turbulencji jest również oparta o tą koncepcję uśredniania przepływu.
Uśredniane parametry przepływu są łatwo mierzalne, co umożliwia łatwą weryfikację eksperymentalną.
Równania Reynoldsa nie są niestety zamknięte, stąd konieczność sformułowania dodatkowych równań i hipotez oraz modeli turbulencji.
Teoria turbulencji jest daleka wciąż od zakończenia. Stąd też wynikła konieczność rozpatrywania uproszczonych równań Naviera - Stokesa np. równań warstwy przyściennej.
Rozwiązania równań Naviera - Stokesa należy traktować dla przypadku ruchu stacjonarnego np. przepływ Hagena - Poisseuille'a jako pewnego rodzaju abstrakcję. Takiego idealnego ruchu nie spotkamy ani w naturze, ani w technice.
Ruchy płynów są zawsze w rzeczywistości niestacjonarne. Ruchy takie jako przepływy stacjonarne realizuje się tylko wtedy, gdy są stateczne (stabilne) względem małych zaburzeń.
Przepływy stabilne względem małych zaburzeń nazywamy zatem laminarnymi (przesuwające się po warstwach, bo lamina- warstwa).
Natomiast przepływy niestabilne i nieuporządkowane nazywamy przepływami turbulentnymi.
Doświadczenie Reynoldsa ---- dowód niestabilności i przejścia do turbulencji
Stateczność ruchu cieczy w rurze o przekroju kołowym.
Szklana rura z zaworem z1 regulacyjnym wydatek wody ze zbiornika A, zbiornik B z zaworem z2 z zabarwioną cieczą o tym samym ciężarze (gęstości). Ciecz tę można wpuszczać do rury szklanej regulując zawór z2.
Jeśli wydatek wody jest dostatecznie mały, to smuga zabarwionej cieczy jest prostoliniowa, nie miesza się z wodą i sprawia wrażenie nieruchomej (Rys. a)
Przy wzroście wydatku wody smuga barwna traci nieruchomość, zaczyna oscylować i falisto wyginać się, nie mieszając się z wodą, granica smugi i otaczającej wody jest ostra i nie rozmyta (Rys. b).
Zwiększając dalej wydatek wody widzimy, że smuga miesza się z wodą tuż za wylotem rurki doprowadzającej zabarwioną ciecz. (Rys. c)
Reynolds wprowadził podział na dwa rodzaje ruchów:
1) Laminarny (Rys. a) (lamina - łuska (łac.)) „warstwy” cieczy nie mieszają się ze sobą, ślizgają się po sobie na kształt łusek
2) Turbulentny (burzliwy) - niestacjonarność, przypadkowość i chaotyczność to główne cechy toru elementów płynu całkowicie różne od siebie, nie można wyróżnić tu niezależnych warstw, występuje silne mieszanie oprócz ruchu głównego. Wzdłuż osi przypadkowe ruchy w poprzek strumienia.
Badania eksperymentalne ruchu płynów wskazują na istnienie dwóch rodzajów ruchu:
- laminarnego
- turbulentnego
W odróżnieniu od przepływu laminarnego ruch turbulentny charakteryzuje się dużym chaosem, mieszaniem się warstw płynu.
Ruch turbulentny płynu opisuje się równaniami Reynoldsa,
otrzymanymi w procesie uśredniania równań Naviera - Stokes'a.
![]()
![]()
Jeżeli dla dowolnej wielkości charakteryzującej przepływ (prędkość, ciśnienie, gęstość) założymy, że jej wartość chwilowa składa się z wartości uśrednionej w czasie i pewnego odchylenia od niej tj. fluktuacji np.:
![]()
![]()
![]()
![]()
![]()
Równania turbulentnego ruchu płynu
![]()
Podstawienie do równań Naviera - Stokes'a równań (1), wykonanie operacji uśredniania prowadzi do równania:
![]()
Dodatkowe składniki w równaniach ruchu są różniczkami odpowiednich składników tensora naprężeń turbulentnych:
Tensor ten jest symetryczny, a zawiera „tylko” sześć nieznanych wartości.
![]()
Równania ruchu płynu uzupełnione równaniami ciągłości przepływu dla przepływu uśrednionego i fluktuacyjnego
i თბ u' = 0
![]()
stanowią układ równań Reynoldsa dla płynu nieściśliwego. Dla przepływu ściśliwego należy ponadto uwzględnić fluktuacje gęstości i temperatury
![]()
i
Dla przepływu nieściśliwego cztery równania Reynoldsa zawierają 10 niewiadomych,
![]()
![]()
uśrednione ciśnienie , trzy składowe uśrednionej prędkości i sześć składowych
![]()
tensora naprężeń turbulentnych
Zamknięcie tego układu równań wymaga wprowadzenia dodatkowych hipotez zamykających określających składowe tensora naprężeń turbulentnych, np.:
- hipoteza Boussinesqa
- hipoteza drogi mieszania Prandtla
- hipoteza drogi mieszania Karmana
- model K - ၥ, itp. ...
![]()
Hipotezy zamykające wnoszą do układu równań nowe równania będące wyrazem zastosowanych modeli turbulencji, ponieważ opisują one własności płynu - podobnie jak hipoteza Newtona lepkości płynu, to równania te można zaliczyć do równań konstytutywnych charakteryzujących przepływ turbulentny.
Tensor naprężeń Reynoldsa
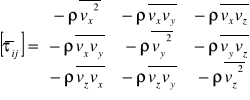
![]()
Obliczmy zatem dowolną składową całkowitą tensora naprężeń w uśrednionym ruchu turbulentnym np. pzx
![]()
Zakładając oczywiście, że tensor prędkości deformacji Td odnosi się do przepływu uśrednionego, wtedy poniższe wyrażenie nazywamy lepkością turbulentną.
Przepływ turbulentny
W odróżnieniu od lepkości dynamicznej (molekularnej) ၭ, która jest wielkością charakteryzującą płyn, a więc stałą materiałową, wielkość A charakteryzuje stan ruchu turbulentnego w danym punkcie.W pobliżu ścianki ciała stałego jest zawsze A = 0, pulsacje turbulentne przy ściance są bowiem równe zeru.
Natomiast w pewnej odległości od ścianki mogą przybierać wartości wielokrotnie wyższe od ၭ. Dlatego też opory przepływu turbulentnego są większe od oporów przepływu laminarnego. Zatem źródłem dodatkowych naprężeń stycznych jest wymiana pędu między warstwami płynu, reprezentowane przez uśrednione iloczyny pulsacji składowych prędkości.
Równania Naviera - Stokes'a opisują zarówno laminarny jak i niestacjonarny ruch płynu, mimo braku zamkniętych rozwiązań tych równań. Równania Reynoldsa są również wyprowadzane z równań Naviera - Stokes'a.Ruch turbulentny jest zawsze trójwymiarowy i niestacjonarny. Rozwiązanie równań Reynoldsa również nie jest proste ani łatwe, gdyż wymagają dodatkowych warunków na składowe tensora naprężeń turbulentnych.
Tensor naprężeń turbulentnych wprowadza do równań Reynoldsa sześć dodatkowych niewiadomych, równania Reynoldsa są zatem otwarte tj. więcej niewiadomych niż równań.
Problem zamknięcia równań Reynoldsa
- uzupełnienie układu równań ruchu
- podstawowa trudność w teorii przepływów turbulentnych.
Rozwiązanie problemu, to kreowanie modeli turbulencji:
Konstruowanie modeli turbulencji
- hipotezy łączące tensor naprężeń turbulentnych z uśrednionymi charakterystykami pola prędkości, zwykle charakter empiryczny- uśrednianie przekształconych równań Naviera - Stokes'a i analiza związków korelacyjnych pomiędzy nimi, są to modele analityczne
Modele eksperymentalne są łatwiejsze, bo można po prostu odpowiednie korelacje prędkości pomierzyć.
Model Bousinesqa
![]()
![]()
ၭB - lepkość turbulentna, wg Boussinesqa wielkość skalarna
![]()
tensor prędkości odkształceń uśrednionych
Pole turbulencji jest jednak trójwymiarowe, stąd ၭB - tensor
Hipotez ta postuluje zatem istnienie „płynu turbulentnego”
Model Prandtla - drogi mieszania
![]()
Dotyczy w zasadzie jednowymiarowego przepływu ścinającego.
![]()
, jeśli założyć
![]()
![]()
to
- droga mieszania
![]()
Wiry turbulentne zderzają się ze sobą na podobieństwo zderzeń międzycząsteczkowych, droga mieszania jest zatem analogiem drogi swobodnej ruchu cząsteczek.
Prandtl postulował lp = ၫ y ၫ - stała wyznaczana empirycznie
Wtedy, w modelu Prandtla współczynnik lepkości zależy od gradientu prędkości.
![]()
Model von Karmana
Dotyczy przepływu ścinającego daleko od ściany Jako funkcje można więc załóżyć, że
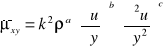
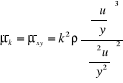
Po analizie wymiarowej a = 1, b = 3, c = - 2, skąd ostatecznie
![]()
A więc droga mieszania
Karman przypuszczał, że współczynnik k jest stałą uniwersalną.
Pomiary jednak tego nie potwierdziły.
Model Kołmogorowa
Model Kołmogorowa - za pomocą analizy wymiarowej dla turbulencji izotropowej i jednorodnejSą one jednak niezależne od równań Naviera - Stokes'a, stanowią więc pewien empiryczny model turbulencji.
l - skala dużych wirów, skala zewnętrzna turbulencji
ၨ - skala małych wirów ulegających dyssypacji
lo - skala molekularna, określająca lepkość molekularną.
Turbulencja - proces podtrzymywany przez przekazywanie energii ruchu głównego do dużych wirów o skali l, a następnie ich rozpad poprzez coraz mniejsze wiry aż do skali ၨ, które ulegają dyssypacji dzięki lepkości zmieniając formę energii kinetycznej tych wirów w energię cieplną na poziomie skali lo
Model Kołmogorowa - za pomocą analizy wymiarowej dla turbulencji izotropowej i jednorodnej. Są one jednak niezależne od równań Naviera - Stokes'a, stanowią więc pewien empiryczny model turbulencji.
l - skala dużych wirów, skala zewnętrzna turbulencji
ၨ - skala małych wirów ulegających dyssypacji
ၸ - skala molekularna, określająca lepkość molekularną.
Intensywność dyssypacji: moc dyssypacji na jednostkę masy
![]()
ၱ - temperatura
![]()
- intensywność objętościowych źródeł entropii
Skale Kołmogorowa
![]()
Skala długości ၮ - lepkość kinematyczna
ၥ - intensywność dyssypacji![]()
skala czasu
![]()
skala prędkości
![]()
Na poziomie wirów dyssypujących się w skali ၨ siły bezwładności są tego samego rzędu co siły lepkości, bo liczba Reynoldsa równa jest jedności.
Proces przekazywania energii z ruchu głównego do poziomu dysypacji następuje z
Intensywnością określoną intensywnością dysypacji ၥ
Model k-ၥ
Model K - ၥ (Spalding - Launder) inaczej model dwurównaniowy
Szeroko stosowany w obliczeniach numerycznych.
Opiera się na dodatkowych półempirycznych równaniach
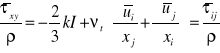
![]()
k - energia kinetyczna ruchu fluktuacyjnego płynu
![]()
ogólnie lepkość turbulentna
ၮt = ၮt (k, ၥ) , a więc ၥ - prędkość dyssypacji
Równania na transport ၥ i k
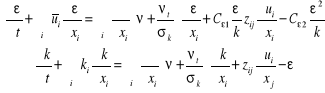
Stałe modelu: Cၭ = 0,09, ၳ k = 1,0, ၳ ၥ = 1,03, Cၥ 1 = 1,44, Cၥ 2 = 1,92
Stałe są wyznaczane przez porównanie z wynikami eksperymentu w stosunkowo prostych geometriach, jak ślad aerodynamiczny lub prosty kanał.
Są to więc równania transportu ၥ i k, energii dysypacji i energii kinetycznej fluktuacji.
Podobieństwo geometryczne - dwa obiekty geometryczne są podobne, gdy można dobrać tak układy współrzędnych dla obu obiektów aby każdemu punktowi jednego obiektu odpowiadał jeden i tylko jeden punkt drugiego obiektu.
Inaczej mówiąc stosunek współrzędnych odpowiadających sobie punktów jest stały.
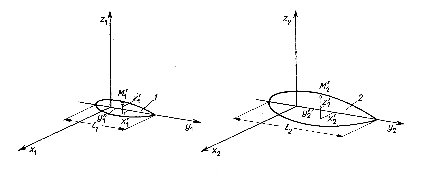
Oba układy muszą być ponadto jednakowe pod względem formalnym (tzn. prawo- lub lewoskrętne jednocześnie)
Ustalony laminarny ruch cieczy lepkiej. Kryteria podobieństwa
![]()
równanie ciągłości
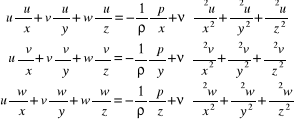
równania ruchu
ၲ = const, ၮ = const
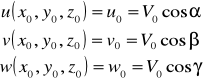
ścianki ciała stałego dane następującym równaniem f(x, y, z) = 0 i dla nich u =v=w=0
Należy następnie sprowadzić do postaci bezwymiarowej:
x = lX, y = lY, z = lZ; u = uV0 v = vV0 w = wV0, p = po P
![]()
Po podstawieniu otrzymamy:
równanie ciągłości
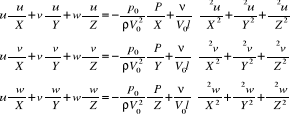
u(Xo, Yo, Zo) = cosၡ, v(Xo, Yo, Zo) = cosၢ, w(Xo, Yo, Zo) = cosၧ
p(Xo, Yo, Zo) = 1 oraz u = v = w = 0 na ścianach f(X, Y, Z) = 0
Kryteria podobieństwa
Dwa przepływy stacjonarne cieczy lepkiej będą podobne, gdy
1) Powierzchnie graniczne będą geometrycznie podobne
2) Bezwymiarowe stałe parametry utworzone ze stałych i charakterystycznych dla przepływu wielkości po, Vo, ၲ, ၮ, l , i będą jednakowe dla obu przepływów
![]()
![]()
3) Kierunki prędkości względem powierzchni brzegowych w dwu odpowiadających sobie punktach będą jednakowe
![]()
![]()
Np. przepływy przez rurę prostoosiową będą równe, gdy
Są to kryteria podobieństwa rozpatrywanych przepływów laminarnych
Bezwymiarowe kombinacje wielkości fizycznych stanowiące o podobieństwie nazywamy parametrami podobieństwa.Kryterium podobieństwa oznacza zatem równość odpowiednich parametrów podobieństwa porównywanych zjawisk.Parametry te noszą zwykle nazwy od nazwisk uczonych, którzy pierwsi je wprowadzili i używali
![]()
Re- liczba Reynoldsa
![]()
Eu - liczba Eulera
Opór ciała opływanego cieczą lepką
Całka po całej powierzchni ciała i po wprowadzeniu wzorów na składowe
![]()
opór ciśnienia opór tarcia
A więc opór całkowity X jest sumą dwóch składników
X = Xc + Xt
W cieczy nielepkiej opór tarcia Xt = 0, bo nie występują naprężenia styczne, zaś opór ciśnienia na mocy paradoksu d'Alamberta jest też równy zeru.
W cieczy lepkiej oba składniki oporu są różne od zera.
Pojęcie oporu profilowego Xp
Dodatkowo pojęcie oporu profilowego Xp
Różnica pomiędzy oporem całkowitym ciała X opływanego cieczą lepką a oporem Xid jakiego doznawałoby ciało opływane cieczą doskonałą bez obszaru zastoju
X = Xp + Xid
W przepływie płaskim opór całkowity ciała o wymiarach ograniczonych jest równy oporowi profilowemu bowiem opór Xid jest równy zeru na mocy paradoksu d'Alamberta.
Podobnie jest dla ciał płaskich półnieskończonych.
Oderwanie warstwy przyściennej
Oderwanie warstwy przyściennej (laminarnej, stacjonarnej)
Wynika bezpośrednio z równań Prandtla i warunków brzegowych.
W punktach na ściance,
![]()
![]()
gdzie i
![]()
mamy
![]()
znak jest zatem jednoznacznie określony znakiem gradientu ciśnienia
wzdłuż ścianki.
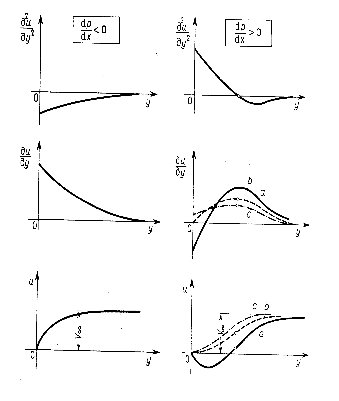
Podstawowa różnica:
![]()
1. Krzywa wypukła
![]()
2. krzywa ma zawsze
punkt przegięcia.
Oderwanie przepływu nastąpi w przypadku 2 a), czyli jako obszar z ujemną prędkością u(y)
Za punkt oderwania przepływu uznajemy
![]()
punkt, w którym
Interpretacja, dwie siły działają na element płynu poruszający się wzdłuż ścianki
- siły tarcia o ściankę
- siły normalnej do ścianki ciała stałego wynikającej z różnicy ciśnień na przedniej i tylnej ściance elementu płynu
W przypadku dp/dx > 0 obie te siły są przeciwne do zwrotu prędkości elementu płynu. Element traci swą energię kinetyczną i zatrzymuje się, a elementy podążające za nią (i on sam) odrywają się od ścianki.
Dla dp/dx < 0 siła wynikająca z różnicy ciśnień na przedniej i tylnej ściance elementu jest zgodna z prędkością tego elementu i oderwanie nie następuje.
Opływ wokół profilu: a) bez oderwania b) z oderwaniem
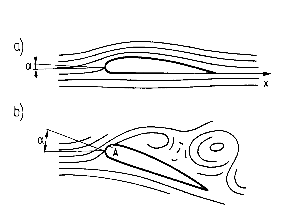
Warstwa przyścienna
Koncepcja warstwy przyściennej
W przypadku dużych liczb Reynoldsa nie można linearyzować równania Naviera - Stokesa za pomocą uproszczeń prowadzących do równania Stokes'a i Oseena tj. odrzucenia członu nieliniowego lub zostawienie tylko jego części
![]()
![]()
Każda część członu nieliniowego może być większa od , zaś odrzucenie członu ၄v/Re prowadzi do równania Eulera, a więc w ogóle nie uwzględnia lepkości.
Koncepcja Prandtla
W całkowitym obszarze przepływu wyróżnił dwa podobszary:
- sąsiedztwo ścianek ciała - warstwa przyścienna (graniczna), siły lepkości w tym obszarze są co najmniej tego rzędu co siły masowe, wpływają istotnie na ruch płynu-obszar poza warstwą przyścienną, w którym siły lepkości są pomijalnie małe w porównaniu z siłami masowymi, płyn w tym obszarze może być traktowany jako nielepki
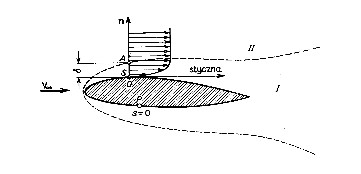
ၤ - grubość warstwy przyściennej - odległość od ścianki punktu, w którym prędkość przepływu różni się nieznacznie od prędkości przepływu potencjalnego, zwykle jest to różnica ~ 1%
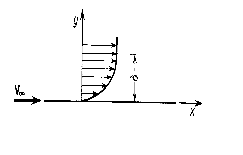
Czyli vA = 0,99 vCD, tj. vCD - gdyby ciało było opływane cieczą doskonałą.
Równania Pradtla -
uproszczone równania Naviera - Stokes'a
Dla dwuwymiarowego ustalonego ruchu
![]()
równanie ciągłości
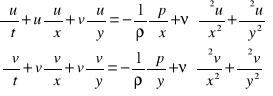
równania ruchu
Ocenimy rząd wielkości poszczególnych składników w tych równaniach w obszarze warstwy przyściennej opierając się na założeniu, że grubość warstwy przyściennej jest mała.
Zakres zmienności y to (0, ၤ)
Zakres zmienności x to (0, l) l - długość ciała.
![]()
![]()
![]()
![]()
, oraz ,
![]()
oraz
Rząd wielkości drugiej składowej
![]()
![]()
![]()
oraz
![]()
![]()
A wtedy
![]()
![]()
Wyrazy i są małe i odrzucamy je
Ponadto wyrazy w składowej y równania ruchu są mniejsze od takich samych składników w równaniu składowej x, a zatem ostatecznie
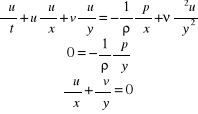
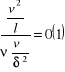
![]()
Porównajmy siły bezwładności (masowe) i siły lepkości są tego samego rzędu w warstwie przyściennej
Niech
![]()
-co oznacza, że grubość warstwy przyściennej jest odwrotnie proporcjonalna do liczby Reynoldsa.
Zgodnie z drugim równaniem ciśnienie w warstwie przyściennej jest stałe wzdłuż normalnej do ścianki, co oznacza, że ciśnienie w warstwie przyściennej jest równe wartości ciśnienia przepływu „nielepkiego” na granicy warstwy.
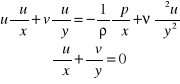
równanie Prandtla dla dwuwymiarowej warstwy
przyściennej z przepływem stacjonarnym
Jest to układ równań trzeciego rzędu, typu parabolicznego p(x) - znana funkcja współrzędnej x
![]()
Przepływ na zewnątrz warstwy przyściennej może być potencjalny lub wirowy, traktując go jako nielepki można wykorzystać równanie Eulera
![]()
które obowiązuje na ściance ciała opływanego cieczą doskonałą. Z tego równania dla przepływu ustalonego
Podstawiając do dalej otrzymamy następnie równania Prandtla

W podsumowaniu można powiedzieć:
Opływ zadanego ciała cieczą lepką można podzielić na dwa następujące zagadnienia (w oparciu o koncepcję warstwy przyściennej i równania Prandtla)
1. Wyznaczenie przepływu nielepkiego wokół ciała (np. przepływ potencjalny) a w szczególności wyznaczenie rozkładu prędkości u wzdłuż ciała lub ciśnienia.
2. Wyznaczenie rozwinięcia u(x, y) i v(x, y) równań Pradtla przy stosownych warunkach brzegowych.
Warunki brzegowe dla równań Prandtla
u(x, 0) = v(x, 0) = 0
u(x, ၤ) = u(x)
Drugi warunek jest uzgodnieniem prędkości na granicy warstwy przyściennej i przepływu zewnętrznego.
Ponadto należy uzupełnić warunkiem
u(xo, y) = uo(y)
określającym rozkład prędkości na pewnej linii łączącej ściankę z granicą warstwy. Rozkład prędkości musi być zatem zadany w pewnym przekroju x = xo warstwy, a rozwiązania dają przedłużenie tego rozkładu na inne wartości x.
Przejście laminarno - turbulentne w warstwie przyściennej.
(eksperyment)
- proces silnie nieliniowy rozpoczynający się etapem liniowego wzrostu zaburzeń tzw. fal Tollmiena - Schlichtina. Następnie tworzenie się trójwymiarowych zaburzeń aby skończyć pojawieniem się tzw. plamek turbulencji, które wreszcie „zlewają się” w przepływ turbulentny
Typy przejścia laminarno-turbulentnego
1) Naturalne (przepływ zewnętrzny z bardzo małym poziomem zaburzeń)
2) by-pass zależne od poziomu zaburzeń w strumieniu zewnętrznym w stosunku do warstwy przyściennej
Fala uderzeniowa
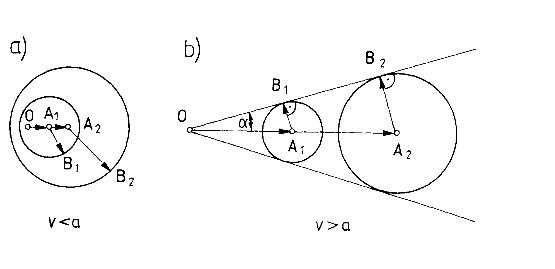
Rozchodzenie się zaburzeń w gazie ruchomym
a) prędkość poddźwiękowa
b) prędkość naddźwiękowa
a) przepływ poddźwiękowy
Zaburzenia (fale) dźwiękowe rozprzestrzeniają się po całej przestrzeni
b) przepływ naddźwiękowy
Fale dźwiękowe (kuliste) wypełniają stożek o wierzchołku O i nie wydostają się poza stożek Macha
Czoło fali uderzeniowej - największe znaczenie w aerodynamice przepływów naddźwiękowych.
Przez tę powierzchnię przepływa gaz
v1u Ⴙ 0 v2u Ⴙ 0 (gdy v1u = v2u = 0, powierzchnia poślizgu)
Zmieniają się skokowo vu, ၲ, p
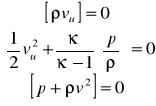
czoło fali uderzeniowej
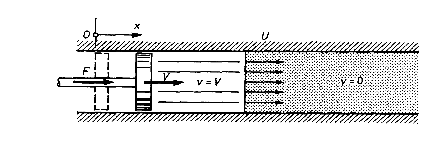
Powstawanie prostopadłej fali uderzeniowej w rurze z tłokiem
Gaz idealny, doskonały początkowo w spoczynku.
Tłok zaczyna się przemieszczać z prędkością v, to powoduje zaburzenie (zgęszczenie) gazu przed tłokiem i jego ruch (gazu) z pełną prędkością. Obszar zaburzeń powiększa się z czasem, czoło fali propaguje się z pewną prędkością u(t), poza tym obszarem gaz dalej nieruchomy.
W obszarze zaburzeń parametry gazu zmieniają się tzn. są funkcją współrzędnej x i czasu t. Prędkość propagacji zaburzeń w każdym przekroju x i w różnych chwilach czasu inna i równa lokalnej prędkości dźwięku a. Zmiana parametrów dokonuje się adiabatycznie, izentropowo, sprężaniu się gazu towarzyszy nagrzewanie się gazu. Ponieważ a ~ , a więc każda następna fala przemieszcza się względem gazu z nieco większą prędkością, zatem jedna fala dogania drugą i nakłada się na nią. W rezultacie po pewnym czasie od uruchomienia tłoka tworzy się powierzchnia silnej nieciągłości parametrów (nie tylko skokowa zmiana pochodnych ale i samej funkcji).
Interesuje nas zmiana parametrów gazu po przejściu fali.
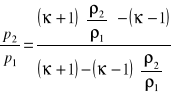
![]()
![]()
Fala uderzeniowa traktowana jest jako powierzchnia, w gruncie rzeczy jest to warstwa o grubości drogi swobodnej cząsteczek gazu.
ၲ1 v1 = ၲ2 v2
Układ zamknięty, trzy równania i trzy niewiadome p2, ၲ2, v2
Rugując prędkości otrzymamy równanie adiabaty uderzeniowej Hugoniota
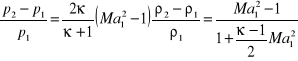
Przejście fali uderzeniowej powoduje wzrost ciśnienia, gęstości i temperatury, natomiast prędkość maleje. Proces sprężania nie jest izentropowy, zachodzi nieodwracalna przemiana energii mechanicznej w ciepło, nawet dla gazu idealnego a zatem i przyrost entropii
![]()
Uderzenie hydrauliczne
Ściśliwość cieczy i odkształcalność rurociągu mają tu istotne znaczenie, natomiast pominiemy siły masowe i tarcie
![]()
![]()
![]()
Zdefiniujmy rozprzestrzenianie się małych zaburzeń w rurociągu
![]()
a - prędkość rozprzestrzeniania się małych zaburzeń
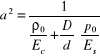
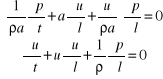
Można policzyć
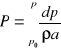
Po przekształceniach układ równań zachowania ma następującą postać
Definiując następnie funkcję ciśnienia
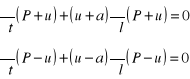
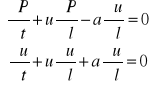
Wyrażenia c1 = P + u i c2 = P - u tzw. niezmienniki Riemanna
![]()
![]()
i
co oznacza, że wielkości c1 i c2 są przenoszone odpowiednio z prędkościami u + a i
u - a, co inaczej oznacza, że w układzie l, t wartości c1 i c2 zachowują stałą wartość wzdłuż tzw. charakterystyk
![]()
![]()
i
![]()
Funkcję ciśnienia P obliczymy następująco:
![]()
wtedy
![]()
![]()
Funkcja P została obliczona z dokładnością do członu liniowego p - po. A zatem i
![]()
Jeśli w rurociągu w chwili to nastąpi nagłe jego zamknięcie, to w chwili zamknięcia p = po, i u = 0, co oznacza, że wartość c2 = 0 rozprzestrzenia się w górę przepływu, a c1 = 0 z prędkością u + a zgodnie
c2 = 0 oznacza skąd p = po + ၲo u a
p = po + ၲo u a - fala ciśnienia tzw. uderzenie hydrauliczne
Natomiast w dół przepływu rozprzestrzenia się fala rozrzedzeniowa, c1 = 0,
![]()
a zatem p = po - ၲo u a
Groźniejsza z obu fal jest fala ciśnieniowa, bo może zniszczyć rurociąg,natomiast fala rozrzedzeniowa może spowodować co najwyżej kawitację.
![]()
Dla częściowego zamknięcia rurociągu u = uo - ၄u w chwili to, c1 = - u + ၄u
wtedy => p = po + ၲo a ၄u fala ciśnienia
Z uwzględnieniem lepkości fala ciśnieniowa będzie słabsza, bo lepkość doprowadzi do pewnej dyssypacji energii.
Środki zabezpieczające przed konsekwencjami uderzenia hydraulicznego
- zbiorniki powietrzne
- wieże wyrównawcze
- zawory bezpieczeństwa
ale też przedłużenie czasu zamykania (otwierania) zaworu skrócenie długości przewodu
Zawór bezpieczeństwa - otwiera się podczas uderzenia hydraulicznego i wypuszcza część wody z rurociągu, a więc obniża ciśnienie w rurociągu
Niestacjonarne przepływy w rurociągach
Uderzenie hydrauliczne.
Metoda przepływów jednowymiarowych - chętnie stosowana w hydraulice, jako uproszczenie modelu trójwymiarowego.Dokładność tego modelu zależy od precyzji definicji wartości średnich stosowanych w metodzie jednowymiarowej.
Zalety:
- prostsze równania + łatwo uzyskiwane rozwiązania obarczone jednak często bliżej nieznanym błędem
- syntetyczność informacji i rezultatów
W hydraulice wiele modeli jest jednowymiarowych, dokładność rezultatów wystarczająco dobra
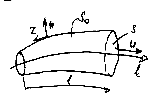
Objętość płynna w 1 D modelu
![]()
Równania zachowania
Dowolny parametr P i jego zmiana w czasie
![]()
![]()
- prędkość średnia
Deformacja liniowa elementu płynu
Równanie zachowania masy
![]()
![]()
![]()
Ale wtedy
![]()
![]()
![]()
Przekształcając można uzyskać inne postacie równania ciągłości
![]()
![]()
![]()
![]()
Albo jeszcze inaczej po scałkowaniu
Równanie zachowania pędu 1 D (jednowymiarowo)
i po przekształceniach: Sc = So + S1 + S2
![]()
Sc = l c
![]()
lub po uwzględnieniu równania zachowania masy:
![]()
Przy czym uśrednianie
Przepływ niestacjonarny dla rurociągu
![]()
![]()
![]()
bo z rozwiązania przepływu Hagena - Poisseuille'a
Uwzględniając ściśliwość cieczy i odkształcalność rurociągu, w układzie będzie za mało równań, bo tylko 2, a 4 niewiadome u, ၲ, S, p.
Znajdźmy zatem te dodatkowe związki
![]()
![]()
Ec i ES - moduły sprężystości cieczy i materiału rurociągu
D/d - stosunek średnicy rurociągu do grubości ścianki
Mamy zatem cztery równania.
Konieczne są poza tym warunki początkowe:
p = p(l) u = u(l)
i warunek brzegowy:
określenie na każdym z dwóch końców rurociągu jednej z funkcji p = p(t) i u = u(t)
W zasadzie należy ten układ równań rozwiązać numerycznie. Jeden przypadek tzw. uderzenie hydrauliczne można rozwiązać analitycznie. Uderzenie hydrauliczne tj. nagłe zamknięcie zaworu na rurociągu. Wówczas mamy do czynienia z gwałtownym przyrostem ciśnienia w miejscach zamknięcia rurociągu i rozprzestrzenianiem się fali ciśnienia w górę rurociagu.
Przepływy w kanałach otwartych
Kanały otwarte dzieli się na naturalne i sztuczne
Naturalne - rzeki, strumienie, potoki
Sztuczne - kanały kanalizacyjne, melioracyjne (nawadniające, odwadniające), komunikacyjne
Różnice między przepływem w przewodach a kanałach otwartych:
W przewodzie płyn wypełnia cały przekrój poprzeczny przewodu, w kanale otwartym ciecz wypełnia tylko część tego przekroju niezależnie, czy jest to rurociąg czy odkryty kanał. Zatem w kanale istnieje swobodna powierzchnia cieczy, na powierzchni cieczy jest zwykle pewne ciśnienie, najczęściej ciśnienie atmosferyczne
Przepływ w kanale otwartym odbywa się wyłącznie pod działaniem siły grawitacji, bezwładności i tarcia, musi też wystąpić spadek dna wzdłuż jego długości
W kanałach otwartych trudne jest analityczne ujęcie ruchu,
w kanałach naturalnych niemożliwe ze względu na nieregularność koryta kanału i nieznaną chropowatość.
Rozważania ograniczymy do kanałów sztucznych.
Ruch wody w kanałach
- zmienny (nierównomierny)
- jednostajny (równomierny)
Gdy przekrój strugi ulega zmianie - ruch zmienny
Gdy przekrój strugi stały - ruch jednostajny
Ruch zmienny - ustalony lub nieustalony (zmienny w czasie)
Rozpatrujemy dalej tylko ruch jednostajny, ma on najczęściej charakter turbulentny.
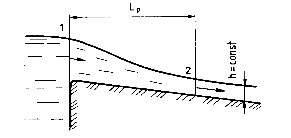
Odcinek początkowy Lp - na takim odcinku formuje się ruch.
v2 = const h = const
Analiza długości odcinka początkowego możliwa tylko na podstawie rozwiązania równań Naviera - Stokes'a.
![]()
Równanie Bernoulli'ego dla przekroju 1 i 2
hstr - różnica poziomów równoważna wskutek tarcia na długości L.
![]()
Dla ruchu jednostajnego linie prądu, w tym i powierzchnia swobodna, są równoległe do dna, a więc p1 = p2 i v1 = v2 i wtedy hstr = ၄h = z1 - z2
Spadek hydrauliczny
I = i = sinၡ - ၡ kąt nachylenia dna do poziomu.
![]()
Podaje się go też w % lub ‰.
Wzór Chézy'ego - średnia prędkość przepływu
![]()
c - współczynnik Chézy'ego , rH - promień hydrauliczny [m]
![]()
![]()
Strumień objętości wody
![]()
Opór tarcia w przewodach wg wzoru Darcy - Weissbacha
![]()
Skąd można wyznaczyć
Zwykle w obliczeniach nie korzysta się ze współczynnika ၬ, a tylko bezpośrednio ze współczynnika Chézy'ego c.
![]()
![]()
![]()
![]()
![]()
![]()
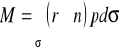
![]()
![]()
![]()
bo r n1 i r n2
Następnie całka po objętości bo r F
natomiast bo vn = 0, nieprzenikliwość łopatki
![]()
![]()
Korzystając z definicji iloczynu wektorowego r× n = r n sin(r, n)
Dalej M = ρ Q (r1 c1 cosα1 - r2 c2 cosα2) = ρ Q (r1 c1n - r2 c2n)
![]()
Praca mechaniczna w jednostce czasu (moc)
Mω = ρ Q ω (r1 c1n - r2 c2n) = hL ρ g Q
Jeśli M i ω zwroty zgodne, praca dodatnia → silnik
M i ω +/- zwroty przeciwne, praca ujemna → maszyna robocza
![]()
![]()
![]()
Rozważmy - Stacjonarny przeplyw przez dwie maszyny, które są geometrycznie podobne, ale mają różne wymiary i różne obroty
Skala wymiarów liniowych λ = d2/d1
Skala obrotów (czasu) ν = n2/n1
Aby przepływ był kinematycznie podobny, to trójkąty prędkości w obu maszynach
powinny być podobne
![]()
![]()
![]()
![]()
![]()
![]()
![]()
bo
![]()
![]()
dla ρ2 = ρ1 natomiast będzie
![]()
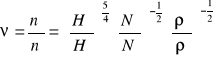
Przyjmując nastepnie n” = ns, H” = Hs = 1 m, N” = Ns = 1 kM
n' = n, H' = H, N' = N
Otrzymamy wtedy
wyróżnik szybkobieżności N [kM] n [obr/min] H [m]
dla silników
Wyróżnik dla maszyn roboczych zamiast mocy N wydatek Q
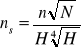
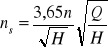
Różne ns dla różnych silników (turbin) np:
ns = 1 ÷ 10 koło wodne
ns = 450 ÷ 1000 turbina Kaplana
5 ÷ 40 turbina Peltona
60 ÷ 450 turbina Francisa
![]()
![]()
Kreska nad symbolem oznacza wartość średnią, symbol prim ` oznacza chwilowe odchylenie od wartości średniej.
Wartość średnią określamy jako:
przy czym okres całkowania powinien być tak duży, aby wartość średnia nie była zależna od wyboru t1 i t2.
Wartość średnia odchylenia u' jest równa zeru:
Natomiast powtórzony proces uśredniania wartości średniej nie zmienia jej wartości
![]()
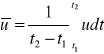
![]()
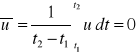
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
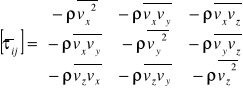
![]()
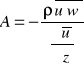
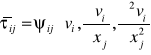
![]()
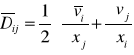
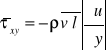
![]()
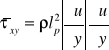
![]()
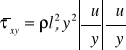
![]()
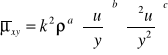
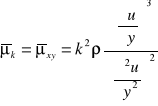
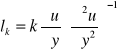
![]()
![]()
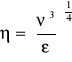
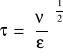
![]()
![]()
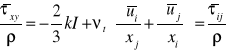
![]()
![]()
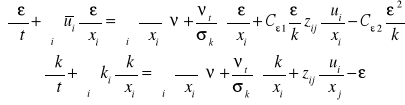
![]()
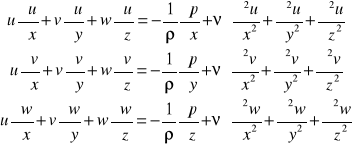
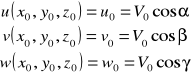
warunki brzegowe
![]()
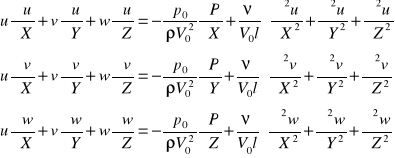
Równanie pędu
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
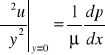
![]()
![]()
![]()
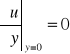
![]()
![]()
![]()
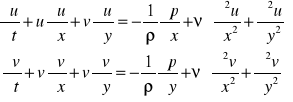
![]()
![]()
![]()
![]()
![]()
![]()
![]()
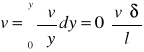
![]()
![]()
![]()
![]()
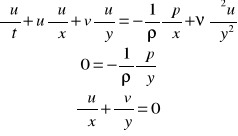
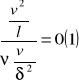
![]()
![]()
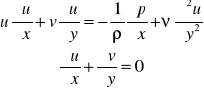
![]()
![]()
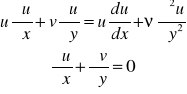
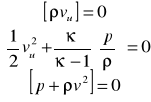
![]()
![]()
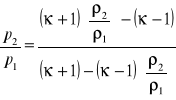
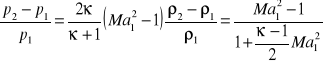
![]()
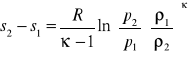
![]()
![]()
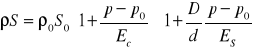
![]()
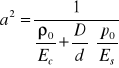
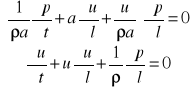
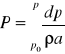
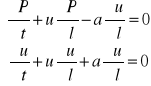
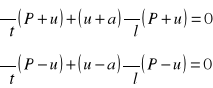
![]()
![]()
![]()
![]()
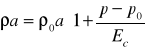
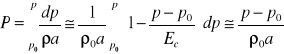
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
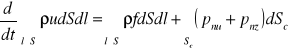
![]()
![]()
![]()
![]()
![]()
![]()
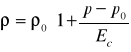
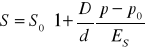
![]()
![]()
![]()
![]()
![]()
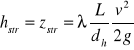
![]()
![]()
Wyszukiwarka
Podobne podstrony:
sciaga egz, Mechanika płynów rok 2
Płyny pytania, Mechanika płynów rok 2
płyny, Mechanika płynów rok 2
plyny-egzamin, Mechanika płynów - spis pytań, 1) Różnice między zjawiskami podobnymi i analogicznymi
zadania z wykladow, Mechanika płynów rok 2
15 płyny ruchome, mechanika plynów
zadania z cwiczen, Mechanika płynów rok 2
płyny ściąga, Mechanika płynów Bryszewska wykład
11 płyny nieprzesuwne, mechanika plynów
Pomoce do mechaniki plynow, I rok, mechanika
plyny-egzamin, Mechanika płynów - do egzaminu, 1) Różnice między zjawiskami podobnymi i analogicznym
plyny cd, Mechanika Plynow
Równanie równowagi płyny, mechanika plynów
anaconda, mechanika płynów, plyny~, plyny, N12 - sprawko
+Mechanika Płynów - Zad.dom.2 - 2 Rok V+, Mechanika Plynow
więcej podobnych podstron