Równanie równowagi płyny:

W cieczy znajdującej się w spoczynku wyznaczamy sześcian o krawędziach dx, dy, dz równoległych do odpowiednich osi układu współrzędnych. Na sześcian działają następujące siły:

- powierzchniowe normalne;

- masowe;

Ciśnienie p znajduje się w punkcie M będącym środkiem sześcianach prostopadłych do osi x odległych o -1/2dx i 1/2dx wynoszą:

i

Natomiast siły powierzchniowe wynoszą:

Siły masowe działające na sześcian otrzymujemy przez przemnożenie jednostkowej siły masowej x, y, z przez masę elementu.

dF_x = ρ_xdxdydz

dF_y = ρ_ydxdydz

dF_z = ρ_zdxdydz

Z warunków równowagi wynika, że suma sił działających na element (powierzchniowych powierzchniowych masowych) na dowolnie wybrany kierunek musi być równa zero. Wyprowadzenie jest takie samo na każdą oś x, y, z.

Wyprowadzenie na oś x:

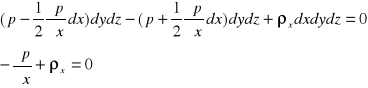
Wyliczamy analogicznie równanie na osi y i z

i

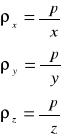
układ równania różniczkowego Eulera

Po przemnożeniu przez dx, dy, dz i dodając

różniczka zupełna ciśnienia

równanie równowagi płynu