Politechnika Warszawska
Wydział Fizyki

22

Laboratorium Fizyki I płd.
Irma Śledzińska

POMIAR SZEROKOŚCI SZCZELINY ORAZ NIEPRZEZROCZYSTEGO PASKA

NA PODSTAWIE ZJAWISKA DYFRAKCJI ŚWIATŁA

1. Podstawy fizyczne

W opisie zjawisk interferencji i dyfrakcji światło traktujemy jako rozchodzącą się

w przestrzeni falę elektromagnetyczną opisywaną jako periodyczne zmiany w przestrzeni
i czasie wektorów natężenia pola elektrycznego E i indukcji magnetycznej B.

Najprostszym przykładem fali elektromagnetycznej jest fala płaska, sinusoidalna,

rozchodząca się wzdłuż osi 0x, o równaniu:

E(x,t) = E

0

sin(ωt – kx)

(1a)

gdzie E

0

jest amplitudą natężenia pola elektrycznego fali, argument funkcji sinus

ϕ = (ωt – kx) nazywamy fazą fali, ω – częstością kołową, k – jest liczbą falową związaną
z długością fali zależnością:

λ

π

2

=

k

(1b)

Równanie (1a) opisuje falę rozchodzącą się wzdłuż osi 0x a więc wektor natężenia

pola elektrycznego, który w ośrodku jednorodnym jest zawsze prostopadły do kierunku
rozchodzenia się fali (fala elektromagnetyczna jest falą poprzeczną), zmienia się tylko
wzdłuż osi 0x a jest stały w płaszczyznach yz prostopadłych do tej osi. Każda taka
płaszczyzna, będzie powierzchnią o stałej wartości fazy

ϕ.

Powierzchnię o stałej fazie nazywamy powierzchnią falową lub czołem fali. Falę,

której powierzchnia falowa jest płaszczyzną nazywamy falą płaską.

Posługując się pojęciem fali płaskiej, musimy zdawać sobie sprawę, że jest to zawsze

pewne przybliżenie, ponieważ większość rzeczywistych źródeł wysyła promieniowanie we
wszystkich kierunkach. Najprostszym opisem tego typu fal są fale kuliste, których
powierzchnie falowe są koncentrycznymi sferami. Dlatego o fali płaskiej możemy mówić
tylko wtedy, gdy rozpatrujemy wycinek sfery o bardzo dużej odległości od źródła, bądź gdy
za pomocą odpowiedniego układu optycznego zmienimy kształt czoła fali.

Zasada Huygensa

mówi że, wszystkie punkty czoła fal można uważać za źródła

nowych fal kulistych

. Położenie czoła fali po czasie t będzie określone przez powierzchnię

styczną do powierzchni tych fal kulistych. Musimy jednak zdawać sobie sprawę, że zasada
Huygensa sformułowana w wyniku obserwacji fal na wodzie w 1678 roku (czyli na długo
przed odkryciem fal elektromagnetycznych) jest pewnym przybliżonym modelem
pozwalającym na opis szeregu zjawisk falowych bez posługiwania się skomplikowanym
aparatem matematycznym. Wymienić należy dwa zasadnicze uproszczenia tej zasady:
1. Zgodnie z zasadą Huygensa, a wbrew obserwacjom, wtórne fale kuliste mogą rozchodzić

się również do tyłu. Aby obejść tą trudność przyjmuje się, że natężenie fal kulistych nie
jest jednakowe we wszystkich kierunkach lecz zmienia się w sposób ciągły od maksimum

Pomiar szerokości szczeliny oraz nieprzezroczystego paska na podstawie zjawiska dyfrakcji światła

2

dla kierunku zgodnego z kierunkiem rozchodzenia się fali pierwotnej do zera w kierunku
przeciwnym.

2. Przy rozchodzeniu się fali elektromagnetycznej w próżni, elementarne źródła nowych fal

kulistych nie mają określonego sensu fizycznego.

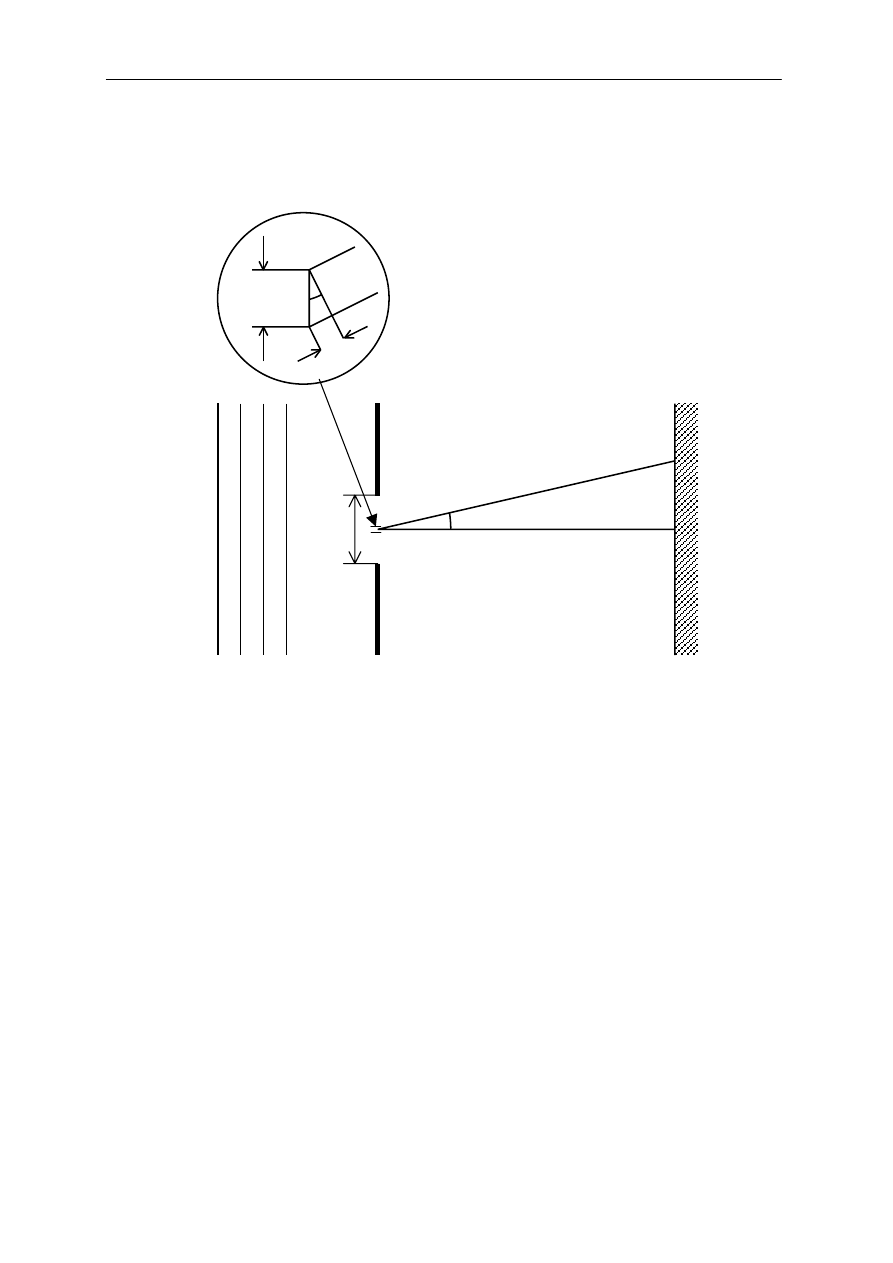
Ekran

Δ

y

Θ

Fala padaj

ąca

P

L>>a

a

Θ

Δ

y

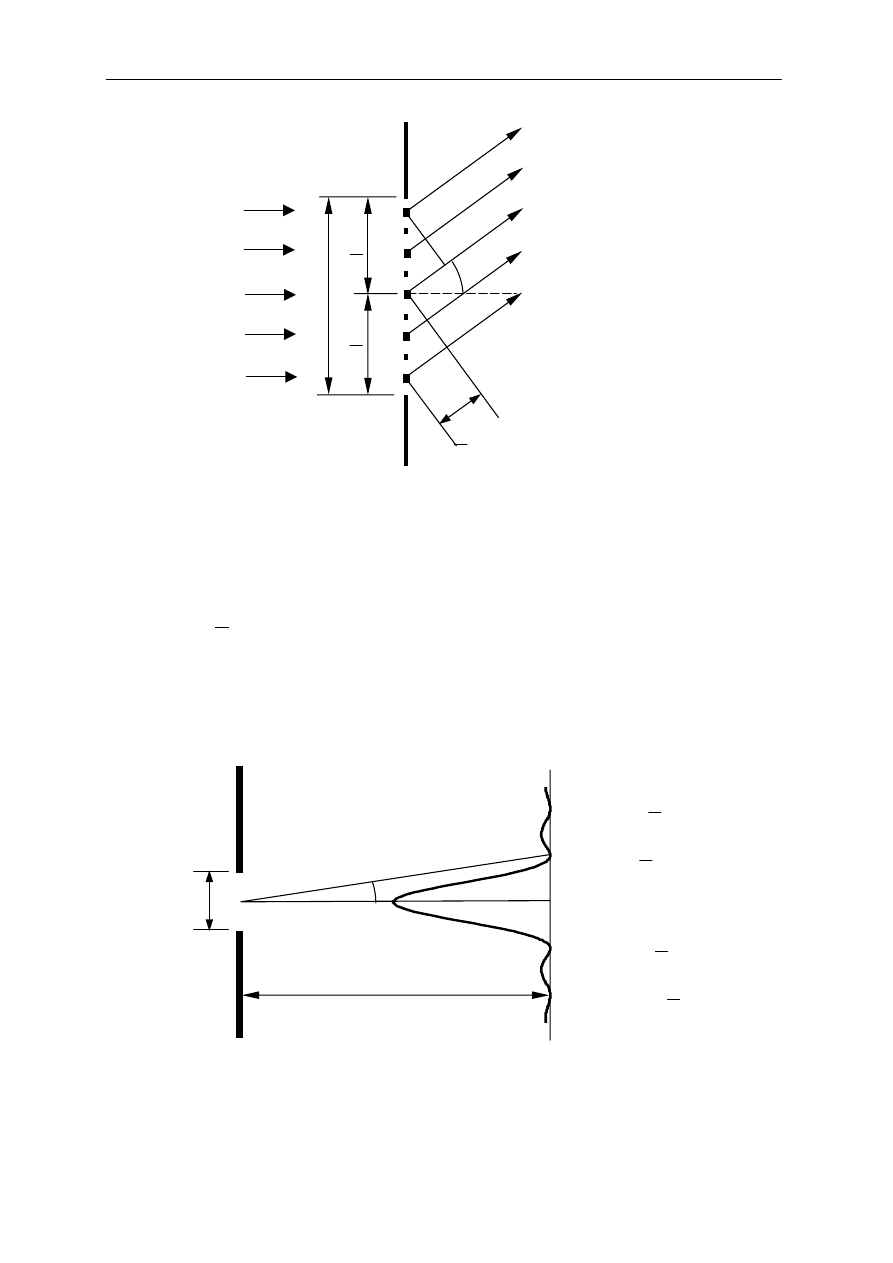
Rys. 1 Nieprzezroczysta przesłona ze szczeliną o szerokości a. W kółku pokazano dokładniej
pasek o szerokości

Δ

y.

Kiedy fala płaska pada na nieprzeźroczystą przesłonę z wąską szczeliną o szerokości a

(rys.1) to czoło tej fali ulega odkształceniu, co obserwujemy jako zmianę rozkładu energii
niesionej przez falę. Ma wówczas miejsce zjawisko dyfrakcji. Zgodnie z zasadą Huygensa –
Fresnela, natężenie promieniowania we wszystkich odległych punktach za przesłoną będzie
takie samo, jak by było wytworzone przez jednorodny rozkład źródeł na całej powierzchni
szczeliny, przy czym fale wysyłane przez te źródła są w jednakowej fazie. Jednak
w szczelinie nie ma żadnych rzeczywistych źródeł. Dlaczego więc przy tak niefizycznym
założeniu otrzymujemy poprawny opis zjawiska?

Wyobraźmy sobie, że w przesłonie pokazanej na rysunku 1 nie ma żadnego otworka,

nie przepuszcza więc ona zupełnie światła. Dzieje się tak dlatego, że padająca na lewą stronę
przesłony fala płaska o amplitudzie natężenia pola elektrycznego, E

ź

, indukuje w niej drgające

dipole wysyłające dodatkowe promieniowanie, E

p

. Pole tego promieniowania nakłada się

na pole fali padającej, w wyniku czego otrzymujemy po prawej stronie przesłony pole
o zerowym natężeniu, czyli:

E

ź

+ E

p

= 0 .

(2a)

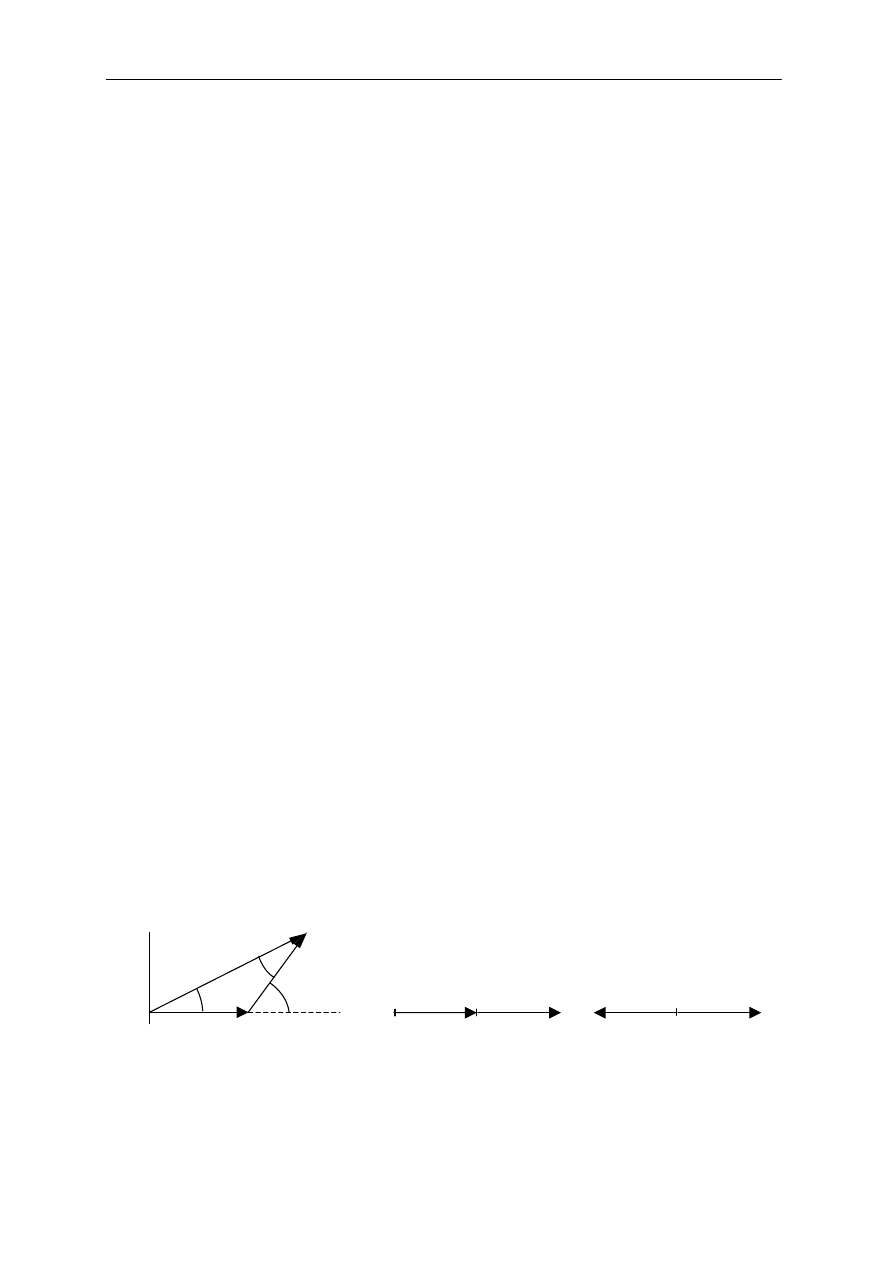
Pomiar szerokości szczeliny oraz nieprzezroczystego paska na podstawie zjawiska dyfrakcji światła

3

Jeśli fala padająca jest falą płaską, to fala wtórna, która tak dokładnie znosi się z falą

padającą musi pochodzić od jednorodnie rozłożonych na całej przesłonie źródeł.

Przyjmijmy, że przesłona składa się z nieprzeźroczystego paska zasłaniającego

szczelinę i z otoczenia tego paska. Wytwarzają one pole odpowiednio o natężeniu E

np

i E

ot

,

przy czym:

E

p

= E

np

+ E

ot

,

(2b)

a więc zgodnie z równością (2a) mamy:

E

ź

+ E

np

+ E

ot

= 0 .

(2c)

Usuńmy teraz nieprzeźroczysty pasek zasłaniający szczelinę. Usuniemy tym samym

część E

np

promieniowania fali wtórnej. Wówczas wypadkowe natężenie po prawej stronie

przesłony wyniesie:

(E

ź

+ E

np

+ E

ot

) – E

np

= 0 – E

np

= -E

np

.

(2d)

Jak wynika z równania (2d), efekt będzie taki sam, jakbyśmy dodali równomiernie

rozmieszczone w szczelinie źródła promieniowania wysyłające fale z fazą przeciwną.

Jeśli zostawimy nieprzeźroczysty pasek a usuniemy jego otoczenie to okaże się,

że natężenie promieniowania I (I ~ E

2

) padającego na odległy ekran będzie takie samo jak

w przypadku szczeliny. Możemy to wykazać przeprowadzając następujące rozumowanie:
Usuwając otoczenie szczeliny mamy:

(E

ź

+ E

np

+ E

ot

) – E

ot

= 0 – E

ot

= -E

ot

,

(3a)

ale z równania (2c) wynika, że:

E

ź

= - E

np

- E

ot

.

(3a)

Ostatnią równość możemy wyrazić w następujący sposób. Jeśli mamy dwie

uzupełniające się przesłony takie, że otwory jednej odpowiadają ściśle częściom w drugiej
przesłonie, to suma zaburzeń pochodzących od tych dwóch przesłon jest taka sama jak
w nieobecności jakiejkolwiek przesłony. Twierdzenie to nosi nazwę zasady Babineta.
Oznacza ona, że w obszarze gdzie nie pada wiązka pierwotna, czyli tam gdzie E

ź

= 0,

zachodzą równości E

np

= -E

ot

i I

ot

= I

np

. Czyli obrazy dyfrakcyjne pochodzące od przesłony

i szczeliny w miejscach ekranu, na które nie pada wiązka pierwotna będą takie same.

E

O

E

O

E

O

E

O

E

O

E

O

E

W

Δφ

β

β

a)

b)

c)

Rys. 2 Graficzne dodawanie dwóch fal o amplitudach E

o

i różnicy faz

Δφ

: a)

Δφ

= 2

β

,

b)

Δφ

= 0, E

w

= 2E

o

, c)

Δφ

=

π

, E

w

= 0. E

w

jest amplitudą wypadkową.

Pomiar szerokości szczeliny oraz nieprzezroczystego paska na podstawie zjawiska dyfrakcji światła

4

Przeanalizujemy teraz dokładnie dyfrakcję na szczelinie o szerokości a (rys.1).

Aby zapewnić warunek jednakowych faz na całej szerokości szczeliny, oświetlimy ją za
pomocą lasera wytwarzającego wąską wiązkę światła spójnego.

Do obliczenia rozkładu natężeń obrazu dyfrakcyjnego na ekranie zastosujemy metodę

graficzną, którą zilustrujemy na przykładzie dwóch źródeł (rys.2).

Natężenie pola E opisywane równaniem (1a) można przedstawić za pomocą wektora,

którego długość wynosi E

0

, a kąt

ϕ, jaki tworzy on z osią poziomą będzie określał jego fazę.

Ponieważ faza zmienia się w czasie, wektor ten będzie obracać się przeciwnie do wskazówek
zegara. Efekt dodania dwóch fal o takiej samej amplitudzie E

0

i różnicy faz

Δϕ ilustruje

rys.2a. Z zależności geometrycznych dla trójkąta równoramiennego otrzymujemy:

2

cos

2

0

ϕ

Δ

= E

E

w

.

(6a)

Maksymalne, wypadkowe natężenie promieniowania (I

w

~E

w

2

) otrzymamy wówczas,

gdy

1

2

cos

±

=

⎟

⎠

⎞

⎜

⎝

⎛ Δ

ϕ

, czyli gdy różnica faz będzie równa (patrz rys. 2b):

π

ϕ

m

2

=

Δ

,

,...

3

,

2

,

1

,

0

±

±

±

=

m

(6b)

Porównując wzory (1a) i (1b) łatwo zauważyć że zmiana odległości o

λ

=

Δx

powoduje zmianę fazy o

π

2

radianów, czyli zmiana fazy o

π

m

2

radianów odpowiada

różnicy dróg :

λ

m

x 2

=

Δ

.

(6c)

Natomiast zerowe natężenie wystąpi gdy

0

2

cos

=

⎟

⎠

⎞

⎜

⎝

⎛ Δ

ϕ

(rys.2b), czyli gdy:

π

ϕ

)

1

2

(

+

=

Δ

m

(6d)

lub

2

)

1

2

(

λ

+

=

Δ

m

x

.

(6e)

Podzielmy szczelinę na N równoległych pasków o szerokości y

Δ . Paski te są źródłem

wtórnych fal Huygensa i wytwarzają wypadkowe natężenie w punkcie P, którego położenie
na ekranie możemy określić za pomocą kąta

θ . Jeśli paski będą dostatecznie wąskie,

to możemy przyjąć, że odległość od ekranu wszystkich punktów na jednym pasku jest taka
sama, a więc światło z danego paska po dotarciu do ekranu będzie miało tą samą fazę.

Różnicę między sąsiednimi paskami policzymy z zależności:

różnica faz

różnica dróg

2

π

λ

(7)

czyli jak widać na rysunku 1:

θ

θ

λ

π

ϕ

sin

sin

2

⋅

Δ

⋅

=

⋅

Δ

=

Δ

y

k

y

.

(8a)

Pomiar szerokości szczeliny oraz nieprzezroczystego paska na podstawie zjawiska dyfrakcji światła

5

Różnica faz między falami pochodzącymi od brzegów szczeliny będzie wynosić:

ϕ

Δ

=

Φ N

.

(8b)

E

w

= E

m

(

a

)

E

w

E

m

(

b

)

E

w

= 0

(

c

)

E

w

(

d

)

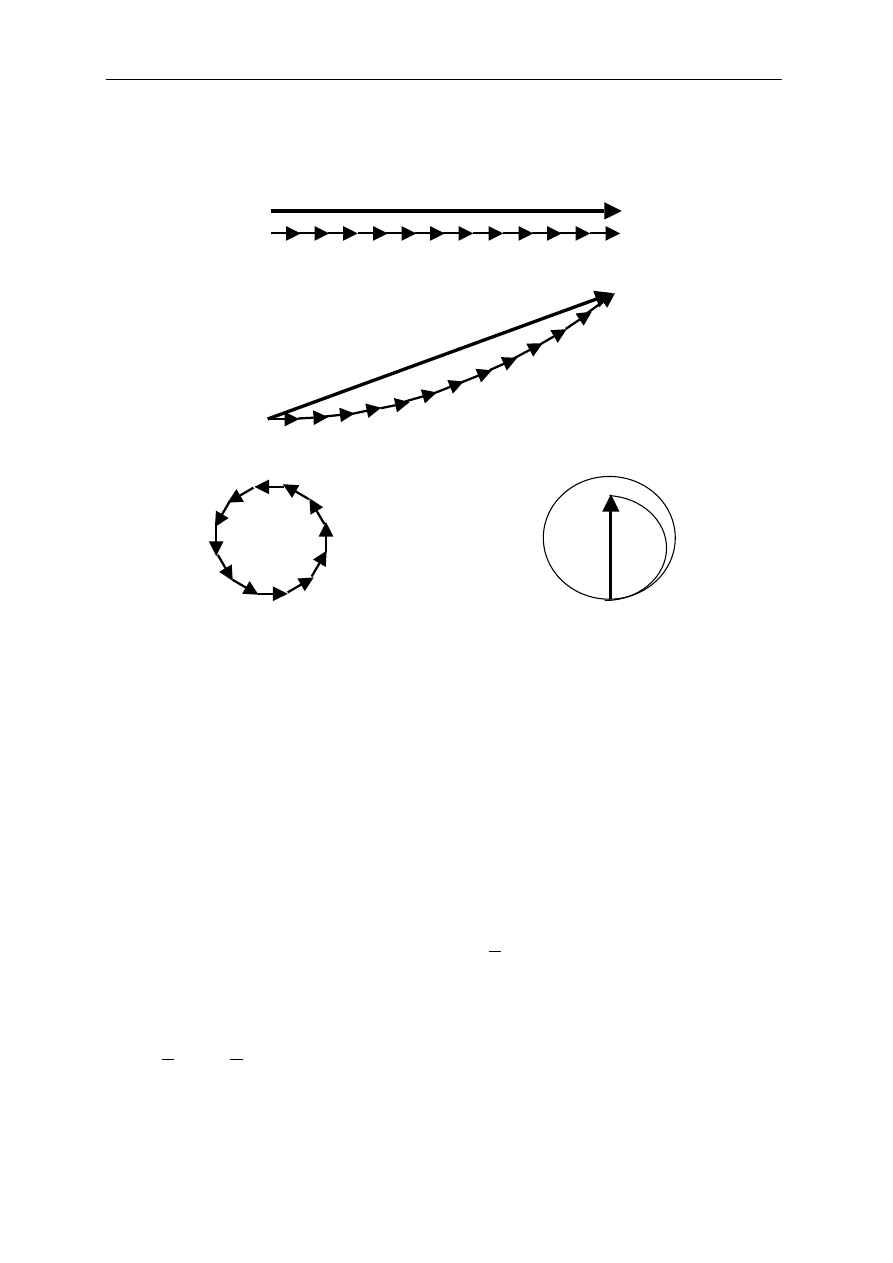
Rys.3 Diagramy wektorowe ilustrujące dodawanie fal pochodzących ze szczeliny, różnice faz

między falami pochodzącymi z brzegów szczeliny wynoszą odpowiednio:

a)

, maksimum główne b)

0

=

Φ

φ

Δ

=

Φ N

, c)

π

2

=

Φ

, pierwsze minimum d)

π

3

=

Φ

pierwsze maksimum boczne.

Wypadkową amplitudę otrzymamy dodając wektorowo natężenia pochodzące

od poszczególnych pasków. Z równania (8a) wynika, że gdy

0

=

θ

to

0

=

Δ

φ

i na wprost

szczeliny otrzymamy maksimum natężenia promieniowania (rys.3a). Kolejne rysunki 3b, 3c
i 3d ilustrują wypadkowe amplitudy przy wzroście kąta

θ , a co za tym idzie i różnicy faz Δϕ.

Rys.(3c) ilustruje przypadek, gdy wektory amplitud „zwijają” się w pełny okrąg. Odpowiada
to oczywiście całkowitej różnicy faz

π

2

=

Φ

.

Aby otrzymać położenie pierwszego minimum wygodnie jest podzielić szczelinę

na połowę (rys.4). Rozpatrzmy dwie fale 1 i 3 pochodzące z dolnego brzegu szczeliny i z jej
środka.

Fala 1 przebędzie do ekranu drogą dłuższą o

θ

sin

2

a

od fali 3. Taka sama różnica dróg

wystąpi między falami 2 i 4 oraz 3 i 5.

Jeśli ta różnica dróg będzie równa:

2

sin

2

λ

θ

=

a

,

(9a)

czyli:

λ

θ

=

sin

a

,

(9b)

Pomiar szerokości szczeliny oraz nieprzezroczystego paska na podstawie zjawiska dyfrakcji światła

6

2

a

2

a

a

θ

θ

sin

2

a

1

2

3

4

5

Rys.4 Dyfrakcja światła na szczelinie o szerokości .

a

to natężenia fal pochodzących z jednej połowy szczeliny będą się znosić z natężeniami
z drugiej połowy (porównaj rys.2b i 3c). Otrzymaliśmy w ten sposób warunek na położenie
pierwszego minimum:

a

λ

θ

=

sin

.

(9c)

Widzimy, że położenie pierwszego minimum zależy bezpośrednio od szerokości

szczeliny. Im węższa szczelina tym większy jest kąt, pod którym obserwujemy pierwsze
minimum, a więc tym szersze jest środkowe maksimum.

a

L

y

1

y

2

-y

1

-y

2

0

a

λ

θ

2

sin

=

a

λ

θ

2

sin

−

=

a

λ

θ

=

sin

a

λ

θ

−

=

sin

0

sin

=

θ

Θ

Rys.5 Położenia minimów w obrazie dyfrakcyjnym szczeliny.

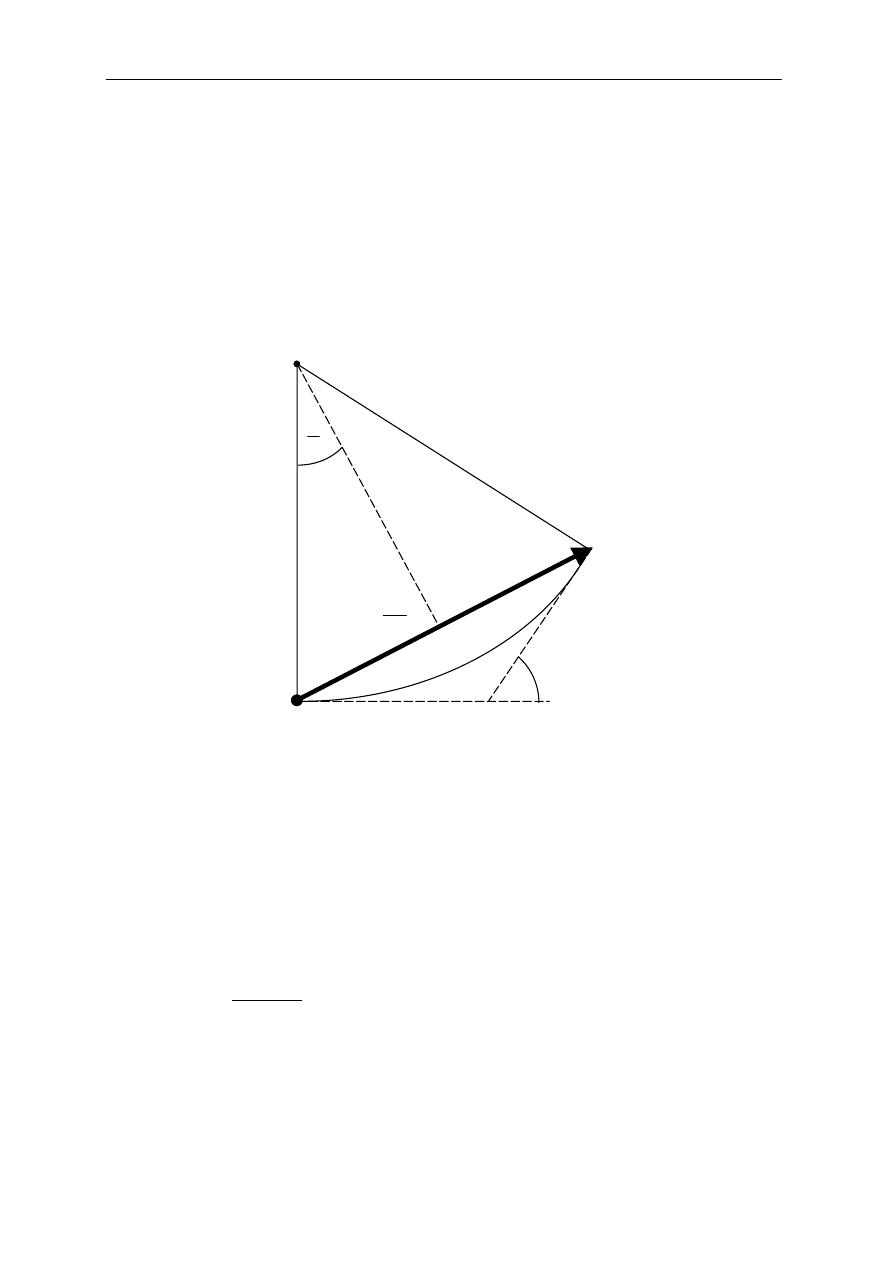
Pomiar szerokości szczeliny oraz nieprzezroczystego paska na podstawie zjawiska dyfrakcji światła

7

Dzieląc szczelinę na 4 części i przeprowadzając podobne rozumowanie otrzymamy położenie
drugiego minimum:

λ

θ

2

sin

=

a

(rys.5). Ogólny warunek na położenia minimów możemy

zapisać jako:

λ

θ

m

a

=

sin

...

3

,

2

,

1

±

±

±

=

m

(9d)

W przypadku dyfrakcji na otworze kołowym o średnicy a, ze względu na inną

symetrię, uzyskujemy inne wyrażenia na położenia minimów dyfrakcyjnych:

λ

θ

p

a

=

sin

p = 1,22 2,33 3,24 4,24...

(9e)

O

R

R

2

θ

E

m

2

w

E

Φ

Rys.6 Geometryczna konstrukcja służąca do obliczania natężeń obrazu dyfrakcyjnego

szczeliny.

Wyznaczymy teraz rozkład natężeń obrazu dyfrakcyjnego. Ponieważ szczelinę

podzieliliśmy na N wąskich pasków, wypadkowa amplituda E

w

będzie sumą wektorową N fal

różniących się o fazę

Δϕ. Wektory te będą leżały na łuku, którego długość będzie równa

maksymalnej amplitudzie E

m

=NE

0

(rys.3). Kąt środkowy

Φ , odpowiadający temu wycinkowi

okręgu, jest równy różnicy faz między paskami na dwóch brzegach szczeliny. Jak widać
na rys.6 wypadkowa amplituda wynosi

)

2

/

sin(

2

Φ

= R

E

w

, a kąt

Φ w mierze łukowej jest

równy: czyli

)

/

(

R

E

m

=

Φ

)

/

(

Φ

=

m

E

R

i stąd otrzymujemy:

)

2

/

(

)

2

/

sin(

Φ

Φ

=

m

w

E

E

(10)

Ponieważ

jest różnicą faz między skrajnymi falami dla których różnica dróg wynosi

asin

Θ

, stąd:

Φ

θ

sin

⋅

⋅

=

Φ

a

k

(11)

Pomiar szerokości szczeliny oraz nieprzezroczystego paska na podstawie zjawiska dyfrakcji światła

8

To równanie, łącznie z równaniem (10) daje nam wartość amplitudy fali wypadkowej

dla obrazu dyfrakcyjnego pojedynczej szczeliny. Natężenie promieniowania I

w

jest

proporcjonalne do kwadratu amplitudy czyli:

2

2

)

2

/

(

)

2

/

(

sin

Φ

Φ

=

m

w

I

I

(12)

Dla kątów ,...

3

,

2

,

1

,

2

±

±

±

=

=

Φ

m

m

π

wyrażenie (12) będzie równe zero ze

względu na zerowanie się licznika. Korzystając z zależności (11) i (12), otrzymamy warunek
na występowanie minimów dyfrakcyjnych wyrażony wzorem (9d).

0,0

0,2

0,4

0,6

0,8

1,0

I

Θ

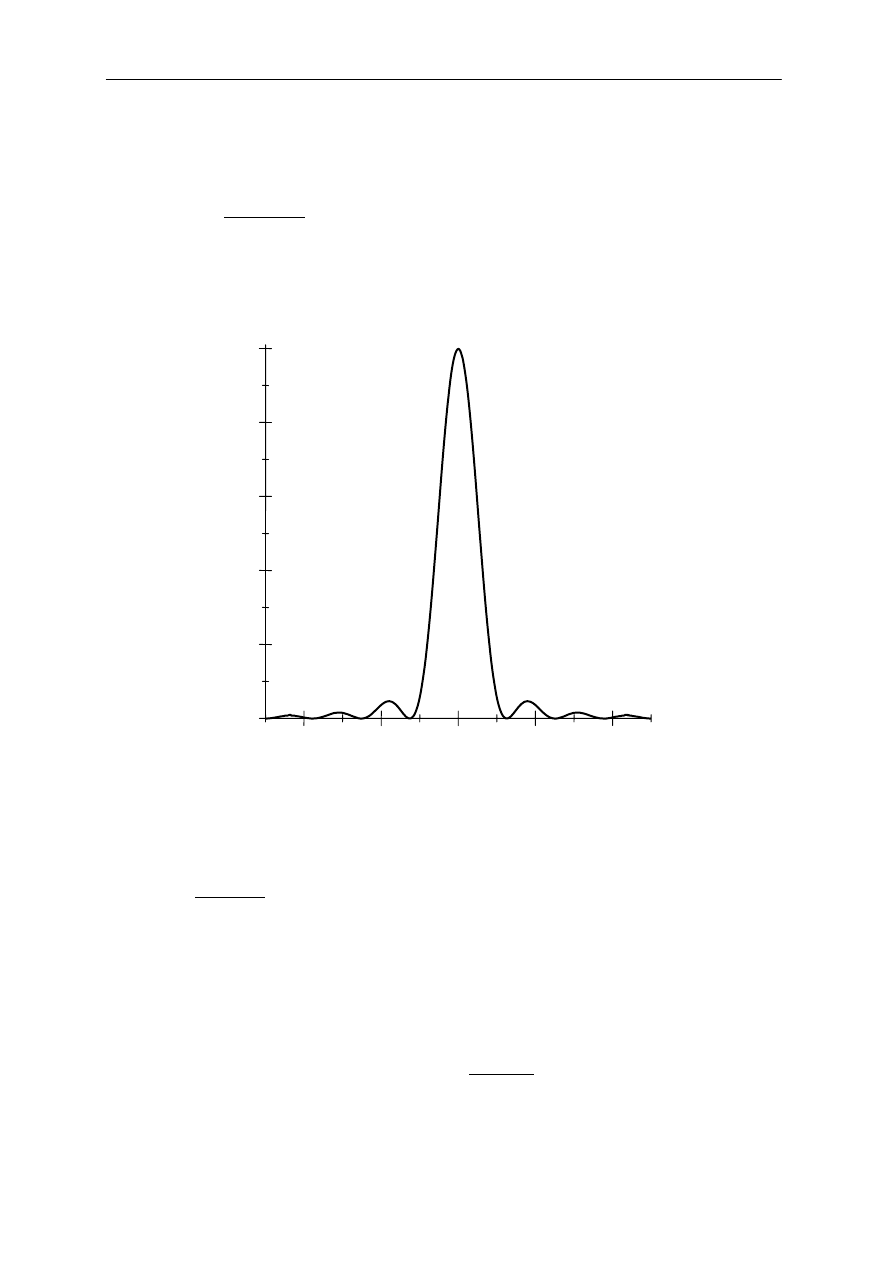
Rys.7 Wykres natężenia promieniowania I w funkcji kąta ugięcia

θ

Dla kąta

(co odpowiada kątowi

Θ

= 0), natężenie fali ugiętej jest maksymalne

i wynosi I

0

=

Φ

m

ponieważ:

1

2

/

)

2

/

sin(

lim

0

=

Φ

Φ

→

Φ

.

(13)

Kolejne maksima dyfrakcyjne będą występować dla kątów

Φ , dla których licznik

wyrażenia (12) przyjmuje maksymalną wartość równą 1, to jest dla

,...

3

,

2

,

1

,

0

)

1

2

(

±

±

±

=

+

=

Φ

m

m

π

. Ponieważ jednocześnie wartość wyrażenia

w mianowniku (12) wzrasta, natężenia kolejnych maksimów szybko maleją wraz ze wzrostem
kąta ugięcia

Θ

(rys.7). I tak, na przykład dla pierwszego maksimum bocznego występującego

przy

π

3

=

Φ

, mamy zgodnie ze wzorem (12)

2

)

2

/

3

(

π

m

I

I

=

, co stanowi mniej niż 5

% I

m

.

Pomiar szerokości szczeliny oraz nieprzezroczystego paska na podstawie zjawiska dyfrakcji światła

9

2. Opis ćwiczenia

W ćwiczeniu wykonujemy pomiary rozkładu natężeń promieniowania w obrazach

dyfrakcyjnych w funkcji kąta ugięcia

Θ

. Układ pomiarowy składa się z lasera, którym

oświetlamy szczelinę bądź włos zasilacza fotoelementu i mikroamperomierza. Występujący
we wzorach (9d) i (9e) kąt ugięcia

Θ

, można powiązać z wielkościami mierzonymi

bezpośrednio w doświadczeniu, a więc odległością L ekranu od szczeliny i odległością y

m

kolejnego minimum dyfrakcyjnego od środka obrazu.

Wiedząc, że

L

y

tg

m

m

=

θ

obliczyć wartości kątów ugięcia

Θ

m

odpowiadające

zmierzonym minimom dyfrakcyjnym. Wykonać wykres zależności m

λ

od

m

θ

sin

(równanie

(9d) i stosując metodę najmniejszej sumy kwadratów wyznaczyć szerokość szczeliny a
ze współczynnika kierunkowego otrzymanej prostej.

3. Wykonanie ćwiczenia

1. Włączyć laser i w bieg wiązki laserowej wstawić przesłonę ze szczeliną o regulowanej

szerokości. Fotoelement przesłonić metalowym ekranem. Zmieniając szerokość szczeliny
zaobserwować zmiany obrazu dyfrakcyjnego.

2. Odrysować obraz dyfrakcyjny na kartce papieru.
3. Usunąć metalowy ekran, a laser oraz szczelinę ustawić tak, aby zakres ruchu fotoelementu

na śrubie mikrometrycznej pokrywał prążek zerowy wraz z prążkami 1, 2, 3, i 4 rzędu.

4. Włączyć zasilacz układu pomiarowego oraz transformator oświetlenia skali

mikroamperomierza. Napięcie zasilacza ustawić tak, aby natężenie prądu odpowiadające
maksimum prążka zerowego można było zmierzyć na największym zakresie
mikroamperomierza. Zmieniając położenie fotoelementu co 0,5 mm zmierzyć rozkład
natężeń obrazu dyfrakcyjnego w zakresie czterech prążków, łącznie z zerowym,
zmieniając odpowiednio zakres mikroamperomierza.

5. Między laserem i ekranem umieścić włos i znaleźć położenia minimów i maksimów

obrazu interferencyjnego.

6. W bieg wiązki laserowej wstawić przesłonę z otworkiem kołowym, zasłonić fotoelement

ekranem i odrysować uzyskany na ekranie obraz.

7. Zmierzyć odległość L między przedmiotem i ekranem i oszacować błąd L.

Δ

4. Opracowanie wyników

1. Narysować wykres natężenia światła (proporcjonalnego do natężenia prądu płynącego

przez fotoelement) od wartości kąta ugięcia

Θ

. Znaleźć szerokość szczeliny,

wykorzystując metodę najmniejszej sumy kwadratów. Długość fali światła emitowanego
przez laser He-Ne jest równa 638,8nm.

2. Wyznaczyć przybliżoną wartość grubości włosa i średnicy otworu kołowego.
3. Na podstawie zmierzonego rozkładu natężeń obrazu dyfrakcyjnego wyznaczyć stosunek

natężeń w kolejnych maksimach dyfrakcyjnych względem maksimum środkowego.

4. Otrzymane wyniki porównać z obliczeniami wykonanymi na podstawie wzoru (12).

Podać źródła ewentualnych rozbieżności.

Pomiar szerokości szczeliny oraz nieprzezroczystego paska na podstawie zjawiska dyfrakcji światła

10

5. Pytania kontrolne

1. Dlaczego obrazy dyfrakcyjne pochodzące od szczeliny i nieprzeźroczystego paska o tej

samej co szczelina szerokości są takie same ?

2. Wyjaśnij dlaczego pierwsze minimum w obrazie dyfrakcyjnym otrzymujemy pod kątem,

dla którego

a

λ

θ

=

sin

?

3. Zilustruj za pomocą diagramów wektorowych powstawanie maksimów i minimów

w obrazie dyfrakcyjnym.

4. Wyjaśnij dlaczego natężenie promieniowania w kolejnych maksimach dyfrakcyjnych jest

coraz słabsze?

6. Literatura

1. D.Halliday i R.Resnick, Fizyka PWN (1984r.) t.II, rozdział 45, 46.
2. J.Orear, Fizyka, PWN (1990r.) t.II, rozdział 22.