Sprawozdanie z ćwiczeń laboratoryjnych

z fizyki.

ĆWICZENIE NR 1

Temat: Wyznaczanie szerokości szczelin, stałych siatek dyfrakcyjnych i długości fali sprężystej w szkle w badaniach dyfrakcji promieniowania laserowego.

GRUPA T - 13

SEKCJA 6

Michał Pluta

Arkadiusz Król

1. WSTĘP TEORETYCZNY.

Podczas emisji spontanicznej lub wymuszonej może odbywać się wypromieniowanie energii przez wzbudzoną cząstkę. Spontaniczna emisja ma miejsce w przypadku samoistnego przejścia ze stanu energetycznie wzbudzonego E_m do stanu o niższej energii E_n z wypromieniowaniem światła o energii:
,gdzie: h - stała Plancka,
- częstotliwość fali promieniowania elektromagnetycznego.

Warunkiem zajścia emisji wymuszonej promieniowania elektromagnetycznego o energii określonej powyższym wzorem, przez atomy lub cząstki jest obecność w ich najbliższym otoczeniu promieniowania elektromagnetycznego o tej samej energii kwantów co określona tym wzorem. Przy tym promieniowanie to musi mieć odpowiednio dużą gęstość. Proces emisji wymuszonej wykorzystuje się w laserach.

Laserami nazywamy źródła spójnego promieniowania elektromagnetycznego o dużym natężeniu. Spójność promieniowania można określić jako stabilność fazy fali, zarówno w przestrzeni jak i czasie. Prócz spójności, innym parametrem opisującym jakość uzyskiwanej wiązki laserowej są długość fali promieniowania laserowego i jej rozmycie, moc wiązki, rozbieżność wiązki.

Zjawisko dyfrakcji polega na ugięciu fali na przeszkodzie (szczelina, siatka dyfrakcyjna), której rozmiary są porównywalne z długością tej fali. W wyniku tego zjawiska powstaje obraz dyfrakcyjny w postaci jasnych i ciemnych prążków.

Siatka dyfrakcyjna to układ równoległych szczelin o równej szerokości. Na każdej z tych szczelin zachodzi zjawisko dyfrakcji światła. Fale ugięte na kolejnych szczelinach mogą interferować ze sobą (czyli nakładać się) przy czym dla powstania tzw. prążka jasnego musi być spełniony warunek, że padająca fala jest falą płaską:

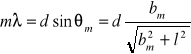
m - kolejny nr prążka, d - odległość 2 kolejnych szczelin w siatce (od siebie), θ_m - kąt ugięcia fali pod jakim propaguje m-ty promień ugięty na siatce, b_m - odległość m-tego prążka od prążka zerowego, l - odległość ekranu od siatki, λ - długość fali.

W przypadku fali dyfrakcji na szczelinie położenie jasnego prążka określa równanie:

,

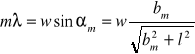
w - szerokość szczeliny, α_m - kąt ugięcia fali świetlnej, m - numer prążka.

2. PRZEBIEG ĆWICZENIA.

Wyznaczenie stałej siatki dyfrakcyjnej.

1. Umieściliśmy siatkę dyfrakcyjną w uchwycie zamocowanym na ławie optycznej i ustawiliśmy uchwyt tak, aby w zakresie przemieszczania fotoogniwa znalazły się prążki dyfrakcyjne od trzeciego rzędu z lewej strony do trzeciego rzędu z prawej strony.

2. Zmierzyliśmy odległość l siatki dyfrakcyjnej od fotoogniwa ustawionego w miejscu zerowego prążka dyfrakcyjnego.

3. Zmierzyliśmy położenie prążków dyfrakcyjnych na podstawie obserwacji wartości sygnału napięciowego pochodzącego od fotoogniwa umieszczonego w centrum kolejnych prążków dyfrakcyjnych i trzykrotnie wykonaliśmy pomiary dla wszystkich prążków leżących w zakresie przemieszczeń fotoogniwa.

3. OPRACOWANIE WYNIKÓW.

1. Średnia wartość odległości badanej siatki dyfrakcyjnej od fotoogniwa oraz jej odchylenie standardowe:

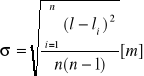
Obliczona wartość wynosi: l=(0,20±0,00) [m]

2. Wyznaczenie wartości średnich oraz ich odchyleń standardowych dla wyników pomiarów położenia m-tego zarejestrowanego prążka dyfrakcyjnego

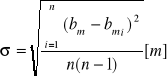
Prążek	bm⋅10^-2 [m]	Δbm⋅10^-2 [m]
L3	8,2	0,2
L2	11,1	0,2
L1	13,6	0,2
0	16,1	0,2
P1	18,5	0,0
P2	21,1	0,2
P3	24,1	0,1

3. Obliczenie średnich odległości b_m lewego i prawego m-tego prążka dyfrakcyjnego od prążka zerowego:

Wyniki obliczeń:

Prążek	bm0 - bml ⋅10^-2 [m]	bmp - bm0 ⋅10^-2 [m]	bm ⋅10^-2 [m]	y=mλ ⋅10^-6 [m]	x=bm(bm^2+l^2)^-1/2
1	2,5	2,4	2,45	0,63	0,12
2	5,0	5,0	5,00	1,26	0,24
3	7,9	8,0	7,95	1,89	0,37

4. Sporządzenie wykresu zależności y=mλ od x=b_m(b_m²+l²)^-1/2 , czyli zależności iloczynu rzędu prążka i długości fali światła od sinusa kąta ugięcia światła dla danego prążka dyfrakcyjnego - WYKRES I.

Dane do wykresu w tabeli w punkcie 3.

5. Aproksymacja wyników przedstawionych na wykresie y=mλ od x=b_m(b_m²+l²)^-1/2

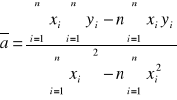
[m]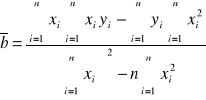
[m]

[m²]

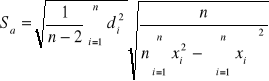
[m]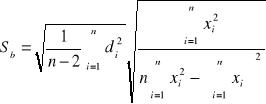
[m]

Obliczeń dokonaliśmy w programie EXCEL.

Współczynniki prostej mλ=a⋅b_m(b_m²+l²)^-1/2+b mają następujące wartości:

a=(5,27±0,58)⋅10^-6 [m]

b=(0,24±0,06)⋅10^-6 [m]

6. Wyznaczenie odległości dwóch kolejnych szczelin w badanej siatce, czyli stałej siatki dyfrakcyjnej:

,

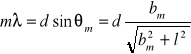
porównując powyższy wzór z prostą mλ=a⋅b_m(b_m²+l²)^-1/2+b i pomijając wartość współczynnika b , otrzymujemy:

d=a [m]
[m]

d=5,27⋅10^-6 [m] , Δd=0,58⋅10^-6 [m]

d=(5,27±0,58)⋅10^-6 [m]

4. WNIOSKI.

Zależność iloczynu rzędu prążka i długość fali świetlnej od sinusa kąta ugięcia światła dla każdego zbadanego prążka dyfrakcyjnego jest liniowa. Wyznaczenie stałej siatki dyfrakcyjnej przeprowadzono na podstawie znajomości przebiegu tej zależności.

W ćwiczeniu uzyskaliśmy następujące wyniki:

-współczynniki prostej aproksymującej:

a=(5,27±0,58)⋅10^-6 [m]

b=(0,24±0,06)⋅10^-6 [m]

-stała siatki dyfrakcyjnej:

d=(5,27±0,58)⋅10^-6 [m]

Niedokładności jakie wystąpiły przy obliczeniu odległości pomiędzy prążkami wynikają z niedokładności odczytu skali oraz złego ustawienia odległości siatki dyfrakcyjnej od fotoogniwa.

---