Sprawozdanie

Politechnika Śląska

Wydział AE i I

Kierunek A i R

ćwiczenie laboratoryjne z fizyki:

Wyznaczanie energii maksymalnej promieni  metodą absorbcyjną. Badanie Statystycznego charakteru rozpadu promieniotwórczego.

Grupa 4 Sekcja 9

Ewa Sobieraj

Gliwice 25-03-95

1.Część Teoretyczna

Rozpad beta polega na przemianie jednego neutronu w jądrze atomu w proton, której towarzyszy emisja promieniowania  (czyli elektronu naładowanego ujemnie e- lub dodatnio e+) i odpowiednio antyneutrina (
) lub neutrina (). pierwiastka.

Widmo energetyczne elektronów w czasie rozpadu promieniotwórczego  jest widmem ciągłym , o ściśle określonej energii maksymalnej (Emax). Maksymalna energia widma odpowiada sytuacji, gdy elektron unosi całą dostępną energię równą energi przejścia . Energie elektronów promieniowania  obejmują szeroki zakres wartości - od energii rzędu 104[eV] do 10[MeV] dla różnych izotopów promieniotwórczych. Ponieważ masa elektronów jest mała, ich energia spoczynkowa wynosi zaledwie 0,51 MeV . Wynika stąd , że już elektrony o energii 104[eV] muszą być opisywane za pomocą wzorów mechaniki relatywistycznej.Proces przejścia elektronów przez absorbującą substancję jest złożony, a zanim jego energia zmaleje do zera może zderzyć się z wieloma elektronami (lub jądrami).

. Strata energii (w zderzeniach niesprężystych) na jedostkę drogi (zwana zdolnością hamującą ośrodka) dla cząstki o ładunku Ze i przelatującej z prędkością v przez substancję, której atomy mają po Z' elektronów, jest określona wzorem Bethego:
, gdzie: m - masa elektronu, Ei - średnia energia jonizacji atomów danego ośrodka,
, c - prędkość światła w próżni, v - prędkość cząstki,
, e - ładunek elektronu, o - przenikalnność dielektryczna próżni, B - wartość stała.

Zdolność hamująca ośrodka jest tym większa, im większa jest jego liczba atomowa Z'.

2.Przebieg ćwiczenia .

Włączamy przelicznik, a następnie mierzymy tło licznika porzez pomiar liczby zliczeń w czasie 10 minut. Umieszczamy preparat promieniotwórczy w domku ołowianym w odległości ok. 1[cm]. od okienka licznika. Poczym nastawiamy tryb pomiaru czas zliczania [s] zadanej liczby impulsów ,tutaj104. Pomiary wykonujemy najpierw bez absorbenta, a następnie z płytkami aluminiowymi dokładanymi na stos na preparacie. Pomiary rozpoczynamy od najcieńszych płytek. Rysujemy wykres zależności N'=f(d). Następnie wykreślamy zależność ln|N'|=f(d). Przedłużamy wykres do przecięcia się z rzędną ln |Nt|. Określamy zasięg liniowy promieni  w aluminium. Obliczmy zasięg masowy promieni , korzystając ze wzoru Zm=ρZlin. Rysujemy wykres zależności zasięgu masowego promieni  w aluminium od ich energii maksymalnej i określamy energię maksymalną promieni  stosowanego preparatu 204Tl.

3.Opracowanie wyników pomiarowych.

Z pomiaru zliczeń w ciągu 10 minut bez preparatu promieniotwórczego otrzymujemu tło licznika, które wynosi Nt=192. Błąd wyliczenia tła wyznaczamy ze wzoru:
i wyniosi on w naszym przypadku Nt=13.85. Ostatecznie więc tło licznika zapisujemy: Nt=192 ± 13.85 . Następnie aby oliczyć zasięg masowy rysujemy wykres zależnści Ln|N`|=f(d). Otrzymujemy prostą o równaniu:

y=(-6.96±0.10)x+(13.37±0.02). Zaznaczając na wykresie wartość logarytmu naturalnego tła licznika: Ln|Nt|=5.25±2.29, w miejscu przecięcia się lini otrzymujemy zasięg liniowy równy Z=1.27±0.36[mm]. Mnożąc zasięg masowy przez gęstość aluminiu ρ=270, otrzymujemy zasięg masowy i błąd jego wyliczenia: Zm=344,02±97.19. Następnie sporządzamy wykres zależności energi maksymalnej od zasięgu masowego. Otrzymano prostą o równaniu:

y=(0.45±0.01)x+(-49.96±7.02). Odczytujemy maksymalną energię i błąd jej wyliczenia: Emax=865,8±213.5 [keV].

4.Statystyczny charakter rozpadu promieniotwórczego

Oznaczony preparat umieszczamy w domku ołowianym, w odległości ok. 2 [cm] od okienka licznika. Wyjmujemy panel przelicznika i włączamy układ pamięciowy, włączamy przelicznik. w trybie[T] ( t = 1s). Notujemy 382 kolejne wskazania przelicznika.

Wyniki opracowujemy i grupujemy w tabeli:

I	Xi	ni	nti
0	0	0	0
1	0	0	0
2	1	1	1
3	2	3	3
4	3	5	8
5	4	18	16
6	5	22	26
7	6	36	36
8	7	51	44
9	8	56	48
10	9	46	48
11	10	36	43
12	11	32	35
13	12	25	27
14	13	19	19
15	14	10	12
16	15	11	8
17	16	8	4
18	17	3	2

gdzie Ni - wartość zliczeń (odczyt z przelicznika), ni - liczba powtórzeń, nti - toretyczna liczba powtórzeń: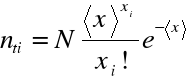
, gdzie <x>- średnia wartość liczby powtórzeń,
,

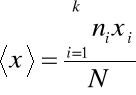
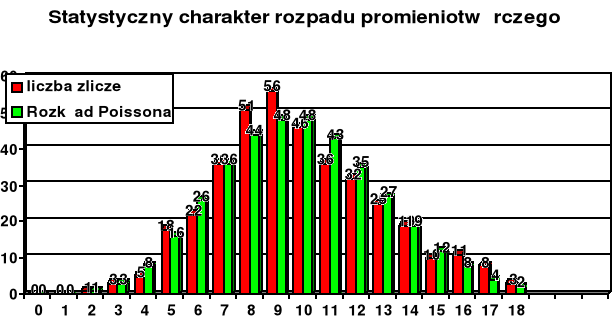
Rysujemy histogram ni = f(Ni) oraz wykres rozkładu Poissona:

5.Podsumowanie.

W pierwszej części wyżej opisanego ćwiczenia wyznaczaliśmy maksymalną energię promieniowania  metodą absorbcyjną. Energia stosowanego preparatu 204Tl określona przez nas równa jest:Emax=865,8±213.5 [keV]..

Wynik ten obarczony jest błędem wynikłym z niedokładności zliczeń w rozpadzie promieniotwórczym, odległością preparatu od okienka licznika, niedokładnością pomiaru grubości absorbenta, błędmi związanymi z odczytem wertości z wykresów.

W drugiej części ćwiczenia badaliśmy statystyczny charakter rozpadu promieniotwórczego. Opracowanie wyników przedstawia tabela pomiarowa. Natomiast histogram pokazuje zależność liczby powtórzeń od wartości zliczenia oraz wykres rozkładu Poissona. Na histogramie można zobaczyć różnice między wartościami określonymi doświadczalnie, a teoretycznymi liczbami powtórzeń. Rozbieżności te wyniknęły na skutek niedokładności wskazań przelicznika oraz małej-minimalnej liczbie zanotowanych, kolejnych wskazań przelicznika (382).

---