SPRAWOZDANIE Z LABORATORIUM Z FIZYKI

ĆWICZENIE NR. 4

WYZNACZANIE ELIPSOIDY BEZWŁADNOŚCI CIAŁA SZTYWNEGO.

SEKCJA IX :

MARCIN CHOLEWA

STANISŁAW WAWSZCZAK

WSTĘP TEORETYCZNY:

Ciałem sztywnym nazywamy ciało, którego wszystkie punkty mają stałe położenie względem siebie.

Elipsoida bezwładności jest to powierzchnia zawarta miedzy końcami odcinków r_x; r_y; r_z odłożonych na wszystkich możliwych osiach przechodzących przez środek masy ciała.

Odcinki odłożone na osiach x, y, z muszą być różnej długości i muszą odpowiadać równaniom:

;
;

gdzie: I_xx, I_yy, I_zz - momenty bezwładności względem osi x, y, z.

Moment bezwładności jest to suma iloczynów mas przez kwadraty odległości od osi obrotu przechodzącej przez środek masy.

PRZEBIEG ĆWICZENIA:

1. Mierzymy czas 10 wahnięć wahadła skrętnego nieobciążonego

2. Pomiar powtarzamy gdy w ramce wahadła zamocujemy sześcian, a następnie prostopadłościan (dla prostopadłościanu mierzymy czas 10 wahnięć dla trzech głównych osi bezwładności i dla jego przekątnej)

3. Pomiary powtarzamy trzykrotnie.

OPRACOWANIE WYNIKÓW:

Wymiary obciążników :

Prostopadłościan					Sześcian
Lp.	a [m]	b [m]	c = h [m]		a [m]
1	0,04	0,06	0,1		0,05
2	0,0405	0,061	0,101		0,049
3	0,0395	0,0605	0,1005		0,051
4	0,039	0,0595	0,0995		0,0495
5	0,041	0,059	0,099		0,0505
xśr	0,04	0,06	0,1		0,05
δ	0,35⋅10^-3	0,35⋅10^-3	0,35⋅10^-3		0,35⋅10^-3

m = 1884 [g] m = 980 [g]

Obliczamy wartość średnią i odchylenie standartowe:

,

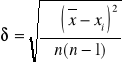
gdzie: n - ilość pomiarów

Czasy 10 wahnięć wahadła skrętnego :

	t [s]
	(1)	(2)	(3)	xśr	δ
wahadło nieobciążone (Io)	7,152	7,152	7,152	7,152	0
Wahadło obciążone sześcianem (Is)	8,995	8,996	8,996	8,9957	3,3⋅10^-4
Wahadło obciążone prostopadłościanem
I główna oś (II)	10,468	10,474	10,495	10,479	2,19⋅10^-2
II główna oś (III)	13,498	13,498	13,499	13,4983	3,3⋅10^-3
III główna oś (IIII)	14,315	14,316	14,316	14,31567	3,3⋅10^-3
Wzdłuż głównej przekątnej (Ia)	11,703	11,712	11,699	11,70467	0,38⋅10^-2

Wyznaczanie wartości głównych momentów bezwładności badanego obciążnika:

ze wzoru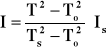

Okres wahania nieobciążonego wahadła

Okres wahania obciążonego sześcianem o m = 980 g

Okres wahania obciążonego prostopadłościanem względem

I głównej osi bezwładności

Moment bezwładności sześcianu obliczamy ze wzoru :

gdzie: a = 0.04 [m] ; M = 980 [g] = 0.98 [kg]

[kg·m²]

[kg·m²]

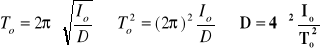
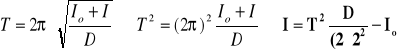
Okres 1 drgania wahadła nieobciążonego:

T_o = 0,715 [s]

Okres 1 drgania wahadła obciążonego sześcianem:

T_s = 0,89957 [s]

Okres 1 drgania wahadła obciążonego prostopadłościanem względem I głównej osi bezwładności:

T_I = 1,0479 [s]

Okres 1 drgania wahadła obciążonego prostopadłościanem względem II głównej osi bezwładności:

T_II = 1,34983 [s]

Okres 1 drgania wahadła obciążonego prostopadłościanem względem III głównej osi bezwładności:

T_III = 1,431567 [s]

Okres 1 drgania wahadła obciążonego prostopadłościanem względem głównej przekątnej osi bezwładności:

T_a = 1,170467 [s]

Obliczamy moment bezwładności nieobciążonej ramki i moment bezwładności prostopadłościanu względem jego głównych osi bezwładności :

PRZEKSZTAŁCAJĄC WZÓR:

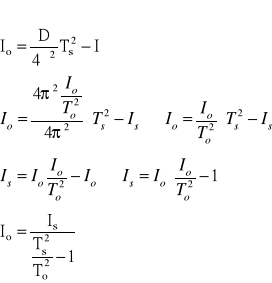
Moment bezwładności ramki nieobciążonej (patrz. TABELA NR 2):

[kg·m²]

Stała kierunkowa (moment kierujący):

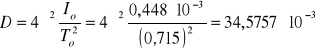
[kg·m² / s²]

Korzystając ze wzoru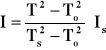
wyznaczymy moment bezwładności względem I głównej osi bezwładności (patrz. TABELA NR 2):

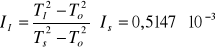
[kg·m²]

Moment bezwładności względem II głównej osi bezwładności (patrz. TABELA NR 2)

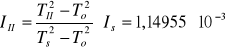
[kg·m²]

Moment bezwładności względem III głównej osi bezwładności (patrz. TABELA NR 2):

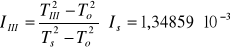
[kg·m²]

Moment bezwładności względem przekątnej prostopadłościanu (patrz. TABELA NR 2):

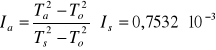
[kg·m²]

Wyznaczamy równanie prostej zawierającej główną przekątną:

Współrzędne wierzchołka prostopadłościanu :

W (x_w; y_w; z_w)

;
;

x_w = 0,02 [m]

y_w = 0,03 [m]

z_w = 0,05 [m]

W (0,02; 0,03; 0,05)

Równanie przekątnej na postać :

Wyznaczamy elipsoidę bezwładności prostopadłościanu o podstawie prostokąta :

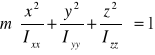
lub równanie elipsoidy

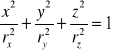
wiemy że I_xx = I_I, I_yy = I_II oraz że I_zz =I_III

więc

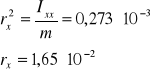
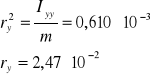
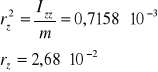
Rozwiązujemy układ równań i wyznaczamy punkty przebicia prostej zawierającej przekątną główną z elipsoidą bezwładności :

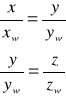
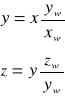
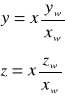
x = 0,788⋅10^-2

x_p = 0,788 ⋅ 10^-2 [m]

y_p = 1,182 ⋅ 10^-2 [m]

z_p = 1,973 ⋅ 10^-2 [m]

Równanie elipsoidy bezwładności ma postać :

Punkt przebicia prostej z elipsoidą bezwładności ma współrzędne:

P (0,788 ⋅ 10^-2; 1,182 ⋅ 10^-2; 1,973 ⋅ 10^-2)

Obliczamy moment bezwładności względem przekątnej głównej prostopadłościanu wynosi :

I_a = 0,7532·10^-3 [kg·m²]

Ten sam moment można obliczyć ze wzoru :

I_ap = 1,1136·10^-3 [kg·m²]

I_a = I_ap

[kg·m²]

Obliczamy błąd procentowy

Przy porównaniu dwóch wyników momentu bezwładności względem głównej przekątnej wystąpiła różnica rzędu
0,3604·10^-3 [kg·m²], jest to bardzo duża różnica wynikającą z niedokładności pomiarów i podawania przybliżonych wartości poszczególnych obliczeń.

Schematyczne obliczenie pochodnej momentu I_x względem T_x, T_o, T_s

I_s = 0,2613·10^-3 [kg·m²] T_s = 0,89957 [s]

I_I = 0,5147·10^-3 [kg·m²] T_I = 1,0479 [s]

I_II = 1,14955·10^-3 [kg·m²] T_II = 1,34983 [s]

I_III = 1,34859·10^-3 [kg·m²] T_III =1,431567[s] I_a = 0,7532·10^-3 [kg·m²] T_a = 1,170467 [s]

T_o = 0,715 [s]

[s]

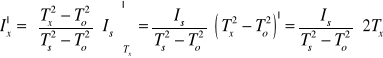
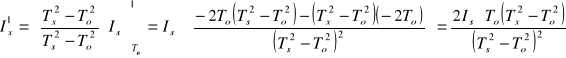
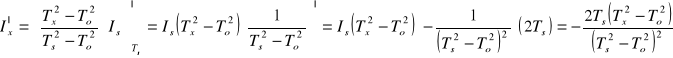
Niepewności jakimi obarczone są wyznaczone wartości momentów bezwładności ciała :

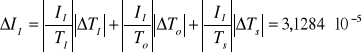
[kg·m²]

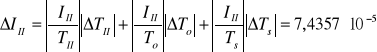
[kg·m²]

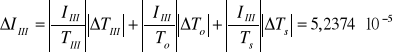
[kg·m²]

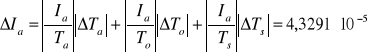
[kg·m²]

Zestawienie wyników :

- pomiary obciążników i czasy wahnięć podane w tabelach na str.1 i 2

- moment bezwładności sześcianu

I_s = (0,261±0,007) · 10^-3 [kg·m²]

- moment bezwładności względem I głównej osi bezwładności

I_I = (0,515±0,031) · 10^-3 [kg·m²]

- moment bezwładności względem II głównej osi bezwładności

I_II = (1,15±0,07) · 10^-3 [kg·m²]

- moment bezwładności względem III głównej osi bezwładności

I_III = (1,35±0,05) · 10^-3 [kg·m²]

- moment bezwładności względem głównej przekątnej

I_a = (0,753±0,043) · 10^-3 [kg·m²]

- moment bezwładności względem głównej przekątnej obliczony wg wzoru

I_ap = (1,11±0,36) · 10^-3 [kg·m²]

- stała kierunkowa (moment kierujący)

D = 34,576 · 10^-3 [kg·m² / s²]

- równanie elipsoidy:

WNIOSKI:

Celem ćwiczenia było wyznaczyć główne momenty bezwładności sześcianu i prostopadłościanu o podstawie prostokąta co zrobiliśmy. Wyniki uzyskane w czasie pomiarów, a także przy obliczeniach są obciążone błędem obserwatora i zaokrąglaniem wyników.

11