Wstęp teoretyczny

Momentem bezwładności jest miarą bezwładności ciała w ruchu obrotowym. Charakteryzuje rozkład masy w ciele.

Momentem bezwładności ciała względem osi x nazywane jest wyrażenie :

I_x = Σ m_i r_i²

gdzie m_i - masy elementów ciała odległe każda o r_i od osi x

Elipsoida bezwładności jest to powierzchnia charakteryzująca rozkład momentów bezwładności danego ciała względem prostych przechodzących przez wyróżniony punkt O

(przyjmowany najczęściej w początku kartezjańskiego układu współrzędnych).

Dana jest ona równaniem:

I_xx² + I_yy² + I_zz² - 2_xyxy - 2_yzyz - 2_xzxz = 1

gdzie I_x , I_y , I_z to momenty bezwładności względem osi układu x , y , z a I z mieszanymi indeksami to momenty odśrodkowe .

Człony mieszane zerują się przy wyborze układu współrzędnych pokrywającego się

z głównymi osiami bezwładności ciała. Wtedy powyższy wzór przyjmuje postać:

I_xxx² + I_yyy² + I_zzz² = 1

Za pomocą tego wzoru można znaleźć moment bezwładności względem dowolnej osi, jeśli tylko znane są główne momenty bezwładności danej bryły. W przypadku, gdy oś obrotu nie przechodzi przez środek masy ciała stosujemy twierdzenie Steinera:

I = I₀ + md²

gdzie I₀ jest momentem bezwładności dla osi przechodzącej przez środek masy ciała,

d - przesunięciem między daną osią a osią środkową, m - masą ciała .

Długość odcinka poprowadzonego ze środka masy ciała do dowolnego punktu powierzchni elipsoidy wyraża się wzorem:

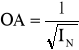
I_n jest w tym wzorze momentem bezwładności danej bryły względem osi pokrywającej się

z tym odcinkiem.

Opis sprzętu pomiarowego

Przedmiotem badań jest stalowy prostopadłościan. W celu wyznaczenia jego momentu bezwładności stosujemy wahadło torsyjne (zwane też skrętnym).

Wahadło zbudowane jest z zawieszonej na dwóch stalowych linkach ramki (2). Wzdłuż prowadnic ramki można przesuwać ruchomą belkę (3). Nakrętki z tulejkami zaciskowymi umożliwiają umocowanie belki na prowadnicach ramki w zależności od wymiarów badanego ciała (4). Pomiar odbywa się poprzez zliczanie impulsów generowanych przez wysięgnik ramki (2) w złączu optoelektronicznym (1). Zliczając co drugi impuls zliczamy tym samym liczbę okresów. Równocześnie ze zwolnieniem ramki następuje uruchomienie elektronicznego zegara. Możemy w ten sposób z dużą dokładnością zmierzyć czas określonej liczby wahnięć.

Zasada pomiaru

Okres drgań wahadła opisuje wzór:

gdzie D jest momentem kierującym wahadła.

W celu wyznaczenia momentu bezwładności należy zmierzyć okres drgań wahadła nieobciążonego:

następnie powtarzamy pomiar obciążając jednocześnie wahadło daną bryłą:

Przekształcając powyższe wzory otrzymamy zależność, z której otrzymujemy wartość szukanego momentu bezwładności:

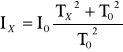
Moment bezwładności wibratora I₀ wyznaczyć można pośrednio mierząc okres drgań układu obciążonego bryłą o znanym momencie bezwładności (kulą lub walcem)

Moment bezwładności ciała o masie m i promieniu R dla osi obrotu pokrywającej się z osią bryły opisują wzory:

Dla kuli :

Dla walca :

Dla tarczy :

Celem ćwiczenia jest sprawdzenie, w jakim stopniu wyznaczenie elipsoidy bezwładności pomaga w wyznaczeniu momentu bezwładności bryły dla dowolnej osi obrotu. Dlatego też po wyznaczeniu momentów bezwładności dla trzech głównych osi bezwładności wyznaczamy ów moment dla zadanej osi obrotu (dla naszego prostopadłościanu może to być np. przekątna PP'). Tak otrzymany wynik weryfikujemy z równaniem elipsoidy (przy zastosowaniu cosinusów kierunkowych dla danej konfiguracji).

gdzie :

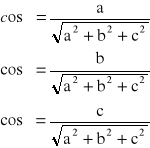
Przebieg ćwiczenia

1. Mierzymy długość krawędzi prostopadłościanu

2. Mierzymy czas 10 okresów drgań wahadła z pustą ramką

3. W ramce wibratora mocujemy walec i mierzymy czas 10 okresów drgań

4. Badany prostopadłościan zamocowujemy w ramce wahadła i mierzymy czas 10 okresów. Pomiary wykonujemy kolejno dla ustawienia bryły zgodnie z trzema głównymi osiami bezwładności

5. Podobne pomiary wykonujemy dla innych osi obrotu

Obliczenia

1. Wyznaczamy moment bezwładności wibratora

2. Obliczamy momenty bezwładności prostopadłościanu dla wszystkich realizowanych zamocowań

3. Obliczamy cosinusy kierunkowe dla poszczególnych konfiguracji bryły

4. Obliczamy moment bezwładności wykorzystując równanie elipsoidy bezwładności i porównujemy otrzymany wynik z wartością eksperymentalną

5. Podobne obliczenia wykonujemy dla wszystkich konfiguracji bryły

6. Przeprowadzamy rachunek błędów.

masa walca m = 1465 g

promień walca R = 24,54 mm

krawędzie a = 40,1 mm

b = 60,2 mm

c = 100,2 mm

Oś obrotu	Czas t = 10T [s]
		Pomiar 1	Pomiar 2	Pomiar 3	średnia
Pusta ramka	9,673	9,673	9,673	9,673
Oś obrotu walca	12,433	12,433	12,433	12,433
Oś x	19,407	10,403	19,393	19,401
Oś y	18,285	18,289	18,289	18,288
Oś z	14,247	14,247	14,242	14,246
Przekątna PP'	15,919	15,923	15,920	15,921

Wartości średnie obliczamy za pomocą wzoru:

Korzystamy ze wzorów: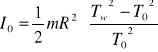
oraz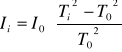

Momenty bezwładności [kg·m^2]	Pomiar 1	Pomiar 2	Pomiar 3	Wartość średnia
Wibratora I0	0,2876421 · 10 ^-3	0,2876421 · 10 ^-3	0,2876421 · 10 ^-3	0,2876421 · 10 ^-3
Elementu względem osi OX IX	0,8701932 · 10 ^-3	0,8697159 ·10 ^-3	0,8685233 · 10 ^-3	0,8694773 · 10 ^-3
Elementu względem osi OY IY	0,7401846 · 10 ^-3	0,7406343 · 10 ^-3	0,7406343 · 10 ^-3	0,7405219 · 10 ^-3
Elementu względem osi OZ IZ	0,3363468 · 10 ^-3	0,3363468 · 10 ^-3	0,3359964 · 10 ^-3	0,3362592 · 10 ^-3
Elementu względem osi PP' Ipp'	0,4914011 · 10 ^-3	0,4917927 · 10 ^-3	0,4914990 · 10 ^-3	0,4915969 · 10 ^-3

Wyliczamy cosinusy kierunkowe i momenty bezwładności I_PP' z równania elipsoidy bezwładności:

cos α = 0,4871

cos β = 0,3245

cos γ = 0,8108

Moment bezwładności [ kg·m^2 ]	Pomiar 1	Pomiar 2	Pomiar 3	Wartość średnia
Ipp'	0,5055486 · 10 ^-3	0,5054827 · 10 ^-3	0,5049693 · 10 ^-3	0,5053566 · 10 ^-3

Różnica pomiędzy wartością wyliczoną a zmierzoną [kg·m^2]	Pomiar 1	Pomiar 2	Pomiar 3	Wartość średnia
ΔIpp'	1,415 · 10 ^-5	1,369 · 10 ^-5	1,347 · 10 ^-5	1,376 · 10 ^-5

Analiza błędów

Wyznaczamy błędy poszczególnych momentów bezwładności:

Moment	Błąd pomiaru 1	Błąd pomiaru 2	Błąd pomiaru 3	Błąd maksymalny ΔI
IX	7,159 · 10 ^-7	2,386 · 10 ^-7	9,54 · 10 ^-7	9,54 · 10 ^-7
IY	3,37 · 10 ^-7	1,124 · 10 ^-7	1,124 · 10 ^-7	3,37 · 10 ^-7
IZ	8,76 · 10 ^-7	8,76 · 10 ^-7	2,628 · 10 ^-7	8,76 · 10 ^-7

Obliczamy błąd momentu I_pp' sposobem różniczki zupełnej:

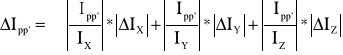
ΔI_pp' = ± 6,648789 ·10^-7

Wnioski:

Zastosowanie wahadła torsyjnego pozwoliło nam w bardzo łatwy sposób wyznaczyć elipsoidę bezwładności badanego prostopadłościanu. Duża dokładność wykonanych przez nas pomiarów dodatkowo potwierdza, iż dane uzyskane w ten sposób są wiarygodne i mogą być źródłem cennych informacji.

6

---