Politechnika Śląska

Wydział AEiI

Kierunek AiR

Ćwiczenia laboratoryjne z fizyki:

Wyznaczanie temperatury Curie dla ferrytów.

Grupa IV, sekcja 3

1.Szymon Ciupa

2.Adam Filipek

Gliwice, 09.04.1999

1. Wstęp teoretyczny:

Ferryty to związki chemiczne zawierające w swojej strukturze metale dwuwartościowe, np. mangan, cynk, magnez. Ich cechą charakterystyczną jest duża oporność właściwa, co pozwala na budowę rdzeni magnetycznych o małych stratach związanych z prądami wirowymi. Własności elektryczne większości ferrytów pozwalają na zakwalifikowanie ich do grupy półprzewodników. Własności magnetyczne zależą do momentów magnetycznych jonów i ich wzajemnego oddziaływania. Rozróżnia się trzy grupy materiałów o własnościach magnetycznych: ferromagnetyki, antyferromagnetyki i ferrimagnetyki.

Ferromagnetyki są to związki, które nawet pod wpływem słabego pola magnetycznego w silnym stopniu ulegają namagnesowaniu. Ferromagnetyki, tym różnią się od dia - i paramagnetyków, że stan namagnesowania jest długo zachowywany nawet po przerwaniu działania zewnętrznego pola magnetycznego. Ciała ferromagnetyczne składają się z atomów mających własne momenty magnetyczne, między którymi w małych obszarach spontanicznego namagnesowania istnieje oddziaływanie porządkujące kierunki momentów magnetycznych atomów. Są one w tym obszarze mikroskopowym ustawione równolegle w określonym kierunku. Takie właśnie obszary spontanicznego namagnesowania noszą nazwę domen. W stanie naturalnym większość ciał ferromagnetycznych nie wykazuje trwałego magnetyzmu. Wielka liczba domen nie wykazuje uporządkowania w całym ferromagnetyku. Dopiero po umieszczeniu takiej substancji w zewnętrznym polu magnetycznym następuje zmiana kierunku magnetycznych momentów poszczególnych domen, wskutek czego namagnesowanie całego ciała wzrasta. Uporządkowanie spinowych momentów magnetycznych w obszarach wewnątrz-domenowych maleje ze wzrostem temperatury i znika całkowicie w temperaturze zwanej temperaturą Curie (Tc). W ferromagnetykach poniżej temp. Curie momenty magnetyczne ustawiają się równolegle do siebie, a zwroty są zgodne. Powyżej temp. Curie intensywne ruchy cieplne zaburzają to uporządkowanie i ferromagnetyk przechodzi w stan paramagnetyczny. Zależność podatności magnetycznej ferromagnetyków od temperatury w zakresie słabych pól opisuje prawo Curie:

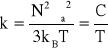
gdzie: N - koncentracja cząsteczek, k_b - stała Boltzmana, T - temperatura, C - stała Curie.

W ogólnym przypadku zależność podatności magnetycznej od temperatury opisuje tzw. prawo Curie - Weissa:

.

2. Schemat układu i opis doświadczenia:

W celu przeprowadzenia doświadczenia zmontowano układ pomiarowy według następującego schematu:

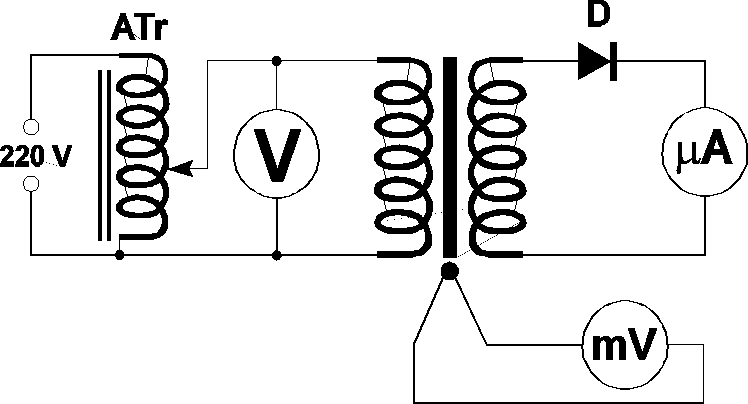
Konstrukcja układu pomiarowego jest następująca. Na rurze ze szkła kwarcowego nawinięto transformator. Wewnątrz rury umieszczono badany, cylindryczny rdzeń ferrytowy. W kontakcie z rdzeniem znajduje się złącze termopary, której drugi koniec posiada temperaturę otoczenia. Prąd płynący w uzwojeniu pierwotnym powoduje powstawanie prądów wirowych wewnątrz rdzenia i jego nagrzewanie się. Ferryt otoczony jest płaszczem izolacyjnym. Temperaturę rdzenia można określić z krzywej cechowania termopary mierząc siłę termoelektryczną miliwoltomierzem.

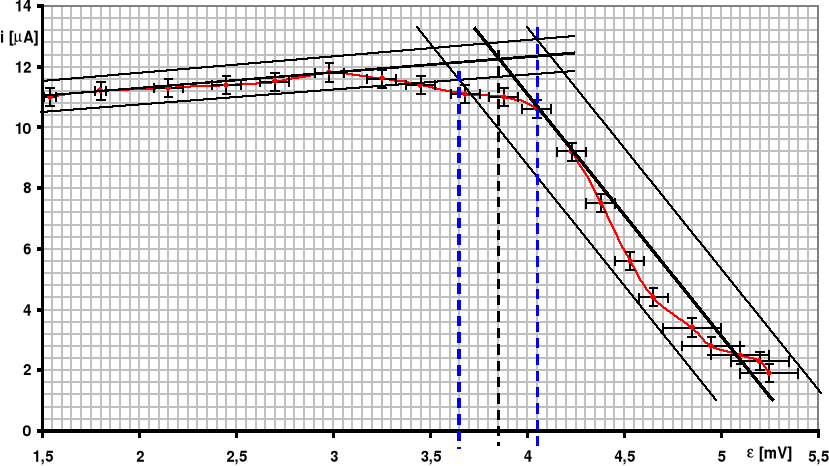
Celem ćwiczenia było wyznaczenie temperatury Curie dla wspomnianego rdzenia ferrytowego. Skorzystano z faktu, że dla temperatury Curie następuje gwałtowny spadek przenikalności magnetycznej rdzenia i natężenie prądu płynącego w uzwojeniu wtórnym transformatora gwałtownie spada. W związku z tym podczas doświadczenia dokonano pomiaru natężenia wspomnianego prądu. Pomiarów dokonywano w jednominutowych odstępach czasu i zakończono je, kiedy wartość natężenia prądu w uzwojeniu wtórnym spadła do 1/5 wartości początkowej. Uzyskane wyniki doświadczenia dostępne są w dalszej części sprawozdania.

3. Tabele pomiarowe, obliczenia i analiza błędów:

Błędy poszczególnych mierników obliczamy z następującej zależności:

I tak do poszczególnych mierników:

- Woltomierz:

• Mikroamperomierz:

• Miliwoltomierz:

- zakres 2 [mV] (t = 1  2)

- zakres 5 [mV] (t = 3  )

- zakres 10 [mV] (t = 16  20)

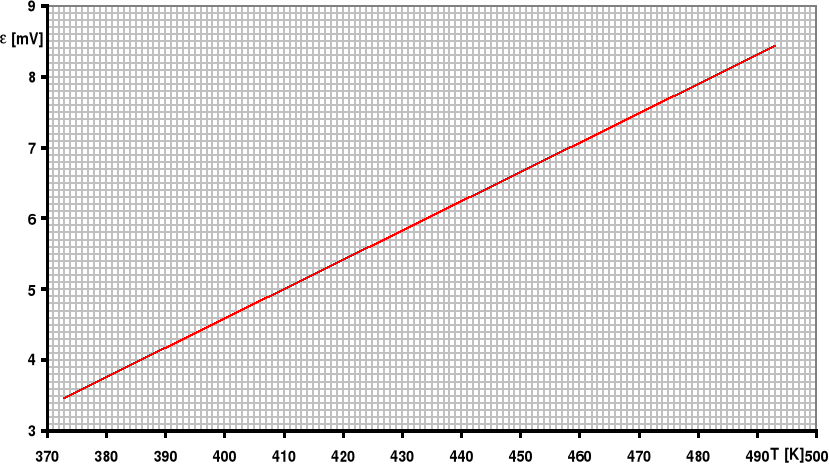
Cechowanie termopary:

 [mV]	T [K]
3,46	373
3,87	383
4,29	393
4,70	403
5,12	413
5,53	423
5,94	433
6,36	443
6,77	453
7,19	463
7,60	473
8,01	483
8,43	493

t [min]	i [A]	 [mV]
1	11,0	1,54
2	11,2	1,80
3	11,3	2,15
4	11,4	2,45
5	11,5	2,70
6	11,8	2,98
7	11,6	3,25
8	11,4	3,45
9	11,1	3,68
10	11,0	3,88
11	10,6	4,05
12	9,2	4,23
13	7,5	4,38
14	5,6	4,53
15	4,4	4,65
16	3,4	4,85
17	2,8	4,95
18	2,5	5,10
19	2,3	5,20
20	1,9	5,25

Wzór na zależność temperatury od siły termoelektrycznej: T=k·++23. Do temperatury wskazanej przez termoparę należy dodać temperaturę otoczenia, ponieważ termopara nie posiadała wzorca temperatury 0°C.

Metodą regresji liniowej na podstawie tabeli cechowania termopary wyznaczamy współczynniki k i  Korzystamy z następujących wzorów:

- wartość średnia pomiaru siły termoelektrycznej  ;

- wartość średnia pomiaru temperatury T;

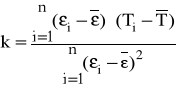
- współczynnik nachylenia charakterystyki;

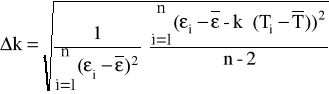
- błąd wyznaczania wartości k;

- współczynnik przesunięcia charakterystyki;

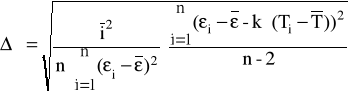
- błąd wyznaczania wartości ;

Uzyskane wyniki obliczeń:

k ± k = (24,16 ± 0,02) [K/mV]; ±  = (289,46 ± 0,08) [K].Wzór na temperaturę Curie ma więc postać: T_C = 24,16·+289,46+23.Wartość siły termoelektrycznej , dla której określamy temperaturę Curie, została odczytana z wykresu i wynosi:  = 3,85 [mV].

Błąd odczytu siły termoelektrycznej  z wykresu wynosi:  = 0,2 [mV]. Błąd wyznaczania temperatury Curie obliczono z różniczki zupełnej:

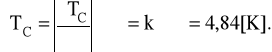
Temperatura Curie badanego ferrytu wyniosła więc: T_C = (405,48 ± 4,84) [K].

4. Wykresy:

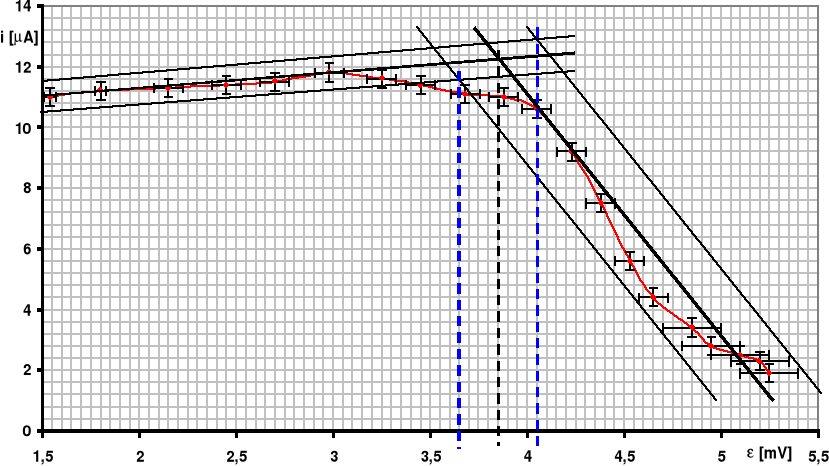
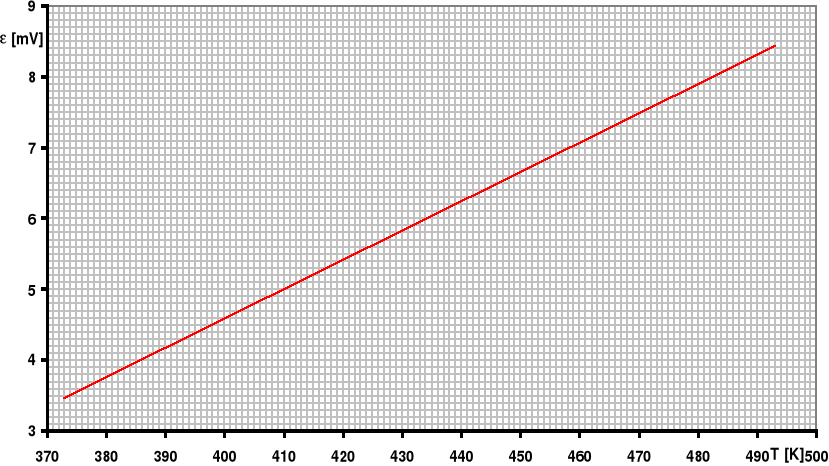
5. Wnioski:

Podczas przeprowadzonego ćwiczenia wyznaczyliśmy temperaturę Curie dla badanego ferrytu, która wynosi Tc = (405,48 ± 4,84) [K].

Na błąd wyznaczania temperatury mogło mieć wpływ to, że termopara mierzyła temperaturę zewnętrzną rdzenia, która była niższa od temperatury wewnątrz rdzenia oraz błędy pomiarowe mierników i nagrzanie rdzenia spowodowane doświadczeniami wcześniejszych sekcji.

8

:

---