Politechnika Śląska

Wydział AEiI

Kierunek AiR

Ćwiczenia laboratoryjne z fizyki:

Dyfrakcja: wyznaczanie stałej siatki dyfrakcyjnej,

pomiar długości światła laserowego,

wyznaczanie szerokości szczeliny.

Grupa IV, sekcja 3

1.Szymon Ciupa

2.Adam Filipek

Gliwice, 23.04.1999

1. Wstęp teoretyczny:

Dyfrakcja jest to ogół zjawisk, w których następuje odstępstwo od prostoliniowego rozchodzenia się fali. Zjawisko dyfrakcji ma miejsce, gdy fala na swojej drodze trafia na tzw. ostre niejednorodności, czyli na wszelkiego rodzaju krawędzie, szczeliny, czyli trafia na przeszkody, co powoduje uginanie się promieni świetlnych.

Ogół zjawisk związanych z dyfrakcją jest tłumaczony w oparciu o zasadę Huygensa-Fresnela: każdy element powierzchni falowej, do którego dochodzi fala, stanowi źródło kulistej fali wtórnej, której amplituda jest proporcjonalna do wielkości tego elementu oraz fale wtórne są spójne. Fale są spójne, gdy różnica faz pomiędzy nimi jest stała w czasie.

Powstające fale wtórne interferują między sobą i zaburzenie w dowolnym punkcie jest wynikiem interferencji fal spójnych.

Na zjawisku dyfrakcji oparte jest działanie siatki dyfrakcyjnej. Siatką dyfrakcyjną nazywa się układ dużej liczby jednakowych szczelin, rozmieszczonych w stałych odległościach od siebie. Odległość między środkami sąsiednich szczelin nazywa się stałą siatki.

W praktyce siatkę dyfrakcyjną otrzymuje się przez porysowanie płasko-równoległej płytki szklanej za pomocą diamentu szeregiem równoległych kresek. Nieprzezroczyste rysy odgrywają rolę zasłon, a przestrzenie między rysami to szczeliny. Promienie ugięte mogą nakładać się czyli interferować ze sobą, gdyż są promieniami spójnymi, znaczy to, że różnice faz między nimi zależą tylko od różnicy dróg geometrycznych, nie zależą od czasu.

Interferencją nazywamy nakładanie się fal, przy czym wychylenie fali wypadkowej jest algebraiczną sumą wychyleń fal składowych. W wyniku interferencji fale mogą się wzmacniać (jeżeli ich fazy są zgodne) lub wygaszać (jeżeli ich fazy są przeciwne).

Maksymalne wzmocnienie (maximum) wystąpi, gdy różnica dróg optycznych będzie wielokrotnością długości fali:

.

Maksymalne wygaszenie (minimum) wystąpi, gdy ta różnica będzie równa wielokrotności połówki długości fali:

2. Opis ćwiczenia:

Celem tego ćwiczenia było wyznaczanie stałej siatki dyfrakcyjnej, pomiar długości światła laserowego i wyznaczanie szerokości szczeliny.

Część 1: obserwowaliśmy obraz dyfrakcyjny uzyskany przy pomocy siatki dyfrakcyjnej. W tym celu umieściliśmy na stoliku obrotowym spektometru siatkę dyfrakcyjną, oświetloną światłem o znanej długości. Płaszczyzna siatki powinna być prostopadła do osi przyrządu. Nie należy dotykać powierzchni siatki! Następnie kręcąc okularem doprowadzaliśmy do pokrycia się linii krzyża pomiarowego z kolejnymi prążkami dyfrakcyjnymi i notowaliśmy kąty ugięcia rzędów na lewo i prawo od prążka zerowego. Pomiary powtarzaliśmy pięciokrotnie. Na podstawie tych danych i dostępnych wzorów należało wyznaczyć stałą badanej siatki dyfrakcyjnej.

Część 2: dokonywaliśmy pomiaru długości światła laserowego. W tym celu należało ustawić siatkę dyfrakcyjną na stoliku w określonej odległości od ekranu, prostopadle do kierunku padania światła laserowego i notować położenia kolejnych jasnych prążków dyfrakcyjnych na lewo i prawo od prążka zerowego.

Część 3: ćwiczenie polegało na wyznaczeniu szerokości szczeliny, na której ugięciu ulegał promień światła laserowego o długości wyliczonej w części drugiej doświadczenia. Skorzystano w tym celu z metody fotoelektrycznej. Detektorem był tutaj fotorezystor zasilany prądem stałym. Natężenie płynącego prądu mierzono multimetrem M-4650CR firmy METEX, który sterowany jest programem stanowiącym wyposażenie miernika. Skorzystano z faktu, że natężenie prądu zależy od natężenia oświetlenia czynnej powierzchni fotorezystora i rośnie ze wzrostem natężenia oświetlenia. Detektor umieszczony był na wysięgniku przesuwnego suportu, którego przesuw zapewnia niskoobrotowy silnik indukcyjny z wielostopniową przekładnią. Dobraliśmy szerokość szczeliny tak, by uzyskać wyrażne prążki dyfrakcyjne z odstępstwem ok. 1[mm]. Przed włączeniem układu ustawiliśmy suport w pozycji krańcowej, zakres miernika ustaliliśmy na 2[mA] oraz ustaliliśmy opcje programu obsługującego miernik. Przesuw zatrzymał się po dojściu do pozycji krańcowej. Wyniki pomiarowe zapisane zostały w zbiorze z rozszerzeniem .prt. Zbiór ten został przekonwertowany za pomocą odpowiedniego programu na zbiór programu kreślącego wykresy, za pomocą którego otrzymaliśmy wykres widma energetycznego prążków dyfrakcyjnych. Dane odczytane z tego wykresu posłużyły nam do wyznaczenia szerokości użytej szczeliny.

Na podstawie otrzymanych wyników i danych wzorów mieliśmy wyznaczyć wartości wspomnianych wielkości. Wyniki doświadczenia i związanych z nim obliczeń są dostępne w dalszej części sprawozdania.

3.Obliczenia i analiza błędów:

Oznaczenia: L - strona lewa n-tego rzędu (jasny prążek n-tego rzędu na lewo od prążka centralnego, P - strona prawa n-tego rzędu (jasny prążek n-tego rzędu na prawo od prążka centralnego).

Część 1: Wyznaczanie stałej siatki dyfrakcyjnej:

Średnie pomiary kąta ugięcia dla poszczególnych stron n-tego rzędu obliczono według wzoru:

,

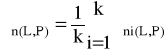
gdzie: k - ilość dokonanych pomiarów.

Błąd średniego pomiaru kąta ugięcia dla poszczególnej strony n-tego rzędu obliczono według wzoru:

,

gdzie: _nmax(L,P) - wartość kąta ugięcia dla poszczególnej strony n-tego rzędu najbardziej różniąca się od wartości średniej kąta ugięcia dla tej strony n-tego rzędu.

Wielkość liczona:	n = 1		n = 2		n = 3
	L	P	L	P	L	P
n(L,P)	6°28'	6°48'	13°12'	13°36'	19°88'	20°80'
n(L,P)	0°22'	0°38'	0°22'	0°34'	0°48'	0°00'

Średnią wartość kąta ugięcia dla poszczególnych rzędów obliczono według wzoru:

.

Błąd średniej wartości kąta ugięcia dla n-tego rzędu obliczono z różniczki zupełnej według wzoru:

.

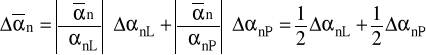
Wielkość liczona:	n = 1	n = 2	n = 3
	6°38'	13°24'	20°34'
	0°30'	0°28'	0°24'

Stałą siatki dyfrakcyjnej dla n-tego rzędu obliczono według wzoru:

,

gdzie:  - średnia wartość długości fali żółtego dubletu sodu = 589,3 [nm].

Błąd wyznaczania stałej siatki dyfrakcyjnej dla n-tego rzędu obliczono z różniczki zupełnej według wzoru:

.

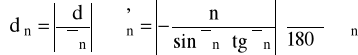
n		n [nm]	dn [nm]
1	0,53  10^-2	5303,18	248,34
2	0,49  10^-2	5146,04	106,88
3	0,42  10^-2	5086,16	57,48

Metodą średniej ważonej obliczono stałą siatki dyfrakcyjnej oraz błąd wyznaczenia tej stałej. Skorzystano z następujących wzorów:

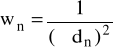
- waga stałej siatki dyfrakcyjnej;

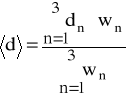
- średnia (ważona) stałej siatki dyfrakcyjnej;

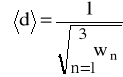
- błąd wyznaczania średniej (ważonej) stałej siatki dyfrakcyjnej.

n	wn [1/nm^2]	dn wn [1/nm]
1	0,17  10^	0,091
2	0,88  10^	0,453
3	3,03  10^	1,542
	4,08  10^	2,086
	202  10^	-

Ostateczny wynik:

.

Część 2: Pomiar długości fali światła laserowego:

Średnią wartość położenia jasnego prążka n-tego rzędu obliczono według wzoru:

.

Błąd wyznaczania średniej wartości położenia jasnego prążka n-tego rzędu obliczono według wzoru:

,

gdzie: x_nmax - wartość najbardziej różniąca się od wartości średniej dla n-tego rzędu.

n	[mm]	 [mm]
1	166,5	0,5
2	344,0	1,0
3	540,0	2,0

Długość fali światła laserowego dla n-tego rzędu obliczono według wzoru:

,

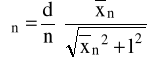
gdzie: d - stała siatki dyfrakcyjnej, obliczona w części 1, l - odległość siatki dyfrakcyjnej od ekranu = (123,5  1) [cm].

Błąd wyznaczania długości fali światła laserowego dla n-tego rzędu obliczono z różniczki zupełnej według wzoru:

.

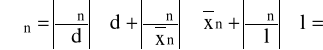
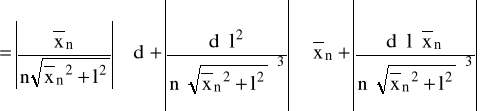
n	n [nm]	n [nm]
1	682,44	14,07
2	685,28	13,66
3	682,10	13,39

Metodą średniej ważonej obliczono długość fali światła laserowego oraz błąd wyznaczenia tej długości. Skorzystano z następujących wzorów:

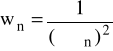
- waga długości fali światła laserowego;

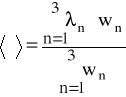
- średnia (ważona) długości fali światła laserowego;

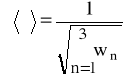
- błąd wyznaczania średniej (ważonej) długości fali światła laserowego.

n	wn [1/nm^2]	n wn [1/nm]
1	0,0050	3,45
2	0,0054	3,68
3	0,0056	3,80
	0,0160	10,93
	0,1265	-

Ostateczny wynik:

.

3. Wyznaczanie szerokości szczeliny:

Średnie wartości n-tego minimum (licząc od prążka centralnego) obliczono według wzoru:

.

N	[mm]
1	2,2200
2	4,3985
3	6,5970
4	8,7820
5	10,9485

Błąd wyznaczania średniej wartości n-tego minimum obliczono z różniczki zupełnej według wzoru:

,

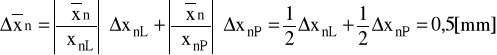
gdzie: x_nL = x_nP = 0,5 [mm] - błędy odczytu wartości x_n określone jako połowa najmniejszej odległości między kolejnymi prążkami dyfrakcyjnymi, która wynosiła około 1 [mm].

Szerokość szczeliny dla n-tego minimum obliczono według wzoru:

,

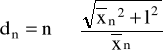
gdzie:  - długość fali światła laserowego, obliczona w części 2; l - odległość fotorezystora od badanej szczeliny = (50  1) [cm].

Błąd wyznaczania szerokości szczeliny dla n-tego minimum obliczono z różniczki zupełnej według wzoru:

.

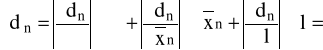
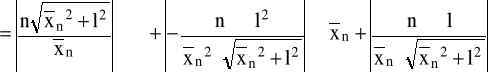
n	dn [nm]	dn [nm]
1	153893,41	39519,36
2	155349,88	22563,22
3	155375,06	16679,81
4	155633,21	13771,59
5	156058,78	12049,83

Metodą średniej ważonej obliczono szerokość szczeliny oraz błąd wyznaczenia tej szerokości. Skorzystano z następujących wzorów:

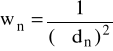
- waga szerokości szczeliny;

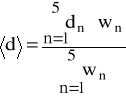
- średnia (ważona) szerokości szczeliny;

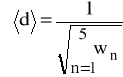
- błąd wyznaczania średniej (ważonej) szerokości szczeliny.

n	wn [1/nm^2]	dn wn [1/nm]
1	0,65  10^-9	9,86  10^-5
2	1,97  10^-9	30,52  10^-5
3	,  10^-9	55,85  10^-5
4	5,28  10^-9	82,07  10^-5
5	6,89  10^-9	107,48  10^-5
	18,36  10^-9	285,76  10^-5
	1,36  10^-4	-

Ostateczny wynik:

.

4. Wnioski:

W wyniku przeprowadzonego doświadczenia i związanych z nim obliczeń otrzymano następujące wartości poszukiwanych wielkości:

• stała badanej siatki dyfrakcyjnej:

d = 5107,72  49,61 [nm];

• długość fali światła laserowego:

 = 683,28  7,91 [nm];

• szerokość szczeliny:

d = 155651,32  7380,39 [nm].

W przypadku części doświadczenia dotyczącej wyznaczenia szerokości szczeliny mała wartość błędu w porównaniu z otrzymaną wartością szerokości świadczy o tym, że zastosowana metoda pomiarowa charakteryzuje się bardzo dużą dokładnością.

9

9

---