Politechnika Śląska w Katowicach

SPRAWOZDANIE

Temat: Wyznaczanie szerokości szczelin, stałych siatek dyfrakcyjnych i długości fali sprężystej w szkle w badaniach dyfrakcji promieniowania laserowego.

GRUPA T - 13

Sekcja VI:

Marcin Cholewa

Stanisław Wawszczak

1. WSTĘP TEORETYCZNY

Siatka dyfrakcyjna to układ równoległych szczelin o równej odległości, porównywalnej z długością padającej fali. Na każdej z tych szczelin zachodzi zjawisko dyfrakcji światła. Fale ugięte na kolejnych szczelinach mogą interferować ze sobą.

Dyfrakcja (nazywana również ugięciem) jest to zjawisko polegające na uginaniu się promieni świetlnych przechodzących w pobliżu przeszkody, takiej jak np. brzeg szczeliny.

Muszą być spełnione dwa warunki aby dyfrakcja zaszła, musi być spójność światła taka jak np. w laserze, oraz szerokość szczeliny musi być porównywalna z długością fali.

Interferencja nakładanie się na siebie fal kulistych. Podczas interferencji na ekranie umieszczonym na drodze fal można zaobserwować ciemne i jasne prążki tj. maxima i minima.

Zasada Huygensa głosi że: wszystkie punkty czoła fali można uważać za źródła nowych fal kuli. Położenia czoła fali po czasie t będzie dane prze3z powierzchnię styczną do tych fal kulistych.

2. PRZEBIEG ĆWICZENIA

1. W uchwycie zamocowanym na ławie optycznej umieszczona zostaje siatka dyfrakcyjna. Odległość siatki dyfrakcyjnej od fotoogniwa jest stała i wynosi 20 [cm].

2. W zaciemnionym pomieszczeniu zmierzyć położenie prążków dyfrakcyjnych obserwując wartości sygnału napięciowego pochodzącego od fotoogniwa umieszczonego w centrum kolejnych prążków dyfrakcyjnych.

3. OPRACOWANIE WYNIKÓW

1. Wyznaczanie stałej siatki dyfrakcyjnej.

Kolejny prążek od lewej do prawej strony m	Odległość między danym prążkiem, a prążkiem zerowym bm [cm]			Napięcie odczytane z miliamperomierza [mA]
m3	8,1	7,9	8.0	9,8	5,7	8,3
m2	5,15	5,1	5,4	50,3	51,2	46,2
m1	2,8	2,55	2,4	109,4	91,3	97,3
m0	0.0	0,0	0,0	122,5	117,7	118,8
m1	2,4	2,5	2,4	115,2	101,3	110,5
m2	4,9	5,05	5,0	48,9	50,2	52,6
m3	7,85	7,9	7,85	11,5	7,9	6,6

Odległość siatki dyfrakcyjnej od fotoogniwa jest stała i wynosi l = 20 [cm]; l = 0,2 [m]

Obliczam wartość średnią położenia m-tego zarejestrowanego prążka dyfrakcyjnego i wartość średnią napięcia odczytanego z miliamperomierza:

b_mśr =
, U_śr =

gdzie: n = 3

Tabela nr1

Kolejny prążek od lewej do prawej strony M	Wartość średnia położenia danego prążka od prążka zerowego bmśr [m]	Wartość średnia napięcia odczytanego z miliamperomierza Uśr [A]
M3	8⋅10^-2	7,933333333⋅10^-3
M2	5,216666667⋅10^-2	49,23333333⋅10^-3
M1	2,583333333⋅10^-2	99,33333333⋅10^-3
M0	0	119,6666667⋅10^-3
M1	2,433333333⋅10^-2	109⋅10^-3
M2	4,983333333⋅10^-2	50,56666667⋅10^-3
M3	7,866666667⋅10^-2	8,666666667⋅10^-3

Obliczamy odchylenia standartowe

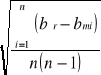
gdzie: n = 3

Tabela nr2

Kolejny prążek od lewej do prawej strony M	Odchylenie standartowe bmśr [m]	Odchylenie standartowe Uśr [A]
M3	0,057735027⋅10^-2	1,197682948⋅10^-3
M2	0,092796073⋅10^-2	1,538758518⋅10^-3
M1	0,116666667⋅10^-2	5,323010844⋅10^-3
M0	0	1,451818783⋅10^-3
M1	0,033333333⋅10^-2	4,082074636⋅10^-3
M2	0,044095855⋅10^-2	1,08371788⋅10^-3
M3	0,016666667⋅10^-2	1,465529862⋅10^-3

Metodą różniczki zupełnej obliczam niepewność wyników uzyskanych w tabeli nr1.

b_mśr =
,

gdzie x,y,z - są to kolejne odczytane odległości prążków od prążka zerowego

Δb_mśr =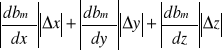
; ΔU_śr =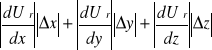

=
=
,

=
=
,

=
=
,

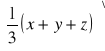
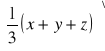
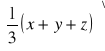
Kolejny prążek od lewej do prawej strony M	Wartość średnia położenia danego prążka od prążka zerowego z uwzględnieniem niepewności bmśr [m]	Wartość średnia napięcia odczytanego z miliamperomierza Uśr [A]
	Δx = 0,1, Δy = -0,1, Δz = 0	Δx = -0,2, Δy = -0,3, Δz = 0,3
M3	Δbmśr = 0	ΔUśr = -0,066666667
	(8±0) ⋅10^-2	(7,933±0,066) ⋅10^-3
	Δx = 0,15, Δy = 0,1, Δz = 0,4	Δx = 0,3, Δy = 0,2, Δz = 0,2
M2	Δbmśr = 0,216666667	ΔUśr = 0,233333333
	(5,2166±0,2166)⋅10^-2	(49,233±0,233) ⋅10^-3
	Δx = -0,2, Δy = -0,45, Δz = -0,6	Δx = 0,4, Δy = 0,3, Δz = 0,3
M1	Δbmśr = 0,416666667	ΔUśr = 0,333333333
	(2,58±0,42) ⋅10^-2	(99,33±0,33) ⋅10^-3
	Δx = 0,1, Δy = -0,1, Δz = 0	Δx = 0,5, Δy = -0,3, Δz = -0,2
M0	Δbmśr = 0	ΔUśr = 0
	0±0	(119,66±0) ⋅10^-3
	Δx = 0,4, Δy = 0,5, Δz = 0,4	Δx = 0,2, Δy = 0,3, Δz = 0,5
M1	Δbmśr = 0,433333333	ΔUśr = 0,033333333
	(2,43±0,43) ⋅10^-2	(109±0,033) ⋅10^-3
	Δx = -0,1, Δy = 0,05, Δz = 0	Δx = -0,1, Δy = 0,2 Δz = -0,4
M2	Δbmśr = 0,016666667	ΔUśr = 0,1
	(4,9833±0,0166) ⋅10^-2	(50,6±0,1) ⋅10^-3
	Δx = -0,15, Δy = -0,1, Δz = -0,15	Δx = 0,5, Δy = -0,1, Δz = -0,4
M3	Δbmśr = 0,133333333	ΔUśr = 0
	(7,87±0,13) ⋅10^-2	(8,66±0) ⋅10^-3

Sporządzamy wykres zależności iloczynu rzędu prążka i długości fali światła od sinusa kąta ugięcia światła dla danego prążka dyfrakcyjnego

y = mλ, x =

gdzie: m - oznacza numer prążka dyfrakcyjnego

b_m - odległość m-tego prążka dyfrakcyjnego od prążka zerowego

l - odległość ekranu od szczeliny ; l = 20 [cm], l = 0,2 [m.]

λ - długość fali światła ; λ = 0,6328⋅10^-6 [m]

M	y = mλ	bmśr [m]	x =
3	1,8984⋅10^-6	8,0⋅10^-2	1,511857892⋅10^-1
2	1,2656⋅10^-6	5,2166⋅10^-2	1,038841399⋅10^-1
1	0,6328⋅10^-6	2,5833⋅10^-2	0,543608733⋅10^-1
0	0	0	0
1	0,6328⋅10^-6	2,433⋅310^-2	0,51375339⋅10^-1
2	1,2656⋅10^-6	4,9833⋅10^-2	0,996999055⋅10^-1
3	1,8984⋅10^-6	7,8633⋅10^-2	1,49021262⋅10^-1

Metodą najmniejszych kwadratów aproksymujemy wykres zależności y = mλ od x =
:

n = 7

y = mλ, x =

x₁+x₂+x₃+x₄+x₅+x₆ = 6,095273089

y₁+y₂+y₃+y₄+y₅+y₆ = 7,5936⋅10^-6

n⋅
n⋅[( x₁ y₁)+(x₂ y₂)+(x₃ y₃)+(x₄ y₄)+(x₅ y₅)+(x₆ y₆) = 62,61352363

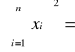
( x₁+x₂+x₃+x₄+x₅+x₆)² = 37,15235403

n⋅
n⋅(x₁²+x₂²+x₃²+x₄²+x₅²+x₆² ) = 49,97369655

y₁²+y₂²+y₃²+y₄²+y₅²+y₆² = 11,2122035⋅10^-6

ā =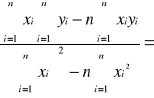
1,273537298

b =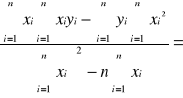
-0,0241368

0,00396622

S_a =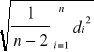

0,030463668

S_b =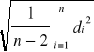

0,03506697

Prosta aproksymująca ma postać:

y = āx + b

y = 1,273537298x - 0,0241368

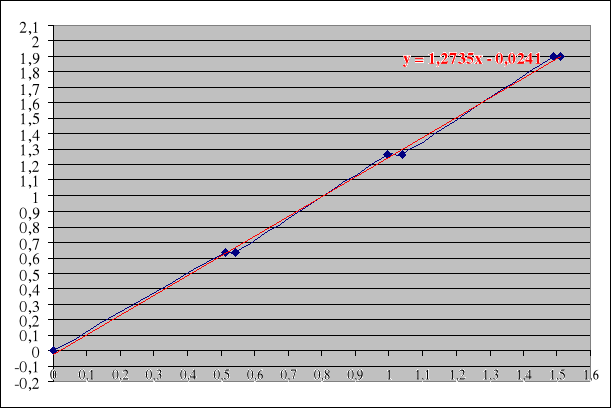
Wykres zależności iloczynu rzędu prążka i długości fali światła od sinusa kąta ugięcia światła dla danego prążka dyfrakcyjnego

Wyznaczam d stałą siatki dyfrakcyjnej

Porównując równanie prostej aproksymującej z równaniem:

mλ = a
+ b

i podstawiając za a = d = (1,273±0,031) ⋅10^-2 [m]

gdzie: d - odległość dwóch kolejnych szczelin w siatce dyfrakcyjnej (zwana także stałą siatki dyfrakcyjnej

Stała siatki dyfrakcyjnej

d = (1,273±0,031) ⋅10^-2 [m]

WNIOSKI:

Z przeprowadzonego ćwiczenia można zaobserwować , że odległość prążka m-tego od prążka zerowego po lewej jak i po prawej stronie różni się niewielkimi wielkościami rzędu około 0,2 [cm]. Podobnie zaobserwowaliśmy dla napięć mierzonych miliamperomierzem cyfrowym. Błędy jakie mogą wystąpić są spowodowane niedokładnością odczytu z przyrządów mierniczych

1

2

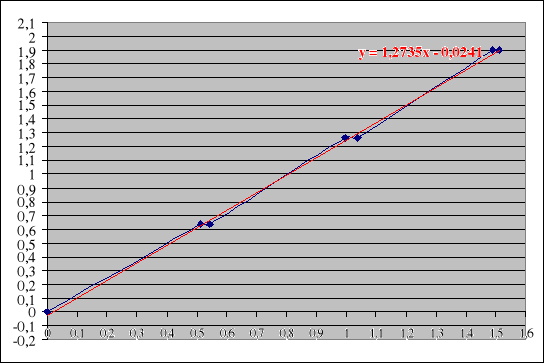
y = 1,273537298 x - 0,0241368

a = (1,274±0,031) ⋅10^-2 [m]

b = - 0,024±0,035

y = mλ

x =