Jesteś tu:

Bossa.pl

Ciąg liczb Fibonacciego i jego zastosowanie na rynkach finansowych

Poniższy artykuł jest fragmentem książki "Zastosowanie teorii Carolana i Fischera na rynku

kapitałowym"

autorstwa J. Nowakowskiego i K. Borowskiego wydanej przez wydawnictwo Difin.

Rozdział 3. Ciąg liczb Fibonacciego i jego zastosowanie na rynkach finansowych

3.1 Ciąg liczb Fibonacciego i jego własności

W XIII wieku włoski matematyk Leonardo Fibonacci (1170 - 1240) odkrył ciąg liczb naturalnych

nazwany następnie jego imieniem:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597,...

Ciąg rozpoczyna się od dwu jedynek, a każda następna liczba stanowi sumę dwu poprzednich:

gdzie n - należy do naturalnych oraz k = 1 i k = 1

0

1

Można pokazać, że

gdzie Φ jest rozwinięciem dziesiętnym

nieskończonym. Za średniowiecznym włoskim matematykiem Lucą Pacioli przyjęto, że przybliżona z

dokładnością do trzech miejsc po przecinku liczba Φ, jest tzw.

lub też złotym

złotym podziałem

środkiem. Stąd też w opracowaniach często podaje się, że Φ=1,618.

Inne ważne wielkości to: 1/Φ=0,618, 1/Φ = 0,382 i Φ = 2,618 będące przybliżeniami odpowiednich

2

2

granic ciągów:

Rysunek 20. Zbieżność ciągów Φ (n = -2, -1, 1, 2)

n

1.

2.

3.

4.

Źródło: opracowanie własne

3.1.1 Własności ciągu liczb Fibonacciego

Liczby ciągu Fibonacciego posiadają cały szereg zdumiewających własności - na ich temat napisano

wiele książek, także w Internecie stosunkowo duża liczba stron opisuje związki i zależności występujące

między tymi liczbami.

Do najważniejszych własności liczby Fibonacciego można zaliczyć:

Złoty podział odcinka stworzony po raz pierwszy przez Euklidesa - patrz Rysunek 21. Zagadnienie

to zostanie szerzej omówione w dalszej części tego rozdziału.

Złoty podział prostokąta - Rysunek 23.

Spirala logarytmiczna - Rysunek 22 (w dowolnym punkcie ewolucji złotej spirali stosunek długości

łuku do jego przekątnej wynosi 1,618, a przekątna pozostaje w takim stosunku do większego

promienia).

Elipsa logarytmiczna - Rysunek 24. Elipsa jest matematycznym opisem owalu. Każdą elipsę można

zdefiniować przy pomocy niewielu parametrów. Skrajną formą elipsy jest parabola opisana przy

pomocy następującego równania: y = 4ax. Punkt P jest odległy o tyle samo od stałego punktu Z i

2

od stałej linii wodzącej ZM. Krzywa jest symetryczna względem osi poziomej.

Rysunek 21. Złoty podział odcinka

Opracowanie własne

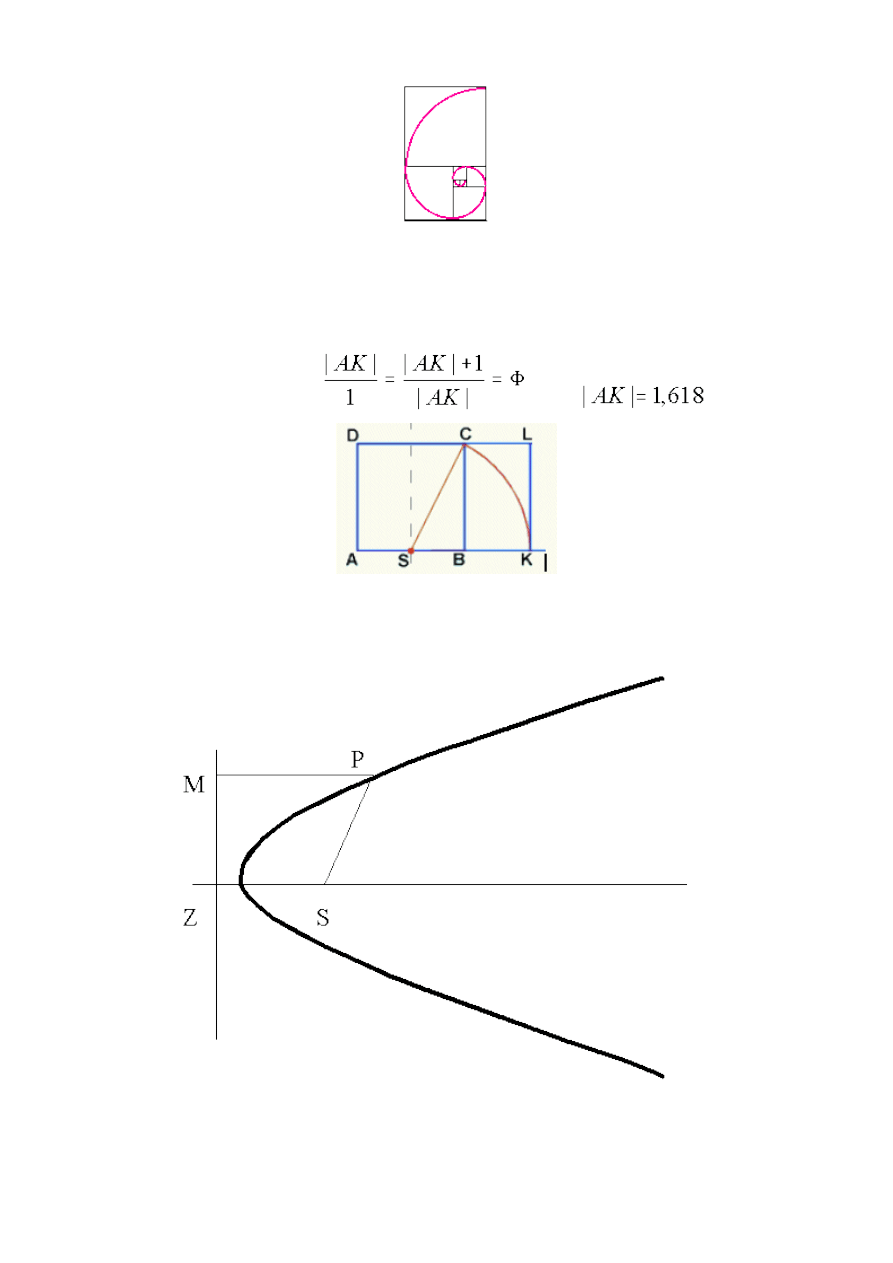
Rysunek 22. Spirala logarytmiczna

Opracowanie własne

Rysunek 23. Złoty podział prostokąta (AS = BS).

Dla odcinka AK zachodzi stosunek złotego podziału), tzn.

jeśli |AD|="1 " to:

czyli:

Opracowanie własne

Rysunek 24. Przykład paraboli logarytmicznej

Źródło: opracowanie własne na podstawie: Huntley, The Divine Proportion, Dover, New York 1970.

Między liczbami Φ zachodzi cały szereg zależności, oto wybrane przykłady:

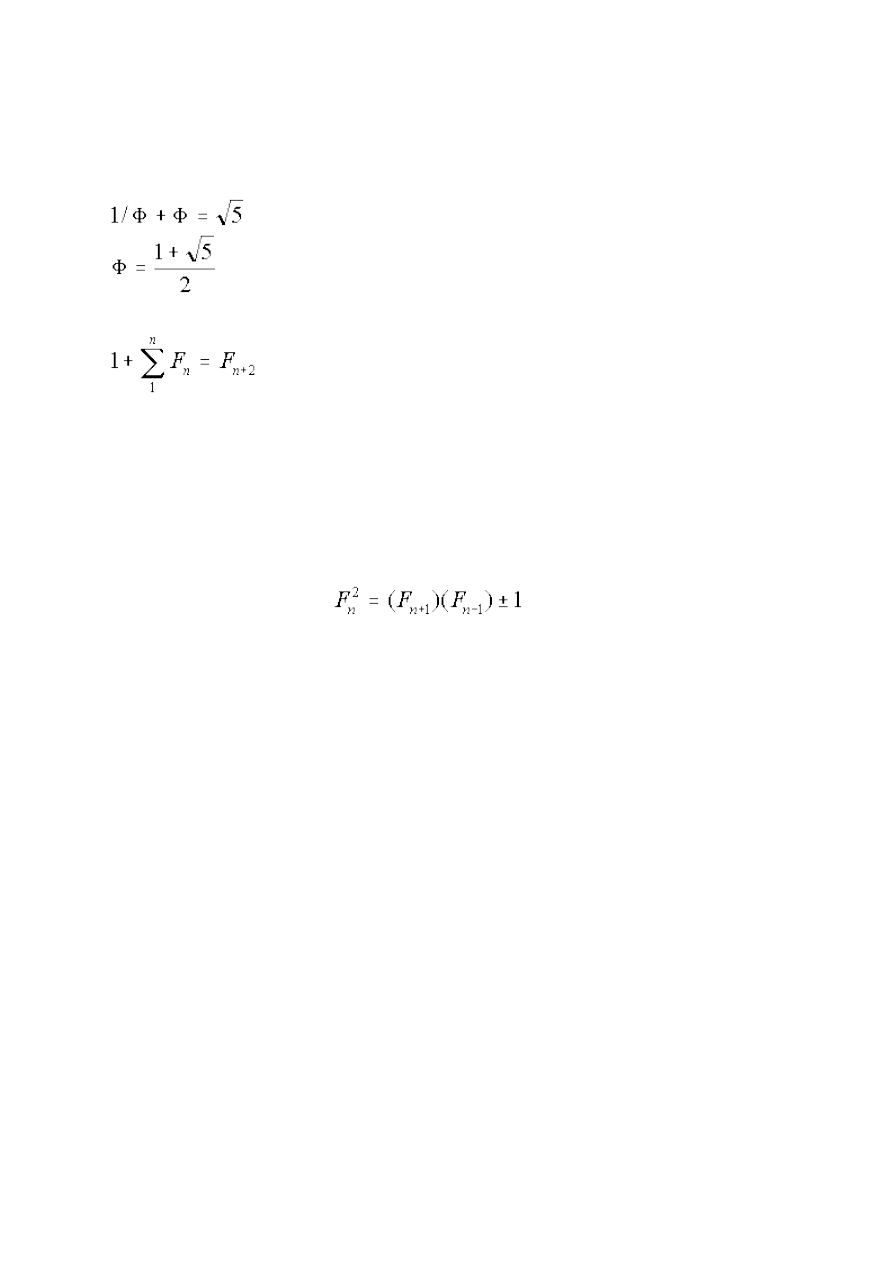
1.

2.

3.

4.

5.

6.
7.

8.

9.

10.

11.

1.

2.

3.

4.

5.

Φ - Φ=1

2

(1 + Φ) = Φ

2

4

1/ Φ + 1 / Φ=1

2

Φ - 1/Φ=1

Dla sumy n pierwszych liczb ciągu Fibonacciego zachodzi następująca tożsamość:

Suma dowolnych dziesięciu kolejnych liczb ciągu Fibonacciego jest podzielna przez 11.

Co trzecia liczba ciągu Fibonacciego jest podzielna przez 2, a co czwarta przez 3, co piąta przez 5,

itd. Kolejne dzielniki są liczbami ciągu Fibonacciego.

Różnica kwadratu liczby ciągu Fibonacciego i iloczynu sąsiednich wyrazów jest stałą, której znak

zmienia się w miarę wzrostu indeksu. Jest to cecha wspólna wszystkich ciągów posiadających

własność addytywności, jednak tylko w ciągu Fibonacciego różnica ta jest równa jeden. Zależność

tę można zapisać następująco:

. Plus i minus pojawiają się na przemian.

Tą samą prawidłowość można odnaleźć w elliottowskiej regule zmienności, która głosi, że złożone

fale korekcyjne występują na przemian z korektami płaskimi, a silne fale impulsu przeplatają się ze

słabymi - patrz rozdział 4.

Dla każdych czterech kolejnych wyrazów ciągu Fibonacciego: A, B, C, D prawdziwa jest

zależność: C - B = A× B

2

2

3.1.2 Złoty podział jako kanon piękna w sztuce

Jakościowa definicja kanonu estetycznego piękna występującego w naturze, została stworzona przez

Tomasza z Akwinu, który pisał, że "... ludzkie zmysły znajdują przyjemność w kontakcie z przedmiotami

zachowującymi właściwe proporcje". W spostrzeżeniu tym zawarta została relacja między poczuciem

piękna a matematyką. Jak się okaże w dalszej części książki relację tę daje się mierzyć i można odnaleźć

ją w naturze.

Typowymi przykładami boskiego kanonu piękna są:

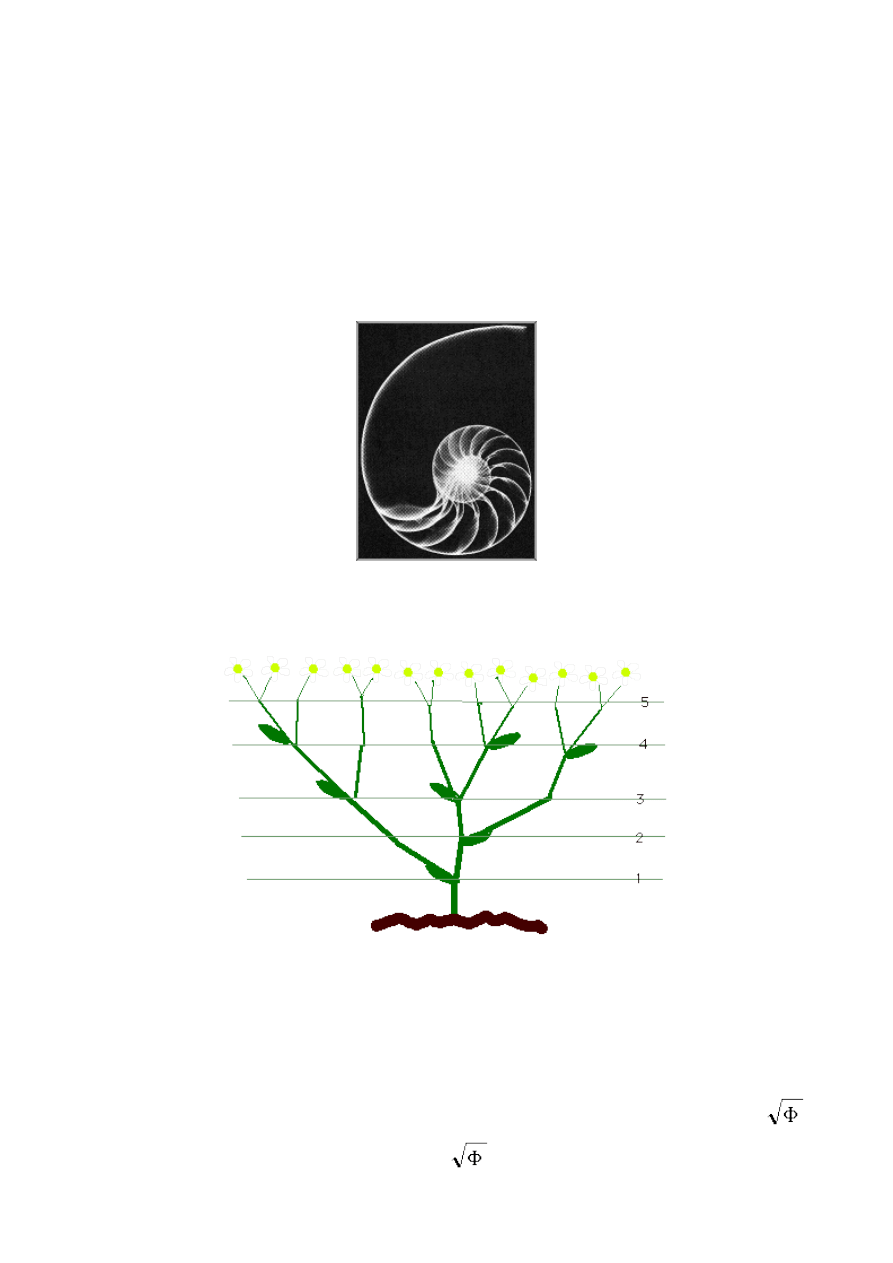
Liczby rozgałęzień wyrastających z łodygi rośliny.

Liczba płatków występujących w kwiatach niektórych roślin

Budowa muszli niektórych skorupiaków (Nautilius Pompilius).

Wzrost populacji królików

5.

6.

7.

8.

9.

10.

11.

12.

Struktura atomowa

Molekuły DNA

Struktura kryształu

Orbity planet i galaktyk

Układ zwojów w szyszce sosny

Proporcje powstające w wirach wodnych

Układ spiral tworzonych przez nasion słonecznika

Proporcje zachodzące pomiędzy poszczególnymi prądami powietrznymi tworzącymi huragany

Rysunek 25. Muszla skorupiaka Nautilius Pompilius

Opracowanie własne

Rysunek 26. Liczba rozgałęzień wyrastających z łodygi

Opracowanie własne

Także starożytni budowniczowie wykorzystywali przy wznoszeniu swoich budowli, proporcje jakie

stwarza ciąg liczb Fibonacciego. Doskonałym przykładem może być tutaj piramida w Gizie czy też

piramidy meksykańskie. Wielka Piramida w Egipcie została zbudowana w proporcjach równych

.

Stosunek wysokości do połowy jej podstawy wynosi

, podobnie jak iloraz wysokości ściany

1.

2.

3.

bocznej do wysokości piramidy. Natomiast stosunek wysokości ściany bocznej do połowy długości

podstawy jest równy Φ. Wymiary wielkiej piramidy są często wyrażane przy użyciu liczby Π. Jest to

możliwe, gdyż

.

3.2 Ciąg liczb Fibonacciego na giełdzie

Istnieją trzy sposoby wykorzystania ciągu liczb Fibonacciego do analizy papierów wartościowych:

metody czasowe - w odniesieniu do upływu czasu - rozdział 3.2.1.

metody cenowe - w odniesieniu do zmiany ceny - rozdział 3.2.2

metody cenowo - czasowe - w odniesieniu do upływu czasu i zmiany ceny - rozdział 3.2.3

Duża liczba metod analizy technicznej stanowi próbę zmierzenia popytu na dany walor i sporządzenia na

tej podstawie prognozy określającej czy cena wzrośnie czy spadnie oraz przy użyciu pewnych

wskaźników, jak długi będzie ten ruch. W tym przypadku stosuje się techniki wykorzystujące proporcje

Fibonacciego w pionie. Metody te nazywamy metodami określającymi wielkość (zasięg) ruchu.

Zaznaczone one zostały na rysunku na osi pionowej - Rysunek 27.

Drugą grupę stanowią metody oparte na analizie cykli oraz wykorzystaniu ciągu liczb Fibonacciego na

osi czasu. Wykorzystuje się je do określenia czasu, w jakim dokona się zmiana trendu. Nazywamy je

metodami określania czasu trwania ruchu cenowego.

Trzecią grupę metod stanowią techniki starające się oszacować jednocześnie potencjalny zakres i czas

trwania ruchu. Metody uniwersalne bardzo często posiadają tę wadę, że dobrze opisują zagadnienie

całościowo, natomiast mało precyzyjnie tłumaczą szczegóły.

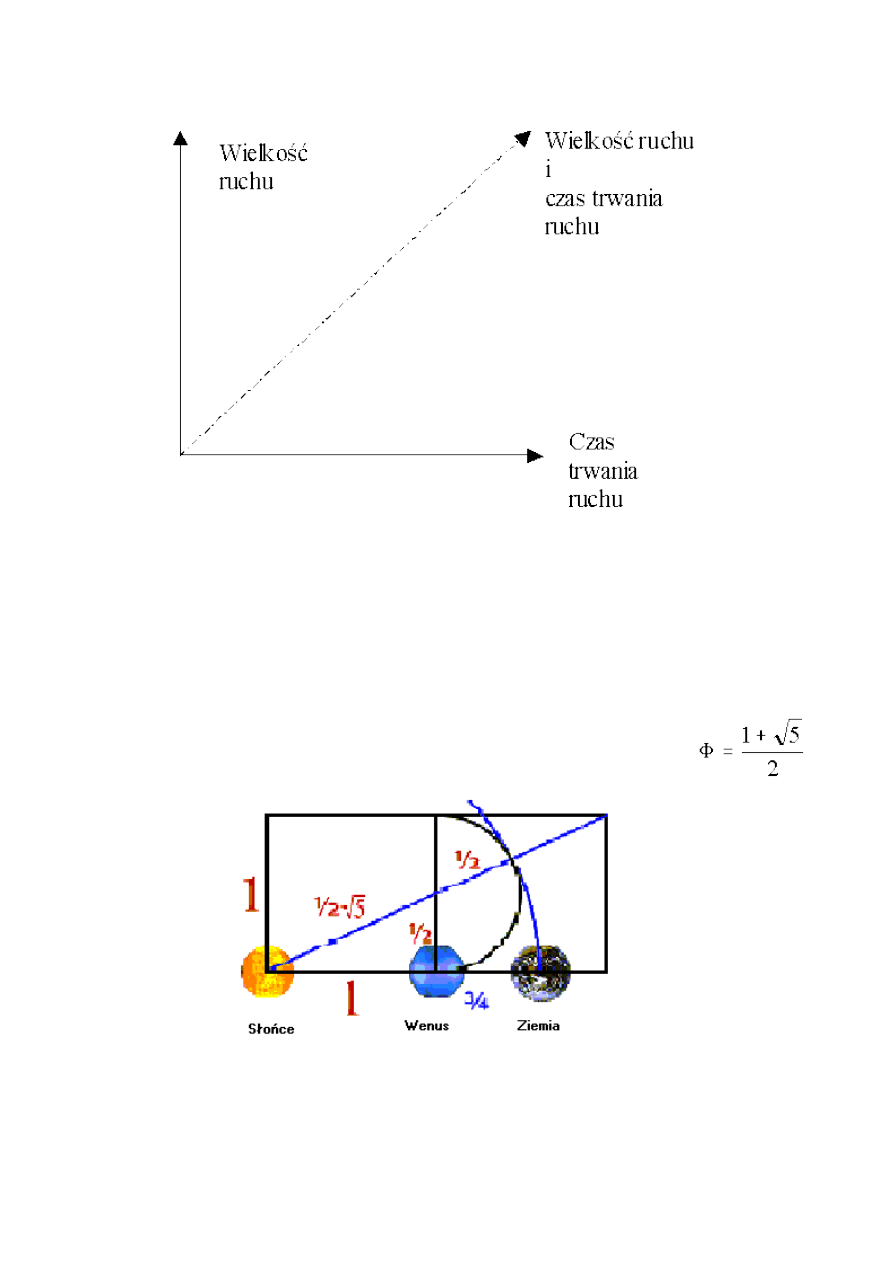
Rysunek 27. Podział metod prognozowania zasięgu ruchu i czasu jego trwania.

Źródło: opracowanie własne

Współczynniki Fibonacciego występują także w okresach orbitalnych planet naszego układu słonecznego.

Odległość księżyców od planety, wokół której krążą (dla systemów planetarnych o więcej niż jednym

księżycu), pozostają w proporcjach opisanych przez odpowiednie potęgi liczby Φ.

Rysunek 28. Wzajemna zależność między odległością Wenus i Ziemi od Słońca:

Źródło: opracowanie własne na podstawie strony internetowej:

 z dnia 05.05.2002

http://www.aeronivest.com

1.

2.

3.

Podobna zależność występuje także w przypadku odległości poszczególnych planet od Słońca - Rysunek

28.

Model D. Bradleya oparty jest na relacjach kątowych między planetami (są to tzw. aspekty) a ich

wpływem na zachowanie uczestników rynków kapitałowych, a zwłaszcza akcji notowanych na Wall

Street. Autor metody stworzył formułę matematyczną obliczającą skumulowany potencjał wszystkich

aspektów planetarnych systemu słonecznego z wykorzystaniem wag odległości planet od ich istotnych

aspektów. Moment czasu, w którym planety ustawiają się w ściśle określony sposób charakteryzuje się

większym prawdopodobieństwem wystąpienia zmiany dotychczasowego trendu. Metoda Bradleya

znalazła zastosowanie w dwu programach komputerowych: Quick Harmonic Trader oraz Galactic Trader.

Rysunek 29 przedstawia wykres ceny kontraktu terminowego na dostawę soji z listopada 1996 r. wraz z

naniesionymi nań liniami:

Liniami wsparcia występującymi co 24 centy z uwagi na fakt, że podział kąta pełnego tj. 360 stopni

przez 15, dokonany po raz pierwszy przez Ganna daje w rezultacie taki właśnie wynik. Z zapisków

tego legendarnego gracza wiadomo, że taki podział szczególnie przypadł mu do gustu. Linie

wsparcia na rysunku mają przebieg zbliżony do horyzontalnego.

Linie cen planet skorelowane wraz długością geocentryczną Saturna. Z uwagi na fakt, że planeta ta

porusza się bardzo wolno przez Zodiak, tworzy ona na wykresie linie ukośne o nieznacznym kącie

nachylenia w stosunku do osi poziomej.

Linie ceny planetarnej dla heliocentrycznej długości Marsa. Planeta ta charakteryzuje się znacznie

szybszym ruchem przez Zodiak, w związku z tym na rysunku utworzy ona linie ukośne o nieco

większym nachyleniu do osi poziomej, które będziemy nazywać diagonalnymi.

Linie cen planet z punktu 2 i 3 stanowią poziomy wsparcia i oporu dla ceny kontraktu na dostawę soji.

Już pobieżna analiza tego rysunku uwidacznia, z jaką precyzją wyznaczają punkty zatrzymania ruchu

ceny kontraktu.

Linie planet mogą być wykorzystane również do określenia potencjalnych poziomów wsparcia i oporu dla

głównych indeksów giełdowych. Rysunek 30 przedstawia linie planet Uran i Mars wraz z wykresem

indeksu S&P.

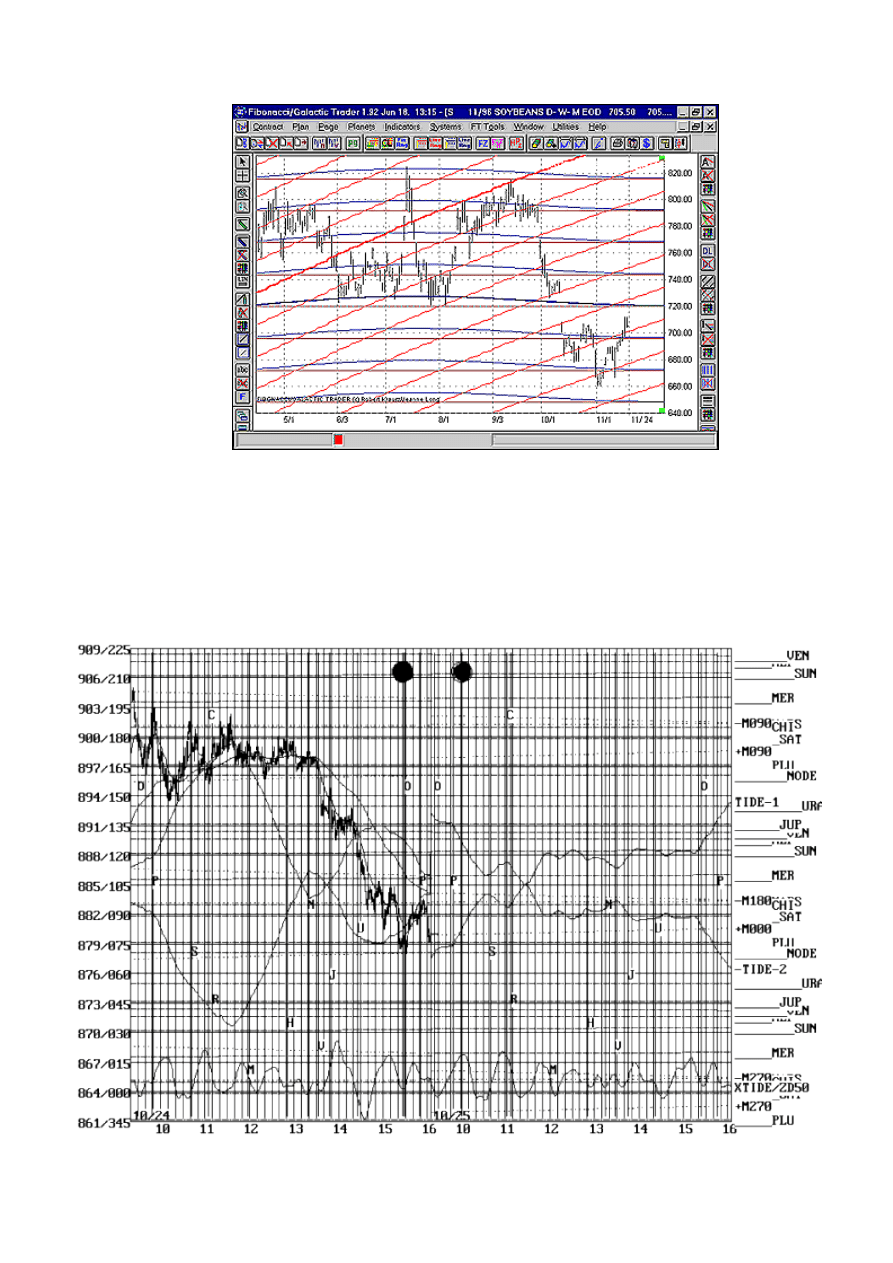
Rysunek 29. Wykres ceny trzymiesięcznych kontraktów terminowych na dostawę soji z listopada

1996 r.

Źródło: opracowanie własne na podstawie strony internetowej:

z dnia 30.09.2002 i programu Galactic Trader v.

http://www.galacticinvestor.com/review/Galactic.htm

3.0.

Rysunek 30. Linie planet na wykresie indeksu S&P. Poziomy wsparcia wyznaczone przez planetę

Uran: 857, 875 i 893 i przez planetę Mars: 861, 883, 901.

Źródło: opracowanie własne na podstawie programu: Larson Chaos Trader.

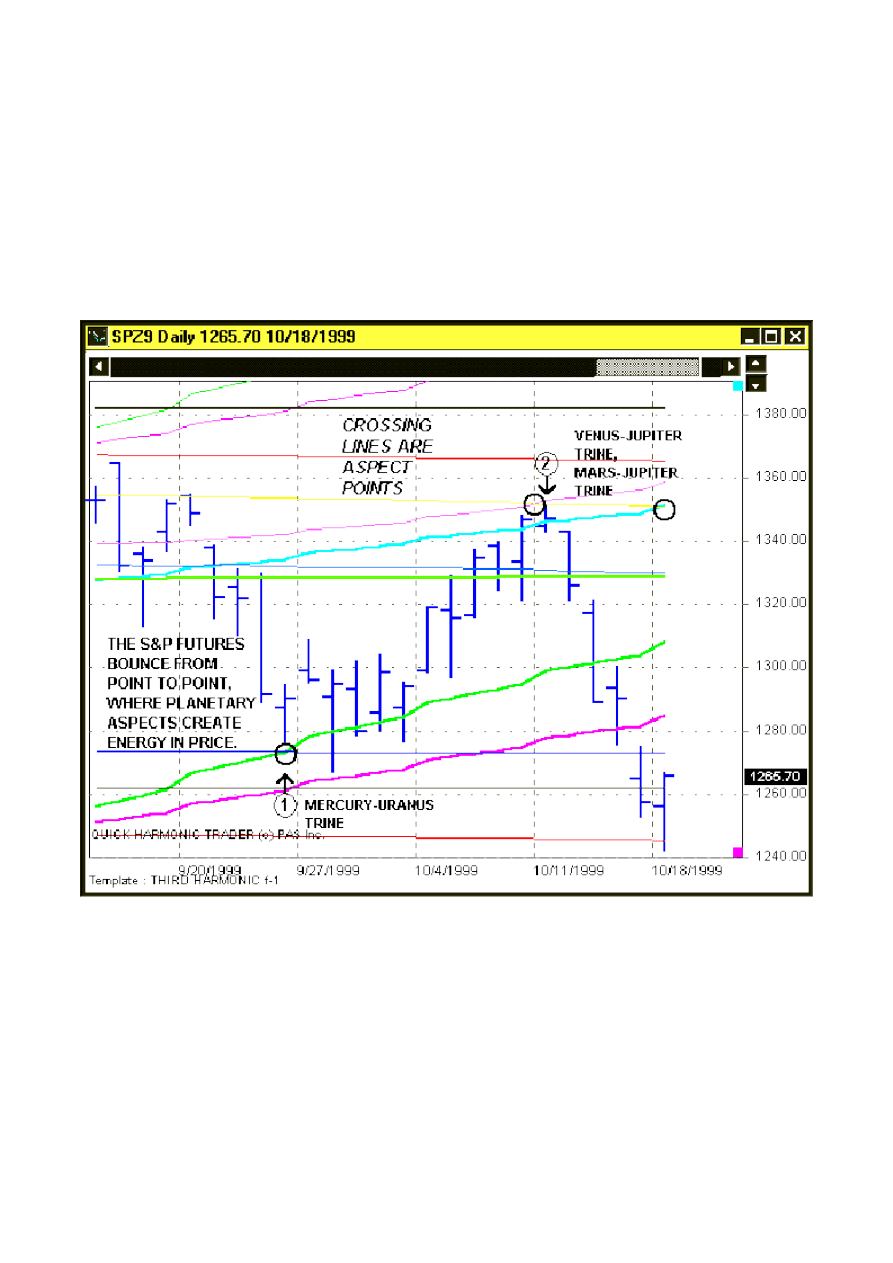
Przy pomocy programu Quick Harmonic Trader można określić potencjalny punkty zwrotne rynku, które

mogą okazać się istotnymi szczytami (kilka współwystępujących harmonii o dużym znaczeniu) lub tylko

lokalnymi ekstremami (mała liczba harmonii). Powstają one zazwyczaj wtedy, gdy aspekty planet i cen

znajdują się w harmonii. Rysunek 31 prezentuje przykład takiej analizy - w dniu 11.10.1999 r. indeks

S&P 500 znajdował się w harmonii z aspektami planet Wenus - Jowisz i Mars - Jowisz. Tego dnia został

uformowany znaczący szczyt. Nieco wcześniej harmonia indeksu z aspektem Merkury - Uran

doprowadziła do krótkotrwałego wybicia w górę.

Rysunek 31. Przykład zastosowania programu Quick Harmonic Trader - indeks S&P

Źródło: opracowanie własne przy wykorzystaniu strony internetowej:

z dnia 30.06.2001.

http://www.marketdetective.com/QHT/qhtinfo.htm

Kolejny przykład przestawia sytuację z 19.07.1999 r. kiedy to wystąpiło przecięcie czwartej harmonicznej

aspektu Saturn - Uran z indeksem DJIA. Tego dnia indeks giełdy nowojorskiej zmienił kierunek - data

okazała się być lokalnym ekstremum indeksu.

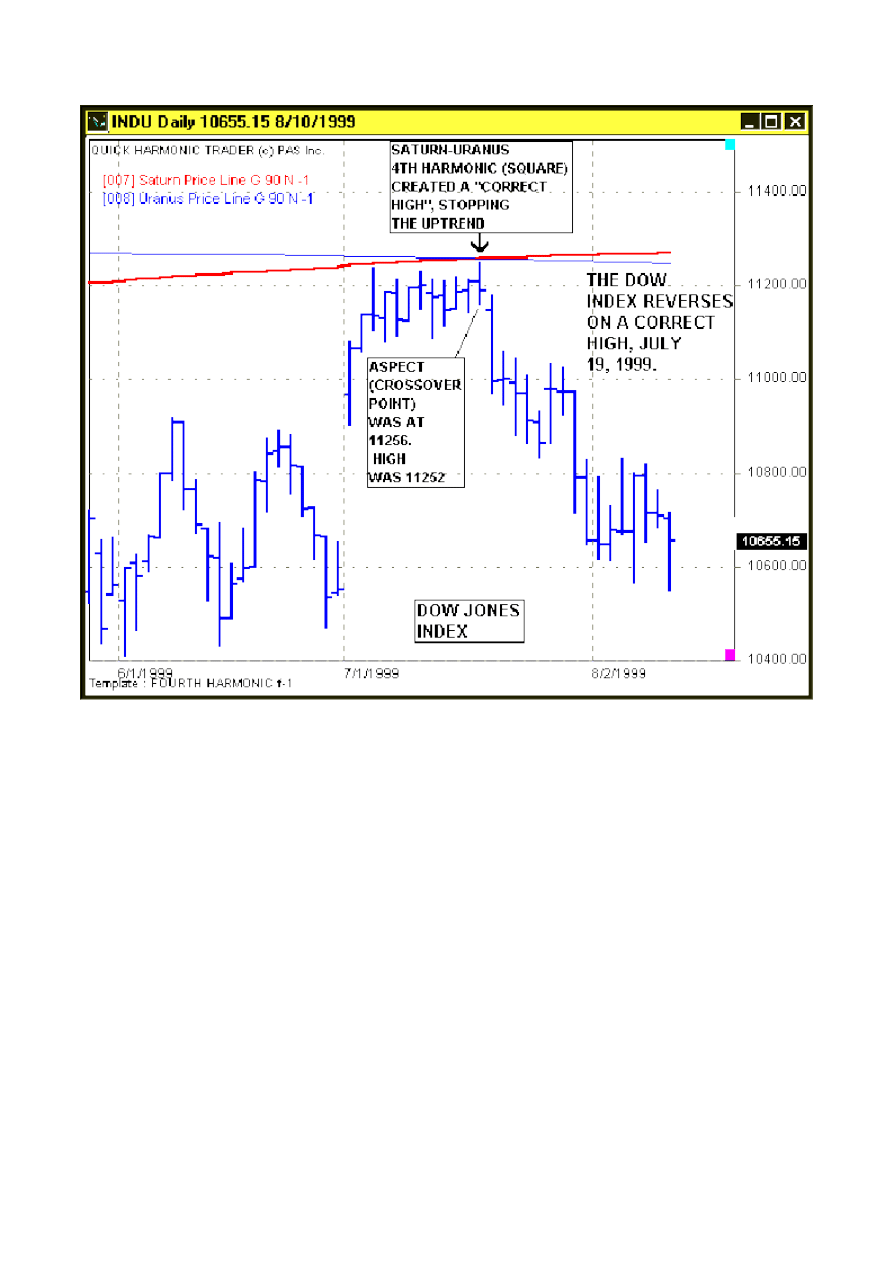
Rysunek 32. Przykład zastosowania programu Quick Harmonic Trader - indeks DJIA

Źródło: opracowanie własne przy wykorzystaniu strony internetowej:

z dnia 30.06.2001.

http://www.marketdetective.com/QHT/qhtinfo.htm

Rysunek 33 przedstawia tzw. geocentryczne koło planetarne stworzone na dzień 26 marca 1998 r. tj.

jedną sesje po silnym spadku indeksu S&P. W jego środku umieszczona została Ziemia, a na obrzeżach

poszczególne ciała niebieskie naszego Układu Słonecznego, oznaczone odpowiednimi literami np. M -

Merkury, V - Wenus, R -Mars i T - Księżyc itd. Wewnętrzne koło reprezentuje zegar ziemski. Linia

pogrubiona oznacza godzinę 16.15 tj. moment zamknięcia notowań indeksu w Nowym Yorku.

W kole geocentrycznym wykreśla się takie figury jak: trójkąty, kwadraty, pentagony i heksagony.

Wzorem o kluczowym znaczeniu w naszym przykładzie jest tzw. wielki krzyż (prostokąt). W jego

wnętrzu znajduje się: linia zamknięcia sesji w Nowym Jorku, dwie fazy Księżyca oraz planety: Wenus,

Uran, Jupiter i Pluton. Drugi wzór stanowi formacja zwana "Y" (yod). Jedno jej ramię zawiera planety:

Uran, Neptun i Wenus. Drugie - Saturna, Marsa, Merkurego i Słońce.

Kosmologiczna interpretacja położenia planet wskazuje na istotny punkt zwrotny.

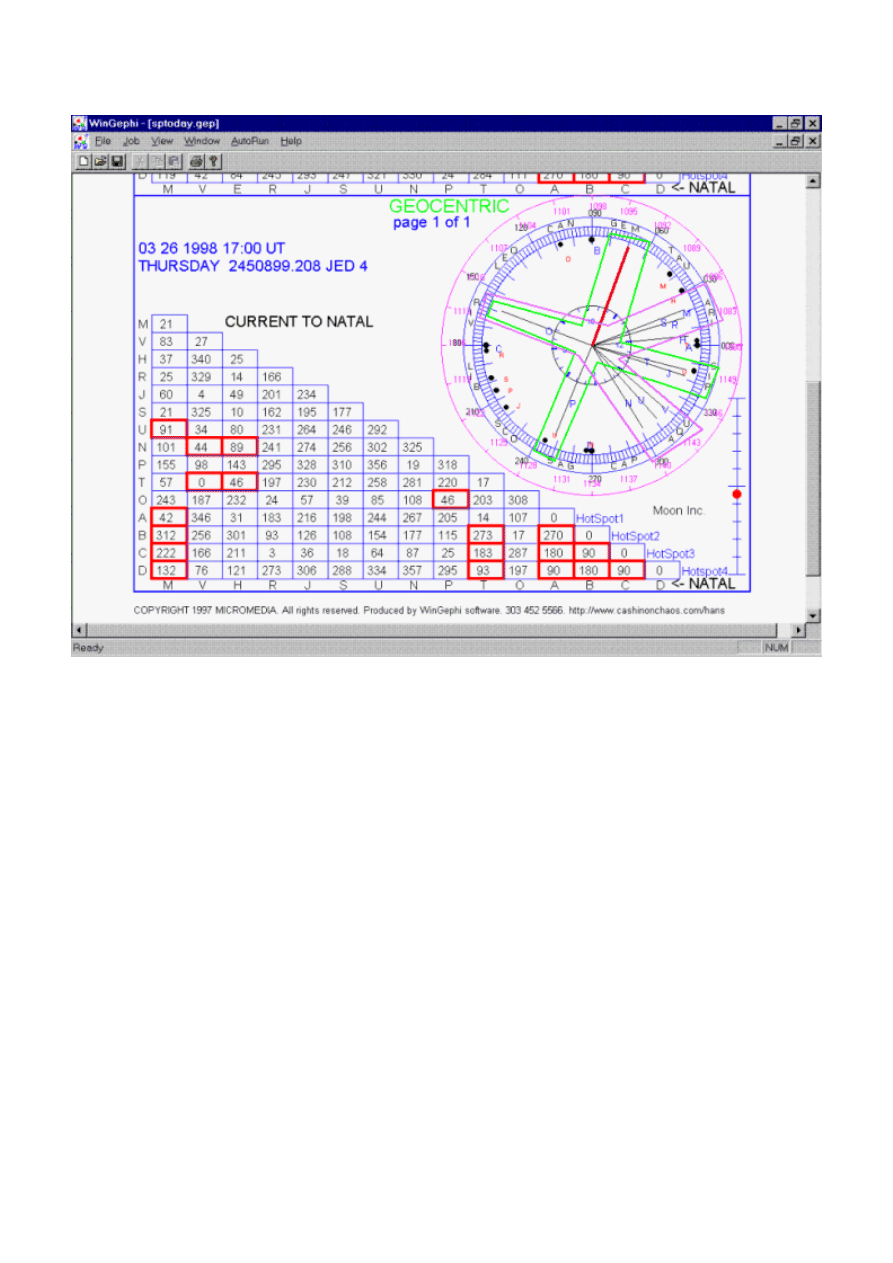
Rysunek 33. Wyznaczenie punktów zwrotnych indeksu S&P przy pomocy wpływu planet na

zachowanie inwestorów.

Źródło: strona internetowa:

z dnia 30.06.2001.

http://www.marketdetective.com/QHT/qhtinfo.htm

Wpływowi planet na zachowanie inwestorów poświęcono stosunkowo dużo pozycji zwracając uwagę, że

oprócz Księżyca także i one silnie oddziałują na ludzkie emocje.

Ponadto wiele firm korzysta także z usług astrologów, którzy na podstawie układu planet prognozują

wydarzenia gospodarcze. "Chodzi tu przede wszystkim o wzajemne położenie Jowisza i Saturna. Np.

razem z koniunkcją obydwu planet w Strzelcu w 1983 r. rozwój gospodarczy uległ przyspieszeniu. Od

stycznia do sierpnia następnego roku Jowisz, Saturn, a także Neptun i Mars tworzyły negatywne aspekty,

czego odbiciem był spadek notowań na giełdach. Kiedy w 1985 r. Jowisz znalazł się w pozytywnych

aspektach z Uranem i Plutonem, wzrosły również notowania giełdowe."

Obecnie wykonuje się także horoskopy dla poszczególnych giełd światowych, które mają wychwycić

korelację odmienną w stosunku do światowej.

3.2.1 Metody cenowe

Teoria fal pozwala zaobserwować proporcje zachodzące między falami kolejnych ruchów cen. W

ogólności fale te dzielą się na tzw. fale główne i następujące po nich fale korekty - istotnym jest, aby oba

rodzaje wzrostów i spadków były tego samego rzędu. Proporcje te można opisać jako kolejne potęgi Φ i

jej odwrotności. Na rynku kapitałowym zazwyczaj do obliczeń wykorzystuje się całkowite wykładniki

potęgi liczby Φ z przedziału <-3, 3> - Tabela 3.

Tabela 3. Współczynniki złotego podziału

Potęga n F - współczynniki złotego podziału

n

Rodzaj ciągu

1

1,618

Ciąg zewnętrzny

2

2,618

3

4,236

-1

0,618

Ciąg wewnętrzny

-2

0,382

-3

0,236

Źródło: Fischer R. "Liczby Fibonacciego na giełdzie", WIG - Press, Warszawa 1996.

Rysunek 34 przedstawia przykłady złotych proporcji rynkowych, będące podstawą analizy cenowej.

Rysunek 34. Proporcje Fibonacciego w formacjach rynkowych. Po lewej stronie przedstawiony został

sposób obliczenia potencjalnego zasięgu ruchu na podstawie fali spadkowej. Po prawej - potencjalny

zasięg korekty następujący po fali wzrostowej.

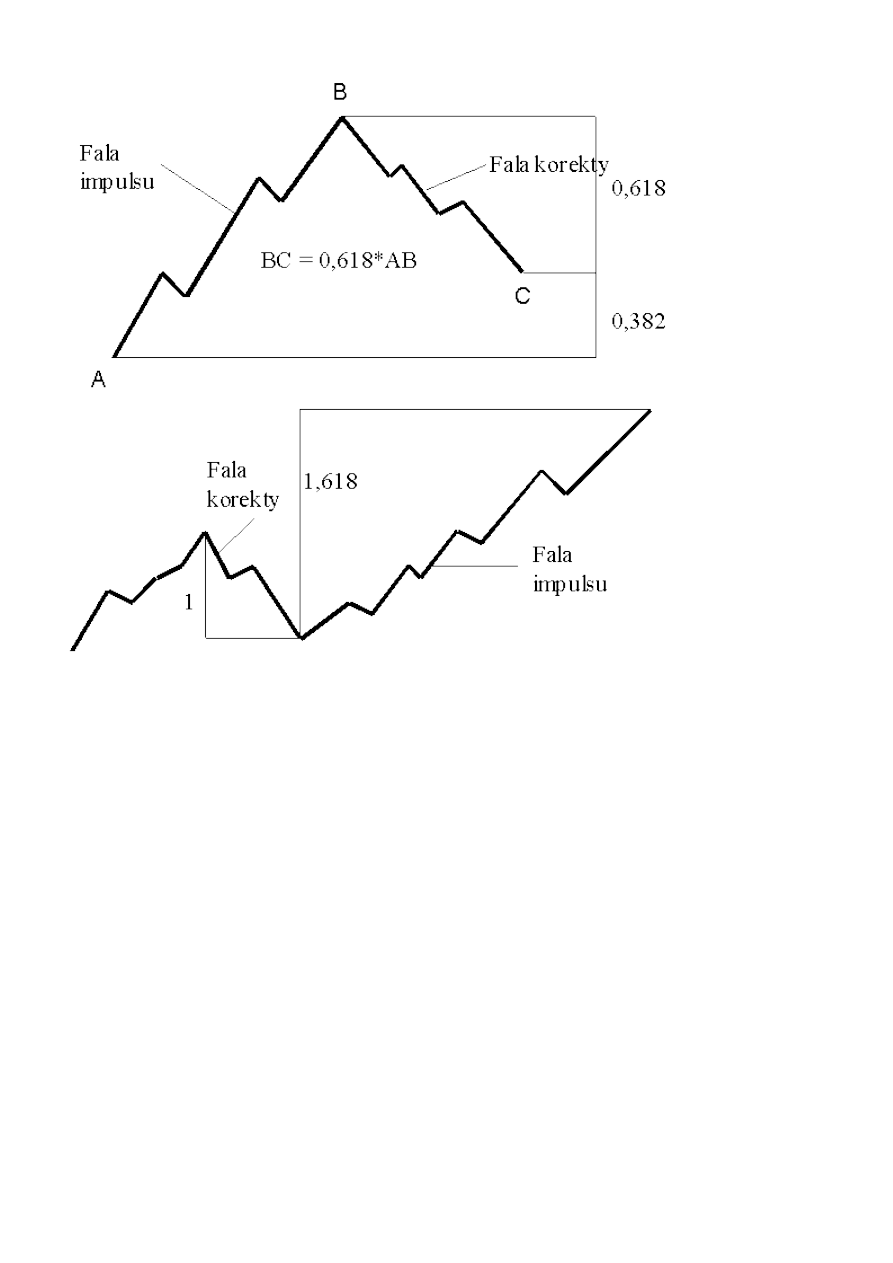
Źródło: opracowanie własne

Podstawową trudnością, z jaką spotykają się analitycy techniczni jest problem określenia z góry, który ze

współczynników powinien być w danym przypadku użyty. Przy zastosowaniu tej metody otrzymujemy

szereg punktów, wokół których, prawdopodobieństwo zmiany trendu jest wyższe.

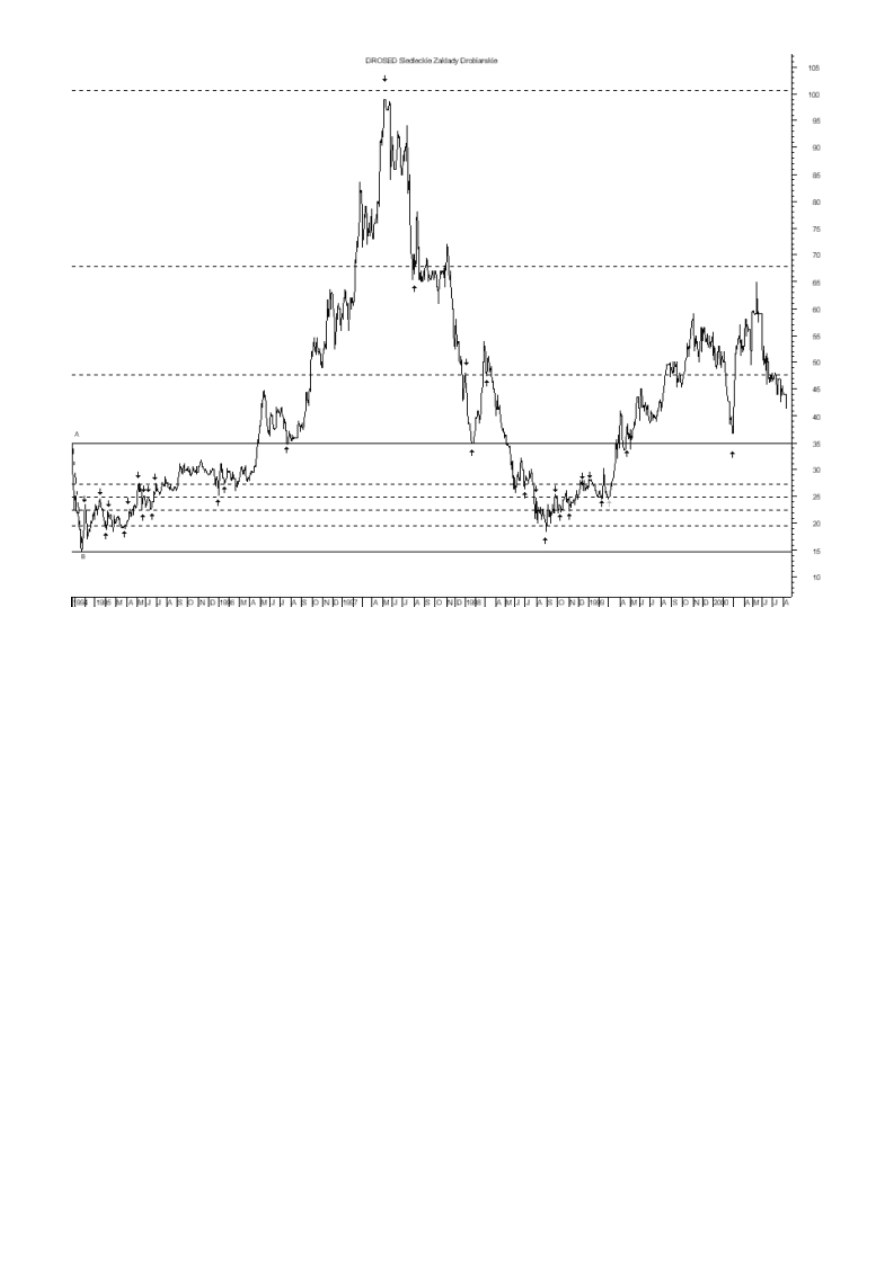
Proporcje Fibonacciego mogą być wykorzystane do wyznaczenia linii odwrotu. Na początku

wyznaczamy linie trendu między dwoma sąsiednimi punktami ekstremum cenowego. Rozpoczynając od

górnego punktu skrajnego wykreślamy 9 linii poziomych przecinających linię trendu na wysokości: 0,0%,

23,6%, 38,2%, 50,0%, 61,8%, 100,0%, 161,8%, 261,8% i 423,6%. Po znaczącym ruchu cenowym (w

górę lub w dół) ceny najczęściej doznają korekty o część wartości pierwotnego ruchu cenowego. W

czasie korekty cen kolejne poziomy wsparcia i oporu wykształcają się w pobliżu poziomu poziomów

odwrotu Fibonacciego - Rysunek 35. Na wykresie zaznaczone zostały poziomy cenowe, które w

przeszłości zadziałały jako poziomy wsparcia (strzałka ↑) i oporu (strzałka ↓).

Rysunek 35. Przykład zastosowania linii odwrotu Fibonacciego na wykresie cen akcji spółki

Drosed.

1.

2.

3.

Źródło: opracowanie własne

Połączenie sygnałów pochodzących z różnych szczytów i dołków cenowych pozwala utworzyć tzw.

zgrupowania sygnałów, w pobliżu których gwałtownie rośnie prawdopodobieństwo zmiany

dotychczasowej tendencji na przeciwną. Rysunek 36 ilustruje poziomy zniesienia Fibonacciego dla kilku

zwyżek cen akcji TP SA:

A - B - listopad 2001

C - D - grudzień 2001 / styczeń 2002

E - Φ - luty / marzec 2002

G - H - kwiecień / maj 2002

Koncentracja zniesień Fibonacciego bardzo dobrze wyznaczyła:

Poziom oporu z maja 2002 roku oznaczony literą H.

Wsparcie z końca kwietnia 2002 r - litera G

Pasmo wsparć z lipca 2002 r. - litery I i J

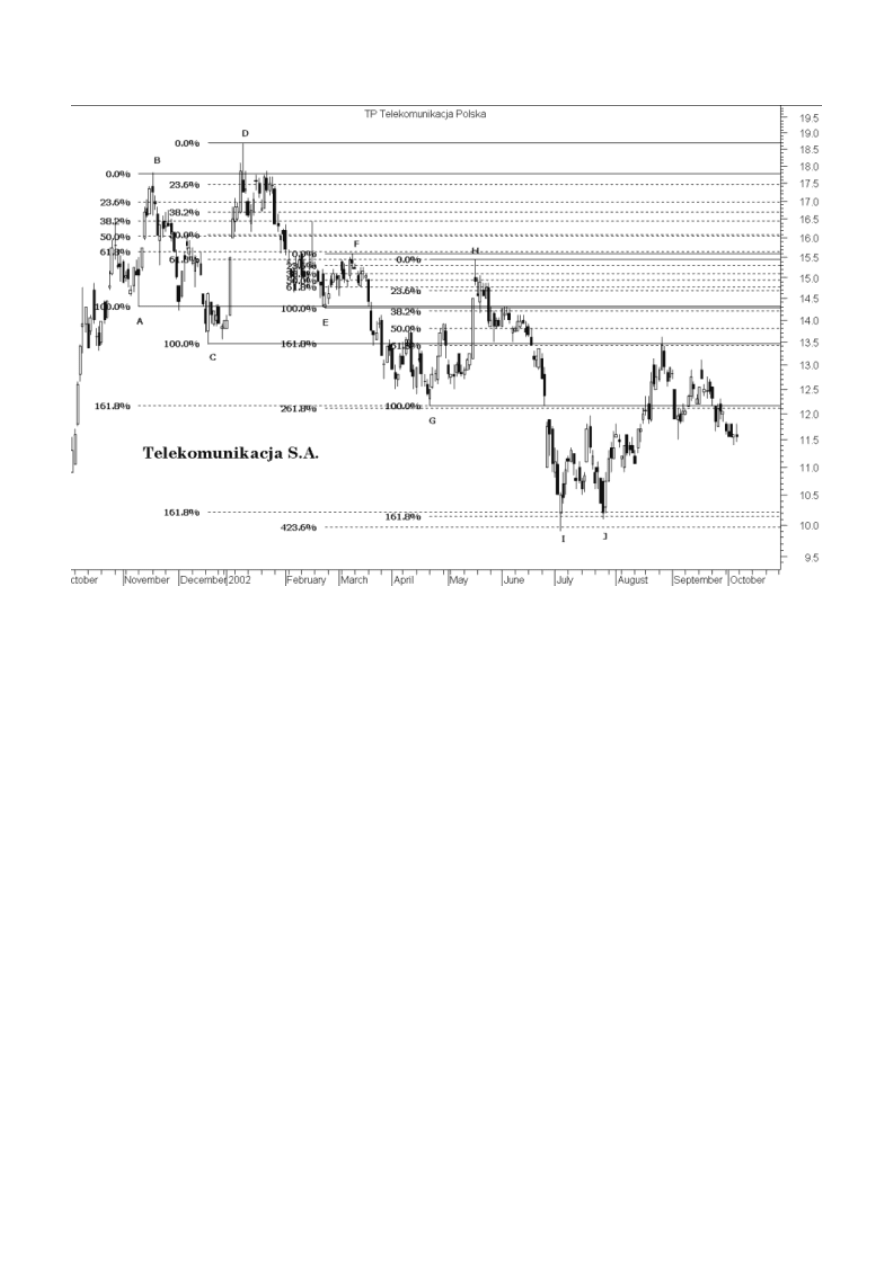
Rysunek 36. Koncentracja poziomów wsparcia i oporu na przykładzie akcji Telekomunikacji SA

Źródło: opracowanie własne

3.2.2 Metody czasowe

Podstawą analizy czasowej jest twierdzenie, że oś czasu podlega złotym podziałom, jeśli za punkty

podziału przyjmie się istotne szczyty i dołki cen lub wartości indeksów giełdowych z przeszłośći -

Rysunek 37. Konsekwencją takiego podejścia jest wyznaczenie potencjalnego dnia zmiany trendu

mającego nastąpić w przyszłości. W literaturze dzien ten nazywany jest dniem docelowym (time goal

day), a ozanczany jako DD.

Pierwsze świadectwa dotyczące występowania na rynku kapitałowym określonych relacji w czasie i

amplitudzie znaleźć można w pracach wielkiego znawcy teorii Dowa, jakim był R. Rhea. Zauważył on

między innymi, że:

"Przedstawione dane (dotyczące wyłącznie średniej przemysłowej) pokazują, że dziewięć rynków byka i

dziewięć rynków niedźwiedzia trwało łącznie 13115 dni kalendarzowych. Rynki byka trwały 8143 dni,

natomiast rynki niedźwiedzia 4972 dni. Stosunek tych liczb wskazuje, że bessa trwała 61,1% okresu

hossy."

Rysunek 37. Wyznaczenie dnia docelowego na bazie odległości między punktami zwrotnymi A i B

oraz współczynnika 1,618.

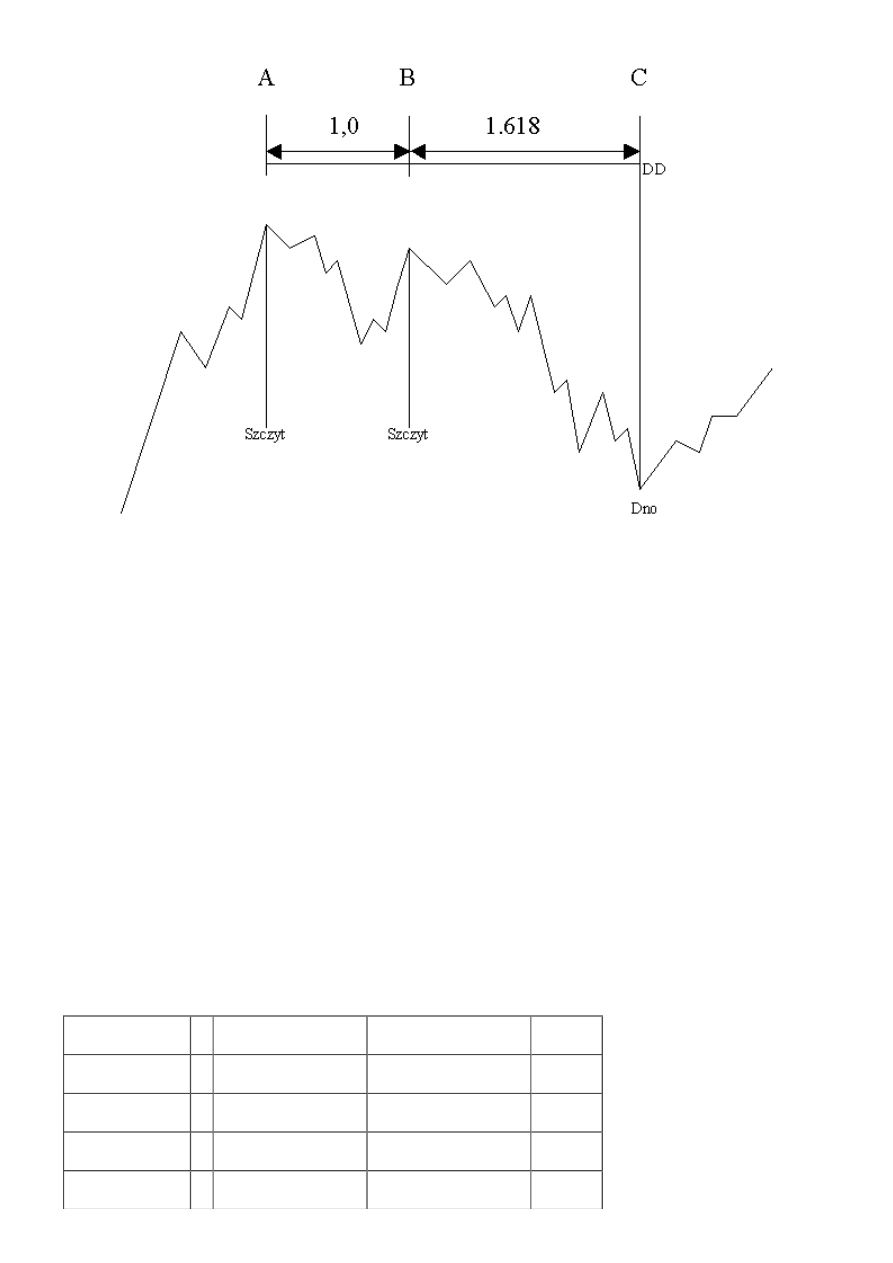
Źródło: opracowanie własne

S. Benner przeprowadził badania statystyczne ruchów cenowych w celu znalezienia odpowiedzi na

pytanie o naturę cykli koniunkturalnych w biznesie. W 1875 r. powstało dzieło "Business Prophecies of

the Futures Ups and Downs in Prices". Benner zauważył, że szczyty koniunktury kształtują się na ogół

zgodnie ze schematem 8 - 9 - 10 lat - Tabela 4. Dla recesji Benner stosował schemat 20 - 18 - 16, ale

mniej poważne dołki na rynku kapitałowym podlegają raczej cyklowi: 16 - 18 - 20, tj. analogicznie do

schematu występowania den kryzysów, którym towarzyszyła panika. Stosując schemat 16 - 18 - 20 do

dołków rynkowych stwierdzamy, że pasuje on bardzo dokładnie do wykresu DJIA w latach 1902 - 1987.

Formuła Bennera sprawdzała się całkiem dobrze przez większość ubiegłego stulecia.

Można stwierdzić, że teoria Bennera jest bardzo bliska sekwencji Fibonacciego, bowiem powtarzający się

schemat 8 - 9 - 10 tworzy liczby Fibonacciego do 377 z dokładnością do 1.

Tabela 4. Ilustracja teorii S. Bennera dla szczytów koniunktury przy wykorzystaniu schematu 8 - 9 - 10

lat.

Schemat 8-9-10   Poszczególne sumy Liczby Fibonacciego Różnica

8

=

8

8

0

+9

=

 

 

 

+10

=

 

 

 

+8

=

35

34

+1

+9

=

 

 

 

+10

=

54

55

-1

...+8

=

89

89

0

...+8

=

143

144

-1

...+9

=

233

233

0

...+10

=

378

377

+1

Źródło: Frost A., Pretcher R. "Teoria fal Elliotta", WIG-Press, Warszawa 1995.

Można zatem przyjąć, że teoria Bennera, oparta na różnych przedziałach czasu dla szczytów i dołków, a

nie stałej periodyczności, mieści się w ramach sekwencji Fibonacciego.

Sam R. Elliott stwierdził, że czynnik czasu potwierdza formację cenową i na tym właśnie polega jego

znaczenie. W analizie fal okresy wynikające z sekwencji Fibonacciego wskazują na możliwe punkty

zwrotne, zwłaszcza jeśli zbiegają się z prognozowanymi poziomami cenowymi i porządkiem fal. W

swojej pracy Nature's Law, R. Elliott przytoczył przykłady okresów wynikających z sekwencji

Fibonacciego, które przedzielały istotne punkty zwrotne rynku - Tabela 5.

Zdaniem M. Czekały aspekt związany z analizą czasu jest raczej wtórny w teorii Elliotta. Główne

twierdzenie w analizie czasu polega na przekonaniu, że również oś czasu podlega złotemu podziałowi,

jeśli za punkty podziału przyjąć istotne szczyty (dołki) cen na akcjogramie.

Tabela 5. Przykłady okresów wynikających z sekwencji Fibonacciego przedstawionych przez R. Elliotta

Okres

Długość

1921 - 1929

8 lat

Lipiec 1921 - listopad 1928

89 miesięcy

Wrzesień 1929 - lipiec 1932

34 miesiące

Lipiec 1932 - lipiec 1933

13 miesięcy

Lipiec 1933 - lipiec 1934

13 miesięcy

Lipiec 1934 - marzec 1937

34 miesiące

Lipiec 1932 - marzec 1937

5 lat (55 miesięcy)

Marzec 1937 - marzec 1938

13 miesięcy

Marzec 1937 - kwiecień 1942

5 lat

1929 - 1942

13 lat

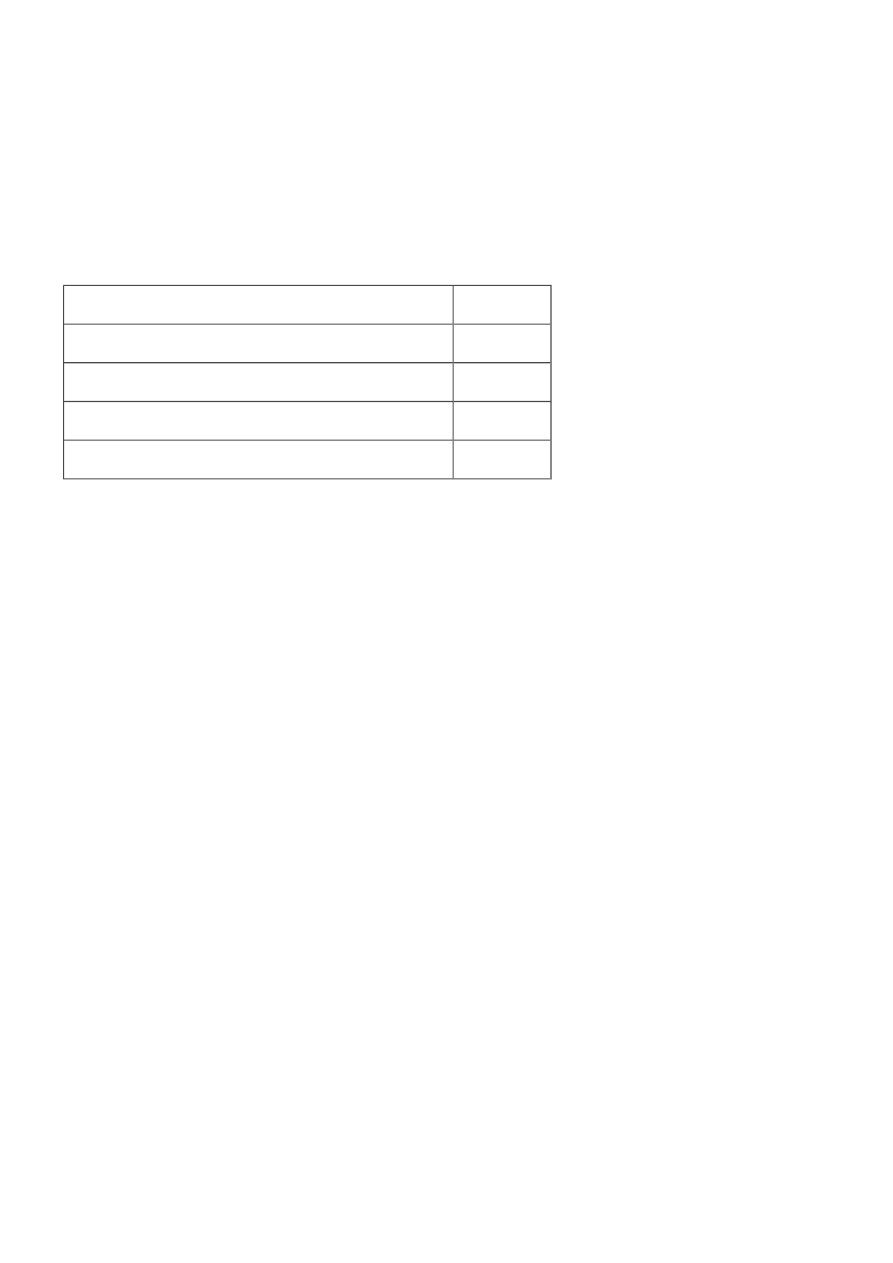
Źródło: Frost A., Pretcher R. "Teoria fal Elliotta", WIG-Press, Warszawa 1995.

R. Russel w Dow Theory Letters z 21.11.1973 przedstawił kilka kolejnych przykładów, w których

poszczególne punkty zwrotne na rynku akcji oddzielone są jednostkami czasu należącymi do zbioru liczb

Fibonacciego - Tabela 6.

Tabela 6. Przykłady okresów wynikających z sekwencji Fibonacciego przedstawionych przez R. Russel'a

Okres

Długość

Dno (panika) z 1907 - dno (panika) z 1962

55 lat

Szczyt z 1947 - dno (panika) z 1962

13 lat

Dno z 1921 (recesja) - dno z 1942 (recesja)

21 lat

Szczyt ze stycznia 1960 - dołek z października 1962 34 miesiące

Źródło: Frost A., Pretcher R. "Teoria fal Elliotta", WIG-Press, Warszawa 1995.

Kolejne potencjalne punkty zwrotne w przyszłości otrzymujemy poprzez dodanie do dat punktów

historycznych odpowiednich wielkości ciągu Fibonacciego. H. Bolton zauważył, że "permutacje czasu

biegną w nieskończoność" i że "dany okres może przebiegać od szczytu do szczytu, od szczytu do dołka,

od dołka do dołka bądź od dołka do szczytu". Podobną koncepcję wysunął W. White w swojej pracy na

temat teorii Elliotta, w której starał się wyznaczyć kolejny punkt zwrotny rynku akcji na rok 1970. W

uzasadnieniu wskazał on następującą sekwencję:

1949+21=1970;

1957+13=1970;

1962+8=1970;

1965+5=1970.

Okazało się, że w maju 1970 r miało miejsce dno indeksu Dow Jones.

Można skonstatować, że powyższe obserwacje dały podwaliny do powstania takiego instrumentu analizy

technicznej, jakim są

, w której daty kolejnych dni docelowych obliczamy

strefy czasowe Fibonacciego

ze wzoru:

C = A + Φ

n

n

gdzie:

A - data dnia zwrotnego tj. dnia zmiany tendencji rynkowej

F - n-ta liczba ciągu Fibonacciego

n

C - data n-tego dnia docelowego (DD)

n

n

Dzień A powinien być tzw. dniem charakterystycznym - ekstremum podstawowym. Poczynając od niego

należy prowadzić proste równoległe do osi ceny w odległościach odpowiadającym kolejnym liczbom

ciągu Fibonacciego - otrzymujemy wtedy ciąg dni docelowych. W pobliżu narysowanych linii poszukuje

się istotnych zmian cen tj. punktów zwrotnych. Im większa jest wartość n liczby ciągu Fibonacciego, tym

otrzymywany sygnał zmiany trendu w dniu docelowym DD jest silniejszy. Kluczowym elementem

n

powodzenia jest poprawne wybranie ekstremów podstawowych. Przykład zastosowania stref czasowych

Fibonacciego został przedstawiony poniżej (Rysunek 38).

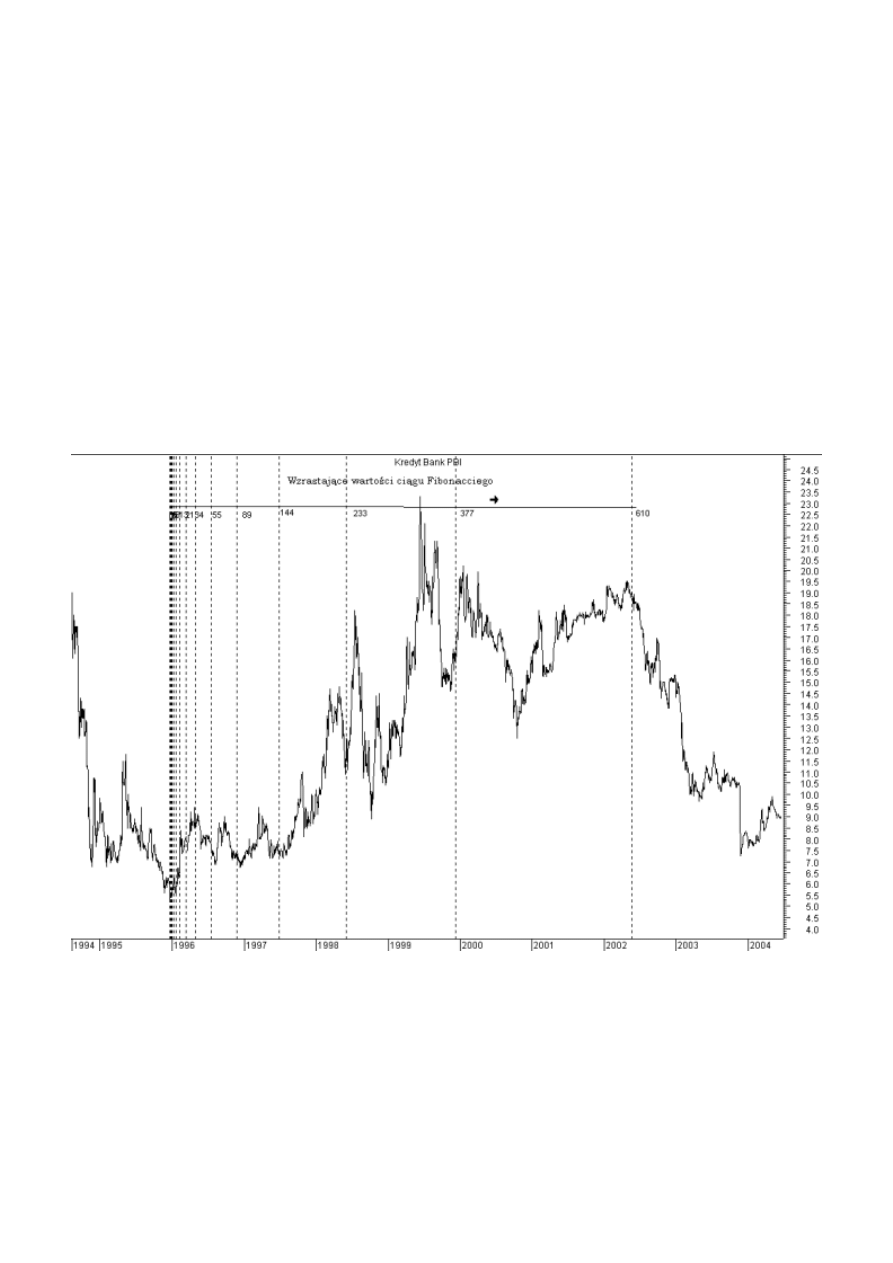
Rysunek 38. Zastosowanie stref czasowych Fibonacciego na przykładzie akcjogramu Kredyt

Banku. Jako punkt początkowy wybrane zostało dno ceny akcji banku z grudnia 1995 r.

Źródło: opracowanie własne

Niektórzy autorzy zamiast daty stosują numer sesji. Na tak skonstruowanych wykresach widoczny jest

brak przesunięcia akcjogramu w lewo spowodowany mniejszą liczbą sesji w pierwszym okresie notowań

na GPW.

1.

2.

3.

4.

Problem równości fal impulsu w czasie, a także proporcji Fibonacciego zachodzących między ujęciami

czasowymi tych fal zostały zauważone przez R. Pretchera i A. Frosta. Autorzy szacowali starali się

przewidzieć potencjalny punkt zwrotny DJIA na podstawie:

Szczytu z października 1974 (21 lat lub 233 miesiące do punktu zwrotnego maj / sierpień 1995)

Dołka z sierpnia 1982 (13 lat lub 144 miesiące do punktu zwrotnego maj / sierpień 1995)

Szczytu z października i grudniowego dołka z 1987 (8 lat lub 89 miesięcy do punktu zwrotnego

maj / sierpień 1995)

Dołka ze stycznia 1991 (5 lat lub 55 miesięcy do punktu zwrotnego maj / sierpień 1995)

Wg nich współczynniki Fibonacciego dotyczące czasu występują znacznie rzadziej, ale na podstawie

wieloletniego analizowania indeksów rynkowych stwierdzili, że amplituda praktycznie każdej fali

(mierzona w skali arytmetycznej lub w procentach) pozostaje stała względem amplitudy fali sąsiedniej,

fali tego samego ruchu biegnącej w podobnym kierunku i / lub swojej podfali w stosunku

odpowiadającym jednemu ze współczynników Fibonacciego.

Poczynione przez nich spostrzeżenia były bardzo bliskie sformułowaniu pojęcia spirali czasowej

występującej na rynku kapitałowym. Niemniej nie rozwinęli oni tego pomysłu w takim zakresie w jakim

uczynił to R. Fischer i C. Carolan. Można więc powiedzieć, że obie metody czasowe wywodzą się

bezpośrednio z teorii Elliotta - problem ten zostanie omówiony w dalszych rozdziałach.

Rynki funkcjonują w kilku ramach czasowych jednocześnie. Rynek może dawać sygnały kupna na

wykresie dziennym, a równocześnie sygnały sprzedaży w ujęciu tygodniowym i vice versa. W takim

przypadku

, a

nadrzędne znaczenie mają sygnały napływające z wykresu o większej ramie czasowej

więc należy badać najpierw układy roczne, kwartalne, tygodniowe, dzienne, godzinowe i minutowe. Jeśli

posługujemy się dwiema ramami czasowymi to powinny one być połączone współczynnikiem 5: krótsza

powinna wynosić 1/5 dłuższej, np. układ tygodniowy (dłuższa) i dzienny (krótsza). W układzie

sporządzonym w szerszej ramie czasowej widoczne będą większe siły, które odpowiednio rozpoznane

można wykorzystać w węższej. Nieco odmienna zasada obowiązuje w przypadku oscylatorów - dla

rozwiania wątpliwości powinniśmy stosować węższe okienko czasowe. Bardzo ciekawą koncepcję

połączenia różnych ram czasowych ze współczynnikami Fibonacciego zaprezentował R. Krausz. Otóż

poziom równowagi (C

) cen w tygodniu n+1 uzyskujemy jako średnią arytmetyczną najwyższej (C ),

PR

H

najniższej (C ) i ceny zamknięcia (C ) w n - tym tygodniu wg następującego wzoru:

L

C

Jeśli przez C

oznaczymy różnicę między ceną najwyższą a najniższą w n-tym tygodniu (C

= C - C ),

DL

DL

H

L

wtedy odpowiednie przedziały wsparcia (C

)i oporu (C

), otrzymane przy zastosowaniu proporcji

PW

PO

Fibonacciego wynoszą:

Zmiana horyzontu czasowego pozwala nam na zastosowanie tego systemu w różnych ujęciach

czasowych.

3.2.3 Metody cenowo - czasowe

Jest to połączenie analizy cenowej i czasowej. Otrzymane w ten sposób punkty - dni odwrotu oznaczane

jako DD, charakteryzują się wyższym prawdopodobieństwem odwrócenia trendu, niż w każdej z

powyższych dwu metod. Warunkiem powstania punktu DD jest otrzymanie takiej samej prognozy

zarówno przy użyciu analizy czasowej, jaki i cenowej. Podstawowym narzędziem tej metody są spirale

cenowe, którym z uwagi na ich rangę został poświęcony osobny rozdział.

Inną metodą łączącą analizę czasową i cenową są łuki Fibonacciego. Dla wykreślenia łuków

Fibonacciego łączymy przy pomocy linii trendu dwa punkty cyklu cenowego, z których jeden jest

lokalnym minimum a drugi lokalnym maksimum cenowym. Następnie biorąc za podstawę drugi z

punktów skrajnych wykreślamy 3 łuki w taki sposób by przecinały one linie trendu na wysokości 38,2%,

50,0% i 61,8% długości tej linii. Lokalizacja poziomów wsparcia i oporu występuje w momencie

osiągnięcia przez ceny poziomu łuków. Przecięcia łuków przez linię kursu potwierdzają zmianę

poprzedniego trendu wyższego rzędu.

Rysunek 39 ilustruje sposób wykorzystania i interpretacji łuków Fibonacciego. Rysując w pierwszym

kroku trend od punku A do punktu B, otrzymujemy w konsekwencji trzy łuki Fibonacciego. Po spadku

cen waloru z punktu B do C, możemy zaobserwować korektę wzrostową do punktu D. Jak widać odbicie

cen zatrzymuje się na jednym z łuków Fibonacciego. Na łuku środkowym dochodziło kilkakrotnie do

krótkoterminowych wzrostów cen akcji. Po przekroczeniu punktu Φ wygenerowany został sygnał

długoterminowy sprzedaży i odwrócenia trendu. Warto podkreślić również fakt, że wzrost cen akcji

spółki w pierwszych miesiącach 1997 r. zatrzymał się w pobliżu drugiego łuku Fibonacciego - niestety tę

informację otrzymujemy dopiero po ukształtowaniu się właściwego szczytu cenowego w punkcie B.

Stanowi ona jednak potwierdzenie istotności tak narysowanych łuków Fibonacciego.

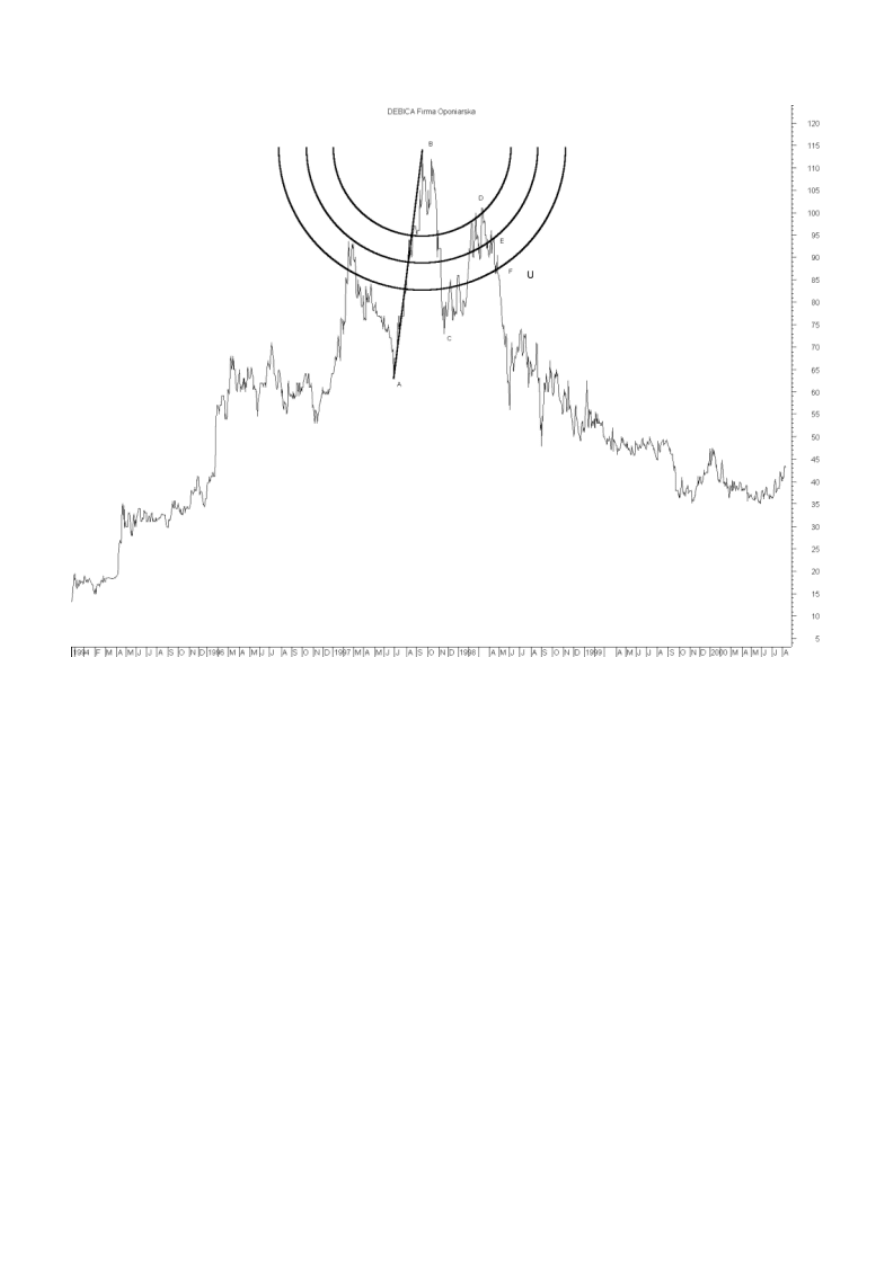
Rysunek 39. Zastosowanie łuków Fibonacciego na akcjogramie spółki Dębica

Źródło: opracowanie własne

Następnym sposobem wykorzystywanym przez analizę czasową i cenową są wachlarze Fibonacciego. W

pierwszej kolejności wyznaczamy linię trendu pomiędzy dwoma sąsiadującymi ekstremami cenowymi.

Następnie przez drugi z otrzymanych punktów prowadzimy "niewidzialną" prostą pionową. Wreszcie z

pierwszego punktu wyprowadzamy trzy linie trendu w ten sposób aby przecięły one "niewidzialną" linię

pionową na wysokości poziomów Fibonacciego 38,2%, 50,0% i 61,8%. Otrzymane proste stanowią

kolejne poziomy wsparcia lub oporu.

Rysunek 40 prezentuje wachlarze Fibonacciego widoczne na wykresie cen akcji Dębicy. Po trendzie

spadkowym od punktu A do punktu B, korekcyjna fala wzrostowa natrafiała na opór w punktach C i E.

Fala korekty wzrostu z odcinka BC zatrzymuje się w punkcie D, który w tym przypadku staje się

poziomem wsparcia.

W. D. Gann (1878 - 1955) był twórcą technik będących połączeniem kątów geometrycznych z danymi

cenowymi i szeregami czasowymi - zagadnienie to zostanie szerzej omówione w dalszej części pracy.

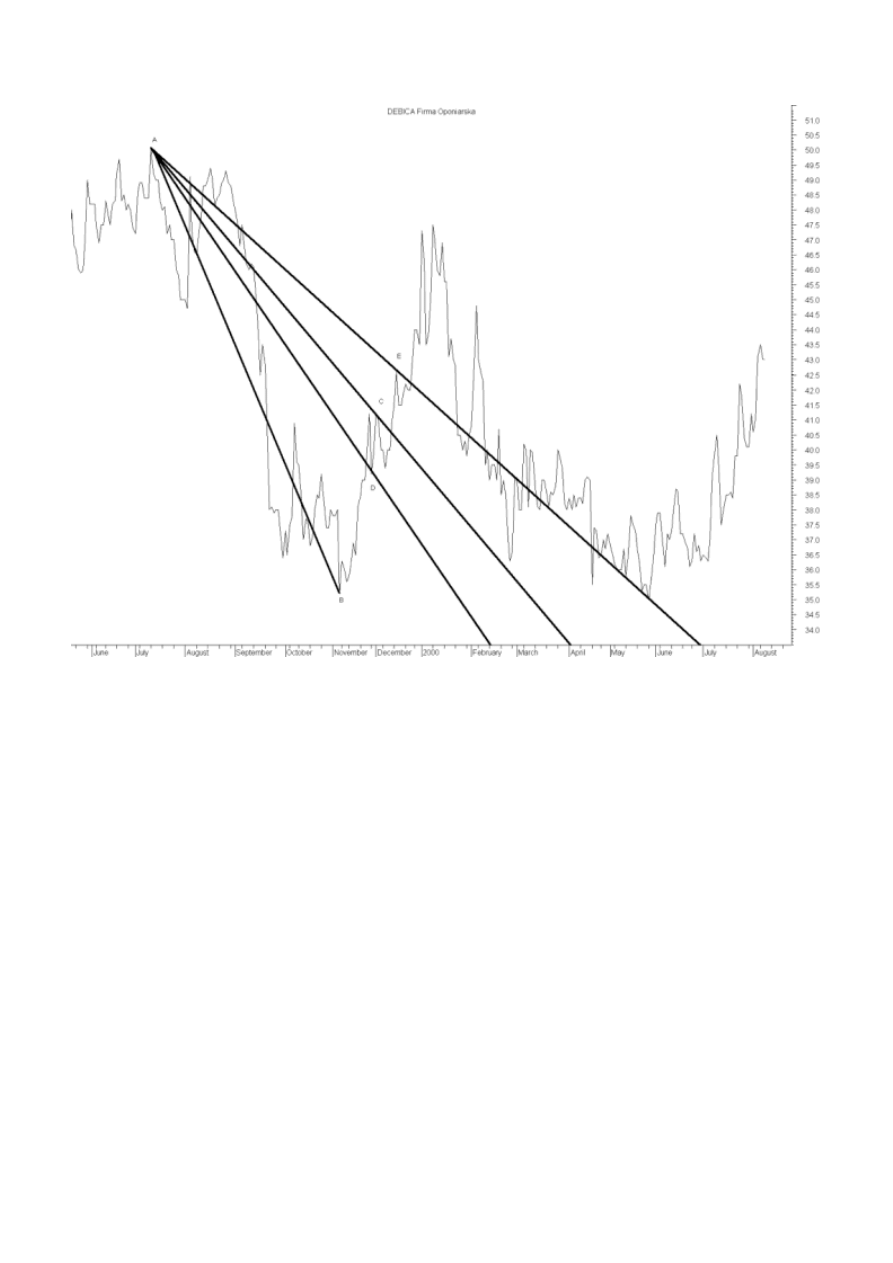
Rysunek 40. Przykład zastosowania wachlarzy Fibonacciego na akcjogramie spółki Dębica

Źródło: opracowanie własne

3.2.4 Dynamiczne zastosowanie ciągu liczb Fibonacciego

Dokonując wyboru istotnych punktów zwrotnych jakie miały miejsce w przeszłości, jesteśmy w stanie

otrzymać prawdopodobne zmiany trendu w przyszłości, zarówno na osi pionowej (cenowej) jak i

poziomej (czasowej). Poniżej przedstawiony został proces rozwijania proporcji Fibonacciego na osi

pionowej i poziomej dla wybranego odcinka AB.

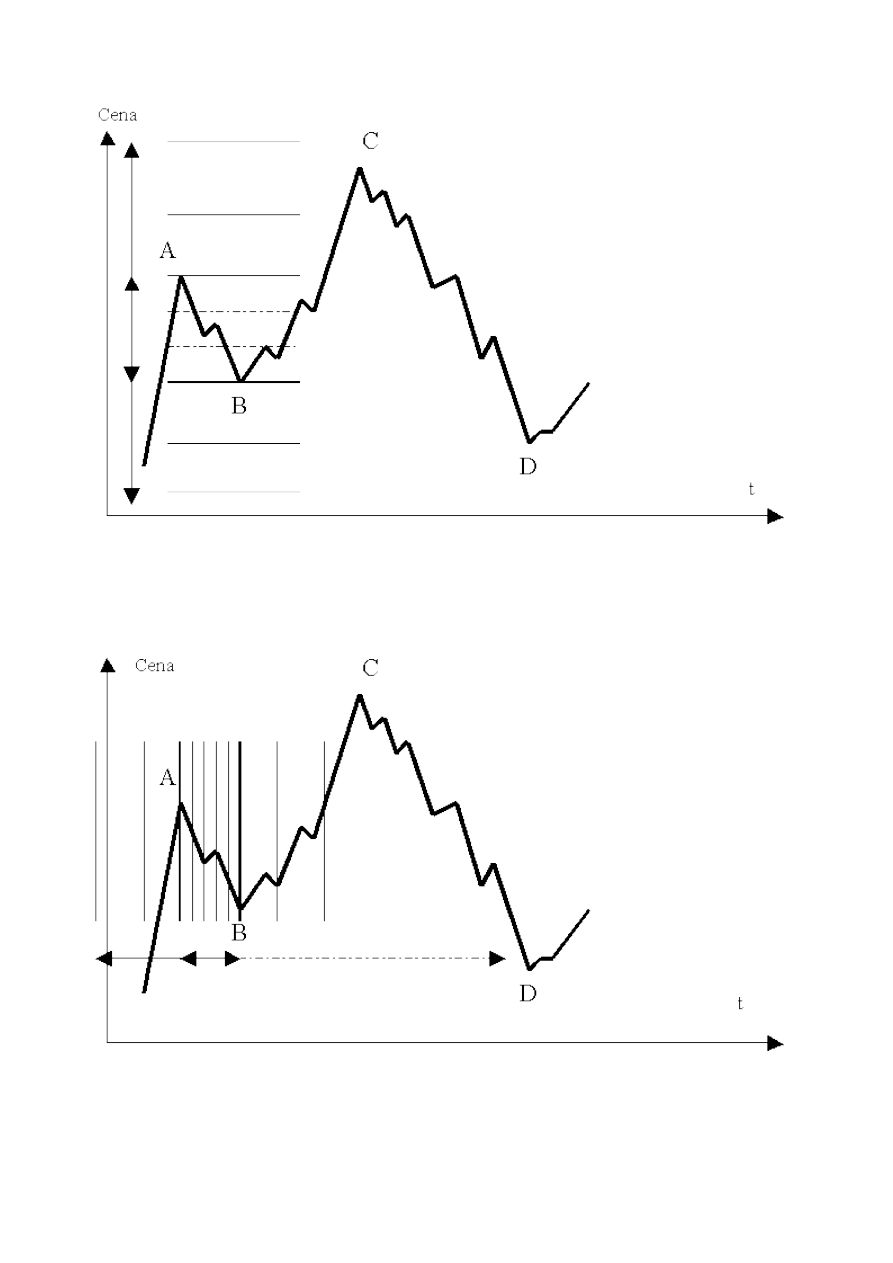
Rysunek 41. Proporcje Fibonacciego na osi pionowej

Źródło: opracowanie własne

Rysunek 42. Proporcje Fibonacciego na osi poziomej

Źródło: opracowanie własne

Wybierając także inne punktu otrzymujemy koncentrację poziomów Fibonacciego zarówno na osi

pionowej jak i poziomej w pobliżu istotnych cen i dat - Rysunek 43 i Rysunek 44

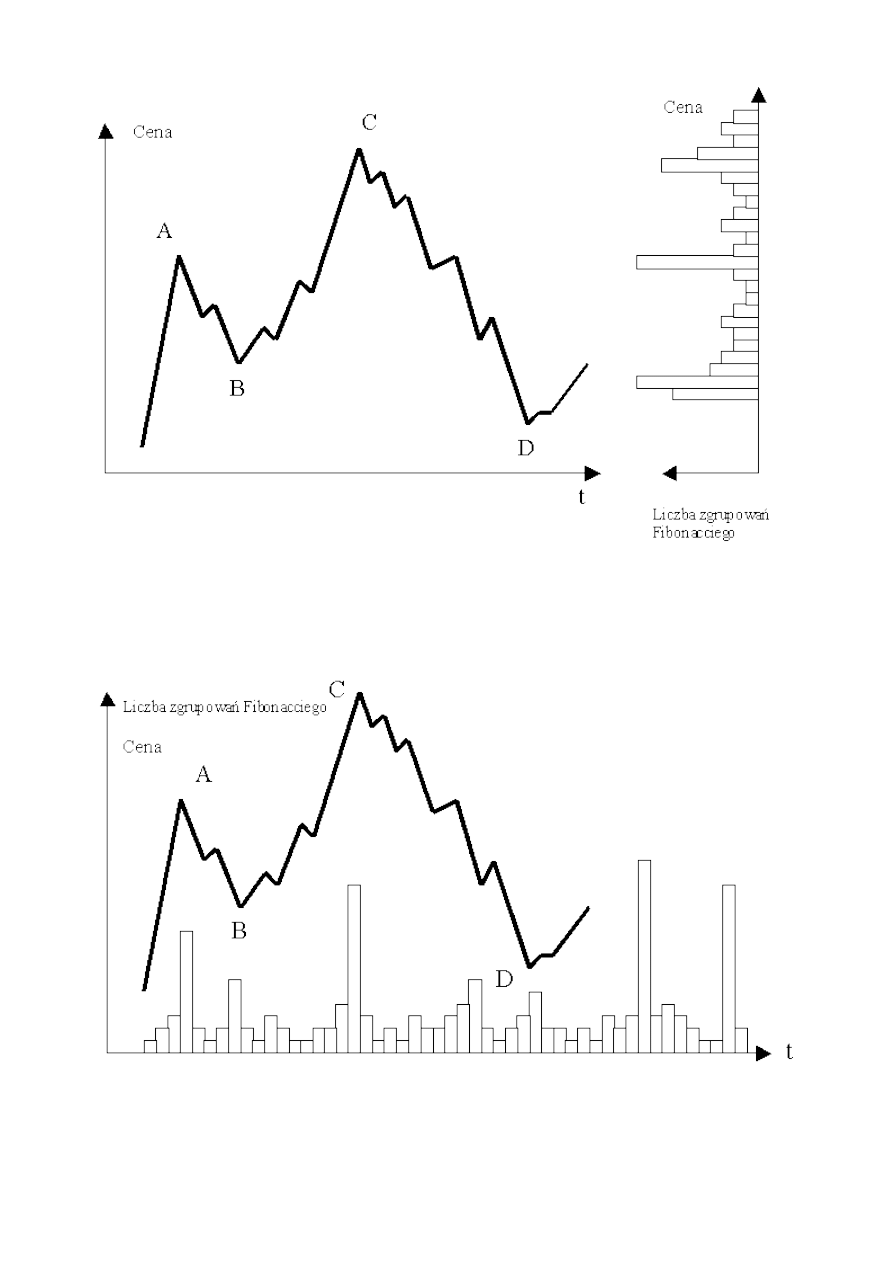
Rysunek 43. Zgrupowanie poziomów Fibonacciego na osi pionowej w pobliżu istotnych cen.

Źródło: opracowanie własne

Rysunek 44. Zgrupowanie poziomów Fibonacciego na osi poziomej w pobliżu istotnych dat.

Źródło: opracowanie własne

Problem polega jednak na tym, że duże zagęszczenie poziomów Fibonacciego prowadzi bardzo szybko

do pogorszenia czytelności wykresu.

W celu przezwyciężenia tych trudności w programie Nature' s Pulse i Fibonacci Trader stworzona została

możliwość dynamicznego stosowania ciągu Fibonacciego tylko dla wybranych szczytów i dołków, co

pozwala uzyskać przejrzysty obraz sytuacji.

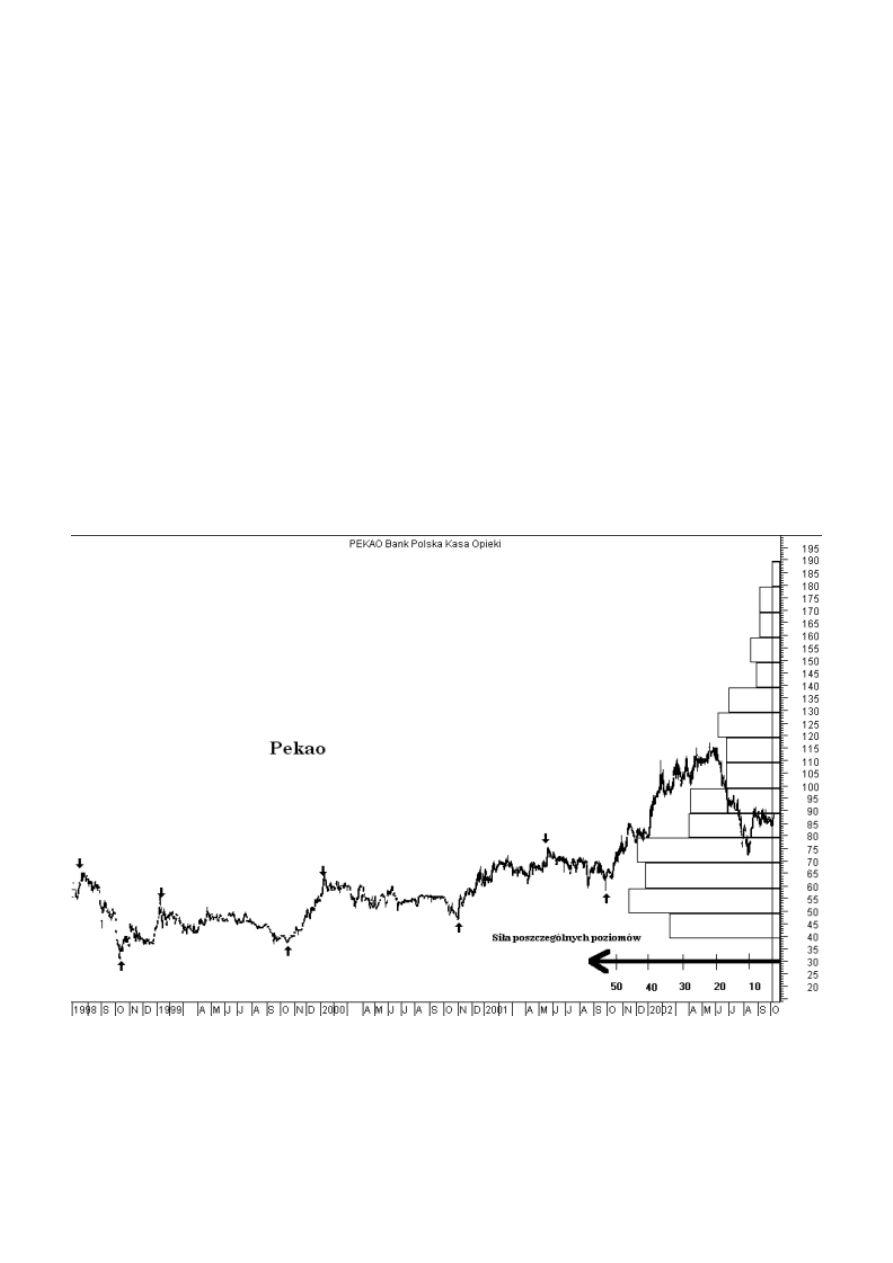
Użytkownik programu Nature's Pulse zaznacza istotne, jego zdaniem, punkty zwrotne, które mają służyć

do przeprowadzenia stosownej analizy. Program odnosi liczby Fibonacciego do wszystkich możliwych

kombinacji wybranych dołków i szczytów. Rysunek 45 przedstawia wybrane szczyty i dołki (strzałki na

dół i w górę) na akcjogramie Pekao SA oraz liczbę linii Fibonacciego zgrupowanych w danym przedziale

cenowym (skok ceny wynosił 10 PLN). Informację tę odczytujemy na dodatkowej, poziomej osi

umieszczonej na wykresie.

Rysunek 45. Wykres zgrupowań poziomów Fibonacciego w ujęciu dynamicznym - obliczenia

wykonane w programie Nature's Pulse i przekonwertowane do programu Metastock.

Źródło: opracowanie własne

Nieco inne ujęcie prezentuje program Fibonacci Trader gdzie poszczególne zgrupowania poziomów

Fibonacciego wyświetlane są bezpośrednio w pobliżu aktualnej ceny. W programie tym waga wybranych

punktów zwrotnych w przeszłości może ulegać zwiększeniu lub zmniejszeniu przy obliczaniu zgrupowań

linii Fibonacciego. Ujęcie dynamiczne może być również wykorzystane do prognozowania momentów

zwrotnych w czasie. Przy wykorzystaniu tych samych punktów zwrotnych co poprzednio (Rysunek 45)

przeprowadzono taką analizę na osi czasowej (Rysunek 47). Wybrane punkty zwrotne zaznaczone zostały

strzałkami. Słupki u dołu wykresu reprezentują liczbę wskazań przypadającą w pobliżu obliczonej daty.

Słupki A, B, C i D, w których doszło do koncentracji wskazań, okazały się istotnymi punktami

zwrotnymi. Na tej podstawie można wyliczyć również inne potencjalne punkty zwrotne w przyszłości.

Rysunek 46 przedstawia przykład wykorzystania programu Fibonacci Trader, gdzie do obliczeń

zastosowane zostało bardzo wąskie okno czasowe obejmujące jedynie 5 sesji. Środek linii w okienku o

numerze n otrzymujemy w wyniku podzielenia cen: najwyższej, najniższej i zamknięcia z okresu

poprzedniego (tj. o indeksie n-1) przez liczbę 3. Pozostałe linie narysowane dla okna cenowego o indeksie

n uzyskujemy w wyniku pomnożenia różnicy ceny najwyższej i najniższej z okienka o indeksie n, przez

wybrane współczynniki Fibonacciego. Linie te stanowią silne poziomy wsparcia i oporu w krótkim

horyzoncie czasowym.

Ujęcie dynamiczne może być również wykorzystane do prognozowania momentów zwrotnych w czasie.

Przy wykorzystaniu tych samych punktów zwrotnych co poprzednio (Rysunek 45) przeprowadzono taką

analizę na osi czasowej (Rysunek 47). Wybrane punkty zwrotne zaznaczone zostały strzałkami. Słupki u

dołu wykresu reprezentują liczbę wskazań przypadającą w pobliżu obliczonej daty. Słupki A, B, C i D, w

których doszło do koncentracji wskazań, okazały się istotnymi punktami zwrotnymi. Na tej podstawie

można wyliczyć również inne potencjalne punkty zwrotne w przyszłości.

Rysunek 46. Zgrupowanie poziomów Fibonacciego w ujęciu dynamicznym - obliczenia wykonane w

programie Fibonacci Trader.

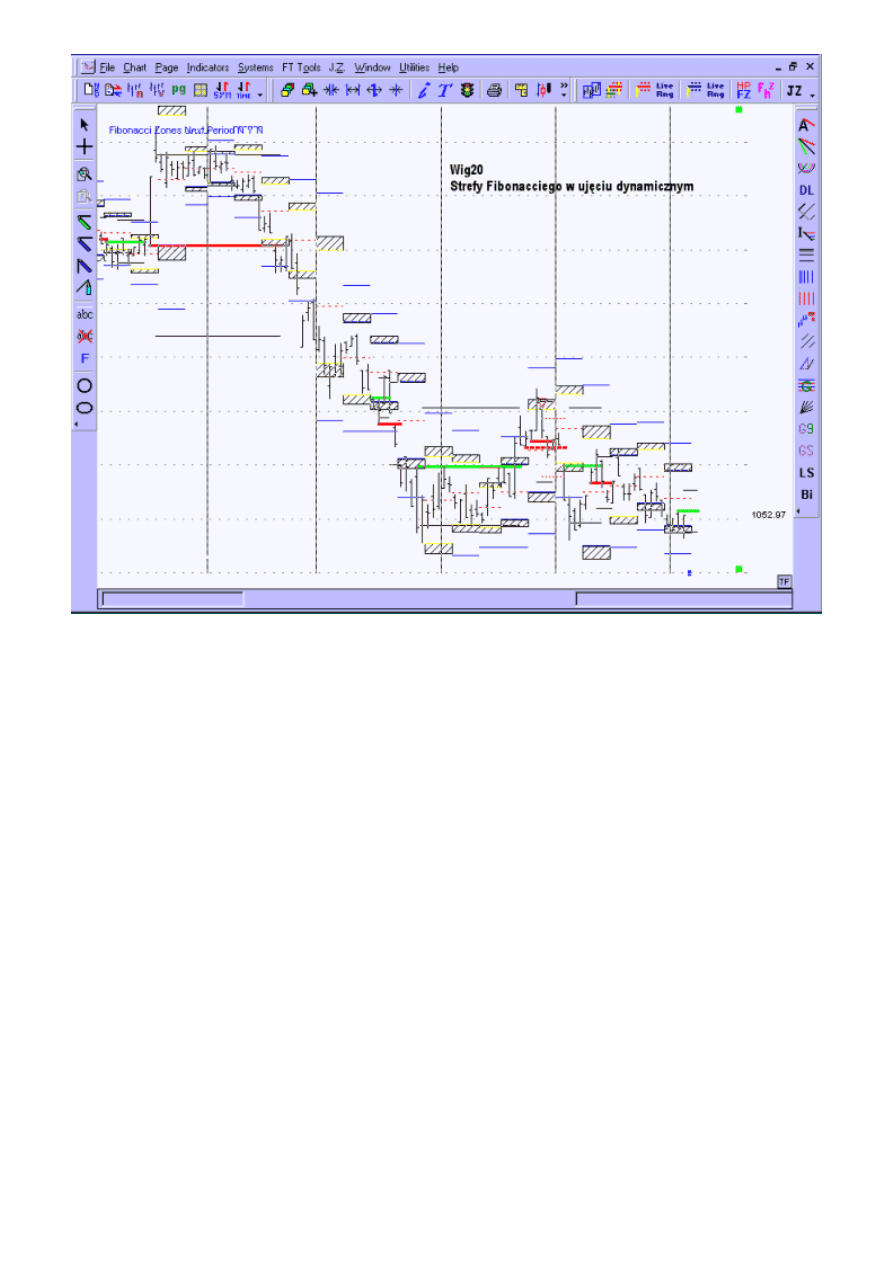
Źródło: opracowanie własne

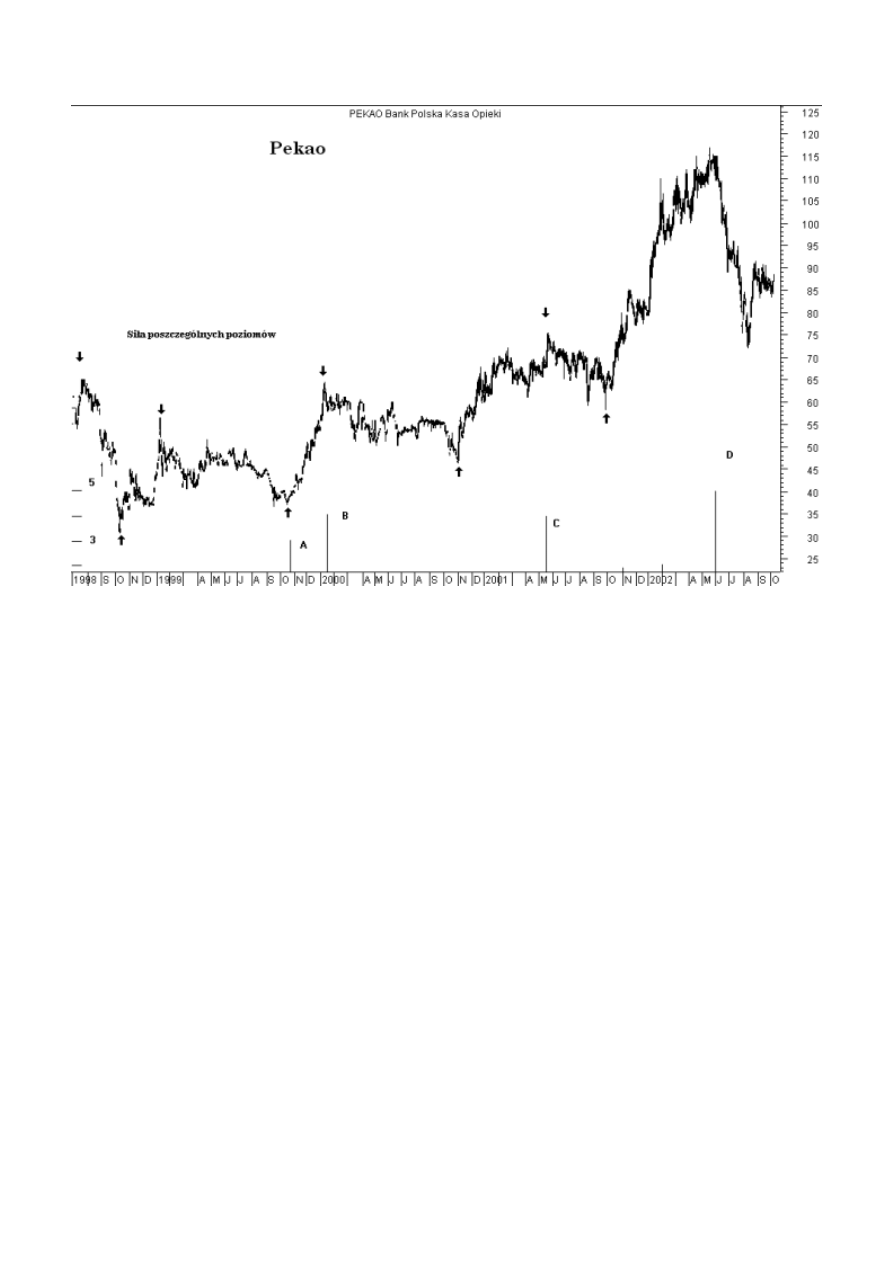
Rysunek 47. Dynamiczne ujęcie liczb Fibonacciego dla wyznaczenia punktów zwrotnych w czasie.

Źródło: opracowanie własne