OBWODY ELEKTRYCZNE PRĄDU STAŁEGO 

POJĘCIA PODSTAWOWE 

Obwód  elektryczny  stanowi  zamkniętą  drogę  służącą  do  przekazywania 

energii elektrycznej ze źródeł do odbiorników. Każdy obwód elektryczny składa 

się z elementów (części) niepodzielnych pod względem funkcjonalnym bez utraty 

ich charakterystycznych cech. 

Elementy  obwodu  można  podzielić  na  elementy  źródłowe-aktywne  oraz 

elementy odbiorcze-pasywne. 

Stosowane  w  obwodach prądu stałego  źródła napięcia posiadają  dwa  zaciski: 

jeden  o  wyższym  potencjale  (+)  i  drugi  o  niższym  (



)  służące  do  przyłączenia  do 

obwodu.  Różnicę  potencjałów  panującą  pomiędzy  zaciskami,  gdy  energia 

elektryczna  nie  jest  z  niego  pobierana  nosi  nazwę  siły  elektromotorycznej  lub 

napięcia źródłowego. 

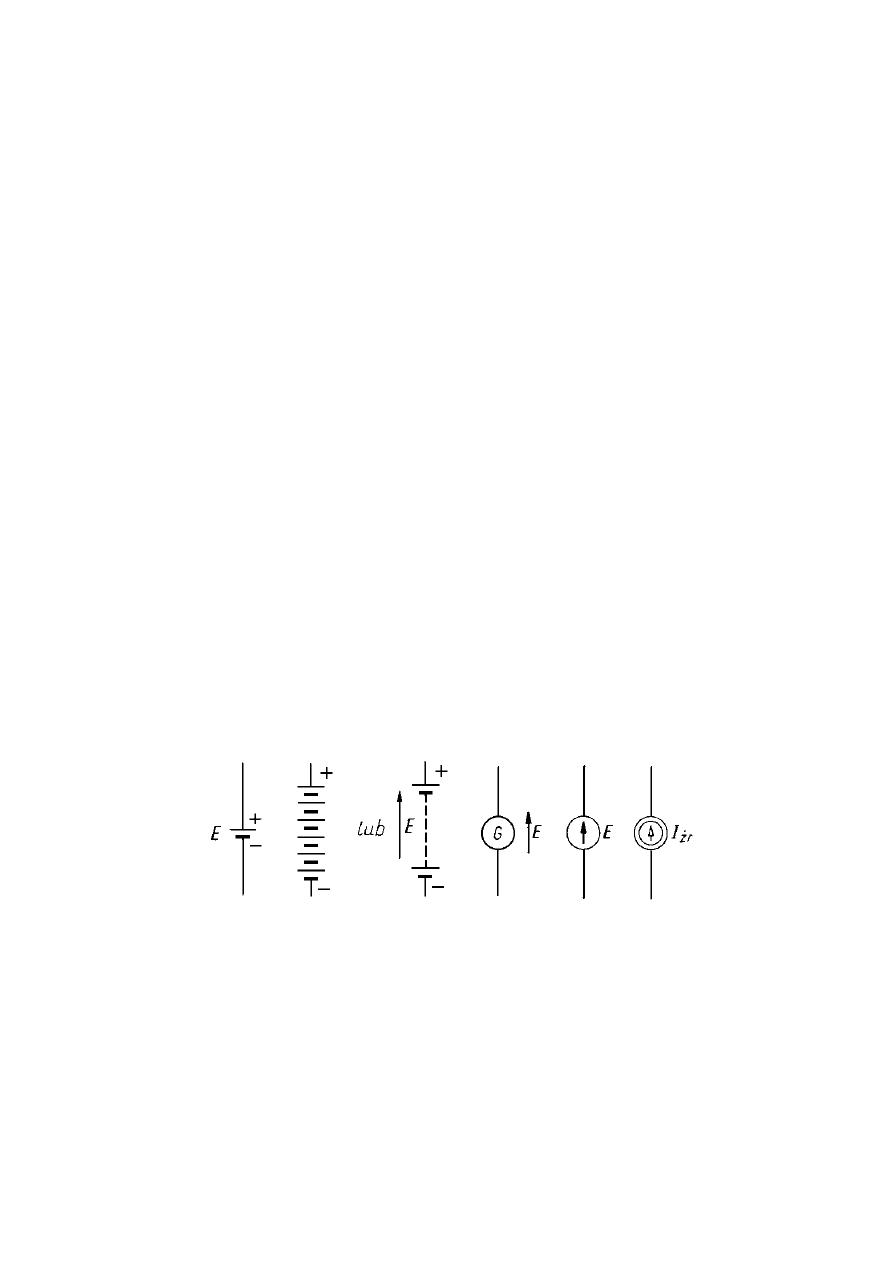
Biegunowość źródeł na schematach elektrycznych jest oznaczana w następujący 

sposób:  biegun  dodatni  znajduje  się  przy  zacisku  oznaczonym  grotem  strzałki  lub 

dłuższą kreską, biegun ujemny przy zacisku z krótszą kreską. 

Różne oznaczenia źródeł napięcia i prądu przedstawia poniższy rysunek: 

 

Symbole źródeł napięcia i prądu wykorzystywane w schematach układów 

elektrycznych 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

ELEMENTY OBWODÓW 

Do  elementów  odbiorczych  wchodzących  w  skład  obwodów  elektrycznych 

zaliczyć można trzy podstawowe grupy elementów: 

1.  Rezystory. Potocznie noszą nazwę oporników. Podczas przepływu prądu przez te 

elementy  następuje  zamiana  energii  elektrycznej  w  energię  cieplną,  która 

następnie jest rozpraszana w środowisku otaczającym rezystor. 

2.  Cewki  i  kondensatory.  Elementy  magazynujące  energię  w  określonej  postaci: 

cewka pod postacią pola magnetycznego, natomiast kondensator elektrycznego. 

3.  Przetworniki  energii  elektrycznej.  W  wyniku  ich  pracy  energia  elektryczna  jest 

przetwarzana  na  inne  postacie  energii:  mechaniczną  (silniki  elektryczne), 

chemiczną  (przepływ  prądu  wykorzystywany  w  procesie  elektrolizy),  świetlną 

(lampy wyładowcze itp.). 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

Obwody  prądu  elektrycznego  w  których  istnieje  tylko  jedna  droga  przepływu 

prądu,  a  tym  samym  tylko  jedna  wartość  natężenia  prądu  nazywa  się  obwodami 

nierozgałęzionymi.  

Innym rodzajem obwodu jest obwód rozgałęziony składający się co najmniej z 

trzech gałęzi i dwóch węzłów. Gałąź utworzona jest z jednego lub kilku połączonych 

ze  sobą  szeregowo  elementów  i  przez  wszystkie  z  nich  przepływa  prąd  o  jednej 

wartości.  

Węzły  stanowią  zakończenia  gałęzi,  do  których  przyłączane  są  pozostałe 

gałęzie. Zwykle obwody elektryczne są obwodami rozgałęzionymi, składającymi się 

z połączonych w określony sposób elementów źródłowych i odbiorników.  

Często  w  analizie  obwodów  stosowane  jest  pojęcie  oczka  obwodu 

elektrycznego. Pod pojęciem tym rozumie się zbiór gałęzi tworzących zamkniętą 

drogę dla przepływu prądu, odznaczającą się tym, że po usunięciu jednej z nich 

pozostałe nie tworzą takiej drogi. 

Obwód  nierozgałęziony  jest  obwodem  jednooczkowym,  natomiast  obwody 

rozgałęzione są obwodami  wielooczkowymi.  Wszystkie  obwody  elektryczne  mogą 

być  przedstawione  za  pomocą  schematów  ukazujących  wzajemne  połączenia 

pomiędzy nimi, tworzonych ze znormalizowanych symboli. 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

POJĘCIA LINIOWOŚCI I NIELINIOWOŚCI OBWODÓW 

Wszystkie  obwody  elektryczne  można  podzielić  na  dwie  zasadnicze  grupy: 

obwody liniowe i nieliniowe. 

Obwód  elektryczny,  którego  wszystkie  elementy  są  elementami  liniowymi 

nazywamy  obwodem  liniowym  (o  prostoliniowej  charakterystyce  napięciowo-

prądowej),  jeżeli  natomiast  co  najmniej  jeden  element  obwodu  jest  elementem  

nieliniowym  (analogicznie  -  nie  będącej  linią  prostą),  to  obwód  taki  jest  obwodem 

nieliniowym. 

Energia  elektryczna  jest  dostarczana  do  obwodu  przez  dowolnego  typu  źródło 

energii. W wyniku jego działania, jeżeli obwód jest obwodem zamkniętym (istnieje 

przynajmniej  jedna  zamknięta  droga  przepływu)  popłynie  prąd  elektryczny.  W 

odniesieniu  do  źródła  stosuje  się  pojęcie  wymuszenia,  z  kolei  przepływający  w 

przewodniku  pod  jego  wpływem  prąd  nosi  nazwę  odpowiedzi  -  źródło  wymusza 

przepływ prądu. 

W  analizie  obwodów  liniowych  znajduje  zastosowanie  zasada  superpozycji. 

Brzmi ona następująco:  

Odpowiedź  obwodu  elektrycznego  na  jednoczesne  działanie  kilku 

wymuszeń jest równa sumie odpowiedzi na każde wymuszenie z osobna. 

Definicję tą ilustrują poniższe zależności: 

 

y

1 

= f(x

1

); y

2

 = f(x

2

) 

 

 

(y

1 

+ y

2

) = f(x

1 

+ x

2

) 

 

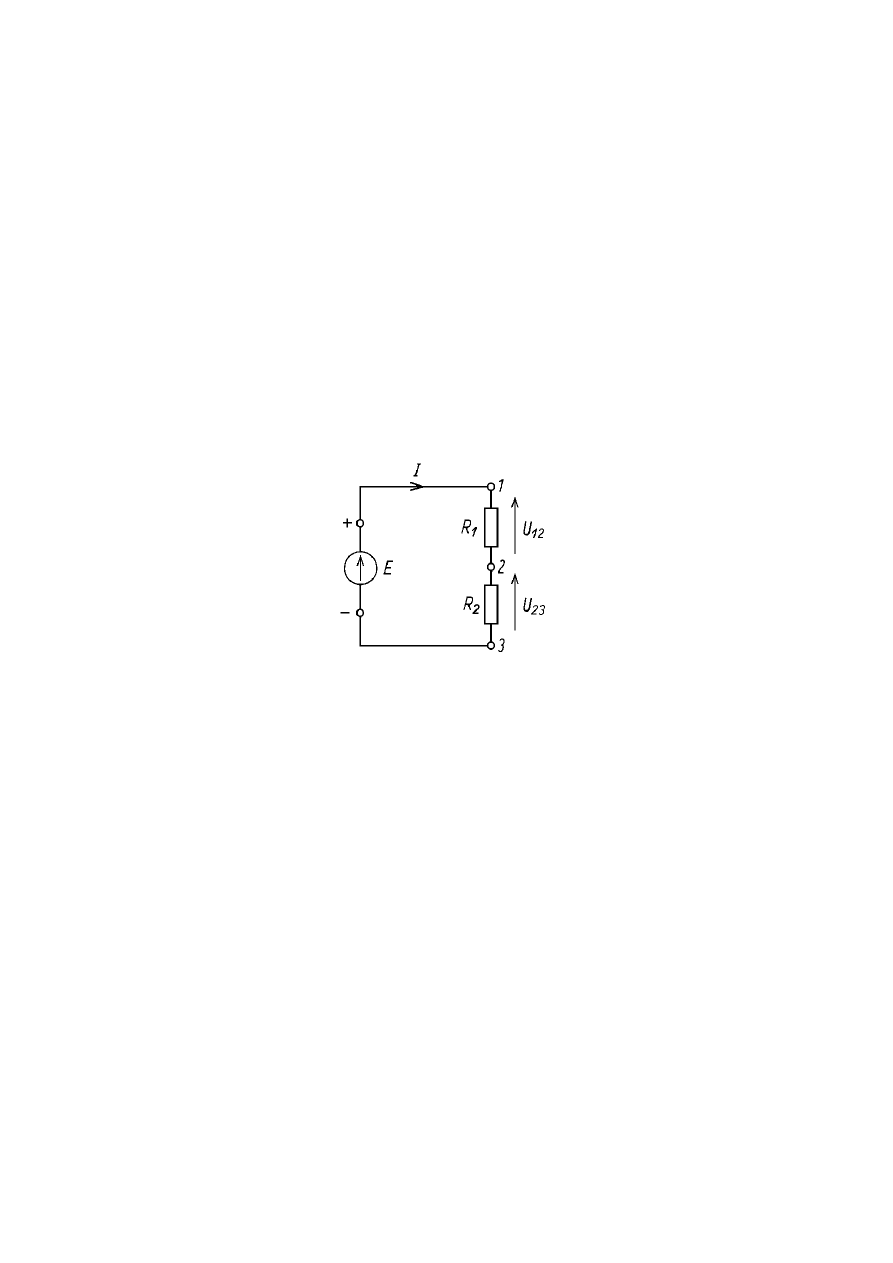
OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

ZNAKOWANIE NAPIĘĆ I PRĄDÓW 

Znakowanie wielkości występujących w obwodach elektrycznych stosuje się w 

celu  zwiększenia  przejrzystości  schematu.  Umownie  zostało  przyjęte  znakowanie 

kierunku przepływu prądu zgodnie z kierunkiem ruchu ładunków dodatnich, czyli od 

zacisku o wyższym potencjale (bieguna dodatniego) do zacisku o potencjale niższym 

(bieguna  ujemnego).  W  rzeczywistości  prąd  elektryczny  jest  ruchem  ładunków 

ujemnych,  więc  jego  przepływ  następuje  w  kierunku  przeciwnym.  Strzałka 

oznaczająca  kierunek  przepływu  prądu  rysowana  jest  jako  nie  zaczerniona,  w 

przewodzie lub obok niego. 

 

Przykład znakowania wielkości występujących w układzie elektrycznym 

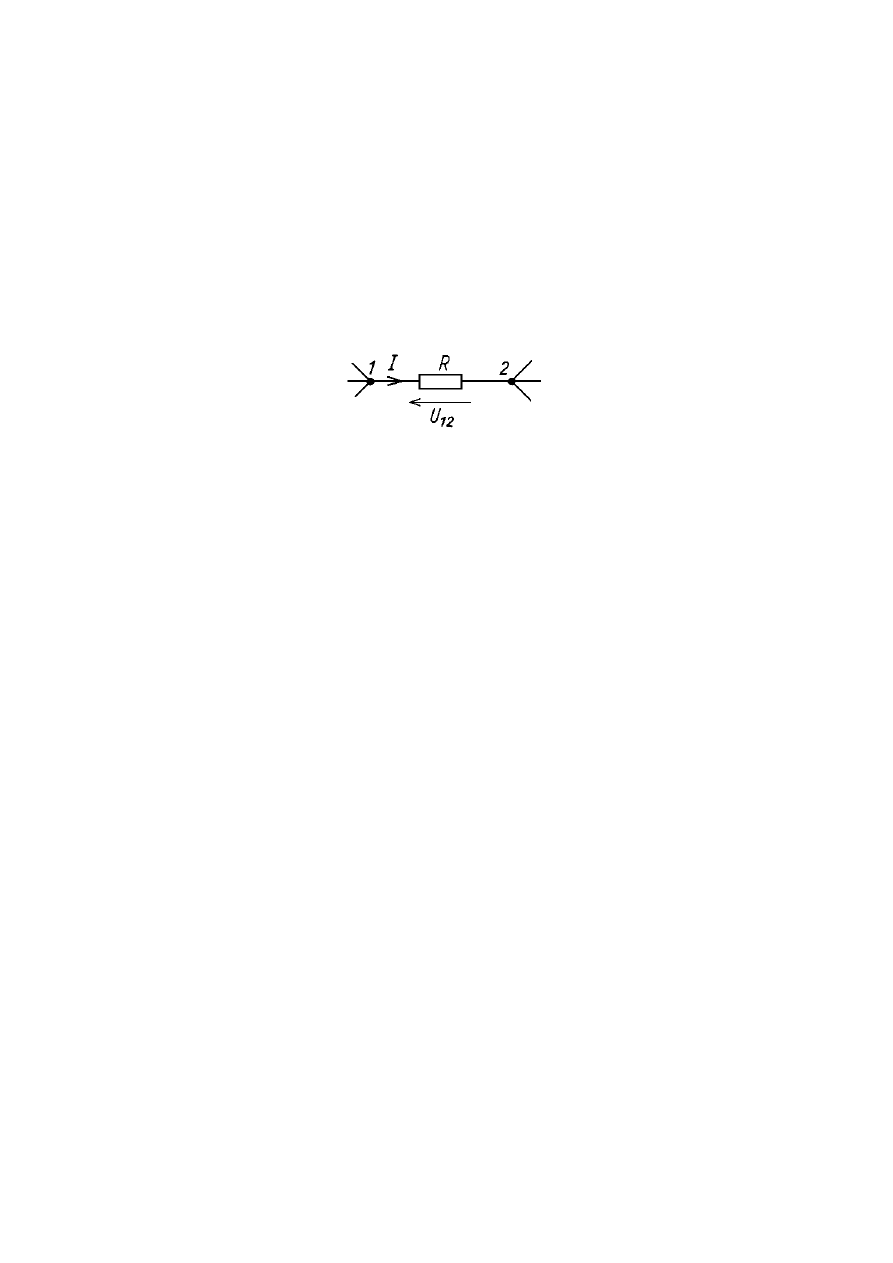
OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

PRAWA DOTYCZĄCE OBWODÓW ELEKTRYCZNYCH 

W celu umożliwienia dokonywania analizy obwodów elektrycznych konieczne 

stało  się  określenie  praw  rządzących  takimi  obwodami.  Jednym  z  podstawowych 

praw  obwodów  jest  wspomniane  wcześniej  prawo  Ohma.  Dla  wyodrębnionej  z 

większego  obwodu  gałęzi  zawierającej  element  pasywny,  przedstawionej  poniżej 

wygląda ono następująco: 

 

Ilustracja prawa Ohma dla wyodrębnionej z układu gałęzi 

 

U

12 

= RI 

 

gdzie: 

U

12

 = 



1

 



 



2

 - różnica potencjałów pomiędzy węzłami gałęzi. 

Niejednokrotnie  zamiast  wartości  rezystancji  danego  elementu  stosuje  się 

wartość będącą jej odwrotnością - konduktancję G: 

 

I = GU

12

 

 

Prawo Ohma podane powyżej  można rozwinąć, jeżeli gałąź nie jest wyłącznie 

gałęzią pasywną, lecz występują w niej elementy aktywne, co w połączeniu z innymi 

prawami dotyczącymi obwodów elektrycznych pozwala dokonywać ich analizy. 

Podstawowymi  obok  prawa  Ohma  są  dwa  prawa  Kirchhoffa  wynikające  z 

zasady zachowania energii. Pierwsze prawo Kirchhoffa dotyczy bilansu prądów w 

rozpatrywanym węźle obwodu. Brzmi ono w następujący sposób:  

Dla  każdego  węzła  obwodu  elektrycznego  suma  algebraiczna  prądów 

wynosi zero. 

 

0

I









 

 

gdzie: 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 



  przyjmuje  wartości  (1,2,...)  odpowiadające  liczbie  gałęzi  zbiegających  się  w 

węźle. 

Prądy do sumy podstawiamy z różnymi znakami, w zależności od zwrotu prądu 

względem  danego  węzła  -  prądy  dopływające  ze  znakiem  plus,  zaś  odpływające 

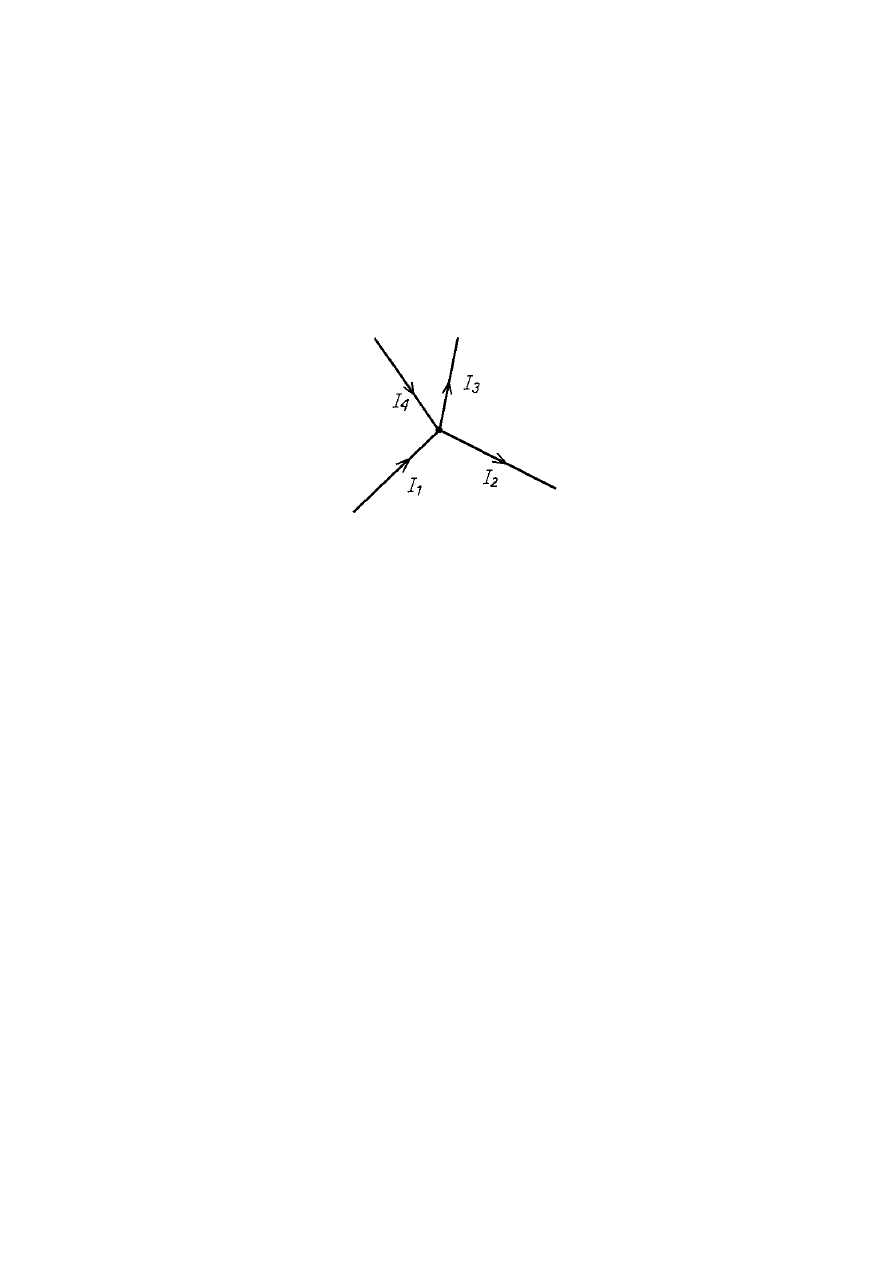
minus.  Przykładowy  zapis  dla  węzła  pokazanego  na  poniższym  rysunku  wygląda 

następująco: 

 

Węzeł obwodu ilustrujący pierwsze prawo Kirchhoffa 

 

0

I

I

I

I

3

2

4

1









 

 

Po  pogrupowaniu  prądów  dopływających  po  jednej  stronie  równania, 

odpływających drugiej otrzymujemy drugą postać prawa Kirchhoffa. 

 

3

2

4

1

I

I

I

I







 

 

Na jego podstawie można prawo sformułować w następujący sposób:  

Dla każdego węzła obwodu elektrycznego suma prądów dopływających do 

węzła równa się sumie prądów odpływających od niego. 

Drugie  prawo  Kirchhoffa  dotyczy  bilansu  napięć  w  oczku  obwodu 

elektrycznego prądu stałego.  

W  dowolnym  oczku  obwodu  elektrycznego  prądu  stałego  suma 

algebraiczna napięć źródłowych oraz suma algebraiczna napięć odbiornikowych 

występujących na rezystancjach równa się zero. 

 

0

I

R

E



















 

 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

gdzie: 



 przyjmuje wartość (1, 2,...) równą liczbie źródeł należących do danego oczka, 



  wartość  (1,  2,...)  równą  liczbie  elementów  rezystancyjnych  wchodzących  w 

skład oczka.  

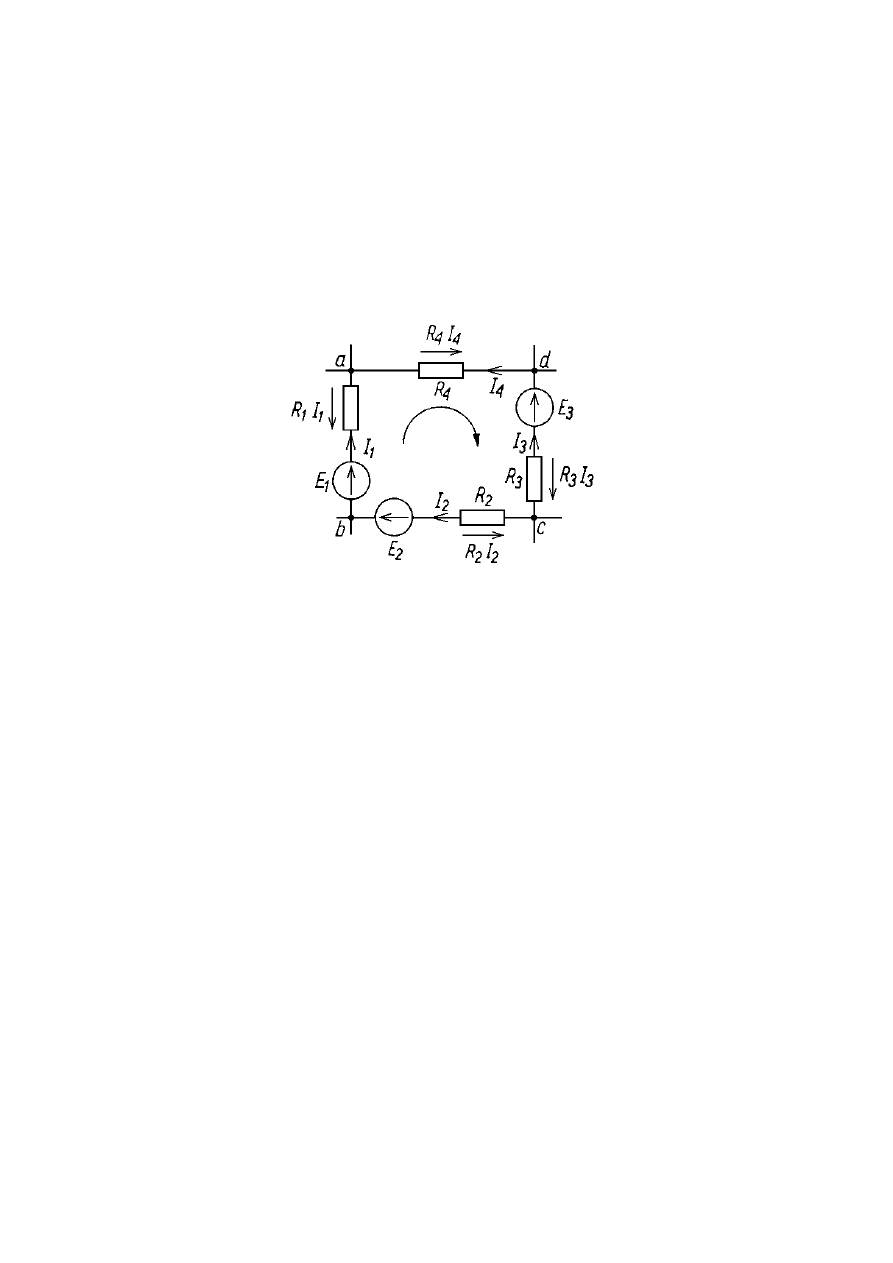
Zilustrować można prawo to korzystając z przykładowego oczka obwodu: 

 

Oczko wyodrębnione z układu (ilustracja drugiego prawa Kirchhoffa) 

Dla oczka tego zapis drugiego prawa Kirchhoffa wygląda następująco: 

 

0

E

I

R

I

R

E

I

R

I

R

E

2

2

2

3

3

3

4

4

1

1

1















 

 

Po  dokonaniu  analogicznych  przekształceń  jak  w  poprzednim  przypadku,  tzn. 

pogrupowaniu  napięć  określonego  rodzaju  stronami  otrzymujemy  alternatywną 

postać drugiego prawa Kirchhoffa: 

 

2

2

3

3

4

4

1

1

2

3

1

I

R

I

R

I

R

I

R

E

E

E













 

 

którą możemy sformułować w następujący sposób:  

Dla  dowolnego  oczka  obwodu  elektrycznego  prądu  stałego  suma 

algebraiczna  napięć  źródłowych  jest  równa  sumie  algebraicznej  napięć 

odbiornikowych. 

Ze  stwierdzenia  tego  wynika  bezpośrednio,  że  w  oczku  obwodu  nie 

zawierającym  źródeł  napięcia  suma  algebraiczna  napięć  odbiornikowych  wynosi 

zero. 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

ŹRÓDŁA ENERGII ELEKTRYCZNEJ 

Wszystkie  stosowane  obecnie  źródła  energii  elektrycznej,  bez  względu  na 

zasadę  działania  odznaczają  się  pewną  rezystancją  wewnętrzną  R

w

.  Najczęściej 

stosowanym  schematem  zastępczym  źródła  energii  elektrycznej  jest  tzw.  schemat 

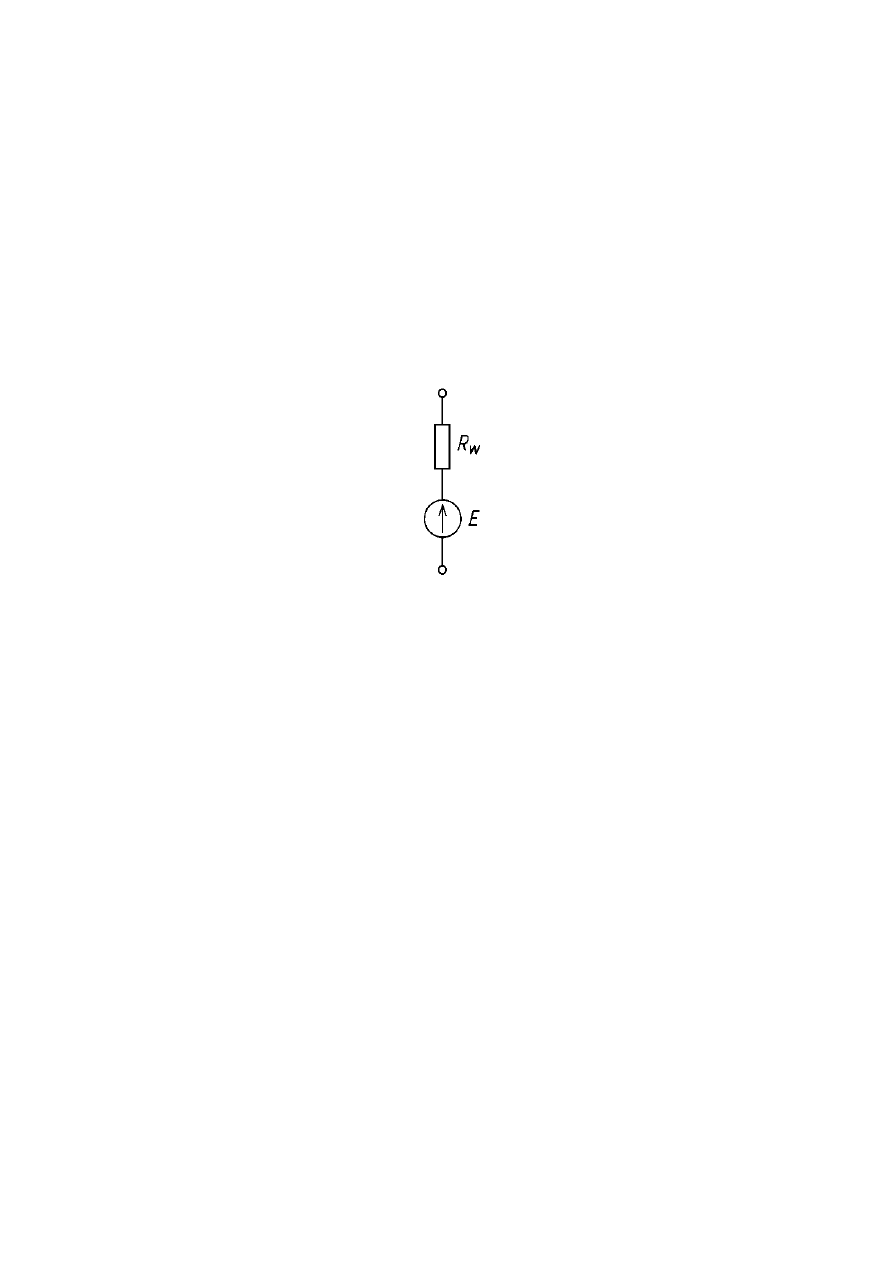
szeregowy,  nazywany  także  źródłem  napięcia. Jak  widać  na  załączonym  rysunku  w 

skład  rzeczywistego  źródła  napięcia  wchodzi  idealne  źródło  napięcia  E  oraz 

rezystancja wewnętrzna R

w

, przy czym połączone są one szeregowo. 

 

Schemat rzeczywistego źródła napięcia 

Źródło  rzeczywiste  staje  się  źródłem  idealnym,  wówczas,  gdy  rezystancja 

wewnętrzna wynosi zero. 

Do zacisków rzeczywistego źródła napięcia można dołączyć rezystor nastawny 

o bardzo dużej rezystancji. Rezystancja ta może być zmieniana w zakresie od zera do 

pełnej  wartości  R  a  także  może  być  rozłączana  dając  przerwę  w  obwodzie.  W 

zależności  od  wartości  rezystancji  odbiornika  źródło  może  pracować  w  różnych 

stanach. 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

Schemat układu z dołączonym odbiornikiem (rezystor nastawny) – układ 

wyjściowy 

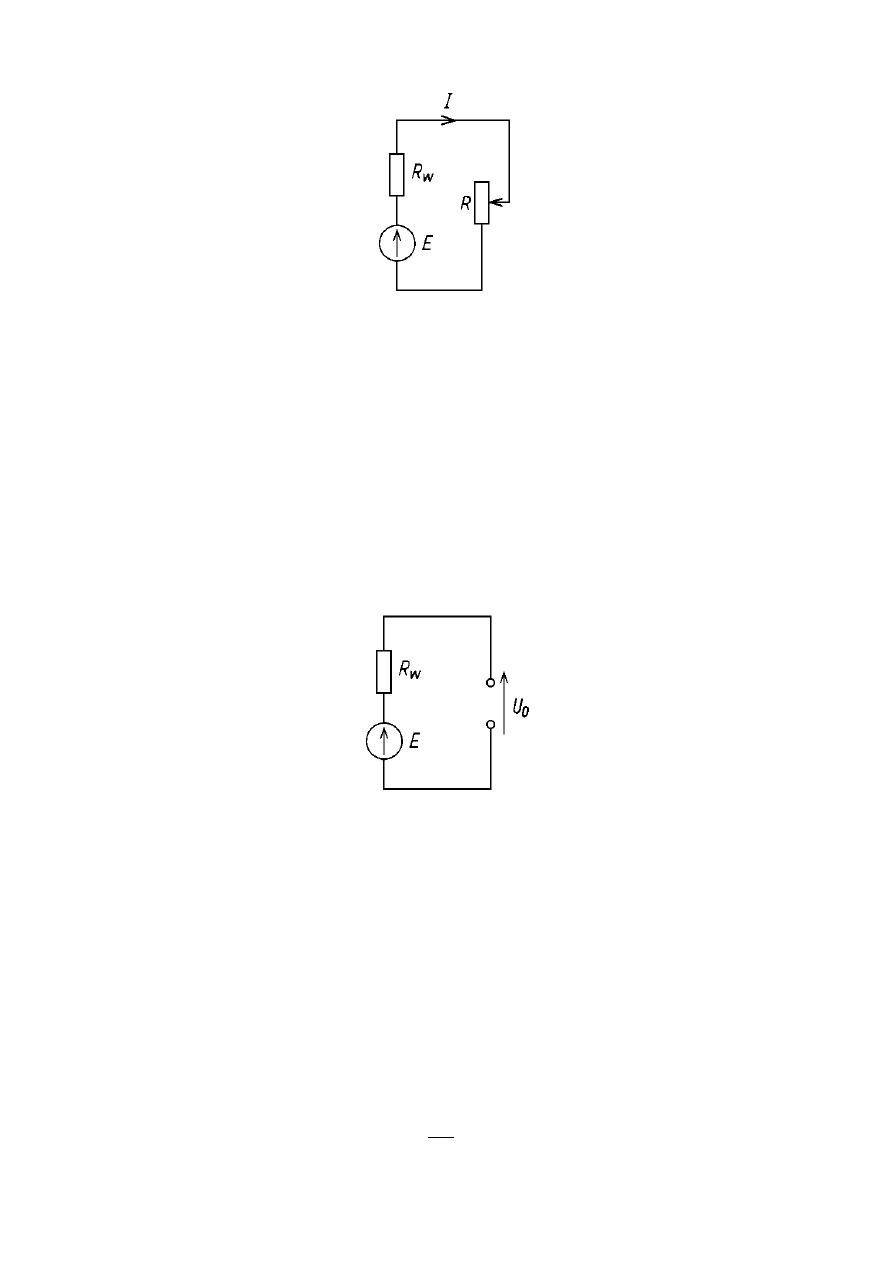
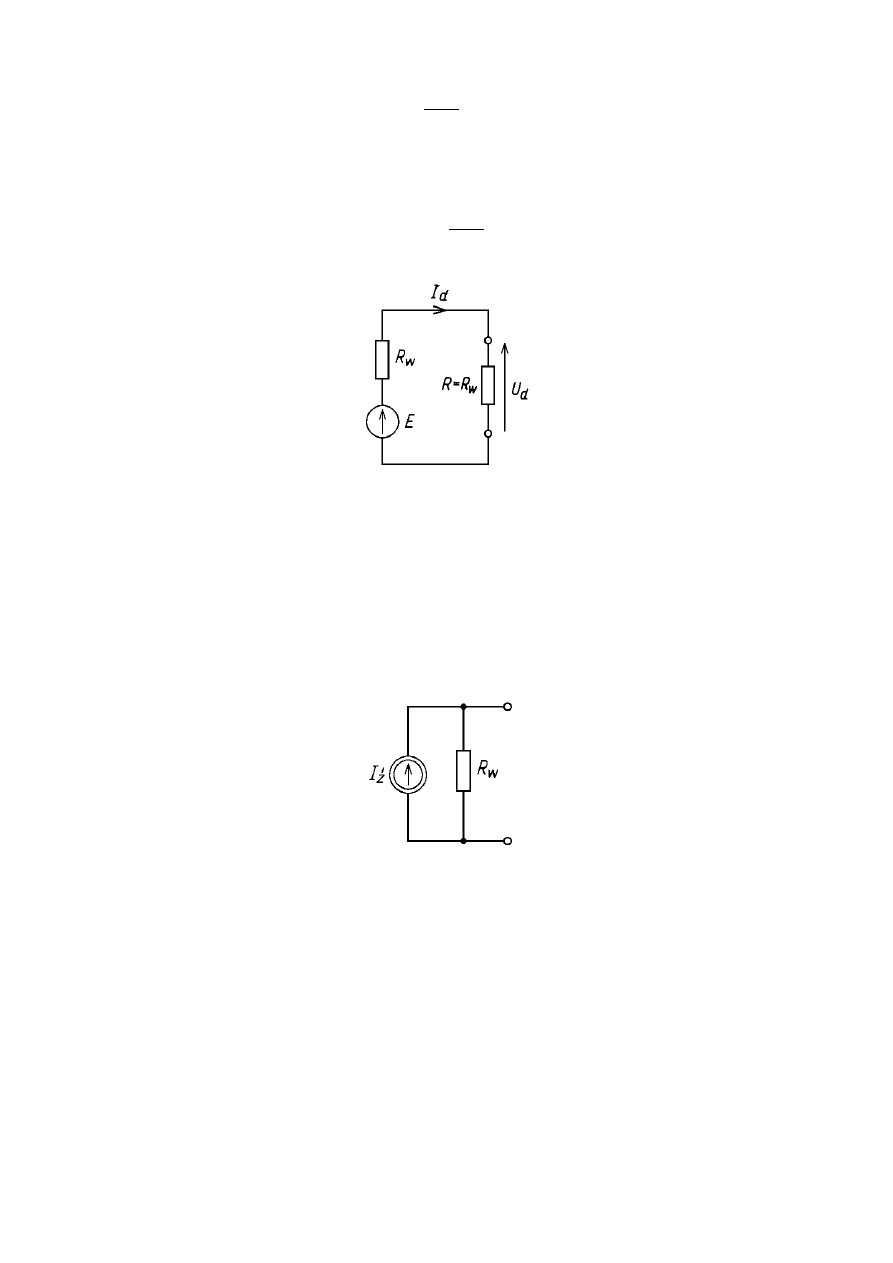
Stanem jałowym nazywa się stan pracy źródła przy rezystancji R równej 

nieskończoności, której odpowiada przerwa w obwodzie.  

W  sytuacji  tej  prąd  w  obwodzie  nie  płynie,  natomiast  napięcie  na  zaciskach 

źródła  jest  równe  napięciu  źródłowemu  E  i  wynosi  U

0

.  Sytuacja  taka  jest 

przedstawiona na poniższym rysunku. 

 

Rzeczywiste źródło napięcia w stanie jałowym 

Jeżeli rezystancja zostanie zmniejszona do wartości zerowej, mamy wtedy do 

czynienia z drugim ze stanów pracy źródła napięcia.  

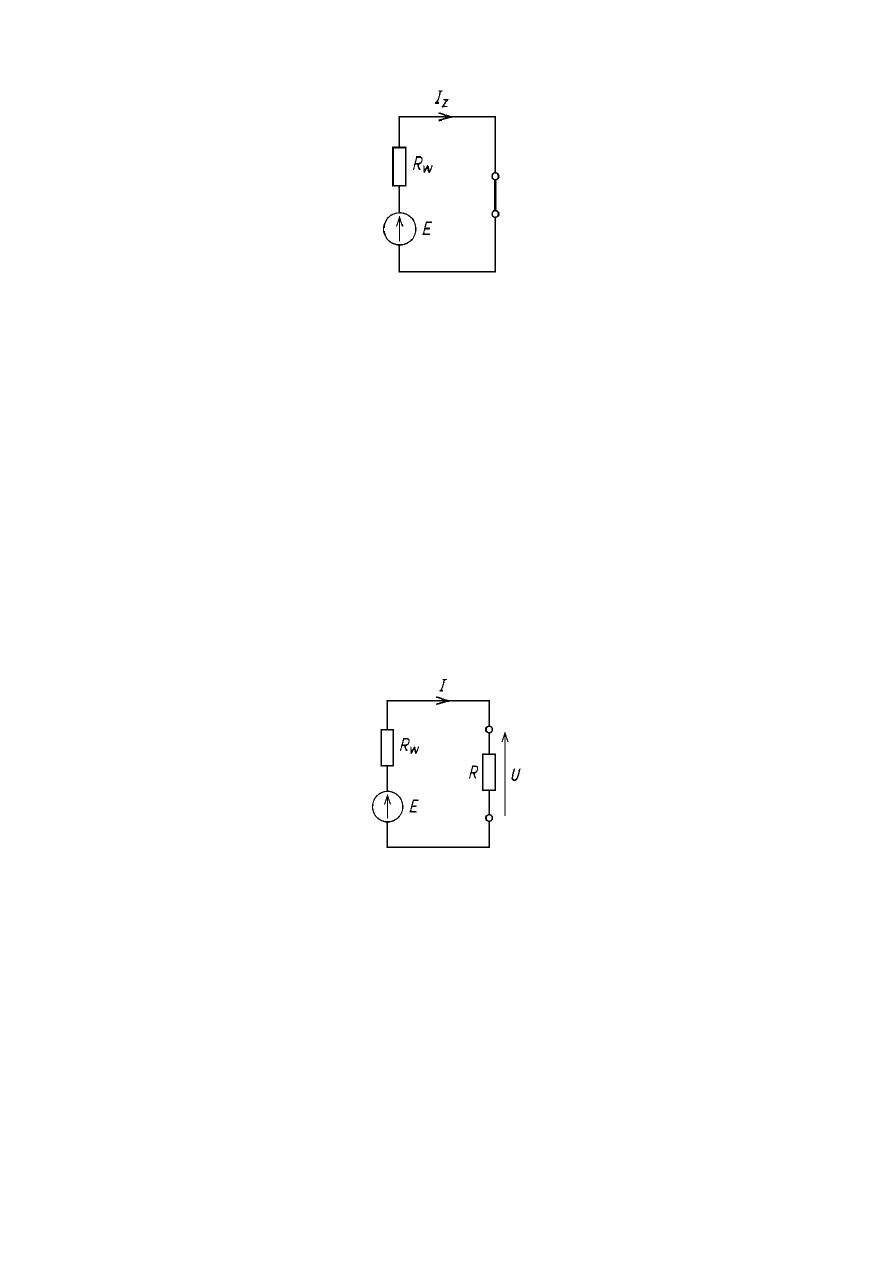
Stan  pracy  źródła  przy  rezystancji  R  równej  zeru,  której  odpowiada 

zwarcie odbiornika nazywa się stanem zwarcia źródła.  

W sytuacji takiej w obwodzie płynie prąd, którego wartość można obliczyć ze 

wzoru: 

 

w

z

R

E

I



 

 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

Stan zwarcia rzeczywistego źródła napięcia 

Z kolei, jeżeli rezystancja posiada wartość większą od zero, a  mniejszą od R 

pracuje w warunkach normalnych.  

Stan pracy źródła napięcia przy dowolnej wartości rezystancji R nazywa 

się stanem obciążenia.  

Podczas  pracy  w  tym  stanie  w  obwodzie  przepływa  prąd,  którego  wartość 

zależy  od  wartości rezystancji obciążenia i  rezystancji  wewnętrznej  źródła. Wartość 

prądu oblicza się na podstawie drugiego prawa Kirchhoffa: 

Dla oczka przedstawionego na rysunku: 

 

Rzeczywiste źródło napięcia obciążone rezystancją R 

Wartość prądu obliczamy następująco: 

 

0

U

I

R

E

w







 

 

 

I

R

E

U

w





 

 

Zgodnie z prawem Ohma, napięcie na zaciskach odbiornika: 

 

I

R

U

w



 

 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

Po  przekształceniach  wzorów  dochodzimy  do  wzoru  na  wartość  prądu 

płynącego w obwodzie: 

 

w

R

R

E

I





 

 

Jak z tego wynika, napięcie na zaciskach jest równe napięciu źródłowemu tylko 

wtedy, gdy prąd I wynosi zero, a więc w stanie jałowym.  

Jeżeli  podczas  współpracy  odbiornika  ze  źródłem  jest  pobierana 

największa moc, wtedy odbiornik pracuje w stanie dopasowania do źródła.  

Wartość  rezystancji  dla  której  występuje  dopasowanie  odbiornika  do  źródła 

może  być  wyznaczona  z  prawa  Joule’a



Lenza  na  podstawie  obliczonej  pochodnej. 

Moc pobierana przez odbiornik: 

 

2

RI

P



 

 

W miejsce prądu wpisujemy zależność 15): 

 





2

w

2

R

R

RE

P





 

 

Pochodna mocy względem rezystancji odbiornika: 

 

3

w

2

w

2

4

w

2

w

2

w

2

)

R

R

(

RE

2

)

R

R

(

E

)

R

R

(

RE

)

R

R

(

2

)

R

R

(

E

dR

dP



















 

 

Pochodna  jest  równa  zero,  gdy  wyrażenie  występujące  w  liczniku  jest  równe 

zero: 

 

0

RE

2

)

R

R

(

E

2

w

2







 

 

czyli dla 

w

R

R



 

Reasumując – jeżeli rezystancja przyłączona do zacisków źródła jest równa jego 

rezystancji  wewnętrznej,  wówczas  odbiornik  pobiera  z  niego  maksymalną  moc. 

Wartość prądu przepływającego w tym momencie w obwodzie można wyznaczyć z 

poniższego wzoru: 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

w

d

R

2

E

I



 

 

Z kolei pobierana moc wynosi: 

 

w

2

2
d

w

R

4

E

I

R

P





 

 

 

Rzeczywiste źródło napięcia pracujące w stanie dopasowania odbiornika 

Obok  wymienionego  schematu  szeregowego  stosuje  się  także  schemat 

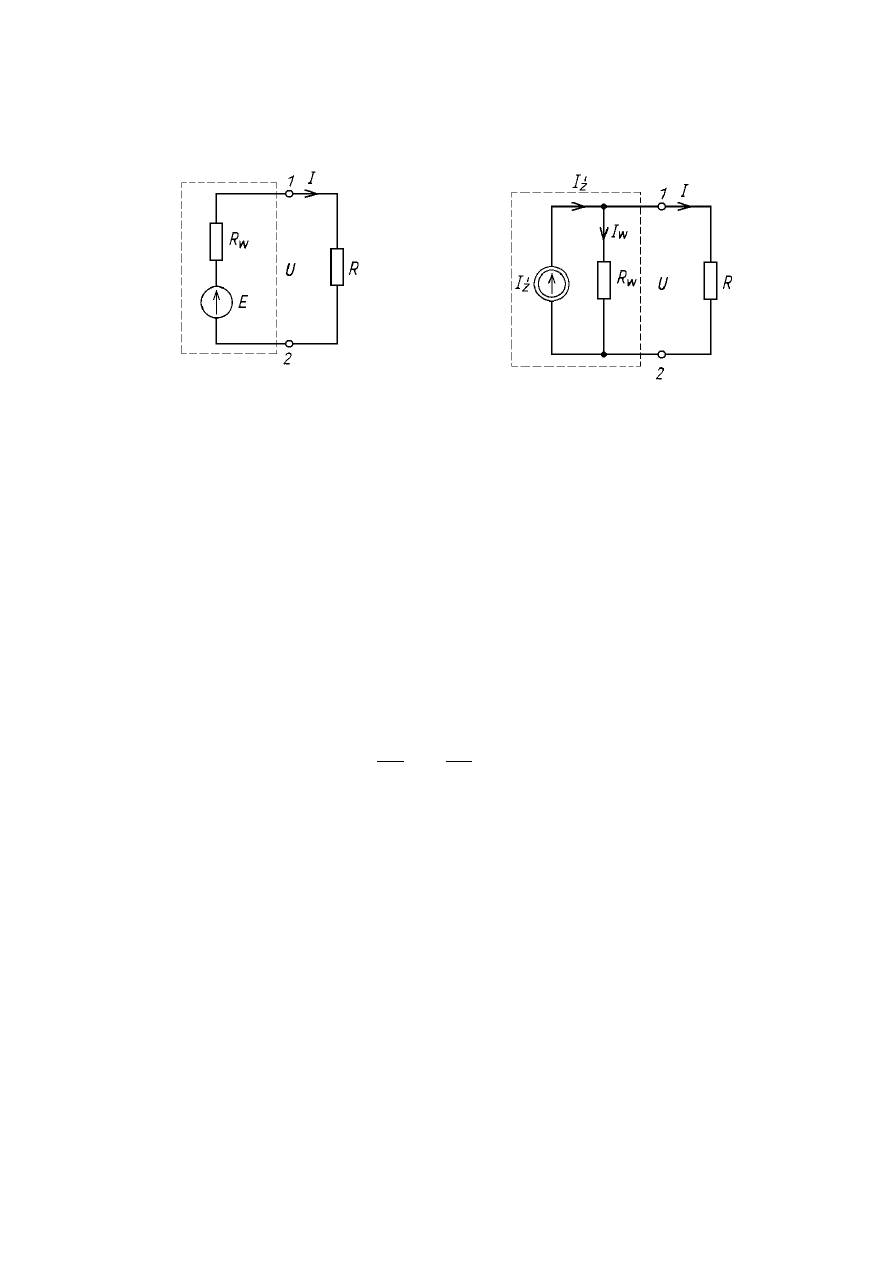
równoległy rzeczywistego źródła energii elektrycznej, który nosi nazwę źródła prądu. 

W układzie tym połączono idealne źródło prądu z włączoną równolegle rezystancją 

wewnętrzną. Schemat takiego połączenia przedstawia rysunek: 

 

Schemat rzeczywistego źródła prądu 

Wielkością charakteryzującą źródło prądu jest prąd źródłowy oznaczany jako I

ź

. 

Analogicznie  jak  źródło  napięcia  może  ono  pracować  w  następujących  stanach: 

stanie jałowym, stanie zwarcia, stanie obciążenia oraz stanie dopasowania. 

W praktyce obliczeniowej stosuje się zamianę rzeczywistego źródła napięcia na 

źródło prądu, przy czym w przypadku tym prąd przepływający przez odbiornik oraz 

napięcie  na  jego  zaciskach  pozostają  stałe.  Rozpatrzymy  następujący  przykład: 

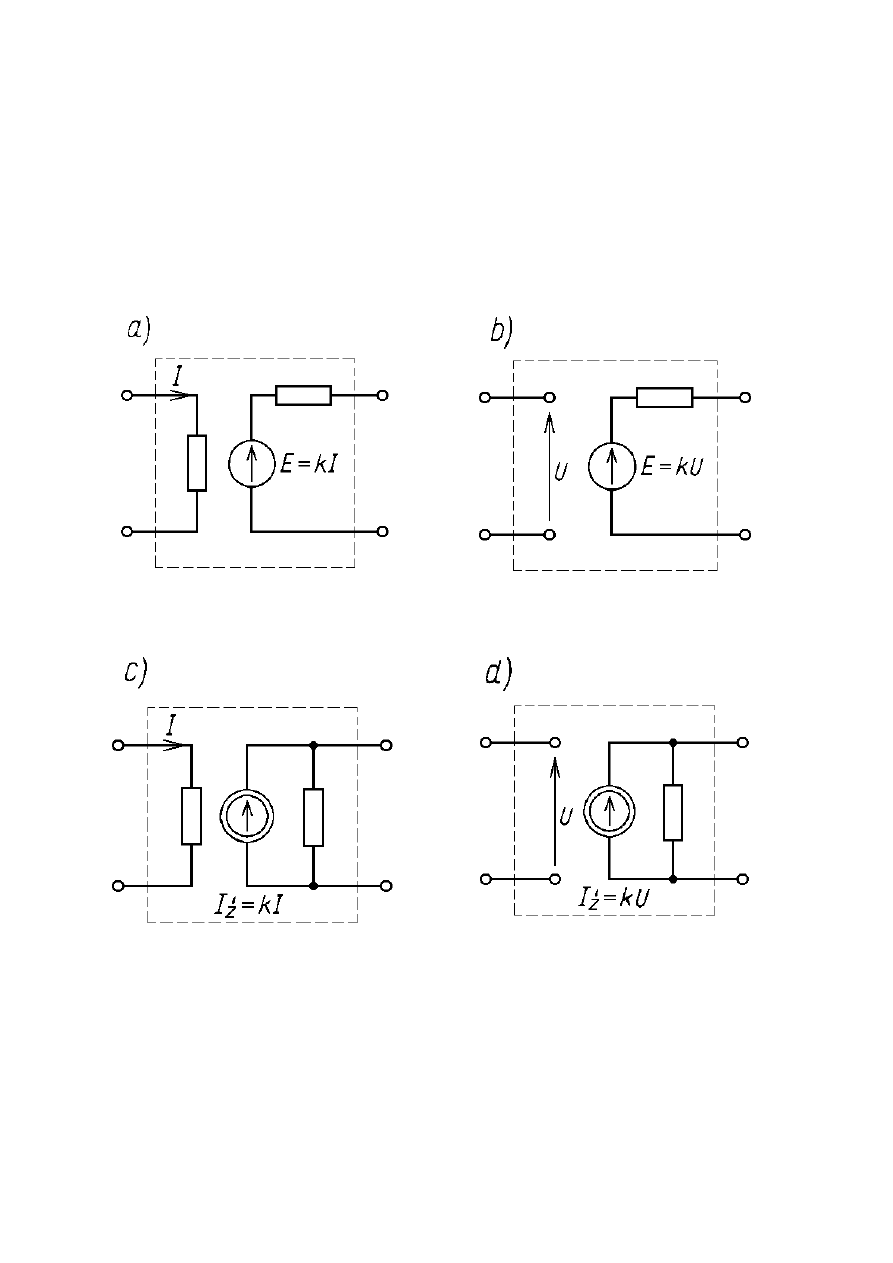
OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

zamiana  źródła  napięcia  na  źródło  prądu.  Schematy  obu  rodzajów  źródeł 

przedstawione są na schemacie: 

a)  

 

 b)   

 

Zastępowanie rzeczywistego źródła napięcia (rysunek a) źródłem prądu 

(rysunek b) 

Zamiana  źródeł  oparta  jest  na  obliczeniach  wynikających  z  prawa  Kirchhoffa. 

Dla układu zawierającego źródło napięcia bilans napięć wygląda następująco: 

 

U

I

R

E

w





E = R

w

I + U 

 

Zakładając, że mamy do czynienia ze źródłem rzeczywistym i jego rezystancja 

wewnętrzna jest różna od zera dokonujemy dzielenia obustronnego przez R

w

. W jego 

wyniku otrzymujemy: 

 

w

w

R

U

I

R

E





 

 

czyli: 

 

w

z

I

I

I





 

 

gdzie: 

I

w 

– prąd przepływający przez rezystancję wewnętrzną źródła prądu, natomiast I 

prąd przepływający przez odbiornik.  

Prąd  źródłowy  I

ź

  wyznacza  się  jako  prąd  zwarcia  źródła  napięcia.  Poprzez 

połączenie  równoległe  idealnego  źródła  prądu  z  rezystancją  R

w

  uzyskujemy  układ 

równoważny dla źródła napięcia. 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

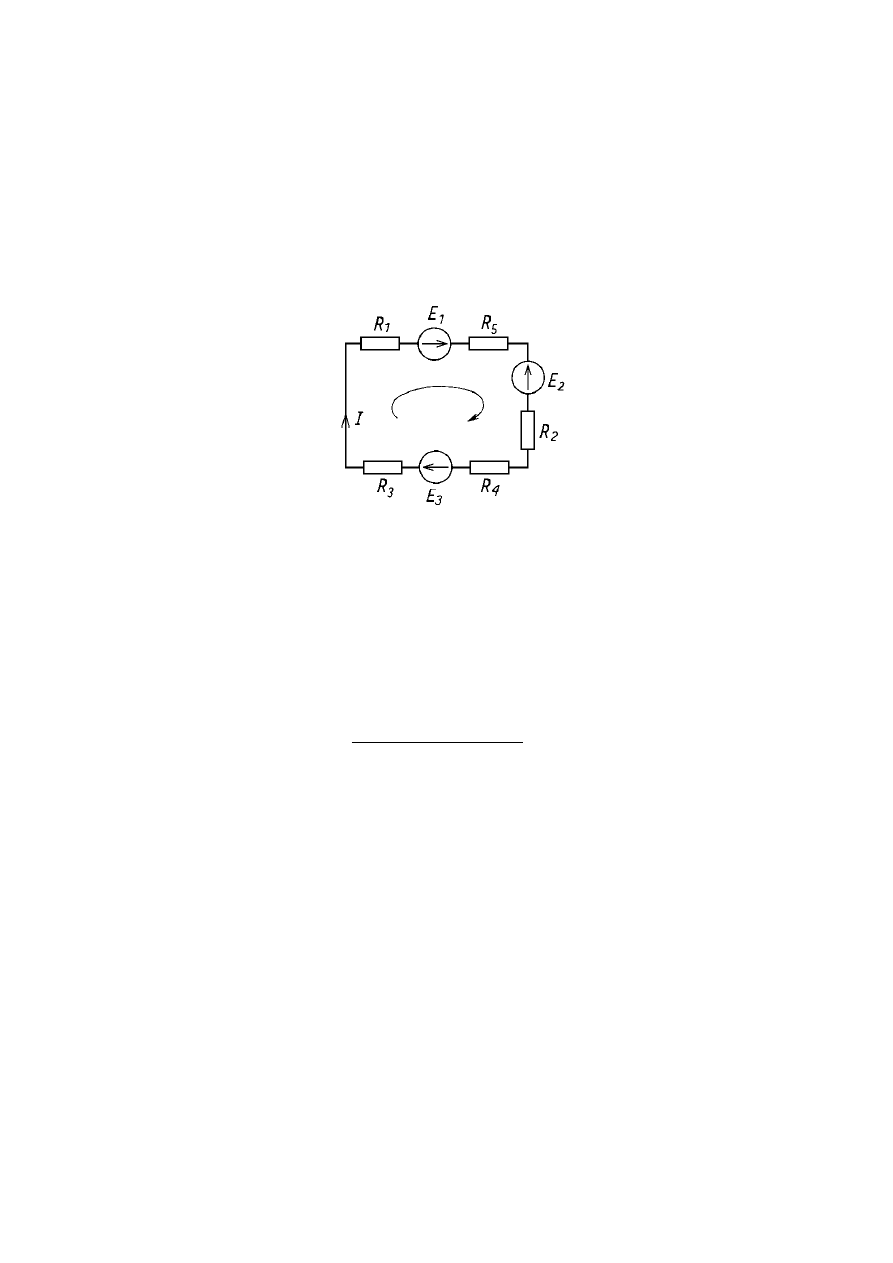
Źródła  napięcia  i  prądu  należą  do  grupy  źródeł  niesterowanych,  obok  których 

stosuje  się  również  źródła  sterowane,  dla  których  wartość  prądu  lub  napięcia 

źródłowego ulegają zmianie w zależności od napięć i prądów występujących w innej 

części  obwodu.  Rozróżnia  się  kilka  rodzajów  źródeł  sterowanych:  źródła  napięcia 

sterowane  napięciowo  lub  prądowo  i  źródła  prądu  sterowane  napięciowo  lub 

prądowo. 

 

Źródło napięcia sterowane prądowo  

 

Źródło napięcia sterowane napięciowo  

 

Źródło prądu sterowane prądowo 

 

Źródło prądu sterowane napięciowo 

Schematy źródeł sterowanych  

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

OBWODY NIEROZGAŁĘZIONE 

Przez wszystkie elementy obwodu połączone w sposób szeregowy przepływa 

prąd o takiej samej wartości. Jako przykład posłużyć może jednooczkowym obwód 

elektryczny  (nierozgałęziony).  Przykład  takiego  obwodu  przedstawia  poniższy 

rysunek: 

 

Schemat obwodu nierozgałęzionego (jednooczkowego) 

Wynikające z drugiego prawa Kirchhoffa równanie napięć wygląda następująco: 

 

E

1 

– R

5

I – E

2

 – R

2

I – R

4

I + E

3

 – R

3

I – R

1

I = 0 

 

Obliczona z tego równania wartość prądu w obwodzie wynosi: 

 

5

4

3

2

1

3

2

1

R

R

R

R

R

E

E

E

I















 

 

Prąd przepływający  w układzie zależy więc zarówno od wartości wypadkowej 

działania źródeł napięcia, jak i wartości rezystancji włączonej w obwód. Obwód taki 

można  przekształcić  do  odpowiadającej  mu  postaci  równoważnej,  poprzez 

pogrupowanie  elementów  i  zastąpienie  ich  elementami  zastępczymi.  Spadki  napięć 

na  poszczególnych  rezystancjach  obwodu  można  wyznaczyć  korzystając  z  prawa 

Ohma,  natomiast  napięcie  na  zaciskach  układu  szeregowo  połączonych  rezystorów 

jest równe sumie napięć na poszczególnych elementach. 

 

U

1

 = R

1

I;      U

2

 = R

2

I       U

3

 = R

3

I 

 

 

U = U

1

 + U

2

 + U

3

 = (R

1

 + R

2

 + R

3

)I 

 

skąd: 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

I

U

= R

1

 + R

2

 + R

3

 

 

Ponieważ: 

I

U

 = R , więc: 

 

R = R

1

 + R

2

 + R

3

 

 

Rezystancja  zastępcza  dla  szeregowo  połączonych  rezystorów  jest  równa 

sumie rezystancji poszczególnych z nich. 

Analogiczna  sytuacja  występuje  w  przypadku  połączonych  źródeł  napięcia. 

Wypadkowa wartość napięcia źródłowego wyniesie dla rozważanego przypadku: 

 

E = E

1 

– E

2

 + E

3

 

 

W  połączeniu  szeregowym  dowolnej  liczby  źródeł  napięcia,  napięcie 

źródłowe  zastępczego  źródła  napięcia  jest  równe  algebraicznej  sumie  napięć 

źródłowych poszczególnych źródeł. 

Osobno  możliwe  jest  rozpatrywanie  bilansu  mocy  danego obwodu.  Aby  tego 

dokonać  wystarczy  pomnożyć  obie  strony  równania  bilansu  napięć  wynikającego  z 

drugiego prawa Kirchhoffa przez wartość prądu I przepływającego w obwodzie. W 

wyniku  tego  uzyskujemy  równanie  będące  zapisem  bilansu  mocy  dla  danego 

obwodu.  

Suma  algebraiczna  mocy  oddawanych  (lub  pobieranych)  przez  źródła 

energii  elektrycznej  jest  równa  mocy  pobieranych  przez  rezystory  stanowiące 

odbiorniki. 

Bilans mocy  może być przeprowadzany także dla obwodów równoważnych, w 

analogiczny sposób jak w tym przypadku. 

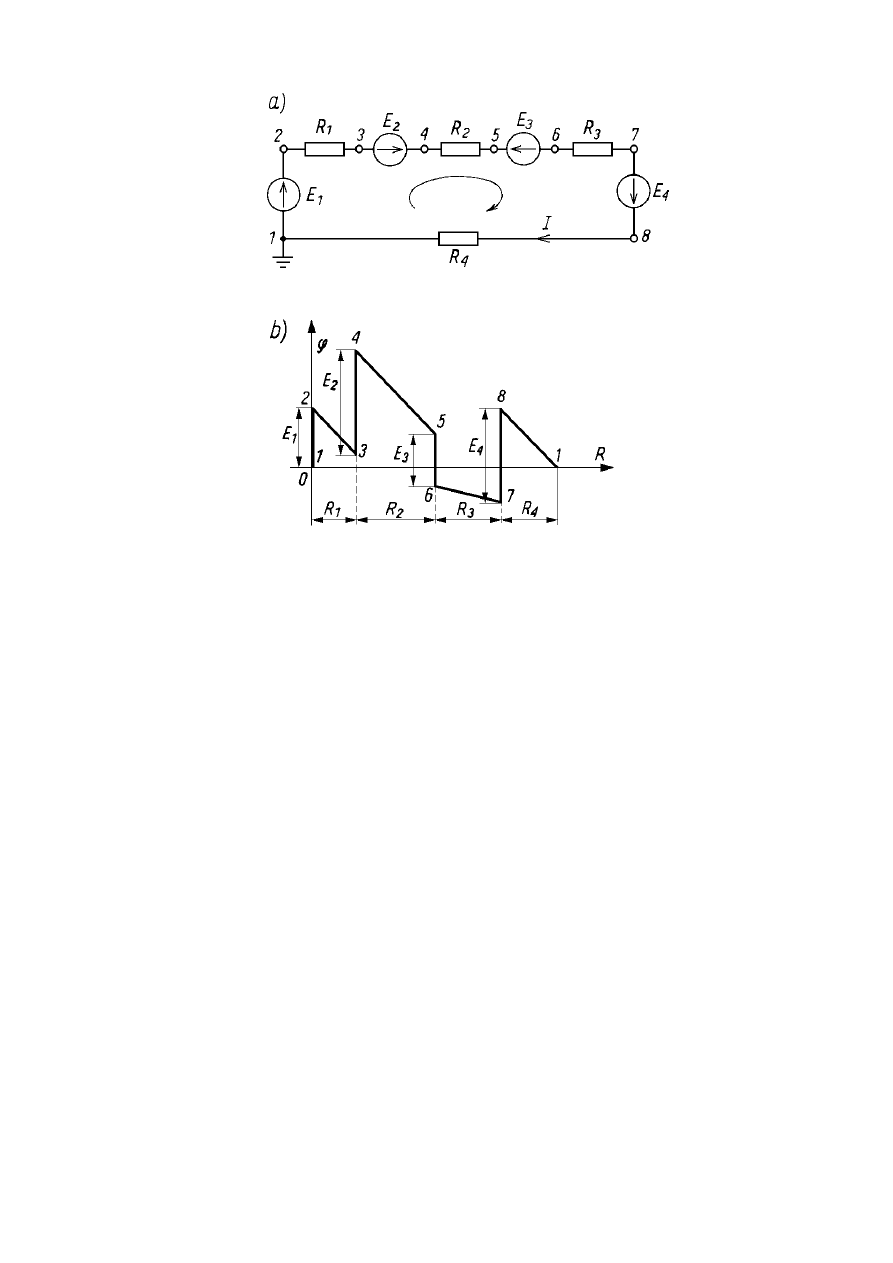
OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

 

Układ nierozgałęziony (a) wraz z wykreślonym wykresem zmienności potencjału 

(b) 

Ze względu na przyjętą zerową rezystancję źródeł wykres w punktach przejścia 

przez  nie  zmienia  się  skokowo.  Obok  metody  wykreślnej  istnieje  możliwość 

wyznaczenia  potencjałów  w  poszczególnych  punktach  w  sposób  analityczny, 

podobnie rozpoczynając z punktu o przyjętym zerowym potencjale. 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

OBWODY ROZGAŁĘZIONE O DWÓCH WĘZŁACH 

W  układach  równoległych  wszystkie  elementy  włączone  są  pomiędzy  tą 

samą  parę  węzłów  i  na  zaciskach  posiadają  to  samo  napięcie  U.  Zgodnie  z 

pierwszym  prawem  Kirchhoffa  suma  prądów  dopływających  do  węzła  jest  równa 

sumie prądów odpływających od niego. Przebieg zjawisk występujących w układzie 

równoległym  przeanalizować  można  na  przykładzie  układu  przedstawionego  na 

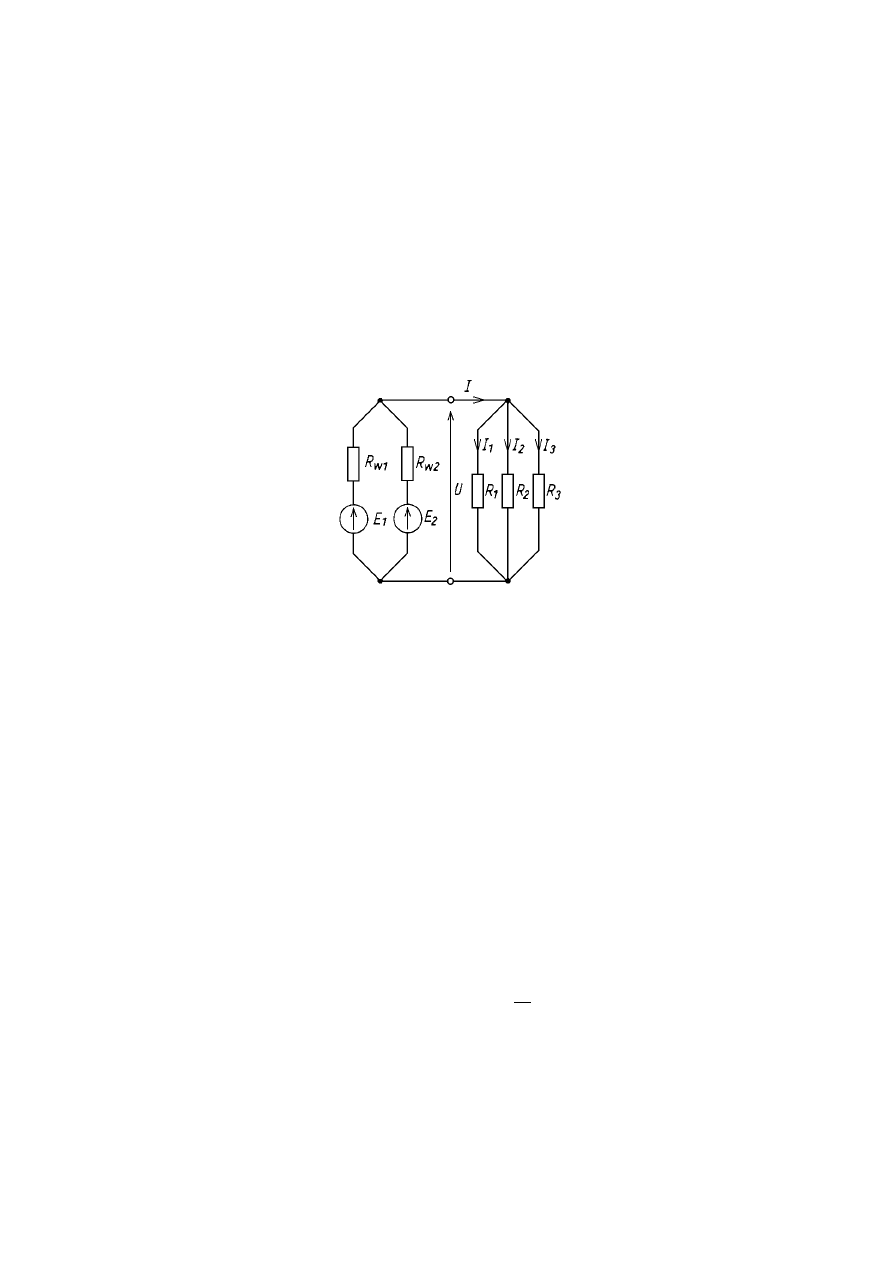
schemacie. 

 

Układ równoległy 

W  praktyce  obliczeniowej  często  zachodzi  konieczność  dokonania  obliczeń 

wielkości  występujących  w  danym  obwodzie,  przy  czym  najczęściej  wyznacza  się 

jego parametry zastępcze. W przypadku ukazanym poniżej wyznaczymy rezystancję 

zastępczą odbiorników oraz parametry zastępczego źródła napięcia.  

Zgodnie  z  prawem  Kirchhoffa  prąd  płynący  od  źródeł  do  odbiorników  jest 

równy sumie prądów przepływających przez odbiorniki: 

 

I = I

1

 +I

2

 + I

3

 

 

Ponieważ  jak  wiadomo  prawo  Ohma  można  przedstawić  w  tzw.  postaci 

przewodnościowej (konduktancyjnej) – gdzie G = 

R

1 , więc: 

 

I

1

 = G

1

U;        I

2

 = G

2

U;        I

3

 = G

3

U 

 

Po podstawieniu powyższych wartości do równania prądów: 

 

I = G

1

U + G

2

U + G

3

U = (G

1 

+ G

2 

+ G

3

)U 

 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

U

I

= G

1 

+ G

2 

+ G

3

 

 

Przekształcając  dalej  powyższy  wzór,  z  uwzględnieniem,  że 

U

I

 = G 

otrzymujemy: 

 

G = G

1 

+ G

2 

+ G

3

 

 

Konduktancja zastępcza dowolnej liczby rezystorów połączonych równolegle 

jest równa sumie konduktancji poszczególnych rezystorów.  

Bezpośrednio  z  tego  wzoru  możliwe  jest  obliczenie  rezystancji  zastępczej  dla 

układu równolegle połączonych rezystorów. 

 

3

2

1

R

1

R

1

R

1

R

1







 

 

Odwrotność  rezystancji  zastępczej  dowolnej  liczby  połączonych 

rezystorów  jest  równa  sumie  odwrotności  rezystancji  poszczególnych 

rezystorów.  

Jednym  z  częściej  stosowanych  wzorów  jest  wzór  na  rezystancję  zastępczą 

dwóch połączonych równolegle rezystorów: 

 

R = 

2

1

2

1

R

R

R

R



 

 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

Układ wyjściowy po zastąpieniu trzech gałęzi z elementami rezystancyjnymi 

jednym 

Przy zastępowaniu układu równoległego układem równoważnym wyznacza się 

także zastępczą wartość źródła napięcia. W tym celu należy zastąpić źródła napięcia 

źródłami  prądu  zgodnie  z  zależnościami  podanymi  przy  okazji  omawiania  tematu 

źródeł  napięcia.  Wartości  prądów  źródłowych  przepływających  w  poszczególnych 

gałęziach wynoszą: 

 

I

ź1

 = 

1

w

1

R

E

=G

w1

E

1

    oraz   I

ź2

 = 

2

w

2

R

E

=G

w2

E

2

 

 

 

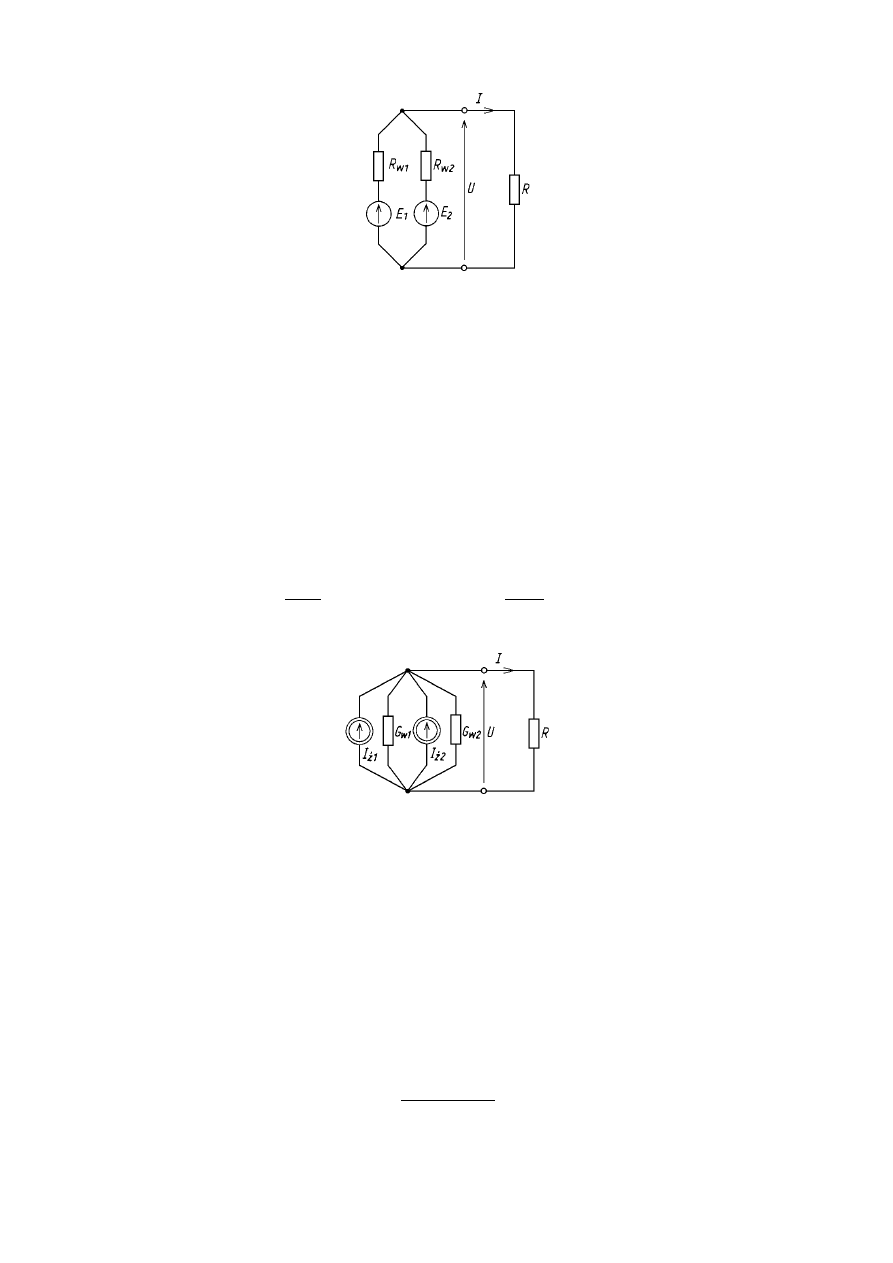
Układ po zastąpieniu dwóch rzeczywistych źródeł napięcia rzeczywistymi 

źródłami prądu 

Zgodnie  z  pierwszym  prawem  Kirchhoffa  zapisujemy  bilans  prądu  dla  węzła 

układu: 

 

I

ź

 = I

ź1

 + I

ź2

 

 

Obliczamy także zastępczą rezystancję wewnętrzną dla układu: 

 

R

w

 = 

2

w

1

w

2

w

1

w

R

R

R

R



  

bądź w postaci konduktacyjnej: 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

G

w

 = G

w1

 + G

w2

 

 

Dzięki  takim  obliczeniom  możliwe  jest  sprowadzenie  układu  wyjściowego  do 

jego prostszej postaci: 

 

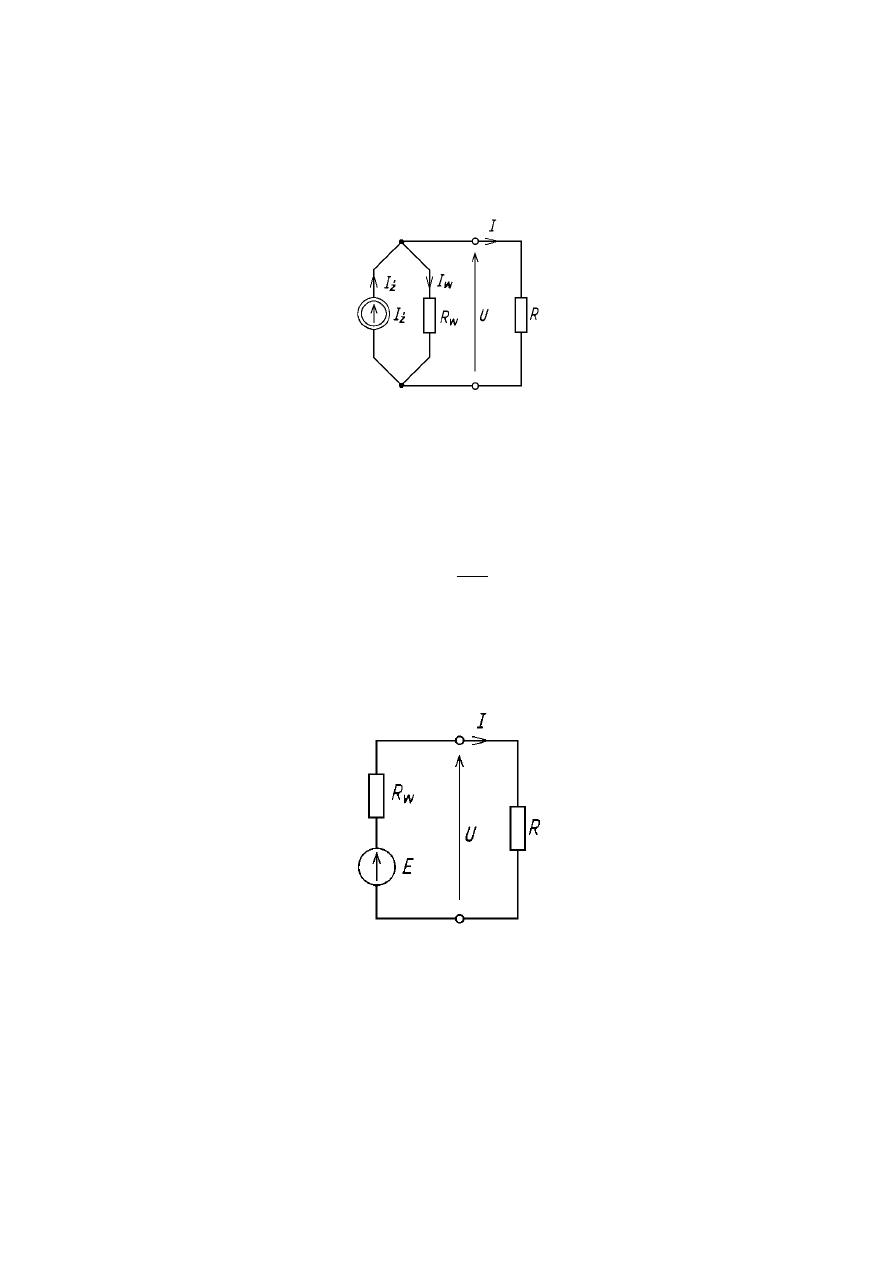
Układ z zastępczą rezystancją wewnętrzna oraz zastępczym źródłem prądu 

W  układzie  tym  występuje  rzeczywiste  źródło  prądu.  Ostatnim  krokiem  jest 

przejście do układu ze źródłem napięcia o napięciu źródłowym: 

 

E = R

w

I

ź

 = 

w

ź

G

I

 

 

W  wyniku  wszystkich  przekształceń  uzyskać  można  schemat  równoważnego 

układu względem układu wyjściowego, co było celem wszystkich operacji. 

 

Układ równoważny wyjściowemu po wszystkich przekształceniach 

Metodę zamiany źródeł i odbiorników na układy równoważne wykorzystuje się 

przy analizowaniu różnego rodzaju układów elektrycznych. 

 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

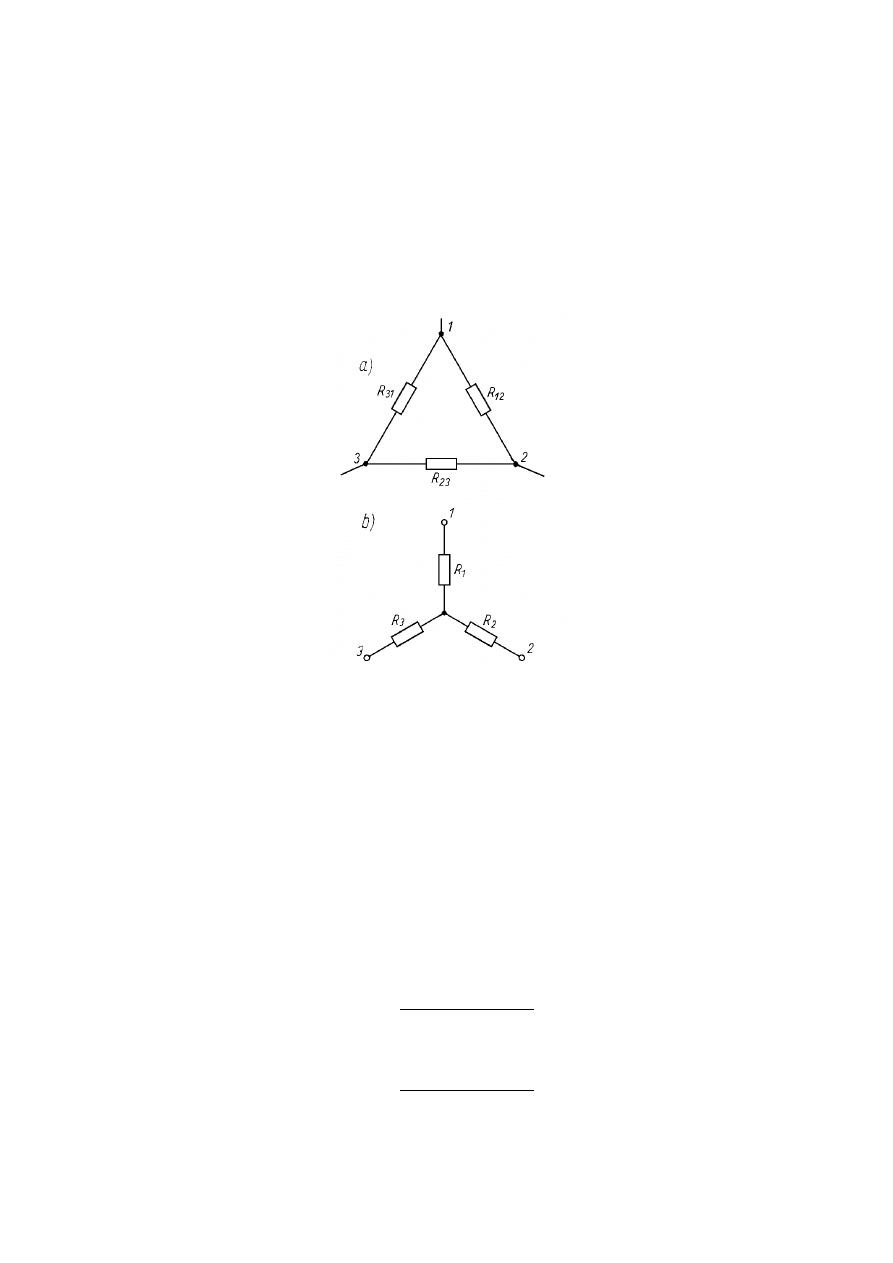
UKŁADY Z POŁĄCZENIEM ELEMENTÓW W GWIAZDĘ LUB TRÓJKĄT 

Obok  połączeń  szeregowego  i  równoległego  elementów  obwodów  spotyka  się 

również  połączenie  w  gwiazdę  (gwiazdowe  –  rysunek  d)  lub  połączenie  w  trójkąt 

(trójkątowe  –  rysunek  a).  Schemat  połączeń  elementów  obydwóch  przypadkach 

przedstawia poniższy rysunek: 

 

Układ elementów przy połączeniu w trójkąt (a) oraz w gwiazdę (b) 

W  układzie  gwiazdowym  rezystancja  pomiędzy  dowolnymi  zaciskami  równa 

jest  sumie  rezystancji  dołączonych  do  tych  zacisków,  natomiast  przy  połączeniu  w 

trójkąt  rezystancja  mierzona  między  zaciskami  jest  równa  rezystancji  układu 

równoległego. 

W  związku  z  tym  dla  poszczególnych  par  zacisków  muszą  być  spełnione 

następujące zależności: 

 

R

1 

+ R

2

 = 

31

23

12

31

23

12

R

R

R

)

R

R

(

R







 

 

 

R

2 

+ R

3

 = 

31

23

12

12

31

23

R

R

R

)

R

R

(

R







 

 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

R

3 

+ R

1

 = 

31

23

12

23

12

31

R

R

R

)

R

R

(

R







 

 

Odejmując  powyższe  równania  od  połowy  ich  sumy  otrzymuje  się  poniższe 

zależności, stosowane przy przekształcaniu trójkąta w gwiazdę: 

 

R

1

 = 

31

23

12

31

12

R

R

R

R

R





 

 

 

R

2

 = 

31

23

12

23

12

R

R

R

R

R





 

 

 

R

3

 = 

31

23

12

31

23

R

R

R

R

R





 

 

W myśl powyższych wzorów:  

Rezystancja  gałęzi  gwiazdy  jest  równa  iloczynowi  rezystancji  gałęzi 

trójkąta  (R

tr

)  schodzących  się  w  tym  samym  węźle,  podzielonej  przez  sumę 

rezystancji wszystkich gałęzi trójkąta.  

Sytuacja  ulega  znacznemu  uproszczeniu,  gdy  rezystancja  wszystkich  gałęzi 

trójkąta jest taka sama. Rezystancja układu gwiazdy (R

gw

) wynosi wtedy: 

 

R

gw

 = R

1 

= R

2 

= R

3 

= 

tr

2
tr

R

3

R

= 

3

R

tr

 

 

W przypadku odwrotnym, tzn. przy zamianie gwiazdy w trójkąt z zależności 50 

-  5.52)  powyżej  tworzy  się  sumę  iloczynów  (R

1

R

2 

+  R

2

R

3 

+  R

3

R

1

),  która  jest 

następnie dzielona kolejno przez  R

1

,  R

2

  i  R

3

.  W  wyniku tych  operacji uzyskuje  się 

równania opisujące wartości poszczególnych rezystancji trójkąta: 

 

R

12

 = R

1

 + R

2

 + 

3

2

1

R

R

R

 

 

 

R

23

 = R

2

 + R

3

 + 

1

3

2

R

R

R

 

 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

R

31

 = R

3

 + R

1

 + 

2

1

3

R

R

R

 

 

Zgodnie  z  nimi  rezystancja  gałęzi  trójkąta  równa  jest  sumie  rezystancji 

gałęzi  gwiazdy  zbiegających  się  w  tej  samej  parze  węzłów  i  iloczynu  tych 

rezystancji  podzielonego  przez  rezystancję  trzeciej  gałęzi.  Podobnie  jak  w 

przypadku  gwiazdy,  tak  i  w  przypadku  trójkąta  wzory  te  upraszczają  się,  gdy 

rezystancje gałęzi gwiazdy są sobie równe: 

 

R

tr

 = 2R

gw

 + 

gw

2
gw

R

R

= 3R

gw

 

 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

OBWODY NIELINIOWE PR

ĄDU STAŁEGO 

Przykładowe  charakterystyki  kilku  elementów  nieliniowych  przedstawia 

poniższy rysunek 

 

 

 

 

 

 

Charakterystyki elementów nieliniowych: diody próżniowej (a); diody 

półprzewodnikowej (b); żarówki z włóknem wolframowym (c); termistora (d); 

diody tunelowej (e) 

Jak widać z przytoczonego przykładu niektóre z charakterystyk są symetryczne 

względem początku układu współrzędnych, inne nie, co oznacza, że elementy takie 

mogą odznaczać się różnymi własnościami przy różnych sposobach polaryzacji. 

Niejednokrotnie  dla  ułatwienia  analizy  obwodów  dokonuje  się  uproszczenia 

charakterystyki rzeczywistej elementu poprzez zastąpienie jej charakterystyką idealną 

powstałą  w  wyniku  aproksymacji  liniowej  (w  przedziałach  w  których  przebieg  jest 

zbliżony do liniowego jest on zastępowany linią prostą).  

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

POŁĄCZENIE SZEREGOWE ELEMENTÓW NIELINIOWYCH 

Obwody  nieliniowe  nie  spełniają  zasady  superpozycji  o  której  była  mowa  w 

początkach  rozdziału,  natomiast  słuszne  pozostają  prawa  Ohma  i  Kirchhoffa.  Do 

analizy  układu  szeregowego  oraz  równoległego  zastosować  można  jedną  z  metod 

graficznych  analizy  obwodów  prądu  stałego.  W  obu  przypadkach  celem  jest 

wyznaczenie  charakterystyki  zastępczej  dla  danego  układu  i  przebiegu  wartości 

wielkości (prądów i napięć) występujących w nim. 

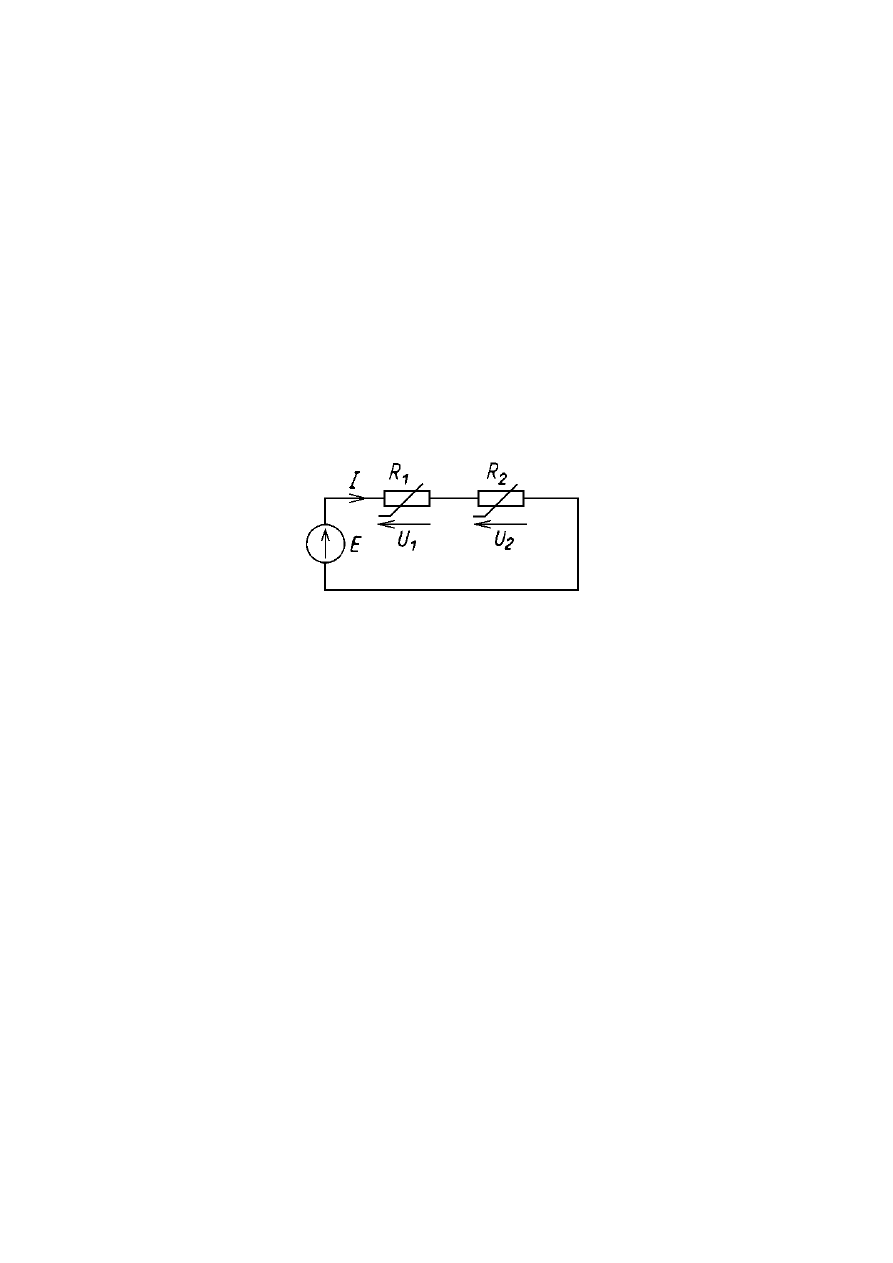
Schemat  połączenia  dwóch  elementów  nieliniowych  połączonych  szeregowo 

przedstawia poniższy rysunek: 

 

Szeregowe połączenie elementów nieliniowych 

 

Dla  obwodu  w  tej  postaci  słuszne  jest  równanie  zapisane  w  oparciu  o  drugie 

prawo Kirchhoffa: 

 

E = R

1

(I)



I + R

2

(I)



I 

 

W równaniu tym: R

1

(I); R

2

(I) – rezystancje elementów nieliniowych zależne od 

wartości prądu w obwodzie. Najczęściej stosowaną w takim przypadku metodą jest 

metoda  charakterystyki  zastępczej.  Charakterystyka  zastępcza  powstaje  poprzez 

sumowanie charakterystyk poszczególnych elementów, czyli dodanie wartości napięć 

dla różnych wartości prądów.  

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

 

Ilustracja wyznaczania charakterystyki zastępczej dwóch połączonych 

szeregowo elementów nieliniowych 

Prosta  równoległa  do  osi  napięcia  przechodząca  przez  punkt  N  przecinając 

charakterystyki  obu  elementów  wyznacza  wartości  występujących  na  nich  spadków 

napięcia przy danej wartości prądu w obwodzie. 

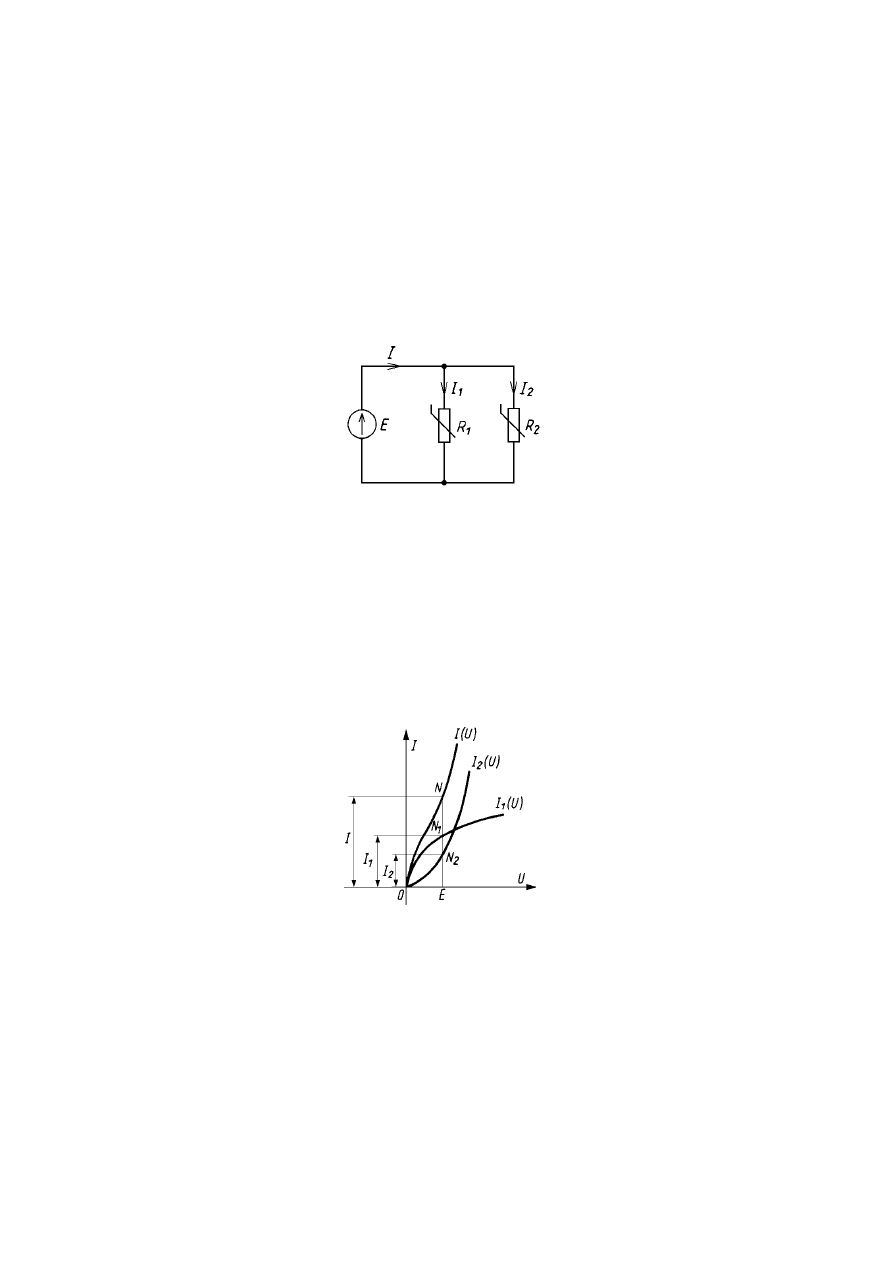
OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

POŁĄCZENIE RÓWNOLEGŁE ELEMENTÓW NIELINIOWYCH 

W  przypadku  połączenia  równoległego  dwóch  rezystancyjnych  elementów 

nieliniowych,  przedstawionego  na  rysunku  oba  elementy  zasilane  są  z  tego  samego 

źródła o napięciu E, w wyniku czego ustalają się na nich takie same spadki napięcia. 

Zgodnie z pierwszym prawem Kirchhoffa prąd dopływający do układu równoległego 

jest sumą prądów przepływających przez poszczególne elementy: 

 

Układ równolegle połączonych elementów nieliniowych 

 

I = I

1

 + I

2

 

 

Charakterystyka  zastępcza  układu  powstaje  jako  suma  charakterystyk  dla 

poszczególnych elementów, czyli poprzez zsumowanie wartości prądów dla różnych 

napięć: 

 

Wyznaczanie charakterystyki zastępczej równolegle połączonych elementów 

nieliniowych 

Podobnie  jak  w  przypadku  układu  szeregowego  przecięcie  charakterystyki 

wypadkowej  z  prostą  odpowiadającą  wartości  napięcia  źródłowego  (punkt  N)  daje 

wartość  prądu  wypadkowego  dopływającego  do  układu.  Z  kolei  rzędne  punktów 

OBWODY ELEKTRYCZNE PRĄDU STAŁEGO

 

przecięcia  z  charakterystykami  poszczególnych  elementów  dają  wartości  prądów 

przepływających przez gałęzie układu.