Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego

Maszyny elektryczne – wykład multimedialny

Autorzy:

Prof. dr hab. inż. Roman Nadolski

Dr inż. Jan Staszak

Dr inż. Krzysztof Ludwinek

Mgr inż. Zbigniew Gawęcki

Lata realizacji 2008-2011

SPIS TREŚCI

2. Transformatory

2.1

Budowa transformatorów

2.2

Analiza pracy transformatora jednofazowego

2.2.1

Równania napięć i prądów

2.2.2

Schemat zastępczy i wykres wektorowy

2.3

Stany pracy transformatora

2.3.1

Stan jałowy

2.3.2

Stan zwarcia

2.4

Transformatory trójfazowe

2.4.1

Sposoby połączeń uzwojeń

2.4.2

Grupy połączeń transformatorów trójfazowych

2.4.3

Przekładnia zwojowa i napięciowa

2.5

Praca równoległa transformatorów

2.6

Zmienność napięcia

2.7

Straty i sprawność transformatorów

LITERATURA

2.1 BUDOWA TRANSFORMATORÓW

Transformator jest urządzeniem elektromagnetycznym przetwarzającym energię

prądu przemiennego na energię prądu przemiennego o innym z reguły napięciu i prądzie, lecz

o tej samej częstotliwości.

Transformatory można podzielić na następujące grupy:

a)

transformatory energetyczne, stosowane do przesyłania i rozdziału energii

elektrycznej,

b)

transformatory małej mocy, stosowane w automatyce, łączności, telemechanice i

urządzeniach elektronicznych,

c)

transformatory specjalne, do których można zaliczyć przekładniki pomiarowe,

transformatory prostownikowe, probiercze, spawalnicze itp.

Rola transformatora w systemie elektroenergetycznym związana jest z koniecznością

przesyłu energii z elektrowni do odbiorców i ograniczeniem strat przesyłowych. Straty przy

przesyle energii są proporcjonalne do I

2

R, aby były one jak najmniejsze należy przesyłać

energie przy małym prądzie I lub małej rezystancji R. Przesył energii liniami o małej

rezystancji, a więc o dużych przekrojach przewodów, byłby zbyt kosztowny, a w przypadkach

dużych mocy trudny lub niemożliwy technicznie do zrealizowania. Energię wytworzoną w

turbogeneratorach umiejscowionych w elektrowniach, której napięcie nie przekracza

zazwyczaj 24kV przesyła się przy stosunkowo wysokim napięciu U i niskim prądzie I.

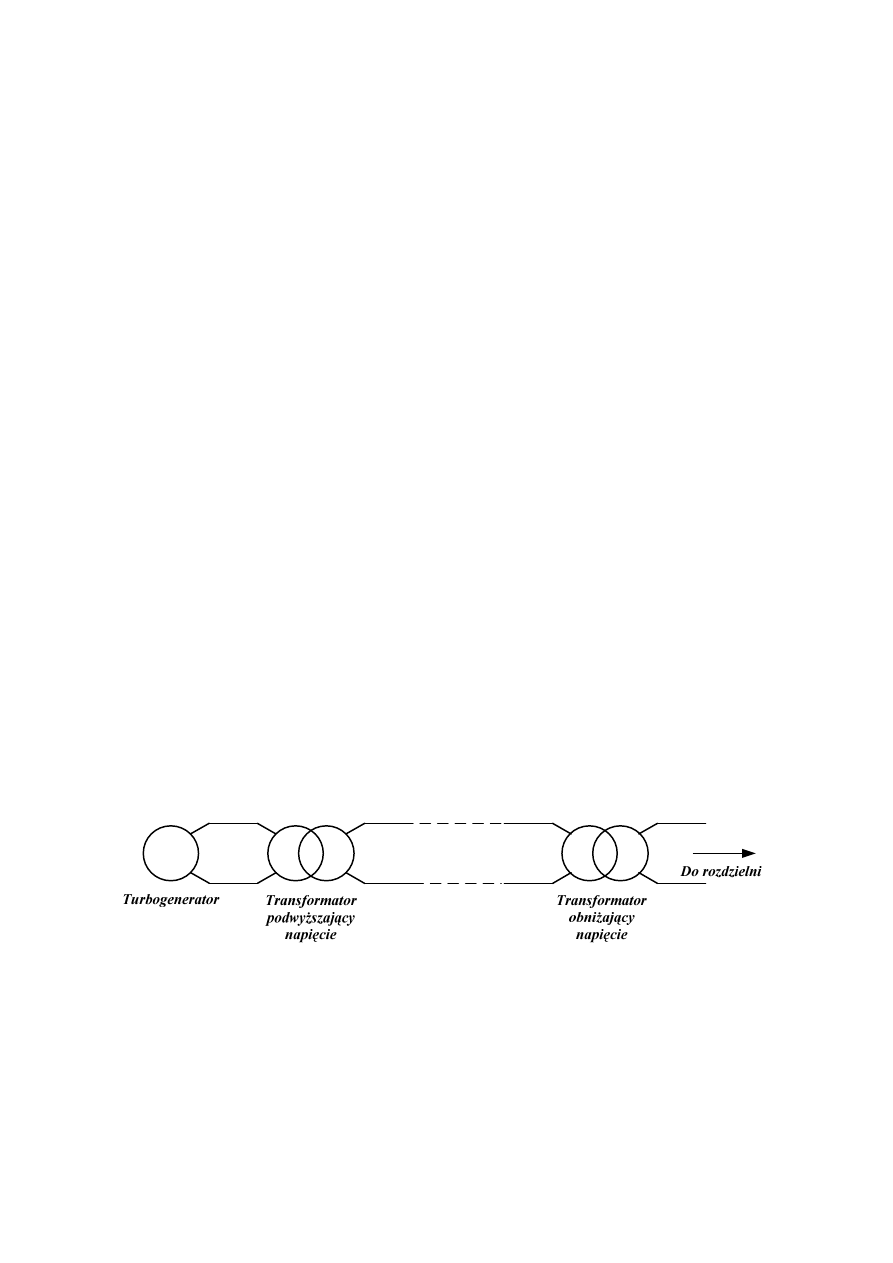
Rys. 2.1. Rola transformatora w systemie elektroenergetycznym

W trakcie przesyłu energii elektrycznej z elektrowni do odbiorców następuje podwyższenie

napięcia do np. 220kV (i zmniejszenia prądu), a następnie obniżenie napięcia do poziomu

napięcia rozdzielni, z której energia rozprowadzana jest liniami do transformatorów

końcowych obniżających napięcie do poziomu użytecznego dla odbiorców. Tak więc energia

od miejsca wytworzenia do miejsca w którym zostanie zużytkowana jest transformowana co

najmniej trzykrotnie.

Zasadniczymi elementami składowymi transformatora są:

•

rdzeń, który przewodzi strumień magnetyczny,

•

uzwojenie, przez które przepływa prąd elektryczny.

Rdzeń transformatora składa się z kolumn na których nawinięte są uzwojenia i z jarzm

łączących te kolumny.

Ze względu na liczbę faz rozróżniamy transformatory:

•

jednofazowe,

•

wielofazowe, wśród których najpowszechniej stosowanymi są transformatory

trójfazowe.

Ze względu na liczbę uzwojeń rozróżnia się transformatory:

•

jednouzwojeniowe, nazywane autotransformatorami,

•

dwuuzwojeniowe, najczęściej spotykane,

•

trójuzwojeniowe lub czterouzwojeniowe.

W transformatorach dwuuzwojeniowych można wyróżnić:

•

uzwojenie pierwotne – uzwojenie do którego doprowadza się energię,

•

uzwojenie wtórne – uzwojenie z którego odprowadza się energię.

Uzwojenie wyższego napięcia nazywa się uzwojeniem górnego napięcia, a uzwojenie

niższego napięcia uzwojeniem dolnego napięcia. Jeżeli napięcie wtórne jest wyższe od

napięcia pierwotnego to taki transformator nazywa się transformatorem podwyższającym

napięcie, jeżeli natomiast napięcie wtóre jest niższe od napięcia pierwotnego to taki

transformator nazywa się transformatorem obniżającym napięcie.

Transformatory mogą być budowane jako:

•

rdzeniowe,

•

płaszczowe.

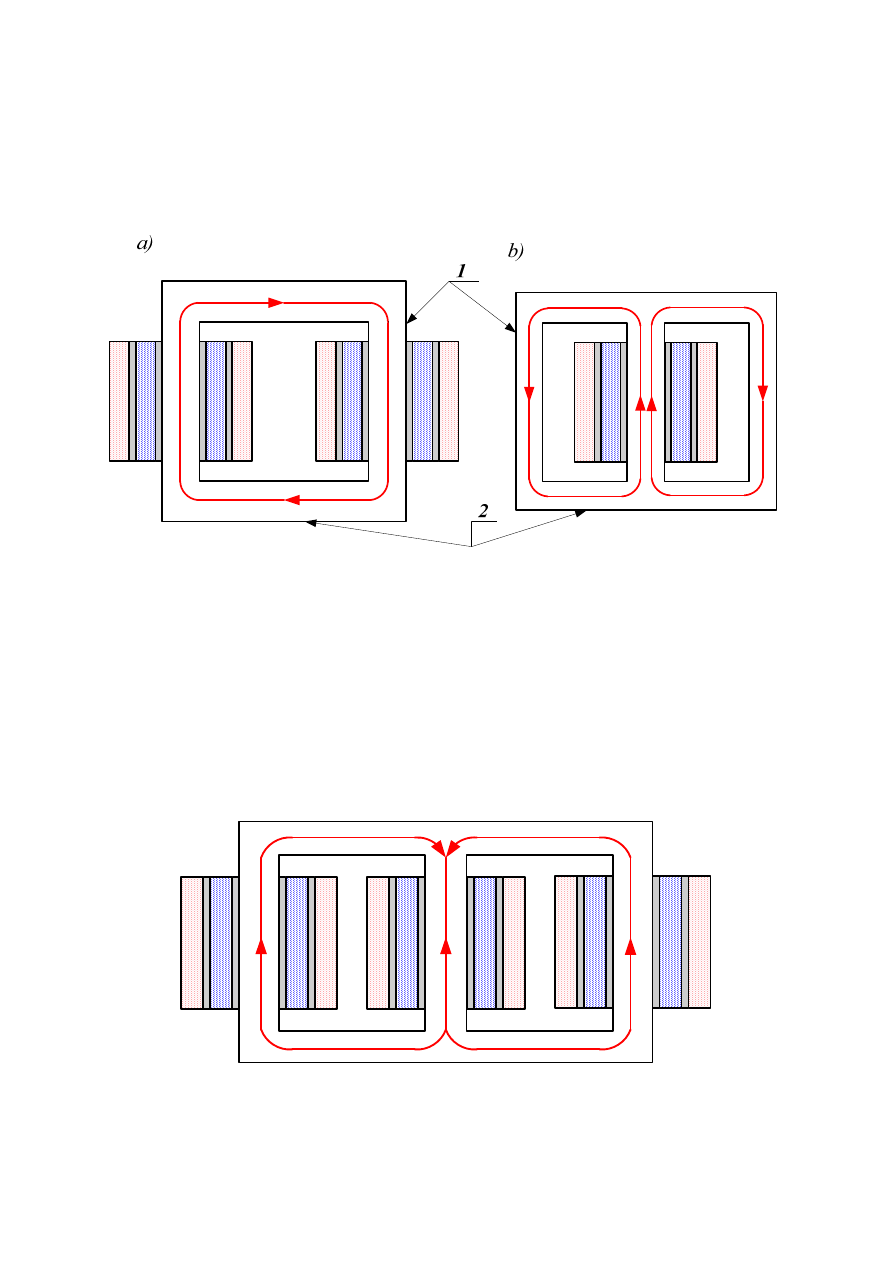
W jednofazowym transformatorze rdzeniowym (rys.2.2a)) na każdej kolumnie znajdują się po

dwa uzwojenia, w transformatorze płaszczowym (rys. 2.2b)) uzwojenia są nawinięte na

kolumnie środkowej, kolumny skrajne służą tylko do przewodzenia strumienia

magnetycznego.

Rys. 2.2. Transformator jednofazowy: a) rdzeniowy, b) płaszczowy; 1-kolumny, 2-jarzma

W transformatorze trójfazowym rdzeniowym (rys.2.3.) na każdej kolumnie znajduje się jedno

uzwojenie pierwotne i jedno uzwojenie wtórne. Z uwagi na to, że kolumna środkowa ma

mniejszą reluktancję w stosunku do kolumn skrajnych z jarzmami, transformator nie jest

symetryczny, ale nie ma to istotnego wpływu na pracę transformatora.

Rys. 2.3. Transformator trójfazowy rdzeniowy (niesymetryczny)

W przypadkach przesyłania dużych mocy w sieciach trójfazowych o wysokim napięciu

niekiedy stosuje się zespoły transformatorów jednofazowych, a czasem transformatory

trójfazowe wykonane jako pięciokolumnowe (rys 2.4)

Rys. 2.4. Transformator trójfazowy pięciokolumno

wy

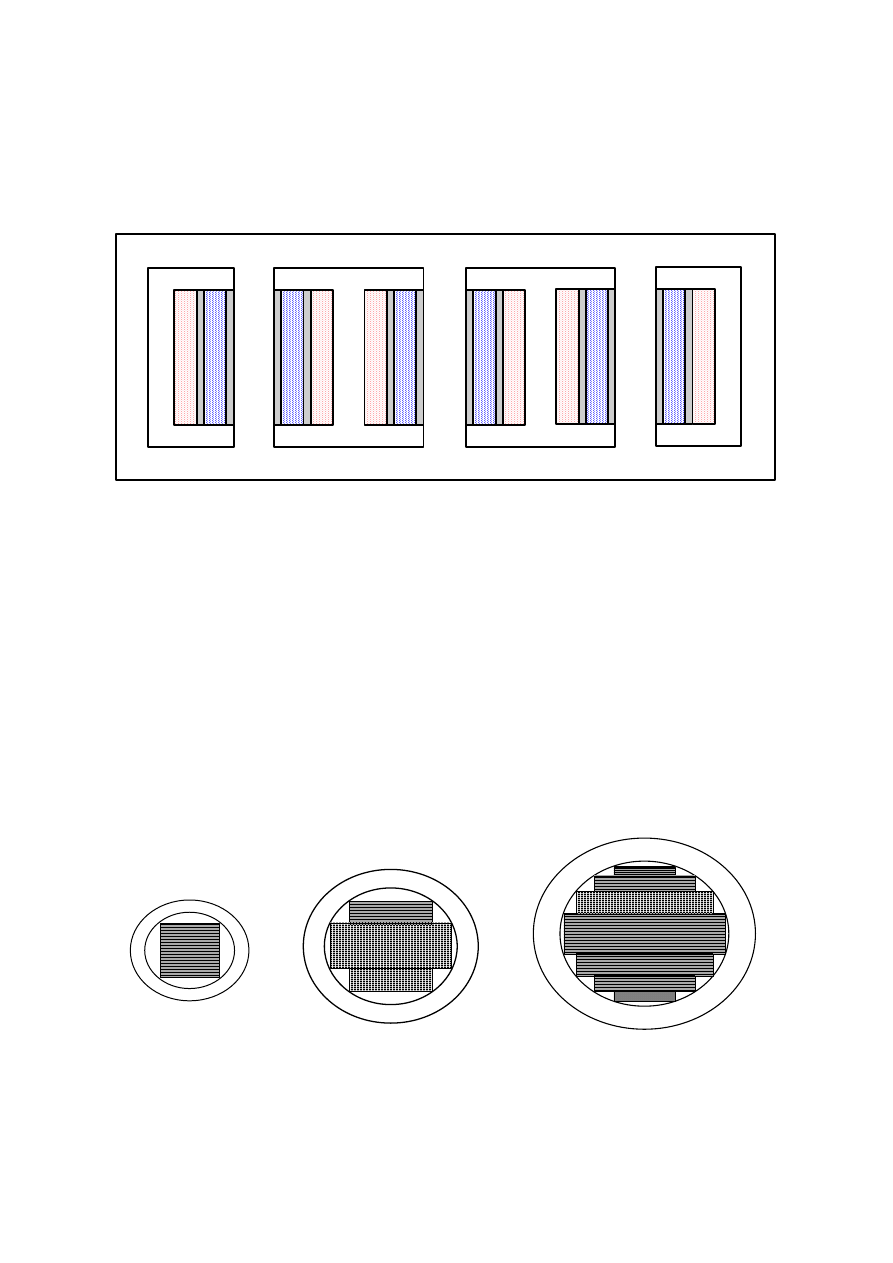
Naturalnym kształtem uzwojenia transformatora ze względu na skutki działań

elektrodynamicznych jest kształt kołowy, dlatego przekrój kolumny, na których nawinięte jest

uzwojenie powinno mieć kształt zbliżony do kołowego. Jedynie w transformatorach małych

mocy stosuje się kolumny o przekroju kwadratowym lub krzyżowym (rys.2.5a), 2.5b)),

natomiast w transformatorach średnich i dużych mocy stosowane są kolumny o przekrojach

schodkowych (rys. 2.5. c)), przy czym liczba schodków zależy od mocy transformatora i ma

wpływ na koszt jego wytworzenia.

a)

b)

c)

Rys.2.5. Przekroje rdzeni transformatorów: a) kwadratowy, b) krzyżowy, c) schodkowy

Rdzeń transformatora wykonywany jest z blachy transformatorowej o grubości

0.3÷0.5mm. Z uwagi na zmienny strumień magnetyczny blachy pokrywane są warstwami

materiału izolacyjnego (np. lakieru) i układane w pakiety. Izolacja pomiędzy pojedynczymi

blachami, powoduje zmniejszenie strat wiroprądowych, a tym samym nie pozwala na zbytnie

nagrzewanie się rdzenia.

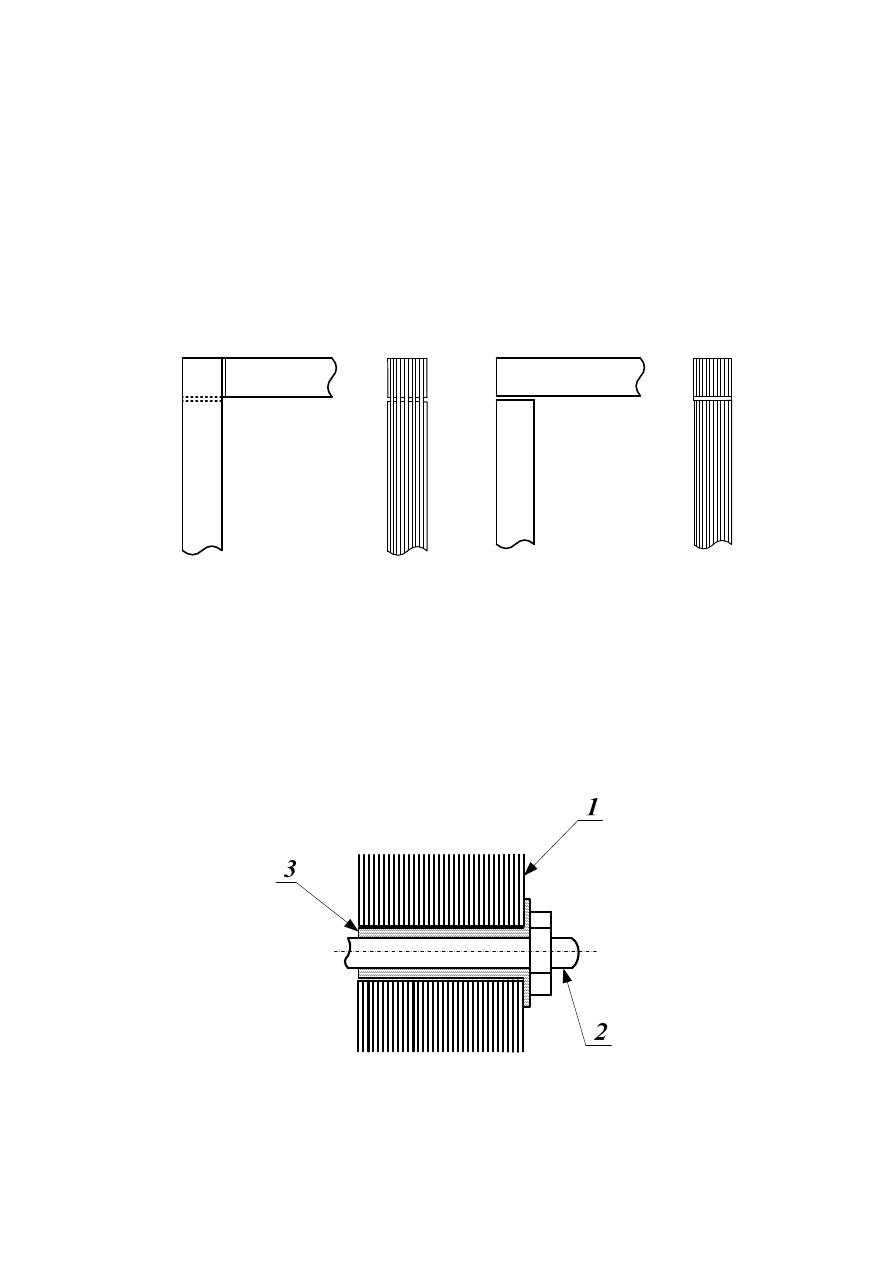
Blachy jarzm mogą być łączone z blachami kolumn „na zakładkę” (rys.2.6 a) lub „na styk”

(rys.2.6b)).

a)

b)

Rys. 2.6. Składanie jarzm i kolumn: a) „na zakładkę”, b) „na styk”

Przy połączeniu „na zakładkę” zmniejszeniu ulega szczelina powietrzna na drodze strumienia

magnetycznego, lecz koszt wykonania takiego rdzenia jest wyższy w stosunku do rdzenia

łączonego „na styk”. Miejsca styku jarzm i kolumn wykłada się materiałem izolacyjnym, aby

uniknąć zwarć.Blachy po pakietowaniu mocowane są zwykle za pomocą śrub przechodzących

na wskroś przez cały pakiet (rys.2.7).

Rys. 2.7. Sposób mocowania pakietu blach za pomocą śruby:1-pakiet blach, 2-śruba, 3-tuleja

izolacyjna

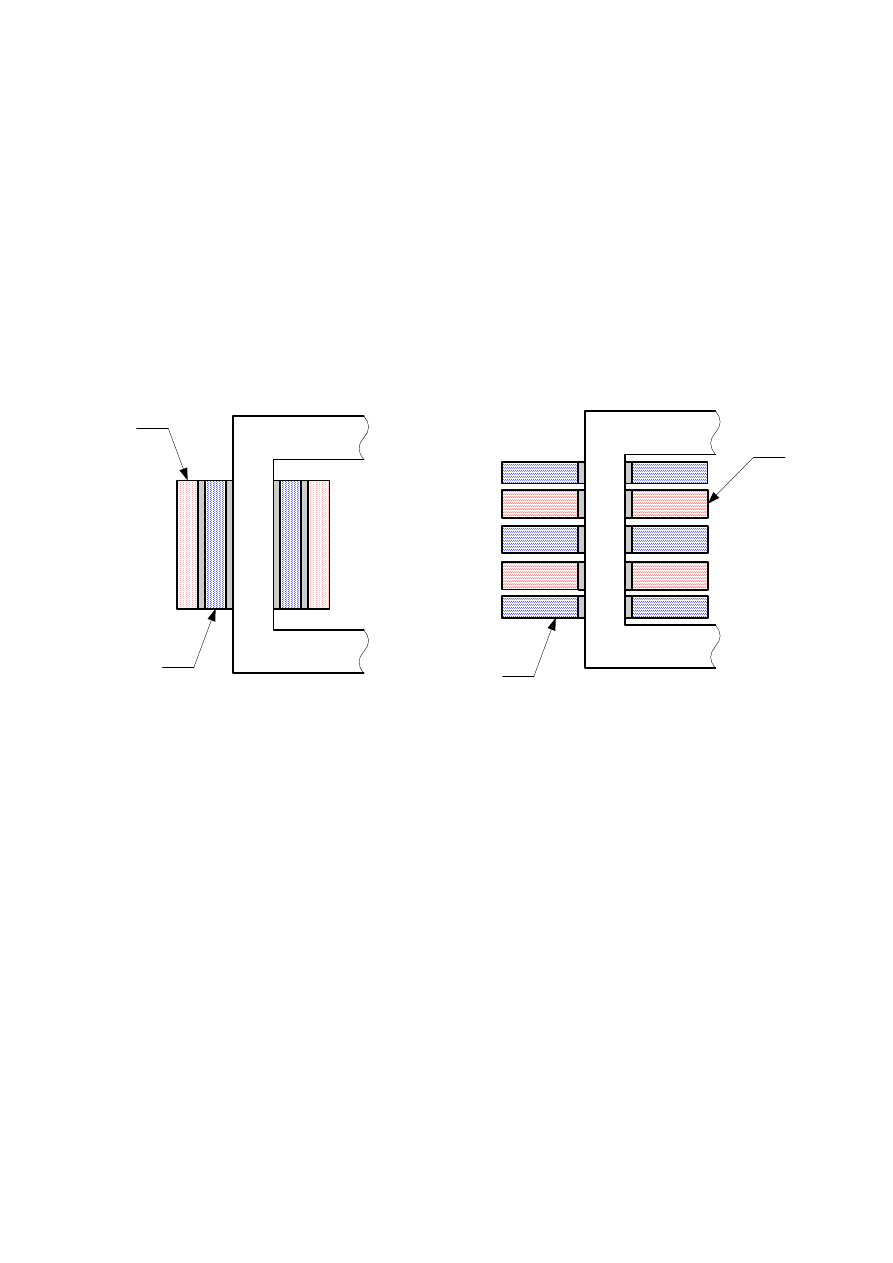
Uzwojenia transformatorów mogą być wykonane jako cylindryczne lub krążkowe (rys.2.8).

W uzwojeniu cylindrycznym, ze względu na koszt izolacji bliżej rdzenia leży uzwojenie

niższego napięcia. W uzwojeniu krążkowym cewki uzwojeń niskiego i wysokiego napięcia

leżą naprzemiennie, bliżej jarzma znajdują się zawsze cewki niższego napięcia.

Uzwojenia wykonuje się z miedzi lub aluminium. Przy małych przekrojach przewodów

stosuje się drut okrągły, natomiast przy większych prostokątny.

1

2

a)

b)

1

2

Rys. 2.8. Uzwojenia transformatorów: a) cylindryczne, b) krążkowe; 1-uzwojenie dolnego napięcia, 2-

uzwojenie górnego napięcia

W trakcie pracy transformatora powstają straty mocy w rdzeniu i w uzwojeniach, objawiające

się ich nagrzewaniem to powoduje konieczność chłodzenia.

Ze względu na sposób chłodzenia rozróżniamy transformatory:

•

transformatory suche – rdzeń i uzwojenie chłodzone jest powietrzem (chłodzenie

naturalne lub z wymuszonym obiegiem powietrza), szczególnym wykonaniem są

transformatory żywiczne, w których uzwojenia zalane są żywicą.

•

transformatory gazowe – elementy transformatora umieszczone są w hermetycznej

kadzi wypełnionej sześciofluorkiem siarki (SF

6

),

•

transformatory olejowe – rdzeń i uzwojenie zanurzone są w oleju mineralnym lub

syntetycznym niepalnym (chłodzenie naturalne do mocy ok. 1600kVA, dla większych

jednostek chłodzenie z wymuszonym obiegiem).

2.2. ANALIZA PRACY TRANSFORMATORA JEDNOFAZOWEGO

2.2.1. Równania napięć i prądów

Zasadę działania transformatora wygodnie jest przedstawić na przykładzie transformatora

jednofazowego dwuuzwojeniowego (rys.2.9).

Rys. 2.9. Układ transformatora jednofazowego dwuuzwojenioweg

o

Uzwojenie pierwotne transformatora o liczbie zwojów N

1

jest zasilone napięciem

sinosoidalnym U

1

o częstotliwości f

1

. Uzwojenie wtórne o liczbie zwojów N

2

jest obciążone

odbiornikiem o impedancji Z

obc

. Jeżeli do zacisków uzwojenia pierwotnego zostanie

przyłożone napięcie U

1

, to w uzwojeniu tym popłynie prąd I

1

. Prąd ten a właściwie przepływ

1

1

1

I

N

=

Θ

(2.1)

I

1

I

2

U

1

U

2

R

1

R

2

E

1

E

2

E

1

σ

E

2

σ

Φ

1

σ

Φ

2

σ

Z

obc

Φ

g1

Φ

g2

Φ

Φ = Φ Φ

g1

g2

-

Φ = Φ

Φ

g1

g2

-

U

R1

U

R2

wytworzy strumień magnetyczny

Φ

1

=

Φ

g1

+

Φ

1

σ

. Składowa główna

Φ

g1

tego strumienia

zamyka się w rdzeniu transformatora, natomiast składowa

Φ

1

σ

zwana strumieniem

rozproszenia zamyka się poza rdzeniem i skojarzona jest tylko z tym uzwojeniem.

Jeżeli uzwojenie wtórne transformatora zostanie obciążone odbiornikiem Z

obc

, wówczas

popłynie prąd I

2

w tym uzwojeniu. Prąd ten a właściwie jego przepływ

2

2

2

I

N

=

Θ

(2.2)

wytworzy strumień

Φ

2

=

Φ

g2

+

Φ

2

σ

, skierowany przeciwnie do strumienia

Φ

1

. Strumień

główny

Φ

g2

, podobnie jak w uzwojeniu pierwotnym, zamyka się w rdzeniu transformatora.

Natomiast strumień rozproszenia

Φ

2

σ

zamyka się poza rdzeniem i sprzęga się tylko z

uzwojeniem wtórnym.

W rdzeniu transformatora wystąpi strumień wypadkowy

Φ

zwany strumieniem głównym,

będący różnicą strumieni

Φ

g1

i

Φ

g2

)

sin(

2

1

t

m

g

g

ω

Φ

=

Φ

−

Φ

=

Φ

(2.3)

gdzie:

Φ

m

– amplituda strumienia,

ω

– pulsacja napięcia zasilającego.

Strumień wypadkowy w rdzeniu transformatora, podobnie jak i jego składowe

Φ

g1

i

Φ

g2

ma

przebieg sinusoidalny. Strumień ten sprzęga się zarówno z uzwojeniem pierwotnym jak i

wtórnym i indukuje w nich napięcia

)

cos(

1

1

1

1

t

N

t

d

d

N

t

d

d

e

m

ω

ω

Φ

=

Φ

=

Ψ

=

(2.4)

)

cos(

2

2

2

2

t

N

t

d

d

N

t

d

d

e

m

ω

ω

Φ

=

Φ

=

Ψ

=

(2.5)

gdzie:

Ψ

1

,

Ψ

2

– odpowiednio, strumień skojarzony z uzwojeniem pierwotnym i wtórnym

transformatora.

Amplitudy napięć indukowanych wynoszą

m

m

N

E

Φ

=

ω

1

1

(2.6)

m

m

N

E

Φ

=

ω

2

2

(2.7)

W praktyce posługujemy się nie amplitudami napięć lecz wartościami skutecznymi, które

wynoszą odpowiednio

m

m

m

f

N

N

E

E

Φ

=

Φ

=

=

1

1

1

1

2

2

1

2

π

ω

(2.8)

m

m

m

f

N

N

E

E

Φ

=

Φ

=

=

2

2

2

2

2

2

1

2

π

ω

(2.9)

Z zależności (2.3)

÷

(2.5) wynika, że napięcia indukowane w uzwojeniach transformatora e

1

i

e

2

są ze sobą w fazie oraz są względem strumienia

Φ

przesunięte o kat

π

/2.

Z równań (2.8) i (2.9) wynika, że stosunek napięć indukowanych E

1

i E

2

jest równy

stosunkowi liczby zwojów N

1

i N

2

n

N

N

E

E

=

=

2

1

2

1

(2.10)

Wielkość n nazywamy przekładnią zwojową transformatora. Zgodnie ze wzorem (2.10)

możemy napisać

'

2

2

2

2

1

1

E

n

E

E

N

N

E

=

=

=

(2.11)

Wielkość E

’

2

jest wartością skuteczną napięcia indukowanego w uzwojeniu wtórnym

transformatora, sprowadzoną na stronę uzwojenia pierwotnego

n

E

E

2

'

2

=

(2.12)

Strumienie rozproszenia

Φ

1

σ

i

Φ

2

σ

, zamykające się poza rdzeniem, nie biorą udziału w

przenoszeniu energii. Jednak podobnie jak strumień główny

Φ

, również strumienie

rozproszenia obu uzwojeń indukują napięcia rozproszenia. Wartości skuteczne tych napięć,

zgodnie ze wzorem (2.8) wynoszą

σ

σ

π

1

1

1

2

Φ

=

f

N

E

(2.13)

σ

σ

π

2

2

2

2

Φ

=

f

N

E

(2.14)

Strumienie rozproszenia

Φ

1

σ

i

Φ

2

σ

są proporcjonalne i są w fazie z wywołującymi je

przepływami

σ

σ

σ

1

1

1

1

1

1

2

Λ

=

Λ

Θ

=

Φ

I

N

m

(2.15)

σ

σ

σ

2

2

2

1

2

2

2

Λ

=

Λ

Θ

=

Φ

I

N

m

(2.16)

gdzie:

Λ

1

σ

,

Λ

2

σ

- przewodności magnetyczne dla strumieni rozproszenia, odpowiednio

uzwojenia pierwotnego i wtórnego

Podstawiając zależności (2.13) i (2.14) do równań (2.8) i (2.9), otrzymujemy

1

1

2

1

1

2

I

N

f

E

σ

σ

π

Λ

=

(2.17)

1

2

2

2

2

2

I

N

f

E

σ

σ

π

Λ

=

(2.18)

Uwzględniając, że wyrażenia

σ

σ

1

2

1

1

Λ

=

N

L

(2.19)

σ

σ

2

2

2

2

Λ

=

N

L

(2.20)

są indukcyjnościami rozproszenia uzwojenia pierwotnego i wtórnego, równania (2.14) i (2.15)

można zapisać w postaci

1

1

1

1

1

2

I

X

I

L

f

E

σ

σ

σ

π

=

=

(2.21)

2

2

2

2

2

2

I

X

I

L

f

E

σ

σ

σ

π

=

=

(2.22)

Napięcia E

1

σ

i E

2

σ

są przesunięte względem wywołujących je prądów o kąt

π

/2.

Na podstawie schematu transformatora (rys.2.9) możemy napisać równania napięć

transformatora dla strony pierwotnej i wtórnej transformatora

σ

1

1

1

1

1

E

I

R

E

U

+

+

=

(2.23)

σ

2

2

2

2

2

E

I

R

E

U

+

+

=

(2.24)

Uwzględniając zależności (2.21) i (2.22) równania te możemy zapisać w postaci

1

1

1

1

1

1

I

X

j

I

R

E

U

σ

+

+

=

(2.25)

2

2

2

2

2

2

I

X

j

I

R

E

U

σ

+

+

=

(2.26)

Strumień magnetyczny w rdzeniu jest skutkiem działania przepływu wypadkowego

Θ

0

, który

jest różnicą geometryczą przepływów

Θ

1

i

Θ

2

2

1

0

Θ

−

Θ

=

Θ

(2.27)

Przepływ wypadkowy

Θ

0

jest wytworzony przez prąd I

0

, zwany prądem jałowym

transformatory, który płynie w uzwojeniu o liczbie zwojów N

1

2

2

1

1

0

1

2

2

2

I

N

I

N

I

N

−

=

(2.28)

Dzieląc obustronnie równanie (2.28) przez

N

2

otrzymujemy

'

2

1

2

2

2

1

0

I

I

I

N

N

I

I

−

=

−

=

(2.29)

Prąd

'

2

I jest prądem wtórnym transformatora przeliczonym na stronę pierwotną

n

I

I

N

N

I

2

2

2

2

'

2

=

=

(2.30)

Mnożąc obustronnie równanie (2.26) przez przekładnię zwojową n, otrzymuje się

n

I

n

jX

n

I

n

R

n

E

n

U

2

2

2

2

2

2

2

2

σ

+

+

=

(2.31)

Uwzględniając zależności (2.12) i (2.30) oraz wprowadzając oznaczenia

n

U

U

2

'

2

=

2

2

'

2

n

R

R

=

2

2

'

2

n

X

X

σ

σ

=

(2.32)

równanie (2.31) przyjmie postać

'

2

'

2

'

2

'

2

'
2

'
2

I

jX

I

R

E

U

σ

+

+

=

(2.33)

gdzie:

'
2

U

−

napięcie po stronie wtórnej transformatora sprowadzone na stronę pierwotną,

'

2

R

,

'

2

σ

X

−

rezystancja i reaktancja rozproszenia uzwojenia wtórnego sprowadzone na

stronę pierwotną transformatora

2.2.2

Schemat zastępczy i wykres wektorowy

Napięcie indukowane w uzwojeniu pierwotnym E

1

można przedstawić jako napięcie na

reaktancji magnesowania X

m

przez którą przepływa prąd magnesujący I

m

m

m

m

m

I

X

I

L

f

E

E

=

=

=

π

2

'

2

1

(2.34)

Indukcyjność magnesowania oblicza się z zależności

Fe

Fe

Fe

m

m

l

S

N

N

L

µ

2

1

2

1

=

Λ

=

(2.35)

gdzie:

Λ

m

– przewodność magnetyczna rdzenia transformatora,

µ

Fe

– przenikalność

magnetyczna rdzenia, l

Fe

, S

Fe

– długość rdzenia i przekrój poprzeczny rdzenia.

Ze względu, że

µ

Fe

>>

µ

0

, to reaktancja magnesowania rdzenia jest dużo większa od reaktancji

rozproszenia uzwojenia czyli X

m

>>X

1

σ

. Napięcia indukowane E

1

i E

2

są ze sobą w fazie i

wyprzedzają strumień główny a tym samym prąd magnesujący o kąt

π

/2.

Uwzględniając zależności (2.25), (2.33) i (2.34) równania napięciowe transformatora można

zapisać w postaci

(

)

m

m

I

X

j

I

X

j

R

E

I

X

j

I

R

U

+

+

=

+

+

=

1

1

1

1

1

1

1

1

1

σ

σ

(2.36)

(

)

m

m

I

X

j

I

jX

R

E

I

jX

I

R

U

+

+

=

+

+

=

'

2

'

2

'

2

'
2

'

2

'

2

'

2

'

2

'
2

σ

σ

(2.37)

Równaniom (2.36) i (2.37) odpowiada schemat zastępczy transformatora o parametrach

sprowadzonych do strony pierwotnej (rys. 2.10).

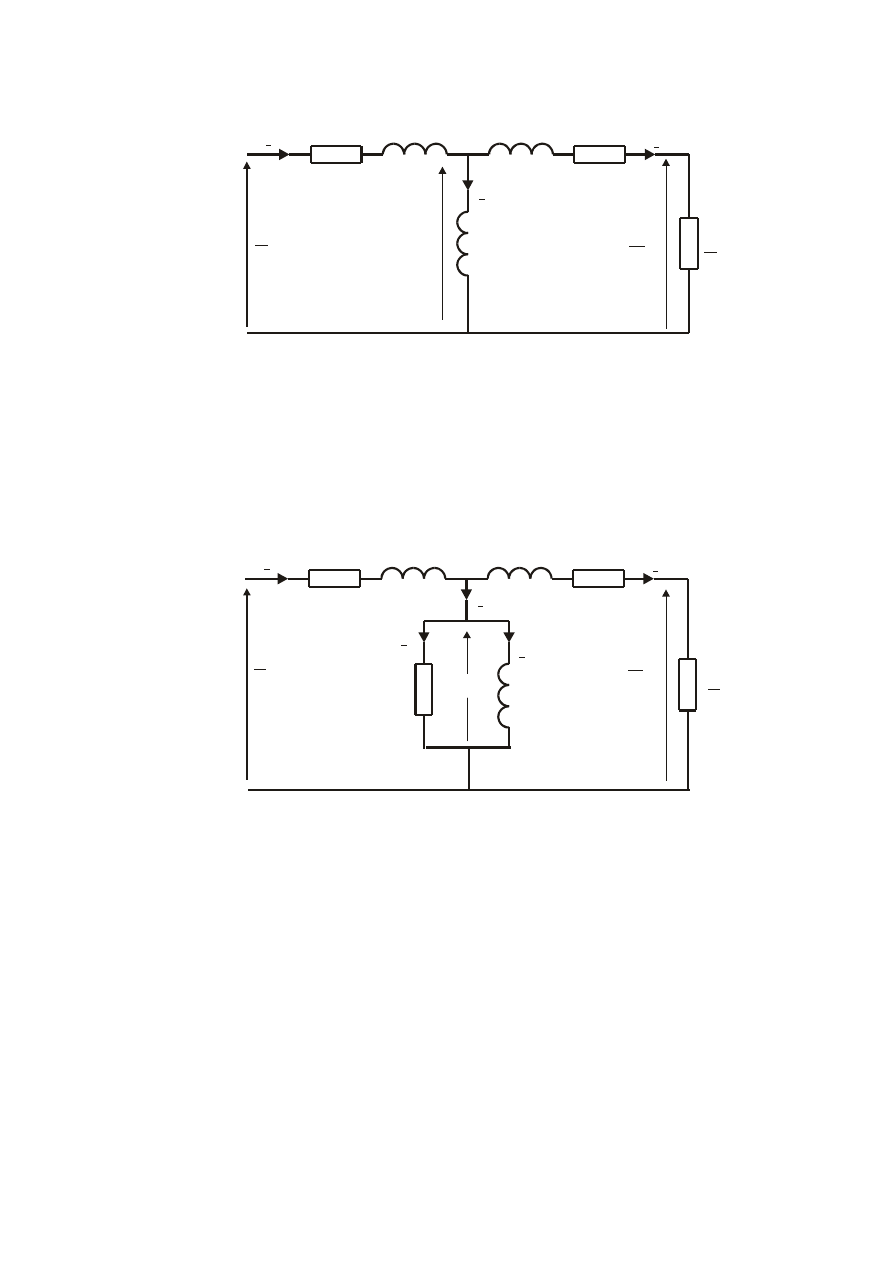
Rys. 2.10. Schemat zastępczy transformatora

Schemat zastępczy przedstawiony na rys. 2.10 nie uwzględnia strat w rdzeniu transformatora.

Schemat ten należy uzupełnić o gałąź poprzeczną, z elementem rezystancyjnym R

Fe

reprezentującym straty w rdzeniu, przez którą przepływa prąd I

Fe

(rys. 2.11).

Rys. 2.11. Schemat zastępczy transformatora z uwzględnieniem strat w rdzeniu

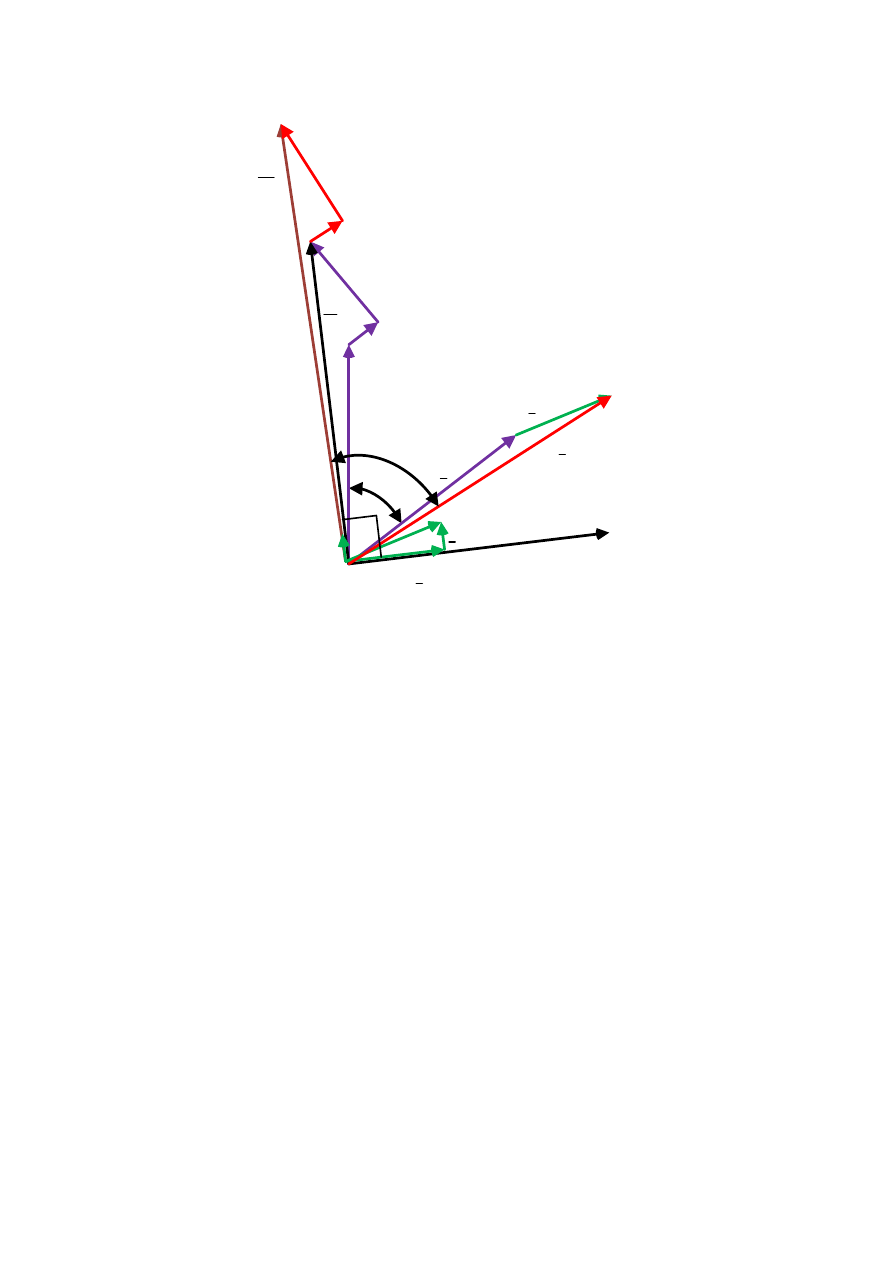
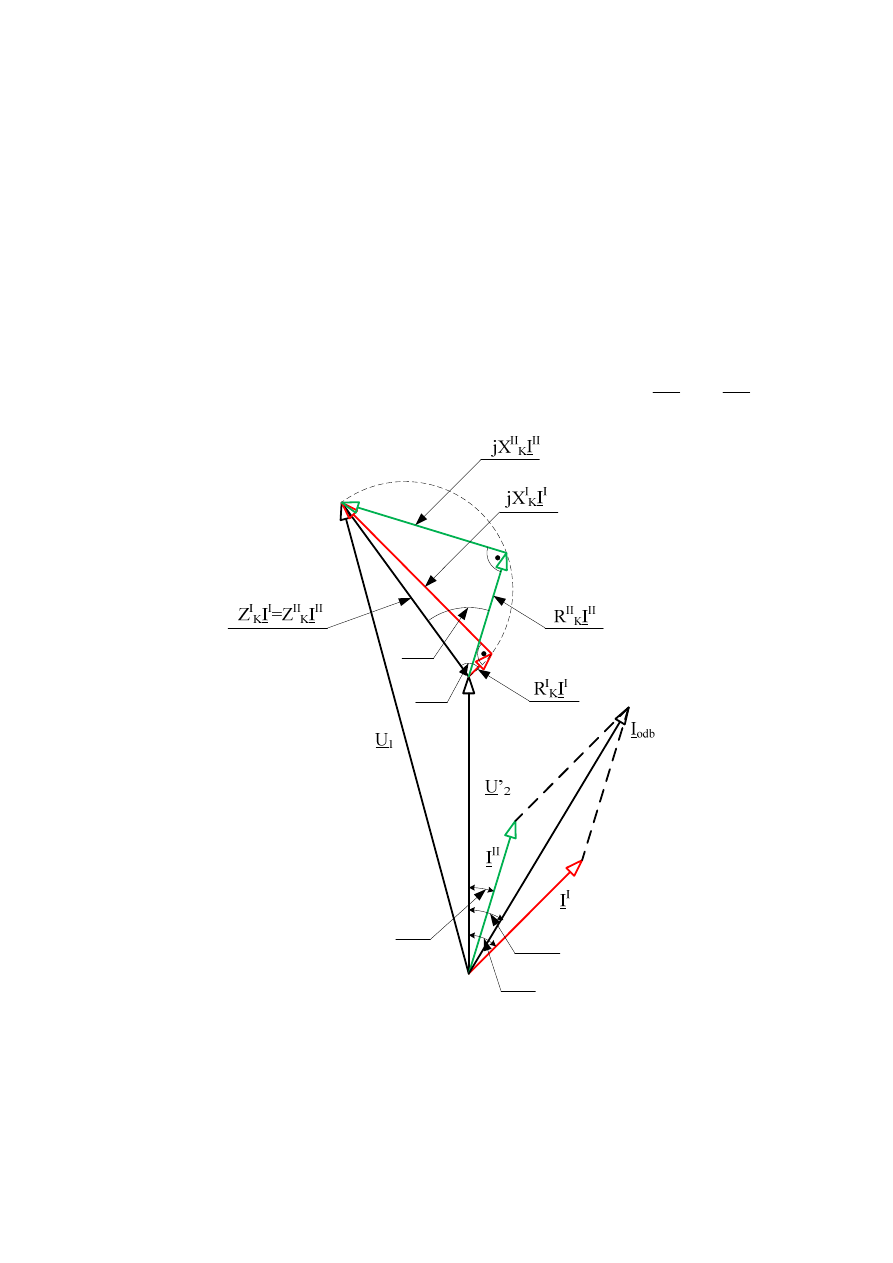
Na podstawie równań napięciowych i schematu zastępczego transformatora można sporządzić

wykres wskazowy prądów i napięć (rys. 2.12.) dla zadanych wartości U

2

, I

2

, cos

ϕ

2

i znanych

parametrów schematu zastępczego.

X

m

X

’

2

σ

R

1

X

1

σ

I

1

I

’

2

R

’

2

U

1

U’

2

E =E

1

2

'

I

m

Z

'

obc

X

m

X

’

2

σ

R

1

X

1

σ

I

1

I

’

2

R

’

2

U

1

U’

2

E =E

1

2

'

I

m

Z

'

obc

I

Fe

R

Fe

I

0

Φ

'

'

2 2

R I

'

'

2

2

X

I

σ

'
2

U

1

E

1

I

'
2

I

0

I

1

U

1 1

R I

1

1

X

I

σ

Fe

I

m

I

2

ϕ

1

ϕ

Rys. 2.12. Wykres wektorowy transformatora w stanie obciążenia

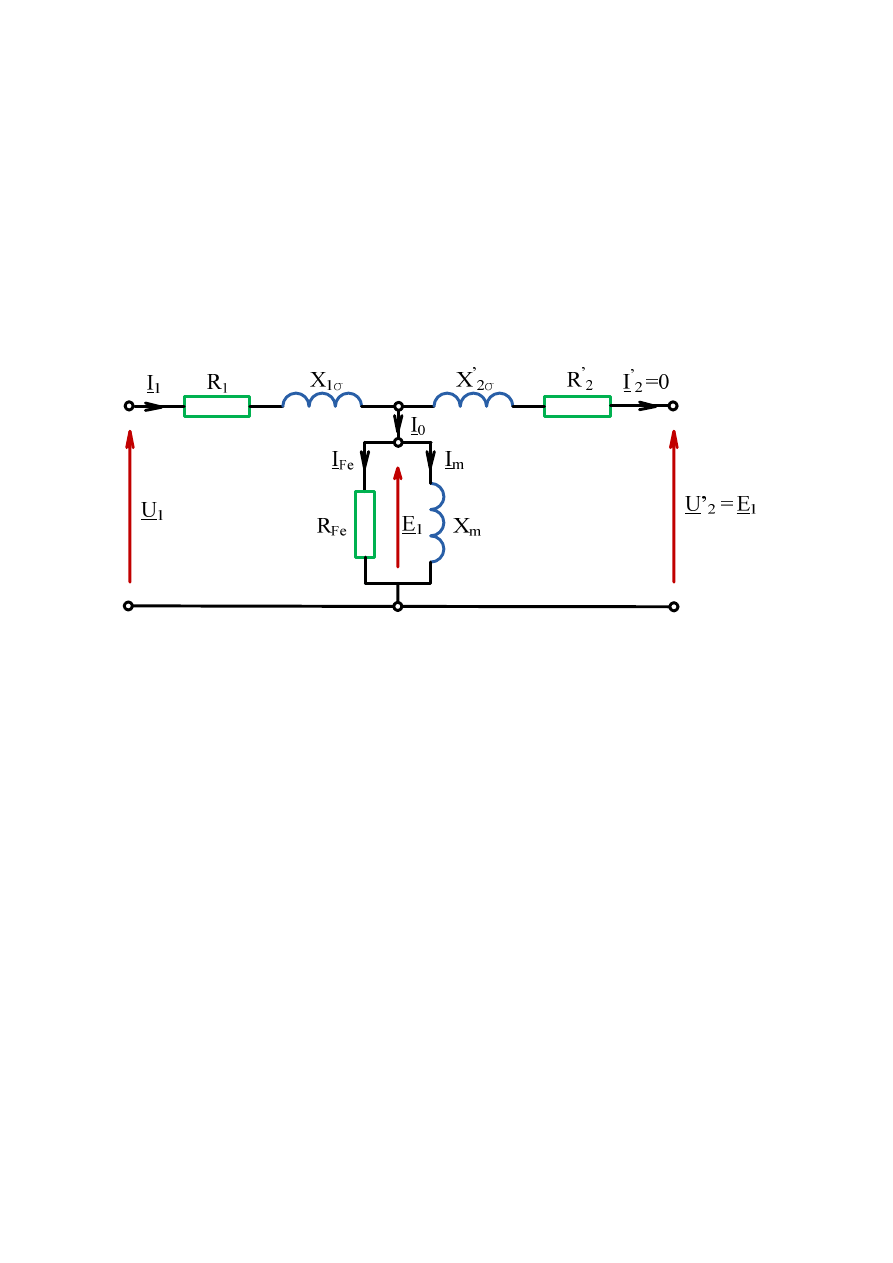
2.3. STAN PRACY TRANSFORMATORA

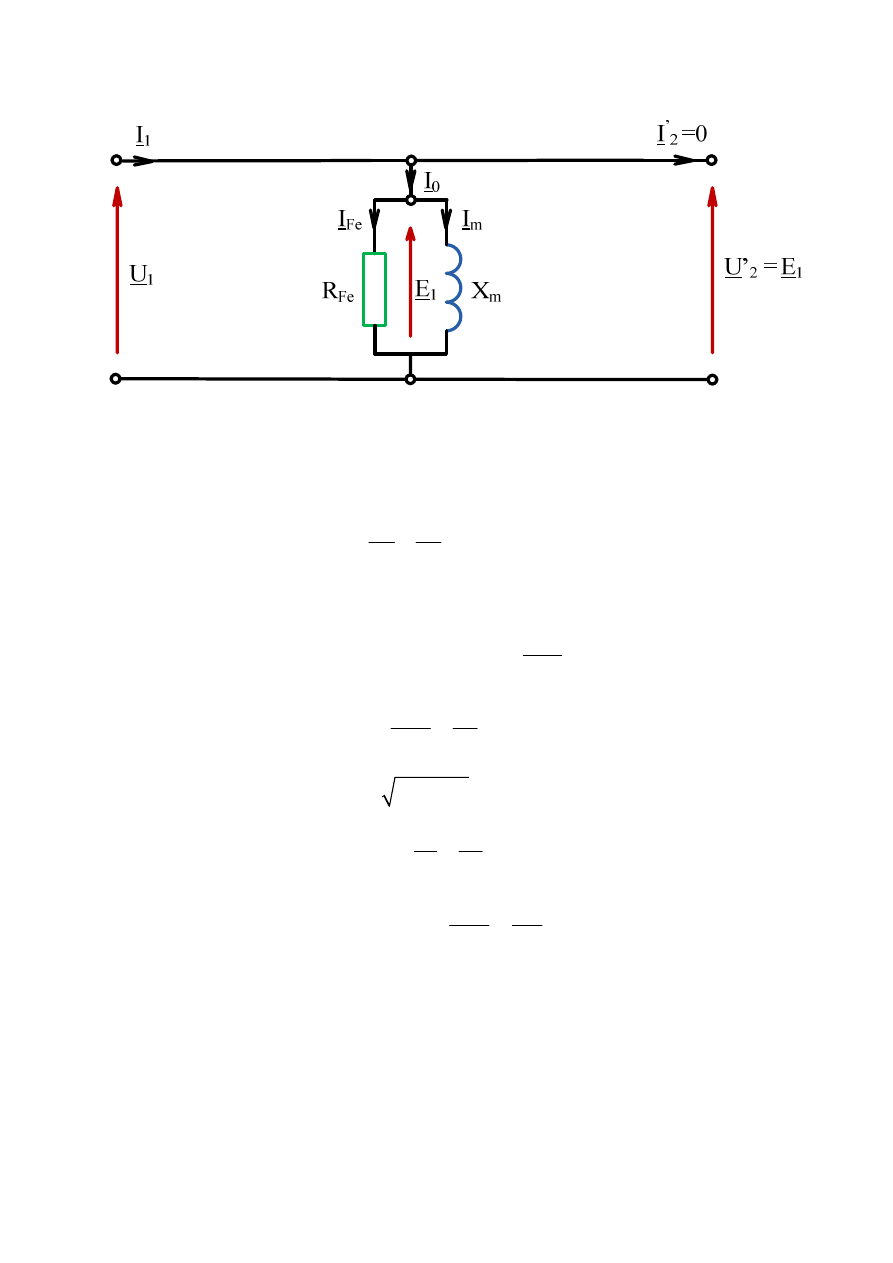
2.3.1. Stan jałowy pracy transformatora

Stanem jałowym pracy transformatora nazywamy taki stan, w którym strona wtórna

transformatora jest rozwarta, czyli I’

2

=0.

Wynika stąd, że U

2

= E

1

,

a prąd pobierany z sieci I

1

jest równy prądowi gałęzi poprzecznej I

0

.

Schemat zastępczy transformatora w stanie biegu jałowego przedstawia rys. 2.13.

Rys. 2.13. Schemat zastępczy transformatora w stanie biegu jałowego

Przedstawione na rys. 2.13 parametry transformatora mogą być przyjęte jako stałe za

wyjątkiem

X

m

tj. reaktancji magnesowania transformatora, która zależy od stanu nasycenia.

Poszczególne parametry transformatora oznaczają:

U

1

– napięcie fazowe zasilania strony pierwotnej transformatora,

U’

2

– napięcie fazowe strony wtórnej transformatora,

I

0

, I

Fe

, I

m

- prądy

odpowiednio: biegu jałowego,

odpowiedzialny za straty mocy w rdzeniu

transformatora, magnesowania

E

1

– napięcie fazowe gałęzi poprzecznej strony pierwotnej transformatora,

R

1

– rezystancja uzwojenia strony pierwotnej transformatora,

R’

2

– sprowadzona na stronę pierwotną rezystancja strony wtórnej transformatora,

R

Fe

– rezystancja obrazująca straty mocy w rdzeniu transformatora,

X

1

σσσσ

– reaktancja rozproszenia uzwojenia strony pierwotnej transformatora,

X’

2

σσσσ

– sprowadzona na stronę pierwotną reaktancja rozproszenia strony wtórnej

transformatora,

X

m

– reaktancja magnesowania transformatora.

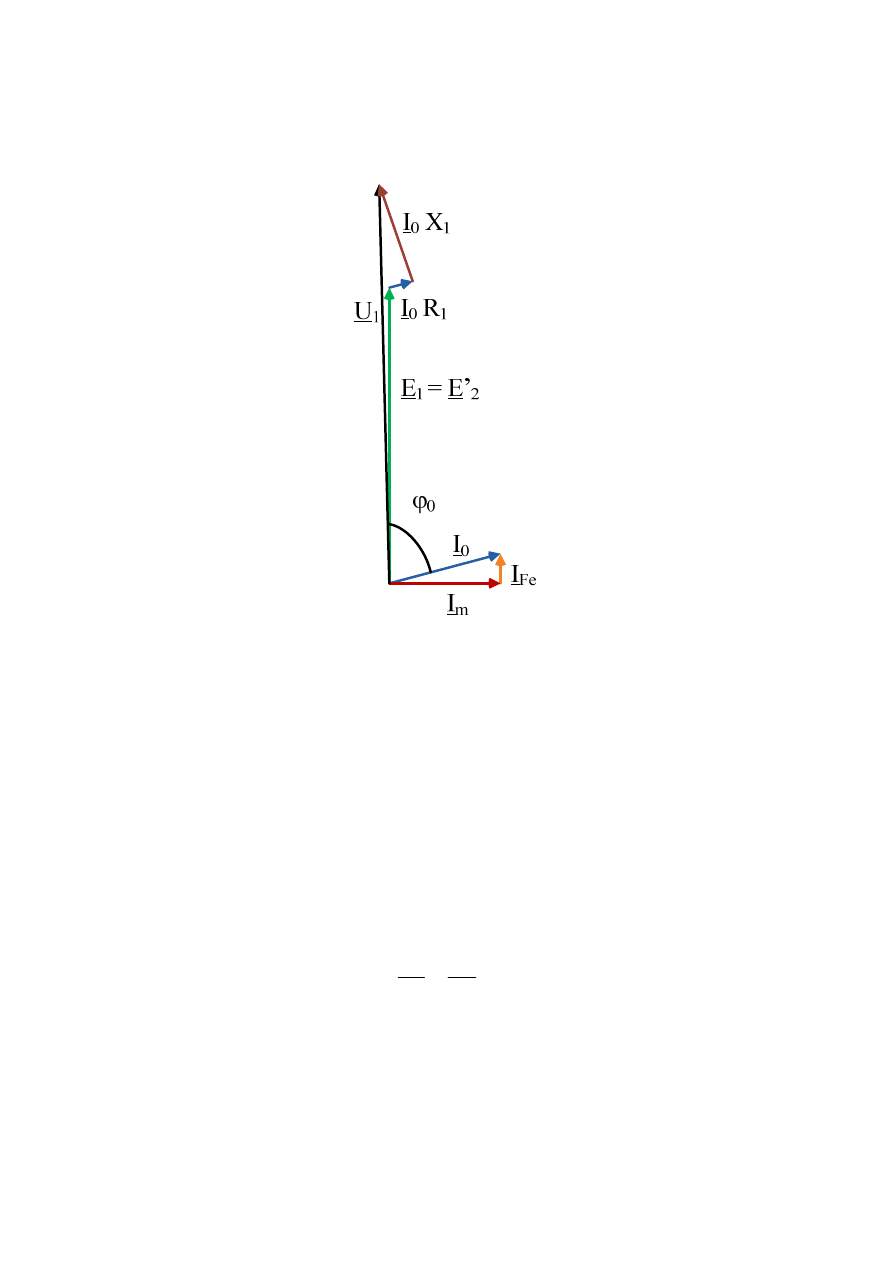
Na rys. 2.14 przedstawiono wykres wskazowy napięć i prądów dla transformatora

pracującego w stanie biegu jałowego.

Rys. 2.14. Wykres wskazowy napięć i prądów dla transformatora pracującego w stanie biegu jałowego

Prąd stanu jałowego dla transformatorów wynosi od około 3 – 12 % prądu znamionowego.

Przy czym większe wartości odnoszą się do małych transformatorów. W przypadku

transformatorów o bardzo małej mocy rzędu kilku watów np. używanych w zasilaczach,

sprzęcie AV prąd biegu jałowego przekracza nawet 60% prądu znamionowego.

W transformatorach większej mocy prąd biegu jałowego jest niewielki stąd pomija się spadki

napięcia na rezystancji i reaktancja uzwojenia strony pierwotnej transformatora. Nawet przy

obciążeniu spadek ten wynosi 2 – 3 % napięcia znamionowego. W tym stanie pracy

wyznacza się przekładnię napięciową, która jest równa przekładni zwojowej.

1

1

2

2

u

E

U

n

K

E

U

=

≈

=

(2.38)

W stanie biegu jałowego moc strat na rezystancji uzwojenia strony pierwotnej transformatora

∆

P

cu

jest do pominięcia w odniesieniu do strat mocy w rdzeniu. Czyli

∆

P

0

≈

∆

P

Fe.

Natomiast

moce

∆

P

cu

oraz

∆

P

Fe

są w przybliżeniu równe dopiero w stanie obciążenia znamionowego.

W stanie jałowym pracy prąd pobierany przez transformator jest praktycznie równy prądowi

magnesującemu I

m

. Czyli

1

m

I N

Hl

=

. Wynika stąd, że

m

I ~ H

.

Na rys. 2.15 przedstawiono charakterystykę magnesowania

Φ

=f(I

m

)

jako U

1

=f(I

0

).

0

m

I

·I

≈

1

U ·

≈Φ

1N

U

0 N

I

Rys. 2.15. Charakterystyka magnesowania

Φ

=f(I

m

) jako U

1

=f(I

0

)

Zależność strat mocy od napięcia zasilania podczas pracy jałowej transformatora przedstawia

charakterystyka na rys. 2.16.

0

P

1

U

1N

U

0

Fe

P

P

= ∆

Rys. 2.16. Zależność strat mocy od napięcia zasilania

Moc stanu jałowego może być określona jako:

2

2

2

2

1 3

.

Fe

h

w

Fe

P

C B f

C B f

C B f

∆

≈

+

≈

(2.39)

Gdzie C

h

oraz C

w

są stałymi zależnymi od rodzaju materiału.

Zasilanie transformatora ze źródła o stałej częstotliwości i regulowanym napięciu prowadzi

do zależności:

1

1

1

1

4 44

E

B

c

c U

S

.

fN

Φ

=

=

≈

(2.40)

Stad przyjmuje się, że starty w rdzeniu są proporcjonalne do kwadratu napięcia zasilania

1

FE

P

cU

∆

≈

.

Przy zachowaniu stałej wartości napięcia zasilania i zmiennej częstotliwości towarzyszyć

będzie zmiana indukcji

1

1

1

4 44

E

c

B

c

S

.

fN

f

Φ

=

=

≈

czyli

2

1

h

h

C

P

C B f

f

∆ ≈

≈

. Natomiast

straty wiroprądowe

2

2

1

w

w

w

P

C B f

C

∆ ≈

≈

. Zatem zależność strat w rdzeniu przy U

1

= const

określa się jako:

1

1

h

Fe

h

w

w

C

P

P

P

C

f

∆

≈ ∆ + ∆ ≈

+

(2.41)

Zmniejszenie

częstotliwości

przy

U

1

=

const

spowoduje

wzrost

strumienia

1

1

4 44

E

c

.

fN

Φ ≈

co z kolei powoduje wzrost prądu magnesującego. Aby tego uniknąć i

utrzymywać wartość strumienia stałą należy regulować zarówno napięcie jak i częstotliwość

1

1

1

1

4 44

E

U

B

c

c

S

.

fN

f

Φ

=

=

≈

(2.42)

Straty podczas pracy w warunkach znamionowych:

2

2

hN

h

N

N

P

C B f

∆

≈

i

2

2

wN

w

N

N

P

C B f

∆

≈

(2.43)

Straty podczas pracy w warunkach innych niż znamionowych:

2

2

h

h

P

C B f

∆ ≈

i

2

2

w

w

P

C B f

∆ ≈

(2.44)

Straty te odniesione do znamionowych wynoszą:

2

2

2

2

2

N

h

hN

hN

N

N

N

N

f

B

f

Bf

P

P

P

B

f

B f

f





∆ = ∆

= ∆









(2.45)

2

2

2

2

2

w

wN

wN

N

N

N

N

B

f

Bf

P

P

P

B

f

B f





∆ = ∆

= ∆









(2.46)

Uwzględniając, że

1

1

1

1

4 44

U

E

.

fz

c Bf

=

=

Φ =

(2.47)

1

1

1

1

4 44

N

N

N

N

N

N

U

E

.

f z

c B f

=

=

Φ =

(2.48)

Czyli:

1

1N

B f

U

B f

U

=

(2.49)

Stąd po podstawieniu otrzymuje się:

2

1

1

N

h

hN

N

f

U

P

P

U

f





∆ = ∆









oraz

2

1

1

w

wN

N

U

P

P

U





∆ = ∆









(2.50)

Całkowite straty mocy

2

2

1

1

1

1

N

h

w

hN

wN

N

N

f

U

U

P

P

P

P

P

U

f

U









∆ = ∆ + ∆ = ∆

+ ∆

















(2.51)

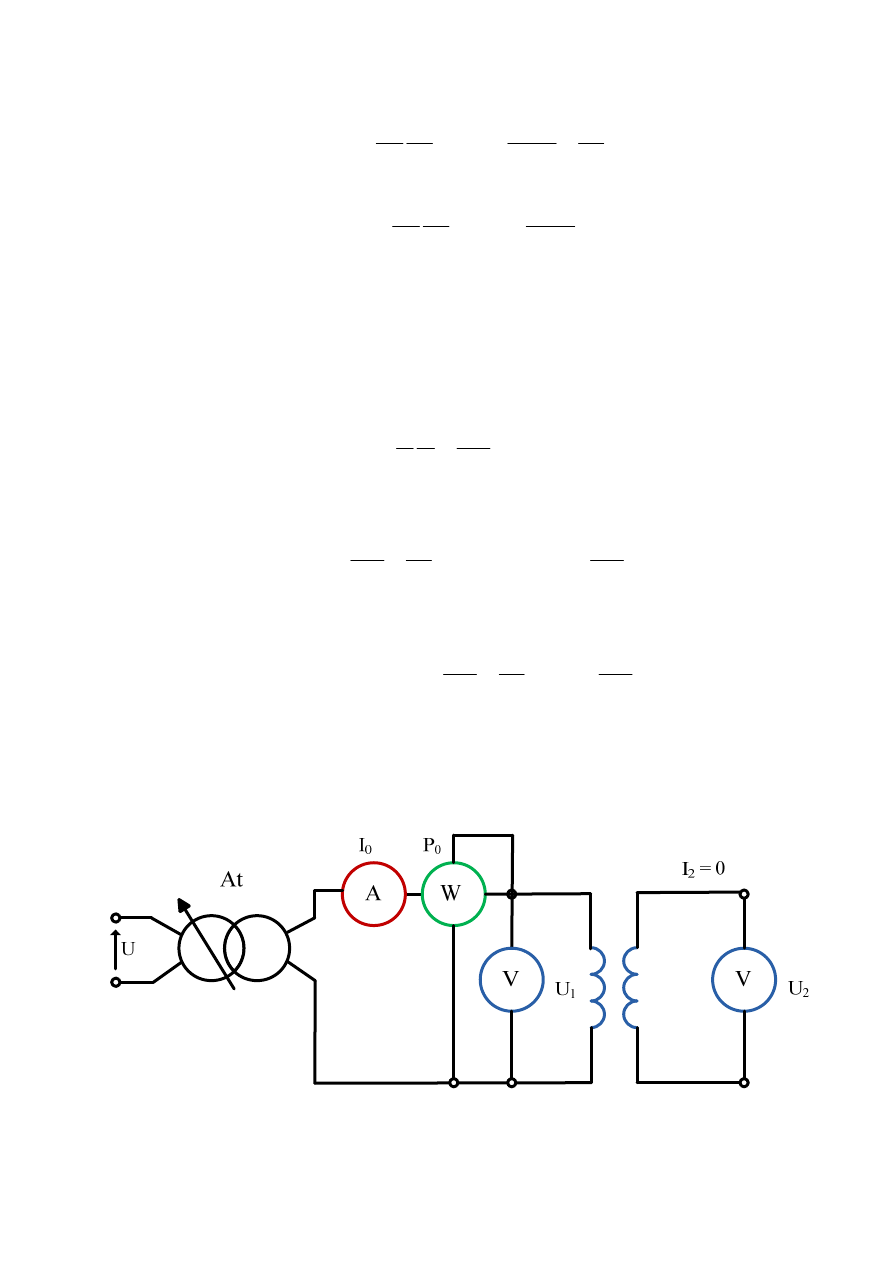
Na podstawie pomiaru napięcia U

1

, prądu I

0

i mocy P

0

w stanie biegu jałowego transformatora

w układzie jak na rys. 2.17. można obliczyć parametry gałęzi poprzecznej schematu

zastępczego jak na rys. 2.18.

Rys. 2.17. Pomiar napięcia, prądu i mocy w stanie biegu jałowego transformatora

Rys. 2.18. Parametry gałęzi poprzecznej schematu zastępczego

W tym stanie oblicza się:

•

Przekładnię transformatora:

1

1

2

2

u

U

Ę

K

n

U

E

≈

=

=

•

Straty w rdzeniu:

0

Fe

P

P

∆

=

•

Współczynnik mocy w stanie jałowym:

0

0

1 0

P

cos

U I

ϕ

=

•

Składową czynną prądu:

0

1

1

Fe

Fe

P

P

I

E

U

∆

=

≈

•

Składową bierną prądu:

2

2

0

m

Fe

I

I

I

=

−

•

Reaktancje magnesowania:

1

1

m

m

m

E

U

X

I

I

=

≈

•

Rezystancję gałęzi poprzecznej:

2

2

1

1

0

m

Fe

E

U

X

P

P

=

≈

∆

2.3.2. Stan zwarcia transformatora

Stanem zwarcia w czasie pracy transformatora nazywamy taki stan, w którym strona

pierwotna jest zasilona ze źródła, natomiast strona wtórna jest zwarta, czyli U’

2

=0. Wynika

stąd, że U

2

= 0, a prąd pobierany z sieci I

1

w przypadku napięcia zasilania bliskiego

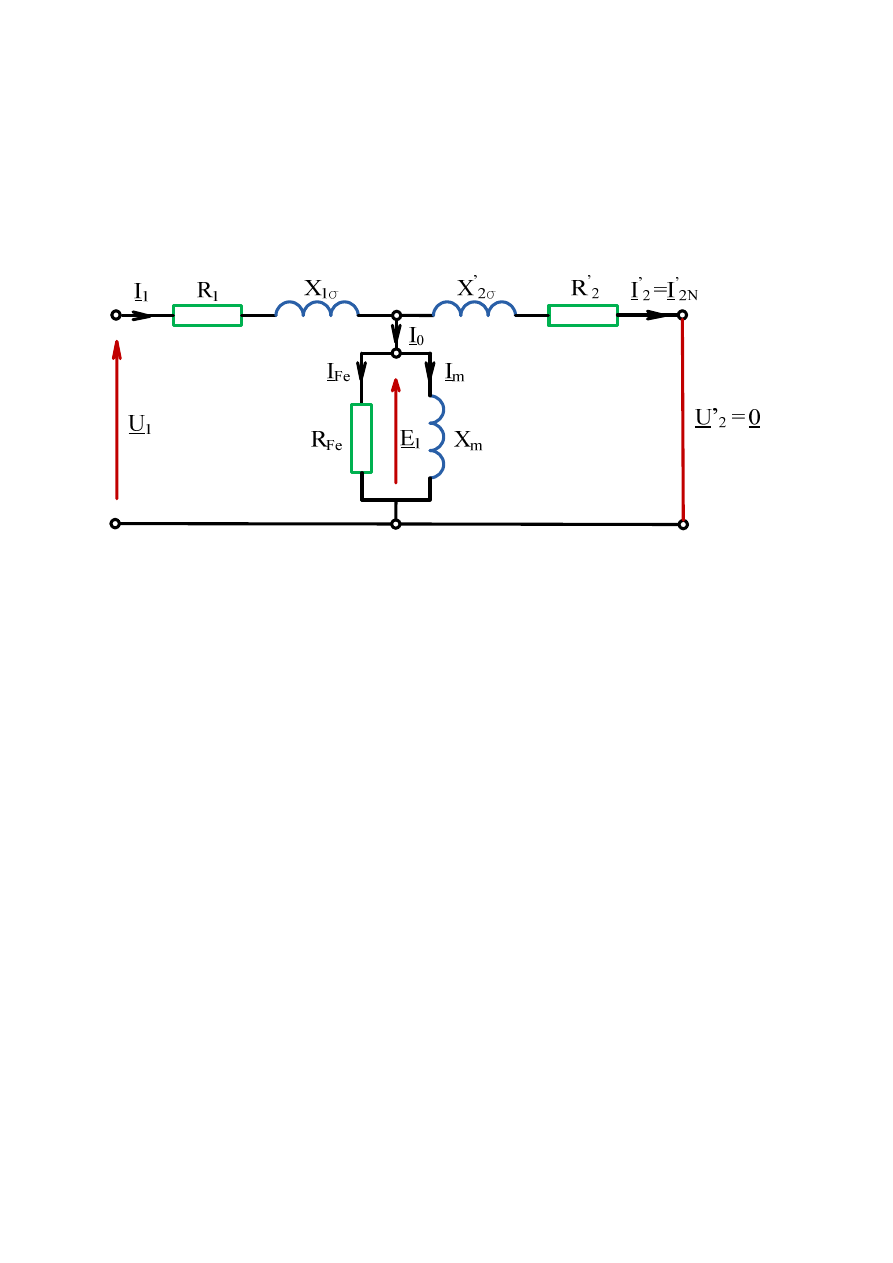
znamionowemu może wynosić kilkanaście czy nawet kilkadziesiąt razy prąd I

N

. Jest to stan

bardzo niebezpieczny. Dlatego w laboratorium przeprowadza się stan zwarcia pomiarowego.

W stanie zwarcia pomiarowego uzwojenie pierwotne zasila się takim napięciem przy którym

w obu uzwojeniach popłyną prądy znamionowe. Schemat zastępczy transformatora w stanie

zwarcia przedstawia rys. 2.19.

Rys. 2.19. Schemat zastępczy transformatora w stanie zwarcia

Przedstawione na rys. 2.19 parametry transformatora mogą być przyjęte jako stałe za

wyjątkiem

X

µµµµ

tj. reaktancji magnesowania transformatora, która zależy od stanu nasycenia.

Poszczególne parametry transformatora oznaczają:

U

1

– napięcie fazowe zasilania strony pierwotnej transformatora,

U’

2

– napięcie fazowe strony wtórnej transformatora,

I

0

, I

Fe

, I

m

- prądy

odpowiednio: biegu jałowego,

odpowiedzialny za straty mocy w rdzeniu

transformatora, magnesowania

E

1

– napięcie fazowe gałęzi poprzecznej strony pierwotnej transformatora,

R

1

– rezystancja uzwojenia strony pierwotnej transformatora,

R’

2

– sprowadzona na stronę pierwotną rezystancja strony wtórnej transformatora,

R

Fe

– rezystancja obrazująca straty mocy w rdzeniu transformatora,

X

1

– reaktancja uzwojenia strony pierwotnej transformatora,

X’

s2

– sprowadzona na stronę pierwotną reaktancja strony wtórnej transformatora,

X

m

– reaktancja magnesowania transformatora.

Napięcie zwarcia wynosi od 4 – 12% U

N

. Dlatego pomija się gałąź poprzeczną.

Uproszczony schemat zastępczy transformatora w stanie zwarcia przedstawia rys. 2.20.

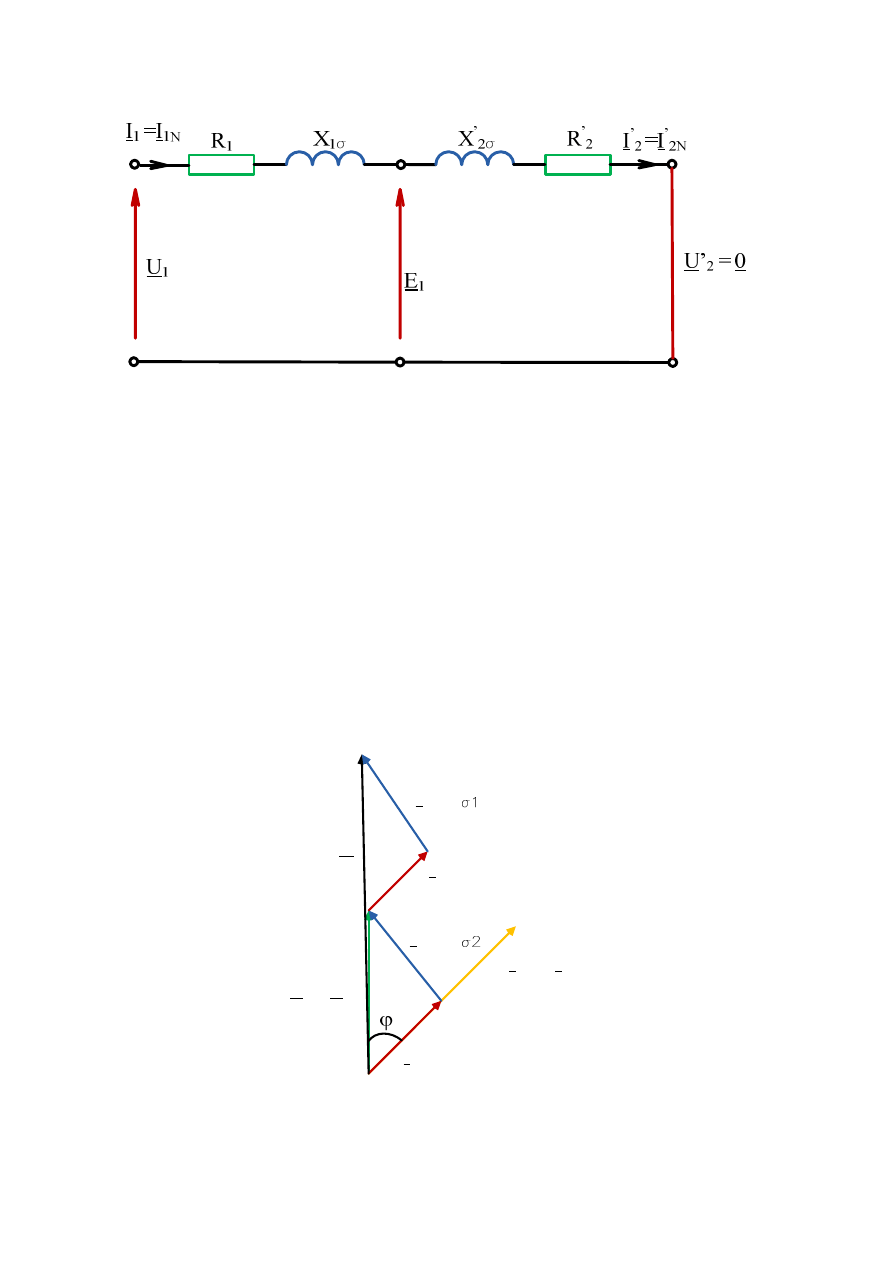
Rys. 2.20. Uproszczony schemat zastępczy transformatora w stanie zwarcia

W stanie zwarcia można napisać zależność:

1

1

1 1

1

1

N

K

K

U

E

R I

jX

I

σ

=

+

+

(2.52)

2

2

2

2

2

0

K

K

E'

R' I '

jX I '

σ

=

+

+

(2.53)

Oraz

1

2

K

K

I

I '

=

(2.54)

Na rys. 2.21 przedstawiono wykres wskazowy napięć i prądów dla transformatora

pracującego w stanie zwarcia. Przy czym: Rezystancja zwarcia

R

K

=R

1

+R’

2

oraz

reaktancja

zwarcia

X

K

=X

σ

1

+X’

σ

2.

E

1

= E’

2

K

U

1

I’

2K

R’

2

I

1K

= I’

2K

I

1K

R

1

I’

2K

X’

I

1K

X

Rys. 2.21. Wykres wskazowy napięć i prądów dla transformatora pracującego w stanie zwarcia

Schemat zastępczy z rys. 2.20 i wykres z rys. 2.21 można uprościć do przedstawionych na

rys. 2.22.

R

K

X

U

1K

I

1K

=I

1N

Rys. 2.22. Uproszczony schemat zastępczy z rys. 2.20 i wykres z rys. 2.21

2

2

1K

R

X

U

U

U

=

+

(2.55)

Gdzie:

1

R

K

K

U

R I

=

oraz

1

X

K

K

U

X I

=

Przy napięci zasilania U

1

=U

1N

prąd zwarcia

1

1

N

K

K

U

I

Z

=

Przy napięci zasilania U

1

=U

1K

prąd zwarcia

1

1

K

N

K

U

I

Z

=

Stąd

1

1

1

1

N

K

K

N

U

I

U

I

=

(2.56)

W jednostkach względnych

1

1

1

r

K

K

N

I

I

I

=

(2.57)

1

1

1

r

K

K

N

U

U

U

=

(2.58)

Czyli:

1

1

1

r

K

r

K

U

I

=

(2.59)

1

1

1

1

1

1

N

r

N

N

K

K

r

N

K

K

K

U

I

Z

I

I

I

Z

Z

Z

=

=

=

=

(2.60)

W stanie zwarcia moc pobierana jest mocą strat na rezystancji uzwojeń strony pierwotnej i

wtórnej transformatora

∆

P

cu

.

2

2

2

2

1

1

2

2

1

1

2

2

'

'

K

cu

K

K

K

K

P

P

I

R

I

R

I

R

I

R

= ∆

=

+

=

+

(2.61)

Czyli

2

2

1

1

2

1

(

' )

K

K

K

K

P

I

R

R

I

R

=

+

=

(2.62)

Zależność strat mocy od napięcia zasilania podczas pracy transformatora w stanie zwarcia

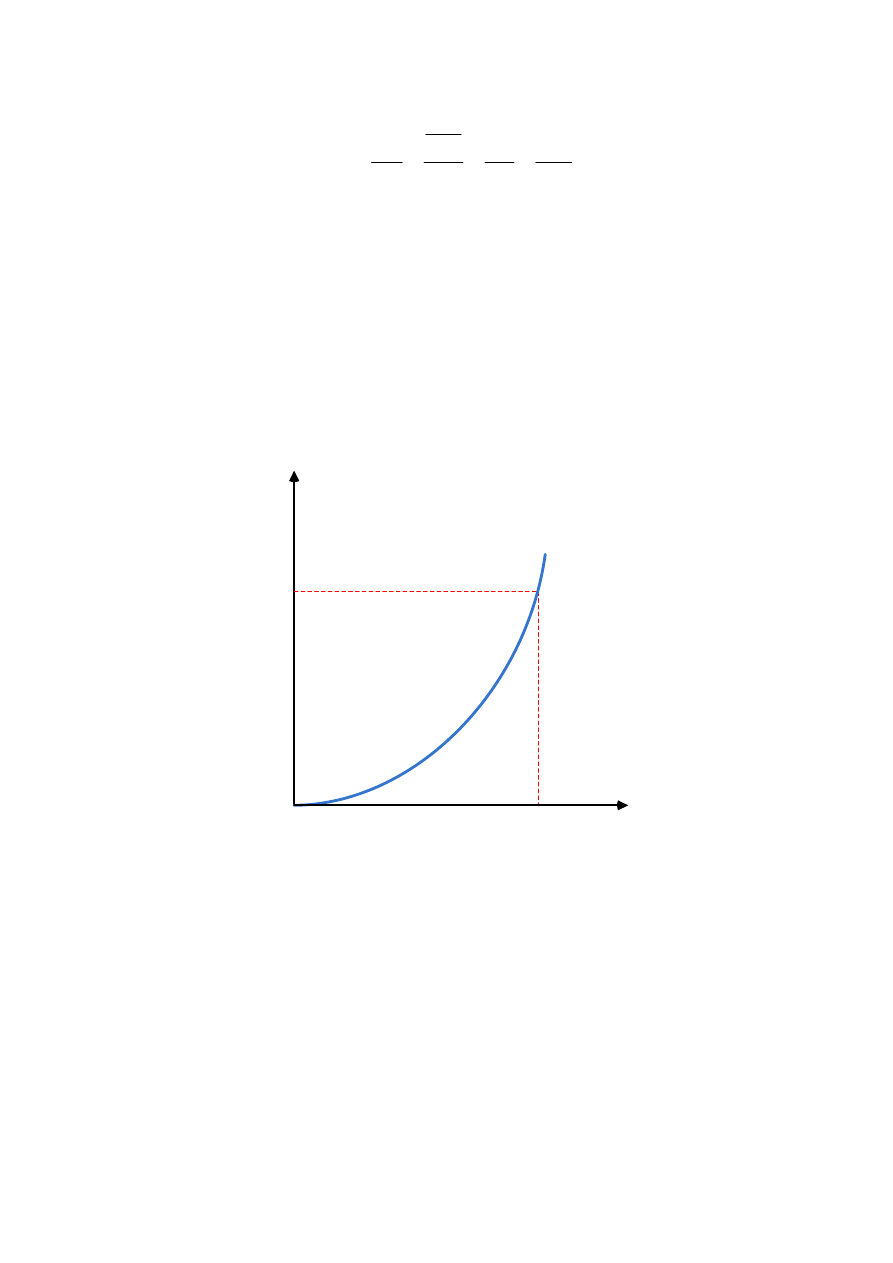
przedstawia charakterystyka na rys. 2.23.

K

P

1

U

1K

U

K

cu

P

P

= ∆

Rys. 2.23. Zależność strat mocy od napięcia zasilania

Na podstawie pomiaru napięcia U

1

, prądu I

K

i mocy P

K

w stanie zwarcia transformatora

w układzie jak na rys. 2.24 można obliczyć parametry gałęzi podłużnej schematu zastępczego

jak w układzie z rys. 2.25.

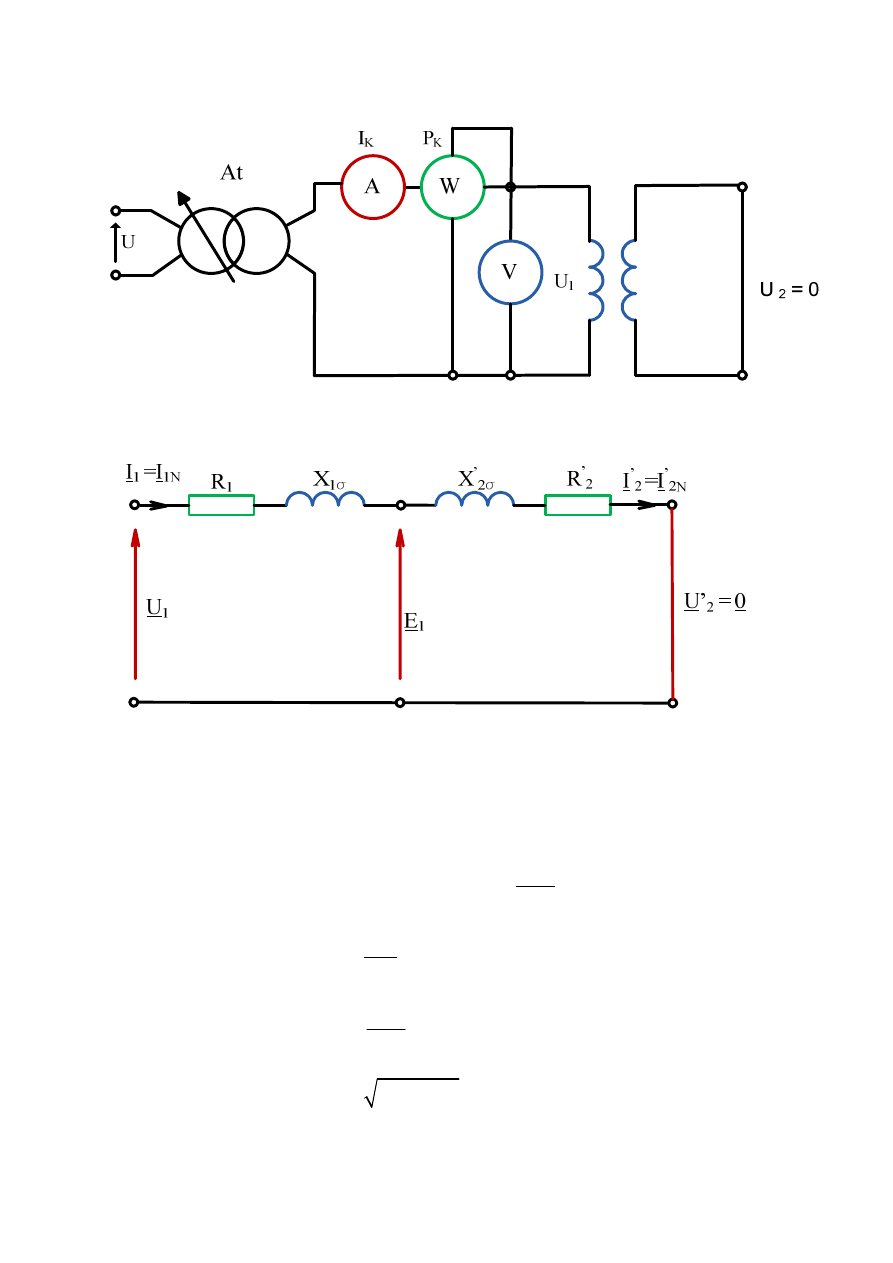
Rys. 2.24. Pomiar napięcia, prądu i mocy w stanie zwarcia transformatora

Rys. 2.25. Parametry gałęzi podłużnej schematu zastępczego

W tym stanie oblicza się:

•

Straty w uzwojeniu:

cu

K

P

P

∆ =

•

Współczynnik mocy w stanie zwarcia:

0

0

1 0

P

cos

U I

ϕ

=

•

Impedancja zwarcia:

1

1

K

K

N

U

Z

I

=

•

Rezystancję zwarcia:

2

1

cu

K

N

P

R

I

∆

=

•

Reaktancję zwarcia:

2

2

K

K

K

X

Z

R

=

−

Zwykle przyjmuje się:

1

2

2

K

R

R

R'

=

=

(2.63)

1

2

2

K

X

X

X '

σ

σ

=

=

(2.64)

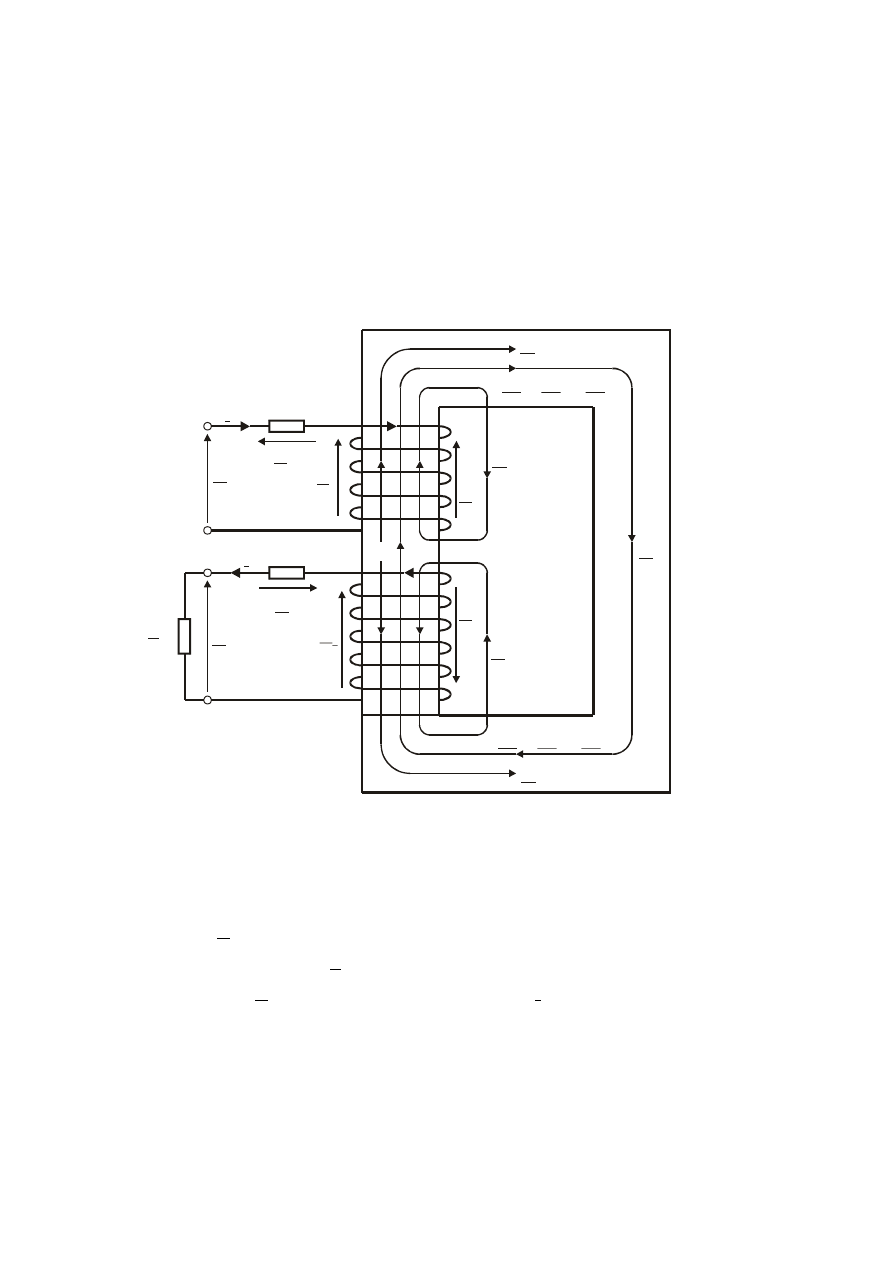
2.4. TRANSFORMATORY TRÓJFAZOWE

2.4.1 . Sposoby połączeń uzwojeń

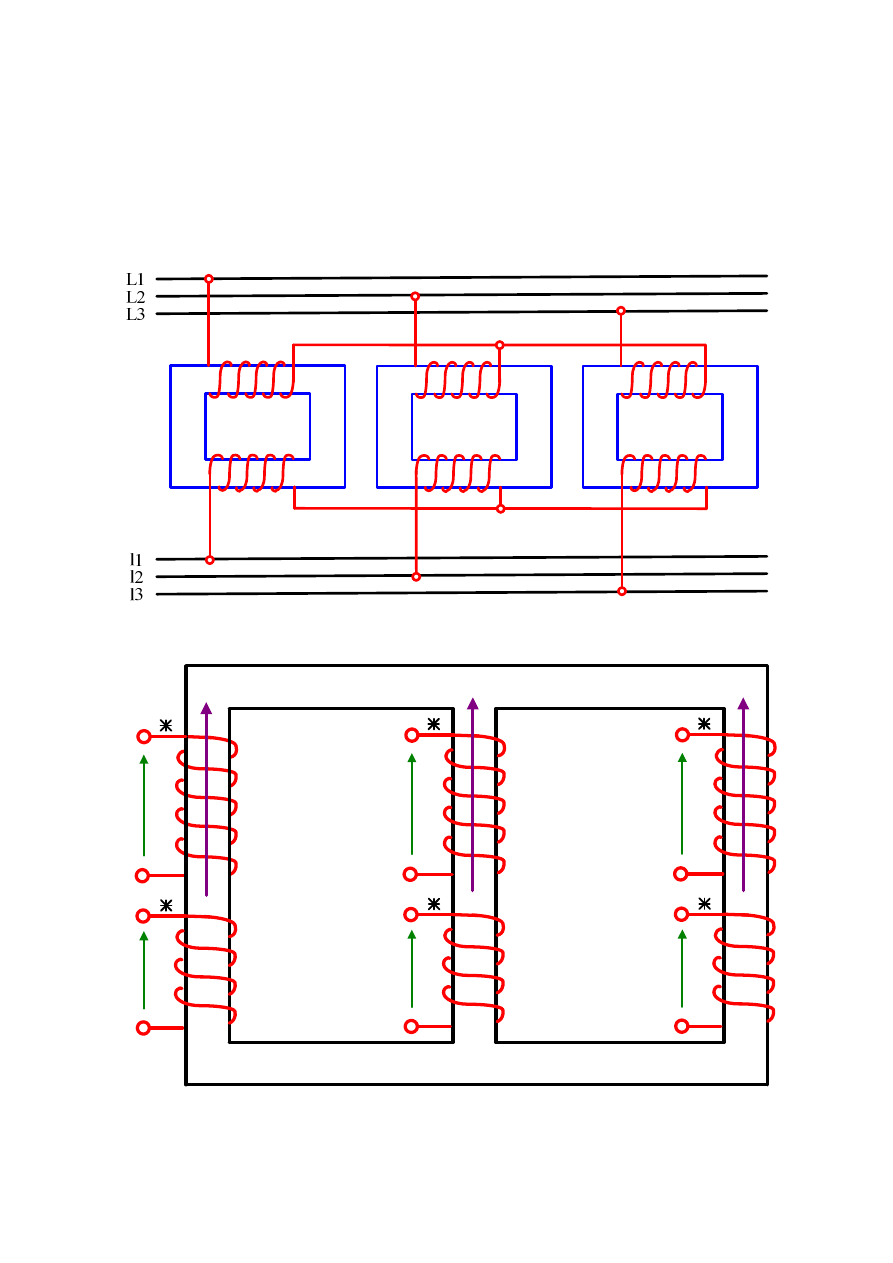
Transformowanie napięć w sieci trójfazowej można dokonać za pomocą trzech

transformatorów jednofazowych jak to pokazano na rys. 2.26 lub jednego transformatora

trójkolumnowego – rys. 2.27- lub pięciokolumnowego.

Rys. 2.26. Transformowanie napięć w sieci trójfazowej można dokonać za pomocą trzech

transformatorów jednofazowych

A

U

a

U

B

U

b

U

C

U

c

U

A

Φ

B

Φ

C

Φ

Rys. 2.27. Transformowanie napięć w sieci trójfazowej można dokonać za pomocą transformatora

trójkolumnowego

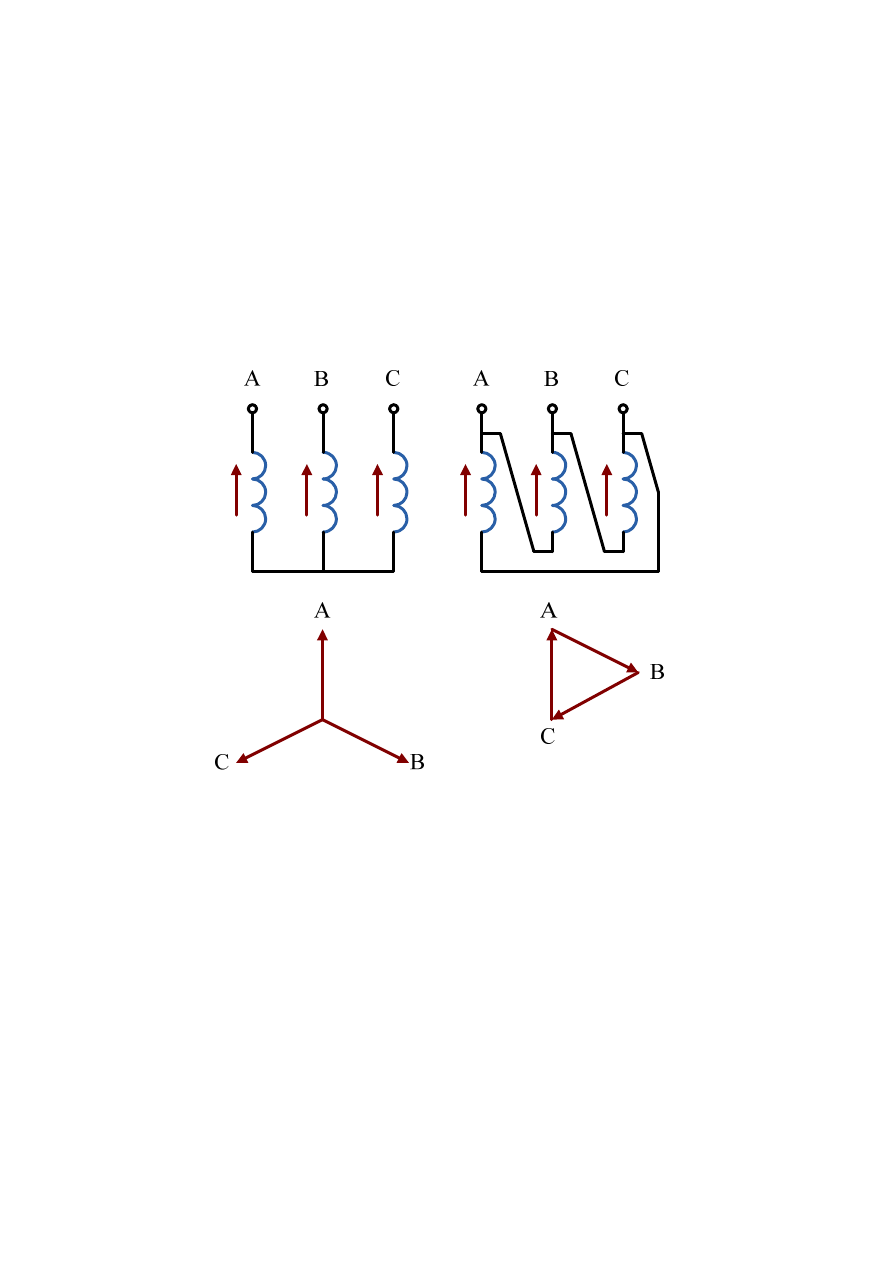
Stosowane są trzy rodzaje grup połączeń:

•

W gwiazdę oznaczone jako: strona pierwotna -

Y

i strona wtórna –

y

,

•

W trójkąt oznaczone jako: strona pierwotna -

D

i strona wtórna –

d

,

•

W zygzak oznaczone jako: strona wtórna –

z

.

Duże litery dotyczą strony pierwotnej, natomiast małe litery strony wtórnej.

Przykład połączeń uzwojeń transformatora w gwiazdę, trójkąt, w zygzak oraz odpowiadające

im wykresy wskazowe napięć przedstawia rys. 2.28.

A

U

A

U

C

U

C

U

B

U

A

U

B

U

C

U

A

U

B

U

C

U

Rys. 2.28. Przykład połączeń uzwojeń transformatora w gwiazdę, trójkąt oraz odpowiadające im

wykresy wskazowe napięć

Przykłady innego połączenia uzwojeń transformatora w trójkąt przedstawiono na rys. 2.29

oraz połączenie strony wtórnej transformatora w zygzak i odpowiadające im wykresy

wskazowe napięć przedstawia rys. 2.30.

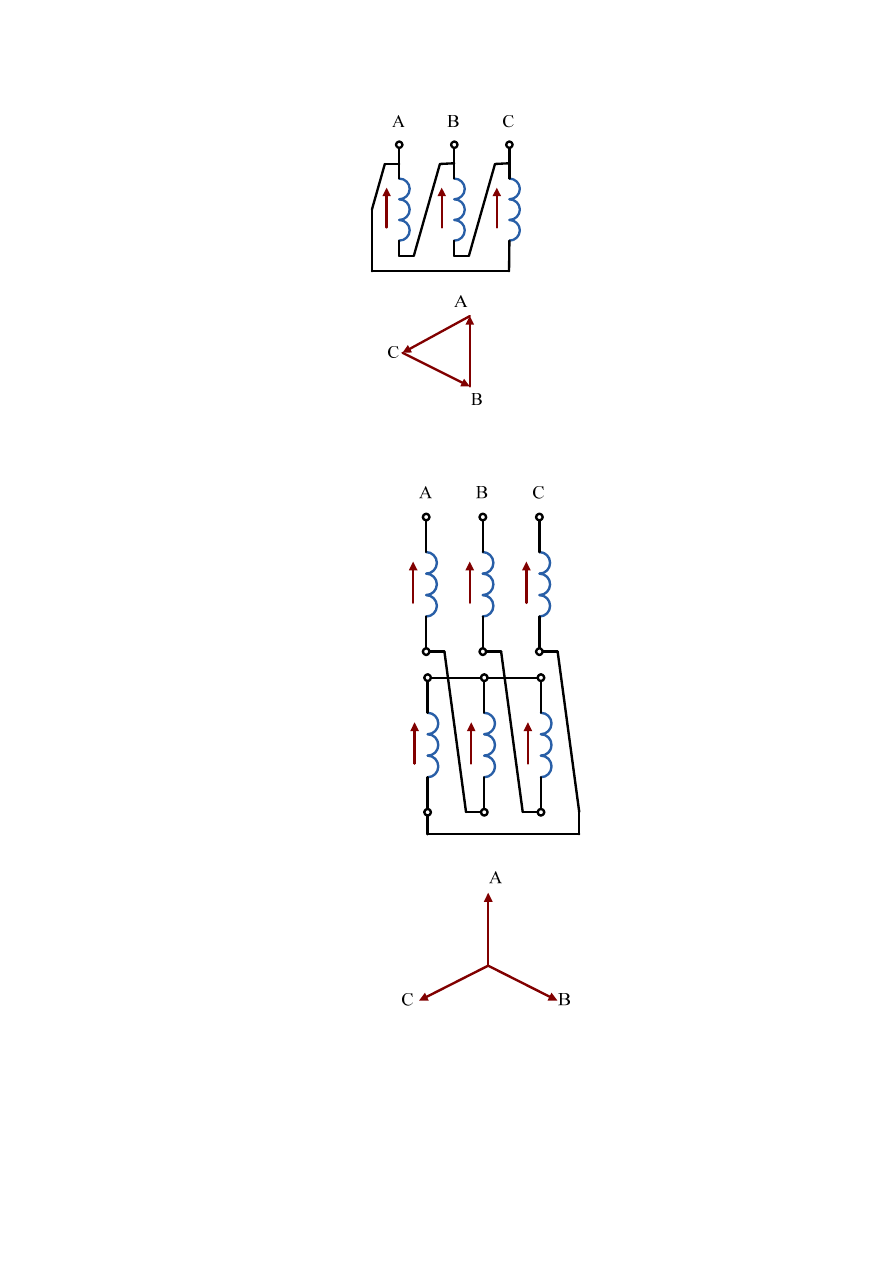
A

U

C

U

B

U

A

U

B

U

C

U

Rys. 2.29. Przykłady połączeń uzwojeń w trójkąt i odpowiadające mu wykres wskazowy napięć

1

2

,

a

a

U

U

1

a

U

1

b

U

1

c

U

2

a

U

2

b

U

2

c

U

1

2

,

b

b

U

U

1

2

,

c

c

U

U

Rys. 2.30. Przykłady połączeń uzwojeń transformatora w zygzak i odpowiadający mu wykres

wskazowy napięć

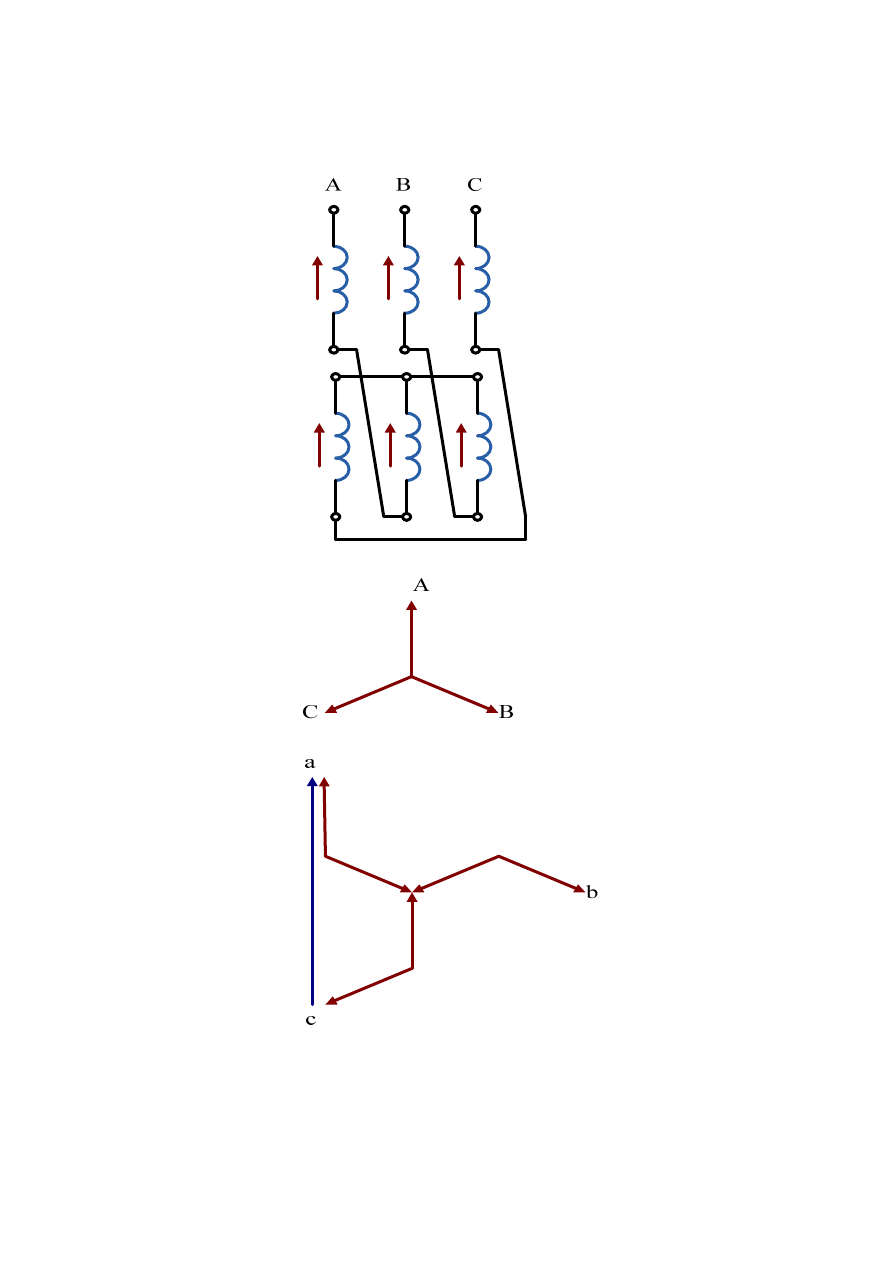
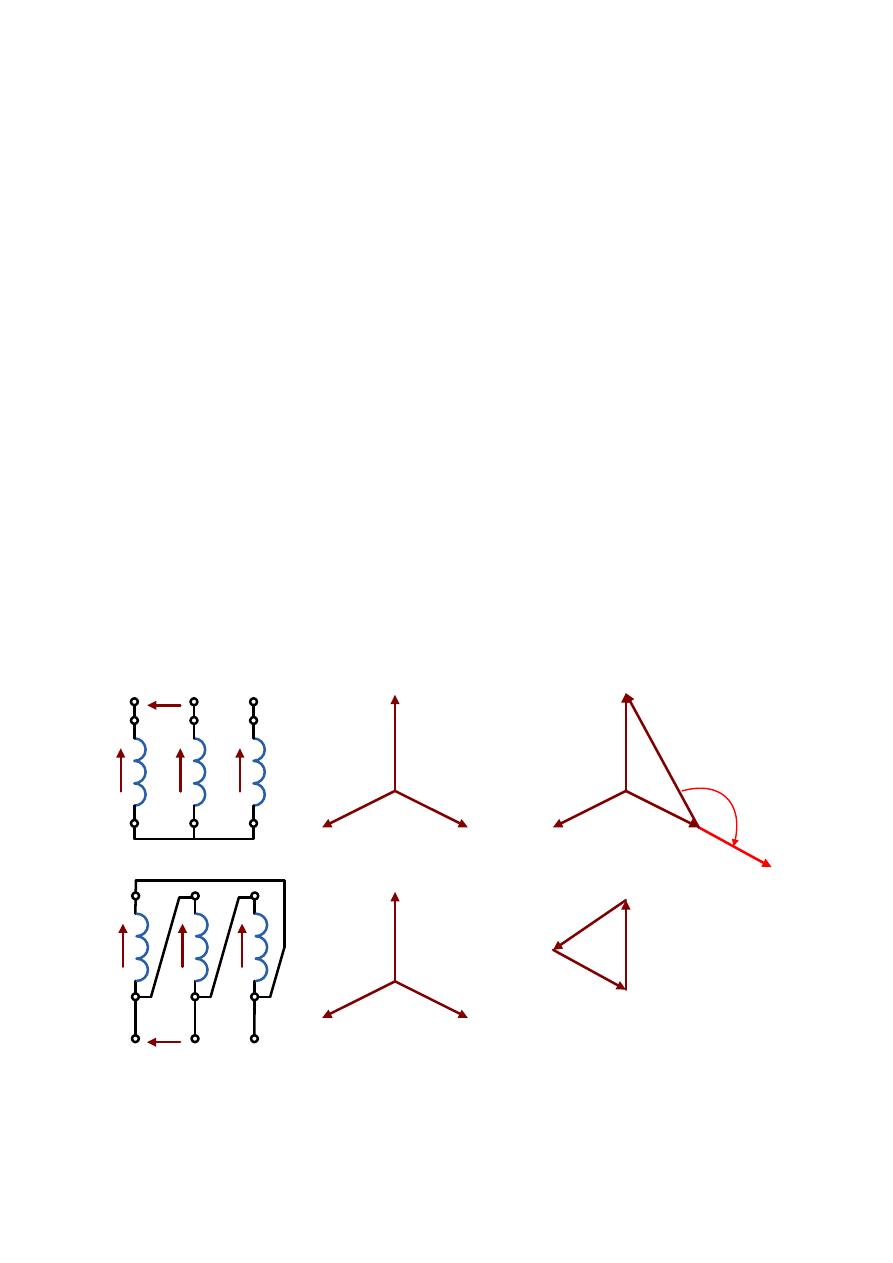
Konstrukcja wykresu wskazowego napięć dla układu połączeń w zygzak przedstawiona jest

na rys. 2.31.

1

2

,

a

a

U

U

1

a

U

1

b

U

1

c

U

2

a

U

2

b

U

2

c

U

1

2

,

b

b

U

U

1

2

,

c

c

U

U

2

a

U

1

c

U

1

a

U

2

b

U

1

b

U

2

c

U

ab

U

Rys. 2.31. Konstrukcja wykresu wskazowego napięć dla układu połączeń w zygzak

2.4.2. Grupy połączeń transformatorów trójfazowych

W zależności o d sposobu połączeń uzwojeń górnego i dolnego napięcia można

otrzymać różne przesunięcie fazowe pomiędzy przebiegami czasowymi napięć uzwojeń

strony pierwotnej i wtórnej.

Stąd dla każdego polaczenia uzwojeń podaje się również kąt przesunięcia fazowego między

odpowiadającymi sobie napięciami międzyprzewodowymi tzn. oznaczonymi tymi samymi

literami

(dużymi dla strony pierwotnej i małymi dla wtórnej).

W układzie gwiazda, trójkąt i zygzak kąty przesunięcia fazowego są zawsze

wielokrotnością 30

o

przy czym

1h=30

o

.

Kąt ten jest mierzony zgodnie z następstwem faz licząc od napięcia górnego do dolnego.

Wyznaczenie grupy połączeń:

•

uzwojenia umieszczone na tym samym słupie rysuje się nad sobą,

•

przy jednokierunkowym nawinięciu uzwojeń należy przyjąć, że początki obu uzwojeń

są u góry lub u dołu,

Wyznaczenie grupy połączeń Yd5 przedstawione jest na rys. 2.32.

a)

b)

c)

A

B

C

A

B

C

A

U

C

U

A

U

B

U

C

U

A1

B1

C1

X1

Y1

Z1

a

U

b

U

c

U

a1

b1

c1

x1

y1

z1

a

b

c

B

U

a

c

a

U

c

U

b

U

b

B

C

A

U

C

U

B

U

a1, z1

a

U

c

U

b

U

AB

U

ab

b

U

U

=

b1, x1

c1, y1

ab

U

150

o

α

=

Z1

Z1 Y1

X1

A

A1

C1

B1

AB

U

ab

U

Rys. 2.32. Wyznaczenie grupy połączeń Yd5: a) układ połączeń, b) wykresy wskazowe napięć

fazowych, c) wykresy topologiczne

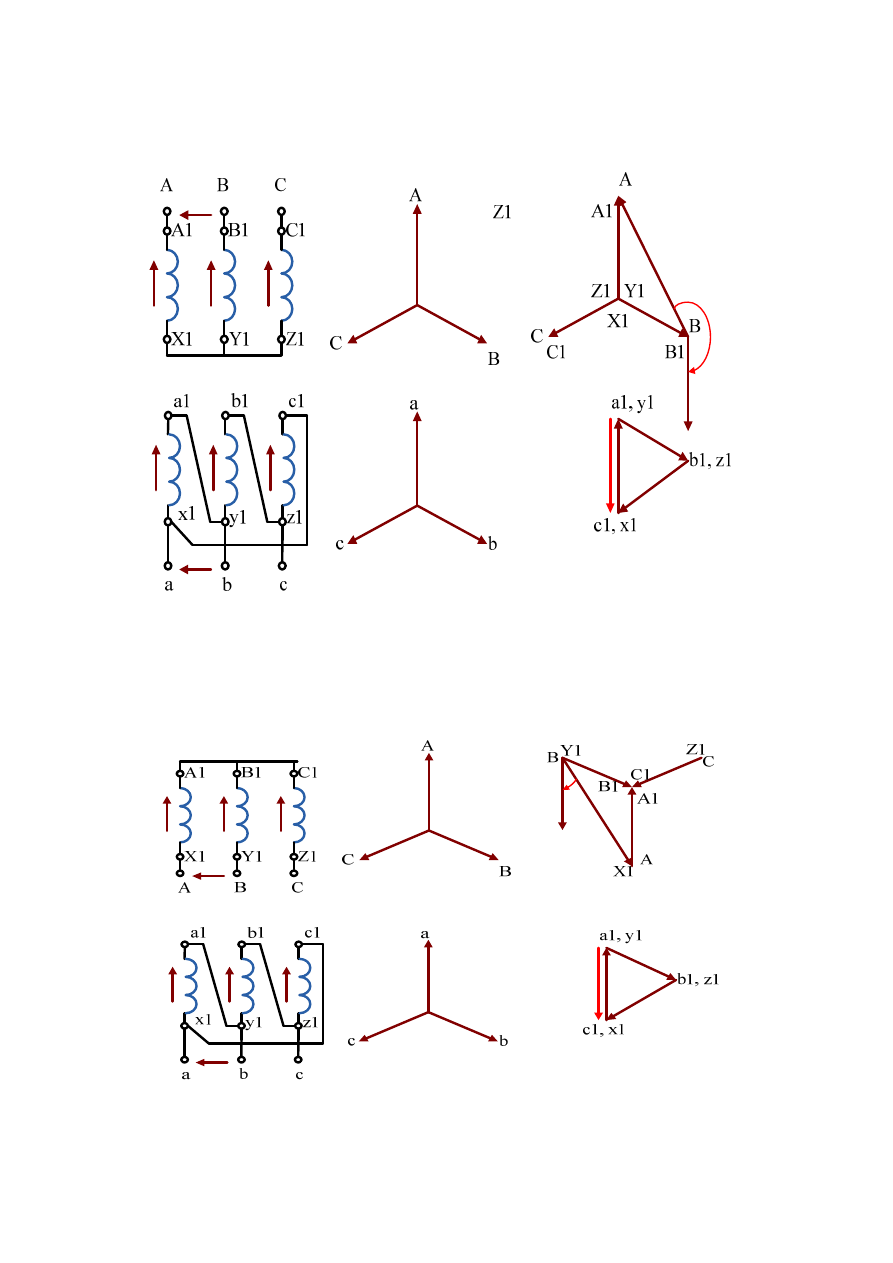
Wyznaczenie grupy połączeń Yd7 przedstawione jest na rys. 2.33.

a)

b)

c)

A

U

C

U

A

U

B

U

C

U

a

U

b

U

c

U

B

U

a

U

c

U

b

U

A

U

C

U

B

U

a

U

c

U

b

U

AB

U

ab

a

U

U

= −

ab

U

210

o

α

=

AB

U

ab

U

Rys. 2.33. Wyznaczenie grupy połączeń Yd7: a) układ połączeń, b) wykresy wskazowe napięć

fazowych, c) wykresy topologiczne

Wyznaczenie grupy połączeń Yd1 przedstawione jest na rys. 8.

a)

b)

c)

A

U

C

U

A

U

B

U

C

U

a

U

b

U

c

U

B

U

a

U

c

U

b

U

A

U

C

U

B

U

a

U

c

U

b

U

AB

U

ab

a

U

U

= −

ab

U

30

o

α

=

AB

U

ab

U

Rys. 2.34. Wyznaczenie grupy połączeń Yd1: a) układ połączeń, b) wykresy wskazowe napięć

fazowych, c) wykresy topologiczne

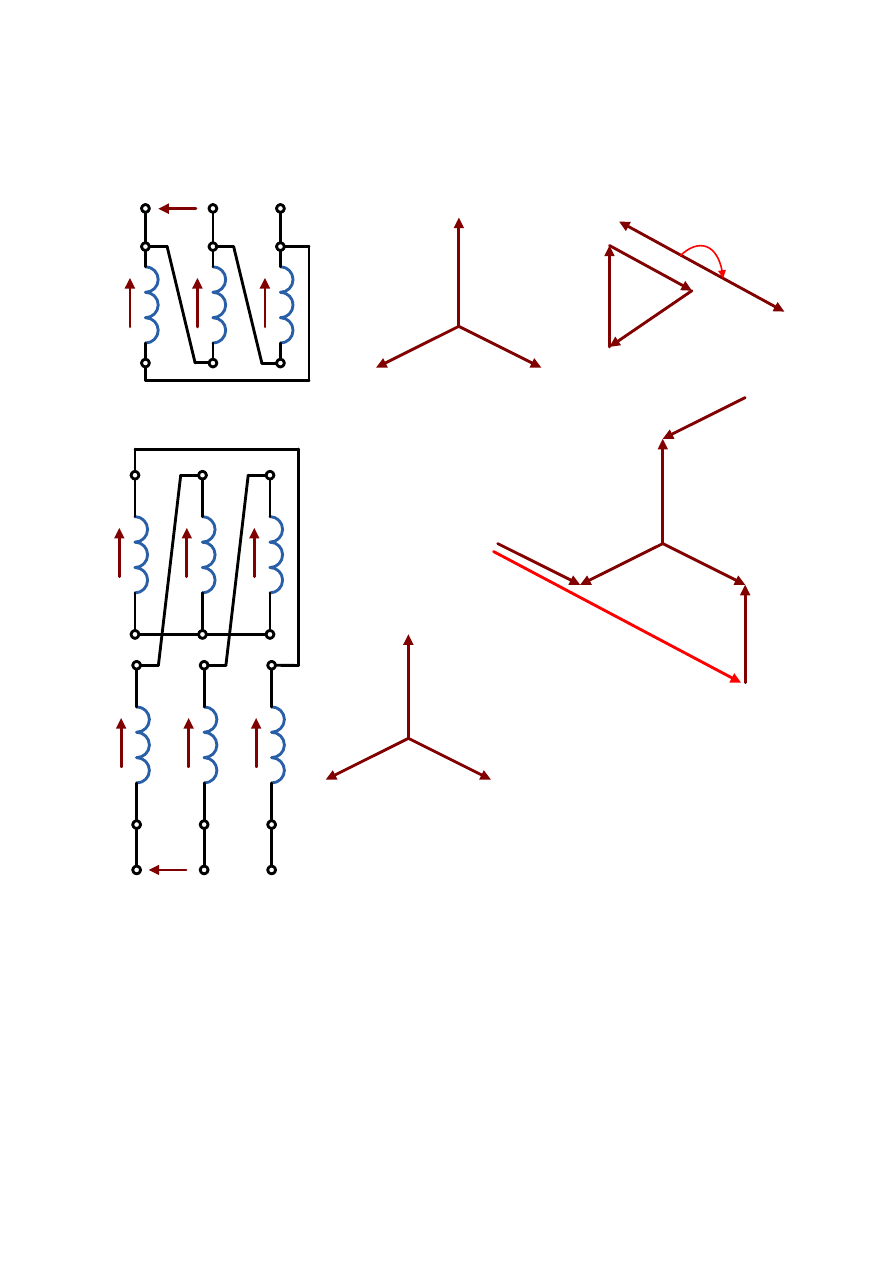
Wyznaczenie grupy połączeń Dz6 przedstawione jest na rys. 2.35.

a)

b)

c)

a

b

c

1

a

U

1

b

U

1

c

U

2

a

U

2

b

U

2

c

U

A

B

C

A

B

C

A

U

C

U

A

U

B

U

C

U

A1

B1

C1

X1

Y1

Z1

B

U

ab

U

AB

U

ab

U

a1

b1

c1

x1

y1

z1

a2

b2

c2

x2

y2

z2

AB

U

180

o

α

=

Z1

Y1

X1

A1

C1

A

U

B

U

C

U

2

a

U

1

c

U

1

a

U

2

b

U

1

b

U

2

c

U

a

b

c

ab

U

c

b

1

2

,

a

a

U

U

1

2

,

b

b

U

U

1

2

,

c

c

U

U

y2

z2

x2

x1

z1

y1

b2

c1

a2

a1

c2

B1

a

Rys. 2.35. Wyznaczenie grupy połączeń Dz6: a) układ połączeń, b) wykresy wskazowe napięć

fazowych, c) wykresy topologiczne

Polskie Nomy zalecają stosować następujące grupy połączeń:

Yy0, Dy5, Yd5, Yz5, Dy11, Yd11, Yz11

2.4.3. Przekładnia zwojowa i napięciowa

Przekładnią napięciową transformatora K

u

nazywamy stosunek znamionowych napięć

przewodowych strony wyższego napięcia U

1

do niższego napięcia U

1.

Natomiast przekładnią zwojową transformatora n nazywamy stosunek liczby zwojów

wyższego napięcia U

1

do liczby zwojów niższego napięcia U

1.

W zależności od sposobu połączeń uzwojeń górnego i dolnego napięcia transformatora

przekładnię napięciową można wyrazić poprzez przekładnię zwojową w następujący sposób:

Układ Yy

1

1

1

2

2

2

3

3

f

f

u

f

f

U

U

U

K

n

U

U

U

=

=

=

=

(2.65)

Układ Dd

1

1

2

2

f

u

f

U

U

K

n

U

U

=

=

=

(2.66)

Układ Yd

1

1

2

2

3

3

f

u

f

U

U

K

n

U

U

=

=

=

(2.67)

Układ Dy

1

1

2

2

3

3

f

u

f

U

U

n

K

U

U

=

=

=

(2.68)

Układ Yz

1

1

1

1

2

2

3

3

2

3

3

3

2

f

u

f

U

U

N

n

K

N

U

U

=

=

=

=

(2.69)

Układ Dz

1

1

1

1

2

2

2

3

3

3

2

f

u

f

U

U

N

n

K

N

U

U

=

=

=

=

(2.70)

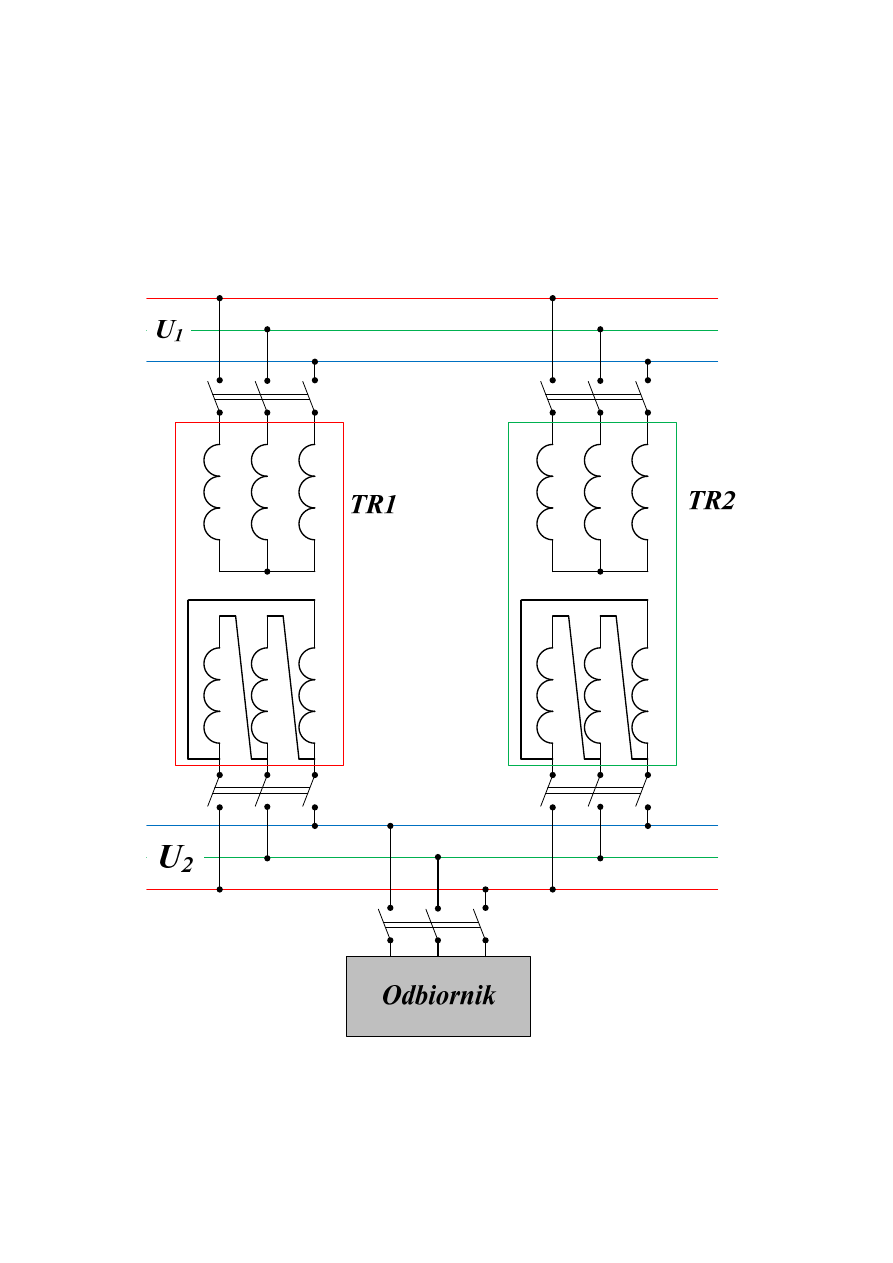
2.5. PRACA RÓWNOLEGŁA TRANSFORMATORÓW

Pracą równoległą transformatorów nazywamy taka pracę, przy której strony pierwotne

dwóch lub większej liczby transformatorów zasilane są ze wspólnych szyn zbiorczych, a

strony wtórne tych transformatorów zasilają odbiory również przez wspólne szyny zbiorcze

(rys.2.36).

Rys.2.36. Praca równoległa transformatorów 3-fazowych

Transformatory przeznaczone do pracy równoległej powinny spełniać określone wymagania:

•

w stanie bez obciążenia (odbiory odłączone) w uzwojeniach stron wtórnych

nie powinny płynąć prądy wyrównawcze, natomiast w uzwojeniach pierwotnych

powinny płynąć jedynie prądy biegu jałowego,

•

w czasie pracy transformatory powinny obciążać się

proporcjonalnie do swoich

mocy znamionowych,

•

prądy obciążenia płynące w uzwojeniach stron wtórnych w czasie pracy

transformatorów

powinny być ze sobą w fazie, czyli prąd płynący przez linię jest

sumą arytmetyczną prądów poszczególnych transformatorów .

Aby w stanie bez obciążenia nie płynęły w uzwojeniach wtórnych prądy wyrównawcze,

transformatory powinny odpowiadać następującym warunkom:

•

napięcia znamionowe pierwotne i wtórne powinny być jednakowe,

•

grupy połączeń transformatorów trójfazowych powinny być takie same,

•

jednoimienne zaciski należy przyłączyć do tych samych szyn zbiorczych.

Zgodnie z normami, do pracy równoległej można łączyć transformatory, których przekładnie

nie różnią się więcej niż ±0.5%, co ogranicza wartość prądów wyrównawczych do (2÷7)I

N

.

II

20

U

I

20

U

II

20

I

20

U

U

=

I

II

I

I

II

I

Rys.2.37. Praca równoległa transformatorów o różnych przekładniach

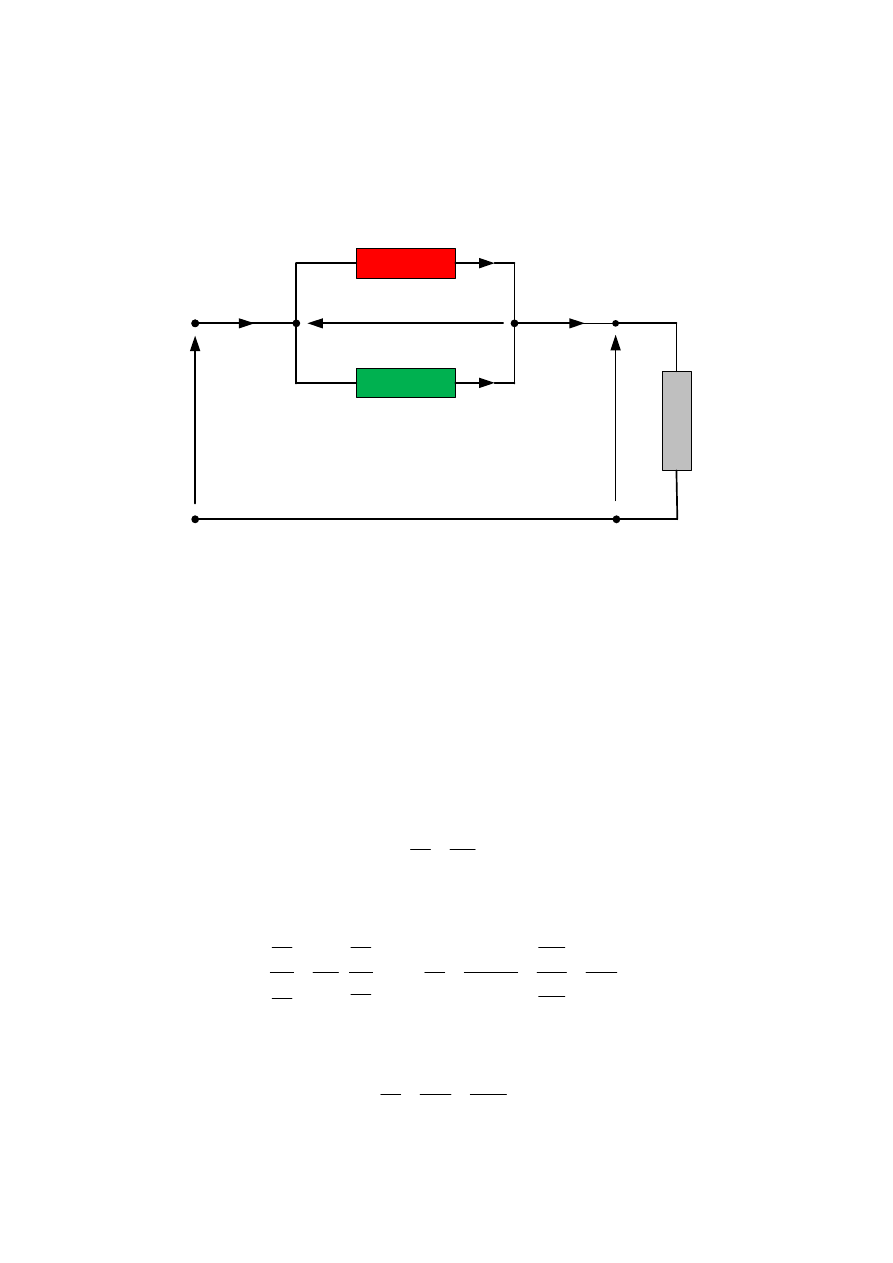
Dla stanu obciążenia transformatorów pracujących równolegle można skorzystać ze schematu

zastępczego zamieszczonego poniżej.

I

I

2

II

I

2

I
2K

Z

II
2K

Z

obc

Z

II
2K

II

I
2K

I

Z

I

Z

I

⋅

=

⋅

2

2

'
1

U

2

U

2obc

I

'
1

I

Rys. 2.38. Praca równoległa transformatorów – schemat zastępczy.

Z równości napięć stron pierwotnych i wtórnych obu transformatorów wynika równość napięć

na impedancjach zwarcia:

II

II
K

I

I
K

I

Z

I

Z

⋅

=

⋅

(2.71)

zatem rozpływ prądów:

I
K

II
K

II

I

Z

Z

I

I

=

(2.72)

Stosując układ jednostek względnych:

I
Kr

II
Kr

I
K

II
K

I

I
K

II

II
K

II
r

I
r

II

I

I
K

II
K

II

II

I

I

U

U

U

U

I

Z

I

Z

I

I

I

1

I

1

Z

Z

I

I

I

I

=

=

⋅

⋅

=

→

⋅

=

N

N

N

N

N

N

N

N

U

U

(2.73)

I
K%

II
K%

I
Kr

II
Kr

II
r

I
r

U

U

U

U

I

I

=

=

(2.74)

lub w odniesieniu do mocy:

I
K

II
K

II

I

I
K%

II
K%

II
r

I
r

Z

Z

S

S

U

U

S

S

=

=

(2.76)

Na podstawie powyższych wzorów można stwierdzić, że przy pracy równoległej

transformatorów prądy i moce wyrażone w jednostkach względnych są odwrotnie

proporcjonalne do napięć zwarcia.

Przy pracy równoległej n transformatorów o różnych napięciach zwarcia obciążenie dla j-tej

jednostki można wyznaczyć z zależności:

K%j

j

N

n

1

j

K%j

j

N

odb

j

∆U

S

∆U

S

S

S

⋅

=

∑

=

(2.77)

U

II
K

I
K

U

U

=

I

II

I

I

r

II

I

r

r

I

II
K

I
K

U

U

>

s

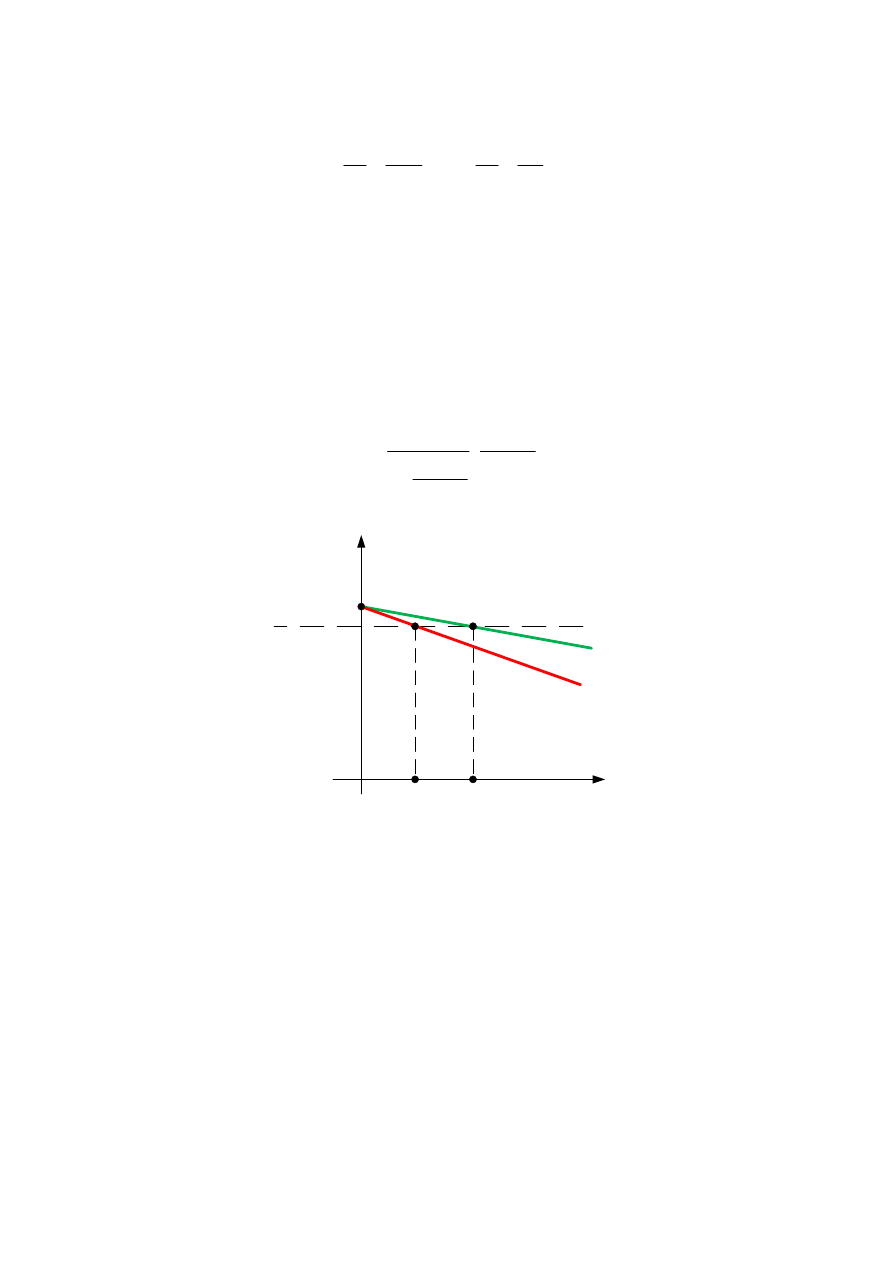
Rys. 2.39. Praca równoległa transformatorów o różnych napięciach zwarcia

II
K

I
K

U

U

>

.

Na postawie powyższej interpretacji graficznej można zauważyć, że transformator II o

mniejszym napięciu zwarcia będzie obciążony większym prądem w stosunku do

transformatora I o większym napięciu zwarcia

(

)

I

II

I

I

r

r

>

.

Aby obciążenie dzieliło się równomiernie pomiędzy pracujące równolegle transformatory,

napięcia zwarcia powinny być jednakowe. Normy dopuszczają odchyłkę ±10% średniej

wartości napięć zwarcia. Jeżeli do pracy równoległej przeznaczy się jednostki o różnych

napięciach zwarcia, wówczas ich współpraca będzie korzystniejsza, jeżeli transformator o

większej mocy znamionowej będzie miał mniejsze napięcie zwarcia.

Spełnienie warunków równości przekładni i napięć zwarcia przy pracy równoległej

gwarantuje brak prądów wyrównawczych w stanie jałowym i równomierny podział mocy w

stanie obciążenia, jednak wymienione warunki nie gwarantują uzyskania mocy stanowiącej

sumę mocy znamionowych współpracujących jednostek.

Przesunięcie fazowe pomiędzy prądami transformatorów pracujących równolegle

wystąpi, jeżeli ich współczynniki mocy są różne:

II

K

I

K

cos

cos

ϕ

ϕ

≠

(rys. 2.40) co jest

równoznaczne z różnicami pomiędzy ich właściwościami wewnętrznymi:

II

K

K

I

K

K

R

X

R

X













≠













.

I

2

ϕ

II

2

ϕ

odb

ϕ

I

K

ϕ

II

K

ϕ

Rys. 2.40. Wykres wektorowy transformatorów pracujących równolegle przy

II

K

I

K

cos

cos

ϕ

ϕ

≠

Przesunięcie to będzie tym większe, im większa będzie różnica współczynników mocy przy

zwarciu. Pokrywanie się prądów jednostek pracujących równolegle można uzyskać, gdy

stosunek ich mocy znamionowych nie będzie większy niż 1:3 (wartość cosφ

K

zależy od

wielkości transformatora i dla transformatorów o takiej samej wielkości będzie taka sama).

Podsumowując, można sformułować następujące warunki pracy równoległej:

•

przynależność do odpowiednich grup połączeń,

•

równość przekładni (z dokładnością do ±0.5%),

•

równość napięć zwarciowych (z dokładnością do ±10%),

•

stosunek mocy znamionowych nie większy niż 1:3.

2.6

. ZMIENNOŚĆ NAPIĘCIA

Jedną z charakterystycznych cech transformatora jest zakres wahań napięcia strony

wtórnej przy przejściu od stanu jałowego do stanu obciążenia. W stanie jałowym

transformatora (I

2

=0) zasilanego napięciem pierwotnym U

1

po stronie wtórnej pojawia się

napięcie U

20

, natomiast w stanie obciążenia I

2

≠0 napięcie po stronie wtórnej będzie miało

wartość inną niż w stanie jałowym (U

2

≠U

20

) z powodu spadków napięć na impedancjach

wewnętrznych transformatora. Jeżeli pominie się prąd magnesujący, co jest równoznaczne

'
2

1

I

I

=

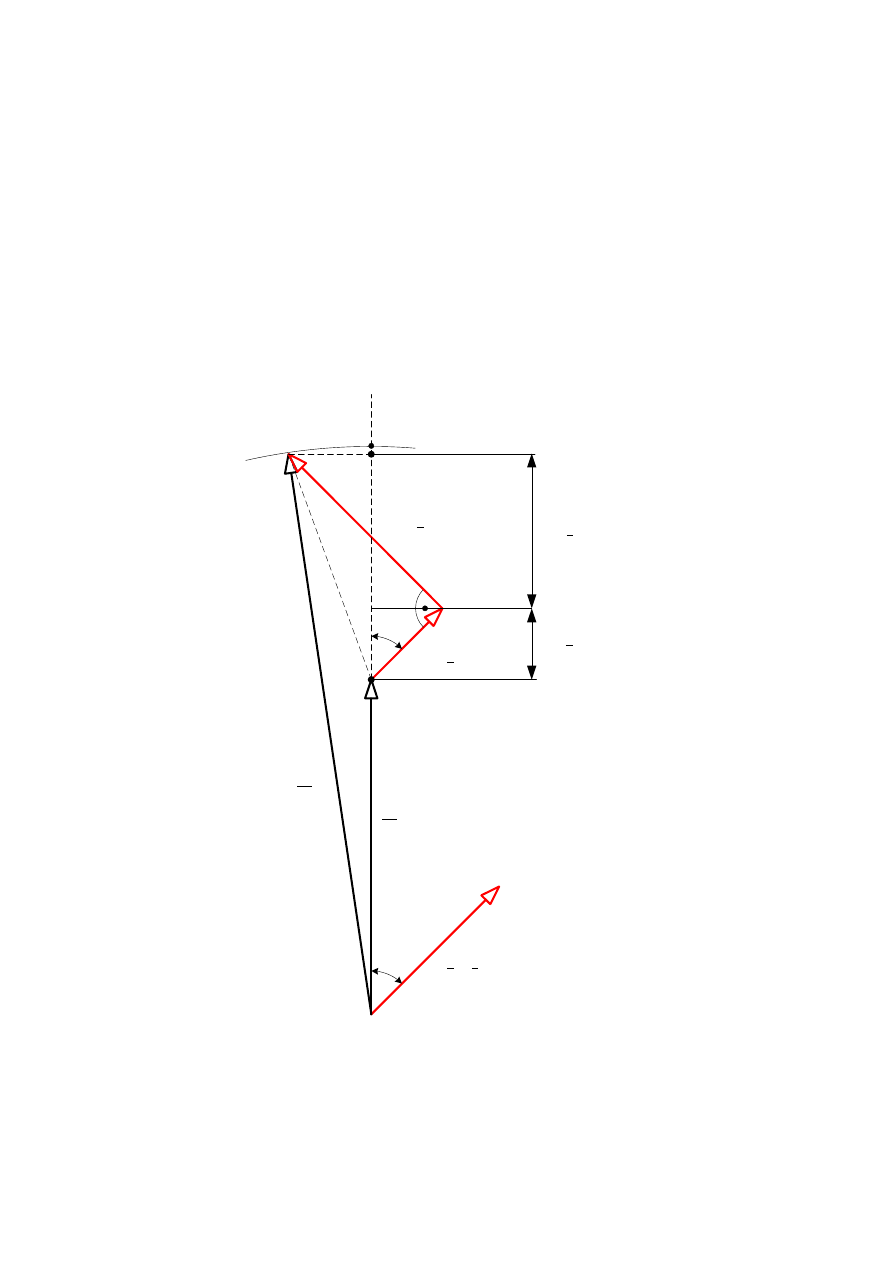
można narysować wykres wskazowy (rys. 2.41).

2

ϕ

2

ϕ

A

B

C

U

1

U’

2

I

1

=I’

2

jX

1K

I’

2

R

1K

I’

2

X

1K

I’

2

sinφ

2

R

1K

I’

2

cosφ

2

Rys. 2.41. Uproszczony sposób wyznaczania zmienności napięcia transformatora

Zmiennością napięcia transformatora ∆U nazywa się algebraiczną różnicę między napięciem

pierwotnym U

1

a odniesionym do obwodu pierwotnego napięciem wtórnym U’

2

przy

przejściu od stanu jałowego do stanu obciążenia przy danym współczynniku mocy cosφ

2

.

2

1

1K

2

1

1K

'

2

1

sin

I

X

cos

I

R

U

U

∆U

ϕ

ϕ

±

=

−

=

(2.77)

lub w jednostkach względnych

2

1

1

1K

2

1

1

1K

1

'

2

1

sin

U

I

X

cos

U

I

R

U

U

U

U

ϕ

ϕ

δ

±

=

−

=

(2.78)

2

1

1N

1N

1

1

1

1K

2

1

1N

1N

1

1N

1N

1K

sin

U

U

I

I

U

I

X

cos

U

U

I

I

U

I

R

δU

ϕ

ϕ

⋅

⋅

±

⋅

⋅

=

(2.79)

[

]

2

X

2

R

sin

U

cos

U

β

α

δ

U

ϕ

ϕ

⋅

±

⋅

⋅

⋅

=

(2.80)

gdzie:

1

1N

U

U

=

α

- współczynnik napięciowy,

1N

1

I

I

=

β

- współczynnik prądowy,

2N

2N

2K

1N

1N

1K

R

U

I

R

U

I

R

U

=

=

- spadek napięcia na rezystancji zwarciowej (czynna strata napięcia),

2N

2N

2K

1N

1N

1K

X

U

I

X

U

I

X

U

=

=

spadek napięcia na reaktancji zwarciowej (bierna strata napięcia),

w powyższym wzorze znak „+” dotyczy obciążenia rezystancyjno indukcyjnego, natomiast

znak „-” obciążenia rezystancyjno-pojemnościowego.

Charakterystykę zmienności napięcia w zależności od współczynnika mocy przedstawia

rys.2.42., na podstawie której można stwierdzić, że maksymalna zmienność napięcia wystąpi

przy współczynniku mocy równym zwarciowemu współczynnikowi mocy transformatora.

Dodatnia wartość zmienności napięcia oznacza spadek napięcia (U

2

<U

20

) po stronie

wtórnej transformatora przy przejściu od stanu jałowego do stanu obciążenia, ujemna

wartość zmienności oznacza wzrost napięcia (U

2

>U

20

) po stronie wtórnej transformatora

przy przejściu od stanu jałowego do stanu obciążenia, ponadto przy pewnym współczynniku

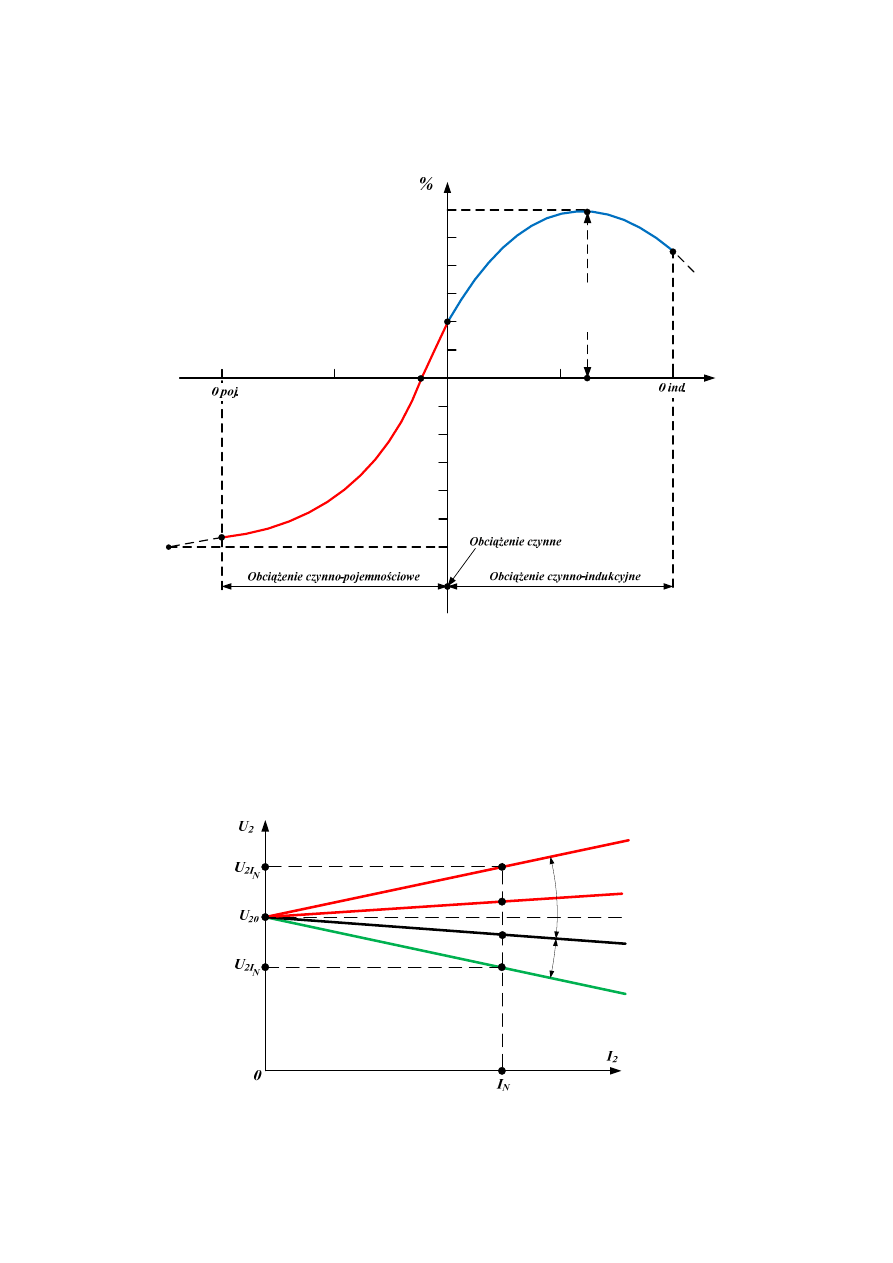
mocy obciążenia zmienność napięcia może wynieść zero, co oznacza że napięcie zarówno w

stanie jałowym jak i w stanie obciążenia będzie miało taką samą wartość.

K

2

cos

cos

ϕ

ϕ

=

2

cos

ϕ

δ

U

m

a

x

δ

U

Rys. 2.42. Charakterystyka zmienności napięcia transformatora od współczynnika mocy cosφ

2

Charakterystyki zewnętrzne transformatora będące zależnością napięcia U

2

po stronie wtórnej

od prądu strony wtórnej I

2

przy danym współczynniku mocy odbiornika przedstawiono na

rys. 2.43.

2poj

cos

ϕ

2ind

cos

ϕ

1

cos

2

=

ϕ

const.

cos

const.,

f

const.,

U

przy

)

f(I

U

2

1

2

2

=

=

=

=

ϕ

Rys. 2.43. Charakterystyka zewnętrzna transformatora przy przejściu od stanu jałowego do stanu

obciążenia

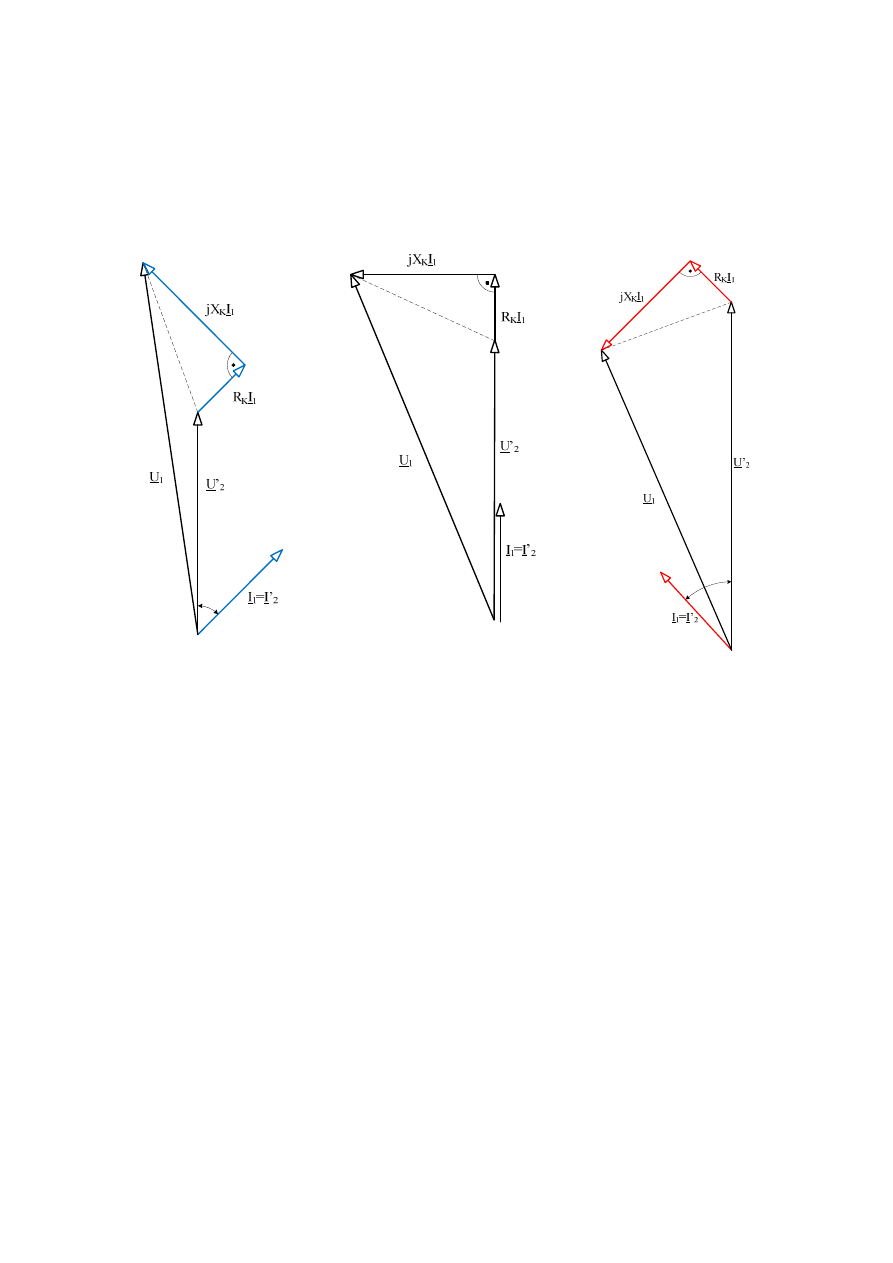
Poniższe wykresy wskazowe ilustrują wpływ zmiany charakteru odbiornika (od obciążenia czynno-

indukcyjnego, poprzez obciążenie czynne do obciążenia czynno-pojemnościowego) na wartość

napięcia po stronie wtórnej transformatora zasilanego z sieci o napięciu U

1

i przy takiej samej wartości

prądu obciążenia I

1

=I’

2

.

a)

2

ϕ

b)

0

2

=

ϕ

c)

2

ϕ

Rys. 2.44. Wykresy wskazowe napięć i prądów transformatora: a) dla obciążenia czynno-

indukcyjnego, b) dla obciążenia czynnego, c) dla obciążenia czynno-pojemnościowego

2.7 STRATY I SPRAWNOŚĆ TRANSFORMATORA

Sprawnością transformatora nazywamy stosunek mocy czynnej oddawanej P

2

do mocy

czynnej pobieranej P

1

przy stałym współczynniku mocy cos

ϕ

2

1

2

P

P

=

η

(2.81)

Sprawność małych transformatorów (kilku kVA) jest rzędu ok. 0.95, natmiast

transformatorów dużych mocy (rzędu kilkudziesięciu MVA) jest bardzo duża i wynosi ok.

0.995. Sposób bezpośredni wyznaczenia sprawności ze wzoru (2.81) dla dużych

transformatorów jest obarczony dużym błędem. Sprawność transformatorów wyznaczana jest

metodą strat poszczególnych.

Uwzględniając całkowite straty mocy wzór (2.81) można zapisać w postaci

P

P

P

P

P

∆

+

=

=

2

2

1

2

η

(2.82)

gdzie:

∆

P

−

całkowite straty mocy, przy czym

Cu

Fe

P

P

P

∆

+

∆

=

∆

(2.83)

Straty w rdzeniu w rdzeniu (jałowe) przy stałej częstotliwości zależą od kwadratu napięcia

2

cU

P

Fe

=

∆

(2.84)

Natomiast straty w uzwojeniu (obciążeniowe) są zależne od kwadratu prądu

z

Cu

R

mI

P

2

2

=

∆

(2.85)

Wprowadzając zależność (2.83) do równania (2.82), sprawność transformatora możemy

określić ze wzoru:

Cu

Fe

P

P

P

P

∆

+

∆

+

=

2

2

η

(2.86)

Wprowadzając zależności

2

2

2

2

2

2

2

cos

cos

ϕ

ϕ

N

N

N

S

I

I

I

mU

P

=

=

(2.87)

CuN

N

z

Cu

P

I

I

R

mI

P

∆













=

=

∆

2

2

2

2

2

(2.88)

oraz oznaczając

N

I

I

2

2

=

β

(2.89)

wyrażenie na sprawność transformatora przy znamionowym napięciu zasilającym można

zapisać w postaci

FeN

CuN

N

N

P

P

S

S

∆

+

∆

+

=

2

2

2

cos

cos

β

ϕ

β

ϕ

β

η

(2.90)

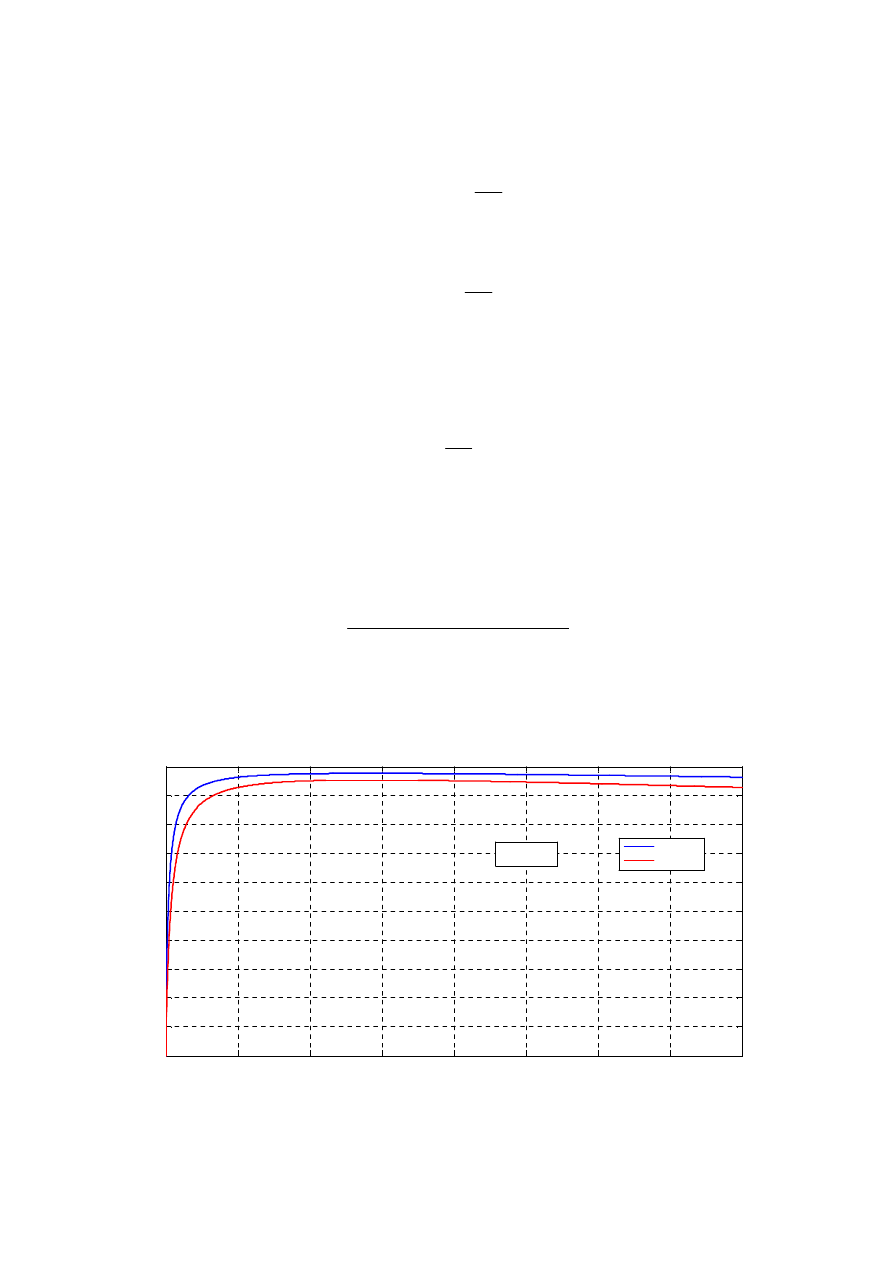
Wyrażenie powyższe pozwala wyznaczyć sprawność transformatora w zależności od prądu

obciążenia

β

i współczynnika mocy cos

ϕ

2

(rys. 2.45).

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

ηηηη

I

2

/I

2N

cos

φ

=1

cos

φ

=0.8

ββββ

opt

=0.57

Rys. 2.45. Zależność sprawności transformatora od obciążenia przy różnych współczynnikach mo

cy

Przy stałym współczynniku mocy maksymalną sprawność transformatora określamy z

warunku

0

=

β

η

d

d

(2.91)

Maksymalna sprawność wystąpi przy współczynniku obciążenia

CuN

FeN

P

P

∆

∆

=

β

(2.92)

czyli

CuN

Cu

N

CuN

FeN

P

P

I

I

P

P

∆

∆

=













=

∆

∆

=

2

2

2

2

β

(2.93)

Skąd:

FeN

Cu

P

P

∆

=

∆

(2.94)

Ze wzoru (2.94) wynika, że maksymalna sprawność wystąpi przy takim obciążeniu przy

którym straty obciążeniowe są równe stratom jałowym.

Niektóre transformatory pracują ze stałym obciążeniem np. transformatory blokowe.

Współczynnik obciążenia tych transformatorów jest zbliżony do jedności

β≈

1. Stąd takie

transformatory zgodnie ze wzorem (2.92) powinny mieć straty w żelazie równe stratom

obciążeniowym

CuN

FeN

P

P

∆

=

∆

(2.95)

Inne transformatory np. zasilające osiedla mieszkaniowe, pracują ze zmiennym obciążeniem

zmieniającym się w szerokich granicach od 0

÷

1. Można założyć średnią wartość obciążenia

β

=0.5. Stąd:

5

.

0

=

∆

∆

=

CuN

FeN

P

P

β

(2.96)

Czyli straty w żelazie w takich transformatorach powinny być równe:

CuN

FeN

P

P

∆

=

∆

25

.

0

(2.97)

LITERATURA

[1]

Bajorek Z.:

Maszyny elektryczne, WNT, Warszawa 1983

[2]

Chapman S.J.:

Electric machinery fundamentals, Third Edition, McGraw-Hill Book

Company, Singapore 1999.

[3]

Fitzgerald A. E., Kingsley Ch. Jr., Stephen D. Umans S.D.:

Electric machinery, Sixth

edition, McGraw-Hill, USA, New York, 2003.

[4]

Gieras J.F., Wing M.:

Permanent magnet motor technology. Design and Application,

Second Edition, Marcel Dekker Inc., New York 2002.

[5]

Krause P.C.:

Analysis of electric machinery, McGraw-Hill Book Company, New York

1986.

[6]

Kurdziel R.:

Podstawy elektrotechniki, WNT, Warszawa 1972

[7]

Latek W.: Teoria

maszyn elektrycznych, WNT, Warszawa 1987

[8]

Plamitzer A.:

Maszyny elektryczne, WNT, Warszawa 1982