Prognozowanie, Tadeusz W.Bołt,
1
3. Wyrównywanie szeregu czasowego za pomocą średnich (skrót)
1
Przedmiotem wykładu będą obecnie metody prognozowania oparte na wygładzaniu. Na pierwszym
wykładzie omawiano strukturę szeregu czasowego zmiennej
t
y
, wyodrębniając składową systematyczną,
cykliczną, sezonową i zakłócenie przypadkowe (losowe). Oryginalne szeregi czasowe zawierają zatem
efekty oddziaływania czynników przypadkowych. Procedura wygładzania jest operacją wykonywaną na
oryginalnych wyrazach szeregu czasowego. Oryginalne wartości są w toku procedury wygładzania
zastępowane przez odpowiednio dobrane funkcje tych wyrazów, które szacują systematyczne i periodyczne
składowe szeregu. Wartości wygładzone możemy interpretować jako wartości oczyszczone z zakłóceń
losowych.
Wszystkie metody prognozowania, które omawiać będziemy w trakcie tego wykładu będą składały się z
dwóch etapów:
wygładzania szeregu,
prognozowania szeregu.
Prognoza na okres
)
(
j
t
, wyznaczona w okresie
t
jest równa dostępnej w tym okresie wartości
wygładzonej szeregu.
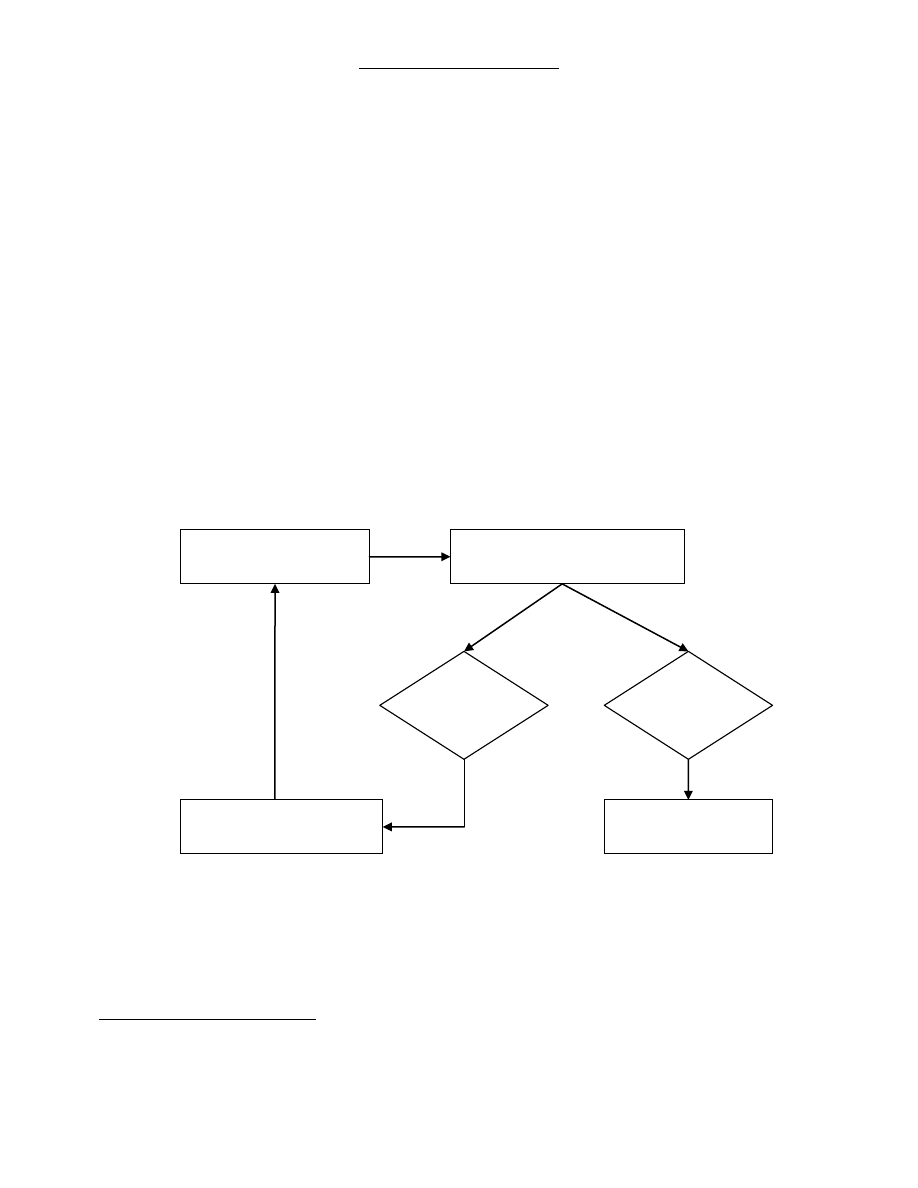
Schemat 3.1 Metody prognozowania oparte na wygładzaniu
Źródło: opracowanie własne
Schemat 3.1 prezentuje algorytm określający sposób postępowania w procedurach wykorzystujących
metody prognozowania oparte na wygładzaniu. Ponieważ apriori trudno jest stwierdzić jaki sposób
wygładzania zapewni najlepszą jakość prognozowania w odniesieniu do danego szeregu czasowego,
algorytm zakłada prognozowanie obserwacji historycznych (ex post) oraz ocenę na tej podstawie
1
Materiał dydaktyczny do wykorzystania przez studentów uczestniczących w wykładach z Prognozowania,
prowadzonych przez Tadeusza W. Bołta.
Wygładzanie szeregu
daną metodą (1)
Prognozowanie obserwacji
historycznych (2)
Prognozy nie -
dopuszczalne
Prognozy
dopuszczalne
Prognozowanie
ex ante (3a)
Wybór nowej metody
wygładzania (3b)
Prognozowanie, Tadeusz W.Bołt,
2
dokładności prognozowania. Jeśli prognozy okazują się niewystarczająco dokładne (niedopuszczalne)
następuje wybór nowego sposobu wygładzania i powrót do pierwszego etapu procedury.
Formalnie rzecz biorąc, dla szeregu czasowego liczącego
T
wyrazów, wygładzanie można opisać w
następujący sposób:
)
,...
,
(
)
(
2
1
t
t
y
y
y
f
y
;
)
,...,
2
,
1
(
T
t
gdzie
)
(
t
y
jest wartością wygładzoną na okres
t
w oparciu o informacje dostępne aż do tego okresu.
Prognozą ex post na okres
)
(
j
t
, wyznaczoną w okresie
t
jest:
)
(
t
p
j
t
y
y
;
)
,...,
2
,
1
(
T
t
.
W trakcie wykładu rozpatrywać będziemy różne sposoby wygładzania liniowego, wykorzystujące
średnie wartości szeregu, które dla porządku pogrupujemy na następujące klasy:
według kryterium sposobu liczenia średniej wyodrębniać będziemy:
a) średnie nieważone,
b) średnie ważone,
według kryterium sposobu aktualizacji próby wyodrębniać będziemy:
a) średnie obliczane rekurencyjnie (przez dołączanie kolejnych obserwacji),
b) średnie ruchome (przez wymianę obserwacji, z zachowaniem stałej szerokości ,,okna’’).
W praktyce zatem każdy sposób wygładzania, który rozpatrywać będziemy w trakcie wykładów, określony
będzie przez dwa wyżej wymienione kryteria. Występować zatem będą średnie nieważone rekurencyjne i
średnie nieważone ruchome oraz średnie ważone rekurencyjne i średnie ważone ruchome.
Cechą średniej nieważonej jest nadawanie tej samej wagi wszystkim obserwacjom z danego podzbioru,
dla którego wyznaczana jest wartość średnia. Cechą średniej ważonej jest nadawanie różnych wag
obserwacjom starszym i nowszym
2
. Cechą średniej obliczanej rekurencyjnie jest uwzględnianie wszystkich
obserwacji dostępnych w okresie
t
, natomiast cechą średniej ruchomej jest odrzucanie najstarszej
obserwacji, za każdym razem, kiedy dołączona jest obserwacja najnowsza.
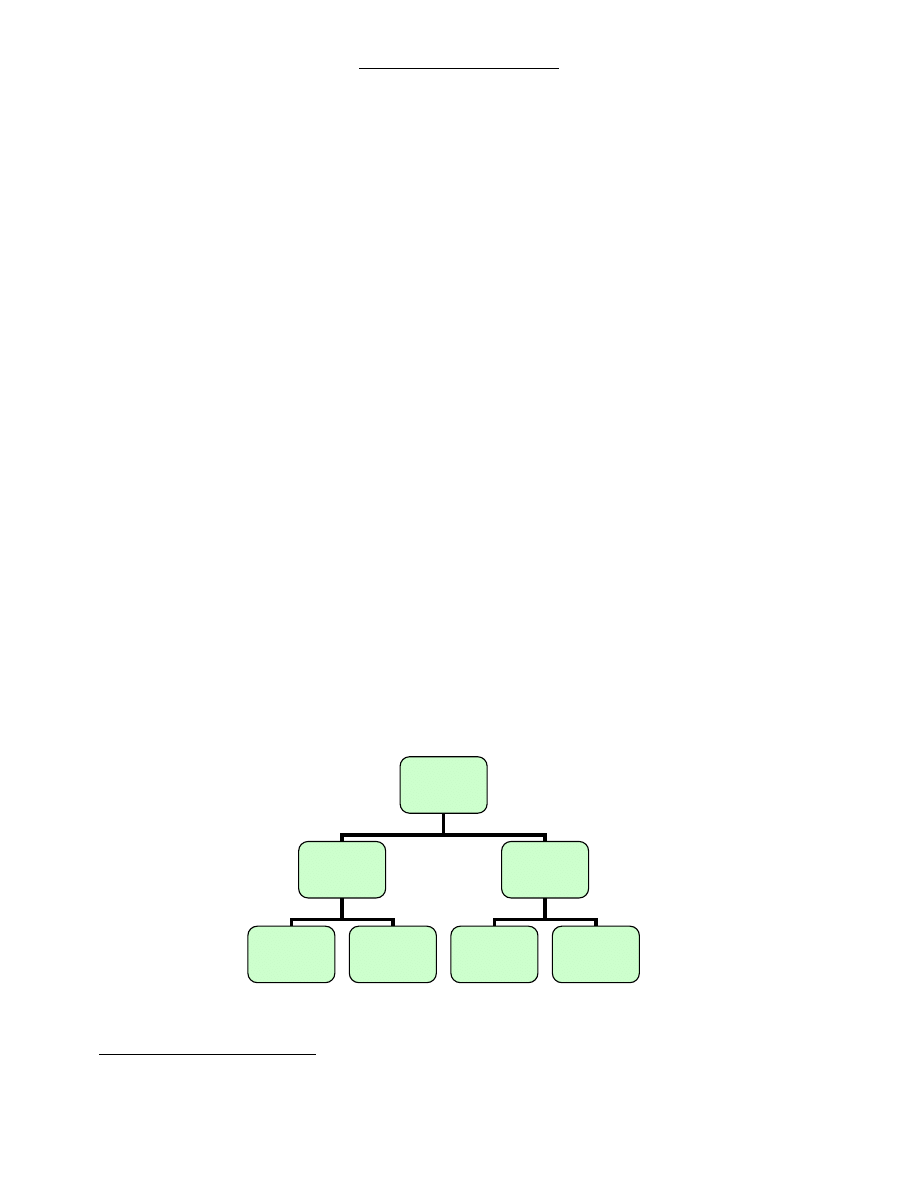
Schemat 3.2
Rodzaje średnich wykorzystywanych w wyrównywaniu szeregów czasowych
Źródło: opracowanie własne
2
Szczegółowo na ten temat w kolejnych punktach wykładu.
Rodzaje
średnich
Rekurencyjne
(SR)
Ruchome
(SM)
Nieważone
(SRN)
Ważone
(SRW)
Nieważone
(SMN)
Ważone
(SMW)
Prognozowanie, Tadeusz W.Bołt,
3
3.1. Średnia arytmetyczna rekurencyjna nieważona
Rekurencyjna średnia arytmetyczna szeregu jest obliczana w następujący sposób:
t
s
s
t
y
t
y
1
1
;
)
,...,
2
,
1
(
T
t
.
Wszystkie obserwacje należące do podzbioru pierwszych
t
elementów szeregu mają wagi równe
)
/
1
( t
.
Rozpisując powyższą równość dla kolejnych
t
otrzymujemy:
1
1
y
y
)
(
2
1
2
1
2
y
y
y
)
(
3
1
3
2
1
3
y
y
y
y
………………………….
)
...
(
1
2
1
T
T
y
y
y
T
y
y
.
Przeszacowanie średniej na kolejny okres czasu następuje zatem w ślad za dołączeniem kolejnej
obserwacji. Można zapisać rekurencyjną formułę średniej arytmetycznej w następujący sposób:
t
t
t
t
s
s
t
y
t
y
t
t
y
y
t
y
1
)
1
(
)
(
1
1
1
1
;
)
,...,
3
,
2
(
T
t
.
Wykorzystamy obecnie wygładzone wartości do prognozowania ex post, zgodnie z następującą formułą:
t
p
j
t
t
y
y
|
;
,.....)
,
;
,....,
,
(
2
1
2
1
j
j
T
t
.
Prognozą na okres
)
(
j
t
, wyznaczaną w okresie
t
jest dostępna w tym okresie ocena średniej
arytmetycznej (nieważonej) szeregu czasowego.
Błędem prognozy ex post jest:
t
j
t
p
j
t
t
j
t
p
j
t
t
y
y
y
y
|
|
;
,.....)
,
;
,....,
,
(
2
1
2
1
j
j
T
t
.
Do opisu błędów ex post wykorzystywać będziemy, omówione w części poprzedniej, mierniki
dokładności prognoz ex post, wraz z dekompozycjami prognostycznymi Theila.
W prognozowaniu ex ante wykorzystywana będzie dostępna w momencie wyznaczania prognozy średnia
arytmetyczna. Ogólnie możemy zapisać, że:
T
p
j
T
T
y
y
|
;
,.....)
2
,
1
(
j
.
Prognozowanie, Tadeusz W.Bołt,
4
Wyznaczone dla błędów ex post miary dokładności wykorzystywać będziemy do (przybliżonej) oceny
dokładności prognoz ex ante.
3.2. Średnia arytmetyczna rekurencyjna ważona
Wygładzanie średnią nieważoną, jak pokazaliśmy w punkcie poprzednim, niesie zagrożenie wystąpienia
systematycznego błędu przeszacowania/niedoszacowania składnika systematycznego w przypadku, gdy
szereg czasowy jest niestacjonarny (z tendencją malejącą/rosnącą). Jednym ze sposobów eliminacji tego
typu błędów jest ważenie obserwacji. Intuicyjnie rzecz biorąc, z punktu widzenia wyznaczenia wartości
wygładzonej na okres
t
, informacje starsze powinny mieć mniejszą wagę niż obserwacje nowsze, w
szczególności obserwacja bieżąca.
Średnią arytmetyczną ważoną
)
~
(
t
y
, wyznaczoną na okres
t
, definiuje następująca równość:
t
s
s
t
s
t
y
w
y
1
~
;
)
,...,
2
,
1
(
T
t
,
gdzie
t
s
w
oznacza wagę przypisaną obserwacji o numerze
s
, w szeregu zawierającym
t
obserwacji.
O wagach zakładamy, że każda z nich jest unormowana na przedziale
1
;
0
oraz że sumują się do
jedności, co zapiszemy:
1
0
t
s
w
;
t
s
t
s
w
1
1
.
W wielu przypadkach, choć nie jest to bezwzględnie konieczne, zakładać będziemy
3
, że wagi
monotonicznie maleją jak rośnie odległość danego okresu od okresu bieżącego
t
, co zapiszemy:
t
t
t
t
t
t
w
w
w
w
1
2
1
......
.
Rozpisując wzór na średnią dla kolejnych okresów otrzymujemy:
1
1
1
1
1
~
y
y
w
y
2
2
2
1
2
1
2
~
y
w
y
w
y
3
3
3
2
3
2
1
3
1
3
~
y
w
y
w
y
w
y
……………………………
T
T
T
T
T
T
y
w
y
w
y
w
y
....
~
2
2
1
1
.
W literaturze przedmiotu najczęściej omawiane są trzy rodzaje wag
4
:
wagi harmoniczne
)
(
t
s
wh
,
wagi liniowe
)
(
t
s
wl
,
wagi geometryczne
)
(
t
s
wg
.
3
W przypadku omawianych w częściach następnych wag w wygładzaniu metodą wyrównywania wykładniczego, wagi
nie muszą spełniać tego warunku.
4
Zob. np. Z.Czerwiński, B.Guzik, Prognozowanie ekonometryczne, PWE Warszawa, 1980, str. 216-218.
Prognozowanie, Tadeusz W.Bołt,
5
Wszystkie trzy rodzaje wag spełniają trzy wymienione wyżej warunki. Różnica między nimi polega
na różnym tempie wygasania w miarę oddalania się od okresu bieżącego. Wagi harmoniczne charakteryzują
się tym, że ich przyrosty są odwrotnie proporcjonalne do czasu. Wagi liniowe mają stałe przyrosty,
natomiast wagi geometryczne stałe ilorazy.
Wagi harmoniczne definiowane są następująco:
0
0
t
wh
;
)
1
(
1
1
s
t
t
wh
wh
t
s
t
s
;
)
,...,
1
;
,...,
2
,
1
(
t
s
T
t
.
W tablicy 3.1 podane są wagi harmoniczne dla szeregów czasowych liczących od
1
t
do
8
t
obserwacji. Jak widać wszystkie wagi są unormowane, monotoniczne i sumują się do jedności. Przykładowe
obliczenia dla
3
t
podajemy poniżej:
0
3
0
wh
;
9
1
)
1
1
3
(
3
1
3
0
3
1
wh
wh
;
18
5
6
1
9
1
)
1
2
3
(
3
1
3
1
3
2
wh
wh
;
18
11
3
1
18
5
)
1
3
3
(
3
1
3
2
3
3
wh
wh
.
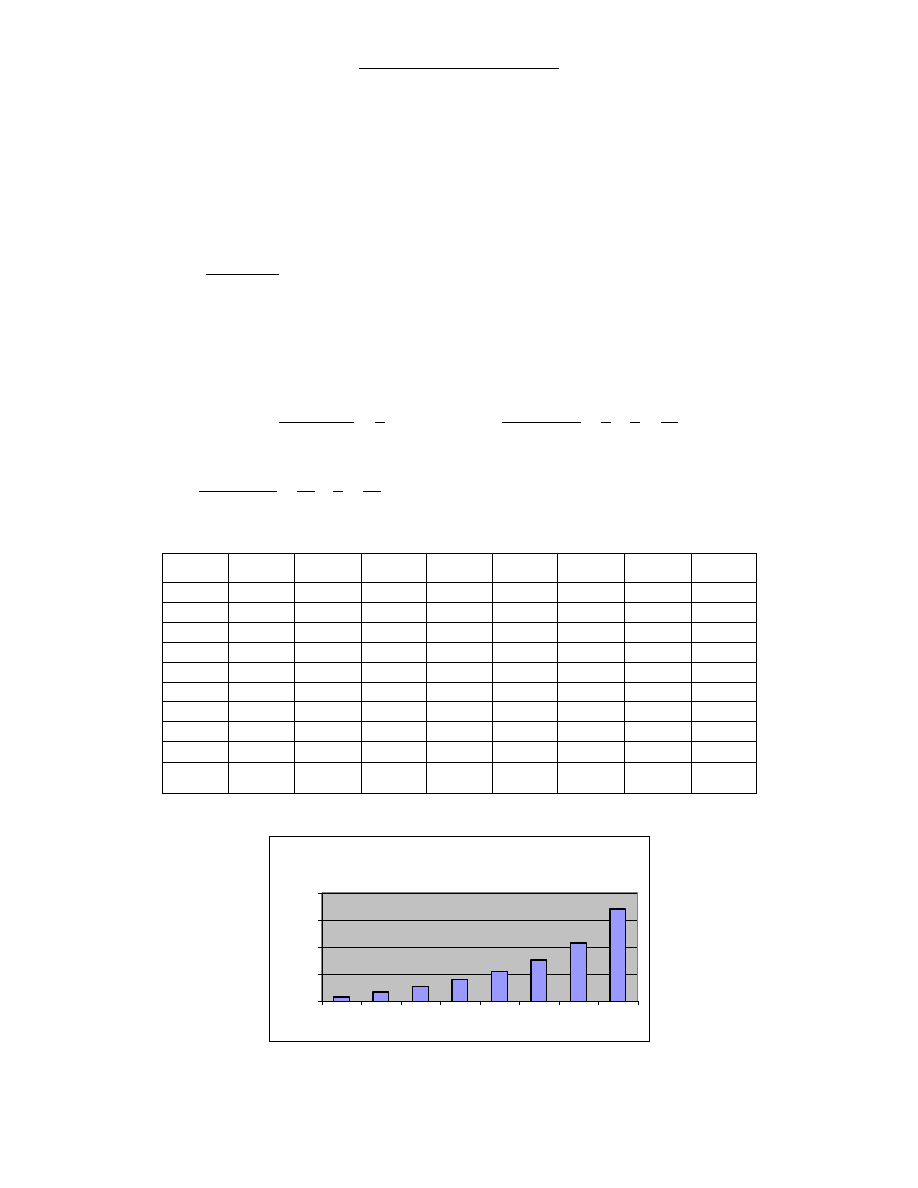
Tablica 3.1 Wagi harmoniczne
t
s,
1
s
wh
2
s
wh
3
s
wh
4
s
wh
5
s
wh
6
s
wh
7
s
wh
8
s
wh
1
1,000
0,250
0,111
0,063
0,040
0,028
0,020
0,016
2
0,750
0,278
0,146
0,090
0,061
0,044
0,033
3
0,611
0,271
0,157
0,103
0,073
0,054
4
0,521
0,257
0,158
0,109
0,079
5
0,457
0,242
0,156
0,111
6
0,408
0,228
0,152
7
0,370
0,215
8
0,340
....
1,000
1,000
1,000
1,000
1,000
1,000
1,000
1,000
Źródło: opracowanie własne
Rysunek 3.1 Wagi harmoniczne
0,000
0,100
0,200
0,300
0,400
1
2
3
4
5
6
7
8
Źródło: opracowanie własne
Prognozowanie, Tadeusz W.Bołt,
6
Wagi liniowe
)
(
t
s
wl
dane są wzorem:
t
i
t
s
i
s
wl
1
;
)
,...,
2
,
1
;
,...,
2
,
1
(
t
s
T
t
,
przy czym
2
1
1
)
(
t
t
i
t
i
.
W tablicy 3.2 podane są wagi harmoniczne dla szeregów czasowych liczących od
1
t
do
8
t
obserwacji. Przykładowe obliczenia dla
3
t
podajemy poniżej:
12
2
)
1
3
(
3
2
3
1
wl
;
12
4
)
1
3
(
3
4
3
2
wl
;
12
6
)
1
3
(
3
6
3
3
wl
.
Widać wyraźnie, że wagi te, dla ustalonego
t
mają stałe przyrosty.
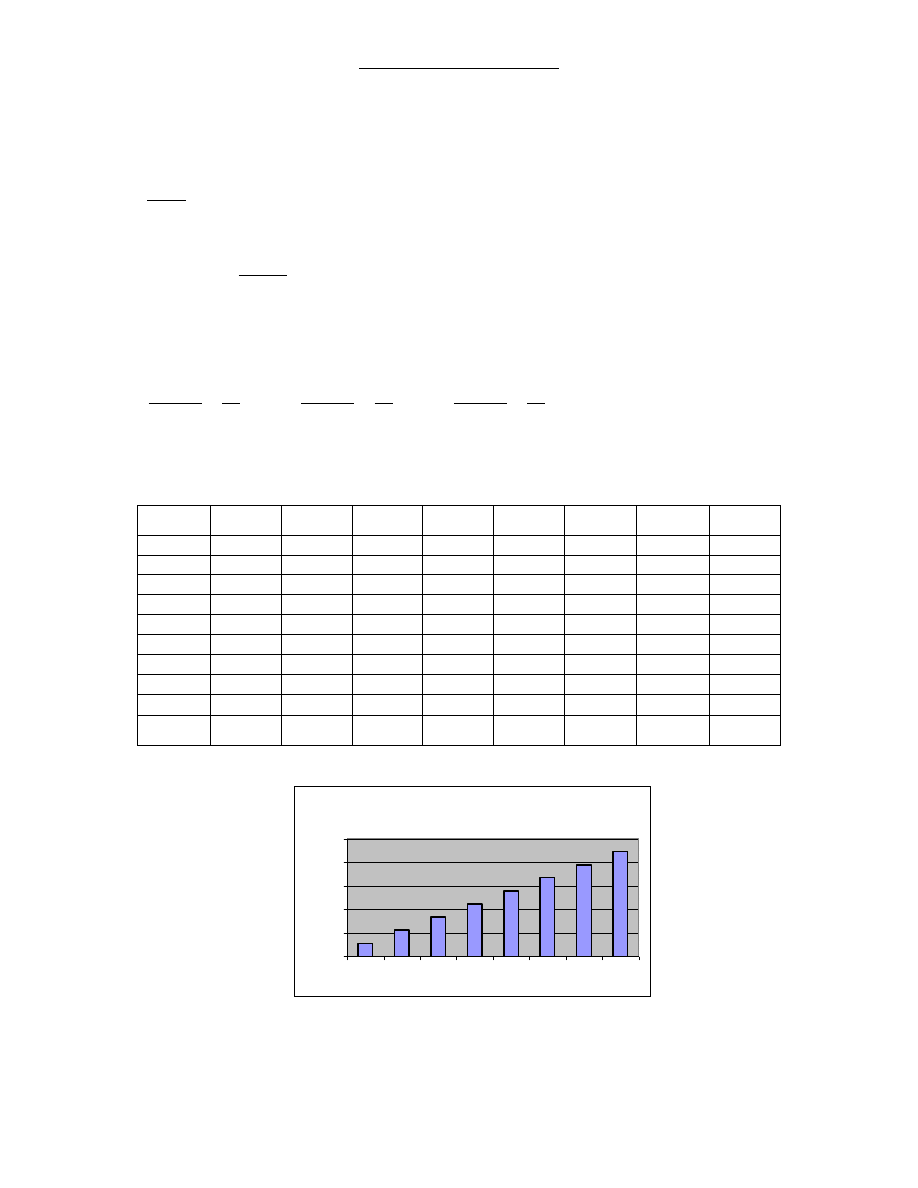
Tablica 3.2. Wagi liniowe
t
s,
1
s
wl
2
s
wl
3
s
wl
4
s
wl
5
s
wl
6
s
wl
7
s
wl
8
s
wl
1
1,000
0,333
0,167
0,100
0,067
0,048
0,036
0,028
2
0,667
0,333
0,200
0,133
0,095
0,071
0,056
3
0,500
0,300
0,200
0,143
0,107
0,083
4
0,400
0,267
0,190
0,143
0,111
5
0,333
0,238
0,179
0,139
6
0,286
0,214
0,167
7
0,250
0,194
8
0,222
....
1,000
1,000
1,000
1,000
1,000
1,000
1,000
1,000
Źródło: opracowanie własne
Rysunek 3.2 Wagi liniowe
0,000
0,050
0,100
0,150
0,200
0,250
1
2
3
4
5
6
7
8
Źródło: opracowanie własne
Wagi geometryczne
)
(
t
s
wg
definiowane są za pomocą wzoru:
Prognozowanie, Tadeusz W.Bołt,
7
)
1
(
)
1
(
t
s
t
t
s
q
q
q
wq
;
)
,...,
2
,
1
;
,...,
2
,
1
;
1
0
(
t
s
T
t
q
.
Zmienność wag geometrycznych zależy od parametru
q
. Wziąwszy
q
bliskie zera, co pokazuje tablica
3.3, otrzymujemy wagi szybko zbiegające do zera, w miarę wzrostu odległości od okresu bieżącego
t
.
Biorąc
q
bliskie jedności, co pokazuje tablica 3.5, otrzymujemy wagi wolno malejące w miarę wzrostu
odległości od okresu bieżącego. Obliczenia dla
3
t
oraz
10
,
0
q
i
90
,
0
q
podajemy poniżej:
001
,
0
999
,
0
009
,
0
)
1
,
0
1
(
1
,
0
*
9
,
0
3
2
3
1
wg
;
090
,
0
999
,
0
090
,
0
)
1
,
0
1
(
1
,
0
*
9
,
0
3
1
3
2
wg
;
900
,
0
999
,
0
9
,
0
)
1
,
0
1
(
1
,
0
*
9
,
0
3
0
3
3
wg
,
299
,
0
271
,
0
081
,
0
)
9
,
0
1
(
9
,
0
*
1
,
0
3
2
3
1
wg
;
332
,
0
271
,
0
090
,
0
)
9
,
0
1
(
9
,
0
*
1
,
0
3
1
3
2
wg
;
369
,
0
271
,
0
100
,
0
)
9
,
0
1
(
9
,
0
*
1
,
0
3
0
3
3
wg
.
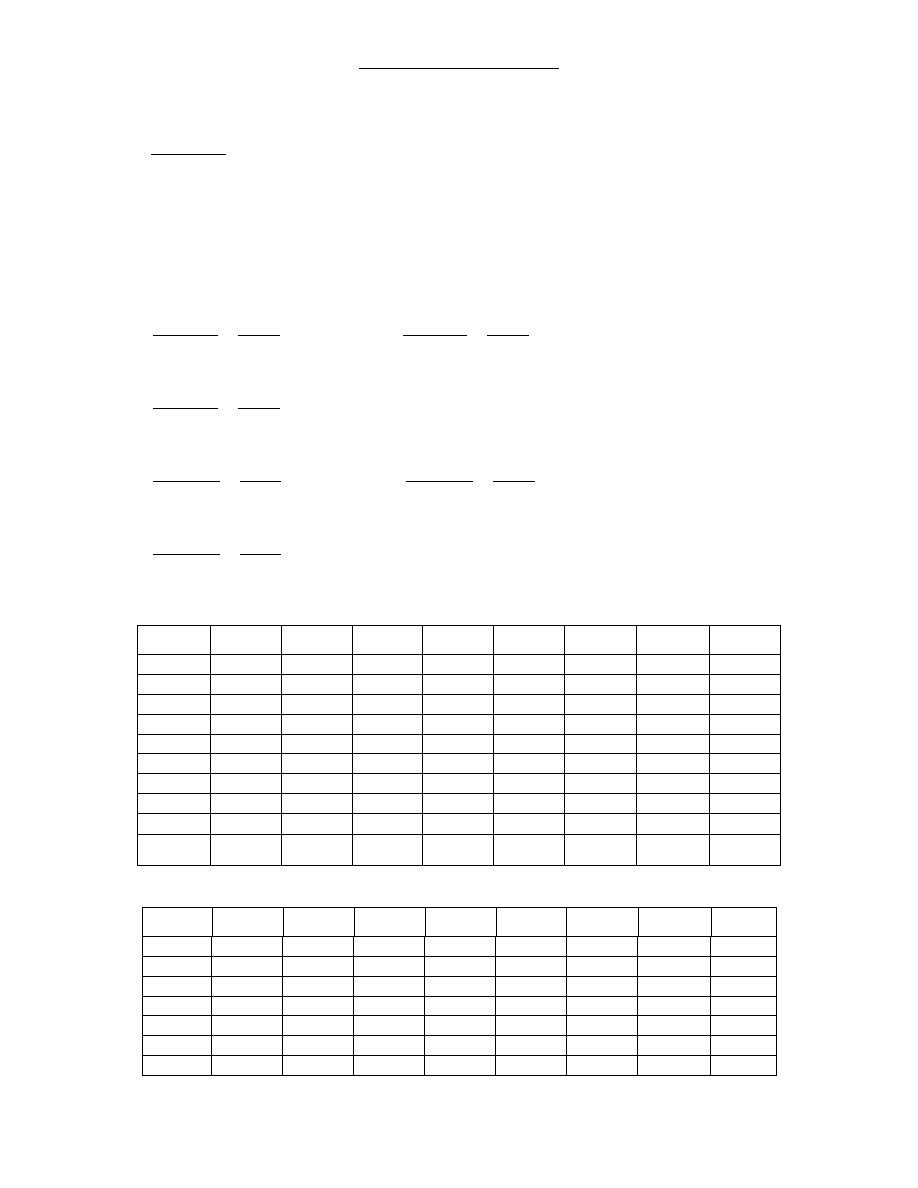
Tablica 3.3. Wagi geometryczne,
10
,
0
q
t
s,
1
s
wg
2
s
wg
3
s
wg
4
s
wg
5
s
wg
6
s
wg
7
s
wg
8
s
wg
1
1,000
0,091
0,009
0,001
0,000
0,000
0,000
0,000
2
0,909
0,090
0,009
0,001
0,000
0,000
0,000
3
0,901
0,090
0,009
0,001
0,000
0,000
4
0,900
0,090
0,009
0,001
0,000
5
0,900
0,090
0,009
0,001
6
0,900
0,090
0,009
7
0,900
0,090
8
0,900
....
1,000
1,000
1,000
1,000
1,000
1,000
1,000
1,000
Źródło: opracowanie własne
Tablica 3.4 Wagi geometryczne,
50
,
0
q
t
s,
1
s
wg
2
s
wg
3
s
wg
4
s
wg
5
s
wg
6
s
wg
7
s
wg
8
s
wg
1
1,000
0,333
0,143
0,067
0,032
0,016
0,008
0,004
2
0,667
0,286
0,133
0,065
0,032
0,016
0,008
3
0,571
0,267
0,129
0,063
0,031
0,016
4
0,533
0,258
0,127
0,063
0,031
5
0,516
0,254
0,126
0,063
6
0,508
0,252
0,125
7
0,504
0,251
Prognozowanie, Tadeusz W.Bołt,
8
8
0,502
....
1,000
1,000
1,000
1,000
1,000
1,000
1,000
1,000
Źródło: opracowanie własne
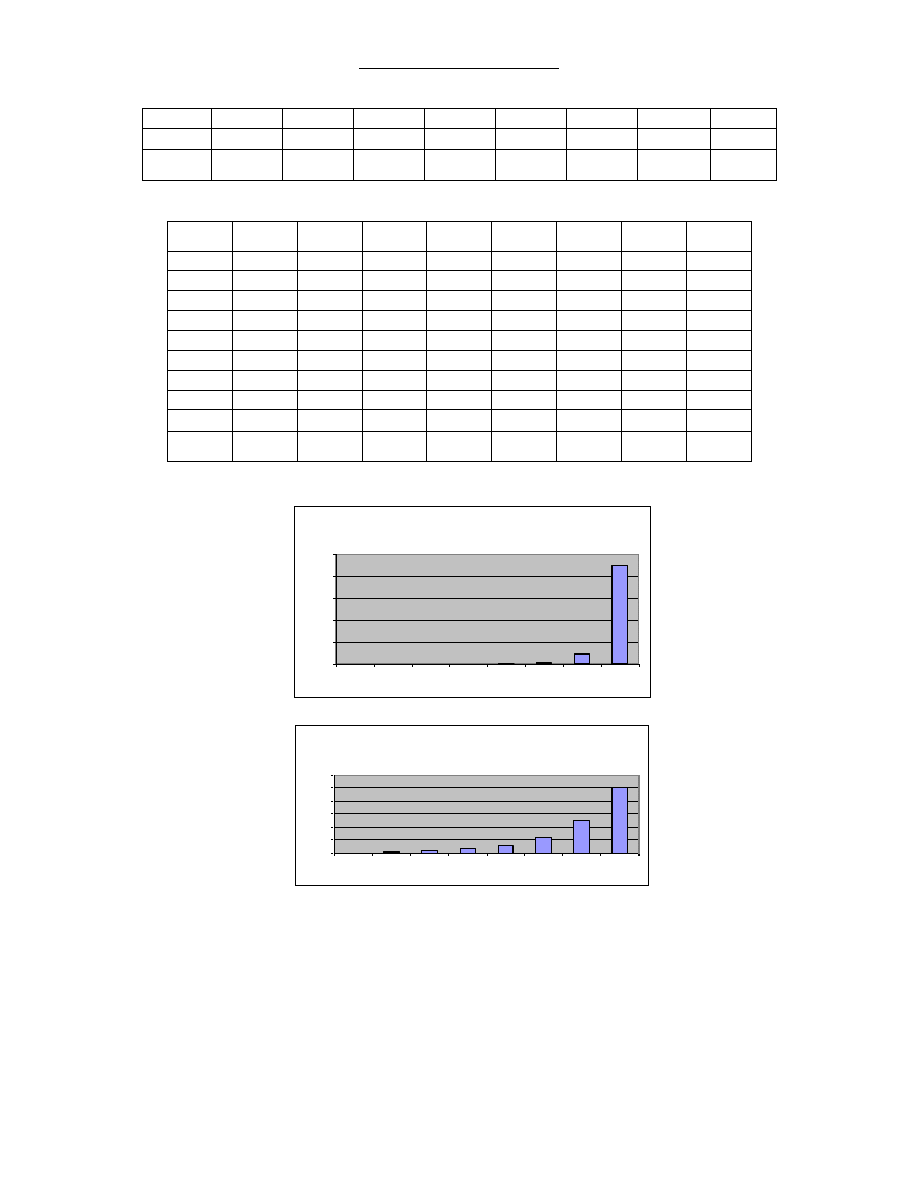
Tablica 3.5 Wagi geometryczne,
90
,
0
q
t
s,
1
s
wg
2
s
wg
3
s
wg
4
s
wg
5
s
wg
6
s
wg
7
s
wg
8
s
wg
1
1,000
0,474
0,299
0,212
0,160
0,126
0,102
0,084
2
0,526
0,332
0,236
0,178
0,140
0,113
0,093
3
0,369
0,262
0,198
0,156
0,126
0,104
4
0,291
0,220
0,173
0,140
0,115
5
0,244
0,192
0,155
0,128
6
0,213
0,173
0,142
7
0,192
0,158
8
0,176
....
1,000
1,000
1,000
1,000
1,000
1,000
1,000
1,000
Źródło: opracowanie własne
3.3 Wagi geometryczne q=0,10
0,000
0,200
0,400
0,600
0,800
1,000
1
2
3
4
5
6
7
8
Źródło: opracowanie własne
3.4 Wagi geometryczne q=0,50
0,000
0,100
0,200
0,300
0,400
0,500
0,600
1
2
3
4
5
6
7
8
Źródło: opracowanie własne
Prognozowanie, Tadeusz W.Bołt,
9
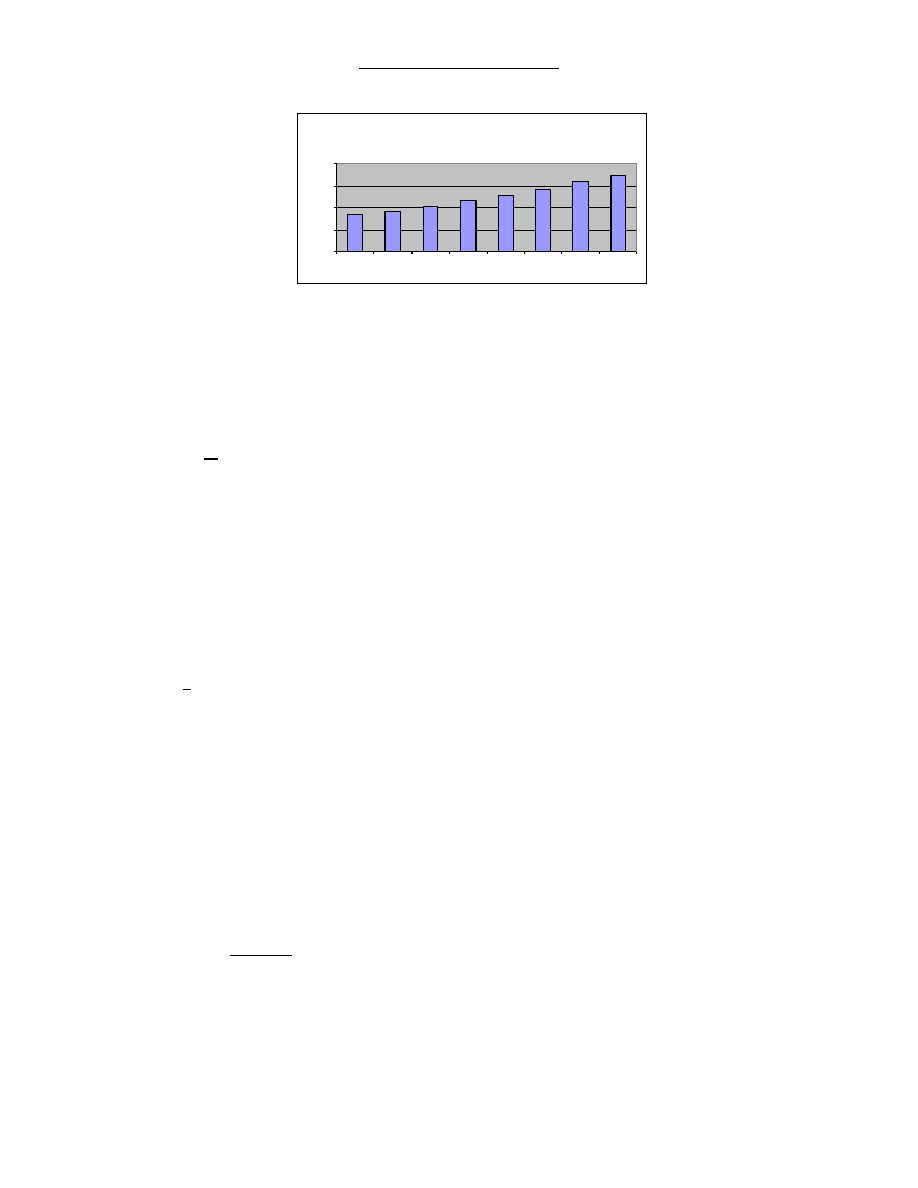
3.5 Wagi geometryczne q=0,90
0,000
0,050
0,100
0,150
0,200
1
2
3
4
5
6
7
8
Źródło: opracowanie własne
Wagi geometryczne są zatem bardzo elastyczne, bowiem dobierając odpowiednią wartość parametru
q
otrzymujemy bardzo różne sposoby ważenia obserwacji historycznych. Powstaje problem, jakie wagi
wybrać oraz jakie kryterium wyboru przyjąć? Odpowiedź na to pytanie wynika z analizy błędów ex post.
Jak w każdej metodzie prognozowania opartej na wygładzaniu, prognoza jest wyznaczana na poziomie
dostępnej w okresie
t
wartości wygładzonej. W naszym przypadku zapiszemy:
t
p
j
t
t
y
y
~
|
;
,...)
2
,
1
;
,...,
2
,
1
(
j
j
T
t
.
Błąd prognozy ex post obliczymy jak poprzednio:
p
j
t
t
j
t
p
j
t
t
y
y
|
|
,
,...)
2
,
1
;
,...,
2
,
1
(
j
j
T
t
.
Zauważmy, że prognoza jest funkcją wag, gdyż wartości średniej ważonej zależą od wag. Zapiszemy
symbolicznie, że:
)
(
~
)
(
|
w
y
w
y
t
p
j
t
t
.
Błąd prognozy ex post będzie zatem także funkcją wag:
)
(
)
(
|
|
w
y
y
w
p
j
t
t
j
t
p
j
t
t
.
W konsekwencji wszystkie parametry rozkładu błędów prognoz ex post będą funkcjami wag. Zatem
naturalnym sposobem wyboru wag będzie optymalizacja wybranego miernika rozkładu błędów względem
wag. Jako kryterium wyboru możemy przyjąć na przykład:
minimalizację średniego kwadratowego błędu prognozy, wtedy zapiszemy:
min
))
(
(
1
1
)
(
1
1
2
w
T
t
p
j
t
p
j
w
j
T
w
MSE
,
minimalizację średniego absolutnego, procentowego błędu prognozy, co zapiszemy:
Prognozowanie, Tadeusz W.Bołt,
10
j
T
t
w
p
j
t
p
j
w
j
T
w
MAPE
1
min
|
)
(
|
1
)
(
,
maksymalizację współczynnika korelacji liniowej Persona (kwadratu tego współczynnika)
pomiędzy realizacjami zmiennej prognozowanej a prognozami wyprzedzeniem j okresów, co
zapiszemy:
min
)
(
,
w
y
y
w
r
p
j
.
W tablicach 3.22 – 3.33 przedstawiono wyniki procesu prognozowania stopy inflacji z wyprzedzeniem
jednego okresu z wykorzystaniem różnych ważonych średnich rekurencyjnych.
3.3. Średnia ruchoma nieważona
Wyrównywanie (wygładzanie) szeregu czasowego omówioną w punkcie poprzednim metodą średniej
arytmetycznej szeregu daje wyniki obciążone systematycznym błędem, szczególnie w przypadku
niestacjonarnych szeregów czasowych, charakteryzujących się występowaniem tendencji rosnącej
(malejącej). Jak pokazaliśmy, w przypadku tendencji malejącej wyrównanie średnią arytmetyczną daje
systematyczne przeszacowanie realizacji szeregu czasowego, w przypadku tendencji rosnącej odwrotnie.
Dlatego też często stosowanym, elastycznym sposobem wygładzania szeregu czasowego jest zastosowanie
średniej ruchomej.
Załóżmy, że dysponujemy szeregiem czasowym
t
y
,
)
,...,
2
,
1
(
T
t
. Średnią ruchomą nieważoną
nazywać będziemy ciąg średnich (arytmetycznych) szeregu wyznaczonych w następujący sposób
5
:
t
k
t
s
s
t
t
k
t
k
t
k
t
y
k
y
y
y
y
k
y
1
1
2
1
1
1
)
...
(
)
(
;
)
,...,
(
T
k
t
,
gdzie
2
k
jest parametrem nazywanym ,,szerokością okna’’ wygładzania
6
. Wybór stałej
k
przesądza o
tym w jaki sposób następować będzie wygładzanie szeregu. Przyjmując małe
k
otrzymujemy tzw. średnią
szybką, tj. liczoną na podstawie niewielkiej liczby okresów, szybko reagującą na wymianę informacji.
Przyjmując
k
duże, otrzymujemy tzw. średnią wolną, tj. liczoną na podstawie dużej liczby okresów, gdzie
wymiana obserwacji nie wpływa na istotne przeszacowanie średniej.
Rozpisując dla kolejnych t otrzymujemy:
)
...
(
)
(
k
k
k
y
y
y
k
y
2
1
1
)
...
(
)
(
1
3
2
1
1
k
k
k
y
y
y
k
y
)
...
(
)
(
2
4
3
2
1
k
k
k
y
y
y
k
y
……………………………
5
Górny indeks w nawiasie
)
(k
oznacza szerokość okna wygładzania.
6
Wybór
1
k
sprowadza omawianą metodę do prognozowania bez wygładzania, omówionego jako ,,metoda
naiwna’’ w trakcie wykładu 2.
Prognozowanie, Tadeusz W.Bołt,
11
)
...
(
)
(
T
k
T
k
T
k
T
y
y
y
k
y
2
1
1
Przykład dla k=2:
)
(
)
(
2
1
2
2
2
1
y
y
y
)
(
)
(
3
2
2
3
2
1
y
y
y
)
(
)
(
4
3
2
4
2
1
y
y
y
……………………………
)
(
)
(
T
T
T
y
y
y
1
2
2
1
Średnia ruchoma jest to zatem średnia liczona dla kolejnych, przesuwanych po osi czasu przedziałów,
kiedy w kolejnym przedziale czasowym najstarsza obserwacja jest odrzucana, natomiast kolejna najnowsza
jest dołączana.
Dla szeregu czasowego liczącego
T
wyrazów, liczba wyznaczonych średnich ruchomych wynosi zatem
)
1
(
k
T
.
Prognozę ex post wyznaczymy w następujący sposób:
)
(
|
k
t
p
j
t
t
y
y
;
,...)
,
;
,...,
(
2
1
j
j
T
k
t
.
3.4. Średnia ruchoma ważona
Średnią ruchoma ważoną
)
~
(
)
(k
t
y
, wyznaczoną na okres
t
, definiuje następująca równość:
t
k
t
s
s
k
i
k
t
y
w
y
1
)
(
~
;
)
,...,
;
,...,
(
k
i
T
k
t
1
,
gdzie
k
i
w oznacza wagę przypisaną obserwacji o numerze i , w szeregu zawierającym k obserwacji.
O wagach zakładamy, że każda z nich jest unormowana na przedziale
1
;
0
oraz że sumują się do
jedności, co zapiszemy:
1
0
k
i
w
;
k
i
k
i
w
1
1.
Ponieważ w średniej ruchomej szerokość okna jest ustalona i równa ,,k’’, zatem wagi zależą od ,,k’’ i są
ustalone dla całej próby. Rozpisując dla kolejnych t otrzymujemy:
k
k
k
k
k
k
k
y
w
y
w
y
w
y
...
~
)
(
2
2
1
1
Prognozowanie, Tadeusz W.Bołt,
12
1
3
2
2
1
1
k
k
k
k
k
k
k
y
w
y
w
y
w
y
...
~
)
(
2
4
2
3
1
2
k
k
k
k
k
k
k
y
w
y
w
y
w
y
...
~
)
(
……………………………
T
k
k
k
T
k
k
T
k
k
T
y
w
y
w
y
w
y
...
~
)
(
2
2
1
1
Przykład dla k=2:
2
2
2
1
2
1
2
2
y
w
y
w
y
)
(
~
3
2
2
2
2
1
2
3
y
w
y
w
y
)
(
~
4
2
2
3
2
1
2
4
y
w
y
w
y
)
(
~
……………………………
T
T
T
y
w
y
w
y
2
2
1
2
1
2
)
(
~
Wagi harmoniczne definiowane dla ustalonego k są następująco:
0
0
k
wh
;
)
(
1
1
1
s
k
k
wh
wh
k
s
k
s
;
)
,...,
(
k
s 1
.
Przykład wag harmonicznych dla dla
2
k
:
0
2
0
wh
;
25
0
1
1
2
2
1
2
0
2
1
,
)
(
wh
wh
;
75
0
50
0
25
0
1
2
2
2
1
2
1
2
2
,
,
,
)
(
wh
wh
Wagi liniowe dla ustalonego
k
)
(
k
s
wl
dane są wzorem:
k
i
k
s
i
s
wl
1
;
)
,...,
,
(
k
s
2
1
,
przy czym
2
1
1
)
(
k
k
i
k
i
.
Przykład wag liniowych dla
2
k
:
3
1
1
2
2
2
2
1
)
(
wl
;
3
2
1
2
2
4
2
2
)
(
wl
.
Prognozowanie, Tadeusz W.Bołt,
13
Wagi geometryczne dla ustalonego k
)
(
k
s
wg
definiowane są za pomocą wzoru:
)
(
)
(
k
s
k
k
s
q
q
q
wq
1
1
;
)
,...,
,
;
(
k
s
q
2
1
1
0
.
Przykład wag geometrycznych dla
2
k
:
)
(
)
(
2
2
1
1
1
q
q
q
wq
;
)
(
)
(
)
(
)
(
2
2
0
2
2
1
1
1
1
q
q
q
q
q
wq
.