Dwójłomność

1

Dwójłomność

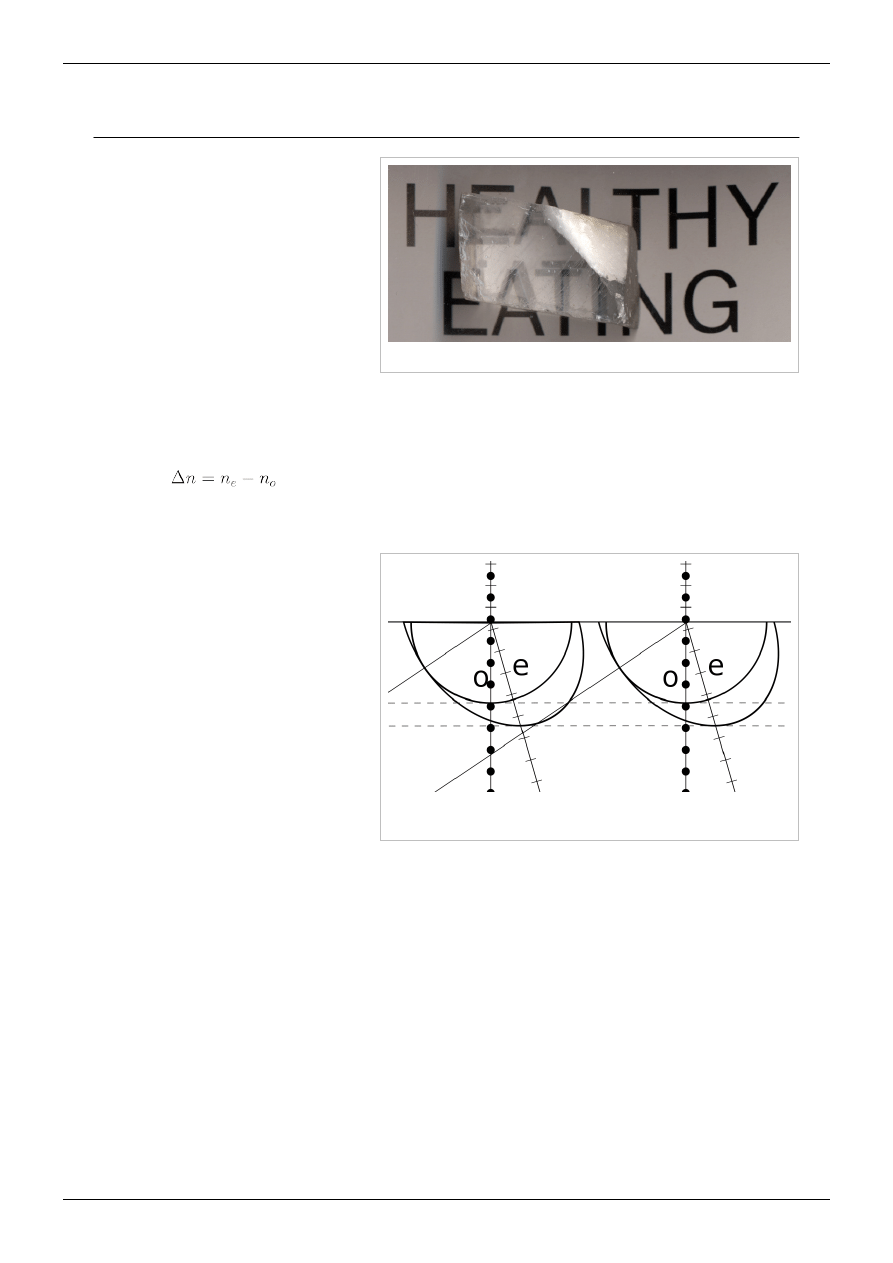
"Podwójny" obraz widziany przez dwójłomny kryształ kalcytu

Dwójłomność – zdolność ośrodków

optycznych do podwójnego załamywania

światła (rozdwojenia promienia świetlnego).

Substancje, dla których zjawisko zachodzi

nazywamy substancjami dwójłomnymi.

Zjawisko dwójłomności odkrył w 1669 roku

Rasmus Bartholin a wyjaśnił Augustin J.

Fresnel w pierwszej połowie XIX w wieku.

Dwójłomność wykazuje wiele substancji

krystalicznych, a także wszystkie ciekłe

kryształy. Przykładami substancji dwójłomnych mogą być kryształy rutylu i kalcytu.

Miarą dwójłomności jest różnica między współczynnikiem załamania promienia nadzwyczajnego n

e

, a

współczynnikiem załamania promienia zwyczajnego n

o

.

Wyjaśnienie

Schemat 1. Rozdzielenie się promienia padającego prostopadle na powierzchnię

dwójłomnego, jednoosiowego kryształu

Zjawisko to wynika z faktu, że substancja

jest anizotropowa, co oznacza, że

współczynniki przenikalności elektrycznej ε

i wynikająca z niego prędkość światła, a co

za tym idzie współczynnik załamania

światła, w krysztale zależą od kierunku

drgań pola elektrycznego fali

elektromagnetycznej (polaryzacji fali).

W krysztale takim istnieje oś optyczna. Jest

to kierunek, w którym biegnące światło nie

rozdziela się na dwa promienie, ponieważ

prędkość światła poruszającego się w tym

kierunku nie zależy od kierunku polaryzacji.

Kierunek tej osi nie zależy od kształtu kryształu. Istnieją kryształy jedno- i dwuosiowe.

Wprowadza się pojęcie: płaszczyzna główna kryształu. Jest to płaszczyzna przechodząca przez dany promień

światła i przecinającą go oś optyczną. Innymi słowy jest to płaszczyzna wyznaczona przez dwie proste - zawierającą

promień światła oraz oś optyczną. Na schematach jest to płaszczyzna rysunku.

Dwójłomność

2

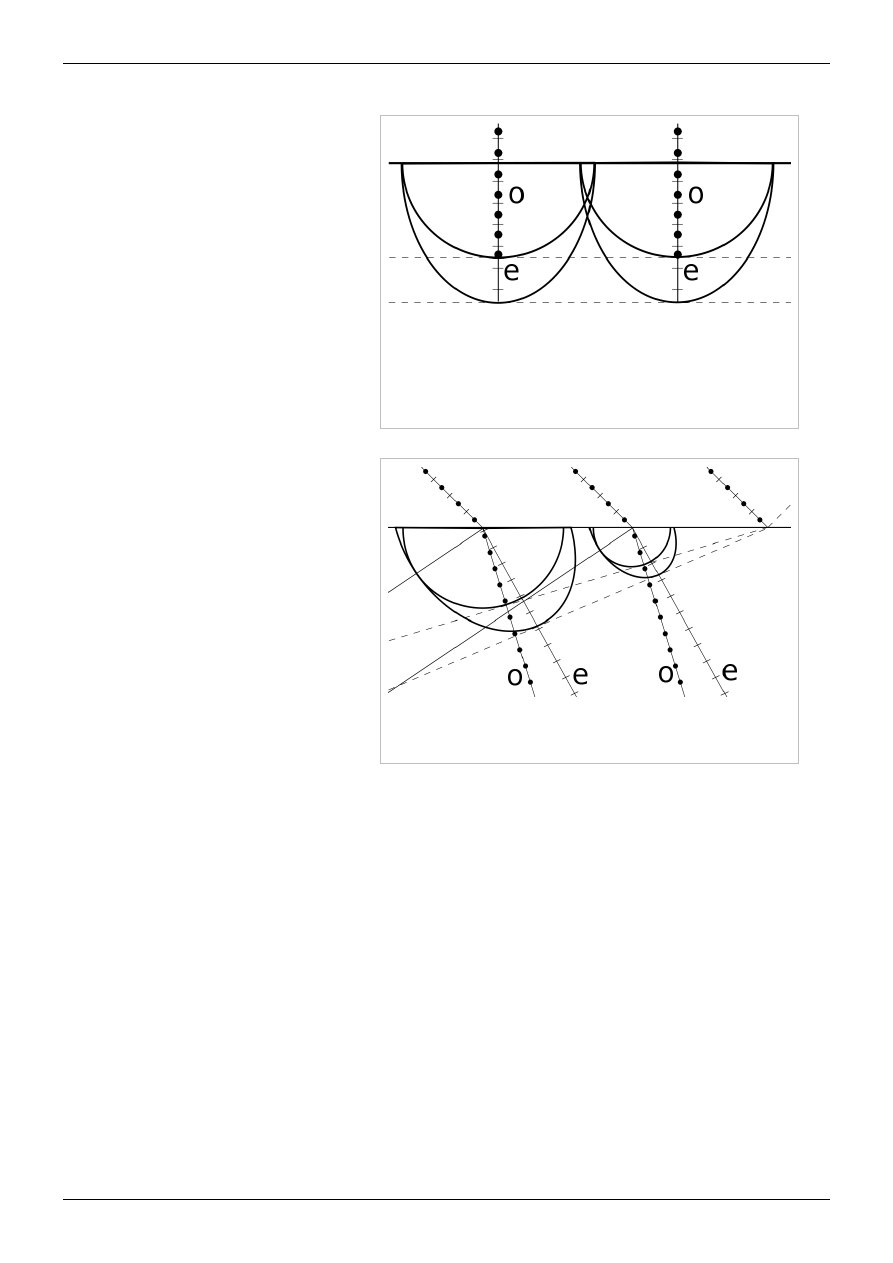
Schemat 2. Zasada działania płytek ćwierć- i półfalowych. Oś optyczna kryształu

skierowana jest równolegle do powierzchni kryształu. Promień pada prostopadle

do tej powierzchni. Po wejściu do kryształu, składowe promieniowania o różnych

polaryzacjach rozchodzą się w nim z różnymi prędkościami, ale po tej samej

drodze. Następuje więc przesunięcie jednej polaryzacji względem drugiej.

Schemat 3. Wyjaśnienie podwójnego załamania za pomocą zasady Huygensa.

Należy zauważyć, że jest to przypadek szczególny – promień nadzwyczajny leży w

płaszczyźnie padania.

Przyczyny mikroskopowe

Istnienie dwójłomności (osi optycznej) w

krysztale wynika z jednakowego kierunku

ustawienia jego anizotropowych cząsteczek.

Cząsteczki takiego kryształu mają

zazwyczaj wydłużony kształt i ułożone są
regularnie. Oś optyczna jest kierunkiem osi

symetrii tych cząsteczek. Zjawisko

dwójłomności może się także pojawić pod

wpływem czynników zewnętrznych, jak

pole elektryczne (elektrooptyczne zjawisko

Kerra), pole magnetyczne (zjawisko

Faradaya, zjawisko magnetooptyczne)), fala

elektromagnetyczna (optyczne zjawisko

Kerra). Wynika to z faktu, że anizotropowe

cząsteczki nie są ułożone regularnie, ale

mogą posiadać ładunki na swoich końcach

(są dipolami), wtedy pod wpływem pola

elektrycznego układają się momentami

dipolowymi równolegle do niego. Zjawisko

to wykorzystywane jest w ekranach LCD.

Nieuszeregowane cząsteczki mogą być

także uporządkowane pod wpływem

ściskania lub rozciągania materiału (tak jak

pozwijane nitki prostują się, kiedy są

rozciągane).

Promień zwyczajny i nadzwyczajny

W krysztale jednoosiowym podczas załamania promień wchodzący do kryształu rozdziela się na dwa. Jeden z nich

to promień zwyczajny, spełnia on prawo Snelliusa, leży w płaszczyźnie padania, oznaczany jest symbolem o (ang.

ordinary). Dla tego promienia kierunek drgań pola elektrycznego jest prostopadły do jego płaszczyzny głównej.

Drugi promień to promień nadzwyczajny. Nazywa się go tak, bo w ogólności nie spełnia on prawa Snelliusa,

oznacza się go przez e (fr. extraordinaire). Promień ten nie musi leżeć w płaszczyźnie padania. Co więcej – może

się załamać nawet wówczas, gdy promień pada prostopadle do powierzchni kryształu. To w jaki sposób zmieni on

kierunek przy takim padaniu, zależy od kierunku osi optycznej w krysztale. Nie załamie się, jeśli oś optyczna jest

prostopadła lub równoległa do powierzchni, na którą pada promień. Dla promienia nadzwyczajnego kierunek drgań

pola elektrycznego jest równoległy do jego płaszczyzny głównej. Warto zauważyć, że ponieważ płaszczyzny główne

obu promieni mogą być inne, polaryzacje obu promieni nie muszą być do siebie prostopadłe.

W krysztale dwuosiowym oba promienie zachowują się jak promienie nadzwyczajne.

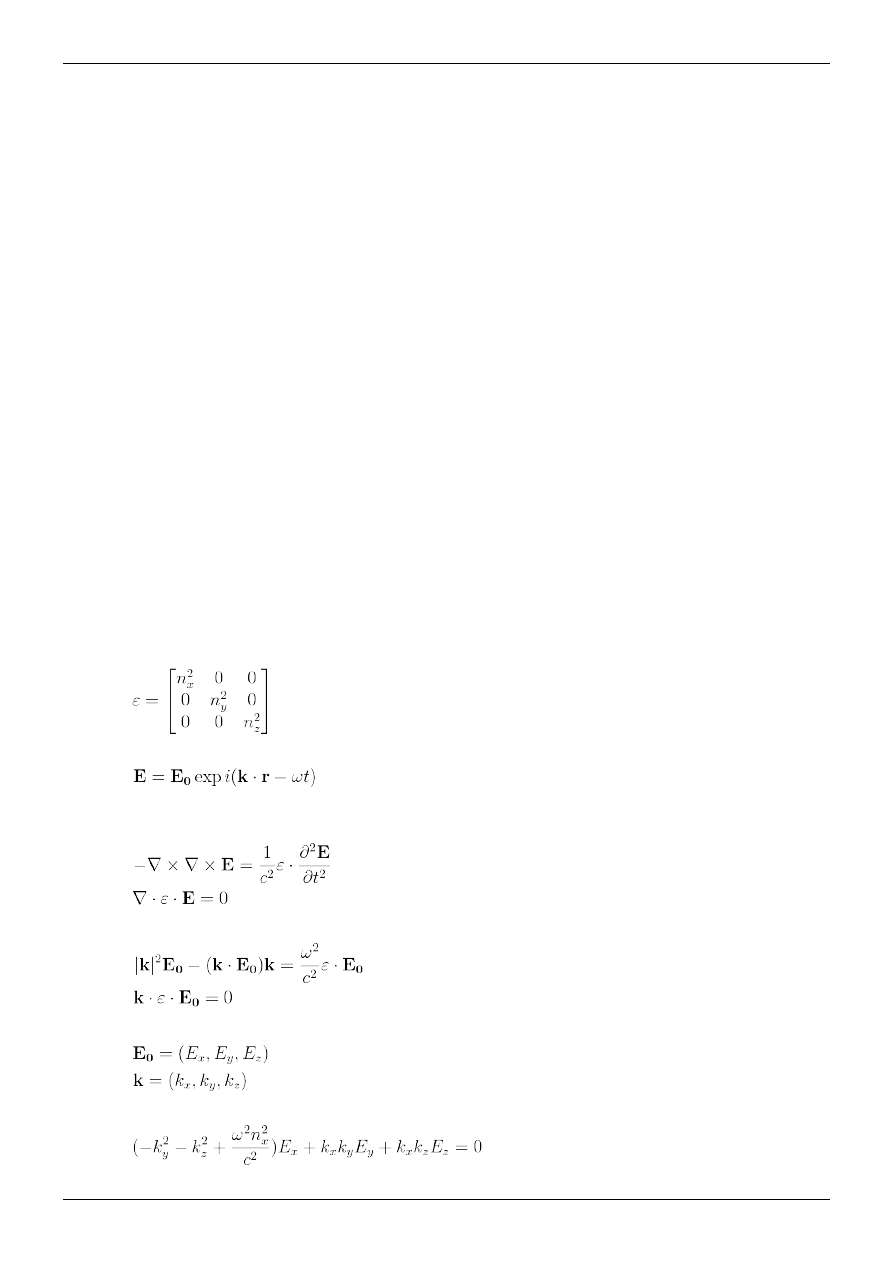
Dwójłomność

3

Zasada Huygensa a dwójłomność

Zasada Huygensa jest spełniona w krysztale dwójłomnym jednoosiowym, z tym, że dla promieni nadzwyczajnych

punkty nie emitują fal kulistych, ale fale elipsoidalne. Jest to elipsoida z osią symetrii wyznaczoną przez oś optyczną

przechodzącą przez emitujący punkt. Wynika to z faktu, że prędkość promienia nadzwyczajnego jest różna w

różnych kierunkach. Dla promienia zwyczajnego jest taka sama we wszystkich kierunkach, emitowana jest więc fala

kulista. Jeśli prędkość światła promienia nadzwyczajnego wzdłuż prostej prostopadłej do osi optycznej jest mniejsza

od prędkości światła promienia zwyczajnego, to kryształ taki nazywa się optycznie dodatnim. Widać, że wtedy

współczynniki załamania promienia nadzwyczajnego spełniają warunek:n

e

jest większy od współczynnika promienia

zwyczajnego n

o

. Jeśli ta prędkość jest większa, kryształ jest optycznie ujemny, a n

e

jest nie większe niż n

o

.

Dzięki zasadzie Huygensa widać też, dlaczego prawo Snelliusa nie jest spełnione dla promienia nadzwyczajnego i

dlaczego promień może się załamać, padając prostopadle na powierzchnię kryształu.

Dla kryształu dwuosiowego emitowane są elipsoidy o trzech różnych osiach, dla których podaje się trzy różne

współczynnik załamania (dwa wzdłuż obu osi i jeden dla kierunku prostopadłego do nich).

Oznaczenia użyte w schematach

• Najcieńsza linia wskazuje kierunek osi optycznej kryształu.

• Kropki i kreski symbolizują kierunek polaryzacji fali elektromagnetycznej, kropki to polaryzacja prostopadła do

powierzchni rysunku, a kreski to polaryzacja równoległa.

• Linie przerywane symbolizują czoło fali.

• Okręgi i elipsy to przykładowe fale cząstkowe narysowane, aby ukazać działanie zasady Huygensa.

Wyprowadzenie z równań Maxwella

Najogólniej dwójłomność można określić przyjmując, że współczynnik przenikalności elektrycznej i współczynnik

załamania światła są tensorami. Bazą są tu wektory własne, co nie zmniejsza ogólności równań

  (1)

Rozważmy rozchodzenie się w takim ośrodku fali płaskiej:

  (2)

gdzie r promień wektora wodzącego, a t to czas. Wtedy wektor falowy k i pulsacja fali ω, muszą spełnić równania

Maxwella

  (3a)

  (3b)

gdzie c to prędkość światła w próżni. Podstawienie równania (2) do 3a-b prowadzi do następujących warunków:

  (4a)

  (4b)

Aby znaleźć dozwolone wartości k, podstawiamy ε i rozpisujemy wektory E

0

i k w bazie ε:

Wtedy równanie 4a rozkłada się na układ równań:

   (5a)

Dwójłomność

4

  (5b)

   (5c)

Będzie on miał rozwiązanie jeśli wyznacznik macierzy będzie równy zero:

  (6)

Po przekształceniu:

  (7)

Dla kryształów jednoosiowych, gdzie n

x

=n

y

=n

o

i n

z

=n

e

, można to równania przekształcić do:

  (8)

Pierwsza część równania definiuje sferę - tak rozchodzi się promień normalny, druga część to elipsoida - tak

rozchodzi się promień nadzwyczajny.

Dla substancji dwuosiowych równanie (7) nie może być przekształcone w taki sposób i opisuje bardziej

skomplikowaną parę powierzchni.

Przykłady substancji dwójłomnych

Dane dla światła o długości fali około 590 nm (okolice światła żółtego),

Substancja jednoosiowa

n

o

n

e

Δn

beryl

1,602 1,557 -0,045

kalcyt CaCO

3

1,658 1,486 -0,172

kalomel Hg

2

Cl

2

1,973 2,656 +0,683

lód H

2

O

1,309 1,313 +0,014

niobian litu LiNbO

3

2,272 2,187 -0,085

fluorek magnezu MgF

2

1,380 1,385 +0,006

kwarc SiO

2

1,544 1,553 +0,009

rubin Al

2

O

3

1,770 1,762 -0,008

rutyl TiO

2

2,616 2,903 +0,287

perydot

1,690 1,654 -0,036

szafir Al

2

O

3

1,768 1,760 -0,008

azotan sodu NaNO

3

1,587 1,336 -0,251

turmalin

1,669 1,638 -0,031

cyrkon, (wsp. maksymalny) ZrSiO

4

1,960 2,015 +0,055

cyrkon, (wsp. minimalny) ZrSiO

4

1,920 1,967 +0,047

Dwójłomność

5

Substancja dwuosiowa

boraks

1,447 1,469 1,472

sól gorzka MgSO

4

·7(H

2

O) 1,433 1,455 1,461

mika, biotyt

1,595 1,640 1,640

mika, muskowit

1,563 1,596 1,601

oliwin (Mg, Fe)

2

SiO

1,640 1,660 1,680

perowskit CaTiO

3

2,300 2,340 2,380

topaz

1,618 1,620 1,627

uleksyt

1,490 1,510 1,520

Zastosowanie

Zjawisko znajduje zastosowanie w produkcji materiałów polaryzujących (np. pryzmatu Nicola), między innymi

półfalówek, ćwierćfalówek i ekranów LCD. Dwójłomność odgrywa także dużą rolę w optyce nieliniowej (może być

wywołana poprzez duże natężenie światła).

Dwójłomność minerałów ma zasadniczy wpływ (obok grubości preparatu) na ich barwy interferencyjne

obserwowane w tzw. płytkach cienkich (preparatach mikroskopowych o grubości 0,02 mm, wykorzystywanych

przez geologów i petrologów). Określenie rodzaju barw interferencyjnych i dwójłomności umożliwia identyfikację

minerałów w płytkach cienkich

[1]

.

Ta sekcja jest zalążkiem. Jeśli możesz, rozbuduj ją

[2]

.

Zobacz też

• fotoelastyczność

• pleochroizm

• właściwości fizyczne i chemiczne minerałów

Bibliografia

• B.M Jaworski, A.A. Dietłaf Fizyka - Poradnik encyklopedyczny rozdział V 4.2

• Richard P. Feynman, Robert B. Leighton, Matthew Sands Feynmana Wykłady z Fizyki, Tom I, Część 2

Przypisy

[1] T.Penkala: Zarys Krystalografii. 1983.

[2] http:/

/

en.

wikipedia.

org/

wiki/

Dw%C3%B3j%C5%82omno%C5%9B%C4%87

Źródła i autorzy artykułu

6

Źródła i autorzy artykułu

Dwójłomność  Źródło: http://pl.wikipedia.org/w/index.php?oldid=21488408  Autorzy: Birczanin, Bogumisia, CiaPan, Filu, Fizykaa, ImreKiss, Karol007, Kluka, KrzysiekS, LMB, Micgryga,
Mpfiz, Mzopw, Petros, Polimerek, Sfu, Siałababamak, Stepa, Stok, Teodozjan, Tommy Boy, Vikom, W2023, Zureks, 8 anonimowych edycji

Źródła, licencje i autorzy grafik

Plik:Calcite.jpg  Źródło: http://pl.wikipedia.org/w/index.php?title=Plik:Calcite.jpg  Licencja: nieznany  Autorzy: Conscious, Duesentrieb, Lzur, Pieter Kuiper, Ra'ike, Saperaud, Sfu, Wutsje, 5
anonimowych edycji

Plik:Birefringence-scheme1.svg  Źródło: http://pl.wikipedia.org/w/index.php?title=Plik:Birefringence-scheme1.svg  Licencja: Creative Commons Attribution-Sharealike 2.5  Autorzy: Sfu

Plik:Birefringence-scheme2.svg  Źródło: http://pl.wikipedia.org/w/index.php?title=Plik:Birefringence-scheme2.svg  Licencja: GNU Free Documentation License  Autorzy: user:Sfu

Plik:Birefringence-scheme3.svg  Źródło: http://pl.wikipedia.org/w/index.php?title=Plik:Birefringence-scheme3.svg  Licencja: Creative Commons Attribution-Sharealike 2.5  Autorzy: Sfu

Plik:Wiki letter w.svg  Źródło: http://pl.wikipedia.org/w/index.php?title=Plik:Wiki_letter_w.svg  Licencja: GNU Free Documentation License  Autorzy: User:Jarkko Piiroinen

Licencja

Creative Commons Attribution-Share Alike 3.0 Unported
http:/

/

creativecommons.

org/

licenses/

by-sa/

3.

0/