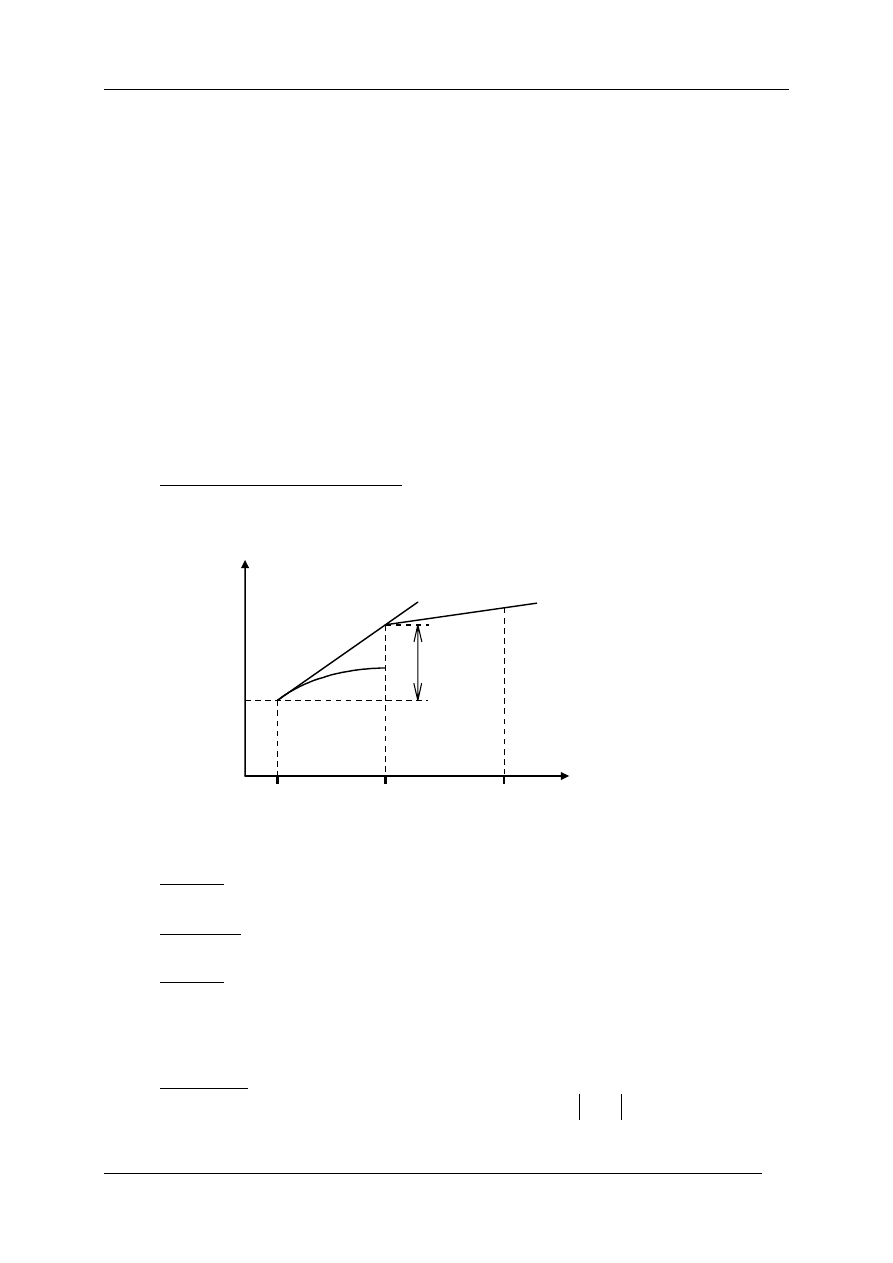
Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
39
7. Równania różniczkowe zwyczajne
7.1 Przybliżenie pierwszego i drugiego rzędu
Przyjmujemy, że rozpatrywane równanie ma postać:
(7.1)
(
)
y
f x y x
'
, ( )
=
; gdzie
f x y
( , )
jest znaną funkcją.
Rozwiązywanie równania różniczkowego (a więc wyznaczanie
y x
( )
gdy znamy
(
)
y
f x y x
'
, ( )
=
) nazywamy całkowaniem równania różniczkowego (7.1) [4].
Problem który będziemy dalej rozpatrywać, zdefiniowany jest następująco:
- znane jest rozwiązanie
y x
y
( )
0
0
=
- należy znaleźć:
1
0
1
)
(
)
(
y
h
x
y
x
y
=
+
=
A. Przybliżenie pierwszego rzędu
W tej metodzie, zwanej metodą Eulera, postępuje się wg algorytmu:
y
x
0
x
1
=x
0
+h
x
2
x
N
1
y
0
∆
y
N
2
T
0
A
0
M
1
0
Rys. 7.1 Metoda Eulera
1
°
oblicz:
(
)
p
f x y
0
0
0
=
,
2
°
przyjmij
M
N
1
1
≈
3
°
oblicz
(
)
∆
∆
y hp
hf x y
y
y
y
=
=
=
+
0
0
0
1
0
,
;
Przy takim postępowaniu popełnia się dwa rodzaje błędów:
błąd metody
wynikający ze sposobu obliczeń (jest to odległość
MN
na rysunku);
Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
40
błąd zaokrąglenia
pojawia się przy obliczaniu
(
)
f x y
0
0
,
(są to na ogół czynniki pomijane przy
mnożeniach i dzieleniach).
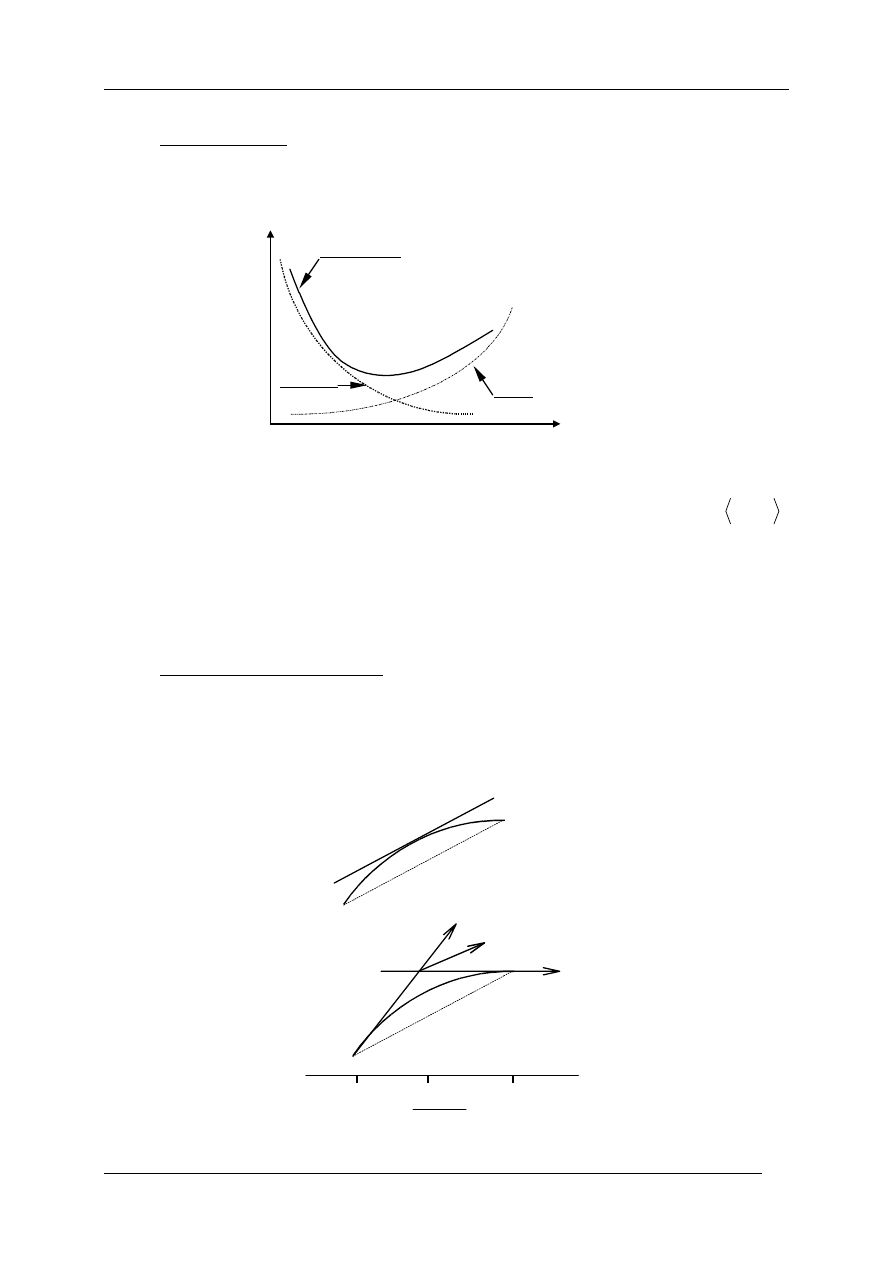
ε
y
0
Błąd całkowity
Błąd
zaokrągleń
Błąd
metody
0
Krok h
Rys. 7.2 Wpływ długości kroku h na błędy popełniane przy rozwiązywaniu równań
różniczkowych
Gdy krok całkowania
h
zmniejsza się, to w celu pokrycia całego przedziału
x b
0
,
,
w którym poszukujemy rozwiązania, zwiększa się liczbę punktów podziału.
Zmniejszenie
h
powoduje zmniejszenie błędu metody, ale powiększa błędy
zaokrągleń. Gdy
h
jest dostatecznie małe, to błąd zaokrągleń jest przeważający i
dalsze zmniejszenie kroku nie daje poprawy dokładności, a może nawet dać
pogorszenie wyników. Przykładowe przebiegi błędów przedstawiono na Rys. 7.2.
B. Przybliżenie drugiego rzędu
Dla paraboli o osi równoległej do osi
y
prawdziwe są następujące twierdzenia:
1
°
Styczna do łuku M M
0
1
w punkcie P o odciętej będącej średnią arytmetyczną
odciętych punktów
0
M
i
1
M
jest równoległa do
M M
0
1
M
0
M
1
M
0
M
1
T
1
T
T
0
2
x
x
1
0
+
x
0
x
1
Rys 7.3 graficzna interpretacja własności paraboli
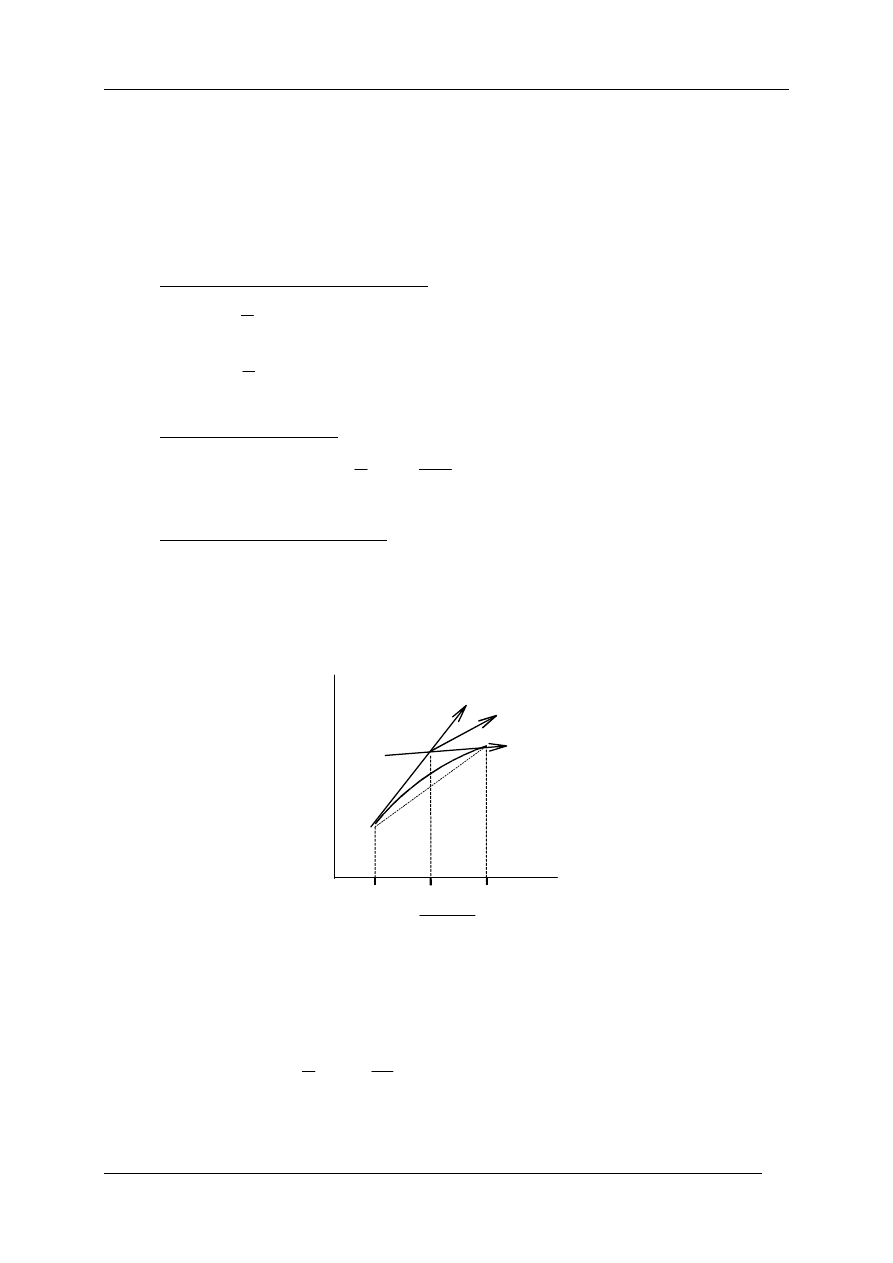
Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
41
2
°
Współczynnik kierunkowy siecznej
M M
0
1
jest średnią arytmetyczną
współczynników kierunkowych stycznych
M T i M T
0 0
1 1
Bazując na tych twierdzeniach konstruuje się wzory dające błąd będący małą trzeciego
rzędu dla dowolnej krzywej. Algorytm postępowania jest następujący:
1
°
oblicza się współrzędne punktu P’
(
)
x
x
h
y
y
h
p
p
f x y
'
'
,
,
=
+
=
+
=
0
0
0
0
0
0
2
2
2
°
znajduje styczną w P’
(
)
+
+
=
′
′
=
′
2
,
2
,
0
0
0
hp
y
h
x
f
y
x
f
p
3
°
oblicza współrzędne punktu
1
M
x
x
h
y
y
hp
1
0
1
0
=
+
=
+
'
Interpretację graficzną tego postępowania przedstawiono na rysunku poniżej.
P
′
M
0
M
1
T
1
T
T
0
2
1
0
x
x
+
x
0
x
1
Rys. 7.4 Graficzna interpretacja przybliżenia drugiego rzędu
Podsumowując, należy liczyć:
(7.2)
(
)
k
hf x y
k
hf x
h
y
k
y
y
k
1
0
0
2
0
0
1
1
0
2
2
2
=
=
+
+
=
+
,
,

Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
42
7.2. Wzory Rungego-Kutty
Stosuje się uogólnienie postępowania przedstawionego poprzednio,
przyjmując:
(7.3)
(
)
(
)
(
)
...
,
,
,
3
3
2
2
1
1
0
1
2
1
0
0
3
1
0
0
2
0
0
1
+
+
+
+
=
+
+
+
=
+
+
=
=
k
R
k
R
k
R
y
y
k
k
y
bh
x
hf
k
k
y
ah
x
hf
k
y
x
hf
k
!
γ
β
α
Współczynniki
a b
R R R
, , , , , ,
,
,...
α β γ
1
2
3
dobiera się tak, aby zapewnić
odpowiednią dokładność i stabilność wzorów. Opracowano wiele formuł. Niektóre z
nich podano poniżej.
Formuły drugiego rzędu
:
Przyjmując:
a
R
R
= =
=
=
α
1
2
0
1
1
2
,
,
otrzymuje się wzory (7.2)
wyprowadzone wcześniej:
Formuły trzeciego rzędu:
(7.4)
(
)
(
)
(
)
k
hf x y
k
hf x
h
y
k
k
hf x
h y
k
k
y
k
k
k
1
0
0
2
0
0
1
3
0
0
1
2
1
2
3
2
2
2
1
6
4
=
=
+
+
=
+
− +
=
+
+
,
,
,
∆

Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
43
Formuły czwartego rzędu
:
(7.5)
(
)
(
)
(
)
k
hf x y
k
hf x
h
y
k
k
hf x
h
y
k
k
hf x
h y
k
y
k
k
k
k
1
0
0
2
0
0
1
3
0
0
2
4
0
0
3
1
2
3
4
2
2
2
2
1
6
2
2
=
=
+
+
=
+
+
=
+
+
=
+
+
+
,
,
,
,
∆
Formuły szóstego rzędu (Milne’a):
(
)
k
hf x y
k
hf x
h
y
k
k
hf x
h
y
k
k
1
0
0
2
0
0
1
3
0
0
2
1
3
3
2
5
6
4
25
=
=
+
+
=
+
+
+
,
,
,
(7.6)
k
hf x
h y
k
k
k
4
0
0
3
2
15
12
1
4
=
+
+
−
+
,
(
)
k
hf x
h
y
k
k
k
k
k
hf x
h
y
k
k
k
k
y
k
k
k
k
5
0
0
4
3
2
1
6
0
0
4
3
2
1
1
3
5
6
2
3
8
50
90
6
81
4
5
8
10
36
6
75
1
192
23
125
81
125
=
+
+
−
+
+
=
+
+
+
+
+
=
+
−
+
,
,
∆
Najpopularniejsze
są formuły czwartego rzędu.
Uwaga Istotną cechą metody Rungego-Kutty jest to, że aby obliczyć wartość
rozwiązania w
x
h
0
+
trzeba obliczać wartości funkcji
f x y x
( , ( ))
w
punktach pośrednich, leżących wewnątrz przedziału
[ ,
]
x x
h
0
0
+
.
Może to być wadą w przypadku gdy obliczenie wartości funkcji
f x y
( , )
jest czasochłonne.
Wolne od tej wady są metody wielokrokowe omawiane dalej.

Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
44
7.3. Metody wielokrokowe
Jeśli scałkujemy rozpatrywane równanie (7.1)
(
)
y
f x y x
'
, ( )
=
w przedziale
[ ,
]
x x
h
n
n
+
to otrzymamy:
(7.7)
( )
(
) ( )
(
)
dx
x
y
x
f
x
y
h
x
y
y
x
f
y
h
x
x
h
x
x
n
n
n
n
n
n
∫
∫
+
+
=
−
+
→
=
′
)
(
,
,
Niech:
(7.8)
(
)
F x
f x y x
( )
, ( )
≡
.
Ponieważ nie znamy (dopiero chcemy wyznaczyć)
y
y x
h
n
n
+
=
+
1
(
)
, funkcja
F x
( )
nie jest znana w
x
h
n
+
. Przyjmijmy, że są znane:
(7.9)
( )
( )
(
)
( ) (
)
( ) (
)
( ) (
)
n
n
n
n
y
x
f
x
F
F
y
x
f
x
F
F
y
x
f
x
F
F
x
y
x
f
x
F
F
,
,
,
,
2
2
2
2
1
1
1
1
0
0
0
0
=
=
=
=
=
=
=
=
!
W metodach wielokrokowych interpoluje się
( )
F x
wielomianem
( )
F x
∗
za pomocą
wartości
F
F
n
0
...
a następnie oblicza całkę z wyrażenia (7.7) następująco:
(7.10)
(
)
f x y x dx
F x dx
F x dx
x
x h
x
x h
x
x h
n
n
n
n
n
n
, ( )
( )
( )
=
≈
+
+
∗
+
∫
∫
∫
W zależności od sposobu budowania wielomianu
( )
F x
∗
otrzymuje się dwie rodziny
metod: ekstrapolacyjne i interpolacyjne.
Metody ekstrapolacyjne
Dane są:
(
)
(
)
(
)
n
n
n
n
n
y
x
f
F
y
x
y
x
f
F
y
x
y
x
f
F
y
x
,
,
,
1
1
1
1
1
0
0
0
0
0
=
=
=
,
,
,
,
,
,
!

Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
45
Krok I
: Znajdujemy wielomian interpolacyjny
( )
F x
∗
zbudowany na:
x x
x
F F
F
n
n
0
1
0
1
, ,...,
, ,...
Krok II:
Obliczamy:
(
)
y x
h
y
F x dx
n
n
x
x
h
n
n
+ =
+
∗
+
∫
( )
B. Metody interpolacyjne
Dane są:
(
)
(
)
(
)
(
)
,
,
,
,
,
,
,
,
,
h
x
x
y
x
f
F
y
x
y
x
f
F
y
x
y
x
f
F
y
x
y
x
f
F
y
x
n
n
n
n
n
n
n
n
n
n
n
n
+
=
=
=
=
=
+
+
+
+
+
+
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
,
,
,
,
!
Krok I
:
Znajdujemy wielomian interpolacyjny
( )
F x
∗
zbudowany na:
x x
x x
F F
F F
n
n
n
n
0
1
1
0
1
1
, ,..., ,
, ,...
,
+
+
Do punktów interpolacji włączamy punkt
(
,
)
x
F
n
n
+
+
1
1
!
Krok II
: Formułujemy równanie
( )
1
1
)
(
+
+
∗
+
=
+
=
⊗
∫
n
h
x
x
n
n
y
G
dx
x
F
y
y
n
n
Krok III
: Rozwiązujemy równanie nieliniowe
⊗
na ogół metodą kolejnych
przybliżeń.
Poniżej omówiono dokładniej obie rodziny metod.
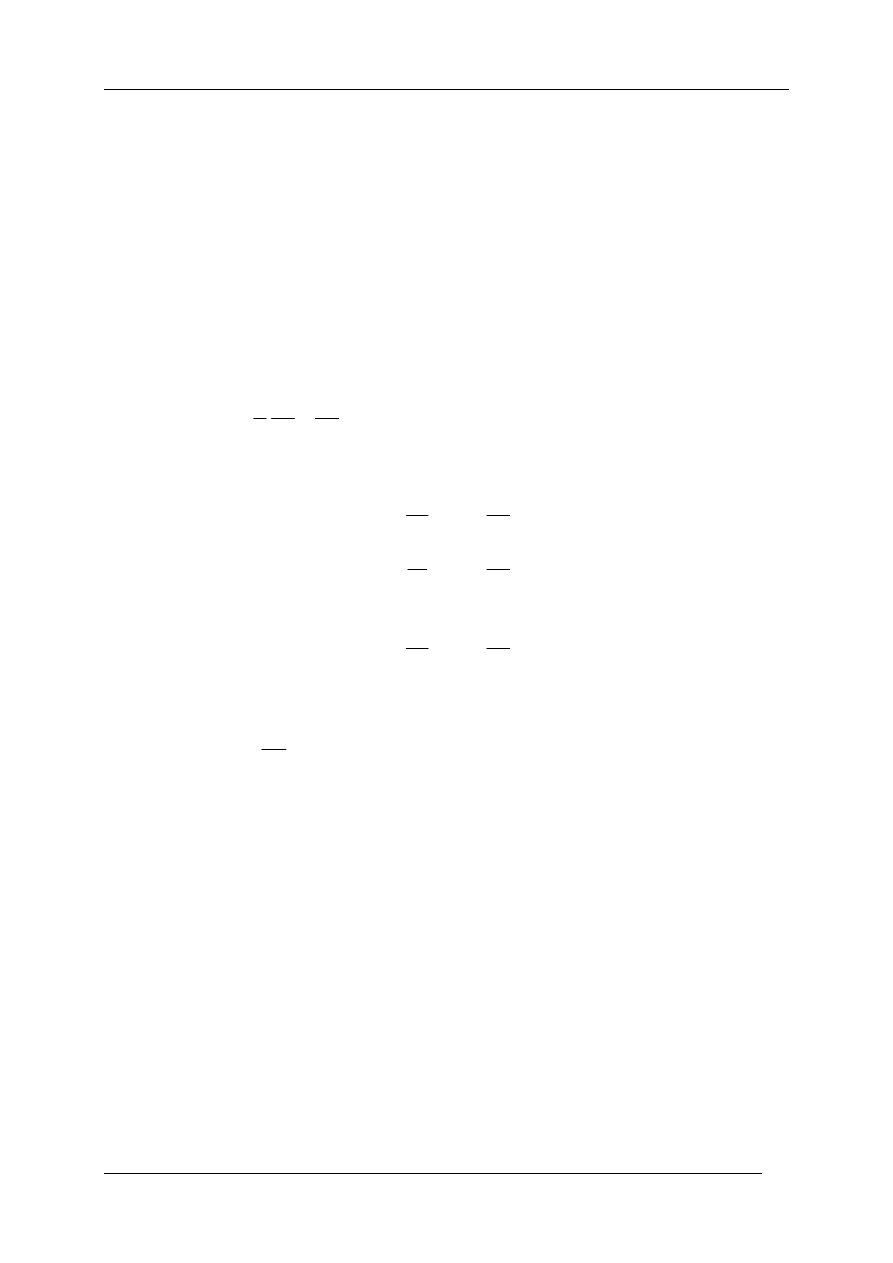
Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
46
7.3.1 Metody ekstrapolacyjne
Dane
są:
n
n
n
F
y
nh
x
x
F
y
h
x
x
F
y
x
,
,
,
,
,
,
0
1
1
0
1
0
0
0
+
=
+
=
!
Budujemy wielomian interpolacyjny w bazie jednomianów, który można ogólnie
przedstawić w postaci:
(7.11)
=
∗
n
n
n
n
F
F
F
h
x
h
x
h
x
x
F
!
1
0
2
2
...
1
)
(
L
gdzie:
=
=
n
n
n
n
n
n
n
n
n
n
h
x
h
x
h
x
h
x
h
x
h
x
n
"
!
!
!
"
#
1
1
1
;
1
1
0
0
V
V
L
1
-
Jeśli wprowadzić oznaczenie:
(7.12)
x
h
dx
J
k
k
k
x
x nh
x h x
n
h
n
n
=
= +
+ = + +
∫
0
0
1
(
)
wówczas
(7.13)
[
]
+
=
+
=
∫
+
∗
+
n
n
n
n
h
x
x
n
n
F
F
F
L
J
J
J
y
dx
x
F
y
y
n
n
!
1
0
1
0
1
...
)
(
Inaczej:
(7.14)
F
y
F
F
F
y
y
n
n
n
n
n
α
α
α
α
+
=
+
+
+
+
=
+
...
1
1
0
0
1
gdzie:
[
] [
]
[
]
α
α α α
= ⋅
≡
=
=
J L
J J J L
F
F F
F
n
n
n
n
n
T
0
1
0 1
0
1
...
;
, ,...,
.
Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
47
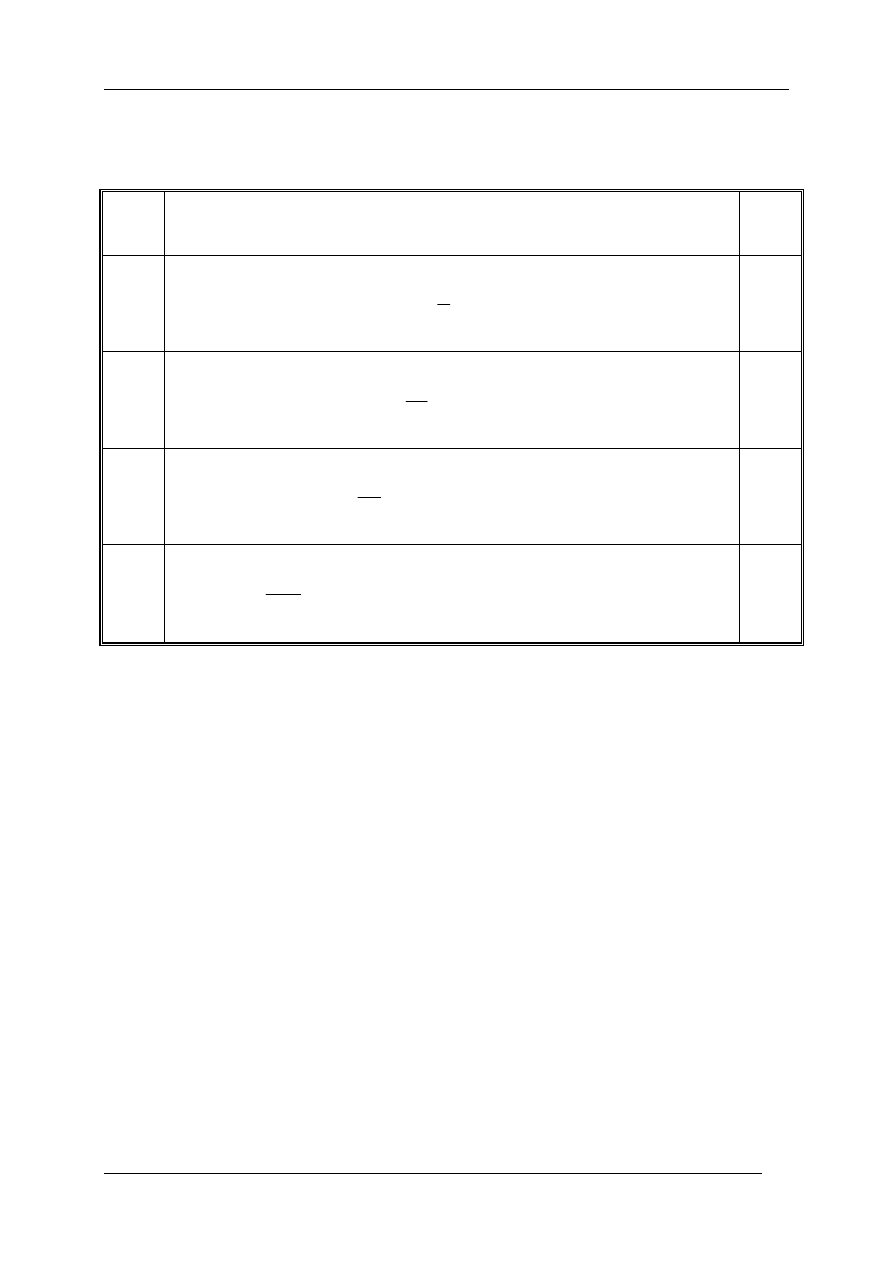
W zależności od liczby n (a więc stopnia wielomianu interpolacyjnego) otrzymuje się
wzory zestawione w poniższej tabeli [5].
Stopień
wielom.
Formuła aproksymacyjna
błąd
n=1
(
)
y
y
h
F
F
2
1
0
1
2
3
=
+
−
+
0(h
3
)
n=2
(
)
y
y
h
F
F
F
3
2
0
1
2
12
5
16
23
=
+
−
+
0(h
4
)
n=3
(
)
y
y
h
F
F
F
F
4
3
0
1
2
3
24
9
37
59
55
=
+
−
+
−
+
0(h
5
)
n=4
(
)
y
y
h
F
F
F
F
F
5
4
0
1
2
3
4
720
251
1274
2616
2774
1901
=
+
−
+
−
+
0(h
6
)

Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
48
7.3.2. Metody interpolacyjne
Dane
są:
1
1
0
1
0
1
1
0
1
0
0
0
,
)
1
(
,
,
+
+
+
+
+
=
+
=
+
=
n
n
n
n
n
n
F
y
h
n
x
x
F
y
nh
x
x
F
y
h
x
x
F
y
x
,
,
,
,
,
!
Wielomian interpolacyjny zbudowany na punktach
( , )
x F
0
0
...
(
,
)
x
F
n
n
+
+
1
1
ma
postać:
(7.15)
=
+
+
+
∗
1
1
0
1
1
2
2
1
)
(
n
n
n
n
n
n
n
F
F
F
F
h
x
h
x
h
x
h
x
x
F
!
"
L
Po zastosowaniu oznaczeń (7.12) można obliczyć:
(7.16)
[
]
+
=
+
+
+
+
1
1
0
1
1
1
0
1
...
n
n
n
n
n
n
n
F
F
F
F
J
J
J
J
y
y
!
L
Jest to równanie nieliniowe z uwagi na zależność:
(7.17)
(
)
F
f x
y
n
n
n
+
+
+
=
1
1
1
,
W celu rozwiązania równania nieliniowego (7.16) należy odpowiednio dobrać
przybliżenie początkowe
y
n
+
1
0
( )
.
Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
49
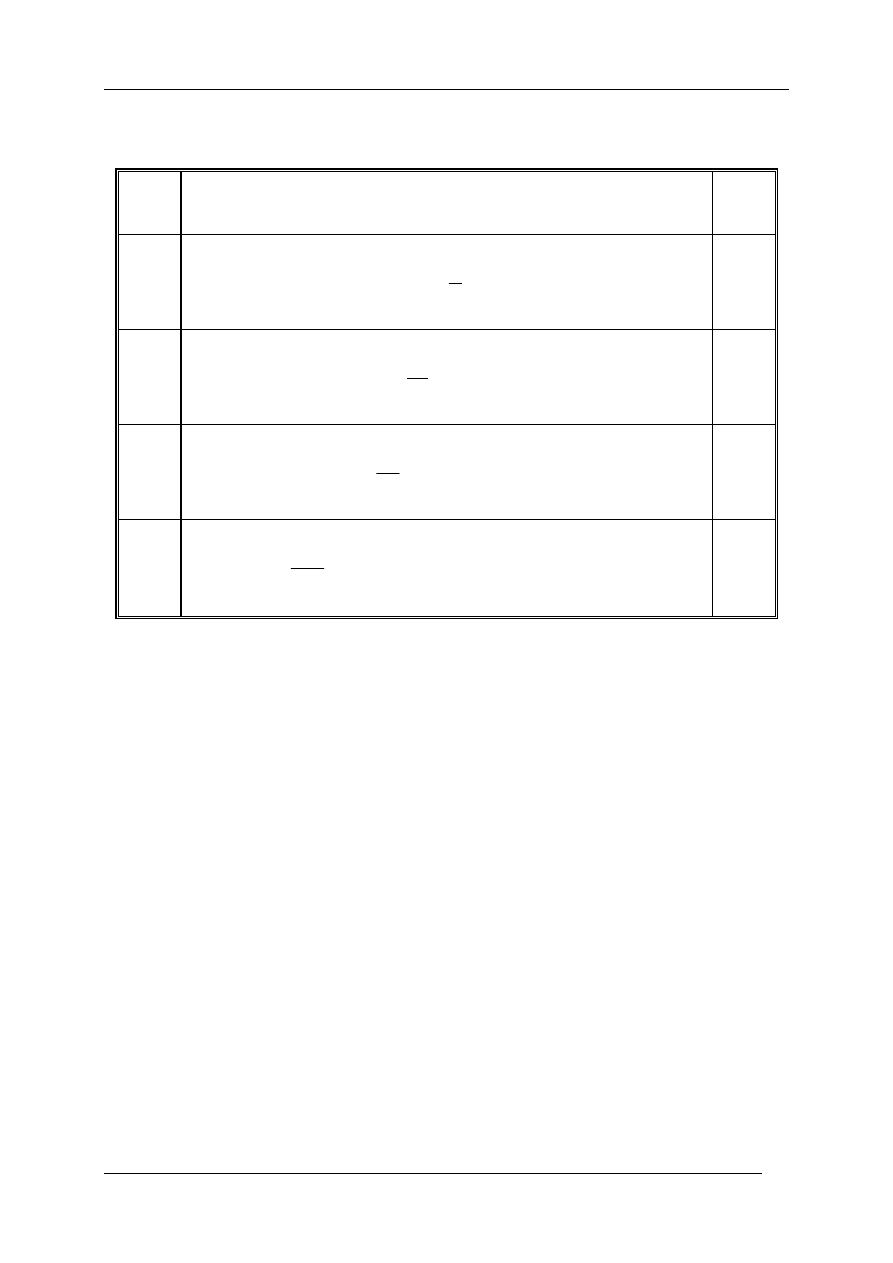
W
zależności od liczby n otrzymuje się wzory zestawione w poniższej tabeli.
Stopień
wielom.
Formuła aproksymacyjna
błąd
n=1
(
)
1
0
0
1
2
F
F
h
y
y
+
+
=
0(h
3
)
n=2
(
)
2
1
0
1
2
5
8
12
F
F
F
h
y
y
+
+
−
+
=
0(h
4
)
n=3
(
)
3
2
1
0
2
3
9
19
5
24
F
F
F
F
h
y
y
+
+
−
+
=
0(h
5
)
n=4
(
)
4
3
2
1
0
3
4
251
646
264
106
19
720
F
F
F
F
F
h
y
y
+
+
−
+
−
+
=
0(h
6
)
Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
50
7.3.3. Metoda obliczeniowa
1
°
Metodą ekstrapolacji wyznacza się
y
n
+
∗
1
na podstawie
y y
y
n
0
1
, ,...,
2
°
Wielkość
y
n
+
∗
1
jest wartością początkową przy rozwiązywaniu metodą kolejnych
przybliżeń równania otrzymanego metodą interpolacyjną:
(
)
[
]
y
y
h
F
F
F
x
y
n
n
n n
n
n
n
n
+
+
+
+
+
=
+
+ +
+
1
0 0
1
1
1
1
β
β
β
...
,
Na ogół wykonuje się tylko jedną iterację w metodzie kolejnych przybliżeń,
otrzymując:
Predyktor:
(
)
y
y
h
F
F
n
n
n n
+
∗
=
+
+ +
1
0 0
α
α
...
Korektor :
(
)
[
]
y
y
h
F
F
f x
y
n
n
n n
n
n
n
+
∗∗
+
+
+
∗
=
+
+ +
+
1
0 0
1
1
1
β
β
β
...
,
Przykład:
n=3
[
]
y
y
h
F
F
F
F
4
3
0
1
2
3
24
9
37
59
55
∗
=
+
−
+
−
+
[
]
(
)
∗
∗
∗
∗
↓
+
+
−
+
−
+
=
4
4
4
3
2
1
0
3
4
,
251
646
264
106
19
720
y
x
f
F
F
F
F
F
h
y
y
Uwagi:
1
°
Dla stosowania metod ekstrapolacyjno-interpolacyjna trzeba znać wartość
y
w
pewnej liczbie punktów początkowych (można zastosować metodę Rungego-
Kutty).
2
°
Metody Rungego-Kutty wymagają obliczenia wartości funkcji
f x y x
( , ( ))
w
punktach pośrednich pomiędzy
x x
h
n
n
,
+
.
3
°
Jeśli obliczanie
f x y
( , )
trwa krótko
−
stosować metody Rungego-Kutty;
Jeśli obliczanie
f x y
( , )
trwa długo
−
stosować metody ekstrapolacyjno-
interpolacyjne.

Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
51
7.4 Sprowadzanie równania wyższego rzędu do układu równań
Rozpatrzmy równanie różniczkowe rzędu n, postaci:
(7.18)
(
)
y
f x y y y
y
n
n
( )
'
''
(
)
, ,
,
,...,
=
−
1
Oznaczmy:
(7.19)
Z
y Z
y
Z
y
n
n
1
2
1
=
=
=
−
;
; ... ;
'
(
)
Można wówczas napisać:
(7.20)
(
)
n
n
n
n
i
i
Z
Z
Z
x
f
Z
Z
Z
n
i
Z
Z
Z
Z
Z
Z
,...,
,
,
1
,...,
2
,
1
2
1
1
1
3
2
2
1
=
′
=
′
−
=
=
′
=
′
=
′
−
+
!
!
Równania (7.20) stanowią układ n równań różniczkowych zwyczajnych pierwszego
rzędu, który można zapisać w następującej ogólnej postaci:
(7.21)
)
,
( Z
G
Z
x
=
′
;
gdzie:
=
=
)
,...,
,
,
(
2
1
3
3
2
2
2
1
n
n
Z
Z
Z
x
f
Z
Z
Z
Z
Z
Z
Z
!
!
!
G
Z

Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
52
Przykład:
Równanie trzeciego rzędu
(
)
y
y
y
x
f
y
′′
′
=
′′′
,
,
,
(*)
zapisujemy jako następujący układ trzech równań pierwszego rzędu”
)
,
,
,
(
(**)
3
2
3
3
2
2
1
Z
Z
Z
x
f
Z
Z
Z
Z
Z
=
′
=
′
=
′
bo:
3
2
1
Z
y
Z
y
Z
y
=
′′
=
′
=
7.5 Rozwiązywanie układów równań różniczkowych zwyczajnych
Układ równań różniczkowych zwyczajnych pierwszego rzędu postaci:
(7.22)
(
)
(
)
(
)
=
=
=
n
n
n
n
n
x
x
x
t
f
dt
dx
x
x
x
t
f
dt
dx
x
x
x
t
f
dt
dx
,...,
,
,
,...,
,
,
,...,
,
,
2
1
2
1
2
2
2
1
1
1
!
można zapisać w postaci macierzowej następująco:
(7.23)
)
,
(
)
,
(
X
F
X
X
F
X
t
t
dt
d
=
≡
=
$
gdzie:
(
)
(
)
(
)
=
=
n
n
n
n
n
x
x
x
t
f
x
x
x
t
f
x
x
x
t
f
x
x
x
,...,
,
,
,...,
,
,
,...,
,
,
;
2
1
2
1
2
2
1
1
2
1
!
!
F
X
Przed przystąpieniem do rozwiązywania równań (7.23) należy określić warunki
początkowe:
(7.24)
0
0
)
(
X
X
=
t

Prof. dr hab. n.t. Stanisław Wojciech ”Elementy metod numerycznych”
Opracowano w ramach projektu TEMPUS S_JEP-09344/95
Politechnika Łódzka filia w Bielsku-Białej
Katedra Mechaniki i Inżynierskich Metod Komputerowych
53
gdzie:
=
)
(
)
(
)
(
0
1
0
1
0
1
0
t
x
t
x
t
x
X
jest wektorem znanych wartości początkowych.
Zagadnienie początkowe dla układu równań różniczkowych zwyczajnych postaci:
(7.25)
0
0
)
(
,
)
,
(
X
X
X
F
X
=
=
t
t
$
można rozwiązywać różnymi metodami. Szczególnie wygodna w programowaniu jest
metoda Rungego-Kutty, która w przypadku formuł IV rzędu prowadzi do wzorów:
(7.26)
(
)
(
)
3
0
0
4
2
0
0
3
1
0
0
2
0
0
1
,
2
1
,
2
2
1
,
2
,
K
X
F
K
K
X
F
K
K
X
F
K
X
F
K
+
+
=
+
+
=
+
+
=
=
h
t
h
h
t
h
h
t
h
t
h
(7.27)
(
)
(
)
4
3
2
1
0
0
1
2
2
6
1
K
K
K
K
X
X
X
+
+
+
+
=
+
=
h
t
Uwaga:
4
3
2
1
1
0
,
,
,
,
,
K
K
K
K
X
X
- są wektorami !
W pracy [2] podano opis procedury RK4SYS.PAS, która całkuje równania (7.25)
metodą Rungego-Kutty rzędu czwartego. Procedura ta dobiera krok całkowania
zapewniający realizację obliczeń z odpowiednią dokładnością
Document Outline
- 1. Wprowadzenie
- 2. Rozwiązywanie równań algebraicznych liniowych
- 3. Interpolacja i aproksymacja funkcji
- 4. Równania nieliniowe
- 5. Numeryczne obliczanie całek
- 6. Numeryczne obliczanie pochodnych
- 7. Równania różniczkowe zwyczajne
- 7.1 Przybliżenie pierwszego i drugiego rzędu
- 7.2 Wzory Rungego-Kutty
- 7.3 Metody wielokrokowe
- 7.3.1 Metody ekstrapolacyjne
- 7.3.2 Metody interpolacyjne
- 7.3.3 Metoda obliczeniowa
- 7.4 Sprowadzanie równania wyższego rzędu do układu równań
- 8. Równania różniczkowe cząstkowe
- 9. Zastosowanie metody różnic skończonych – ugięcia i drgania belek
- 10. Metoda Elementów Skończonych (MES) - ugięcia belek
- Wykłady OnLine
- KM i IMK
Wyszukiwarka
Podobne podstrony:
lekcja 18 id 265103 Nieznany
Grishkova kompetenciya 18 id 19 Nieznany
A, TEST 18 id 49152 Nieznany (2)
5 18 id 39510 Nieznany (2)
zp 121 4 18 id 592509 Nieznany
IMG 18 id 210957 Nieznany
4 18 id 36979 Nieznany (2)
PROJEKT 18 id 397733 Nieznany
Matematyka 18 id 283106 Nieznany
IMG 18 id 211143 Nieznany
Lab 18 id 257446 Nieznany
IMG 18 id 211201 Nieznany
Zestaw 18 id 588002 Nieznany
lekcja 18 id 265103 Nieznany
Grishkova kompetenciya 18 id 19 Nieznany
18 04 2013 WBC(LEUKOCYTY)id 176 Nieznany (2)
Egzamin Zobowiazania (11 18) id Nieznany
c4 18 12 2010 id 97240 Nieznany
EATON 18 wylacznik ppoz id 1496 Nieznany
więcej podobnych podstron