- 1 -

6.5. WZMACNIACZ OPERACYJNY

Jest  to  wzmacniacz  prądu  stałego  o  bardzo  dużym  wzmocnieniu  i  z 

reguły przeznaczony do pracy z zewnętrznym obwodem silnego ujemnego 
sprzężenia zwrotnego.

Za  pomocą  wzmacniacza  operacyjnego  można  realizować  funkcyjne 

operacje  liniowe  i  nieliniowe  na  sygnałach  elektrycznych.  Właściwości 
funkcjonalne  wzmacniacza  operacyjnego  są  kształtowane  przez 
odpowiedni dobór zewnętrznego obwodu ujemnego sprzężenia zwrotnego.

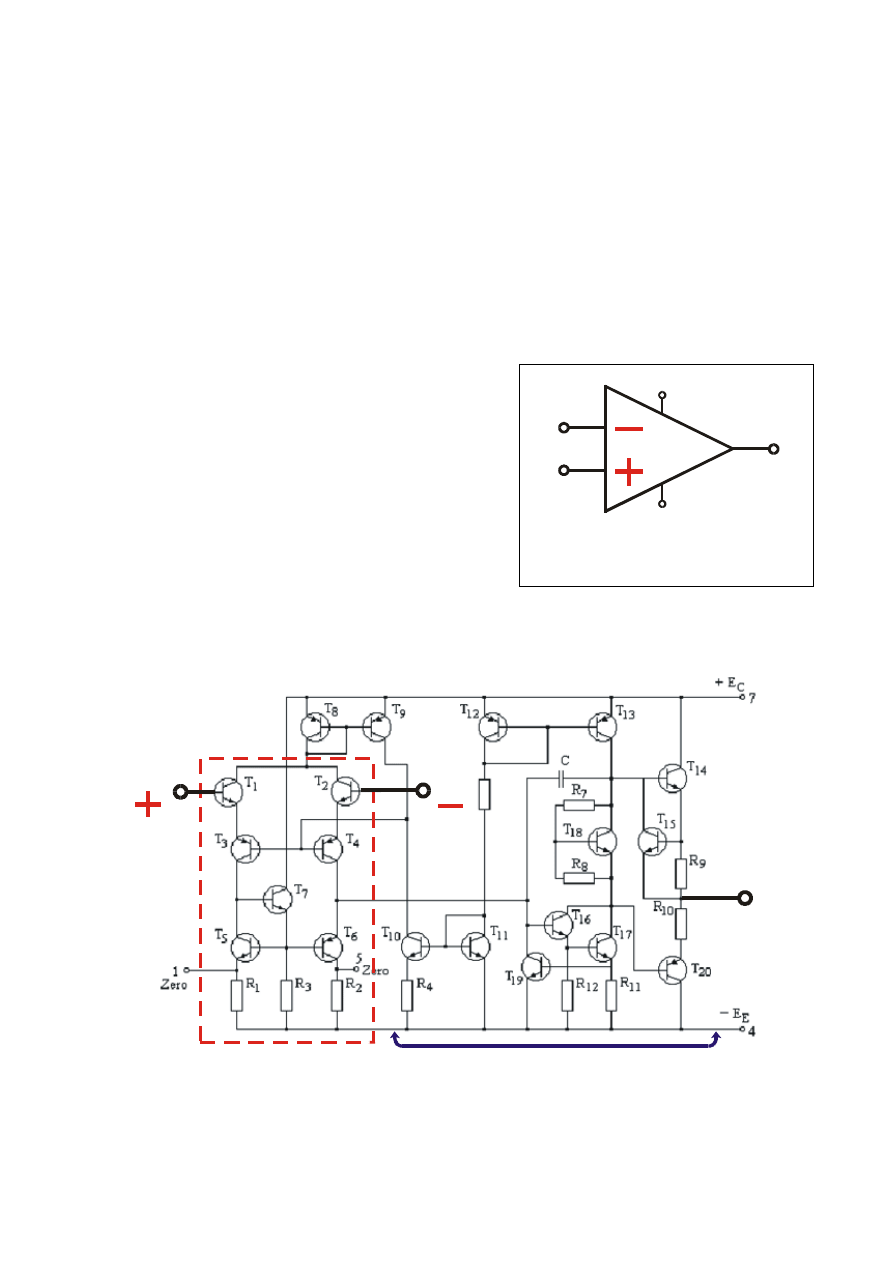
Wzmacniacz  operacyjny  posiada  dwa 

wejścia 

umożliwiające 

symetryczne 

(różnicowe) 

podawanie 

sygnału 

wejściowego  i  niesymetryczne  wyjście. 
Wejście 

We1

  ,  oznaczone  minusem,  jest 

wejściem  odwracającym 

fazę,  a  wejście 

We2

  ,  oznaczone  plusem  –

wejściem 

nieodwracającym

.

WY

We1

We2

+E

C

-E

E

Symbol wzm. operacyjnego

Wzmacniacz  operacyjny  jest  układem  scalonym  w  którym  stopniem 

wejściowym jest wzmacniacz różnicowy.

Wzmacniacz

różnicowy

Układy separujące, wzmacniające,

polaryzujące, dopasowujące

We2

We1

WY

Schemat funkcjonalny wzmacniacza operacyjnego 

A 741

- 2 -

6.5.1. PODSTAWOWE PARAMETRY

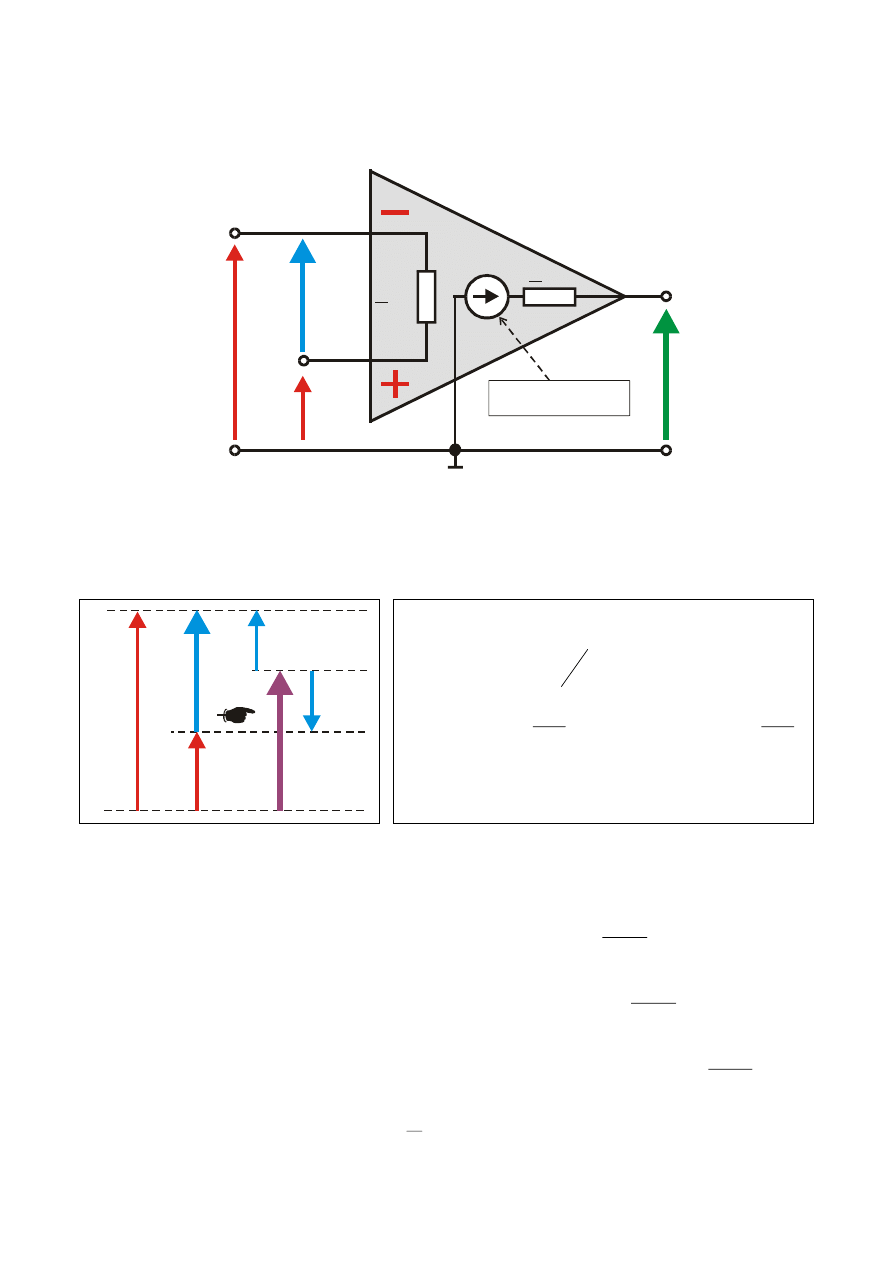
Schemat zastępczy wzmacniacza operacyjnego

WY

We1

We2

Z

 WY

Z

 WE

U

we1

U

we2

U

R

U

wy

K U

UR

R

+

K U

US

S

Zależności  pomiędzy  napięciami  wejściowymi  oraz  tzw.  napięciem 

różnicowym 

U

R

 i wspólnym (sumacyjnym)  

U

S

 obu wejść, można

zobrazować graficznie

i opisać następującymi wzorami:

U

we1

U

we2

U

R

/  U

R

1 2

/  U

R

1 2

U

S

U

R

2

1

We

We

U

U





U

S





2

1

2

1

We

We

U

U





2

1

R

S

We

U

U

U





  oraz  

2

2

R

S

We

U

U

U





U

WY

S

US

R

UR

U

K

U

K





Do  najważniejszych  parametrów  wzmacniacza  operacyjnego

należy:

 Napięciowe 

wzmocnienie różnicowe

R

WY

UR

U

U

K



 Napięciowe 

wzmocnienie sumacyjne

S

WY

US

U

U

K





Współczynnik tłumienia sygnału wspólnego

US

UR

K

K

CMRR





Impedancja wejściowa

WE

Z

- 3 -



Impedancja wyjściowa

WY

Z



Pasma przenoszenia (zakres częstotliwości pracy)

P

S



Maksymalne napięcie wyjściowe

max

WY

U

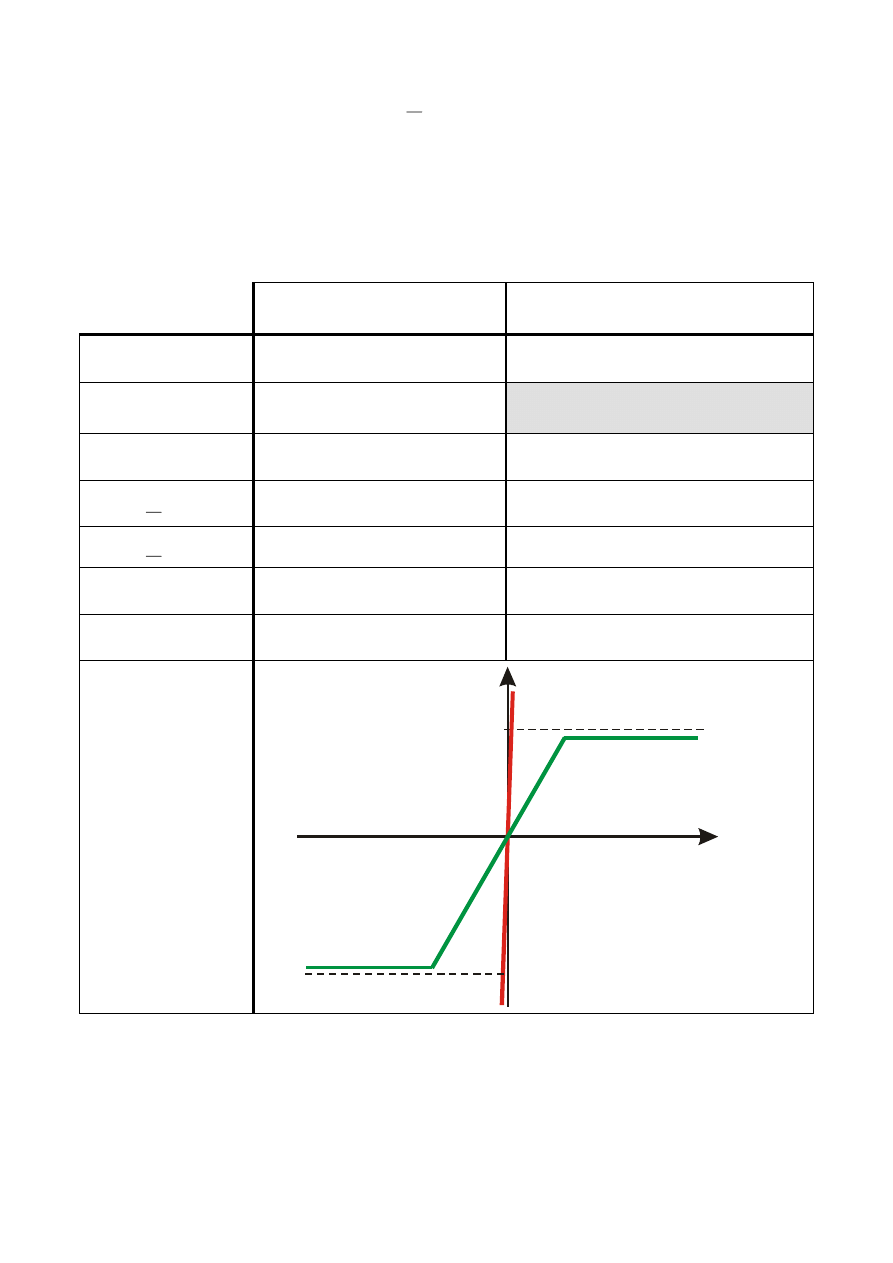
Porównanie parametrów idealnego i rzeczywistego wzmacniacza

IDEALNY

RZECZYWISTY

UR

K



6

4

10

10



  





dB

120

80



US

K

0

bardzo małe -
nie podaje się

CMRR



6

3

10

10



  





dB

120

60



WE

Z







G

k

10

50



WY

Z

0



200

50



P

S

0 

 +



MHz

200

0



max

WY

U

0 

 



 ograniczone napięciami zasilania

Charakterystyka 

przejściowa

U

R

U

WY

+E

C

-E

E

nasycenie

nasycenie

- 4 -

6.5.2. ZASTOSOWANIA WZMACNIACZY OPERACYJNYCH

Prowadząc analizę układów wzmacniacza operacyjnego z dołączonym 

obwodem zewnętrznego sprzężenia zwrotnego, idealizuje się wzmacniacz 
operacyjny zakładając, że:

I.

różnica napięć między jego wejściami jest równa zeru,

II.

jego  wejścia  nie  pobierają  żadnego  prądu  z  obwodów 
zewnętrznych.



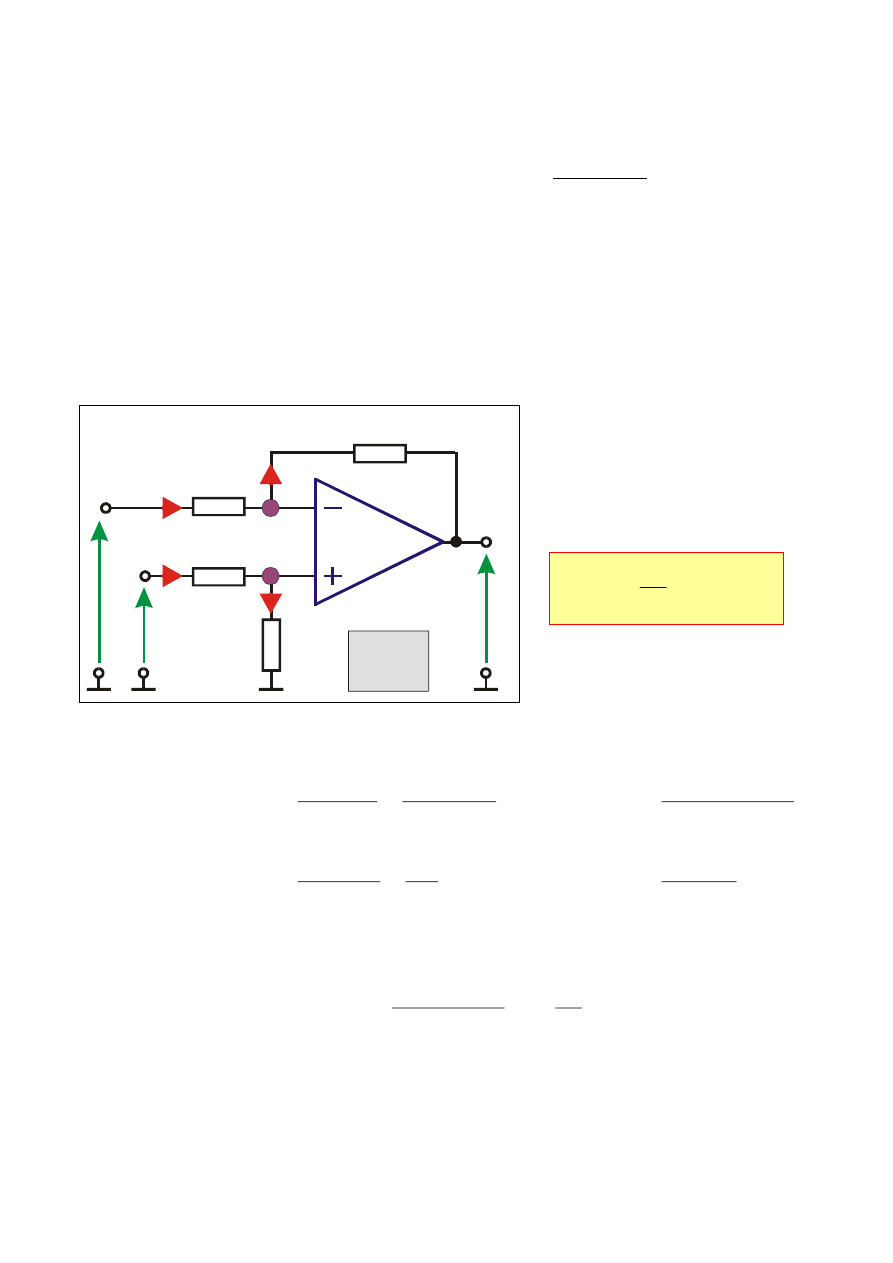
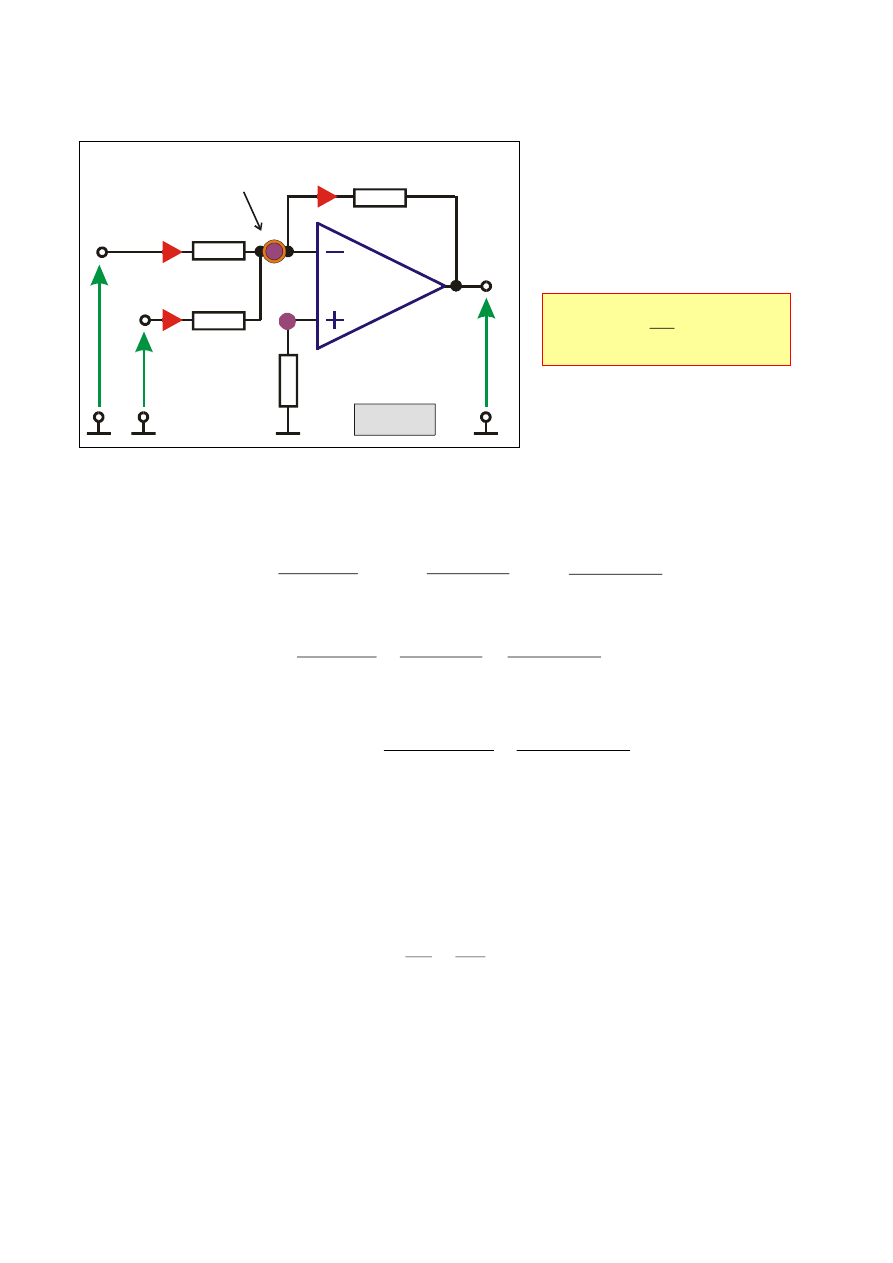
Wzmacniacz ODEJMUJĄCY (różnicowy)

Napięcie wyjściowe

jest wprost proporcjonalne 

do różnicy

napięć wejściowych

U

1

U

A

I

4

I

3

U

B

R

1

R

3

R

2

I

1

I

2

U

2

R

4

U

wy

R =

2

R

1

R =

4

R

3





1

2

1

3

U

U

R

R

U

wy





(6.31)

Z założenia  

II.

  wynika, że :

3

1

I

I



czyli

3

1

1

R

U

U

R

U

U

wy

A

A







stąd

3

1

3

1

1

R

R

R

U

R

U

U

wy

A







4

2

I

I



czyli

4

2

2

R

U

R

U

U

B

B





stąd

4

2

4

2

R

R

R

U

U

B





Natomiast na podstawie założenia  

I.

 można napisać: 

B

A

U

U



zatem









1

3

1

4

2

1

3

1

4

2

R

R

U

R

R

R

R

R

R

U

U

wy









Stosując 

3

4

1

2

,

R

R

R

R





  zależność  opisująca  napięcie  wyjściowe 

przyjmuje postać (6.31).

- 5 -



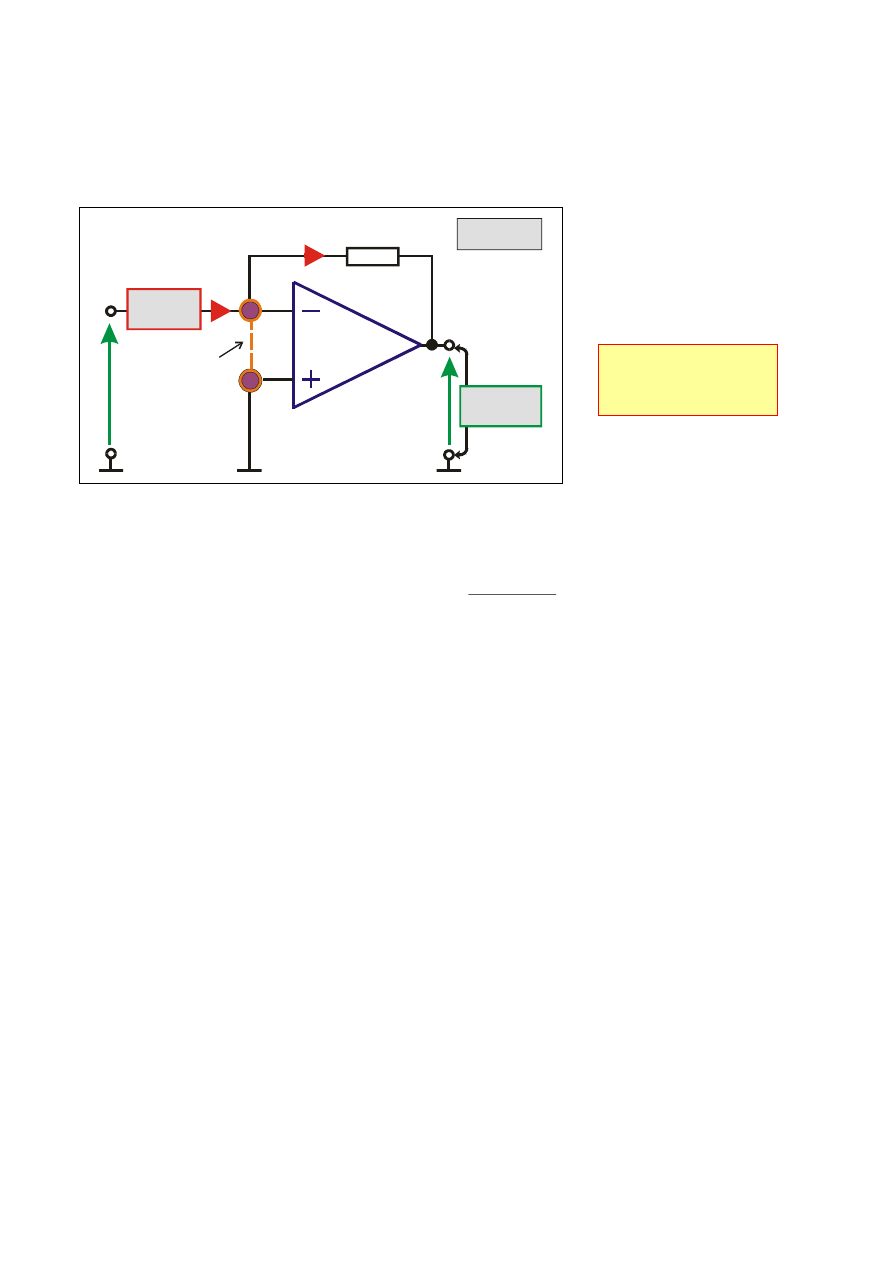
Wzmacniacz SUMUJĄCY

Napięcie wyjściowe

jest wprost proporcjonalne 

do sumy

napięć wejściowych

U

1

I

R

1

R

R

2

I

1

I

2

U

2

R

B

U

wy

R =

2

R

1

U

A

U

B

punkt

masy pozornej

A





2

1

1

U

U

R

R

U

wy







(6.32)

Z założenia  

II.

  wynika, że :    

I

I

I





2

1

gdzie:

1

1

1

R

U

U

I

A





 , 

2

2

2

R

U

U

I

A





 , 

R

U

U

I

wy

A





czyli

R

U

U

R

U

U

R

U

U

wy

A

A

A











2

2

1

1

stąd









2

2

1

1

R

U

U

R

R

U

U

R

U

U

A

A

A

wy











Natomiast na podstawie założenia  

I.

 oraz uwzględniając fakt, że przez 

rezystor R

B

 nie płynie prąd - można napisać:  

0





B

A

U

U

 (dlatego punkt 

A jest nazywany punktem masy pozornej), 

zatem



















2

2

1

1

R

U

R

U

R

U

wy

Stosując 

1

2

R

R

  , zależność opisująca napięcie wyjściowe przyjmuje 

postać (6.32).

- 6 -



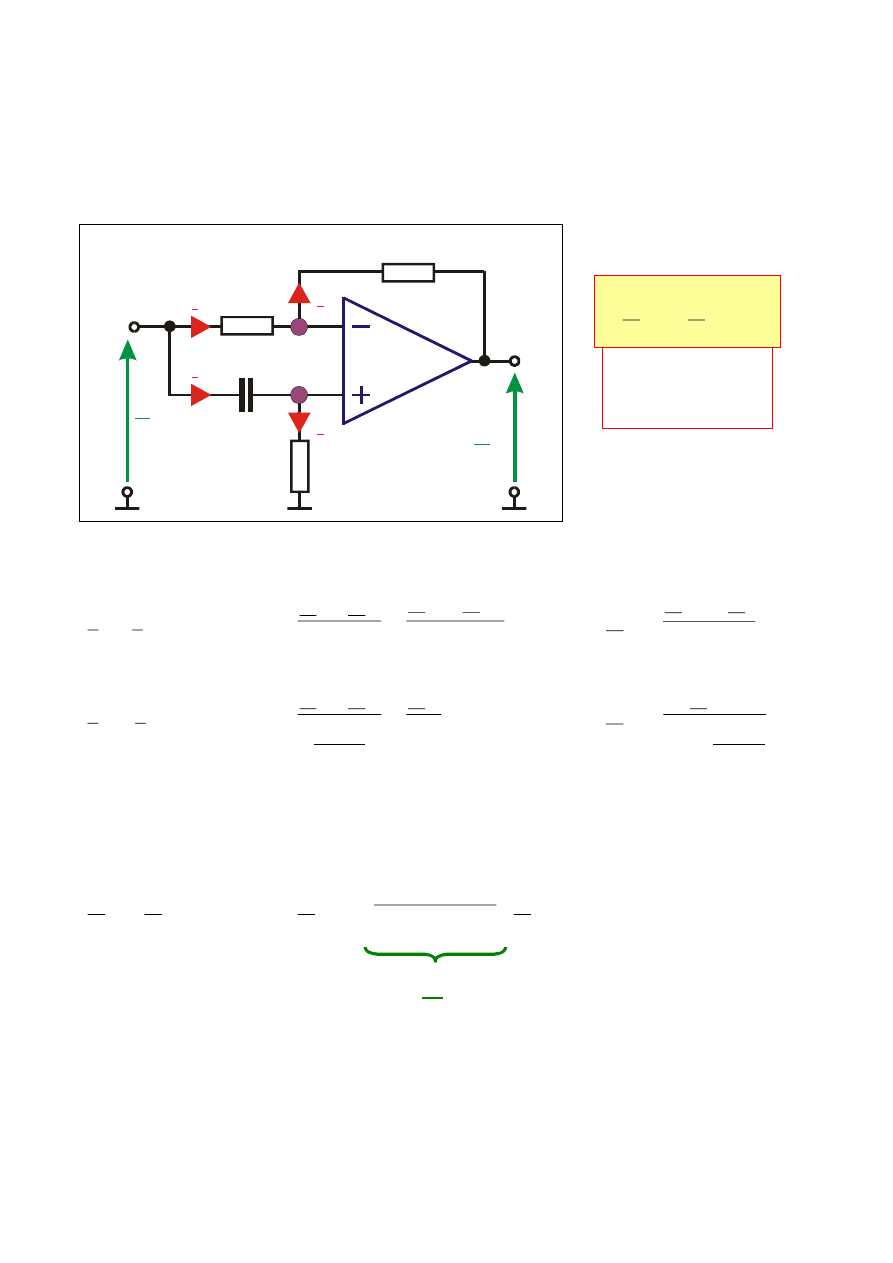
KONWERTER PRĄDOWO-NAPIĘCIOWY

Układ, który przetwarza sygnał prądowy na sygnał napięciowy.

Napięcie wyjściowe

jest wprost 

proporcjonalne do 

prądu

wejściowego

R

F

I

1

U

wy

U

B

I

25

mA

-25

mV

R =1

F



U

A

A

B

pozorne

zwarcie

U

1

1

I

R

U

F

wy





(6.33)

Z założenia  

II.

  wynika, że :    

1

I

I



czyli

F

wy

R

U

U

I





1

1

stąd

wy

F

U

U

R

I





1

1

Ponieważ 

1

U

U

A



, zatem

wy

A

F

U

U

R

I





1

Na  podstawie  założenia   

I.

  oraz  uwzględniając  fakt,  że  punkt  B  ma 

potencjał masy - można napisać:

0





B

A

U

U

dlatego mówi się, że pomiędzy punktami A i B występuje pozorne zwarcie
(zwarcie bezprądowe).

Zatem

wy

F

U

R

I





1

Stąd zależność opisująca napięcie wyjściowe ma postać (6.33).

- 7 -



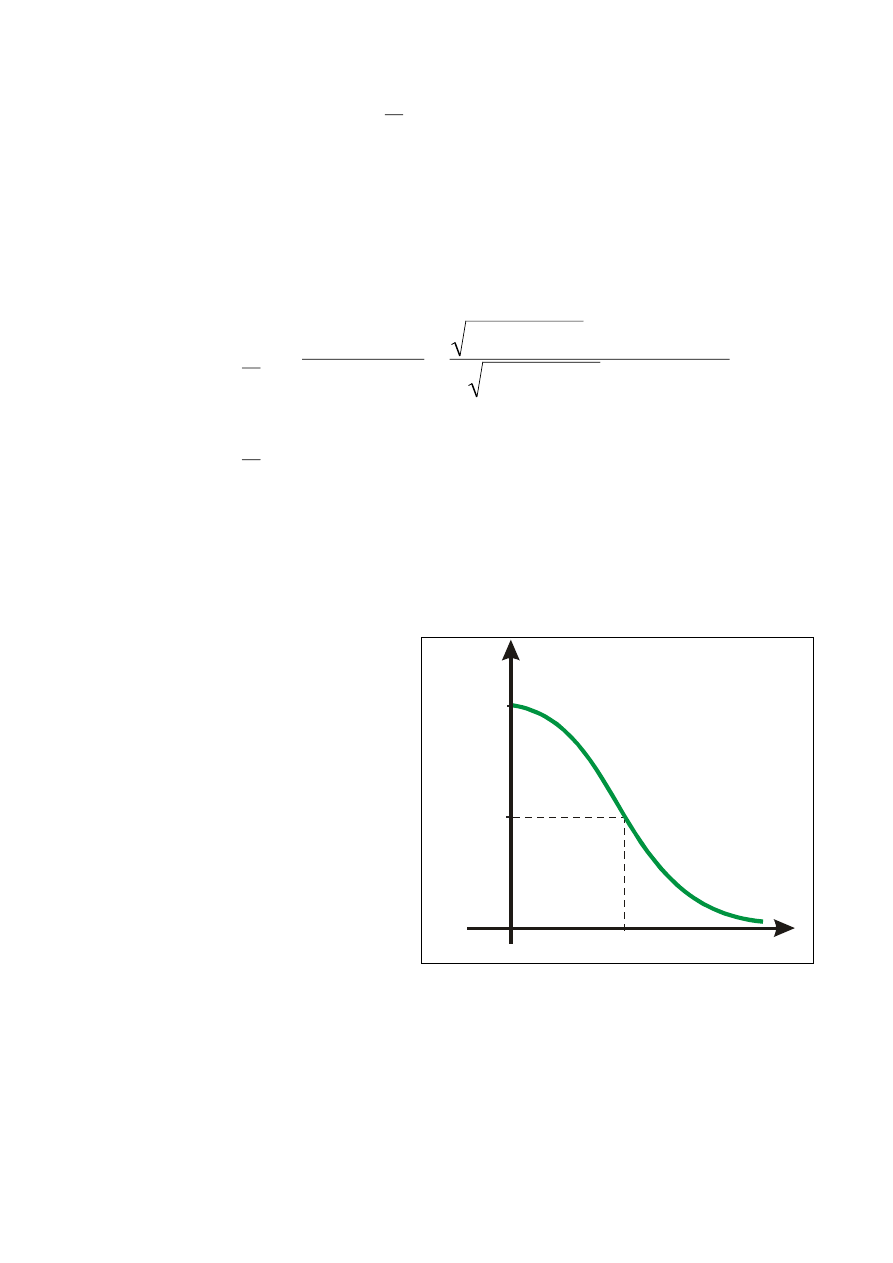
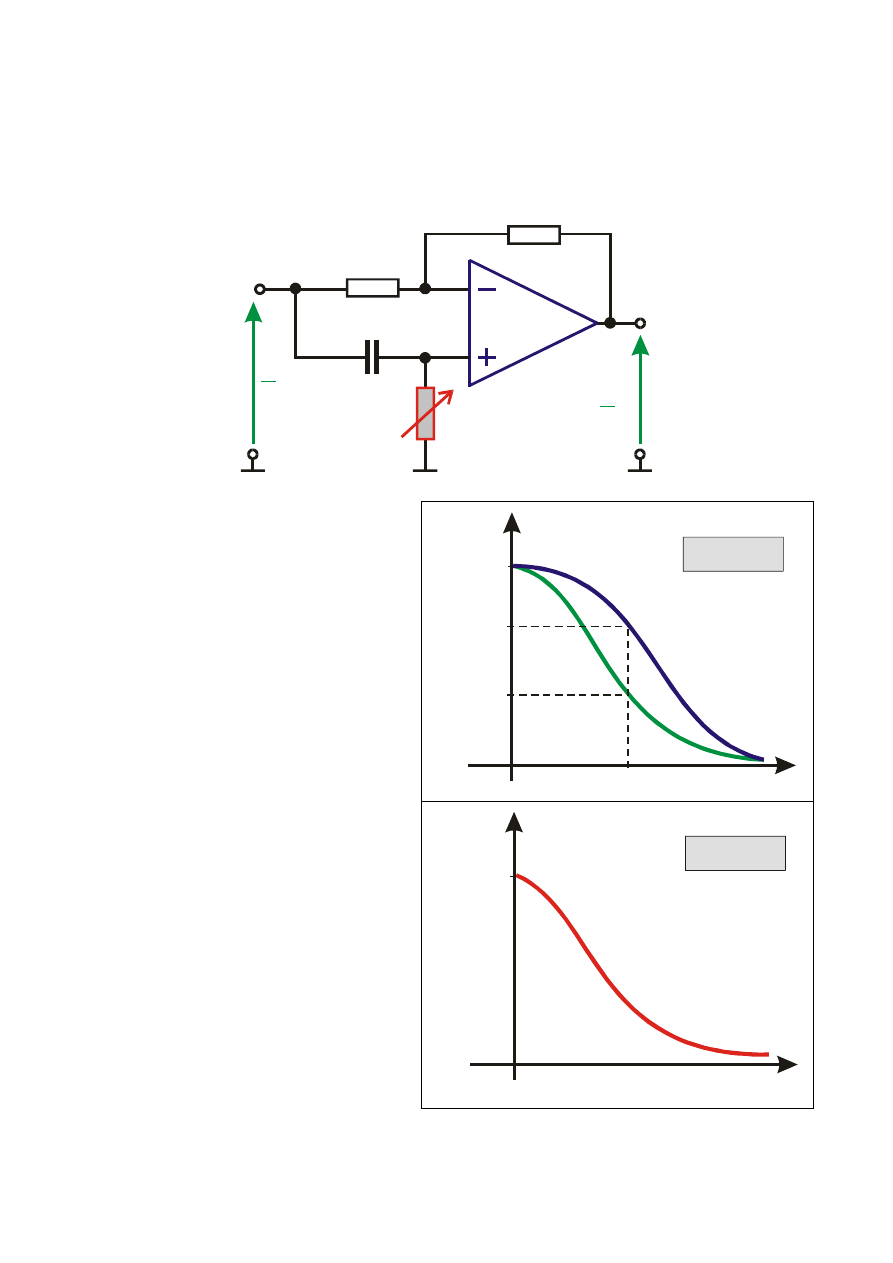
PRZESUWNIK FAZY

Układ, który przesuwa tylko fazę napięcia wyjściowego względem 
napięcia wejściowego.

U

1

U

A

I

4

I

3

U

B

R

1

R

1

C

I

1

I

2

R

2

U

wy



j

wy

e

U

U

1















1

1

wy

wy

U

U

(6.34)

Z założenia  

II.

  wynika, że :

3

1

I

I



czyli

1

1

1

R

U

U

R

U

U

wy

A

A







stąd

2

1

U

U

U

wy

A





4

2

I

I



czyli

2

1

1

R

U

C

j

U

U

B

B







stąd

C

j

R

R

U

U

B



1

2

2

1





Natomiast na podstawie założenia  

I.

 można napisać: 

B

A

U

U



zatem

1

2

2

1

1

U

CR

j

CR

j

U

wy

























K

U

Transmitancja napięciowa przesuwnika

- 8 -

Wiedząc, że



j

U

U

e

K

K



gdzie:

U

K

- moduł transmitancji (wzmocnienie napięciowe)



-

argument  transmitancji  (różnica  faz  początkowych 
napięcia wyjściowego i wejściowego)

Transmitancję napięciową przesuwnika, można przedstawić następująco



U

K













2

2

2

2

2

2

2

2

1

1

1

1

CR

arctg

j

CR

arctg

j

e

CR

e

CR

CR

j

CR

j































U

K

1





2

2

CR

arctg

j

e







Wzmocnienie  napięciowe  przesuwnika  jest  równe  jedności, 

niezależnie od częstotliwości. Natomiast przesunięcie fazowe jest funkcją 
częstotliwości. Czyli

 

1





U

K

 ,   

 

2

2

CR

arctg













Przesunięcie fazowe zmienia 

się  od  180

o

  przy  częstotliwości 

równej  0,  do  0

o

  przy  wielkich 

częstotliwościach,  co  ilustruje 
przebieg charakterystyki fazowo-
czestotliwościowej.

 

( )

/2





1/R C

2

- 9 -

W  rozpatrywanym  układzie  istnieje  możliwość  ustalenia  żądanej 

wartości  kąta  przesunięcia  fazowego  przy  danej  częstotliwości  sygnału. 
Jest to możliwe poprzez zmianę wartości rezystancji R

2

.

U

1

R

1

R

1

C

U

wy

R

2

Po  zwiększeniu  wartości 

rezystancji 

R

2

 

przebieg 

charakterystyki 

fazowo-

częstotliwościowej 

ulega 

zmianie. Okazuje się, że dla tych 
samych 

pulsacji 

sygnału 

występują  mniejsze  przesunięcia 
fazowe.

 

( )





’

”

R

2’

<

R

2’’

0

Z  zależności  przesunięcia 

fazowego  od  rezystancji  R

2

  (dla 

danej pulsacji) wynika, że zwarcie 
wejścia  nieodwracającego  do 
masy 

powoduje 

przesunięcie 

sygnału  wyjściowego  względem 
wejściowego  o  180

o

.  Natomiast 

jego rozwarcie uzyskanie obydwu 
sygnałów w fazie.

(R )

2





const.

R

2

0

- 10 -



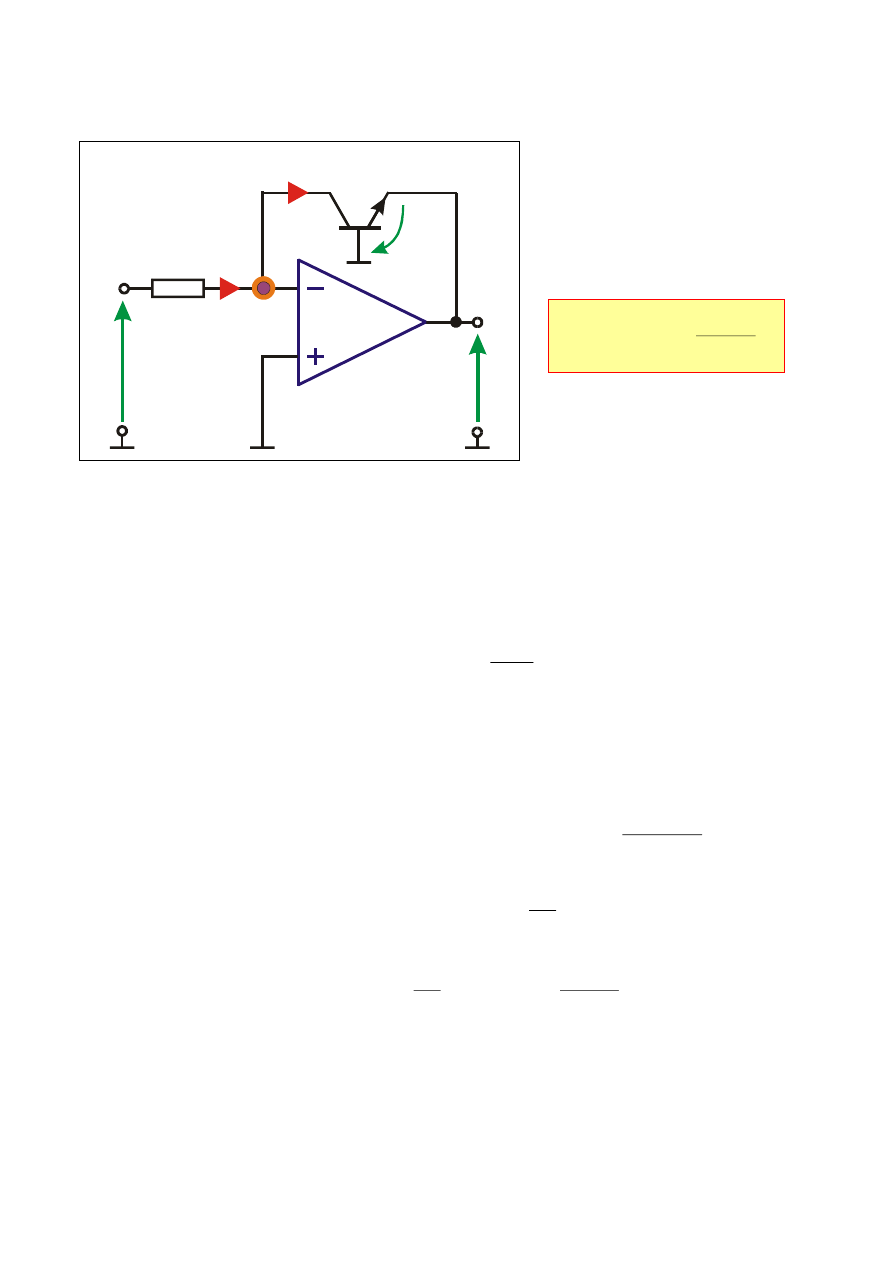
Wzmacniacz LOGARYTMUJĄCY

Napięcie wyjściowe

jest funkcją

logarytmiczną

napięcia wejściowego

I

1

U

wy

A

U

1

R

I

C

U

BE

U

A

















R

I

U

V

U

EB

T

wy

0

1

ln

(6.35)

Jest  to  układ,  w  którym  w  obwodzie  sprzężenia  zwrotnego 

wzmacniacza operacyjnego umieszczono tranzystor bipolarny.

Ponieważ potencjał bazy jest równy potencjałowi kolektora (punkt A 

jest  punktem  masy  pozornej),  to  charakterystykę  tranzystora  opisuje 
zależność















T

BE

EB

C

V

U

I

I

exp

0

gdzie:

0

EB

I

- prąd wsteczny złącza emiterowego, 

BE

U

- napięcie baza-emiter,

T

V

- potencjał elektrokinetyczny.

Z założenia  

II.

  wynika, że :    

1

I

I

C

    gdzie  

R

U

U

I

A





1

1

Zgodnie z założeniem 

I.

  

0



A

U

   czyli   

R

U

I

1

1



Ponieważ  

wy

BE

U

U





  , zatem   











 



T

wy

EB

V

U

I

R

U

exp

0

1

Stąd po przekształceniach napięcie wyjściowe opisuje zależność (6.35).

- 11 -



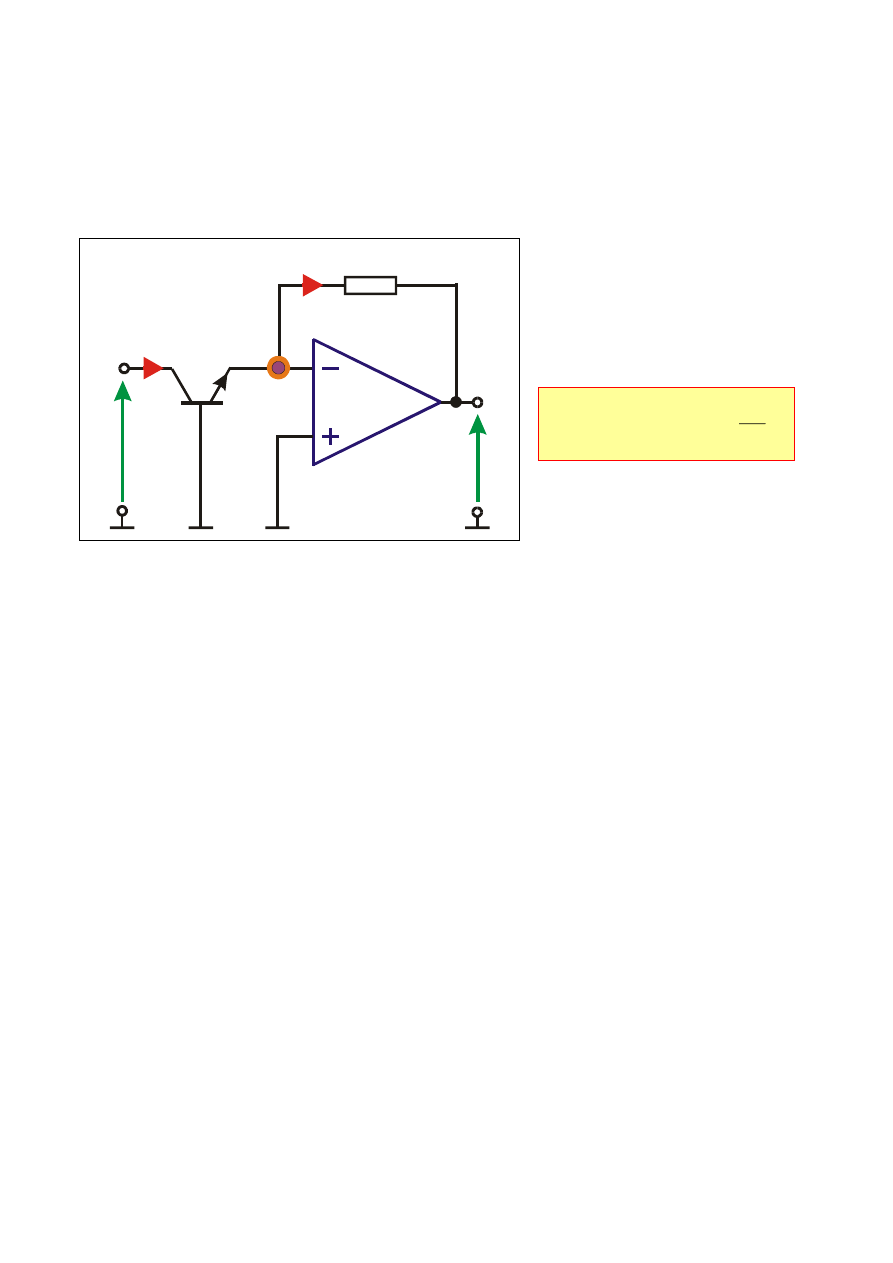
Wzmacniacz ANTYLOGARYTMUJĄCY (wykładniczy)

Zamieniając miejscami tranzystor i rezystor w układzie wzmacniacza 

logarytmującego otrzymuje się wzmacniacz antylogarytmujący.

Napięcie wyjściowe

jest funkcją

wykładniczą

napięcia wejściowego

I

1

U

wy

A

U

1

R

I

U

A

















T

EB

wy

V

U

I

R

U

1

0

exp

(6.36)

PRACA DOMOWA: Wyprowadzić zależność (6.36)

- 12 -

7. FILTRY AKTYWNE I MNOŻNIKI

7.1. FILTRY AKTYWNE

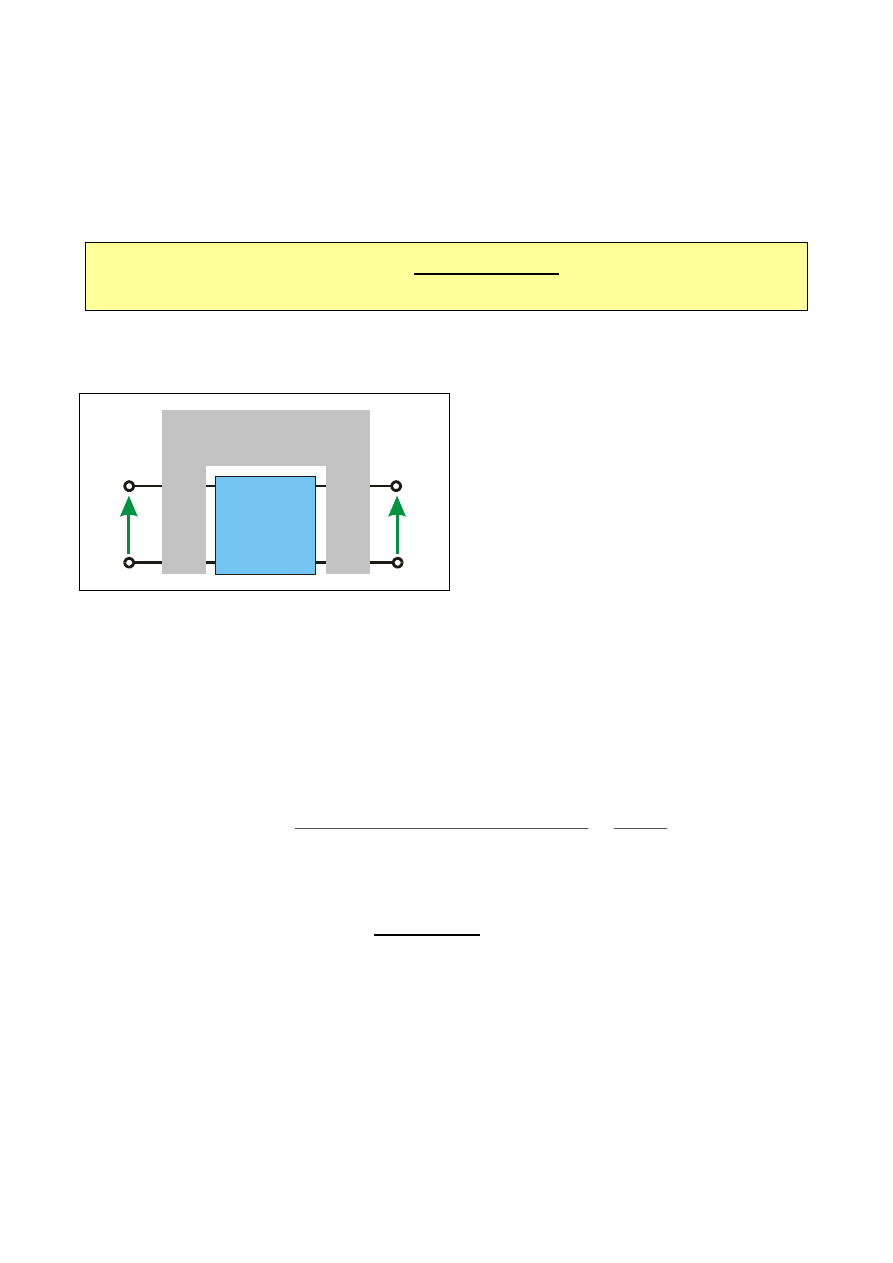
Filtry aktywne

to 

liniowe 

bezindukcyjne 

układy 

realizujące 

transmitancje analogicznie jak filtry RLC

Ogólna struktura filtru aktywnego zawiera: 

U

we

U

wy

Układ

aktywny

Sieć RC

(+ analogów L)

 układ  aktywny  (najczęściej 

wzmacniacz operacyjny);

 sieć  RC  (kombinacje  połączeń 

rezystorów  i  kondensatorów)  i 
czasami  dodatkowo  analogi  L 
(układy 

symulujące 

indukcyjność).

7.1.1. FUNKCJA PRZENOSZENIA FILTRU

W ogólnym przypadku transmitancję filtru można wyrazić jako iloraz 

dwóch wielomianów zmiennej 



j

s



)

(

)

(

)

(

0

1

1

1

0

1

1

1

s

M

s

L

b

s

b

s

b

s

b

a

s

a

s

a

s

a

s

K

m

m

m

m

n

n

n

n

































(6.37)

Równanie algebraiczne M(s)=0 posiada pierwiastki: s

1

, s

2

 ... s

m

 ,

nazywane biegunami transmitancji.

Inaczej – pulsacje, przy których mianownik funkcji przenoszenia staje się 
równy zeru to bieguny.

UWAGA: Liczba biegunów określa tzw. rząd filtru

- 13 -

7.1.2. KLASYFIKACJA FILTRÓW

Podział ze względu na pasmo częstotliwości:

 dolnoprzepustowe,

 górnoprzepustowe,

 środkowoprzepustowe,

 środkowozaporowe.

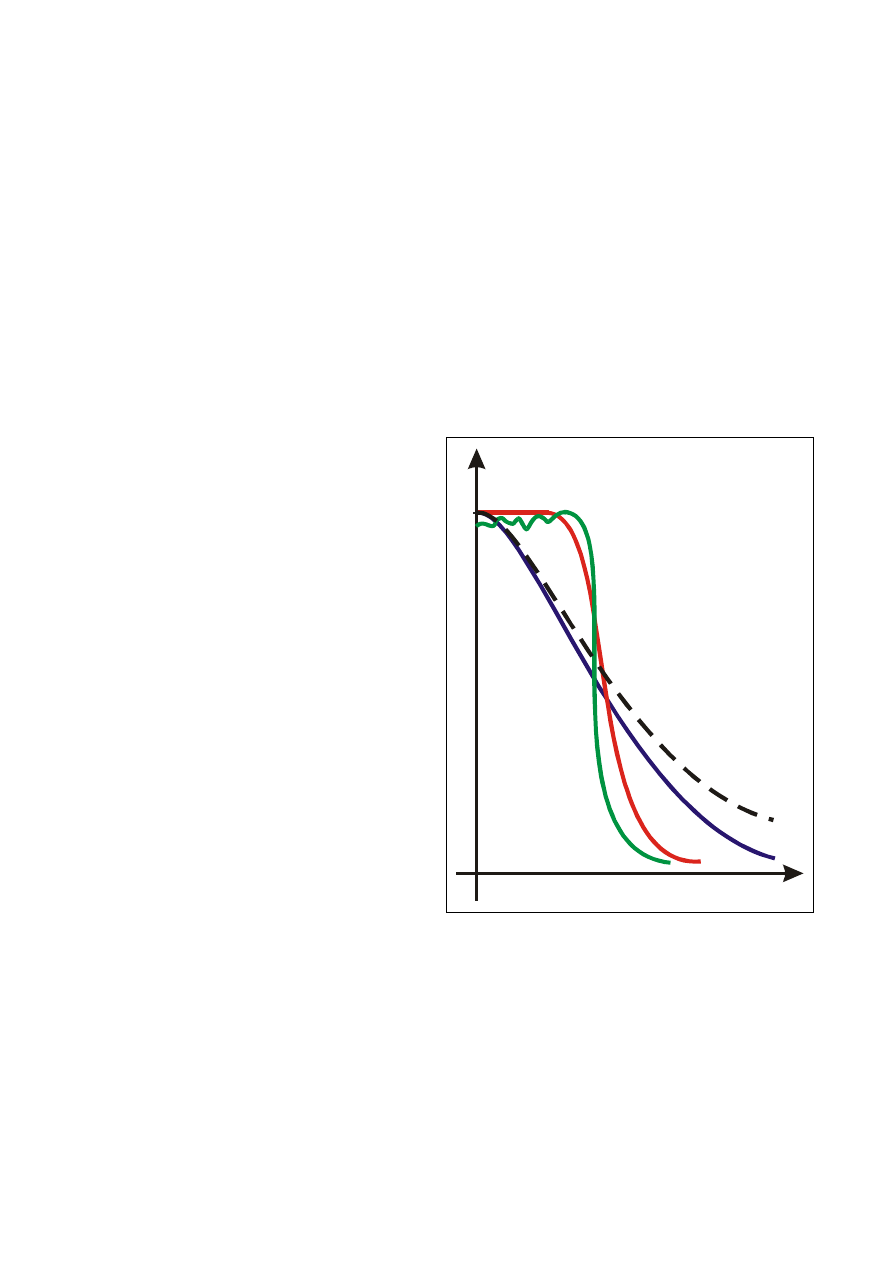
Podział ze względu na cechy charakterystyk częstotliwościowych

Filtry:

 o  maksymalnie  płaskiej  ch-

styce  amplitudowej  w  paśmie 
przenoszenia -

Butterwortha

 o 

maksymalnie 

stromości 

zboczy ch-styki amplitudowej -

Czebyszewa

 o  maksymalnie  płaskiej  ch-

styce  czasu  opóźnienia  w 
funkcji częstotliwości -

Bessela

 wszechprzepustowe  o  płaskiej 

ch-styce  amplitudowej,  lecz  o 
odpowiednio 

ukształtowanej 

ch-styce fazowej 

 o stałym przesunięciu fazowym 

i  odpowiednio  ukształtowanej 
ch-styce amplitudowej 

0

1

K

U

f

RC

Filtry:

 pierwszego rzędu (jednobiegunowe),

 drugiego rzędu (dwubiegunowe),

 ......

- 14 -

7.1.3. WYBRANE UKŁADY FILTRÓW AKTYWNYCH

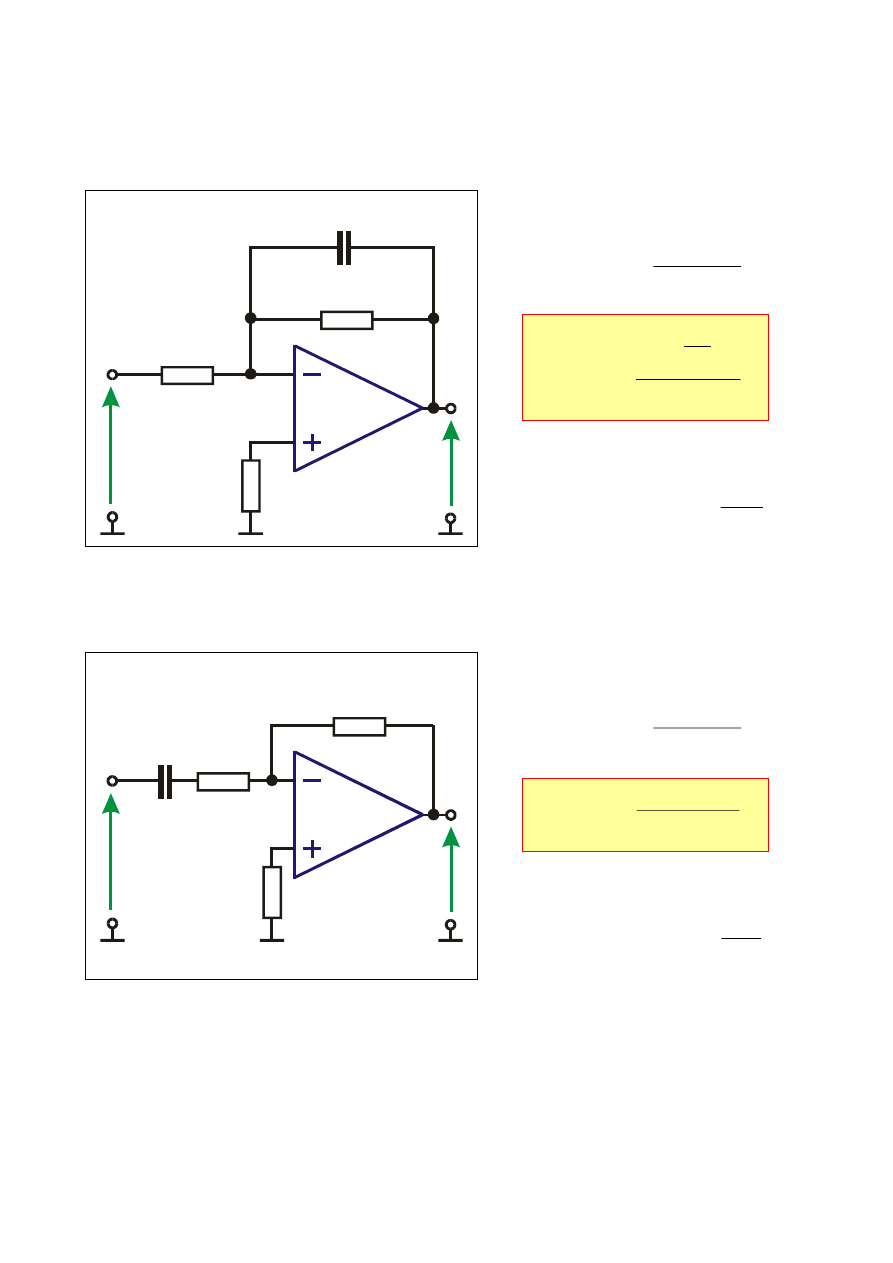
 Filtr dolnoprzepustowy pierwszego rzędu

Funkcja przenoszenia

)

(

)

(

)

(

1







j

U

j

U

j

K

wy

U



R

3

U

wy

U

1

R

2

R

1

C

C

R

j

R

R

j

K

U

3

1

3

1

)

(











(6.38)

biegunem jest 

C

R

g

3

1





 Filtr górnoprzepustowy pierwszego rzędu

Funkcja przenoszenia

)

(

)

(

)

(

1







j

U

j

U

j

K

wy

U



R

3

U

wy

U

1

R

2

R

1

C

C

R

j

C

R

j

j

K

U

1

3

1

)

(











(6.39)

biegunem jest 

C

R

d

1

1





- 15 -

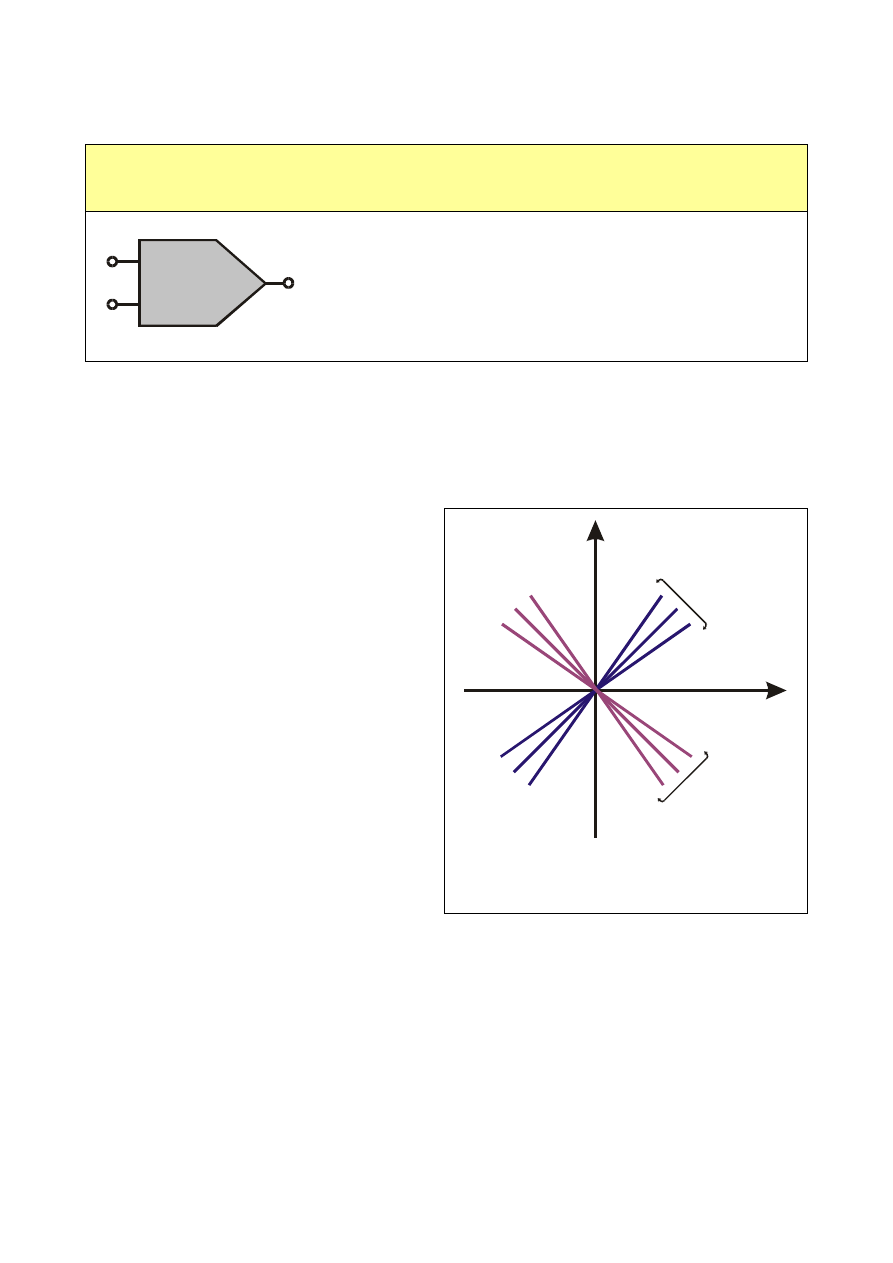
7.2. MNOŻNIKI

Mnożniki to  układy  dające  napięcie  wyjściowe  proporcjonalne  do 

iloczynu dwóch wielkości wejściowych

U

2

U

1

U =k U U

wy

m 1 2

2

1

,U

U

- napięcia wejściowe

wy

U

- napięcia wyjściowe

m

k

- współczynnik skalowania [1/V]

7.2.1. KLASYFIKACJA MNOŻNIKÓW

Podział ogólny mnożników:

 czteroćwiartkowe – wykonują 

mnożenie 

dla  dowolnych 

biegunowości 

napięć 

wejściowych; 

 dwućwiartkowe –  wykonują 

mnożenie gdy 

1

U lub

2

U  ma 

ustaloną biegunowości;

 jednoćwiartkowe –  wykonują 

mnożenie  gdy 

1

U i

2

U   ma 

ustaloną biegunowość.

U

1

U

wy

jest stałą

dodatnią

U

2

jest stałą

ujemną

U

2

Ch-tyka przejściowa układu

czteroćwiartkowego

Podział ze mnożników ze względu na realizację układową, np:

 z zastosowaniem operacji logarytmicznej i wykładniczej,

 z zastosowaniem kwadratorów.

- 16 -

7.2.2. WYBRANE UKŁADY MNOŻNIKÓW

 Układ z zastosowaniem operacji logarytmicznej i wykładniczej

/ realizacja jednoćwiartkowa /

Przy mnożeniu korzysta się zależności:





2

1

2

1

ln

ln

exp

U

U

U

U





(6.40)



U

1

ln x

ln U

1

U

2

ln x

ln U

2

exp x

ln U +

1

ln U

2

U

1

U

2

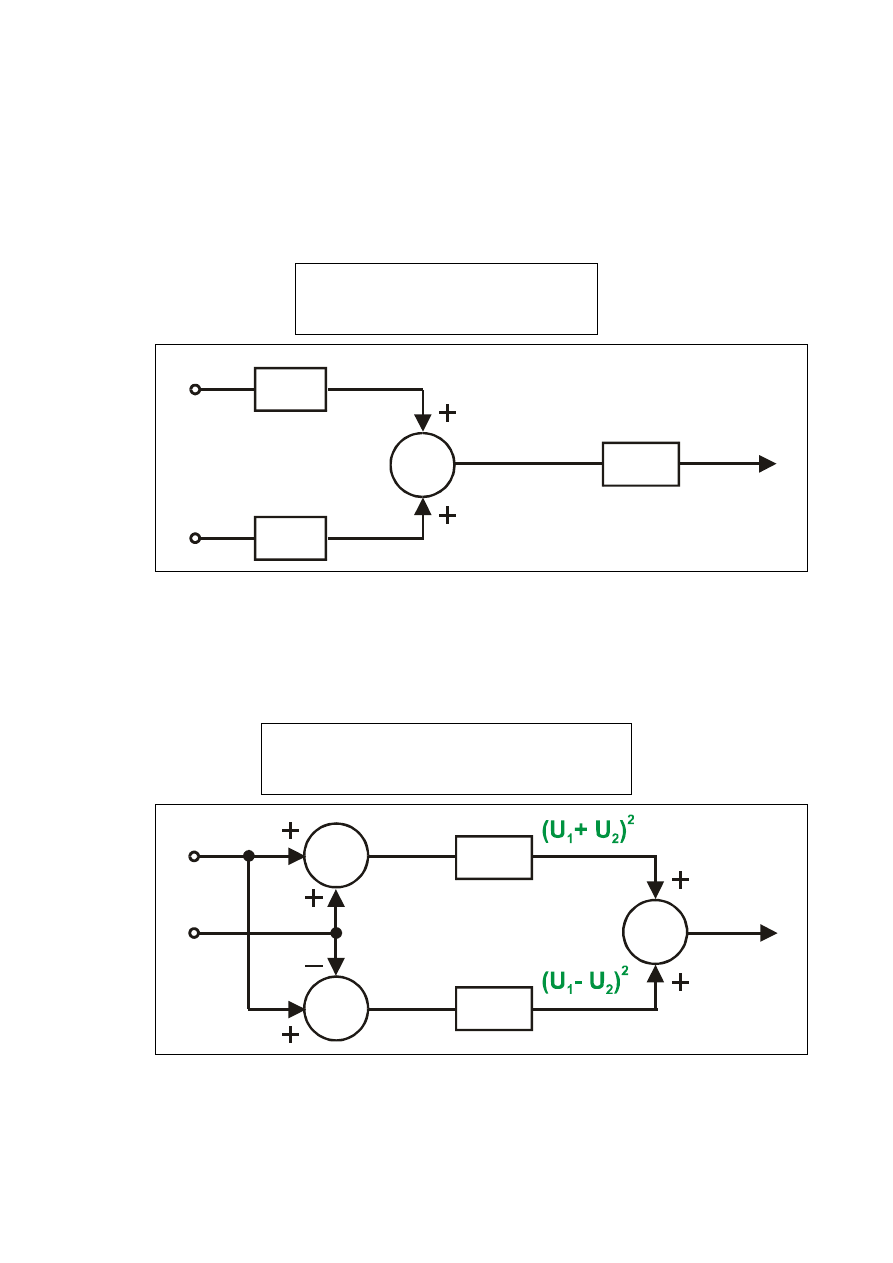
 Układ z kwadratorami   / realizacja dwućwiartkowa /

Przy mnożeniu korzysta się zależności:



 



2

2

1

2

2

1

2

1

4

U

U

U

U

U

U









(6.41)



4U

1

U

2

x

2

U - 

1

U

2

x

2

U + 

1

U

2





U

1

U

2

- 17 -

Operacja potęgowania





we

U

A

A

we

wy

e

U

U

ln





czyli operację potęgowania można zrealizować za pomocą trzech operacji













we

U

A

we

we

we

e

U

A

U

U

ln

ln

ln







1. logarytmowania

2. zmiany skali 
(wzmacniania np.x2)

3. oper. wykładniczej