Cząsteczki 2011

1

CZĄSTECZKI

•

klasyczne jądra

•

kwantowe elektrony

•

funkcja falowa

ψ

(r

1

, r

2

, r

3

, ... r

n

) - dla chmury elektronowej

•

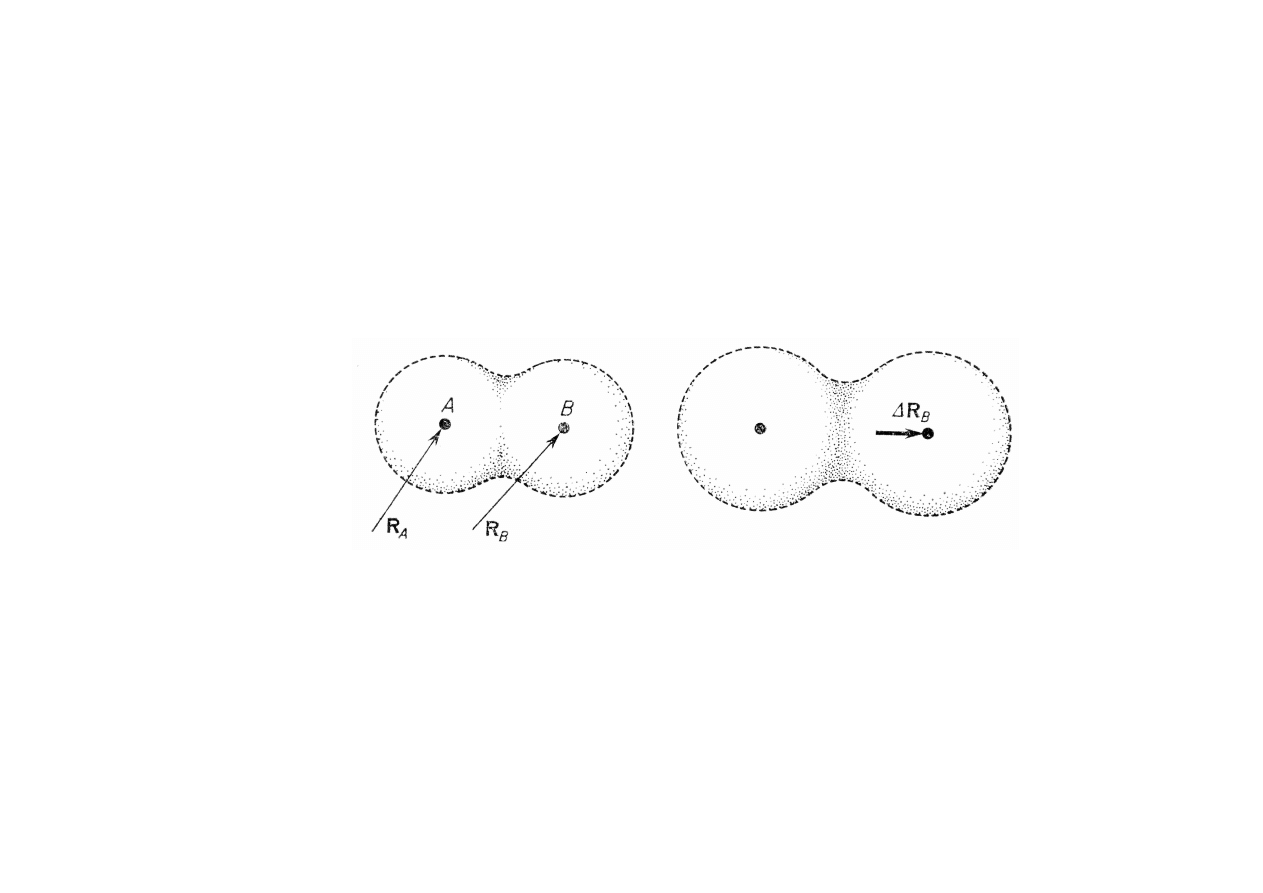
w stanie podstawowym wypadkowa siła (wywierana przez
pozostałe jądra i wszystkie elektrony) działająca na każde jądro
jest równa 0

•

zmiany kształtu chmury elektronowej nadążają za zmianami
położeń jąder

Cząsteczki 2011

2

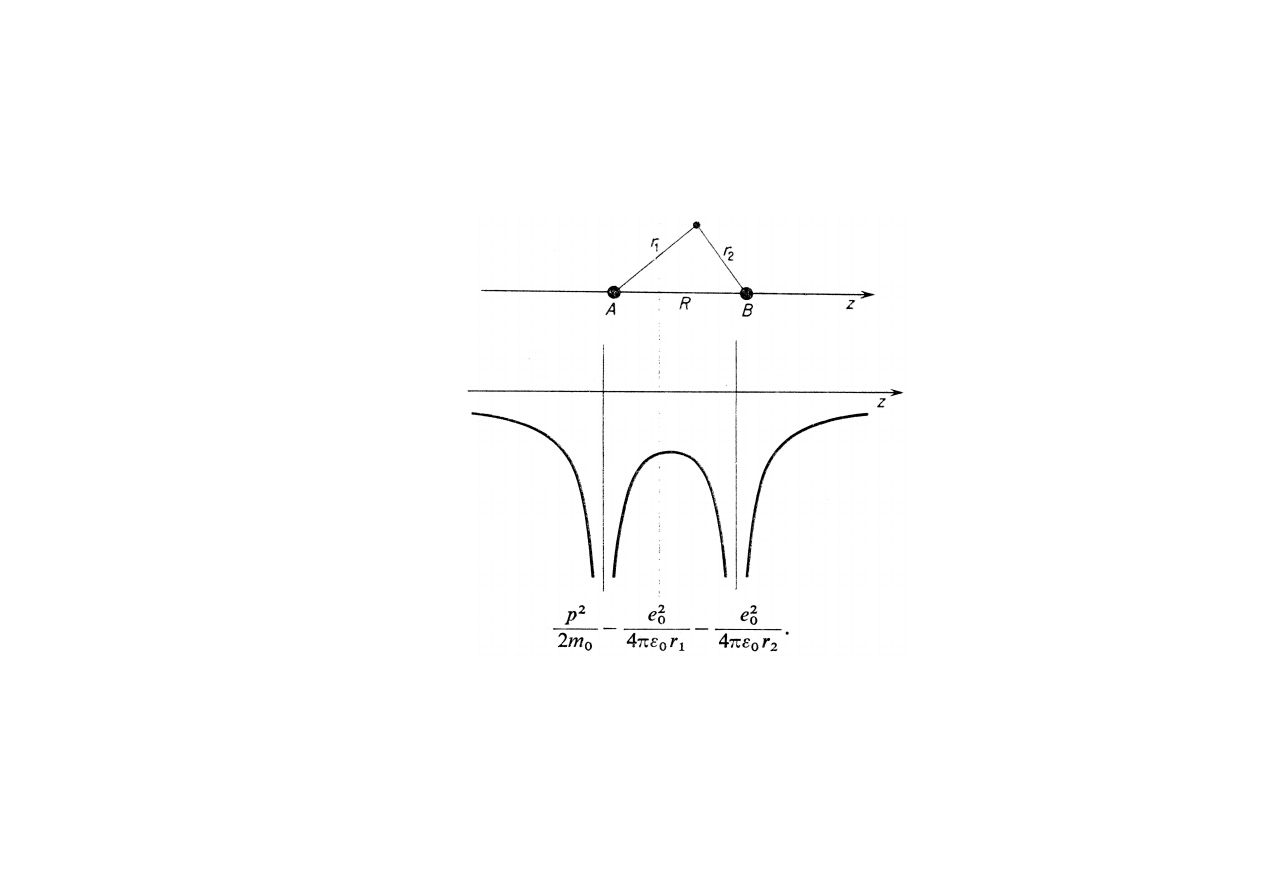
NAJPROSTSZA CZĄSTECZKA

Zjonizowana cząsteczka wodoru H

2

+

Cząsteczki 2011

3

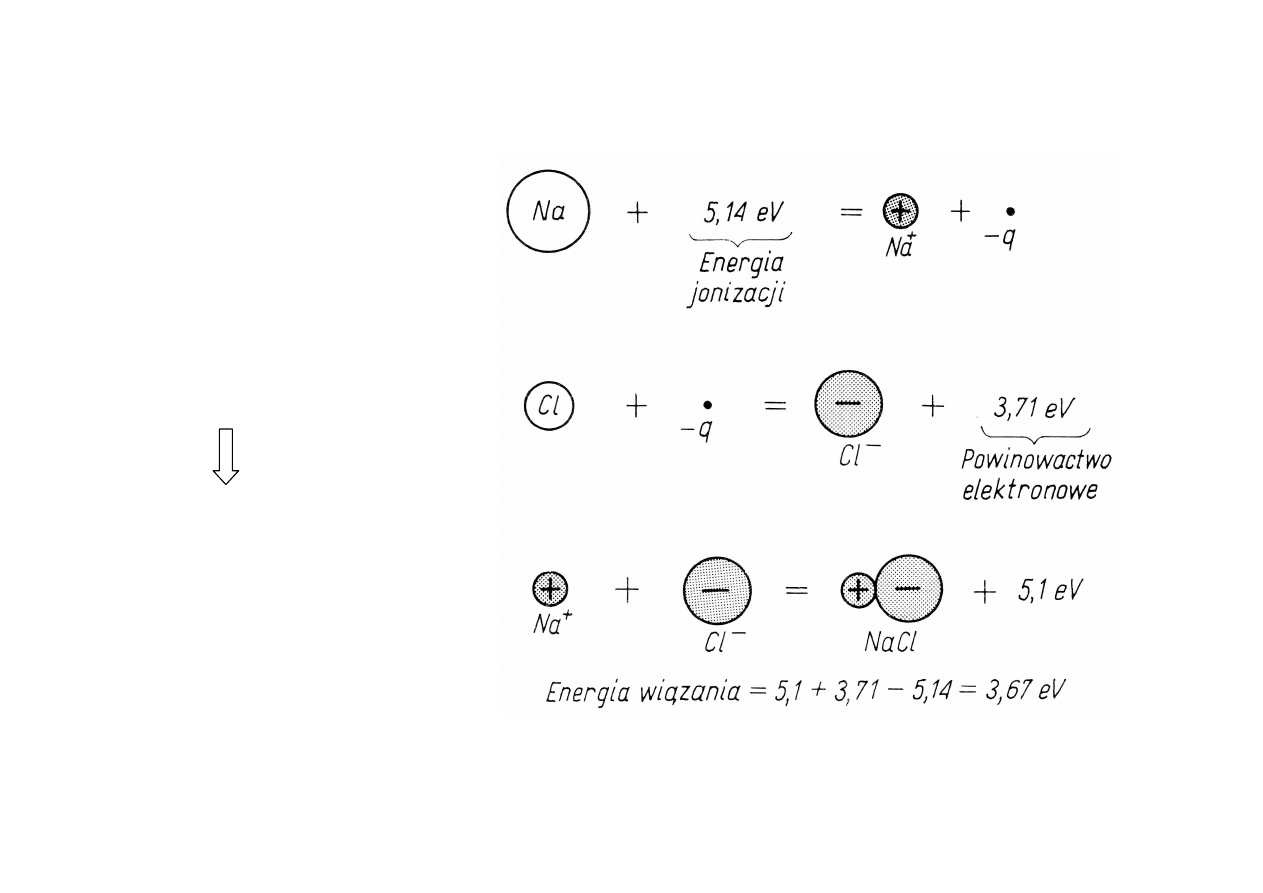
WIĄZANIA JONOWE

Opis rysunku - J.Hennel „Podstawy elektroniki półprzewodnikowej

”

Przykład NaCl:

Na - 1s

2

2s

2

2p

6

3s

1

Cl - 1s

2

2s

2

2p

6

3s

2

3p

5

Na

+

- 1s

2

2s

2

2p

6

Cl

−−−−

- 1s

2

2s

2

2p

6

3s

2

3p

6

Cząsteczki 2011

4

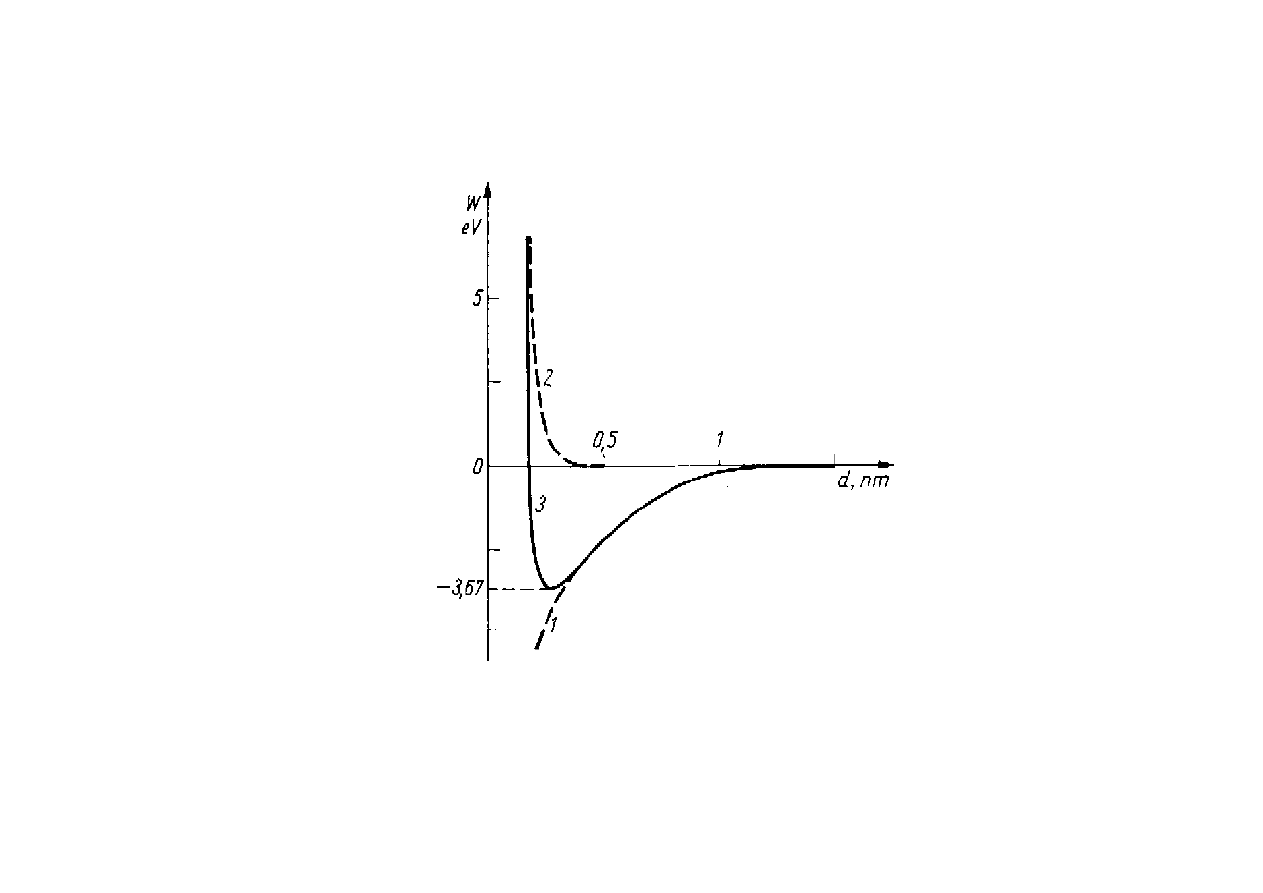
WIĄZANIA JONOWE

Rys. - J.Hennel

Zależność energii potencjalnej od odległości między środkami
ciężkości jonów

1 – energia przyciągania

elektrostatycznego jonów

2 – energia odpychania powłok

elektronowych

3 – wypadkowa energia potencjalna

Cząsteczki 2011

5

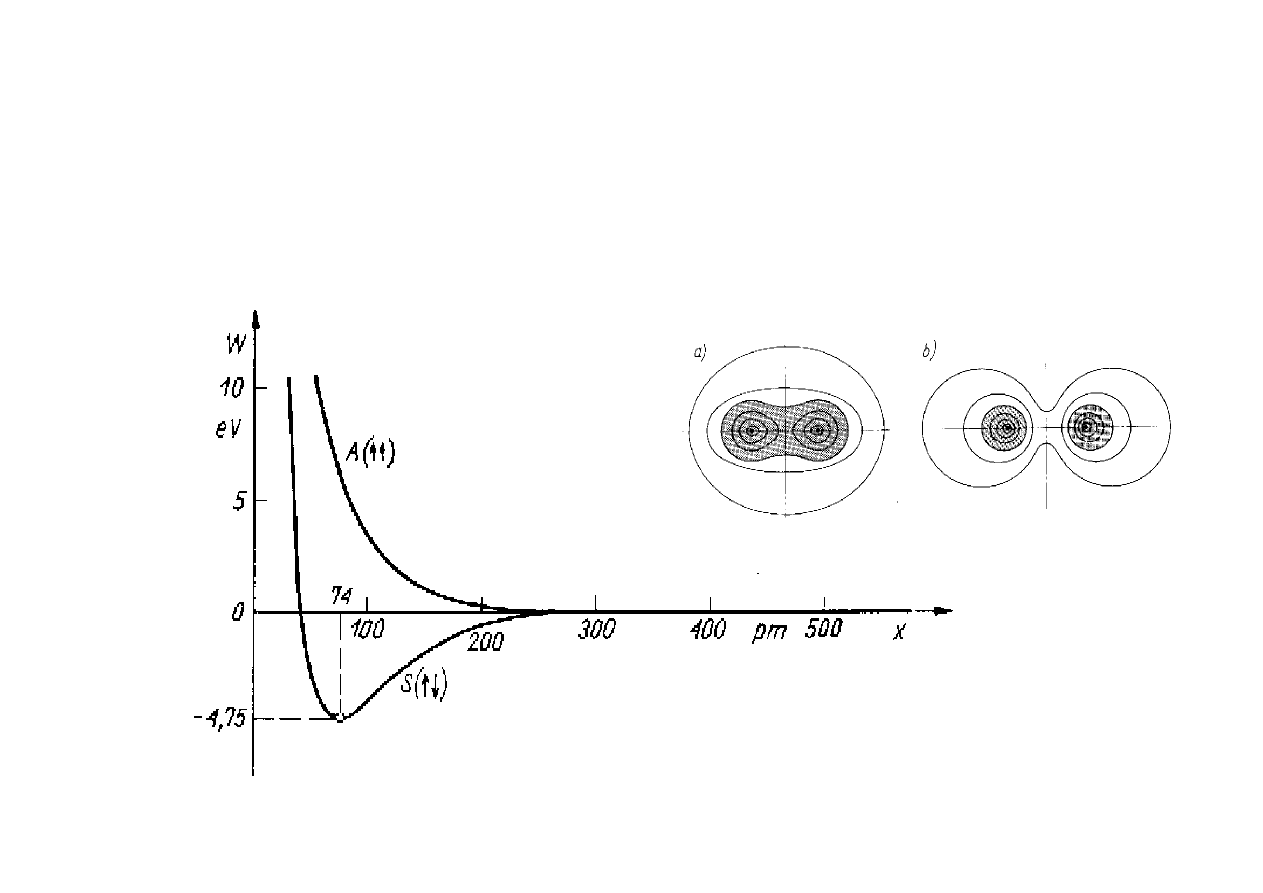
WIĄZANIE KOWALENCYJNE

Wiązanie tworzy wspólna para elektronów o przeciwnie
skierowanych spinach

Orbitale molekularne

H

2

:

orbital wiążący

orbital antywiążący

Zależność energii potencjalnej
od odległości między jądrami

Rys. - J.Hennel

Cząsteczki 2011

6

ORBITALE MOLEKULARNE

Przykładowe rozkłady gęstości ładunku elektronowego:

Przybliżenie:

1, 2

3

1

2

3

1

1, 1

2

2, 2

,

(

, ,..., ; ,

, ,...,

)

(

)

(

) .....

(

)

n

n

n

n

n

r r r

r s s s

s

r s

r s

r s

µ

ψ

ψ

ψ

ψ

=

⋅

⋅

⋅

r r r

r

r

r

r

Cząsteczki 2011

7

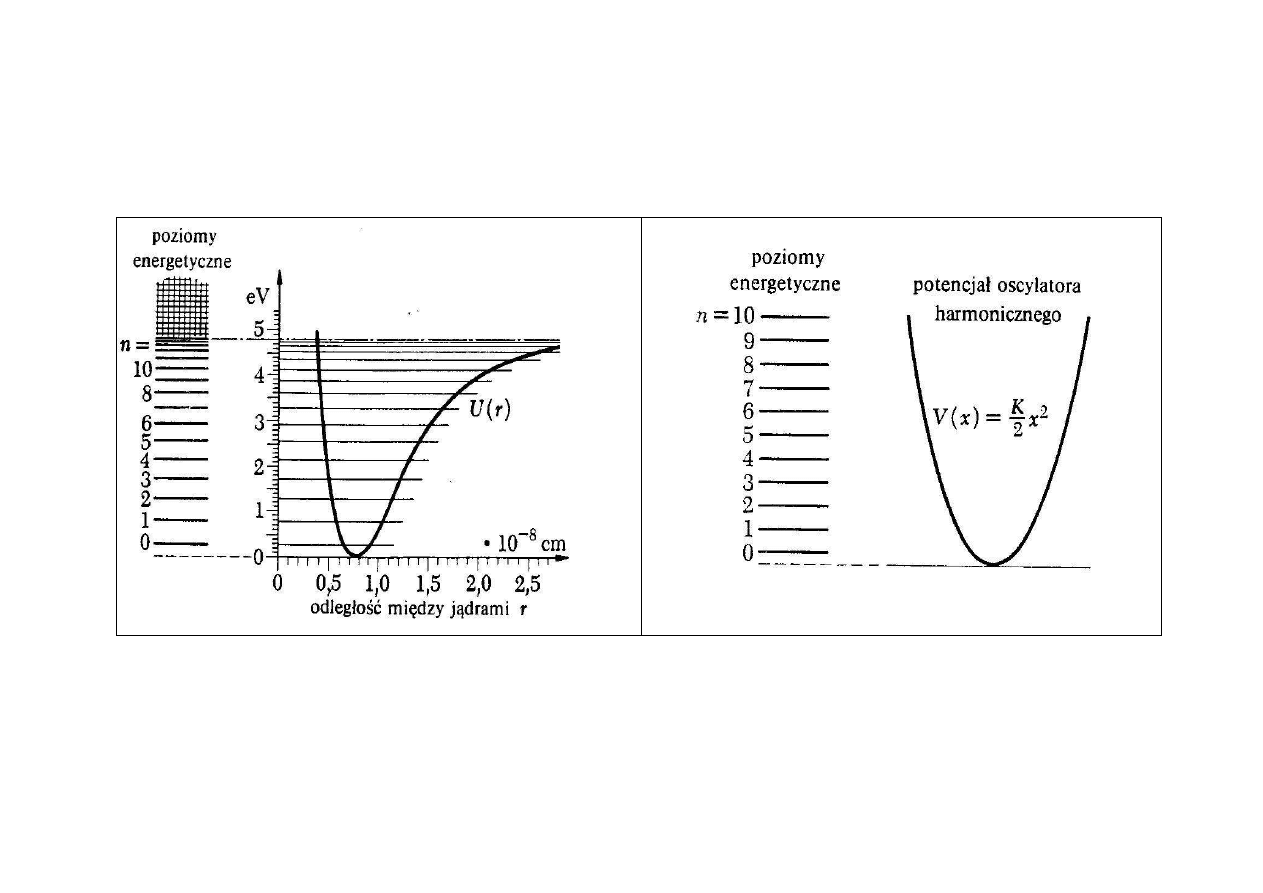
DRGANIA JĄDER W CZASTECZKACH

Energia potencjalna cząsteczki i energia potencjalna oscylatora

harmonicznego (energia drgań harmonicznych)

Cząsteczki 2011

8

OSCYLATOR KWANTOWY

Równanie Schrödingera

(

)

0

2

2

2

2

=

ψ

−

+

ψ

U

W

m

dx

d

h

Energia potencjalna drgań oscylatora harmonicznego :

U(x) = -k x

2

/2 = -

m

ω

2

x

2

/2

n

n

n

n

u

E

u

x

m

dx

u

d

m

=

+

−

2

2

2

2

2

2

2

ω

h

Cząsteczki 2011

9

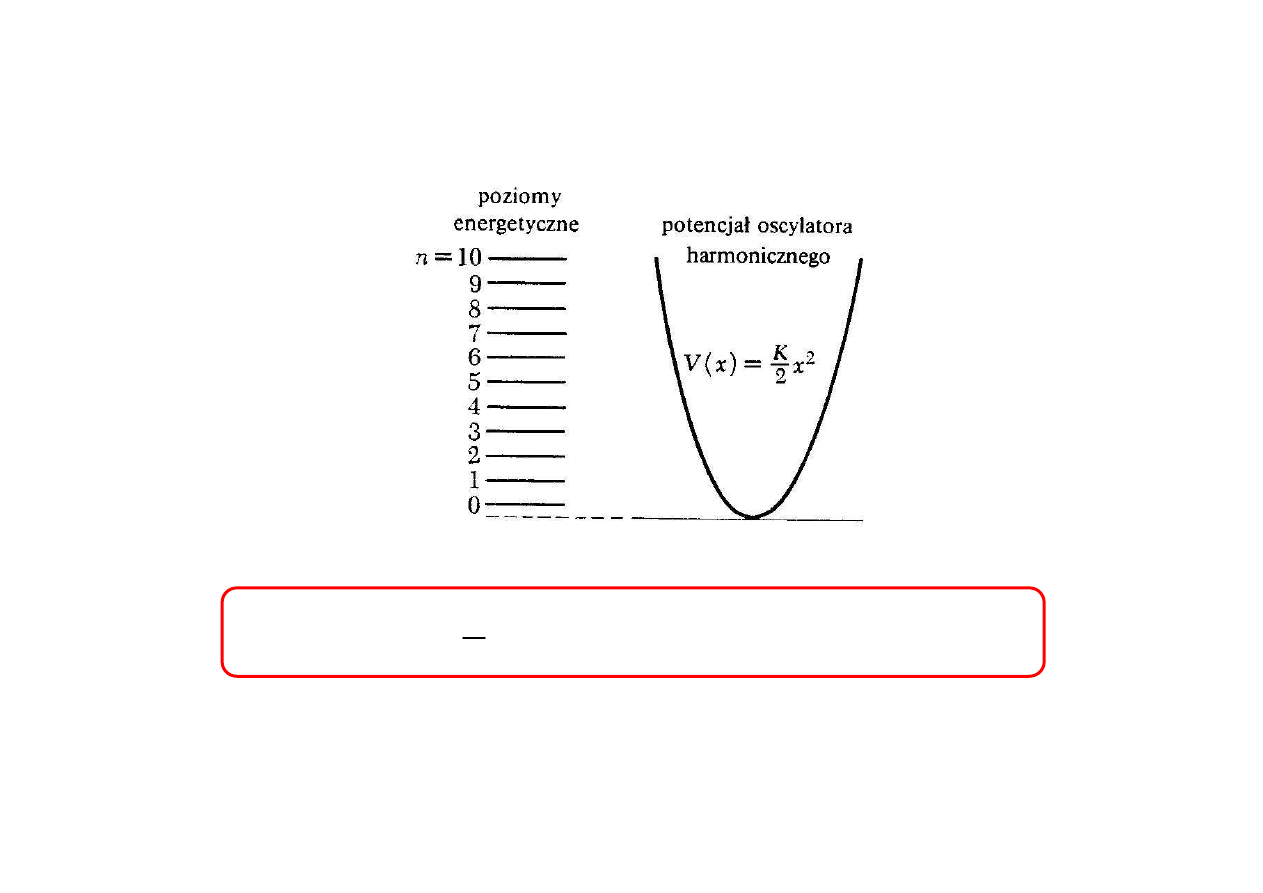
POZIOMY ENERGETYCZNE OSCYLATORA

....

,

2

,

1

,

0

)

(

2

1

=

+

=

n

n

E

n

ω

h

Najniższa możliwa energia jest różna od zera

(drgania „zerowe” dla n=0)

Cząsteczki 2011

10

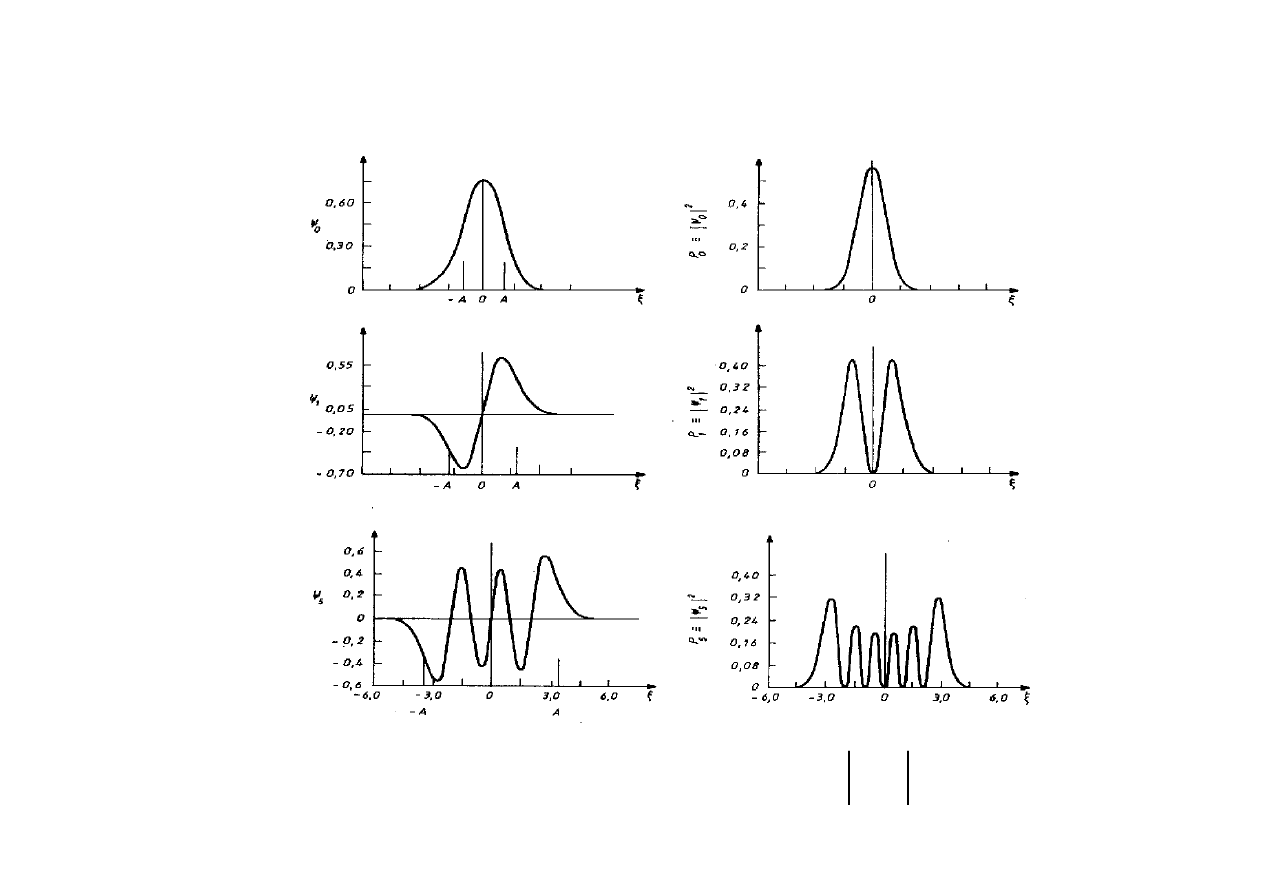
FUNKCJE FALOWE OSCYLATORA

2

n

n

u

u

Cząsteczki 2011

11

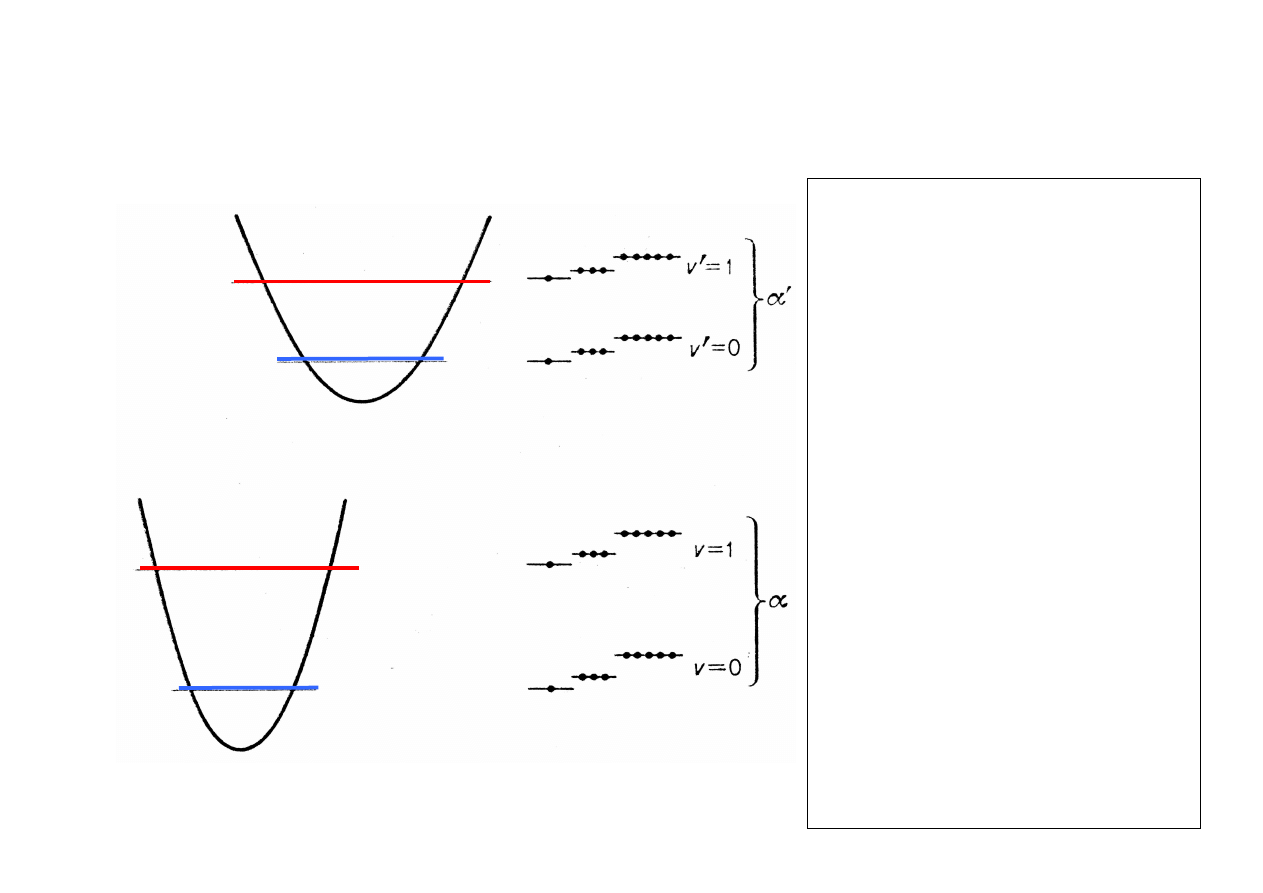
STANY ENERGETYCZNE CZĄSTECZEK

α

i

α

’

dwa stanu energetyczne

chmury elektronowej

v = 0 i v =

1 poziomy

energetyczne drgań cząsteczki dla
stanu podstawowego chmury
elektronowej

v’ = 0 i v’ = 1

poziomy

energetyczne drgań cząsteczki dla
stanu wzbudzonego chmury
elektronowej

poziomy energetyczne drgań
cząsteczki (poziomy
oscylacyjne) są rozszczepione
z powodu różnych poziomów
energii ruchu obrotowego
(poziomy rotacyjne).

Cząsteczki 2011

12

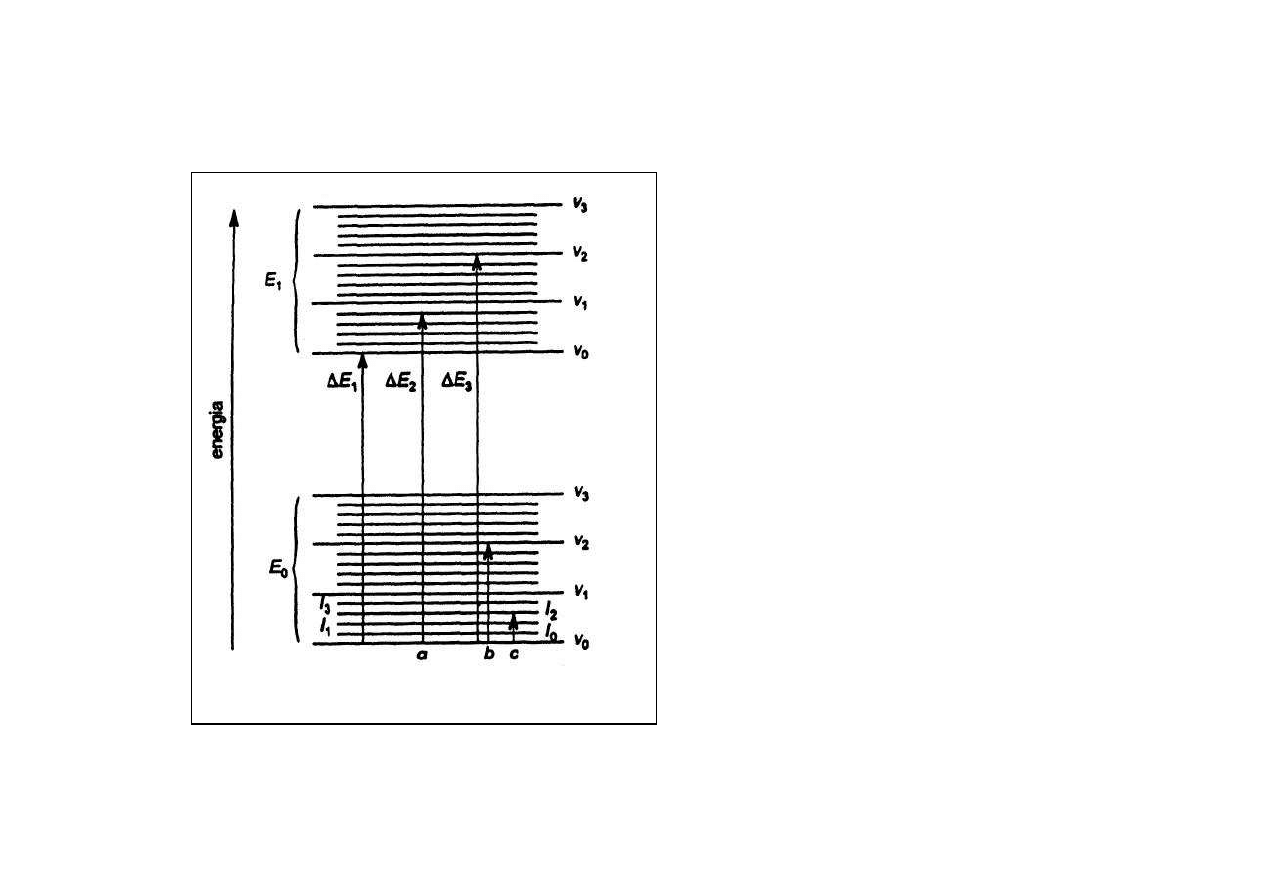
WIDMA CZĄSTECZKOWE

Całkowita energia cząsteczki

E = E

e

+ E

os

+ E

rot

E

e

- energia elektronowa

∆

E

e

kilka eV

E

os

- energia oscylacyjna

∆

E

os

~ 0,01- 0,1 eV

E

rot

- energia rotacyjna

∆

E

rot

~ 0,001eV

E

e

: E

os

: E

rot

= 1000 : 10 : 1

Promieniowanie z zakresu

dalekiej podczerwieni

może powodować tylko zmiany

energii rotacji; powstaje wtedy

widmo rotacyjne

. Zaabsorbowana energia nie

wystarcza do zmiany energii oscylacji i energii elektronowej.

Promieniowanie z zakresu

bliskiej podczerwieni

, o większej energii, powoduje

przejścia pomiędzy poziomami oscylacyjnymi. Ponieważ zmianom energii
oscylacyjnej towarzyszą zmiany energii rotacyjnej, powstają

widma oscylacyjno-

rotacyjne.

Zmiany energii elektronowej może wywołać tylko promieniowanie z zakresu

widzialnego i nadfioletu

. Zmianom tej energii towarzyszą zazwyczaj zmiany energii

oscylacyjnej i rotacyjnej i powstaje

widmo elektronowo-oscylacyjno-rotacyjne

Cząsteczki 2011

13

WIDMA CZĄSTECZKOWE

Widmo cząsteczki składa się z pasm
odpowiadających kolejnym przejściom
elektronowym