WYKŁAD 15 i 16

Podstawy programowania w języku MATLAB

Patrz przykłady zamieszczone na tej stronie:

prog1.m ... prog7.m

oraz

cw_0.m ... cw_12.m

Tomasz Zieliński

KOMPILATOR vs. INTERPRETER

(przypomnienie)

C/C++

=

kompilatory

• tłumaczą od razu cały program na kod maszynowy
• potem dopiero program jest wykonywany
• stosowane kiedy jest już znany algorytm rozwiązania

Basic

=

interpretery

Matlab

• tłumaczona i wykonywana jest linia po linii programu
• stosowane kiedy jest poszukiwany algorytm rozwiązania

Zalety

Wady

Kompilator

• S

zybkie działanie programu

•

Możliwość optymalizacji kodu

programu, np. minimalizacji
potrzebnej pamięci

Długa droga do pomysłu do
jego weryfikacji

Interpreter

Krótka droga do pomysłu do
jego weryfikacji

Wolne działanie programu

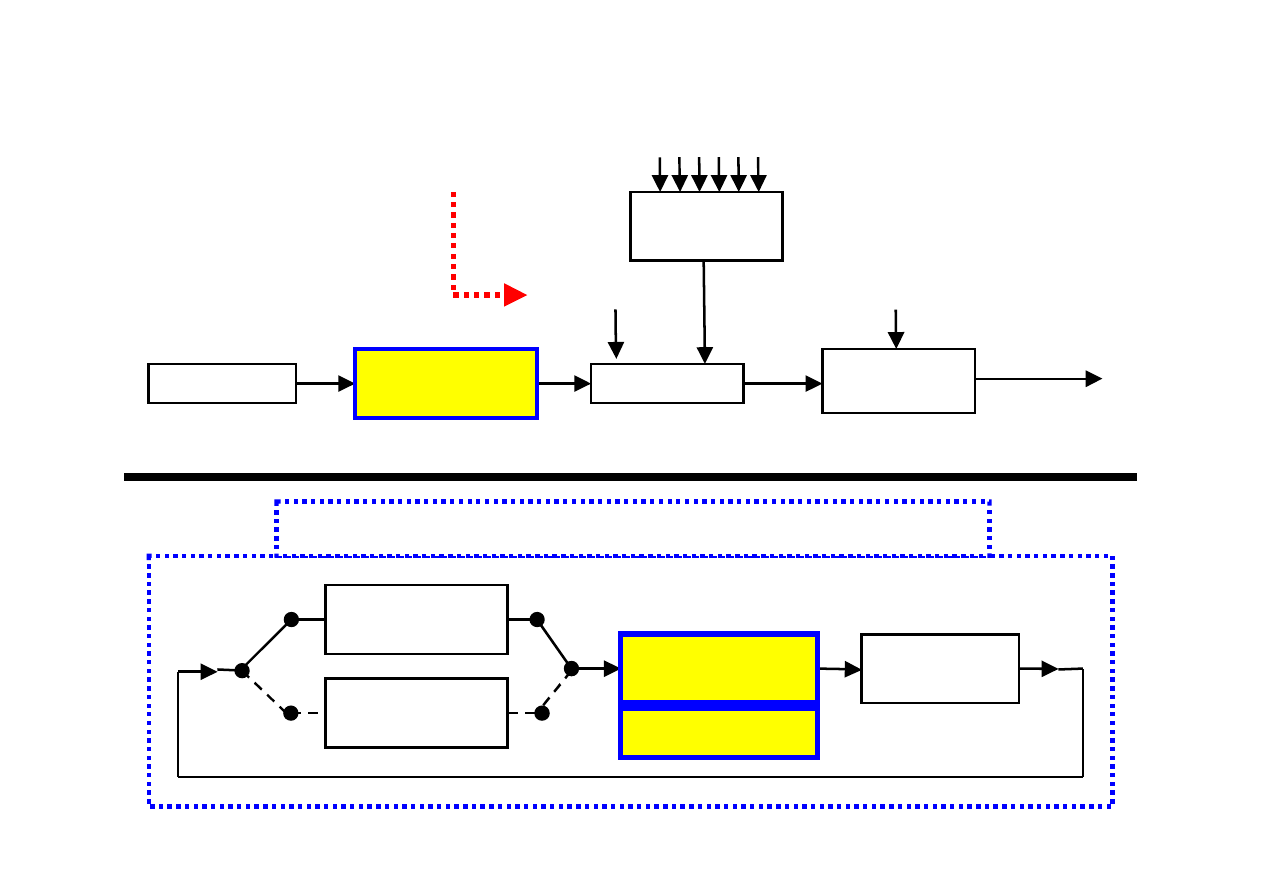
PRACA NAD PROGRAMEM: kompilator vs. interpreter

Linker

Edytor tekstu

prog.c

KOMPILATOR

programu

prog.obj

my.lib

prog.exe

Lib Maker

Konsolidator

f1.obj, f2.obj,

...

system.lib

System

operacyjny

wykonanie
całego
programu

my.dll

statyczne (lib)
i dynamiczne (dll)
dołączanie bibliotek

Interpreter

linii

INTERPRETER to oddzielny program / aplikacja

INTERPRETER

linii

Egzekutor

linii

Edytor

linii

Program

czyli zbiór linii

1

2

1

2

>> ...?... (CR)

system.dll

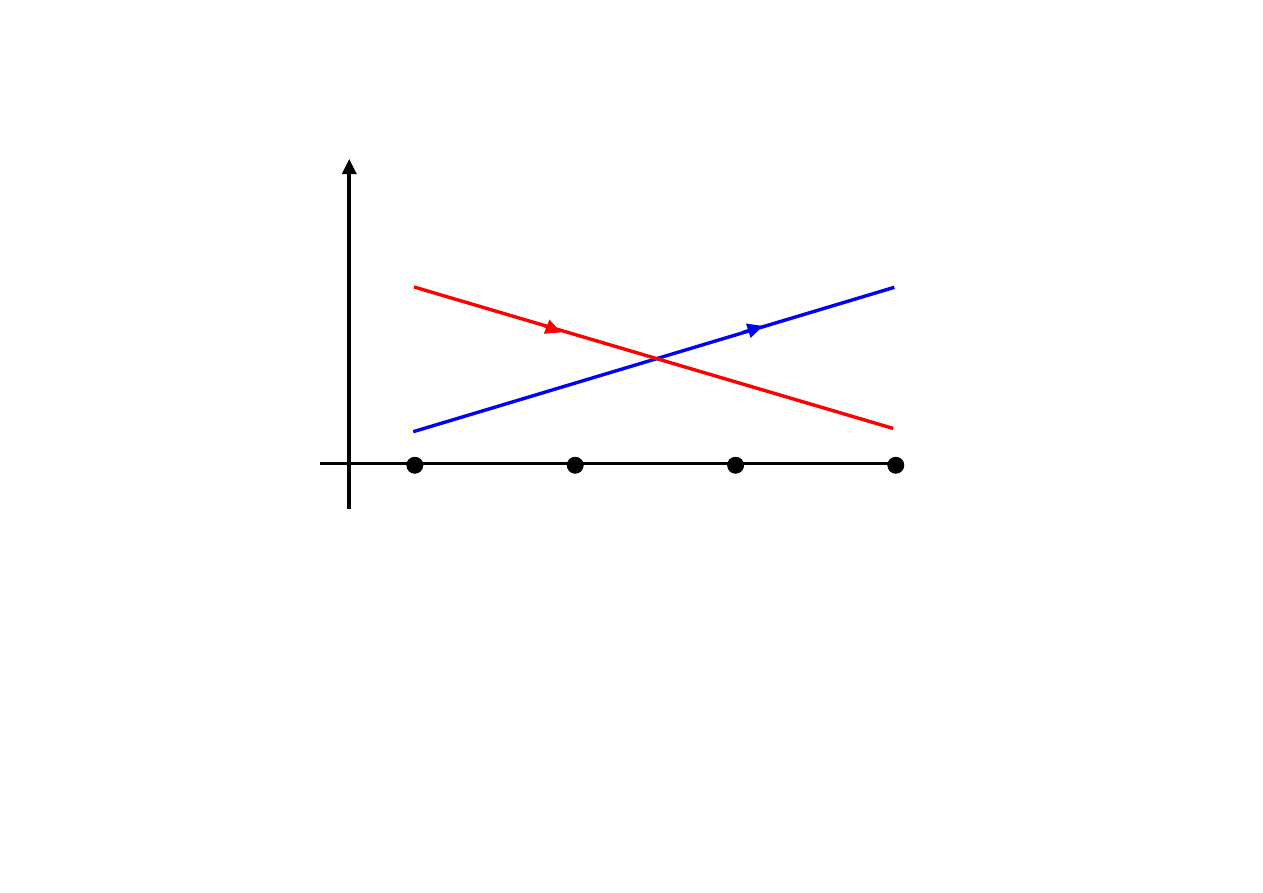
SZYBKOŚĆ PISANIA vs. SZYBKOŚĆ DZIAŁANIA

Asembler

czas napisania i

uruchamiania

(usunięcia błędów)

programu

czas

wykonania

programu

Język C/C++

Matlab

Simulink

WNIOSEK:
♦ kiedy poszukuję rozwiązania problemu, wybieram język wysokiego

poziomu, nawet graficzny, z dużą liczbą bibliotek (

szybko piszę program,

który wolno działa

)

♦ kiedy znam rozwiązanie problemu wybieram język niskiego poziomu

(

wolno piszę program, który szybko działa

)

ZALETY MATLABA:

1)

Obliczenia numeryczne (inżynierskie):

• zapis wektorowo-macierzowy: A*x = b, x = inv(A)*b, C = A*B

• olbrzymia, wiarygodna biblioteka funkcji matematycznych:

algebra liniowa, całkowanie, różniczkowanie, optymalizacja, ...

• kompromis pomiędzy prostotą, dokładnością, szybkością

2)

Zaawansowana wizualizacja 2D/3D danych

, prosta w użyciu.

3)

Biblioteki specjalistyczne

(toolboxes)

pisane przez ekspertów

światowych

z zakresu elektroniki, telekomunikacji, automatyki, ...

4)

Simulink,

Stateflow, SimEvent, SimPower, Link to ModelSim

(VHDL,

FPGA, ASIC) - okienkowo-zorientowane środowiska graficzne do
uruchamiania algorytmów na podstawie ich schematów blokowych,
wyposażone w liczne biblioteki (blocksets).

5)

Otwarta architektura

:

• m-zbiory dostępne w kodzie źródłowym
• łatwość dołączania swoich funkcji
• mnogość interfejsów do różnych typów danych (wav, avi, DICOM,...)

6)

C-maker, Real-Time Workshop

, procesory DSP (TI Composer Studio)

Z języka C do Matlaba (1)

Zbiór dyskowy: prog1.m
%--------------------------------------------------------------------------------------------

% Program prog1: budżet rodziny

osoby = 3

;

% liczba osób

kasa = 1500.45

;

% łączny przychód

moje = kasa/osoby

,

pause

% moje kieszonkowe

disp

(

'moje kieszonkowe = '

), disp(moje), pause

% display

%--------------------------------------------------------------------------------------------

Uwagi:
1) Brak jest specjalnych słów początku i końca programu.

Program jest zbiorem linii zapisanych w osobnym zbiorze na dysku
o rozszerzeniu

*.m

2) Brak deklaracji zmiennych. Wszystkie są typu

double

.

3)

%

stanowi znak początku komentarza (za nim do końca linii).

4) Znak

;

informuje, żeby nie wyświetlać wyniku operacji.

5) Znak

...

na końcu linii informuje, że następna linia jest kontynuacją

bieżącej.

6) Instrukcja

disp()

służy do wyświetlania tekstu lub wartości

zmiennej.

Zbiór dyskowy: prog2.m
%--------------------------------------------------------------------------------------------

% Program prog2: budżet rodziny

osoby = 3;

% liczba osób

kasa =

input

(

'ile do podziału ? '

); % komunikat, czytaj z klawiatury

moje = kasa/osoby, pause

% oblicz, pokaż wynik gdyż brak ;

%--------------------------------------------------------------------------------------------

Uwagi:
1) W instrukcji

input

po wyświetleniu na ekranie tekstu

„ile do

podziału?”

jest wczytywana liczba z klawiatury, której wartość jest

podstawiana do zmiennej kasa.

Z języka C do Matlaba (2)

Zbiór dyskowy: prog3.m
%-----------------------------------------------------------------------------------------
osoby = 3;
kasa = input(

'ile do podziału ? '

);

moje =

wzor3

( kasa, osoby ), pause

% wywołanie funkcji wzor3()

%----------------------------------------------------------------------------------------

Zbiór dyskowy: wzor3.m
%----------------------------------------------------------------------------------------

function

kieszen =

wzor3

( forsa, osoby )

% Moja funkcja, licząca kieszonkowe
% Wejście: forsa - budzet rodzinny
% Wyjście: kieszen - moje kieszonkowe

kieszen = forsa/osoby;

% wyjście = funkcja wejścia

%----------------------------------------------------------------------------------------

Uwagi:

1) Każda funkcja jest osobnym plikiem na dysku.

Od programu różni się tym, że rozpoczyna ją słowo

function

.

2) Przykładowa budowa:

function

[ x, y, z ] =

zróbcoś

(

a, b, c)

% komentarz co funkcja robi, wyświetlany podczas

help

zróbcoś

x = a + b;

% wyraź parametry wyjściowe {x, y, z}

y = a - b;

% poprzez parametry wejściowe {a, b, c}

z = c;

% czyli {x, y, z } = funkcja( a, b, c)

Z języka C do Matlaba (3)

Zbiór dyskowy: prog4.m
%-----------------------------------------------------------------------------------------

clear all

;

% wyzeruj wszystkie zmienne

global

osoby

;

% deklaracja zmiennej globalnej,
% dostępnej także w funkcjach

osoby = 3;

% ustaw liczbę osób

kasa = input(

' ile do podziału ? '

);

% wczytaj wartość budżetu

moje =

wzor4

( kasa ), pause

% oblicz moje kieszonkowe

%-----------------------------------------------------------------------------------------

Zbiór dyskowy: wzor4.m
%-----------------------------------------------------------------------------------------

function

kieszen =

wzor4

( forsa )

global

osoby

kieszen = forsa/osoby;
%-----------------------------------------------------------------------------------------

Uwagi:

1) Aby wartość zmiennej była dostępna w także w funkcji, zmienna ta

musi być zadeklarowana jako

global

(w programie i w funkcji)

Z języka C do Matlaba (4)

Zbiór dyskowy: prog5.m
%-------------------------------------------------------------------------------------------

clear all

;

% wyzeruj wszystkie zmienne

global

osoby;

% deklaracja zmiennej globalnej

osoby = 3;

% ustaw liczbę osób

kasa = input(

'ile do podziału ? '

);

% wczytaj wartość budżetu

[tata, mama, ja] =

wzor5

( kasa ), pause

% kilka zwracanych wartości

%-------------------------------------------------------------------------------------------

Zbiór dyskowy: wzor5.m
%-------------------------------------------------------------------------------------------

function

[osoba1, osoba2, osoba3] =

wzor5

( forsa )

% Moja funkcja, licząca kieszonkowe
% Wejście: forsa - budżet rodzinny
% Wyjście: osoba1, osoba2, osoba3 - kieszonkowe trzech osób

global

osoby

srednia = forsa/osoby;
osoba1 = 1.25 * srednia;
osoba2 = 1.00 * srednia;
osoba3 = 0.75 * srednia;
%--------------------------------------------------------------------------------------

Uwagi:

1) W tym przypadku obliczamy w funkcji kieszonkowe dla wszystkich

członków rodziny, które zwracamy do programu głównego.

Z języka C do Matlaba (5)

Zbiór dyskowy: prog6.m
%-------------------------------------------------------------------------------------------

clear all

;

% wyzeruj wszystkie zmienne

global

osoby;

% zadeklaruj zmienną globalną osoby

imiona = [

'tata'

;

'mama'

;

'ja '

];

% imiona członków rodziny

osoby = 3;

% liczb osób

kasa = input(

'ile do podziału ? '

);

% wczytaj budżet, wstaw do kasy

rodzina =

wzor6

( kasa ), pause

% funkcja teraz zwraca tablicę

disp(

'tata = '

); disp( rodzina(1) );

% kieszonkowe taty

disp(

'mama = '

); disp( rodzina(2) );

% kieszonkowe mamy

disp(

'ja = '

); disp( rodzina(3) ); pause

% kieszonkowe moje

for

i = 1 : osoby

% pętla

for-end

: wyświetlanie

% if( i == 2) break; end

%

break

to wyjście z pętli for

disp( [

'osoba nr '

num2str(i)

',czyli '

imiona(i,:)

' = '

num2str(rodzina(i))

] );

end

if

( rodzina(2) > rodzina(3) )

% warunek logiczny

if-else-end

disp(

'Mama ma więcej niż ja!'

);

else

disp(

'Mam co najmniej tyle co mama'

);

end

while

( rodzina(1) > rodzina(2) )

% pętla

while-end

;

break

ją kończy

disp(

'Tata ma więcej od mamy'

);

break

;

end

plot( 1:osoby, rodzina,

'b*--'

);

% rysunek (x, y)

xlabel(

'nr czlonka rodziny'

);

% opis osi x

ylabel(

'kieszonkowe [PLN]'

);

% opis osi y

title(

'BUDŻET RODZINNY'

);

% tytuł

pause

% pauza

%-------------------------------------------------------------------------------------------

Z języka C do Matlaba (6)

Zbiór dyskowy: wzor6.m
%-------------------------------------------------------------------------------------------

function

czlonkowie

= wzor6( forsa )

% Moja funkcja, licząca kieszonkowe
% Wejście: forsa - budżet rodzinny
% Wyjście: czlonkowie[] - kieszonkowe członków rodziny

global

osoby

srednia = forsa/osoby;

czlonkowie( 1 )

= 1.25 * srednia;

czlonkowie( 2 )

= 1.00 * srednia;

czlonkowie( 3 )

= 0.75 * srednia;

%-------------------------------------------------------------------------------------------

Zbiór dyskowy: prog7.m
%-------------------------------------------------------------------------------------------

load

rodzina.dat

% wczytaj ze zbioru

rodzina.dat

dwie liczby

kasa =

rodzina(1);

% podstaw pierwszą z nich do zmiennej kasa

osoby =

rodzina(2);

% a drugą - do zmiennej osoby

moje = kasa/osoby, pause

% oblicz moje kieszonkowe

save

kieszonkowe.dat moje /ascii

% zapisz je do zbioru

%

kieszonkowe.dat

%-------------------------------------------------------------------------------------------

Zbiór dyskowy: rodzina.dat
%-------------------------------------------------------------------------------------------
1500.45 3
%-------------------------------------------------------------------------------------------

Zbiór dyskowy: rodzina.dat
%-------------------------------------------------------------------------------------------
5.0015000e+002
%-------------------------------------------------------------------------------------------

Macierze w Matlabie (1)

» Cw_0_demo <ENTER>

A = [ 1 2 3; 4 5 6; 7 8 0 ]

% definicja macierzy A 3 x3
% wydruk, gdyż brak na końcu

A = 1 2

3

% średnika

4

5

6

7 8 0

B = A'

% 1) transpozycja i sprzężenie zespolone

% elementów macierzy

B = 1

4

7

% 2) dla macierzy o elementach rzeczywistych

2

5

8

% tylko sprzężenie

3

6

0

%

3) jeśli

.’

to tylko transpozycja

C = A + B

% suma dwóch macierzy

C = 2 6

10

%

10

=

3

+

7

6 10 14
10 14 0

C = A * B

% mnożenie dwóch macierzy

C =

14

32 23

%

14

= 1*1 + 2*2 + 3*3

32

77 68

%

32

= 4*1 + 5*2 + 6*3

23

68 113

%

23

=

7*1 + 8*2 + 0*3

inv(A)

% macierz odwrotna

ans = -1.7778 0.8889 -0.1111
1.5556 -0.7778 0.2222
-0.1111 0.2222 -0.1111

det(A)

% wyznacznik macierzy

ans = 27
rank(A)

% rząd macierzy

ans = 3
cond(A)

% uwarunkowanie macierzy

ans = 35.1059

% (max sv) / (min sv )

Macierze w Matlabie (2)

eig(A)

%

wartości własne

ans = -0.3884
12.1229
-5.7345

[v,d] = eig(A)

% wektory i wartości własne

v = 0.7471 -0.2998 -0.2763
-0.6582 -0.7075 -0.3884
0.0931 -0.6400 0.8791

d = -0.3884 0 0
0 12.1229 0
0 0 -5.7345

svd(A)

% wartości osobliwe

ans = 13.2015
5.4388
0.3760

expm(A)

% eksponenta macierzy

ans = 1.0e+004 *
3.1591 3.9741 2.7487
7.4540 9.3775 6.4858
6.7431 8.4830 5.8672

p = poly(A)

% wielomian charakterystyczny

p = 1.0000 -6.0000 -72.0000 -27.0000

roots(p)

% pierwiastki tego wielomianu

ans = 12.1229

% czyli wartości własne macierzy A

-5.7345
-0.3884

Wektory w Matlabie

x = [ 1 2 3 ]

% definicja wektora poziomego

x =

1

2

3

%

y = [ 4; 5; 6 ]

% definicja wektora pionowego

y =

4

%

5

%

6

%

x * y

% iloczyn skalarny

ans = 32

% 1*

4

+ 2*

5

+ 3*

6

y * x

% iloczyn wektorowy

ans = 4 8 12

%

4

* [ 1 2 3 ]

5 10 15

%

5

* [ 1 2 3 ]

6 12 18

%

6

* [ 1 2 3 ]

x .* y'

% iloczyn odpowiadających sobie

ans = 4 10 18

% elementów: [ 1*

4

, 2*

5

, 3*

6

]

x + y'

% suma odpowiadających sobie

ans = 5 7 9

% elementów: [ 1+

4

, 2+

5

, 3+

6

]

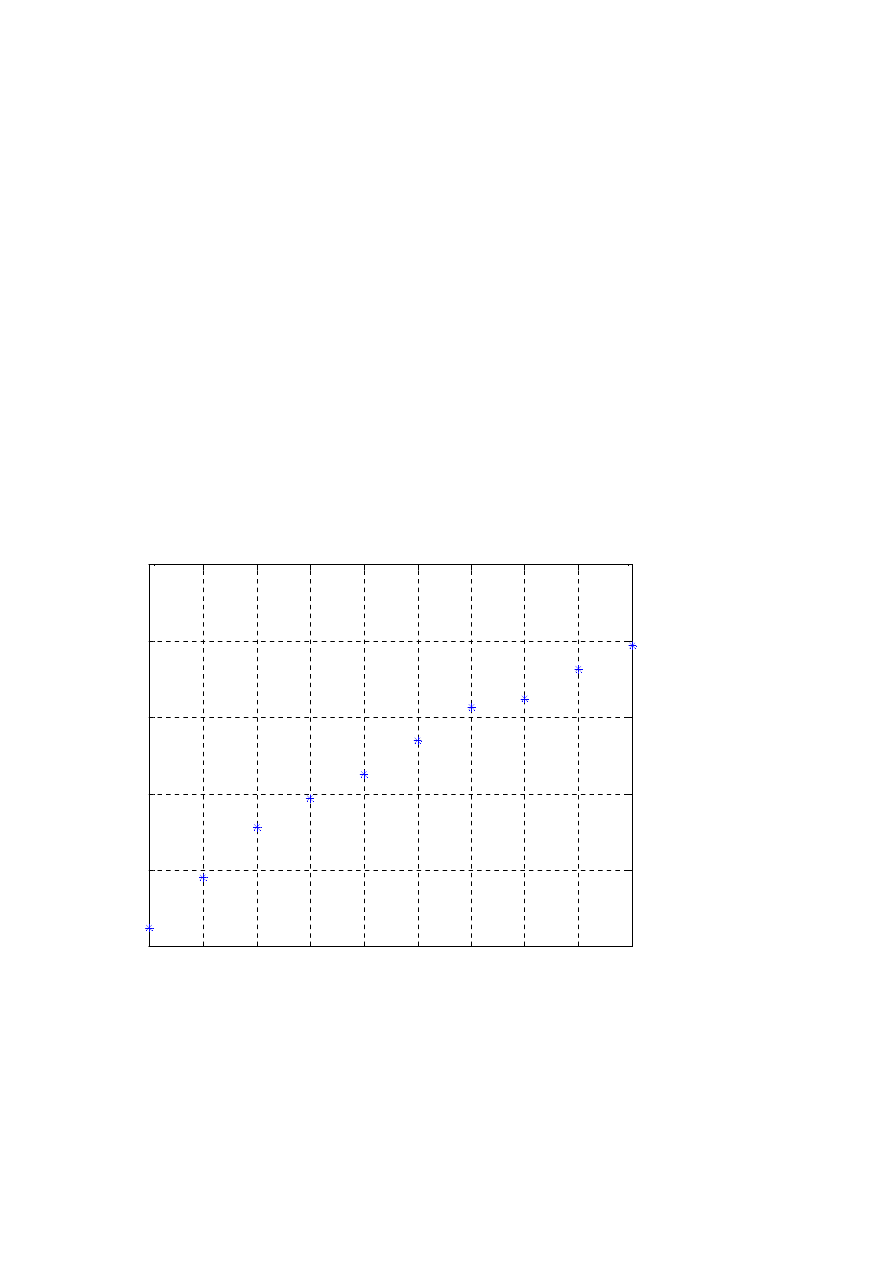
Laboratorium w Matlabie (1)

% W wyniku pomiaru otrzymano następujące liczby :
% ( x = numer pomiaru, y = wartość )

x = [ 1 2 3 4

5 6 7 8 9 10 ];

y = [ 0.912 0.945 0.978 0.997 1.013 1.035 1.057 1.062 1.082 1.097 ];

% W celu lepszej obserwacji przedstawiamy je na rysunku :

plot( x, y, ‘b*’ ) ;

% wykres y = funkcja(x), niebieskie „*”

title( 'DANE POMIAROWE' );

% tytuł

xlabel( 'numer probki' );

% podpis pod osią x

xlabel( 'wartosc' );

% podpis pod osią y

grid;

% siatka

1

2

3

4

5

6

7

8

9

10

0.9

0.95

1

1.05

1.1

1.15

DANE POMIAROWE

numer probki

wa

rt

os

c

pause

% naciśnij jakiś klawisz

clf

% wyzeruj rysunek

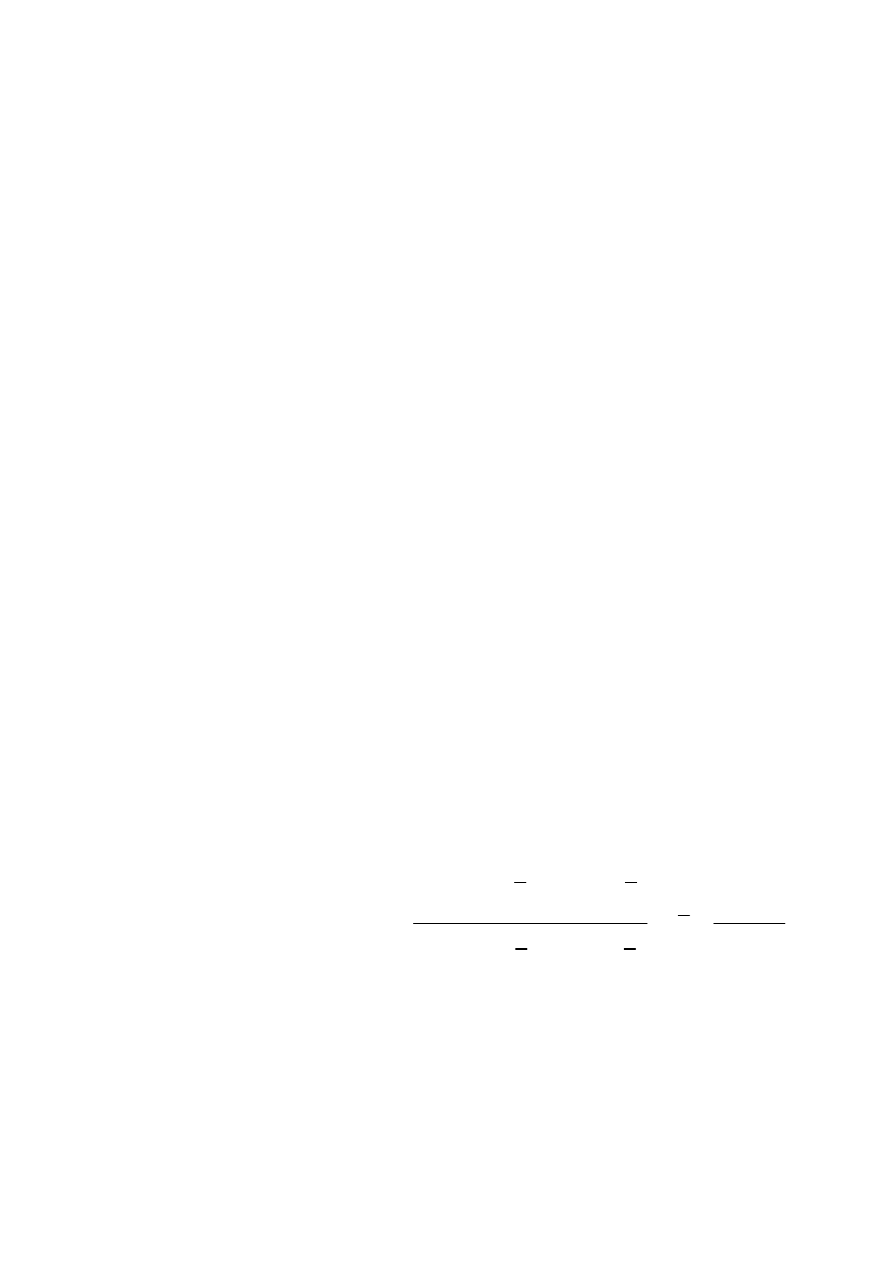
Laboratorium w Matlabie (2)

% Interesuje nas wartość średnia tych liczb
% oraz ich rozrzut wokół wyliczonej wartości średniej :

srednia = mean( y )

% srednia = sum( y ) / length( y )
%

srednia =

% ponieważ brak średnika
% powyżej,

1.0178

% jest wyświetlany wynik

rozrzut = std( y )

% rozrzut = ...
% ... sqrt( sum(

( y - srednia ).^2

) / length( N ) )

rozrzut =

% ponieważ brak jest średnika
% powyżej,

0.0603

% to jest wyświetlany wynik

% Dodatkowo chcielibyśmy wyznaczyć współczynniki a i b linii prostej
% y = a * x + b
% najlepiej aproksymującej otrzymane dane (prosta regresji liniowej).

xm = mean( x );

% średnia wartość wektora x

ym = mean( y );

% średnia wartość wektora y

xr = x - xm;

% wektor x - średnia x (od każdego elementu)

yr = y - ym;

% wektor y - średnia y (od każdego elementu)

a = (xr * yr') / (xr * xr')

% obliczenie wsp a prostej, to samo

% inaczej: a = sum( xr .* yr ) / sum( xr .* xr )

%

(

) (

)

(

) (

)

1

1

1

( )

*

( )

( )

,

( )

* ( )

N

N

n

n

N

n

x n

x

y n

y

x n

a

x

N

x n

x

x n

x

=

=

=

−

−

=

=

−

−

∑

∑

∑

a =

0.0197

b = ym - a * xm

% obliczenie wsp b prostej

b =

0.9096

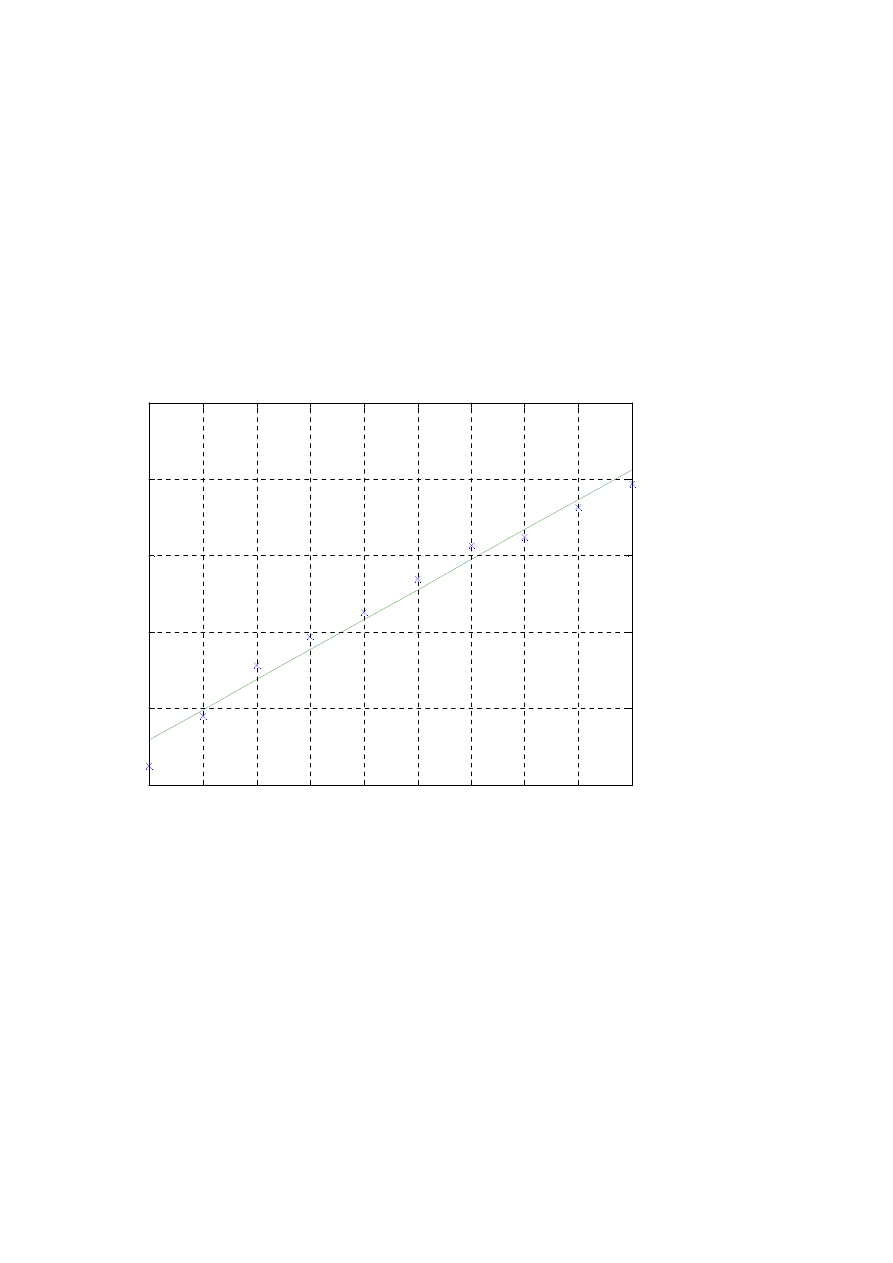
Laboratorium w Matlabie (3)

% Teraz porównamy punkty eksperymentalne z linią regresji liniowej

plot( x, y, 'bx', x, a*x+b, 'k-' )

% niebieskie krzyżyki, linia czarna

title( 'DANE POMIAROWE' )

% tytuł

xlabel( 'numer próbki' )

% podpis pod osią x

ylabel( 'wartość' )

% podpis pod osią y

grid

% siatka

1

2

3

4

5

6

7

8

9

10

0.9

0.95

1

1.05

1.1

1.15

DANE POMIAROWE I PROSTA REGRESJI LINIOWEJ

numer probki

wa

rt

os

c

pause

% naciśnij cokolwiek

clf

% wyzeruj rysunek

echo off

% nie wyświetlaj komend na monitorze

MATLAB - skrót

1)

„

↑↓”

- przewijanie ostatnich linii w linii komend

„>> ....”

2)

„%”

- znak komentarza, za nim do końca linii

3)

„...”

- znak kontynuacji w następnej linii

4)

brak „;”

na końcu instrukcji oznacza polecenia wyświetlenia wyniku operacji

5)

help

instrukcja

- funkcja pomocy

help

: jak się używa

instrukcji

?

6)

„!”

- znak wywołania programu zewnętrznego wewnątrz Matlaba

!edit prog.m

- uruchomienie zewnętrznego edytora i wczytanie prog.m

7)

zerowanie:

clear all

- zawartości wszystki zmiennych (np. na początku prog)

clc

- okna komend

clf

- okien graficznych z rysunkami

8)

format

-

dokładność wydruku wyniku obliczeń

format short

1.3333

short e

1.3333*E+000

long

1.33333333333338

long e

1.33333333333338 * E+000

9)

Stałe predefiniowane

-

pi

= 3.14159...,

eps

= 2.22*10^(-16) (dokładność)

i, j

= sqrt(-1)

10)

Inicjalizacja

:

liczby rzczywiste:

n = 1; m = 10; a = 1.2345; b = 1.2*10^(-6);

liczby zespolone:

z = 3 + 4*

i

; z = 3 + 4*

j

; (dla macierzy: Z = A + B*

i

lub Z = A + B*

i

)

wektory poziome:

x

= [ 1.2 3.4 5.6 ];

y = 0. : 0.1 : 0.4;

otrzymujemy:

od krok do

0., 0.1, 0.2, 0.3, 0.4

z = rand(1, 5);

wektor 1x5 wartości losowych

z = sin( 0 : pi/2 : 2*pi );

0, 1, 0, -1, 0

z = sin(

x

);

wektor 1x3 wartości sin dla

x

z = x(1 : 2);

% podwektor, pobranie wybranych elementów od-do

otrzymujemy: [ 1.2 3.4 ]

wektory pionowe:

y = [ 1.2; 3.4; 5.6 ];

otrzymujemy:

y = [ 1.2

↑ ↑

3.4

znak nowego wiersza

5.6 ]

macierze:

A = [ 1 2 3; 4 5 6; 7 8 9 ];

otrzymujemy:

A = [ 1 2 3

4 5 6
7 8 9 ]

B = rand(5,5);

% macierz liczb losowych o wymiarach 5 x 5

C = eye(10);

% macierz diagonalna o wymiarach 10 x 10

D = A(1 : 2, 2 : 3);

% podmacierz A,

otrzymujemy [ 2 3; 5 6]

B = A’;

% transpozycja, sprzężenie elementów

11)

whos

- lista zmiennych w pamięci, ich wymiary

12)

Operatory arytmetyczne są domyślnie wektorowo-macierzowe.
Jeśli chcemy działać na elementach wektorów/macierzy, to operator
poprzedzamy kropką, np. „ .* „

+, -, *, \ (lewe dzielenie), / (prawe), ^(potęga),

liczby:

c = a

op

b,

gdzie

op

= +, -, *, /, ^

wektory:

z = x

op

y,

gdzie

op

= +, -, *, /,

.*

,

./

macierze:

C = A

op

B,

gdzie

op

= +, -, *, /, \,

.*

,

./

X = B/A

takie, że

X*A=B

X = A/B

takie, że

A*X=B y = A*x;

np. x = [ 1 2 3 ];

y = [ 4 5 6 ];
x + y = [ 5 7 9 ]
y - x = [ 3 3 3 ]
x * y’ = 1*4 + 2*5 + 3*6 = 32
x’ * y = [ 4 5 6

8 10 12
12 15 18 ]

x

.*

y = [ 4 10 18 ]

x

.\

y = [ 4 2.5 2 ]

x

.^

y = [ 1 32 739 ]

x

./

y = [ 0.25 0.4 0.5 ]

x

.^2

= [ 1 4 9 ]

x

/

y = 0.4156

13)

Operatory logiczne

:

<, <=, >, >=, ==, ~=, & (AND), | (OR, ~ (NOT)

np.

if

( (a > b) & ( c ~= d) )

i = 0;

x=y;

while

( i <= 10 )

end

i = i+1;

end

14)

Zapisywanie zmiennych

na dysk i ich odczytywanie (

save, load

):

save temp X Y Z;

% X, Y, Z

→ temp.mat (zbiór binarny Matlaba)

load temp

% inicjalizacja X, Y, Z

xy = [x’ y’];

% złóż wektory w macierz dwu-kolumnową

save temp.dat xy /ascii

% zapisz zmienną xy do zbioru ascii temp.dat

load temp.dat

% wczytaj dane ze zbioru temp.dat

x = temp(:,1);

% x = pierwsza kolumna macierzy temp

y = temp(:,2);

% y = druga kolumna macierzy temp

15)

Przykłady funkcji matematycznych

(użyj

help

funkcja, aby szczegóły):

• sqrt(), log2(), log10(), log()=ln(), exp(), sin(), cos(), tan(), atan(), atan2() -

jeśli na macierzach, to na ich elementach

• mean(), std(), min(), max(), median(), sort(), prod(), cumsum(),

cumprod() -

jeśli na macierzach, to w kolumnach

• expm(A), logm(A), sqrtm(A) -

na całych macierzach

• poly(A), det(A), trace(A), kron(A), eig(A), svd(A)
• diff(), hist(), corrcoef(), cov(), cplxpair()
• abs(), angle(), conv(), deconv(), xcorr(), fft(), ifft(), fftshift(), spectrum(),

psd(), filter()

16)

Przykłady funkcji graficznych

(użyj

help

funkcja, aby szczegóły):

•

2D

: plot(x,y), loglog(x,y), semilog(x,y), polar(x,y), stem(x,y), bar(x,y),

stairs(x,y)

kolory: r, g, b, k, w, i (red, green, blue, black, white, invisible)
linie: - / -- / -. / : (ciągła, przerywana, kreska-kropka, kropkowana)
symbole: +, *, x, o
np. plot(x1, y1, ‘ro’, x2, y2, ‘b--’, x3, y3, ‘k:’

•

3D

: mesh(A), meshc(A), meshz(A), contour(A), surf(A), surfl(A),

waterfall(A), image(A), imagesc(A)

•

ogólne

: title(), xlabel(), ylabel(), text(), axis(),subplot(), hold, grid;

17)

Instrukcje sterujące

(pozostałe to:

pause, break, error, return

):

for-end

for

m = 1 : M

for

n = 1 : N

A(m, n) = 1 / (m+n-1);

end

end

while-end

n=1;

while

( prod(n) < 1*E+100) n=n+1;

end

if-elseif-else-end

if( x==1 )

a=b;

elseif( y<5 )

c=d;

else

e=f;

end

18)

Funkcje

program.m
----------------------------------------------
a1 = 10; a2 = 20; a3 = 30;
[ b1, b2, b3 ] = funkcja( a1, a2, a3);
----------------------------------------------
funkcja.m
----------------------------------------------

function

[x, y, z] = funkcja( a, b, c)

% co robi ta funkcja ?
x = a + b; y = b - c; z = b * c;

DODATKOWE PRZYKŁADY

W JĘZYKU

MATLAB

% PRZYKLAD 1

% Inicjalizacja danych, zapis i odczyt z dysku, rysunek
% Zapisywanie danych na dysk i ich odczytywanie z dysku

x = [ 1 2 3 4 5 ];

% pierwszy wektor

y = [ 0.1 0.2 0.3 0.2 0.1 ];

% drugi wektor

x = x'; y = y';

% odwrócenie obu wektorów do pionu

plot(x, y, '

b

' )

% rysunek y=f(x), niebieska linia

title('y=f(x)')

% tytuł

pause

% czekaj

xy = [ x y ];

% złożenie dwóch kolumn w macierz xy

pause

% czekaj

save wy.dat xy /ascii

% zapis xy na dysk do zbioru wy.dat

load wy.dat

% przeczytaj zbiór z dysku

x1 = wy(:,1);

% podstaw pierwsza kolumnę do x1

y1 = wy(:,2);

% podstaw druga kolumnę do y1

plot( x, y, '

b

', x1, y1, '

r

')

% rysunek y=f(x) i y1=f(x1) - porównanie

title('y=f(x) oraz y1=f(x1)')

% tytuł

pause

% czekaj

% PRZYKLAD 2 - przyklady grafiki dwuwymiarowej

% pojedynczy rysunek - pojedyncza krzywa =================

subplot(111);

% jeden wiersz, jedna kolumna, jeden rysunek

x = 1 : 0.1 : 25 ;

% definicja zmiennej x: od 1 co 0.1 do 20

y = 500 + 400*sin(x);

% oblicz y dla każdego x

plot( x, y, 'k' )

% narysuj wykres y=f(x), linia czarna

title('SINUSOIDA')

% tytuł

xlabel('argument x')

% opis osi x

ylabel('wartość y')

% opis osi y

grid

% siatka

pause

% czekaj na naciśnięcie klawisza

% pojedynczy rysunek z kilkoma krzywymi ==================

plot( x, y, '

r-

', x, 2*y, '

b-

' )

% pierwsza RED, druga BLUE; obie ciągłe

title('DWIE SINUSOIDY')

% tytuł

pause

% 4 rysunki z pojedynczą krzywą
% leżące na szachownicy: dwa wiersze, dwie kolumny (22)
% numer rysunków:

1, 2, 3, 4

(kolejno, wierszami)

subplot(22

1

), plot(x,y,'

b--

')

% RYS - LEWY GÓRNY

title('skala linia, kreska-kreska')

% linia niebieska kreska-kreska

subplot(22

2

), plot(x,y,'

r-.

')

% RYS - PRAWY GÓRNY

title('skala linia, kreska-kropka')

% linia czerwona kreska-kropka

subplot(22

3

), loglog(x,y)

% RYS - LEWY DOLNY

title('skala log x/y')

% skala logarytmiczna x i y

subplot(22

4

), semilogx(x,y)

% RYS - PRAWY DOLNY

title('skala log x ')

% skala logarytmiczna osi x

pause

% czekaj

clf

% wyzeruj ekran graficzny

% PRZYKLAD 3 - prosta grafika trójwymiarowa

subplot(111);

% jeden wiersz, jedna kolumna, jeden rysunek

% definicja X i Y

[ X, Y ] = meshdom( -2 : 0.05 : 2, -2 : 0.05 : 2 );

% def Z = f( X, Y )

Z = sin( 5*(X.^2 +Y.^2) ) .* exp( -0.5*X.^2 -0.5*Y.^2 );

mesh( Z )

% jeden rysunek 3D

title('MAPA 3D')

%

pause

% czekaj

contour( Z )

% jeden rysunek POZIOMICE

title('POZIOMICE 3D')

%

pause

% czekaj

subplot(211); mesh( Z ); title('Rys A'); pause

% kilka RYS na raz

subplot(212); contour( Z ); title('Rys B'); pause

%

subplot(111),
meshc( Z ),

title(

'Funkcja MESHC'

),

pause

meshz( Z ),

title(

'Funkcja MESHZ'

),

pause

surf( Z ),

title(

'Funkcja SURF'

),

pause

surfl( Z ),

title(

'Funkcja SURFL'

),

pause

waterfall( Z ), title(

'Funkcja WATERFALL'

), pause

imagesc( Z ), colormap(

'gray'

), colorbar,

title(

'Funkcja IMAGE (GRAY)'

),

pause

imagesc( Z ), colormap(

'autumn'

), colorbar,

title(

'Funkcja IMAGE (AUTUMN)'

), pause

% Przykład 4 - rozwiązanie równania algebraicznego: A * x = b

A = [ 14 32 23; 32 77 68; 23 68 113 ]

% zdefiniuj macierz A

x = [ 1 2 3 ]

% zdefiniuj wektor x

b = A * x'

% OBLICZ „b” (x: wiersz --> kolumna)

pause

% czekaj

clc

% wyczyść ekran

% ODTWÓRZ „x” - na podstawie A i b

x = inv(A) * b

% za pomocą macierzy odwrotnej

x = A \ b

% oraz poprzez dzielenie macierzowe

pause

% czekaj

% PRZYKLAD 5 - rozkład sygnału na sumę sinusoid

clear all, clf;

% wyzeruj pamięć i ekran graficzny

% Podaj parametry sygnału ==============================
N = 256;

% długość sygnału

fs1 = 250;

% częstotliwość składowej 1 w Hz

fs2 = 500;

% częstotliwość składowej 2 w Hz

fp = 8000;

% częstotliwość próbkowania w Hz

dt = 1/fp;

% odległość między próbkami w sekundach

% Wygeneruj i narysuj analizowane sygnały =================
t = 0 : dt : (N-1)*dt;

% definicja zmiennej czasu t

y1 = 0.4*sin(2*pi*fs1*t + pi/2);

% oblicz składową 1, y1 dla każdego t

y2 = 0.2*sin(2*pi*fs2*t + pi/4);

% oblicz składową 2, y2 dla każdego t

y = y1 + y2;

% suma składowych

plot( t, y ,'

b

')

% narysuj wykres y=f(t)

title('SUMA DWOCH SINUSOID')

% tytuł

xlabel('czas')

% opis osi x

ylabel('sygnał')

% opis osi y

grid

% siatka

pause

% czekaj na „klawisz”

% Rozłóż sygnał na składowe sinusoidalne, transformata Fouriera
Y = fft( y, N );

% widmo sygnału, transformata Fouriera
% SKALOWANIE WYNIKU

Y = 2*abs( Y )/N;

% wartość bezwzględna liczby zespolonej

Y = Y( 1 : N/2 +1 );

% ważna tylko polowa, reszta symetryczna

df = 1/(N*dt);

% co ile herców prążek widma

f = 0 : df : N/2*df;

% częstotliwości prążków widma

% POKAŻ WYNIK

plot( f, Y );

% rysunek widma

title('Rozkład sygnału na sumę sinusoid')

% podpis

xlabel('częstotliwość w [Hz]')

% opis osi x

ylabel('amplituda')

% opis osi y

pause

% czekaj

% Zsyntezuj sygnał ze składowych sinusoidalnych
ys = real( ifft( Y ) ); ys=ys’;

% odwrotna transformacja Fouriera

plot( t, y, '

r

', t, ys, '

b

' );

% porównaj oryginał i kopię

% PRZYKLAD 6 - znajdowanie miejsca zerowego funkcji
%

!!! danej wzorem !!!

% Funkcja FZERO służy do znajdowania miejsca zerowego funkcji
%

% Załóżmy, że interesuje nas funkcja fun_zero(x), zdefiniowana
% w zbiorze fun_zero.m na dysku

x = 0 : .02 : 2;

% zmienność argumentu

y = fun_zero(x);

% zmienność funkcji

plot( x, y, '

b

' )

% rysunek

title( 'Funkcja y=f(x) - zauważ zero w pobliżu x = 1.2' ), grid

% tytuł

pause

% czekaj

% Aby znaleźć zero funkcji w otoczeniu x = 1.2, wołamy FZERO

xokolica = 1.2;

% x, w pobliżu którego szukamy zera

xtoler = eps;

% wymagana tolerancja rozwiązania

z = fzero( 'fun_zero', xokolica, xtoler);

% wyznaczmy argument zera

x = 0.8 : .01 : 1.6;

% x w otoczeniu zera

y = fun_zero(x);

% y w otoczeniu zera

plot( x, y, z, fun_zero(z), '

ro

')

% rysujemy funkcje i obliczone zero

title( 'Zero funkcji funczero(x)' )

% tytuł

grid, pause

% siatka, czekanie

z

% wypisz argument zera

fun_zero(z)

% wypisz wartość zera

% ######################################################
function y = fun_zero( x )

% funkcja, w której miejsc zerowych poszukujemy

y = 1 ./ ((x-.3).^2 + .01) + 1 ./ ((x-.9).^2 + .04) - 6;

% PRZYKLAD 7
% wyznaczanie parametrów znanej funkcji
% jak najlepsze dopasowanie do danych doświadczalnych

global dane

% zmienna globalna - widziana z innych *.m zbiorów

dane = ...

% pary punktów (x,y) otrzymanych doświadczalnie

[ -5 25.5

% np. podczas laboratorium z fizyki

-4 15.2

% pierwsza kolumna to argument x

-3 8.5

% zaś druga, to wartość y

-2 4.3

% jest to zaszumiona funkcja postaci y = a*x^2 + b

-1 0.8
0 0.0
1 0.9
2 4.1
3 8.7
4 15.7
5 24.9 ];

x = dane(:,1);

% „pobranie” wektora argumentów x

y = dane(:,2);

% „pobranie” wektora wartości funkcji y

plot(x,y,'

ro

')

% wykres y w funkcji x, czerwone "o"

% Załóżmy, że zjawisko opisuje zależność: y = f(x;a,b) = a*x^2 + b
% DWIE PARY PUNKTÓW (x1,y1) (x2,y2) wystarczą, aby obliczyć a,b
% Ale ponieważ dane eksperymentalne są ZASZUMIONE,
% przeprowadza się więcej pomiarów.
% Następnie stara się znaleźć takie wartości a i b, aby błąd:
%

błąd = SQRT ( S U M A [ y - f(x; a,b) ]^2 / M )

%

m=1...M

% był jak najmniejszy, tzn. aby funkcja była "jak najlepiej" dopasowana

params = [1 0]';

% startowe wartości a i b

toler = 0.05;

% wymagany błąd

blad = fmins('fun_fi', params, toler);

% procedura minimalizacyjna

a = blad( 1 )

% wynikowe a

b = blad( 2 )

% wynikowe b

fy = a * x.^2 + b;

% oblicz wartości funkcji f(x)
% dla obliczonych a i b

blad = std( fy-y )

% oblicz końcowy błąd

function blad = fun_fi( params )

global dane

% Funkcja wykorzystywana przez przykład cw_7.m
% Ma ona nastepujaca postac : y = a*x^2 + b
% Wejście : parametry a i b
% Wyjście : błąd dopasowania funkcji do danych eksperymentalnych

a = params(1); b = params(2);

% szukane parametry

x = dane(:,1); y = dane(:,2);

% dane z programu głównego

fy = a * x.^2 + b;

% oblicz wartości funkcji f(x)
% dla aktualnych parametrów a i b

blad = std( fy-y );

% błąd dopasowania

% Pokaż postęp w dopasowaniu parametrów funkcji do danych

plot( x, fy, 'w', x, y, 'wo'), grid
xt = 0;
yt = 3/4*max(y);
text( xt, 1.2*yt, ['a = ' num2str( a ) ] )
text( xt, 1.1*yt, ['b = ' num2str( b ) ] )
text( xt, 1.0*yt, ['blad = ' num2str( blad ) ] )
pause

% PRZYKLAD 8 - dopasowanie funkcji do danych
%

jak w przykładzie 7 tylko trudniej

global dane

% zmienna globalna - widziana z innych *.m zbiorów

dane = ...

% pary punktów (x,y), otrzymane z dośw.

[ 0.0000 5.8955

% np. podczas laboratorium z fizyki

0.1000 3.5639

% pierwsza kolumna argument x, np. czas

0.2000 2.5173

% druga kolumna wartość y, np. napięcie

...
1.0000 0.6856
...
2.0000 0.2636 ];

x = dane(:,1);

% „pobranie” wektora argumentów x

y = dane(:,2);

% „pobranie” wektora wartości funkcji y

plot( x, y, '

ro

' )

% wykres y w funkcji x, czerwone "o"

pause

% pauza

% Z teorii wynika, ze dane zjawisko opisuje teoretyczna zależność:
% y = f( x ) = c(1) * exp(-lambda(1)*x) + c(2) * exp(-lambda(2)*x)
% Powyższa funkcja ma dwa parametry liniowe: c(1) i c(2)
% oraz dwa parametry nieliniowe: lambda(1) i lambda(2)
%
% Chcemy wyznaczyć takie wartości tych parametrów, aby funkcja
% y=f(x) była najlepiej dopasowana do danych pomiarowych (x,y)

lambda = [1 0]';

% startowe wartości lambda(1) i (2)

toler = 0.1;

% wymagany tolerancja błędu

blad = fmins('fun_fit', lambda, toler);

% procedura minimalizacyjna

lambda = blad

% wynikowe lambda(1) i (2)

A = zeros( length(x), length(lambda) );

% obliczenia jak w fun_fit.m

for j = 1 : size(lambda)

% dla każdego x i lambda

A(:,j) = exp( -lambda(j) * x );

%

end

%

c = A \ y

%

fy = A * c;

%

blad = std(fy-y)

%

function blad = fun_fit(lambda)

global dane

% Funkcja wykorzystywana przez cw_8.m
% Ma ona następującą postać :
%
% y = c(1)*exp(-lambda(1)*x) + ... + c(n)*exp(-lambda(n)*x)
%
% oraz posiada n parametrów liniowych c(i) i nieliniowych lambda(i)
%
% Wejście : zestaw parametrów lambda
% Wyjście : błąd aproksymacji danych eksperymentalnych przez
%

aktualny zestaw parametrów lambda

%
% Parametry c(i) są wyznaczane na podstawie lambda i danych dośw.

x = dane(:,1); y = dane(:,2);

% podstaw dane
% w programie głównym

A = zeros( length(x), length(lambda) );

% utwórz macierz A, wyzeruj ją
% wierszy tyle ile danych,
% kolumn tyle ile lambda

for j = 1:size(lambda)

% dla każdego x i lambda

A(:,j) = exp( -lambda(j) *x );

% oblicz wartości macierzy A,

end

% takiej że y = A * c

c = A \ y;

% oblicz wektor optymalnych parametrów c
% minimalizujących błąd średniokwadratowy

fy = A * c;

% oblicz wartości funkcji fy dla tego c

blad = std(fy-y);

% oblicz błąd dopasowania
% jak wartości funkcji różnią się od danych dośw.

% Pokaż postęp w dopasowaniu parametrów funkcji do danych

plot( x, fy, 'w', x, y, 'wo' ), grid
xt = max(x)/2; yt = max(y)/2;
text(xt,1.0*yt,['blad = ' num2str( blad )])
pause

% PRZYKLAD 10 - rozw. numeryczne równania różniczkowego

% Funkcje ODE23, ODE45 służą do numerycznego rozwiązywania zwyczajnych
% równań różniczkowych. Metoda rozwiązania Rungego-Kutty-Fehlberga,
% w której krok całkowania numerycznego jest zmieniany automatycznie
% ODE23 wykorzystuje zależności 2 i 3 rzędu - średnia dokładność,
% ODE45 wykorzystuje zależności 4 i 5 rzędu - duża dokładność.

% Załóżmy, że interesuje nas rozwiązanie równania różniczkowego
% van der Pola drugiego rzędu postaci :
%

y'' + (y^2 - 1)*y' + y = 0

% gdzie ' oznacza operator różniczkowania.
% Po przedstawieniu w postaci:
%

y'' = -(y^2 - 1)*y' - y

% równanie to można zastąpić układem dwóch równań rzędu pierwszego
%

y1' = -(y2^2 - 1)*y1 - y2

%

y2' = y1

% gdzie y1 i y2 nazywane są tzw. zmiennymi stanu
%
% Aby zasymulować układ dynamiczny opisany równaniem różniczkowym,
% tworzy się *.m funkcję, która:
% otrzymuje wartości czasu i zmiennych stanu,
% zaś zwraca pochodne wartości zmiennych stanu.
%
% Załóżmy, że nasza funkcja nazywa się fun_diff.m
%
% Aby zasymulować równanie różniczkowe Van Der Pola w przedziale
% czasu 0 < t < 20, wywołujemy funkcję MATLABA ODE23:

t0 = 0;

% czas początkowy obserwacji

tfinal = 20;

% czas końcowy obserwacji

y0 = [ 0 0.25 ]';

% wartości początkowe zmiennych

stanu

tol = 1.e-3;

% dokładność rozwiązania

trace = 1;

% śledzenie

[t,y] = ode23( 'fun_diff', t0, tfinal, y0, tol, trace );
% [t,y] = ode45( 'fun_diff', t0, tfinal, y0, tol, trace );
plot(t,y), title('historia czasowa równania van der Pola'), grid, pause

% funkcja pomocnicza #####################################

function yprime = fun_diff(t,y);

% zwraca pochodne zmiennych stanu y1 i y2 równania Van der Pola

yprime = [ ( (y(2).^2 - 1).*y(1) - y(2) ); y(1) ];