Elementy optyki
relatywistycznej

O czym będzie wykład?

• Pojęcie „relatywistyczny” kojarzy się z bardzo dużymi

prędkościami, bliskimi prędkości światła. Tylko, ze
światło porusza się zawsze z prędkością światła. Więc o
czym tu jeszcze mówić?

• Fala świetlna oddziałując na materię, tek naprawdę

oddziałuje na znajdujące się w niej elektrony, które
pochłaniają energię fali i wprawiane są przez nią w ruch.
Na skutek tego ruchu, te elektrony zaczynają one
emitować falę elektromagnetyczną. Na zjawiska
optyczne takie jak odbicie, czy załamanie można patrzeć
tak, jakby były one skutkiem opisanego tu mechanizmu.

• Przy bardzo dużych energiach fal, prędkość elektronów

może osiągać bardzo duże prędkości, porównywalne z
prędkością światła. Pojawiają się wówczas efekty,
których „normalnie” nie obserwujemy. Tą grupą zjawisk
zajmuje się

optyka nieliniowa

.

• Drugą grupą zjawisk, o której będziemy mówić na

wykładzie są zjawiska relatywistyczne, związane z dużą
prędkością

rozchodzenia

się

promieniowania

elektromagnetycznego lub dużą prędkością źródeł
takiego promieniowania. Przykładem tego typu zjawisk
jest omawiany już wcześniej efekt Dopplera.

Optyka nieliniowa

Dwójłomność samoistna

• Dla większości ciał, prędkośc rozchodzenia się światła i

związany z nią współczynnik załamania nie zależą od
kierunku rozchodzenia się światła. Są to substancje
optycznie izotropowe (bezkierunkowe).

• Istnieją jednak pewne substancje (przeważnie kryształy),

które są optycznie

anizotropowe

(np.. mika, kalcyt,

turmalin).

• W krysztale kalcytu (szpatu islandzkiego) nasrępuje

zjawisko podwójnego załamania, co oznacza, że
pojedyncza wiązka rozszczepia się na dwie wiązki, z
których jedna spełnia prawo załamania (jest to tzw.
promień zwyczajny), a druga go nie spełnia (jest to tzw.
promień nadzwyczajny).

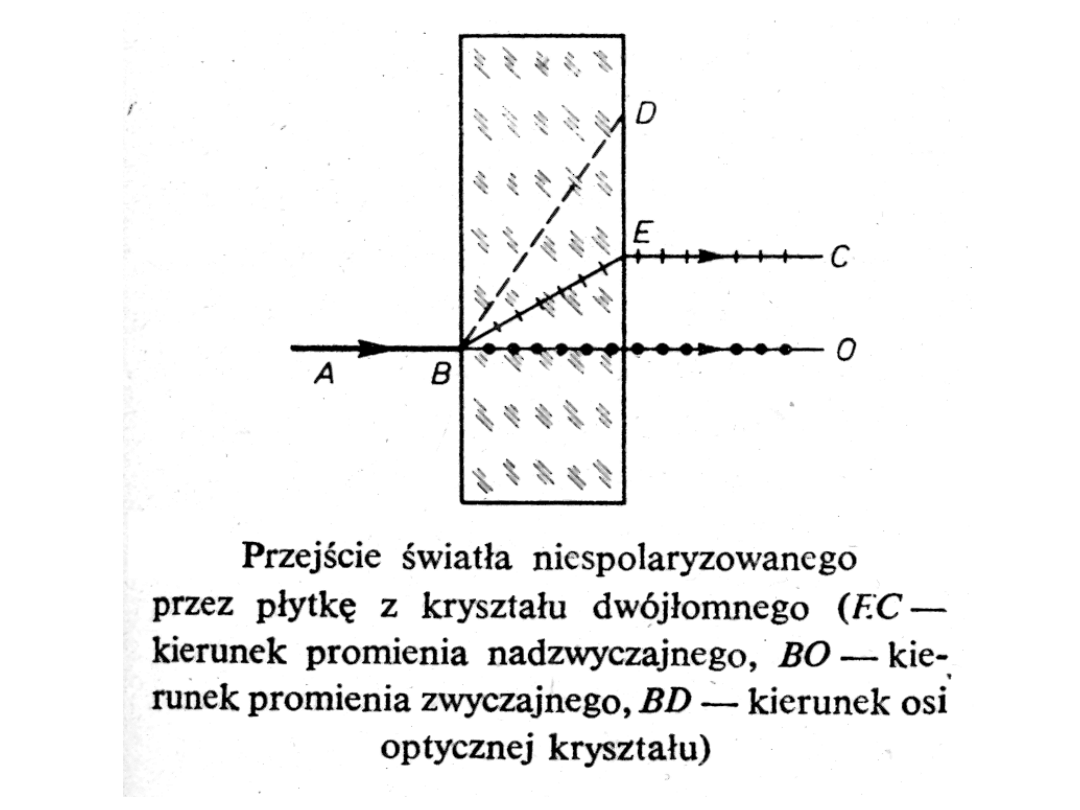
• Zjawisko to wiąże się z istnieniem w krysztale

charakterystycznych

kierunków

zwanych

osiami

optycznymi, związanych z budową kryształu.

• Promień zwyczajny i nadzwyczajny są spolaryzowane

liniowo i ich płaszczyny polaryzacji są do siebie
prostopadła.

• Niektóre kryształy, np.. Turmalin charakteryzują się tym,

że są przezroczyste dla jednego z promieni
spolaryzowanych, a drugi z nich pochłaniają.

Budowa dielektryków

• W dielektrykach brak jest ładunków swobodnych,

mogących swobodnie przemieszczać się. Jednakże
budowa cząsteczek, z których są one zbudowane często
przypomina strukturę dipola elektrycznego.

• Dipolem elektrycznym nazywamy układ dwóch równych

ładunków +q i -q różnoimiennych odległych od siebie o
odcinek l.

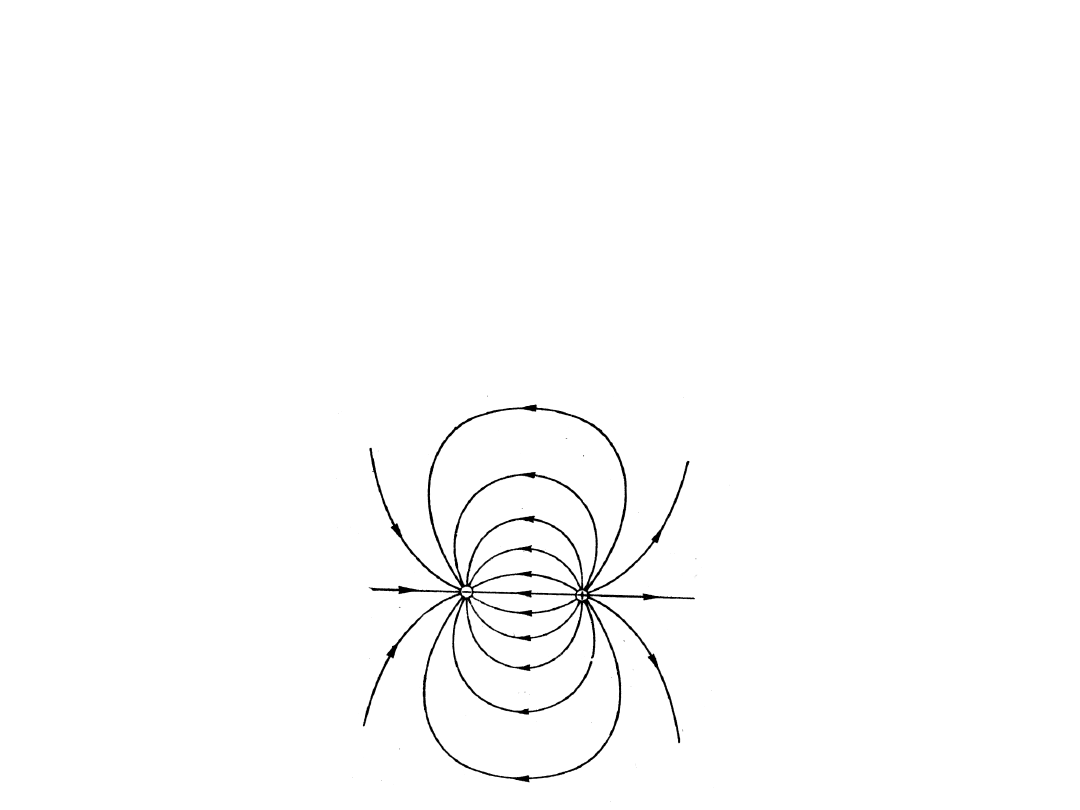
• W dużej odległości r od dipola, w pobliżu jego osi,

natężenie jego pola elektrycznego wytwarzanego przez
dipol wynosi

gdzie

oznacza wektor momentu dipolowego (

jest wektorem o początku w punkciezajmowanym przez
ładunek –q i końcu w miejscu zajmowanym przez
ładunek +q), zaś

θ

jest kątem między wektorem r

(łączącym środek odcinka między ładunkami z punktem
obserwacji) i wektorem l.

• Stan dielektryka opisuje wektor polaryzacji

3

0

2

cos

r

p

E

e

π ε

θ

=

l

l

q

p

e

=

V

p

P

e

∑

=

• W obecności zewnętrznego pola elektrostatycznego

wektor P jest różny od zera i jest on zwykle
proporcjonalny do natężenia pola.

• Pole elektrostatyczne wewnątrz dielektryka jest sumą

pól: zewnętrznego i pola wytworzonego przez dipole
znajdujące się wewnątrz dielektryka:

Stąd mamy:

0

0

ε

P

E

E

−

=

(

)

D

E

E

P

E

E

r

=

=

+

=

+

=

ε

ε

χ

ε

ε

ε

0

0

0

0

0

1

E

P

χ

ε

0

=

• Prędkość światła w ośrodku (i związany z nim

współczynnik załamania) jest zależny od stałej
dielektrycznej ośrodka

Dwójłomność wymuszona

• Pod wpływem czynników zewnętrznych (zewnętrzne

pola magnetyczne lub magnetyczne, siły ściskające)

ciałą optycznie izotropowe stają się anizotropowe.

Przykładami tego typu zjawisk są zjawisko Faradaya i

zjawisko Kerra.

• Zjawisko Faradaya

polega na skręceniu płaszczyzny

polaryzacji światła spolaryzowanego liniowo przy

przejściu światła przez substancję znajdującą się w

polu

magnetycznym

przyłoźonym

w

kierunku

rozchodzenia się fali świetlnej.

• Zjawisko

Kerrra

(elektrooptyczne)

polega

na

podwójnym

załamaniu

światła

w

pierwotnie

izotropowych cieczach lub gazach pod wpływem pola

elektrycznego.

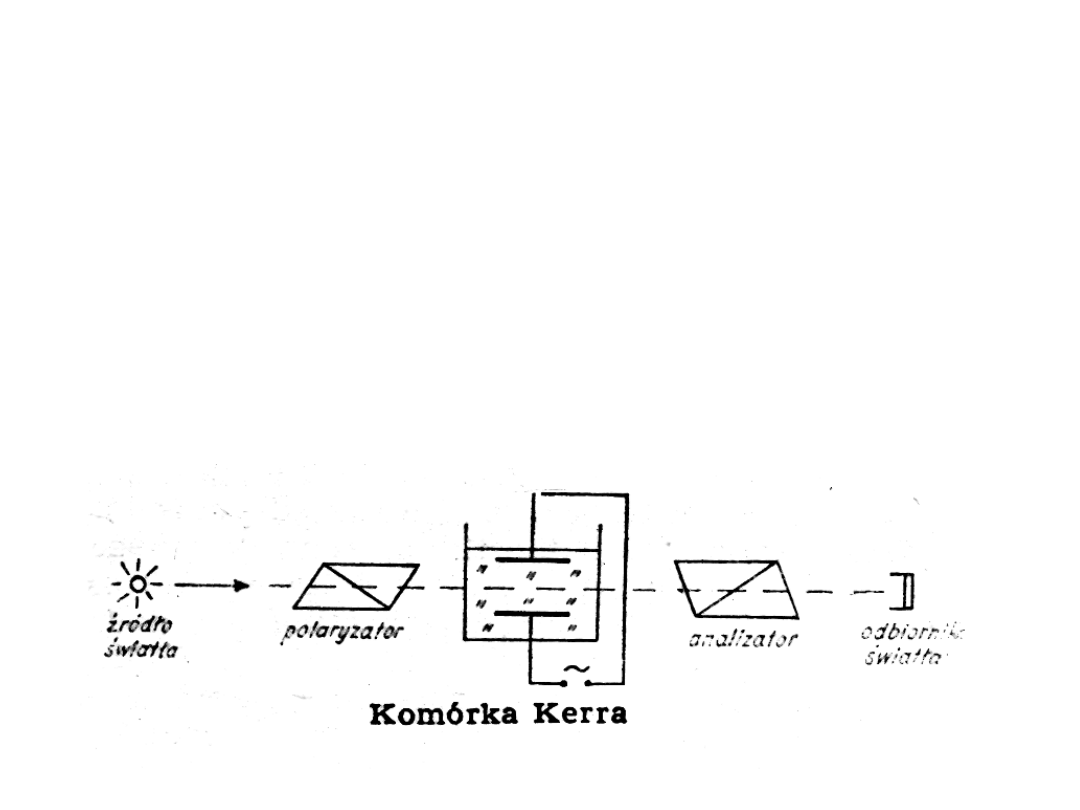
Elektrooptyczne zjawisko Kerra

• W obecności pola elektrostatycznego, dipolowe

cząsteczki dielektryka ustawiają się zgodnie z

kierunkiem pola, czemu towarzyszy pojawienie się

makroskopowej anizotropii: elektrycznej i optycznej.

• Gdy przepuszcza się światło spolaryzowane przez

przezroczystą ciecz znajdującą się między okładkami

naładowanego

kondensatora,

wówczas

względna

różnica dróg optycznych składowych światła -

równoległej

i

prostopadłej

do

kierunku

pola

elektrycznego – po przebyciu drogi l wynosi

gdzie n

r

n

p

– współczynniki załamania dla składowej

równoległej i prostopadłej,

λ

0

– długość fali świetlnej w

próżni, E – natężenie pola elektrycznego, B – stała Kerra

(zależna od

λ

0

i temperatury cieczy)

2

0

0

BlE

n

n

l

p

r

=

−

=

∆

λ

λ

• Zjawisko Kerra zachodzi praktycznie natychmiast –

opóźnienie zmiany

(czas relaksacji) jest rzędu

10

-12

s.

• Zastosowanie: komórka Kerra, stosowana np.. do

modulacji światła z częstotliwością do 1 GHz (w
modulatorach światła), ultraszybkiej fotografia (można
uzyskać impulsy świetlne o czasach trwania od kilku
nanosekund) itp..

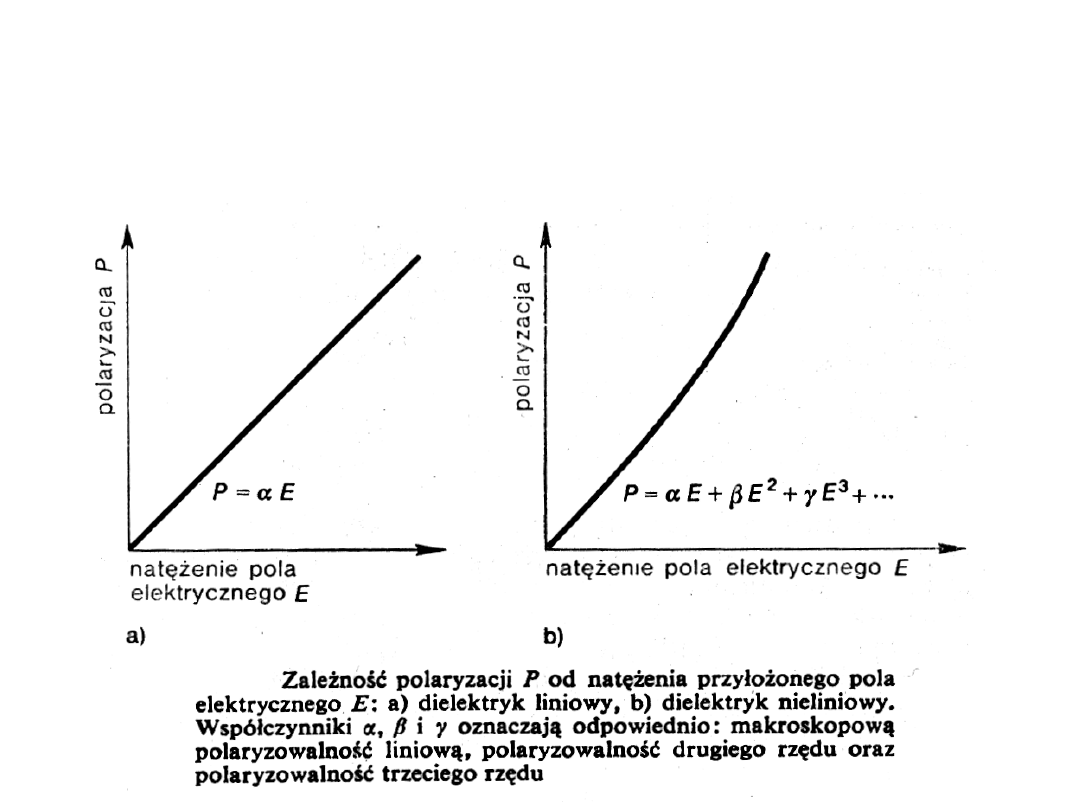
Podstawa optyki nieliniowej

• Polaryzacja dielektryka dla silnych pól elektrycznych nie

jest funkcją liniową

Podwajanie częstotliwości światła

(wytwarzanie drugiej harmonicznej)

• Wartość stałej

β

dla ośrodka anizotropowego jest różna

od zera.

• Jeżeli pole elektryczne fali świetlnej padające na taki

ośrodek zmienia się periodycznie wraz z częstotliwością

ω

, copopisuje funkcja sin(

ω

t), to periodycznie zmienia się

również składowa polaryzacji nieliniowej ośrodka
zależna od kwadratu natężenia pola elektrycznego
padającej fali.

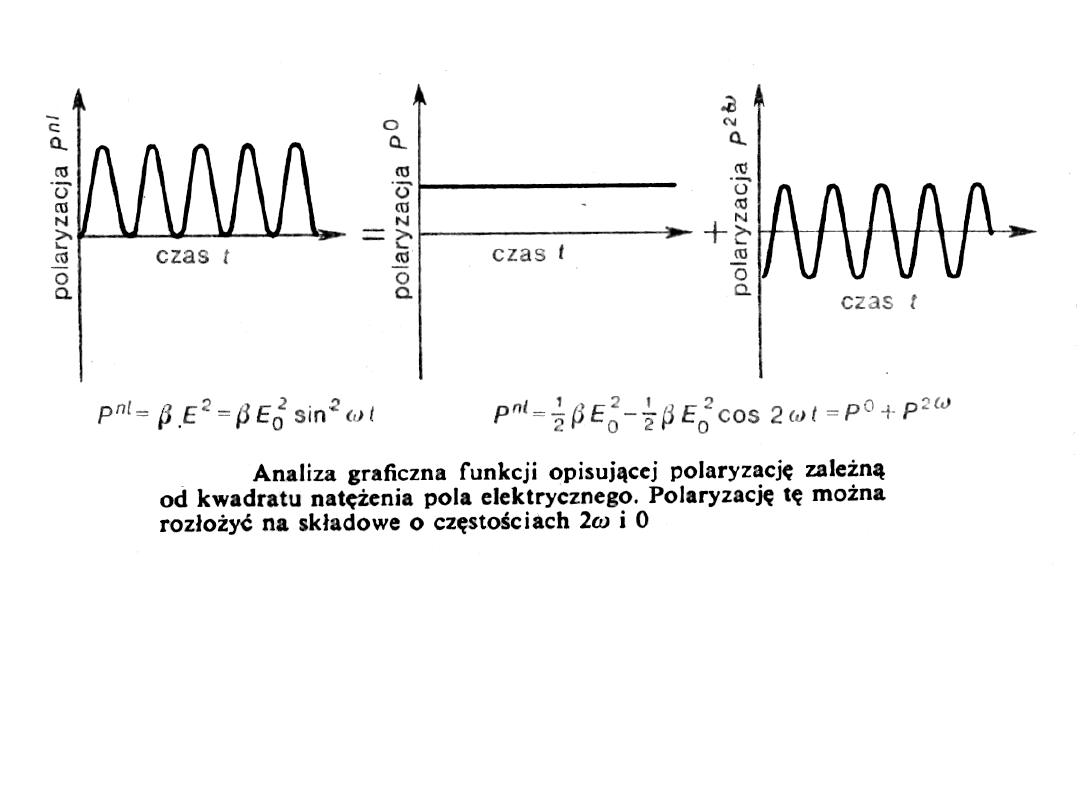
• Takie zmiany polaryzacji ośrodka to nic innego, jak

zmiany momentu dipolowego, a co za tym idzie –

promieniowanie fali elektromagnetycznej

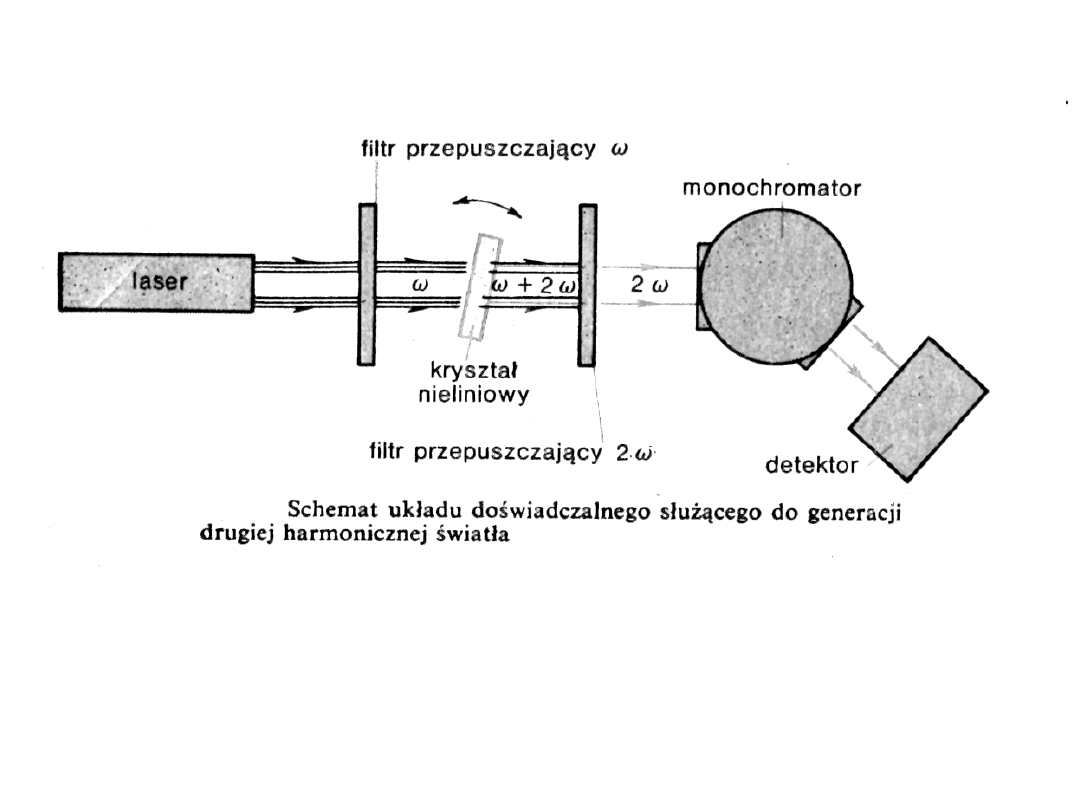
• Podobnie można dokonać potrojenia częstotliwości (do

tego nawet nie trzeba ośrodków anizotropowych).

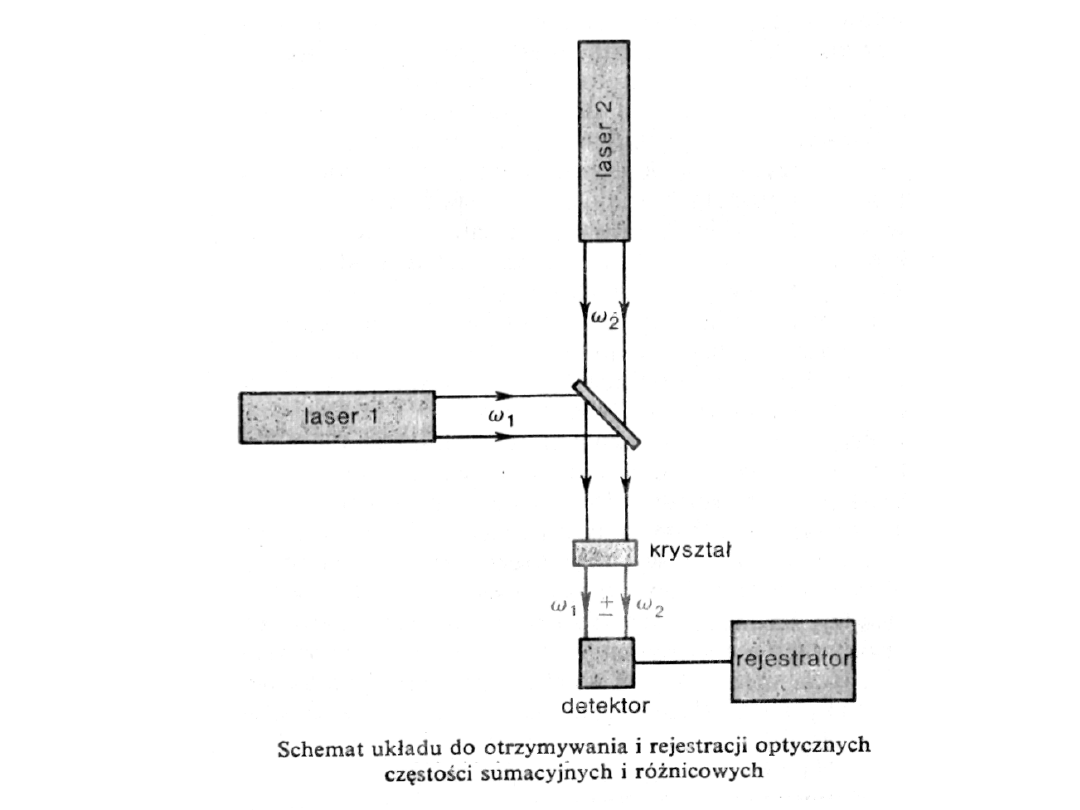
Mieszanie częstotliwości

• Mieszanie częstotliwości jest procesem, polegającym na

uzyskiwaniu fal o częstotliwościach będących sumą i
różnicą częstotliwości mieszanych fal. Jest on możliwy
dzięki nieliniowej charakterystyce polaryzacji ośrodka.

• Podobne

zjawisko

odbywa

się

w

każdym

superheterodynowym

odbiorniku

(radiowym

czy

telewizyjnym), gdzie w tym celu wykorzystuje się układy
elektroniczne

zwane

mieszaczami

iloczynowymi.

Mieszanie zawsze odbywa się na nieliniowej części
charakterystyki takiego układu.

Samoogniskowanie i autokolimacja

• Natężenie światła wiązki laserowej w płaszczyźnie

prostopadłej do kierunku wiązki nie jest stałe – maleje
ono wraz z odległością od środka wiązki.

• Współczynnik

załamania

światła

w

oślodkach

nieliniowych jest funkcją natężenia pola elektrycznego:

i maleje wraz z odległością od środka wiązki

• Promienie świetlne poruszają się więc tym wolniej, im

bliżej leżą środka wiązki.

• Ośrodek działa podobnie do soczewki skupiającej,

kierując światło do środka wiązki.

( )

( )

...

2

2

0

+

+

=

E

n

n

E

n

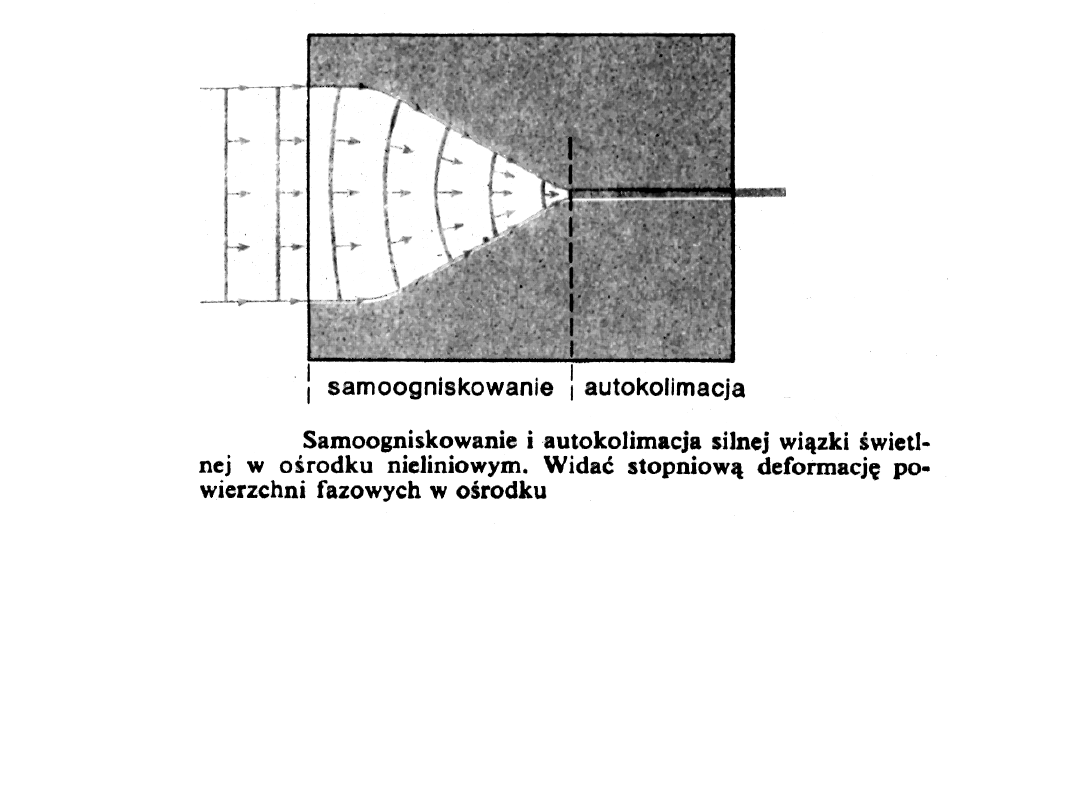
• Analogia między ogniskowaniem przez soczewkę i

samoogniskowaniem kończy się po skupieniu wiązki –
światło rozchodzi się dalej w postaci cienkiej,
skolimowanej nici. Takie zjawisko nazywa się
autoklimacją.

• Nawet skolimowana wiązka laserowa na skutek dyfrakcji

będzie lekko rozbieżna.

• Jeżeli wiązka rozchodzi się w ośrodku nieliniowym, to

współczynnik załamania w obszarze wiązki jest większy
niż na zewnątrz, więc porusza się ona w wytworzonym
przez siebie światłowodzie (falowodzie).

• Jeżeli kąt rozbieżności wiązki wynikający ze zjawiska

dyspersji

jest

większy

od

kąta

granicznego

pozwalającego na całkowite wewnętrzne odbicie od
„granicy” wiązki, to będzie ona rozbieżna. Jeżeli kąty te
będą równe, to szerokość wiązki będzie stała. Jeżeli kąt
rozbieżności będzie mniejszy od kąta granicznego, to
nastąpi zjawisko samoogniskowania i autokolimacji

Nieco inne spojrzenie na

samoogniskowanie i autokolimację

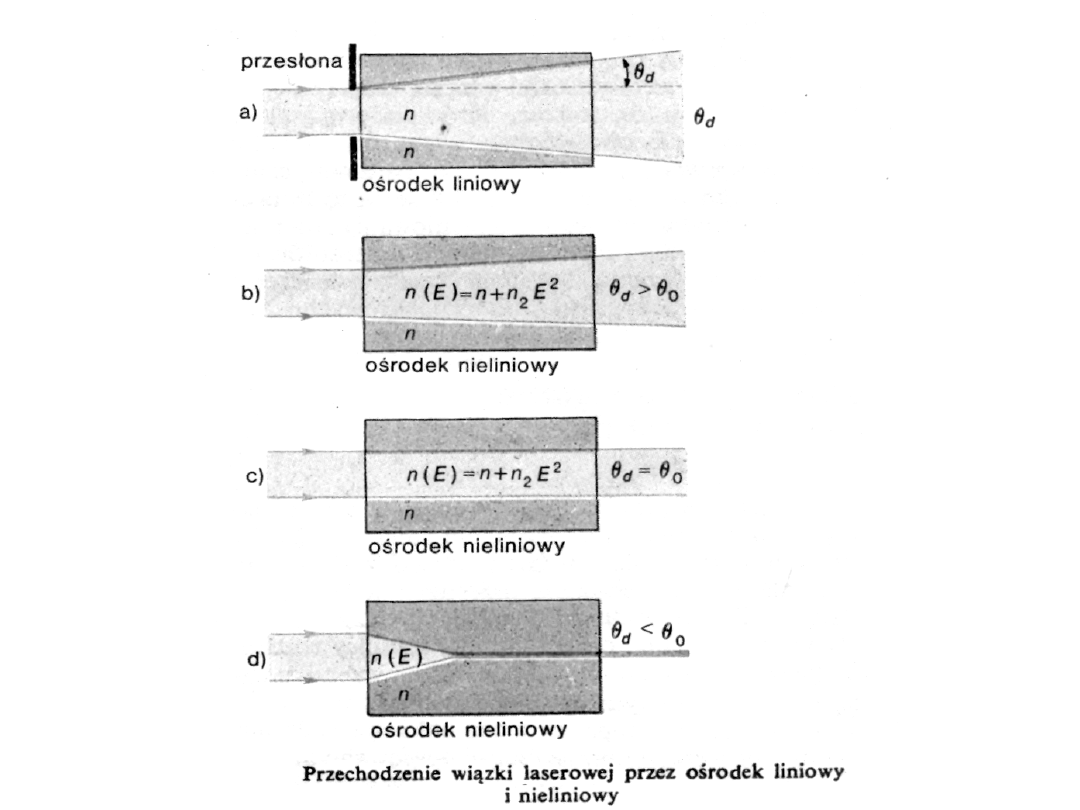
Zjawiska optyczne związane z dużymi

prędkościami

Ciśnienie promieniowania

elektromagnetycznego

• Fala elektromagnetyczna nie ma masy. Jednakże,

zgodnie z wynikami szczególnej teorii względności
przenosi pęd.

• Niech na powierzchnię

∆

S pada w czasie

∆

t

promieniowanie elektromagnetyczne o energii

∆

E.

Strumień energii padającej na tą powierzchnię
definiujemy jako

t

S

E

E

∆

∆

∆

=

σ

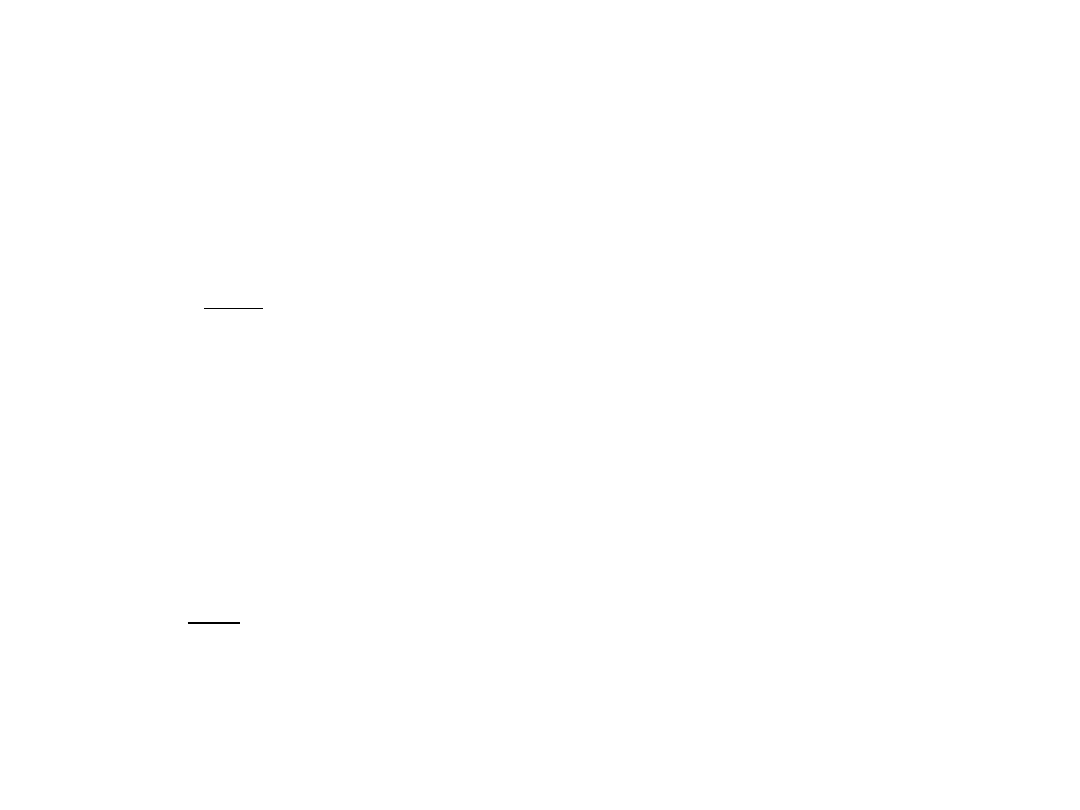
• Załóżmy, że powierzchnia pochłania padające na nią

promieniowanie.

W

czasie

∆

t

promieniowanie

elektromagnetyczne przekazuje powierzchni

∆

S pęd

równy.

• Siła działająca ze strony promieniowania na

rozpatrywaną powierzchnię wynosi więc

c

E

p

∆

=

∆

t

p

F

∆

∆

=

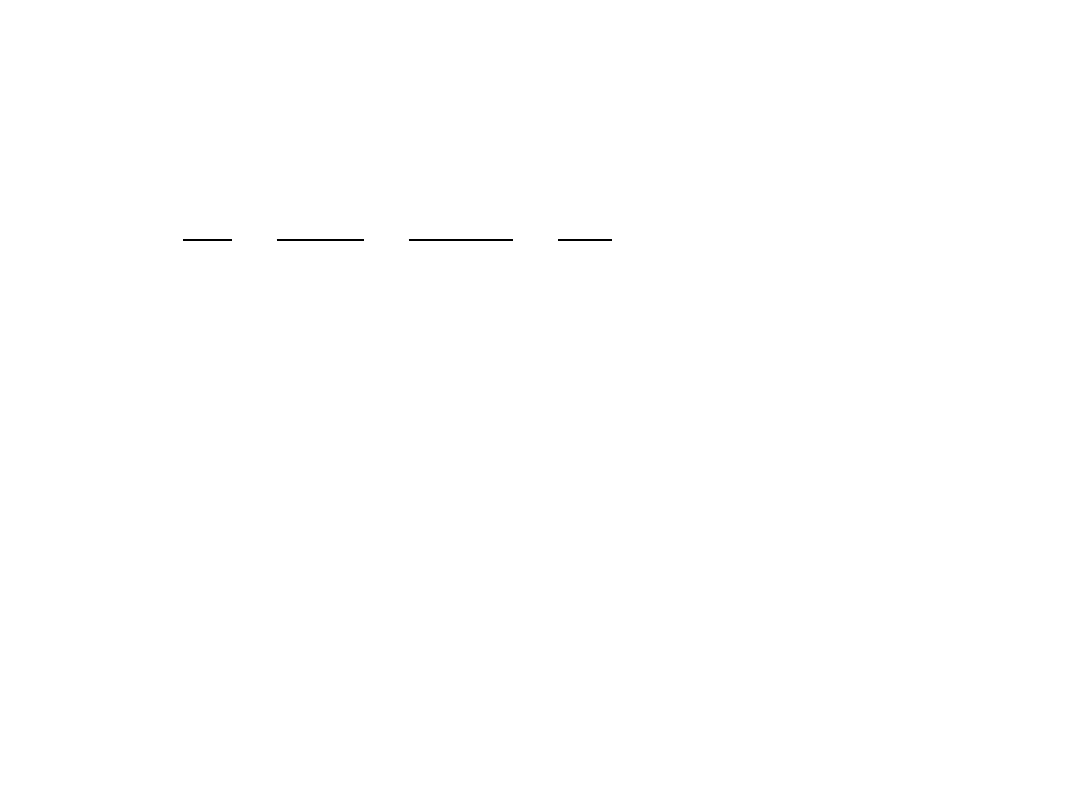
• Ciśnienie wywierane na rozpatrywaną powierzchnię

przez falę elektromagnetyczną wynosi więc

c

t

s

c

E

t

s

p

s

F

p

E

σ

=

∆

∆

∆

=

∆

∆

∆

=

∆

=

Promieniowanie Czerenkowa

• Rozpatrzmy cząstkę naładowaną (np.. elektron), który

wleciał do ośrodka o współczynniku załamania n z
prędkością v większą od c/n.

• Elektron ten nie może poruszać się w tym ośrodku z tak

dużą prędkością (bo jego prędkość jest większa od
prędkości światła). Elektron ten zostanie wyhamowany
(spowolniony) do prędkości v=c/n. Na skutek
hamowania, wyemituje on falę elektromagnetyczną.

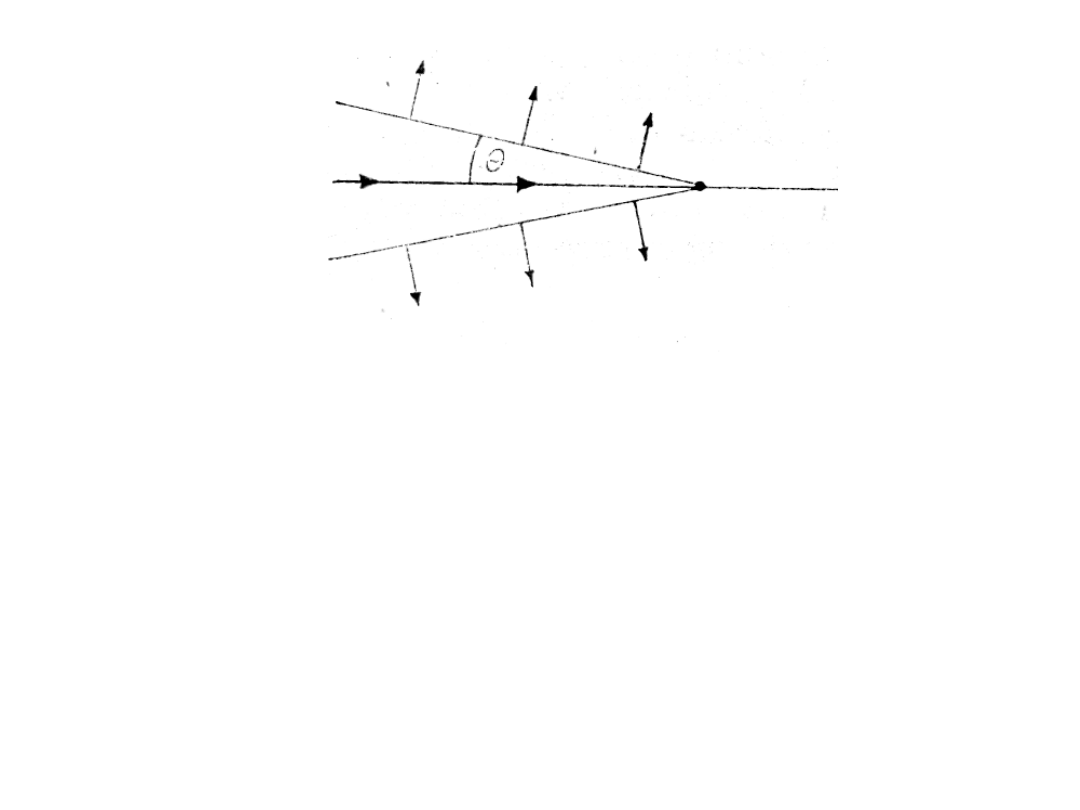
• Powierzchnia falowa promieniowania emitowanego

przez cząstkę stanowi powierzchnię stożka, którego oś
pokrywa się z torem cząstki, a kąt połówkowej
rozwartości spełnia warunek

nv

c

=

θ

cos

• Zauważmy, że cząstka naładowana poruszająca się

ruchem jednostajnym nie wysyła promieniowania
elektromagnetycznego. Wynika to z tego, że wszystkie
układy inercjalne są równouprawnione, więc opisując
zachodzące z nią zjawiska w układzie związanym z tą
cząstką, mówimy że jest ona w spoczynku, a więc nie
wytwarza zmiennego pola elektrycznego, a co za tym
idzie nie promieniuje.

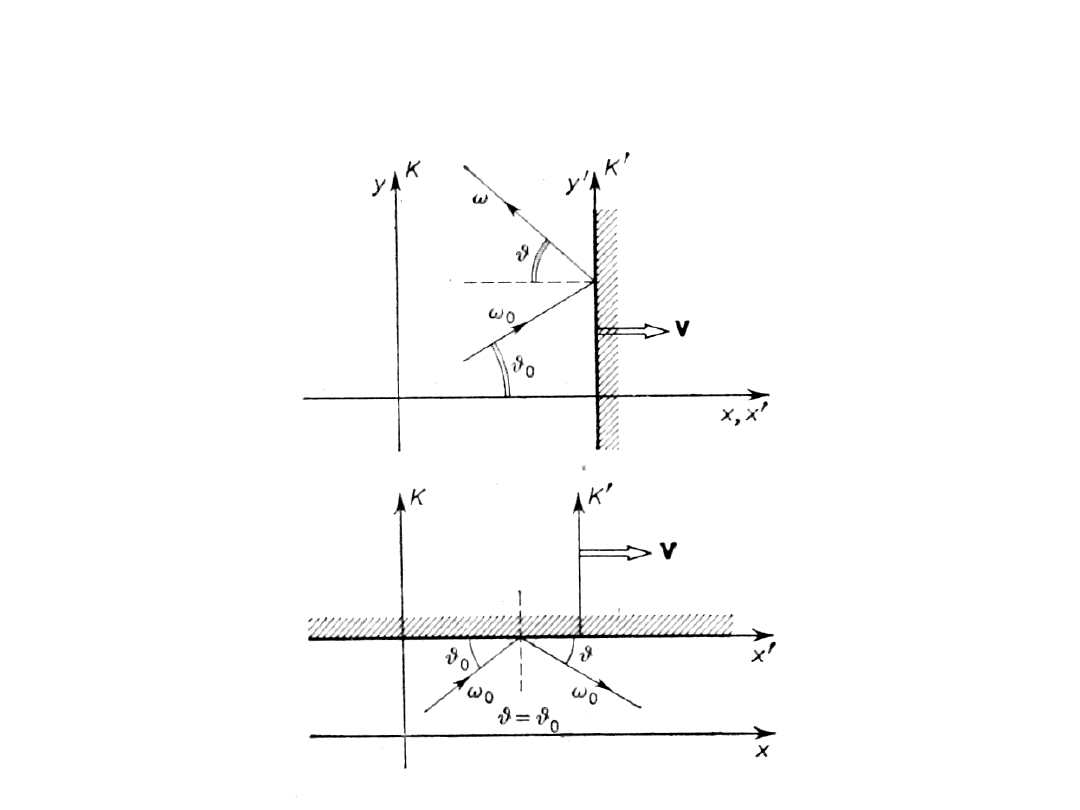
Odbicie od poruszającej się powierzchni

(zwierciadła)

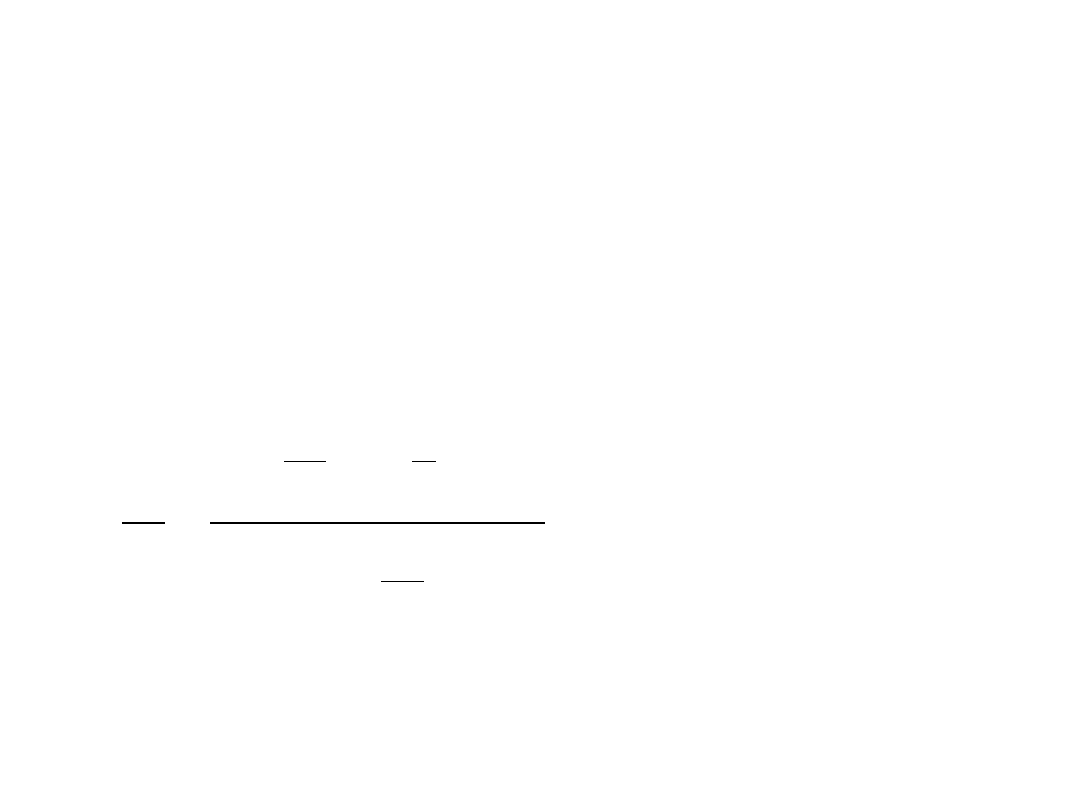
• Jeżeli powierzchnia zwierciadła jest równoległa do

kierunku ruchu, to mamy klasyczne odbicie.

• Jeżeli powierzchnia zwierciadła jest prostopadła do

kierunku ruchu, to mamy ciekawe efekty.

• Zmienia się częstotliwość fali odbitej (w sumie

należałoby tego oczekiwać – efekt podobny do efektu
Dopplera):

2

2

0

2

2

0

1

cos

2

1

c

v

c

v

c

v

f

f

−

−









+

=

ϑ

• Kąt odbicia nie jest równy kątowi padania:

c

v

c

v

c

v

2

cos

1

1

sin

tan

0

2

2

2

2

0

−









+









−

−

=

ϑ

ϑ

ϑ