Fizyka komputerowa I
Dr Mirosław Łątka
Lista 2
Uruchom programy dyskutowane na wykładzie (szereg Taylora funkcji trygonometrycznej, metoda Newtona-Raphsona).
Napisz program obliczający wartość funkcji wykładniczej
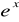
z żądaną dokładnością. Porównaj z wartościami generowanymi przez funkcję wewnętrzną Fortranu 90.
PROJEKT 1 Zbiory Julii
Rozważmy następującą iterację: ![]()
, gdzie ![]()
i ![]()
to liczby zespolone. Wybierzmy początkową liczbę ![]()
i dla ustalonego ![]()
wygenerujmy ciąg liczb zespolonych. Okazuje się, że ciąg ten musi mieć jedną z następujących własności:
ciąg ten jest nieograniczony: elementy ciagu opuszczą każdy okrąg ze środkiem w centrum układu współrzędnych,
ciąg jest ograniczony: istnieje okrąg o środku w centrum układu współrzędnych, którego elementy nigdy nie opuszczą.
Zbiór punktów, z których startując otrzymamy pierwszy rodzaj zachowania, nazywamy zbiorem uciekinierów dla danego c, a zbiór punktów, które prowadzą do drugiego zachowania, nazywamy zbiorem więźniów dla parametru c. Oba zbiory pokrywają pewną część płaszczyzny zespolonej i dodatkowo dopełniają się. Dlatego też granica zbioru więźniów jest jednocześnie granicą zbioru uciekinierów, i ją właśnie nazywamy zbiorem Julii.
Wygeneruj zbiór Julii dla c=(-0.6,0.5). Jako ![]()
wybierz punkty z prostokąta ![]()
, ![]()
. Dla każdej wartości ![]()
powtarzaj iterację do momentu gdy ciąg ucieknie z koła o promieniu R lub gdy zostanie przekroczona maksymalna ilość iteracji N. Do zbioru wynikowego wpisz liczbę iteracji, po których ciąg opuścił okrąg. Przyjmij R=100, N=100. Użyj programu Mathematica do sporządzenia wykresu:
data=ReadList["C:\\Mirek\\FORTRAN\\Julia\\julia.dat",Table[Number,{100}]];
ListDensityPlot[data,Mesh->False]
ListDensityPlot[data,Mesh->False,ColorFunction->Hue]
Wyszukiwarka
Podobne podstrony:
LABORATORIUM, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
POCHODNA FUNKCJI, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
moja pracaq, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
Elektronika 10, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza, Zadania z Fizyki
ZJAWISKO FOTOELEKTRYCZNE, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
poprawka z miernictwa, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
Elektronika 08, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza, Zadania z Fizyki
Stech reakcji i zwiazków-z, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
Elektronika 03, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Zadania z Fizyki
fiele25, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Lab
Pomia napięcia powierzchniowego, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, spr
fiele15, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Lab
lista4elektronika(1), Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka
Sprawozdanie 81, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizy
Sprawozdanie nr12, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fi
Sprawozdanie nr43 fizyka, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdan
Sprawozdanie 12, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizy
Sprawozdanie 57c, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fiz
więcej podobnych podstron