Badanie i pomiary elektroniczny Nieznany

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

MINISTERSTWO EDUKACJI

NARODOWEJ

Agnieszka Ambrożejczyk-Langer

Badanie i pomiary elektronicznych układów cyfrowych
725[01].O1.05

Poradnik dla ucznia

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Recenzenci:
dr inż. Jan Diaczuk
dr Jerzy Gremba

Opracowanie redakcyjne:
mgr inż. Danuta Pawełczyk

Konsultacja:
mgr inż. Gabriela Poloczek

Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej 725[01].O1.05
„Badanie i pomiary elektronicznych układów cyfrowych”, zawartego w modułowym
programie nauczania dla zawodu monter elektronik.

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

SPIS TREŚCI

1. Wprowadzenie

2. Wymagania wstępne

3. Cele kształcenia

4. Materiał nauczania

4.1. Systemy liczbowe

4.1.1. Materiał nauczania

4.1.2. Pytania sprawdzające

4.1.3. Ćwiczenia

4.1.4. Sprawdzian postępów

4.2. Kody liczbowe

4.2.1. Materiał nauczania

4.2.2. Pytania sprawdzające

4.2.3. Ćwiczenia

4.2.4. Sprawdzian postępów

4.3. Podstawowe funkcje logiczne i ich realizacja w technologii bipolarnej

i unipolarnej

4.3.1. Materiał nauczania

4.3.2. Pytania sprawdzające

4.3.3. Ćwiczenia

4.3.4. Sprawdzian postępów

4.4. Układy kombinacyjne

4.4.1. Materiał nauczania

4.4.2. Pytania sprawdzające

4.4.3. Ćwiczenia

4.4.4. Sprawdzian postępów

4.5. Układy sekwencyjne

4.5.1. Materiał nauczania

4.5.2. Pytania sprawdzające

4.5.3. Ćwiczenia

4.5.4. Sprawdzian postępów

4.6. Podstawy techniki mikroprocesorowej

4.6.1. Materiał nauczania

4.6.2. Pytania sprawdzające

4.6.3. Ćwiczenia

4.6.4. Sprawdzian postępów

5. Sprawdzian osiągnięć

6. Literatura

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

1. WPROWADZENIE

Poradnik ten pomoże Ci w przyswajaniu wiedzy z zakresu badania i pomiarów układów

cyfrowych.

W poradniku zamieszczono:

–

wykaz umiejętności, jakie powinieneś mieć przed przystąpieniem do nauki w wybranym
przez Ciebie zawodzie,

–

wykaz umiejętności, jakie ukształtujesz podczas pracy z tym poradnikiem,

–

materiał nauczania – czyli wiadomości dotyczące montowania układów cyfrowych
i badania ich parametrów

–

zestawy pytań, które pomogą Ci sprawdzić, czy opanowałeś podane treści

–

ćwiczenia, które umożliwia Ci nabycie umiejętności praktycznych,

–

sprawdzian postępów, który pomoże ocenić poziom Twojej wiedzy po wykonaniu
ćwiczeń,

–

sprawdzian osiągnięć, który umożliwi sprawdzenie wiadomości i umiejętności nabytych
przez Ciebie podczas realizacji programu jednostki modułowej,

–

wykaz literatury, z jakiej możesz korzystać podczas nauki,
W materiale nauczania zostały omówione zagadnienia dotyczące systemów i kodów

liczbowych, podstawowych elementów cyfrowych, bloków funkcyjnych i ich współpracy
z urządzeniami sterującymi i wyjściowymi.

Nauczyciel pomoże Ci w procesie przyswajania wiedzy wskazując te treści, które są

kluczowe dla Twojego zawodu lub stanowią podstawę dalszego kształcenia.

Poziom przyswojenia Swojej wiedzy możesz sprawdzić, odpowiadając na „Pytania

sprawdzające” kończące „Materiał nauczania”. Pozwolą one ocenić Twoją gotowość do
wykonania ćwiczeń.

Kolejnym etapem badania układów cyfrowych, będzie wykonywanie ćwiczeń, których

celem jest uzupełnienie i utrwalenie informacji z danego zakresu. Wykonując ćwiczenia
przedstawione w poradniku lub zaproponowane przez nauczyciela, poznasz parametry
i zasadę działania elementów i prostych układów cyfrowych, na podstawie:
–

oznaczeń elementów,

–

przeprowadzonych analiz schematów logicznych,

–

przeprowadzonych pomiarów i obserwacji.
Po wykonaniu ćwiczeń, sprawdź poziom swoich postępów rozwiązując test „Sprawdzian

postępów”, zamieszczony po ćwiczeniach. W tym celu:
–

przeczytaj pytania i odpowiedz na nie,

–

wybierz odpowiedź TAK lub NIE wstawiając X w odpowiednie miejsce.

Odpowiedzi TAK wskazują twoje mocne strony, natomiast odpowiedzi NIE informują
o brakach, które musisz nadrobić. Oznacza to także powrót do treści, które nie są dostatecznie
opanowane.
Poznanie przez Ciebie wiadomości i nabycie umiejętności dotyczących układów cyfrowych
będzie stanowiło dla nauczyciela podstawę przeprowadzenia sprawdzianu poziomu
przyswojonych wiadomości i ukształtowanych umiejętności. W tym celu nauczyciel posłuży
się zestawem zadań testowych zamieszczonym w „Sprawdzianie osiągnięć”, który znajduje
się w rozdziale 5 tego poradnika. W jego skład wchodzi również:

−

instrukcja, w której omówiono tok postępowania podczas przeprowadzania sprawdzianu,

−

przykładowa karta odpowiedzi, do której wpiszesz wybrane przez Ciebie odpowiedzi na
pytania znajdujące się w teście;

Będzie to stanowić dla Ciebie trening przed sprawdzianem zaplanowanym przez nauczyciela.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

725[01].O1.06

Analizowanie działania maszyn i urządzeń

elektrycznych

725[01].O1.04

Badanie i pomiary elektronicznych

układów analogowych

725[01].O1.01

Przygotowanie do bezpiecznej pracy

725[01].O1.03

Badanie i pomiary obwodów prądu

przemiennego

725[01].O1.05

Badanie i pomiary elektronicznych

układów cyfrowych

725[01].O1.02

Badanie i pomiary obwodów prądu stałego

725[01].O1

Pomiary parametrów elementów

i układów elektronicznych

Schemat układu jednostek modułowych.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

2. WYMAGANIA WSTĘPNE

Przystępując do realizacji programu jednostki modułowej powinieneś umieć:

–

posługiwać się symbolami graficznymi elementów elektrycznych i elektronicznych,

–

stosować podstawowe prawa elektrotechniki,

–

obsługiwać woltomierz, amperomierz, omomierz i miernik uniwersalny,

–

obsługiwać oscyloskop zgodnie z instrukcją,

–

interpretować obserwowane na oscyloskopie przebiegi sygnałów,

–

planować pomiary w obwodzie elektrycznym,

–

organizować stanowisko pomiarowe,

–

stosować różne sposoby połączeń elektrycznych,

–

łączyć obwód elektryczny zgodnie ze schematem,

–

przedstawiać wyniki pomiarów w formie tabel i wykresów,

–

odczytywać informację z tabeli i wykresu,

–

oceniać dokładność pomiarów,

–

analizować i zinterpretować wyniki pomiarów oraz wyciągnąć praktyczne wnioski,

–

współpracować w grupie,

–

korzystać z różnych źródeł informacji,

–

stosować obowiązującą procedurę postępowania w sytuacji zagrożenia,

–

stosować przepisy bezpieczeństwa i higieny pracy oraz przepisy przeciwpożarowe.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

3. CELE KSZTAŁCENIA

W wyniku realizacji programu jednostki modułowej powinieneś umieć:

–

zakodować liczby w kodzie binarnym, heksagonalnym i BCD,

–

zastosować podstawowe prawa algebry Boole’a,

–

rozpoznać na podstawie symbolu graficznego i katalogowego podstawowe elementy
cyfrowe i technologie ich wykonania,

–

rozróżnić funkcje podstawowych układów cyfrowych,

–

przeanalizować działanie prostych układów cyfrowych na podstawie schematów
logicznych,

–

przeanalizować działanie układów cyfrowych na podstawie schematów blokowych,

–

wskazać podstawowe zastosowania elementów i układów cyfrowych,

–

obsłużyć urządzenia do testowania elementów układów cyfrowych,

–

zinterpretować wyniki pomiarów w układach cyfrowych oraz sformułować praktyczne
wnioski,

–

skorzystać z katalogów układów cyfrowych różnych technologii,

–

połączyć proste układy do badania elementów cyfrowych i bloków funkcjonalnych,

–

wykryć usterki w układach cyfrowych,

–

przewidzieć zagrożenia dla życia i zdrowia w czasie realizacji ćwiczeń,

–

zastosować zasady bhp, ochrony ppoż. i ochrony środowiska podczas wykonywania
badań i pomiarów.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4. MATERIAŁ NAUCZANIA

4.1. Systemy liczbowe

4.1.1. Materiał nauczania

Systemy pozycyjne

Powszechnie używane systemy liczenia to systemy pozycyjne. Każdy system pozycyjny

posiada swoją podstawę p, (np. podstawą systemu dziesiętnego jest 10) oraz zbiór znaków
służących do zapisu liczb. Wartość jaką reprezentuje znak liczby systemu pozycyjnego zależy
od pozycji jaką zajmuje. Każda pozycja ma swoją wagę w czyli znaczenie wyrażone
zależnością:

w = p

gdzie w – waga, p – podstawa systemu, k – pozycja.

W systemie pozycyjnym o podstawie p:

–

liczba znaków graficznych potrzebnych do zapisu dowolnej liczy równa jest podstawie
systemu p,

–

wagi poszczególnych pozycji mają wartość p

gdzie k jest pozycją cyfry.

System dwójkowy (binarny)

Podstawą systemu dwójkowego jest p = 2, liczby zapisywane za pomocą cyfr 0, 1.

Pozycja znaku w zapisie liczby binarnej nazywa się bitem. Skrajna pozycja z lewej strony ma
najwyższą wagę (największe znaczenie) i nazywa się najstarszym bitem – MSB (ang. Most
Significant Bit), natomiast skrajna pozycja z prawej strony ma najniższą wagę (najmniejsze
znaczenie) i nazywa się najmłodszym bitem – LSB (ang. Least Significant Bit).

Zamiana liczby całkowitej dziesiętnej na liczbę w zapisie dwójkowym polega na

dzieleniu jej przez podstawę systemu dwójkowego czyli 2. Wynik dzielenia zapisywany jest
jako część całkowita i reszta. W kolejnym kroku z częścią całkowitą postępujemy jak
poprzednio. Reszta dzielenia jest zawsze równa 1 lub 0. Ciąg tych reszt stanowi liczbę
binarną, przy czym reszta pierwszego dzielenia jest najmłodszym bitem.

Zamiana liczby ułamkowej dziesiętnej na liczbę w zapisie dwójkowym polega na

mnożeniu jej przez podstawę systemu dwójkowego czyli 2. Wynik mnożenia zapisywany jest
jako część całkowita i ułamkowa. W kolejnym kroku z częścią ułamkową postępujemy jak
poprzednio. Część całkowita jest zawsze równa 1 lub 0. Ciąg części całkowitych stanowi
liczbę binarną, przy czym część całkowita pierwszego mnożenia jest najstarszym bitem.

Przykład 1
Wykonać konwersję dziesiętno-dwójkową liczby 215.
215 : 2 = 107 + r.1 LSB
107 : 2 =53 + r.1
53 : 2 =26 + r. 1
26 : 2 =13 + r. 0
13 : 2 = 6 + r. 1
6 : 2=3 + r. 0
3 : 2= 1 + r. 1
1 : 2= 0 + r. 1 MSB

Liczba 215 w zapisie dwójkowym to 11010111

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Przykład 2
Wykonać konwersję dziesiętno-dwójkową liczby 0,125

MSB

↓

⋅

125

0,25

⋅

0,5

⋅

1,0

↑

LSB

Liczba 0,125 w zapisie dwójkowym to 0,001.

W przypadku konwersji dziesiętno-dwójkowej liczb ułamkowych zazwyczaj należy przyjąć
pewne przybliżenie.

Konwersji dwójkowo dziesiętne dokonuje się mnożąc każdy bit liczby binarnej przez

wagę jej pozycji, a następnie sumując uzyskane wartości.

Przykład 3
Wykonać konwersję dwójkowo-dziesiętną liczby 11100011

⋅

1 2

⋅

1 2

⋅

1 2

⋅

0 2

⋅

0 2

⋅

0 2

⋅

1 2

⋅

1 2

⋅

1 64 +

⋅

1 32 +

⋅

1 16 +

⋅

0 8 +

⋅

0 2

⋅

0 4

⋅

1 2 +

⋅

1 1 = 64 + 32 + 16 + 2 + 1 = 115

System binarny wykorzystywany jest między innymi w technice cyfrowej i informatyce.

Działania na liczbach binarnych.

Działania arytmetyczne takie jak: dodawanie odejmowanie, dzielenie i mnożenie

wykonywane są na liczbach binarnych tak jak w systemie dziesiętnym. Należy jedynie
pamiętać, że podstawą systemu jest 2 i wynik każdego działania musi równać się 0 lub 1.

Przykład 4
Należy dodawać liczby binarne 1000111 i 10101.

1000111
+ 10101
––––––––––
1011100

Przykład 5
Należy odjąć od liczby binarnej 1000111 liczbę binarną 10101.

1000111
– 10101
––––––––––
110010

System szesnastkowy (heksadecymalny)

Podstawą systemu szesnastkowego jest p = 16, liczby zapisywane za pomocą znaków ze

zbioru {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}.

W celu dokonania konwersji liczby dziesiętnej na szesnastkową, należy najpierw

dokonać konwersji dziesiętno-dwójkowej, następnie podzielić liczbę binarną na grupy po
cztery bity (poczynając od najmłodszego bit, jeśli grupa z najstarszych bitów jest niepełna,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

należy ją uzupełnić o nieznaczące zera), następnie każdej czwórce bitów należy
przyporządkować znak liczby szesnastkowej.

Przykład 7
Wykonać konwersję dziesiętno-szesnastkową liczby 99.
99

= 1100011

= (0110 0011)

= 0111 0011 = 73

⇓

Konwersję szesnastkowo-dziesiętną przeprowadza się w sposób odwrotny: każdy znak

liczby szesnastkowej konwertuje się na wartość dwójkową, następnie dokonuje się konwersji
dwójkowo-dziesiętnej.

Przykład 8
Wykonać konwersję szesnastkowo-dziesiętną liczby 4A

⇓

0100

1010

= 83

System szesnastkowy wykorzystywany jest między innymi w technice cyfrowej oraz
informatyce.

Działania na liczbach w zapisie szesnastkowym

Zasady wykonywania działań arytmetycznych na liczbach w zapisie szesnastkowym, są

analogiczne jak w systemie dziesiętnym. Należy jedynie pamiętać, że podstawą systemu jest
16, a wynik każdego działania musi można zapisać za pomocą znaków ze zbioru {0, 1, 2, 3, 4,
5, 6, 7, 8, 9, A, B, C, D, E, F}.

Przykład 9
Należy dodawać liczby w zapisie szesnastkowym 2A

oraz 11

+ 11

––––––––––

Przykład 10
Należy w zapisie szesnastkowym od liczby 2A

odjąć liczbę11

+ 11

––––––––––

4.1.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Czym charakteryzuje się pozycyjny system liczenia?
2. Jakie znasz systemy pozycyjne?
3. Jaka liczba jest podstawą systemu binarnego?
4. Za pomocą jakich znaków zapisuje się liczby binarne?
5. Jaka liczba jest podstawą systemu heksadecymalnego?
6. Za pomocą jakich znaków zapisuje się liczby w systemie heksadecymalnym?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.1.3. Ćwiczenia

Ćwiczenie 1

Zapisz w systemie dziesiętnym liczby 10111001

oraz 110001001

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) dokonać konwersji dwójkowo-dziesiętnej,
2) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

kalkulator,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 2

Dodaj liczby binarne 10100110 i 10100.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) dodać dwie liczy binarnie,
2) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

kalkulator,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 3

Zapisz w systemie dziesiętnym liczby podane w systemie szesnastkowym: 5E

oraz

16.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) dokonać konwersji każdego znaku liczby szesnastkowej na liczbę binarną,
2) dokonać konwersji otrzymanej liczby binarnej na liczbę dziesiętną,
3) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

kalkulator,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 4

Dodaj liczby w zapisie szesnastkowym 4C

oraz 12

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) dodać dwie liczy szesnastkowe,
2) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

kalkulator,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 5

Odejmij w zapisie szesnastkowym od liczby 5E

liczbę 13

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) odjąć dwie liczy szesnastkowe,
2) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

kalkulator,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

4.1.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) zapisać liczbę dziesiętna w systemie binarnym?

2) dokonać konwersji dwójkowo-dziesiętnej?

3) zapisać liczbę dziesiętną w systemie heksadecymalnym?

4) dokonać konwersji szesnastkowo-dziesiętnej?

5) wykonać dodawanie liczb w systemie binarnym?

6) wykonać odejmowanie liczb w systemie binarnym?

7) wykonać dodawanie liczb w systemie szesnastkowym?

8) wykonać odejmowanie liczb w systemie szesnastkowym?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.2. Kody liczbowe

4.2.1. Materiał nauczania

Kodowanie to przypisywanie różnym informacjom pewnych symboli. Kodem nazywamy

zestaw symboli przypisanej danej informacji.
Podstawowe kody używane w technice cyfrowej i informatyce to kod binarny prosty, kod
szesnastkowy, kod naturalny BCD, pierwotny kod 1 z n, kod Graya, stosuje się również kod
detekcyjne czyli np. kod kontroli parzystości i kod Hamminga.

Kod binarny prosty jest opisanym wcześniej systemem dwójkowym zapisu liczb.

Kodowanie liczb odpowiada konwersji dziesiętno-dwójkowej za pomocą cyfr 0, 1.

Kod szesnastkowy (heksadecymalny) jest opisanym wcześniej systemem szesnastkowy

(heksadecymalny) zapisu liczb. Kodowanie liczb odpowiada konwersji dziesiętno–
szesnastkowej za pomocą znaków ze zbioru {0, 1, 2, 3, 4, 5, 6,7, 8, 9, A, B, C, D, E, F}.

Kod naturalny BCD

Kod naturalny BCD utworzony jest przez zapisanie kolejnych cyfr dziesiętnych

w systemie dwójkowym. Kod ten nazywany jest również kodem BCD 8421.

Przykład
Zapisać liczbę 967

w kodzie BCD.

Każdej cyfrze należy przyporządkować odpowiednik binarny zatem

⇓

1001

0110

0111

Kod pierwotny 1 z n

Kod pierwotny 1 z n jest często kodem wejściowym urządzenia, n oznacza liczbę bitów

kodu. Liczba zapisana w tym kodzie ma tylko na jednym bicie 1 natomiast pozostałe bity
są równe 0.

Przykład
Zapisać liczby od 0

do 4

w kodzie 1 z 10

w kodzie 1 z 10 odpowiada0000000001

w kodzie 1 z 10 odpowiada0000000010

w kodzie 1 z 10 odpowiada0000000100

w kodzie 1 z 10 odpowiada0000001000

Kody detekcyjne

Kody detekcyjne nazywane są inaczej kodami z zabezpieczeniem. Zabezpieczenie

wprowadza się ze względu na mogące wystąpić zakłócenia podczas transmisji informacji.
Kod detekcyjny posiada charakterystyczną tylko dla siebie cechę, którą można identyfikować.
Konstrukcja kodu z zabezpieczeniami pozwala na odtworzeni informacji pierwotnej nawet
w przypadku wystąpienia błędu. Wśród kodów detekcyjnych najpopularniejsze są kod
Hamminga (czyt. Haminga) oraz kod z bitem kontrolnym (bitem kontroli parzystości).
Informacje w systemach cyfrowych przesyła się w postaci bajtów czyli „paczek” informacji
złożonych z ośmiu bitów, gdzie w przypadku stosowania kodu z bitem kontroli parzystości,
ósmy bit jest bitem kontrolnym, który jest ustawiony tak aby całkowita liczba jedynek

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

w bajcie informacyjnym była parzysta lub równa zero. Kod z bitem kontrolnym umożliwia
wykrycie przekłamania na pozycji pojedynczego bitu w bajcie informacji.
W celu zakodowania informacji w kodzie z bitem kontrolnym i przesłania jej:
–

do każdych siedmiu bitów informacji zostaje dodany ósmy bit – bit kontroli parzystości
ustawiony tak aby całkowita liczba jedynek w bajcie była parzysta lub równa zero np. do
informacji 1001100 zawierającej trzy jedynki dodaje się na najstarszej pozycji bit
kontrolny ósmy równy 1, wtedy zakodowana informacja przyjmuje postać:

11001100

↑

dołączony bit kontrolny

–

po otrzymaniu bajta informacji sprawdzone jest czy zawarta w nim ilość jedynek jest
parzysta bądź równa zero, jeśli tak nie jest powtórzona jest operacja przesłania informacji
lub następuje przerwanie pracy i sygnalizacja błędu parzystości.

Istnieje również kod detekcyjny z kontrolą parzystości realizowaną odwrotnie tzn. bit
kontrolny ustawiany jest tak, aby całkowita ilość jedynek była nieparzysta. Kod taki często
nazywany jest kodem z kontrolą nieparzystości

Kod Graya

Kod Graya (czyt. Graja) zwany też refleksyjnym charakteryzuje się tym, że dwa

sąsiadujące wyrazy kodowe różnią się tylko jednym bitem. Jednobitowy kod Graya posiada
jedynie dwa wyrazy 0 oraz 1.

A
0
1

W celu rozszerzenia go do dwóch bitów należy ponownie lecz w odwrotnej kolejności
przepisać ciąg wyrazów kodu jednobitowego.

0
1
–
1
0

Następnie do początkowych wyrazów dopisać na początku dodatkowy bit 0, a do dopisanych
dopisać na początku dodatkowy bit 1.

A B
0 0
0 1
1 1
1 0
Kod Graya n–bitowy tworzy się analogicznie, powtarzając n–1 bitowy kod Graya

następnie dopisując dodatkowy bit 0 do pierwotnej części, 1 do części dopisanej.

4.2.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Na czym polega kodowanie?
2. Jakie znasz kody stosowane w technice cyfrowej?
3. W jaki sposób koduje się liczby dziesiętnie w binarnym kodzie prostym?
4. Jakie są zasady kodowania liczb dziesiętnych w kodzie heksadecymalnym?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5. W jaki sposób zapisuje się liczbę w kodzie BCD?
6. W jakim celu stosuje się kody detekcyjne?
7. W jaki sposób koduje się informacje w kodzie z kontrolą parzystości?
8. W jaki sposób zapisuje się informacje w kodzie 1 z n?
9. Czym charakteryzuje się kod Graya?

4.2.3. Ćwiczenia

Ćwiczenie 1

Zakoduj w kodzie binarnym prostym liczby 115

oraz 89

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) dokonać konwersji dziesiętno-dwójkowej,
2) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

kalkulator,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 2

Zakoduj w kodzie heksadecymalnym liczby 439

oraz 248

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) dokonać konwersji dziesiętno-szesnastkowej,
2) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

kalkulator,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 3

Zapisz w kodzie BCD liczbę 536

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) dokonać konwersji dziesiętnej–dwójkowej każdej cyfry kodowanej liczby dziesiętnej,
2) zapisać liczbę w kodzie BCD,
3) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 4

Dokonaj konwersji liczby 1001 0011 0111 zapisanej w kodzie BCD na postać dziesiętną.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) dokonać konwersji dwójkowo-dziesiętnej każdej czwórki bitów na cyfrę,
2) zapisać liczbę w systemie dziesiętnym,
3) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

kalkulator,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 5

Zakoduj w kodzie z kontrolą parzystości informację: 1100011, a informację 1000100

w kodzie z kontrolą nieparzystości.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) uzupełnić informację 1100011 o bit kontroli parzystości,
2) uzupełnić informację 1000100 o bit kontroli nieparzystości
3) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 6

Zapisz trzybitowy kod Graya.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) zapisać jednobitowy kod Graya,
2) na jego podstawie stworzyć dwubitowy kod Graya,
3) na podstawie dwubitowego kodu Graya zapisać wyrazy trzybitowego kodu Graya,
4) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

kalkulator,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.2.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) zakodować dowolną liczbę dziesiętną w kodzie binarnym prostym?

2) zakodować dowolną liczbę dziesiętną w kodzie heksadecymalnym?

3) zakodować dowolną liczbę dziesiętną w kodzie BCD?

4) zapisać liczbę kodowaną w kodzie BCD w postaci dziesiętnej?

5) zakodować informację w kodzie z kontrolą parzystości?

6) zakodować informację w kodzie z kontrolą nieparzystości?

7) zapisać kolejne wyrazy w kodzie 1 z n?

8) zapisać wyrazy n–bitowego kodu Graya?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.3. Podstawowe funkcje logiczne i ich realizacja w technologii

bipolarnej i unipolarnej

4.3.1. Materiał nauczania

Zalecenia dotyczące przepisów bezpieczeństwa i higieny pracy

Szczegółowe przepisy bezpieczeństwa i higieny pracy dotyczące pracy z urządzeniami

elektrycznymi i elektronicznymi zostały szczegółowo omówione w jednostkach modułowych
„Przygotowanie do bezpiecznej pracy”, „Badanie i pomiary obwodów prądu stałego” oraz
„Badanie i pomiary obwodów prądu przemiennego” należy jednak pamiętać, że minimalna
niebezpieczna dla człowieka wartość prądu płynącego przez dłuższy czas wynosi:

−

30 mA prądu zmiennego,

−

70 mA prądu stałego.

Przed rozpoczęciem pracy z zespołami elektronicznymi należy usunąć ładunki elektryczne
jakie mogą się zgromadzić na ciele lub odzieży. Wykonuje się to przez dotknięci uziemienia
lub przewodu ochronnego.

Aby zachować bezpieczeństwo podczas pracy przy urządzeniach elektrycznych

i elektronicznych należy zachować następujące podstawowe zasady:
1. wyłączyć napięcie we wszystkich częściach urządzenia przy którym będą prowadzone

prace,

2. zabezpieczyć wyłączniki przed ponownym załączeniem (np. taśmą samoprzylepną),

wyjąć bezpieczniki, wywiesić informację o zakazie załączania,

3. sprawdzić stan napięcia (do sprawdzenia użyciu dwubiegunowego próbnika napięć),
4. osłonić i oddzielić sąsiadujące elementy znajdujące się pod napięciem (można

zastosować maty i folie izolacyjne).

Przed przystąpieniem do wykonywania ćwiczeń praktycznych polegających na wykonywaniu
pomiarów i obserwacji oscylogramów w układach elektronicznych, poprawność
zmontowanego układu powinien sprawdzić nauczyciel, a następnie powinien udzielić zgody
włączenie zasilania.

Algebra Boole’a

Algebra Bool’a (czyt. Bula) operuje zmiennymi dwuwartościowymi o wartościach 1 i 0.

Podstawowe operacje algebry Bool’a to:

−

suma logiczna (alternatywa, dysjunkcja),

−

iloczyn logiczny (koniunkcja),

−

negacja (dopełnienie).
Suma logiczna jest równa 1, gdy którykolwiek ze składników jest równy 1. Sumę

argumentów a i b oznacza się jako a + b.

Iloczyn logiczny jest równy 1, gdy wszystkie czynniki są równe 1. Iloczyn logiczny

argumentów a i b oznacza się jako

⋅

, lub ab.

Suma logiczna i iloczyn logiczny mogą mieć dowolną ilość argumentów.
Negacja jest działaniem jednoargumentowym i równa się 1 gdy argument ma wartość 0.

Negację oznacza się a i czyta „nie a”.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

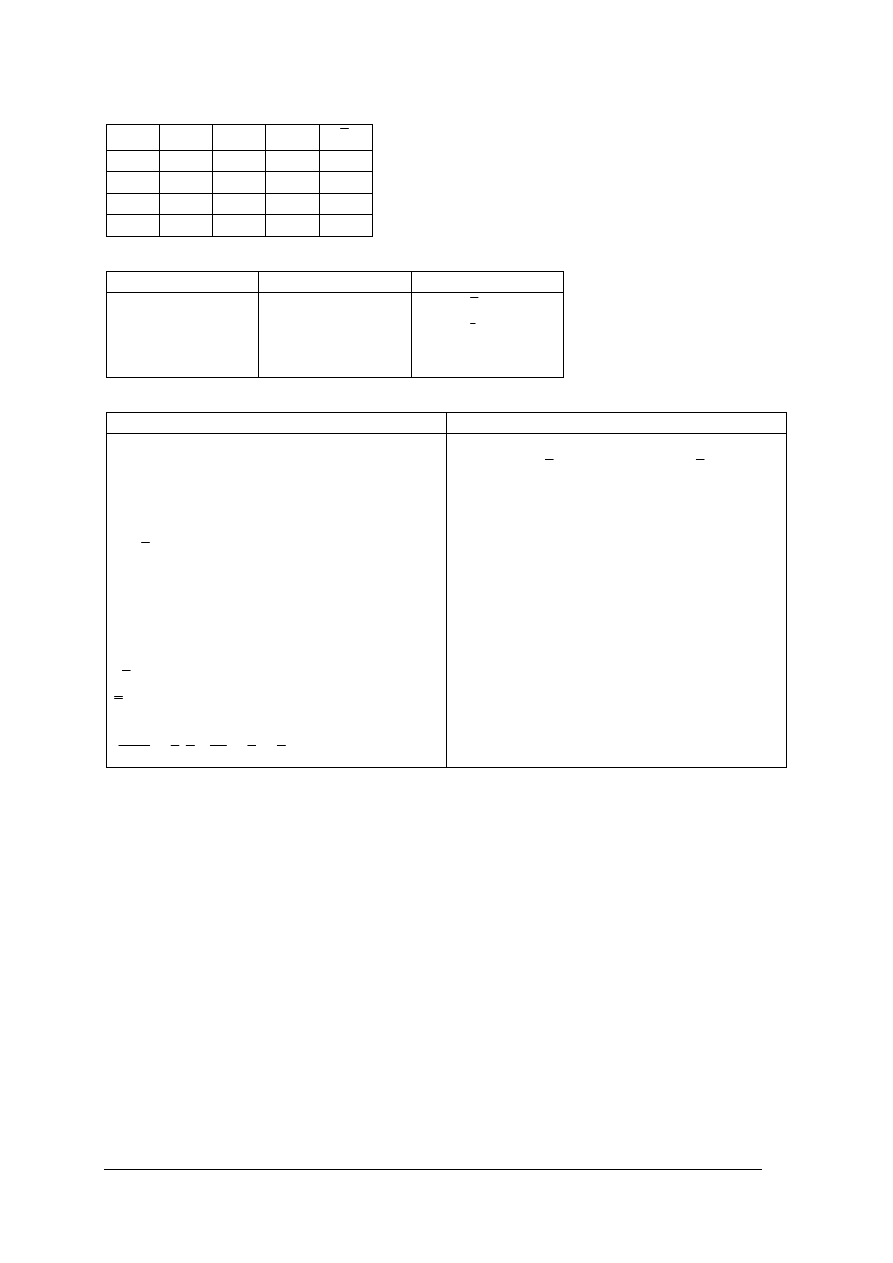
Tabela 1. Definicje operacji bulowskich

a + b

Tabela 2. Własności funkcji logicznych

Suma logiczna

Iloczyn logiczny

Negacja

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1

1 + 1 =1

⋅

Tabela 3. Prawa i twierdzenia algebry Boole’a

Prawa algebry Boole’a

Podstawowe twierdzenia algebry Boole’a

a +b = b + a
a (b + c) = ab + ac
(a + b) + c = a + (b + c)
a + 0 = a
a + 1 = 1

a + a = 1
ab = ba
a +bc = (a + b) (a + c)
(ab) c = a (cb)
a1 =a
a0 = 0

a a = 0

a = a

Prawa de Morgana

= a b ab = a + b

Tw.1. a + ac = a

a (a + b) = a

Tw.2.

a + a b = a + b

a ( a + b) = ab

Tw.3. a + a = a

aa = a

Bramki logiczne

Bramki logiczne nazywamy też funktorami realizują funkcje logiczną jednej lub wielu

zmiennych. Zmienna logiczna to sygnał elektryczny (napięcie) przyjmujący dwa stany.
W konwencji dodatniej niski poziom napięcia oznaczany „L” odpowiada stanowi logicznemu
0, natomiast wysoki poziom napięcia oznaczany „H” odpowiada stanowi logicznemu 1.
W konwencji ujemnej niski poziom napięcia oznaczany „L” odpowiada stanowi logicznemu
1, natomiast wysoki poziom napięcia oznaczany „H” odpowiada stanowi logicznemu 0. Do
analizy układów cyfrowych zazwyczaj stosuje się konwencję dodatnią.
Działanie bramek logicznych opisuje się za pomocą

−

tablic

prawdy,

które

ujmują

wszystkie

kombinacje

sygnałów

wejściowych

i odpowiadające im kombinacje sygnałów wyjściowych.

−

funkcji logicznych wyrażonych w języku algebry Boole’a.

Zbiór funktorów, który pozwala zrealizować dowolną funkcję logiczną nazywa się systemem
funkcjonalnie pełnym.
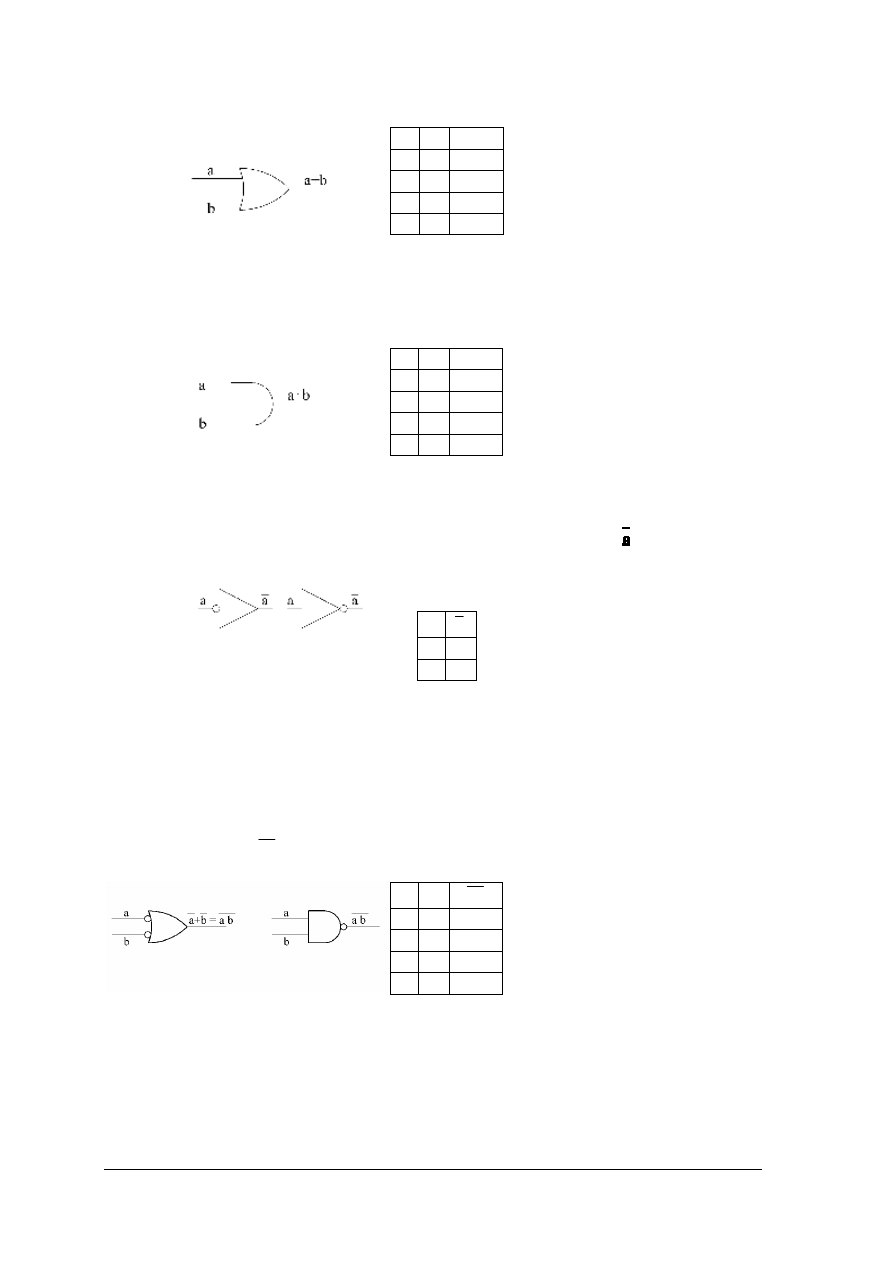
Bramka OR (LUB) może mieć dwa lub więcej wejść, realizuje funkcję sumy logicznej
a + b.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 1. Dwuwejściowa bramka OR a) symbol graficzny, b) tablica prawdy [1, s.34]

Bramka AND (I) może mieć dwa lub więcej wejść, realizuje funkcję iloczynu logicznego ab

Rys. 2. Dwuwejściowa bramka AND a) symbol graficzny; b) tablica prawdy [1, s.34]

Bramka NOT (NIE) posiada jedno wejście i realizuje funkcję negacji

Rys. 3. Bramka NOT a) symbole graficzne; b) tablica prawdy [1, s.34]

W symbolu graficznym bramki NOT można wyróżnić symbol wzmacniacza i kółko (może
być umieszczone na wejściu i na wyjściu) reprezentujące inwersję.

Bramka NAND (NIE I) może mieć dwa lub więcej wejść, realizuje funkcję zanegowanego

iloczynu logicznego ab

Rys. 4. Dwuwejściowa bramka NAND a) symbole graficzne; b) tablica prawdy [1, s.35]

Bramka NAND jest funkcjonalnie pełna, ponieważ realizuje operacje iloczynu AND

i operację negacji NOT.

a b

a + b

0 0

0 1

1 0

1 1

0 0

0 1

1 0

1 1

0 1
1 0

0 0

0 1

1 0

1 1

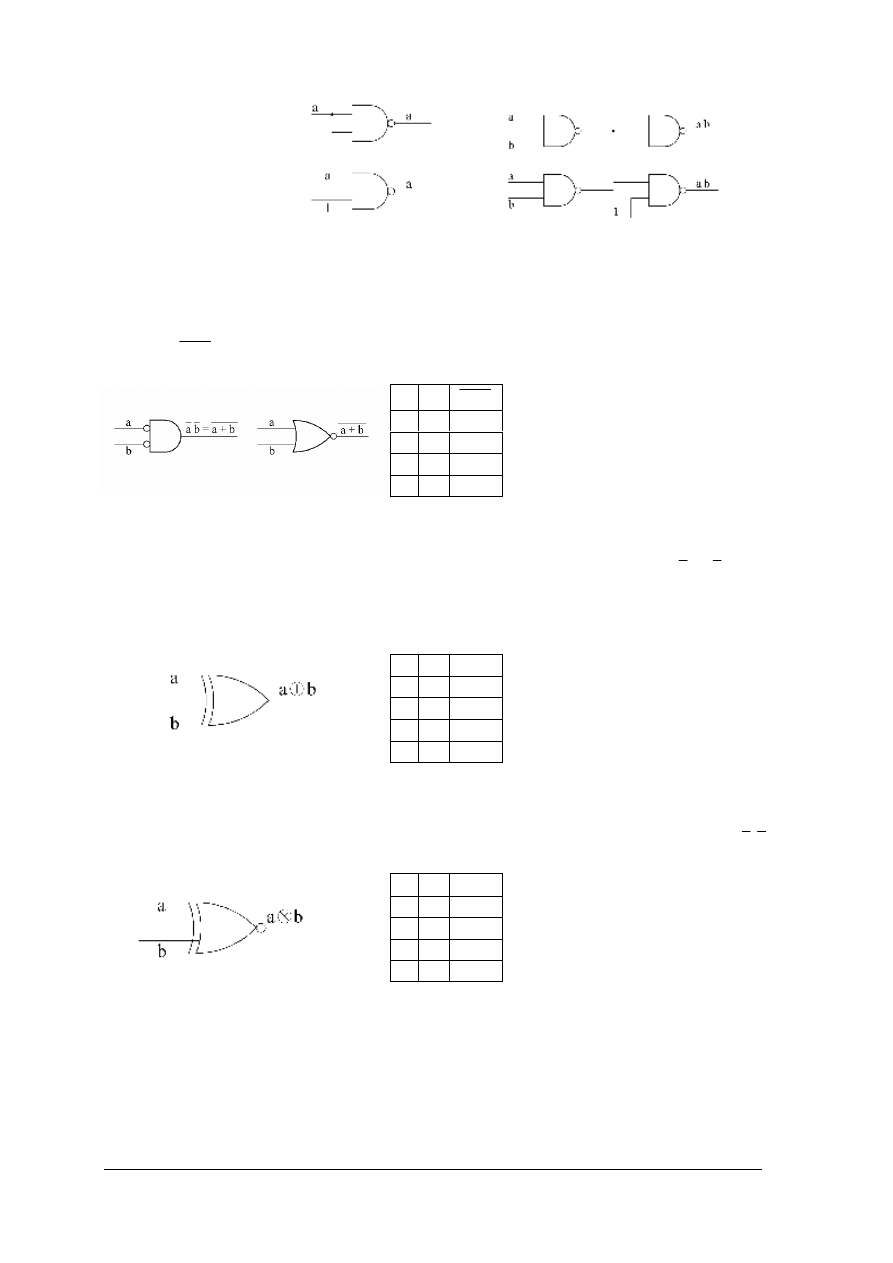
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 5. a) Realizacja negacji za pomocą bramki NAND. [1, s.35] b) Realizacja iloczynu logicznego za

pomocą bramki NAND [3, s.36]

Bramka NOR (NIE LUB) może mieć dwa lub więcej wejść, realizuje funkcję sumy

logicznej

. Bramka NOR jest funkcjonalnie pełna.

Rys. 6. Dwuwejściowa bramka NOR a) symbole graficzne; b) tablica prawdy [1, s.36]

Branka Ex–OR (XOR, ALBO) realizuje funkcję sumy modulo dwa a

⊕

b = a b + a b

Rys. 7. Dwuwejściowa bramka Ex–OR: a) symbol graficzny, b) tablica prawdy [1, s.36]

Branka Ex–NOR (NIE ALBO) realizuje funkcję równoważności a

⊗

b = a

≡

b = ab + a b

Rys. 8. Dwuwejściowa bramka Ex–NOR: a) symbol graficzny; b) tablica prawdy [1, s.36]

Techniki wykonania cyfrowych układów scalonych

Cyfrowe układy scalone mogą być wykonane w technologii bipolarnej lub unipolarnej.

Technologie bipolarne wykorzystują tranzystory bipolarne. Najpopularniejsza z nich to
technologia TTL (ang. Transistor-Transistor Logic) wykorzystująca bipolarne tranzystory
wieloemiterowe. Wcześniejsza była technologia DTL (ang. Diode Transistor Logic)

0 0

0 1

1 0

1 1

b a

⊕

0 0

0 1

1 0

1 1

b a

⊗

0 0

0 1

1 0

1 1

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

wykorzystująca elementy diodowe – obecnie niestosowana z powodu małej obciążalności
i odporności na zakłócenia.
Spośród technologii bipolarnych należy wymienić jeszcze technologie:
–

ECL (ang. Emitter Coupled Logic) – w której wykonane są najszybsze układy
wykorzystujące tranzystory bipolarne,

–

L (ang. Integrated Injection Logic) – wykorzystującą tranzystory bipolarne,

charakteryzuje się dużą gęstością upakowania elementów w strukturze scalonej.

Technologie unipolarne to:
–

MOS (ang. Metal-Oxide-Semiconductor) – wykorzystująca tranzystory unipolarne
z kanałem typu P (PMOS – ang. P-channel Metal-Oxide-Semiconductor) i z kanałem
typu N (NMOS – ang. N-channel Metal-Oxide-Semiconductor). W technice PMOS
i NMOS wykonuje się układy MSI i LSI zawierające całe bloki funkcyjne,

–

CMOS (ang. Complementary MOS) – wykorzystująca unipolarne tranzystory
komplementarne, obecnie równie popularna jak TTL,

–

CTD (ang. Charge Transfer Device) – oparta na technologii MOS, stosowane do budowy
pamięci półprzewodnikowych.

Najczęściej w systemach cyfrowych stosuje się układy wykonane w technologiach TTL oraz
CMOS.

Oznaczenia cyfrowych układów scalonych

Producenci cyfrowych układów scalonych stosują zazwyczaj własne oznaczenia. Polskie

firmy stosują symbolikę zgodna z poniższymi zasadami:
–

pierwszy znak – litera – określa wykonanie: U – układ scalony półprzewodnikowy
monolityczny wykonany w technologii bipolarnej, M – układ scalony półprzewodnikowy
monolityczny wykonany w technologii unipolarnej,

–

drugi znak – litera – określa spełnianą funkcję: C – układy cyfrowe, L – układy
analogowe,

–

trzeci znak – litera – określa zastosowanie: X – prototyp, Y – do sprzętu profesjonalnego,
A – do zastosowań specjalnych,

–

czwarty znak – cyfra – określa numer serii (różny dla TTL i CMOS), dodatkowo mogą
wystąpić jedna lub dwie litery określające rodzaj serii,

–

kolejne znaki – dwie lub trzy cyfry określają rodzaj elementu,

–

ostatnia może wystąpić litera określająca rodzaj obudowy.

Podstawowe parametry układów scalonych

Parametry układów scalonych dzielimy na statyczne i dynamiczne.

Podstawowe parametry statyczne to:
–

straty mocy P

(moc pobierana przez układ, moc rozpraszana) jest to moc tracona

w układzie przy przełączaniu go przebiegiem prostokątnym o wypełnieniu ½ (tzn. czas
trwania impulsu w przebiegu prostokątnym, jest równy czasowi przerwy między
impulsami) i częstotliwości 100 kHz, określa zapotrzebowanie układu na prąd,

–

margines zakłóceń

∆

U – jest to maksymalna wartość amplitudy impulsu zakłócającego,

która dodana do sygnału wejściowego elementu nie powoduje przekroczenia przez sygnał
wyjściowy dopuszczalnych granic,

–

obciążalność N wyjścia układu określa dopuszczalną liczbę wejść innych elementów,
które mogą być z tego wyjścia prawidłowo sterowane.

W katalogach podanych jest jeszcze szereg innych parametrów statycznych takich jak
napięcie zasilania, prąd zasilania w stanie wysokim i niskim, napięcia i prądy wejściowe
w stanie wysokim i niskim, napięcia i prądy wyjściowe w stanie wysokim i niskim.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Podstawowym parametrem dynamicznym jest czas propagacji t

czyli czas upływający

między wystąpieniem sygnału na wejściu i na wyjściu układu. Zazwyczaj określa czasy
propagacji przyzmianie sygnału logicznego na wyjściu z wysokiego na niski i z niskiego
na wysoki. Czas propagacji t

jest najczęściej średnią arytmetyczna tych czasów i określa

szybkość działania układu.
Najczęściej stosuje się w systemach cyfrowych stosuje się układy wykonane w technologiach
TTL oraz CMOS. Układy TTL są szybsze niż CMOS mają też większy margines zakłóceń.
Natomiast układy CMOS charakteryzuje mniejsze straty mocy.

4.3.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Na jakich wartościach operuje algebra Bool’a?
2. Jakie są podstawowefunkcje algebry Bool’a?
3. Jak brzmią prawa de Morgana?
4. Kiedy suma logiczna przyjmuje wartość 1?
5. Jaka bramka realizuje funkcję sumy logicznej?
6. Kiedy iloczyn logiczny przyjmuje wartość 1?
7. Jaka bramka realizuje funkcję iloczynu logicznego?
8. Ilu argumentową jest funkcja negacji?
9. Jaka bramka realizuje negację?
10. Jaką funkcję realizuje bramka Ex–NOR?
11. Jaka jest najpopularniejsza technologia bipolarna realizacji bramek logicznych?
12. Czym charakteryzuje się technologia CMOS?

4.3.3. Ćwiczenia

Ćwiczenie 1

Sprawdź prawdziwość wyrażenia(a + b ) (ac + a b + bc) a b = 0, wykorzystując metodę

przekształceń algebraicznych oraz prawa algebry Bool’a.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) dokonać przekształceń algebraicznych,
2) zaprezentować wyniki pracy.

Środki dydaktyczne:

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 2

Zbadaj właściwości funkcjonalne bramki AND.

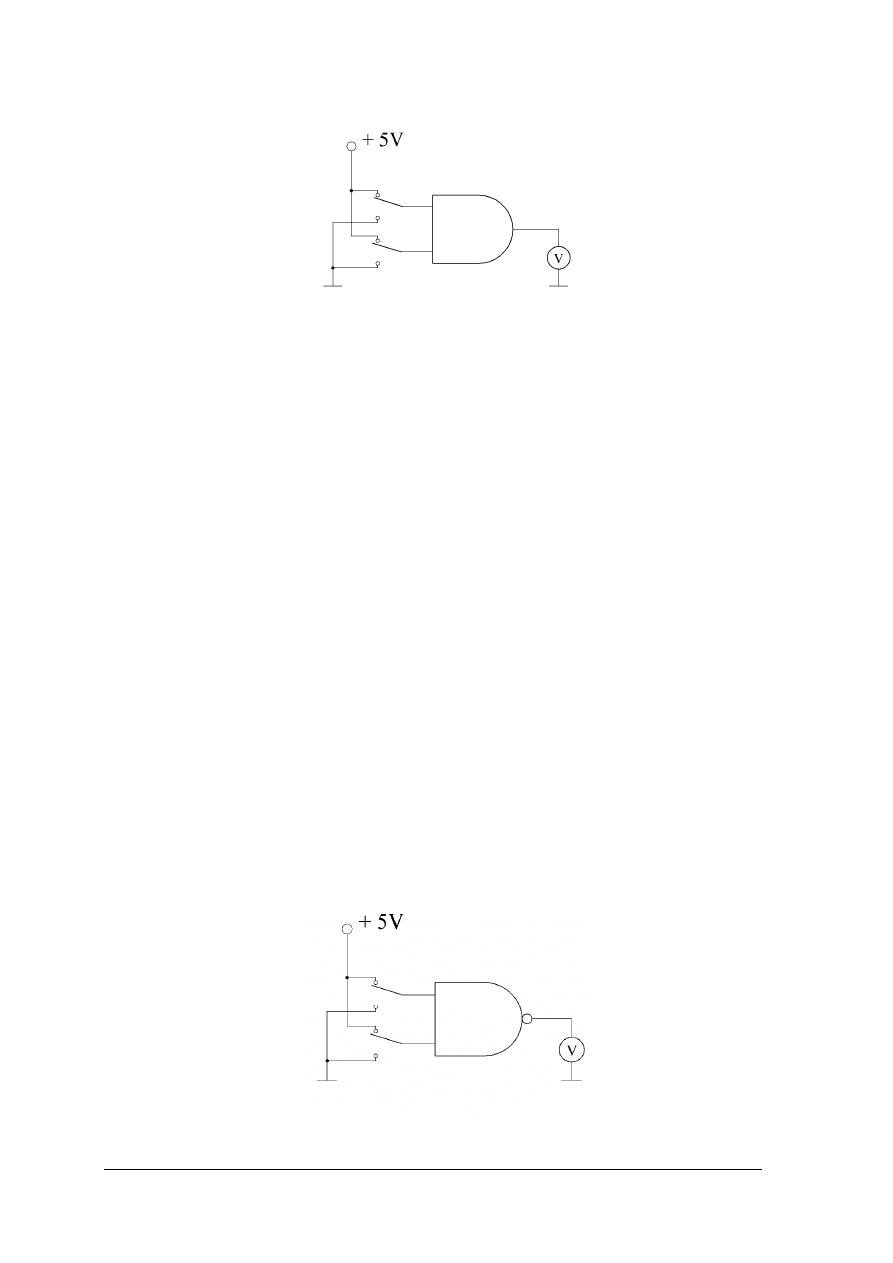
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rysunek do ćwiczenia 2. Układ do badania właściwości funkcjonalnych bramki AND

Uwaga! Przed załączeniem napięcia zasilania układ musi sprawdzić nauczyciel.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) zgromadzić potrzebne elementy i urządzenia,
3) połączyć układ według schematu,
4) zbadać działanie bramki (mierząc napięcie na jej wyjściu) podawać na jej wejścia sygnał

zgodnie z tablicą prawdy dla bramki AND, przyjmując +5 V jako stan 1 logicznej,
0 V jako stan 0 logicznego,

5) sformułować wnioski,
6) sporządzić sprawozdanie z wykonanego ćwiczenia.

Wyposażenie stanowiska pracy:

–

bramka AND (z układu UCY 7408),

–

zasilacz +5 V,

–

dwa przełączniki dwupozycyjne,

–

multimetr uniwersalny,

–

stanowisko do łączenia układów,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 3

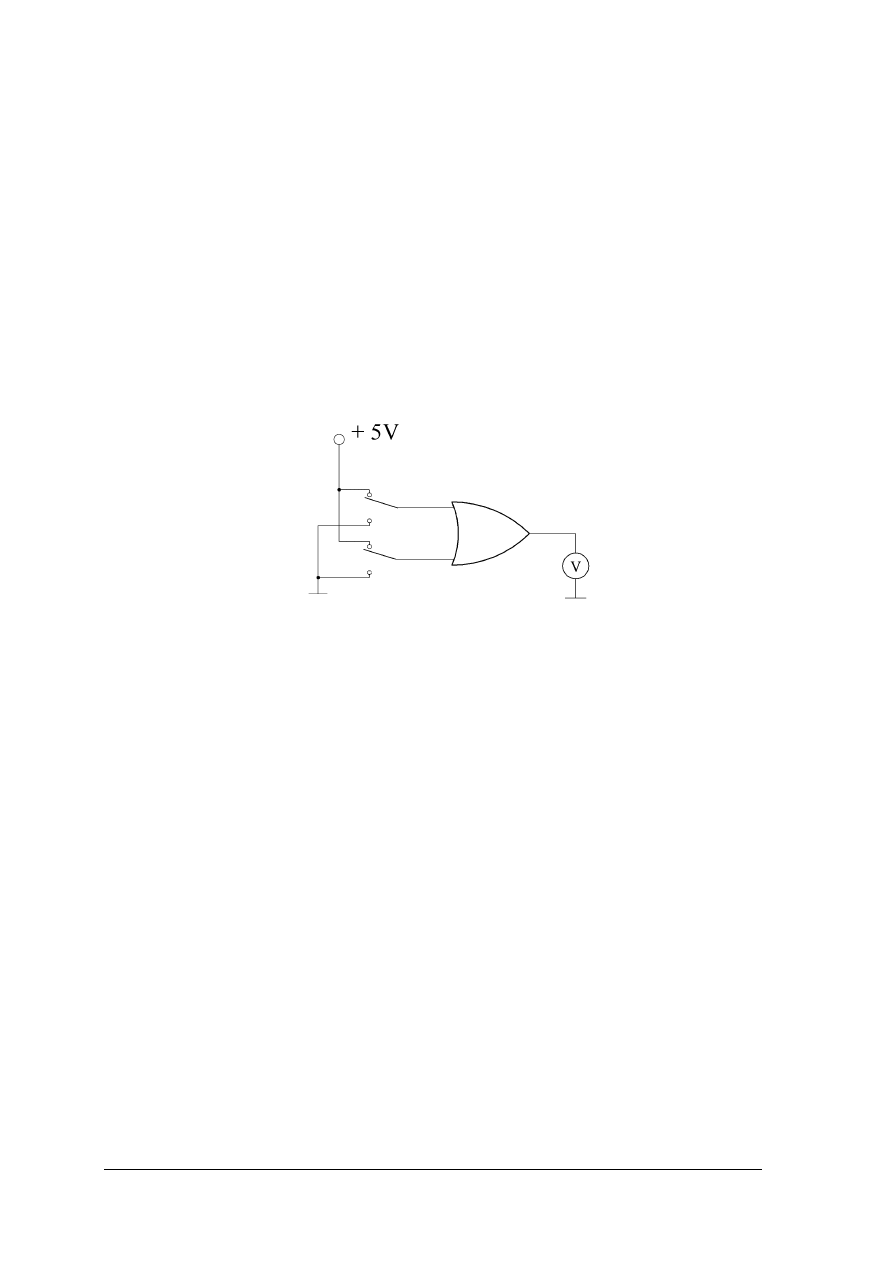
Zbadaj właściwości funkcjonalne bramki NAND.

Rysunek do ćwiczenia 3. Układ do badania właściwości funkcjonalnych bramki NAND

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Uwaga! Przed załączeniem napięcia zasilania układ musi sprawdzić nauczyciel.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zgodnie z tablicą prawdy dla bramki NAND, przyjmując +5 V jako stan 1 logicznej,
0 V jako stan 0 logicznego,

5) sformułować wnioski,
6) sporządzić sprawozdanie z wykonanego ćwiczenia.

Wyposażenie stanowiska pracy:

–

bramka NAND (z układu UCY 7400),

–

zasilacz +5 V,

–

dwa przełączniki dwupozycyjne,

–

multimetr uniwersalny,

–

stanowisko do łączenia układów,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 4

Zbadaj działanie bramki NAND jako negatora.

Rysunek do ćwiczenia 4.

chemat układu realizującego negacjęna bramce NAND [3, s. 31]

Uwaga! Przed załączeniem napięcia zasilania układ musi sprawdzić nauczyciel.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) narysować schemat układu pomiarowego na podstawie rysunku,
3) skompletować potrzebne elementy i aparaturę pomiarową,
4) zbudować układ pomiarowy według zaproponowanego schematu,
5) zmierzyć napięcie U

na wyjściu układu,

6) oszacować dokładność pomiaru,
7) porównać otrzymana wartość z danymi katalogowymi,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

8) sformułować wnioski i sporządzić sprawozdanie z wykonanego ćwiczenia.

Wyposażenie stanowiska pracy:

–

bramka NAND (z układu UCY 7400N),

–

dwa zasilacze regulowane napięcia stałego 0 V

10 V,

–

multimetr cyfrowy,

–

4 rezystory R = 100

Ω

, rezystor R = 5,6 k

Ω

–

stanowisko do łączenia układów,

–

literatura wskazana przez nauczyciela,

–

katalogi elementów elektronicznych,

–

materiały i przybory do pisania.

Ćwiczenie 5

Zbadaj właściwości funkcjonalne bramki OR.

Rysunek do ćwiczenia 5. Układ do badania właściwości funkcjonalnych bramki OR.

Uwaga! Przed załączeniem napięcia zasilania układ musi sprawdzić nauczyciel.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zgodnie z tablicą prawdy dla bramki OR, przyjmując +5 V jako stan 1 logicznej, 0 V jako
stan 0 logicznego,

5) sformułować wnioski,
6) sporządzić sprawozdanie z wykonanego ćwiczenia.

Wyposażenie stanowiska pracy:

–

bramka OR (z układu UCY 7432),

–

zasilacz +5 V,

–

dwa przełączniki dwupozycyjne,

–

multimetr uniwersalny,

–

stanowisko do łączenia układów,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

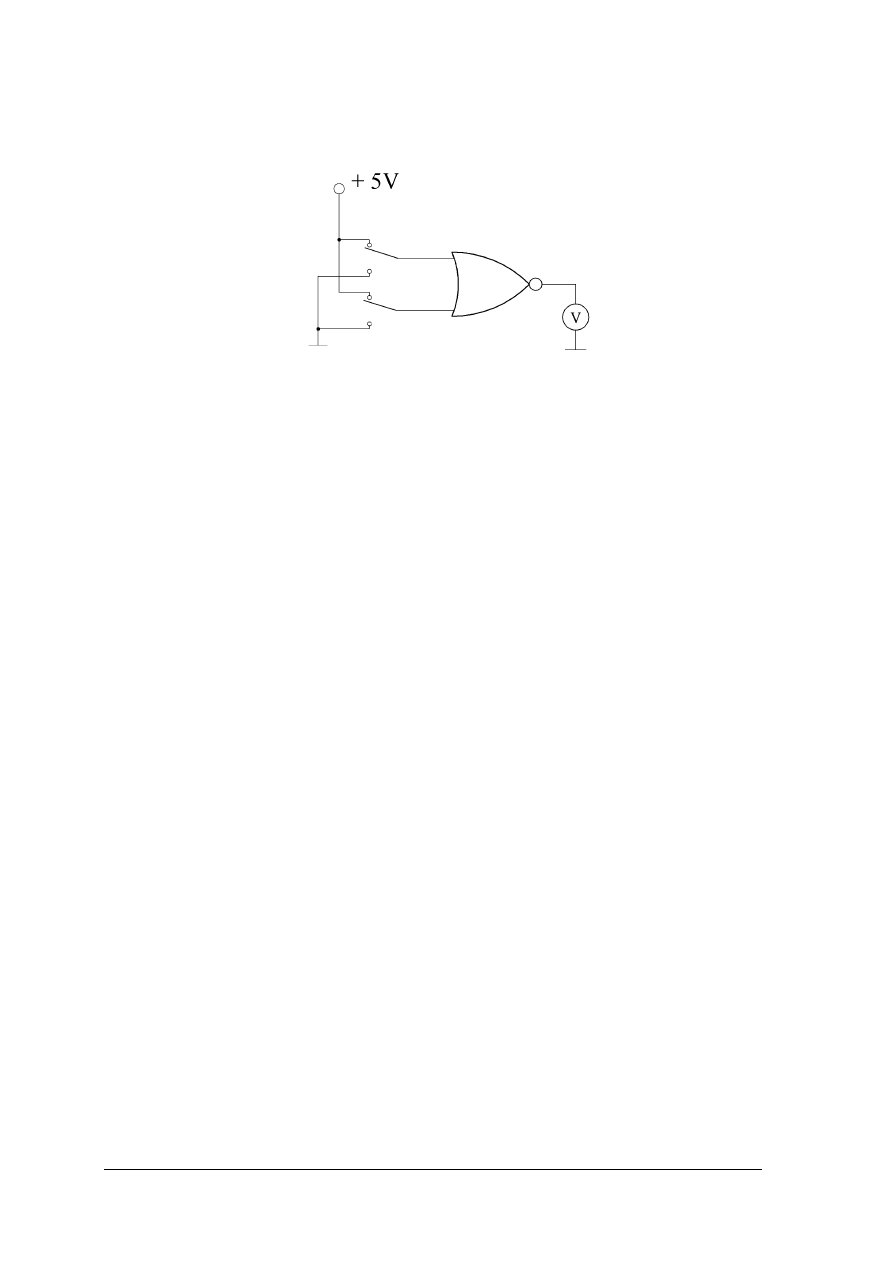
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Ćwiczenie 6

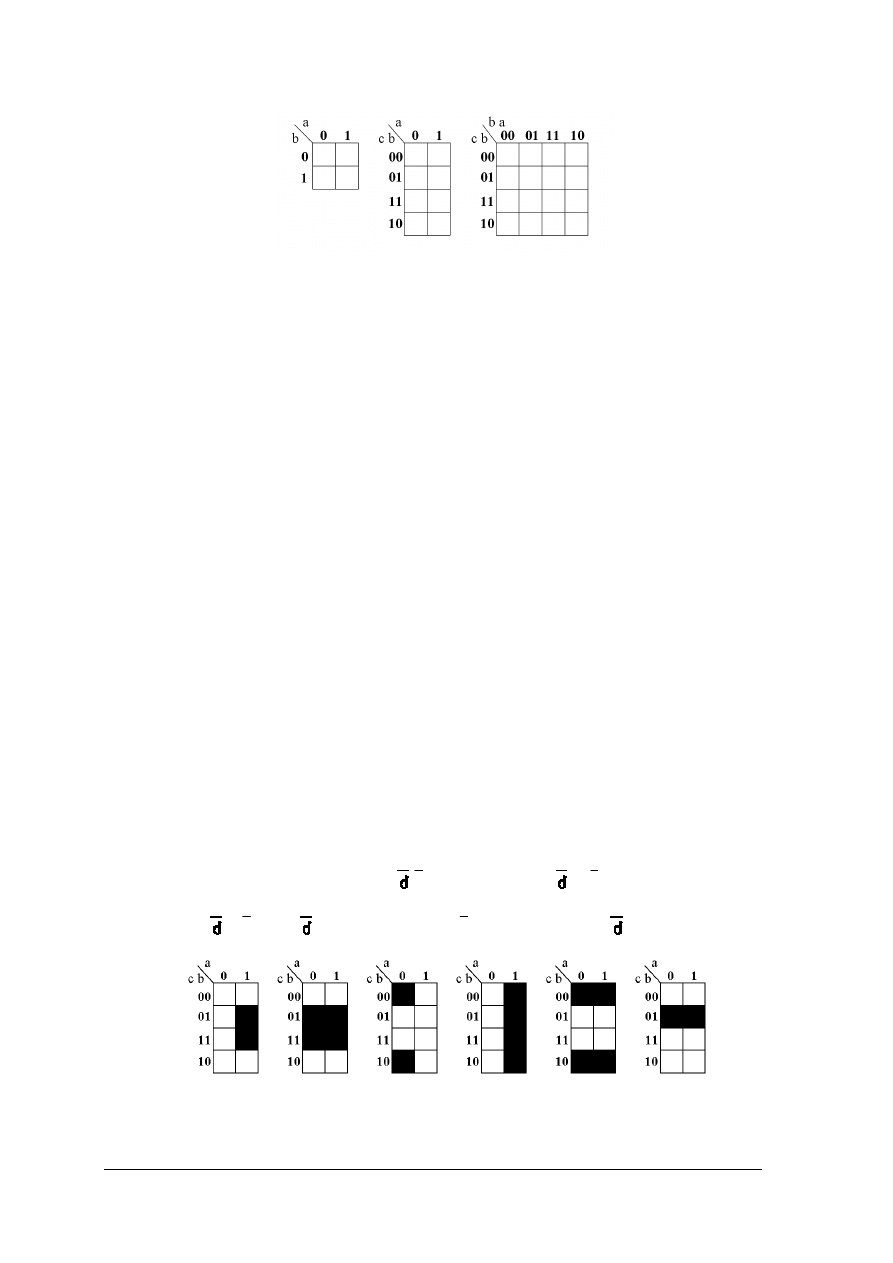
Zbadaj właściwości funkcjonalne bramki NOR.

Rysunek do ćwiczenia 6. Układ do badania właściwości funkcjonalnych bramki NOR.

Uwaga! Przed załączeniem napięcia zasilania układ musi sprawdzić nauczyciel.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

zgodnie z tablicą prawdy dla bramki NOR, przyjmując +5 V jako stan 1 logicznej,
0 jako stan 0 logicznego,

5) sformułować wnioski,
6) sporządzić sprawozdanie z wykonanego ćwiczenia.

Wyposażenie stanowiska pracy:

– bramka NOR (z układu UCY 7402),
– zasilacz +5 V,
– dwa przełączniki dwupozycyjne,
– multimetr uniwersalny,
– stanowisko do łączenia układów,
– literatura wskazana przez nauczyciela,
– materiały i przybory do pisania.

Ćwiczenie 7

Wyjaśnij znaczenie następujących symboli: UCY84LS00N, UCY74LH00N.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) wyjaśnić znaczenia powyższych symboli,
2) sprawdzić w katalogu elementów elektronicznych poprawność analizy znaczeń,
3) zaprezentować wyniki pracy.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Wyposażenie stanowiska pracy:

–

katalogi elementów elektronicznych,

–

materiały i przybory do pisania.

4.3.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) określić wartość sumy logicznej?

2) określić wartość iloczynu logicznego?

3) zastosować prawa algebry Bool’a do minimalizacji wyrażeń?

4) opisać działanie podstawowych bramek logicznych?

5) narysować symbole bramek logicznych?

6) sprawdzić doświadczalnie działanie podstawowych bramek logicznych?

7) rozpoznać typ bramki logicznej na podstawie tablicy prawdy?

8) zrealizować praktycznie negację za pomocą bramek NAND?

9) zrealizować praktycznie iloczyn logiczny za pomocą bramek NAND?

10) określić na podstawie oznaczeń typ cyfrowego układu scalonego?

11) scharakteryzować podstawowe parametry scalonych układów cyfrowych?

12) wyjaśnić znaczenie podstawowych parametrów układów cyfrowych?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.4. Układy kombinacyjne

4.4.1. Materiał nauczania

Układy kombinacyjne to układy cyfrowe, w których każda kombinacja sygnałów

wejściowych określa jednoznacznie kombinację sygnałów wyjściowych.
Kombinacja sygnałów wejściowych jest nazywana stanem wejść układu lub słowem
wejściowym. Kombinacja sygnałów wyjściowych jest nazywana stanem wyjść układu lub
słowem wyjściowym.

Schemat logiczny układu kombinacyjnego można jednoznacznie opisać przy pomocy

funkcji logicznych (funkcji przełączających, funkcji bulowskich). Układy kombinacyjne
buduje się z bramek logicznych.
Działanie układów kombinacyjnych przedstawia się za pomocą:
–

opisu słownego,

–

tablicy prawdy,

–

postaci kanonicznej.

Opis słowny jest pierwotną informacją o funkcjonowaniu układu, nie zawsze jest

on jednoznaczny. Projektowanie układów kombinacyjnych na jego podstawie wymaga
uściśleń.

Tablica prawdy jest wykorzystywana przy opisie działania bramek logicznych. Wiersze

tablicy zawierają wszystkie kombinacje sygnałów wejściowych układu oraz odpowiadające
im stany wyjść układu. Jeśli ze względu na fizyczne działanie urządzenia pewne stany
wejściowe nie mogą zaistnieć, w tablicy prawdy wpisuje się „–”, który traktuje się przy
analizie i minimalizacji funkcji zależnie od potrzeb jako 1 lub 0. Mówimy, że w tym punkcie
funkcja jest nieokreślona.

Tablica prawdy to zwięzły i jednoznaczny opis funkcjonowania układu, bardzo przydatny

przy jego projektowaniu.

Postać kanoniczna jest umownym sposobem opisu obiektów matematycznych. W postaci

tej stosuje się pełne iloczyny czyli iloczyny wszystkich argumentów funkcji i pełne sumy
czyli sumy wszystkich argumentów funkcji.

Wyróżniamy kanoniczną postać sumy będącą sumą pełnych iloczynów funkcji dla

których przyjmuje ona wartość 1 oraz kanoniczną postać iloczynu będącą iloczynem pełnych
sum dla których funkcja przyjmuje wartość 0. Na podstawie postaci kanonicznej można
budować układy kombinacyjne przy użyciu bramek, które jednak ze względu na rozbudowana
strukturę są drogie i zawodne.

Minimalizacja funkcji logicznych
W celu zaprojektowania ekonomicznego i niezawodnego układu kombinacyjnego, czyli

zawierającego jak najmniejszą liczbę elementów i połączeń, stosuje się minimalizacje funkcji
opisującej jego działanie.

Funkcje logiczne można minimalizować stosując prawa algebry Bool’a. Jest to jednak

sposób bardzo pracochłonny i mało efektywny. Istnieją uproszczone sposoby minimalizacji
funkcji logicznej, spośród których najpopularniejszą jest metoda graficzna – tablic Karnaugha
(czyt. Kanacha). Stosuje się ją do minimalizacji funkcji maksymalnie 6 zmiennych. Wiersze
i kolumny tablicy opisane są zmiennymi wejściowymi funkcji zakodowanymi w kodzie
Graya. Każde pole tablicy odpowiada jednej kombinacji zmiennych wejściowych i zawiera
wartość jaką przyjmuje funkcja dla tej kombinacji.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 9. Tablice Karnaugha: a) dwóch zmennych, b) trzech zmiennych, c) czterech zmiennych

Minimalizacja funkcji metodą tablic Karnaugha przebiega w trzech etapach:
1. przygotowanie tablicy dla danej liczby zmiennych i wpisanie w jej pola wartości funkcji,

często na tym etapie bardzo pomocna jest tablica prawdy, której wiersze odpowiadają
odpowiednio opisanym polom tablicy Karnaugha,

2. połączenie w grupy możliwie największych obszarów obejmujących wyłącznie jedynki

lub wyłączne zera logiczne, jeżeli sąsiadujące pola tablicy zawierające te same wartości
(0 lub 1) to odpowiadające tym jedynkom (zerom) pełne iloczyny (pełne sumy) można
skleić – co odpowiada usunięciu litery, która w ramach sklejonej grupy zmienia swoją
wartość,

3. zapisanie funkcji:

–

dla grup jedynek w postaci sumy iloczynów zmiennych wejściowych (jeden iloczyn
odpowiada jednej grupie),

–

dla grup zer w postaci iloczynu sum zmiennych wejściowych (jedna suma
odpowiada jednej grupie).

Zasady zakreślania grup w tablicy Karnaugha:
1. liczba pól elementarnych łączonych ze sobą musi być potęga liczby 2,
2. łączone ze sobą pola muszą by polami sąsiadującymi ze sobą, tzn. linią poziomą,

pionową lub krawędziami tablicy,

3. połączone pola musza mieć kształt symetryczny względem swych osi (kwadraty,

prostokąty),

4. dla tablic 5 zmiennych obowiązuje zasada: jeśli zakreślone pola znajdują się w obu

połówkach tablicy, to w wyniku złożenia tej tablicy względem osi dzielącej ja na dwie
symetryczne części zakreślony obszar powinien się dwukrotnie zmniejszyć i spełniać
zasadę określona w punkcie 3,

5. jeśli w tablicy znajduje się „–” (funkcja jest nieokreślona), to pola takie można łączyć

z jedynkami bądź z zerami.

Grupa 1

c b

Grupa 0

+ a

a + b

Rys. 10. Przykłady sklejania w tablicy trzech zmiennych [1, s. 49]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Projektowanie układów kombinacyjnych

Układ kombinacyjny powinien być projektowany tak, by zawierał jak najmniejszą liczbę

elementów i połączeń, co zapewnia większą niezawodność i niskie koszty wykonania.
W celu zaprojektowania układu kombinacyjnego należy zrealizować kolejno trzy etapy:
1. określić funkcję logiczną rozpatrywanego problemu, może to być postać kanoniczna lub

tablicy prawdy,

2. zminimalizować określoną funkcję logiczna wykorzystując np. tablice Karnaugha,
3. sporządzić schemat połączeń elementów logicznych układu.

Układy komutacyjne

Multipleksery, demultipleksery oraz niektóre przetworniki kodów to układy komutacyjne

czyli układy kombinacyjne umożliwiające przełączanie sygnałów cyfrowych.

Multiplekser służy do wyboru jednego z sygnałów wejściowych i przekazania go na

wyjście układu. Multiplekser posiada:
–

N wejść informacyjnych (danych), na które podawane są sygnały, który należy
przełączać;

–

n wejść adresowych (sterujących), sygnały podane na te wejścia określają numer wejścia
z którego sygnał przeniesiony zostanie na wyjście;

–

wejście zezwalające (strobujące), podanie aktywnego sygnału na nie umożliwia działanie
multipleksera;

–

jedno wyjście.

Adresowanie wejść informacyjnych realizowane jest w naturalnym kodzie binarnym zatem
ilość N wejść informacyjnych multipleksera powiązana jest ilością n wejść adresowych
zależnością:

N = 2

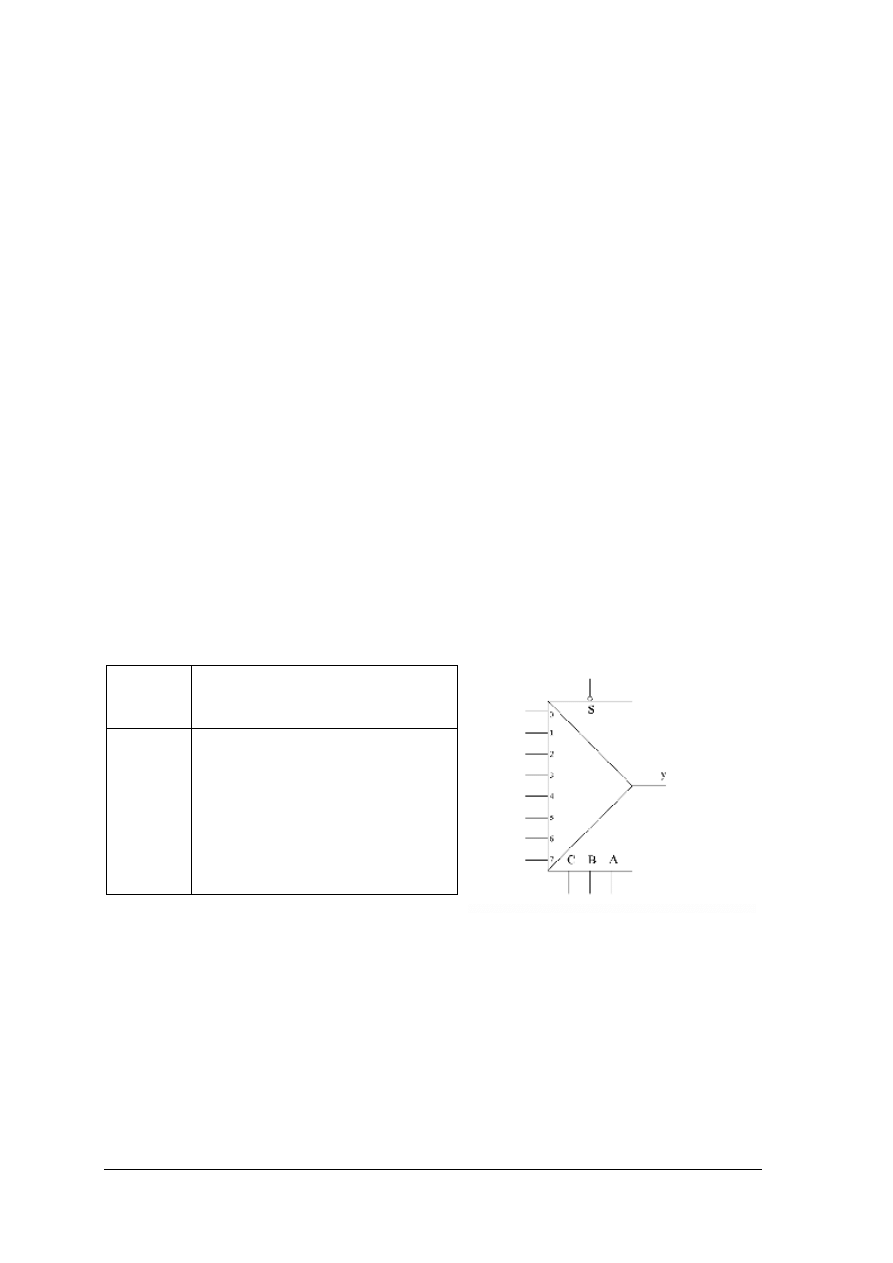
Rys. 11. Multiplekser ośmiowyjściowy a) tablica działania, b) symbol graficzny multipleksera. [1, s. 201]

Demultiplekser umożliwia przekazanie sygnału z wejścia informacyjnego do jednego

z jego wyjść. Demultiplekser posiada:
–

jedno wejście informacyjne;

–

N wyjść;

–

n wejść adresowych (sterujących), sygnały podane na te wejścia określają numer wyjścia
na które sygnał zostanie przeniesiony sygnał z wejścia;

–

wejście zezwalające (strobujące), podanie aktywnego sygnału na nie umożliwia działanie
demultipleksera.

Adresowanie wyjść realizowane jest w naturalnym kodzie binarnym zatem ilość N wyjść
demultipleksera powiązana jest ilością n wejść adresowych zależnością:

wejścia

adresowe

C B A

nr wejścia danych z którego sygnał

pojawi się na wyjściu

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

0
1
2
3
4
5
6
7

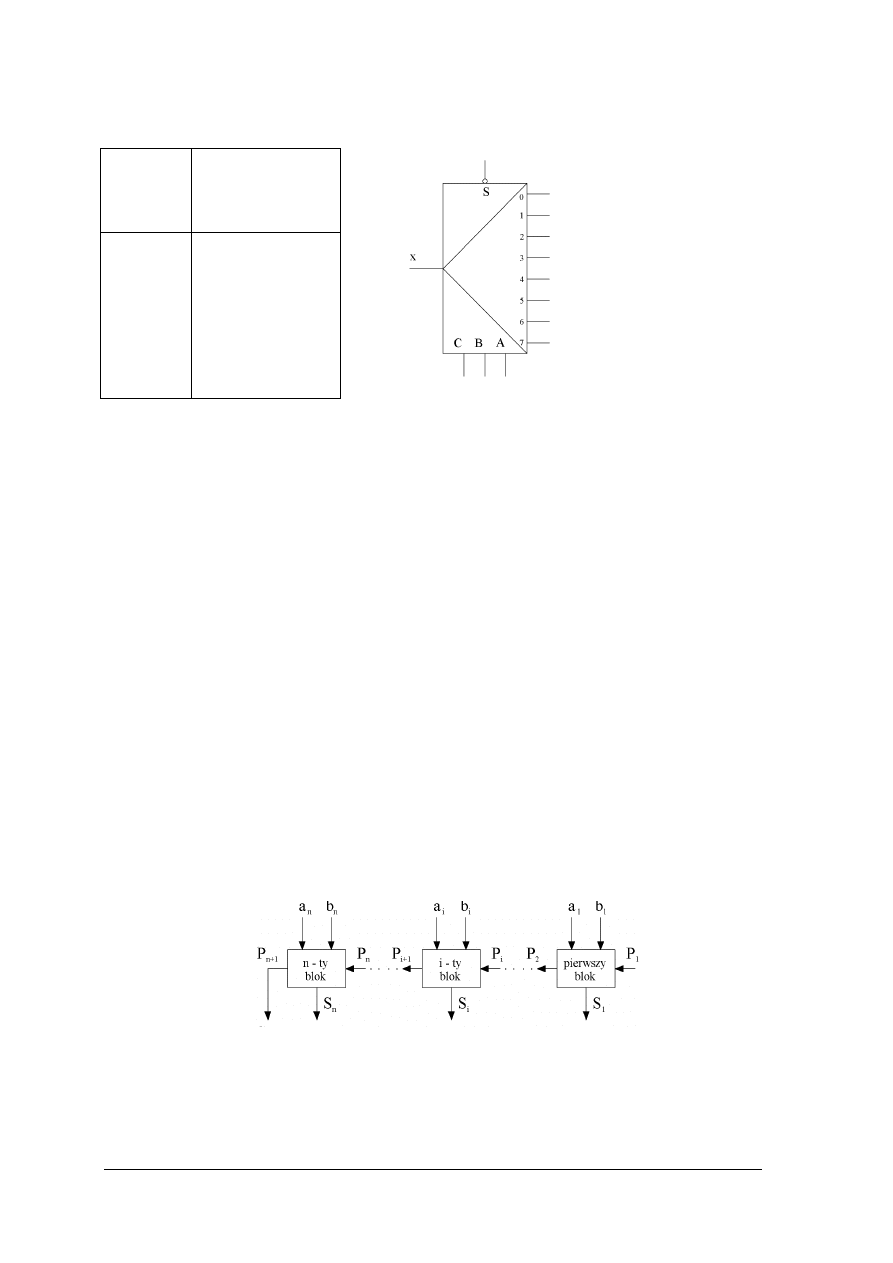
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

N = 2

Rys. 12. Demultiplekser ośmiowejściowy a) tablica działania, b) symbol graficzny. [1, s. 203]

Multipleksery i demultiplekser służą do realizacji funkcji logicznych, adresowania pamięci
i innych układów w systemach cyfrowych.

Przetworniki kodów inaczej zwane konwerterami kodów dokonują zamiany kodów.

Układ realizujący zamianę informacji w kodzie 1 z n na kod wewnętrzny urządzenia nazywa
się koderem (enkoderem).
Układ zamieniający dowolny kod na kod 1 z n nazywa się dekoderem.
Układ zamieniający jeden kod wewnętrznych urządzenia na inny (żaden z nich nie jest kodem
1 z n) nazywa się transkoderem.

Układy arytmetyczne
Układy cyfrowe umożliwiające realizację podstawowych działań arytmetycznych

nazywamy układami arytmetycznymi.

Sumatory to podstawowe układy arytmetyczne to które prócz dodawania mogą

po zastosowaniu dodatkowych przekształceń realizować mnożenie, odejmowanie i dzielenie.
Rozróżniamy sumatory równoległe i szeregowe.

Sumatory równoległe umożliwiają dodawanie dwóch liczb n–bitowych, ponieważ

zbudowane są z n elementarnych sumatorów połączonych kaskadowo, z których każdy dodaje
dwa odpowiednie bity obu liczb. Układ taki nazywamy iteracyjnym.

Rys. 13. Schemat blokowy sumatora równoległego [1, s. 61]

W sumatorze szeregowym dodawane składniki są podawane na wejście kolejno. Układ ten
posiada pamięć oraz układ sterowania. Podstawowy cykl pracy sumatora szeregowego polega
na dodaniu dwóch bitów i określeniu wyniku sumowania i bitu przeniesienia. Powtarzany

wejścia

adresowe

C B A

nr wyjścia

7 6 5 4 3 2 1 0

0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 0
0 0 0 0 0 1 0 0
0 0 0 0 1 0 0 0
0 0 0 1 0 0 0 0
0 0 1 0 0 0 0 0
0 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0

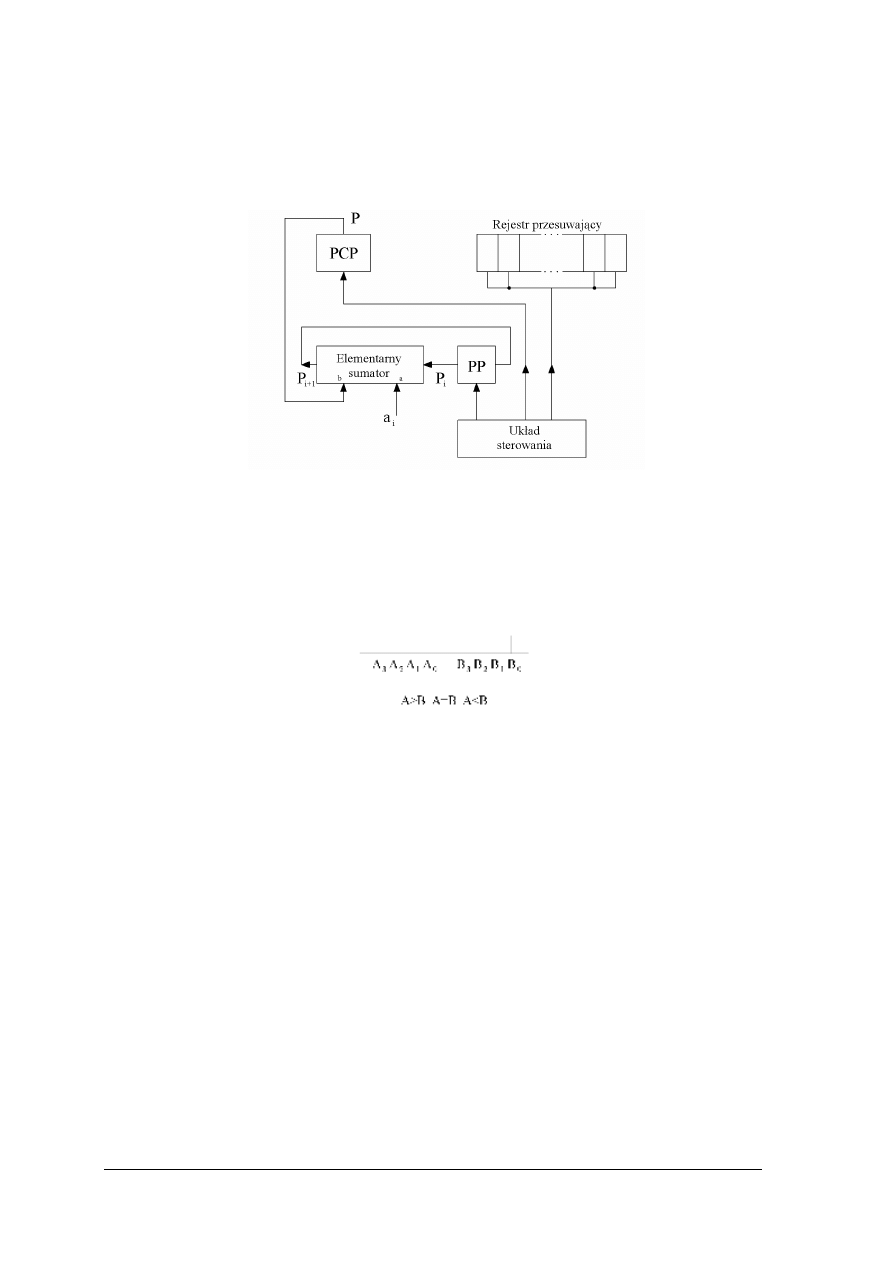
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

n–razy umożliwia dodawanie n–bitowych liczb. Pamięć układu zrealizowana z rejestrów
przesuwających powinna być tak rozbudowana aby pomieściła kolejne wyniki kolejnych
operacji dodawania. Sumator szeregowy może dodawać ciągle nowe składniki (gromadzić
– akumulować) dlatego nazywany jest akumulatorem.

Rys. 14. Schemat funkcjonalny sumatora elementarnego w układzie akumulatora PCP – pamięć cyklu,

podstawowego PP – pamięć przeniesienia [1, s. 123]

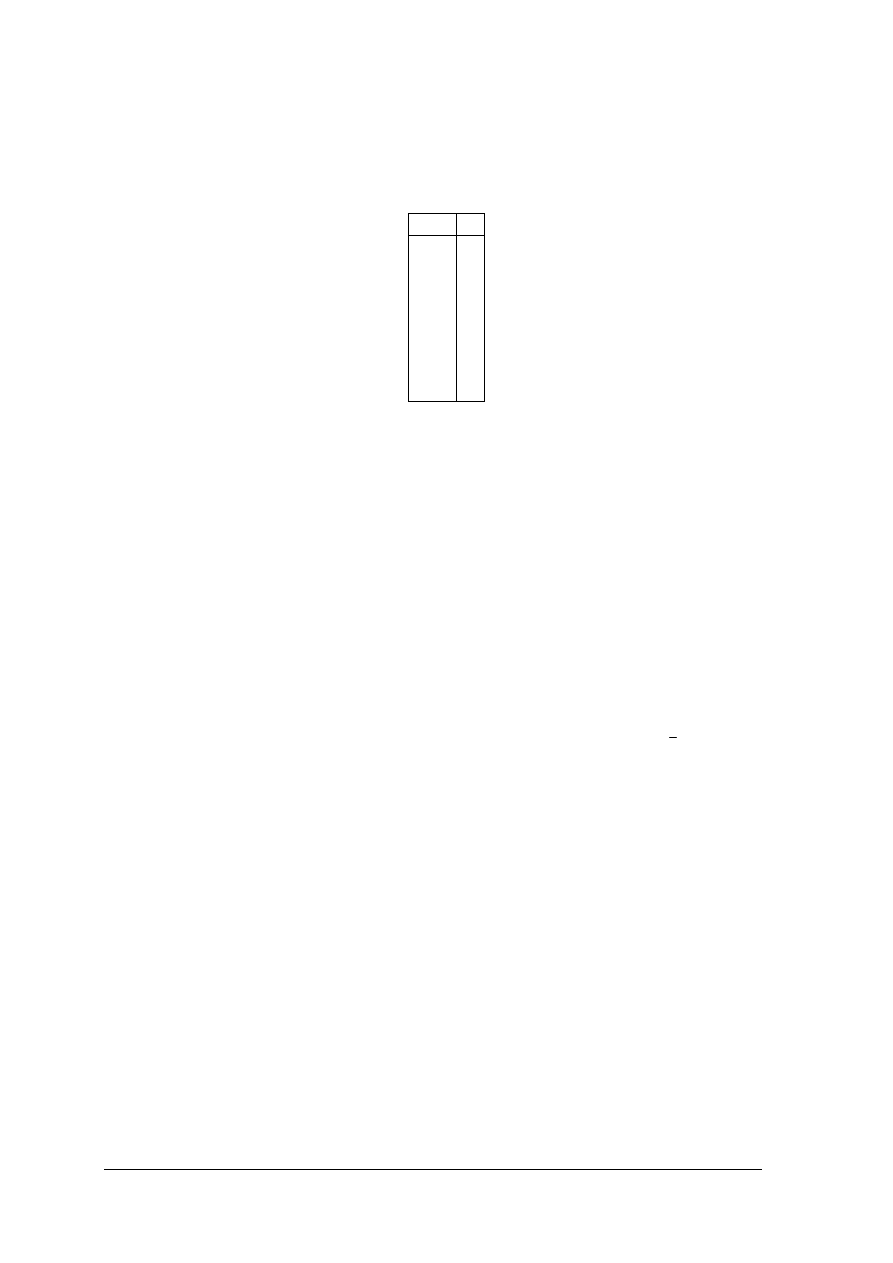
Komparator służy do porównania dwóch liczb. Układ ten posiada dwa wejścia

n–bitowe na które podawane są porównywane liczy A i B oraz trzy wyjścia (A=B), (A>B),
(A<B) gdzie sygnalizowany jest wynik porównania. Komparatory realizuje się jako układy
iteracyjne.

Rys. 15. Symbol graficzny komparatora czterobitowego [1, s. 233]

Układy wyjściowe

Informacja wyjściowa układów cyfrowych jest przetwarzania i służy do wysterowania

pewnych obiektów, bardzo często jest wizualizowana za pomocą układów wyświetlania
zbudowanych z diod świecących lub wskaźników ciekłokrystalicznych. W przypadku diod
LED moc sygnałów wyjściowych z elementów TTL czy MOS jest zbyt mała by je
wysterować.

Wskaźniki elektroluminescencyjne to najczęściej pojedyncze diody LED (ang. Light

Emitting Diode) lub zbudowane z nich wskaźniki alfanumeryczne. Do sterowania diod
świecących można użyć dowolnych bramek TTL z wyjściem przeciwsobnym lub otwartym
kolektorem. Należy pamiętać, że sterują diodą LED ze źródła napięcia stałego, należy
włączyć szeregowo z nią rezystor ograniczający prąd. Wartość rezystora należy dobrać tak,
aby prąd płynący przez diodę nie przekraczał wartości jej prądu przewodzenia i dopuszczalnej
wartości prądu wyjściowego bramki.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 16. Układ sterowania diody LED z bramek TTL z wyjściem przeciwsobnym lub otwartym kolektorem.

[1, s.184]

W przypadku układów CMOS charakteryzujących się niskim prądem wyjściowym wymaga
zastosowania bufora np. układu MCY74050. W układzie tym również stosuje się rezystor
ograniczający prąd płynący przez diodę. Element wskaźników siedmiosegmentowych
ze wspólna anodą mogą być sterowane za pomocą wzmacniacza tranzystorowego,
a ze wspólna katodą za pomocą wtórnika emiterowego.

Rys. 17. Układ sterowania diody LED z układu CMOS za pomocą a) bufora b) wzmacniacza tranzystorowego,

c) wtórnika emiterowego [1, s.188]

Wskaźniki ciekłokrystaliczne wymagają znikomo małych mocy sygnałów sterujących

w porównaniu z mocą sygnałów wyjściowych elementów TTL czy CMOS.

4.4.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Czym charakteryzuje się układ kombinacyjny?
2. Z jakich elementów zbudowane są układy kombinacyjne?
3. Jakie znasz sposoby opisu działania układów kombinacyjnych?
4. Jak zbudowana jest tablica prawdy?
5. Jakie są zasady minimalizacji funkcji za pomocą tablicy Karnaugha?
6. Jakie są etapy projektowania układów kombinacyjnych?
7. Do czego służą układy komutacyjne?
8. Jak działa multiplekser?
9. Jak działa demultiplekser?
10. Co to znaczy, że układ jest iteracyjnym?
11. Czym różni się sumator szeregowy od równoległego?
12. Jaką operację realizuje komparator?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.4.3. Ćwiczenia

Ćwiczenie 1

Zminimalizuj za pomocą tablicy Karnaugha funkcję y – z opisaną tablicą prawdy.

c b a y
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

0
1
–
0
0
1
1
0

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) zbudować tablicę Karnaugha trzech zmiennych,
3) wypełnić jej pola zgodnie z tablicą prawdy,
4) zaznaczyć grupy zer lub jedynek,
5) zapisać postać funkcji y wynikający ze sklejenia grup,
6) zaprezentować wyniki pracy

Wyposażenie stanowiska pracy:

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 2

Zbuduj układ kombinacyjny realizujący funkcję logiczną y = a + c

b . Zbadaj jego

działanie.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) stworzyć tablicę prawdy dla funkcji y,
3) narysować schemat układu kombinacyjnego realizującego funkcję y,
4) zgromadzić potrzebne elementy i urządzenia,
5) zbudować układ według schematu,
6) podająć na jego wejścia kombinacje zmiennych wejściowych, sprawdzić działanie układu

zgodnie z tablicą prawdy,

7) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

układ UCY 7400,

–

układ UCY 7432,

–

zasilacz napięcia stałego +5 V,

–

próbnik stanów logicznych,

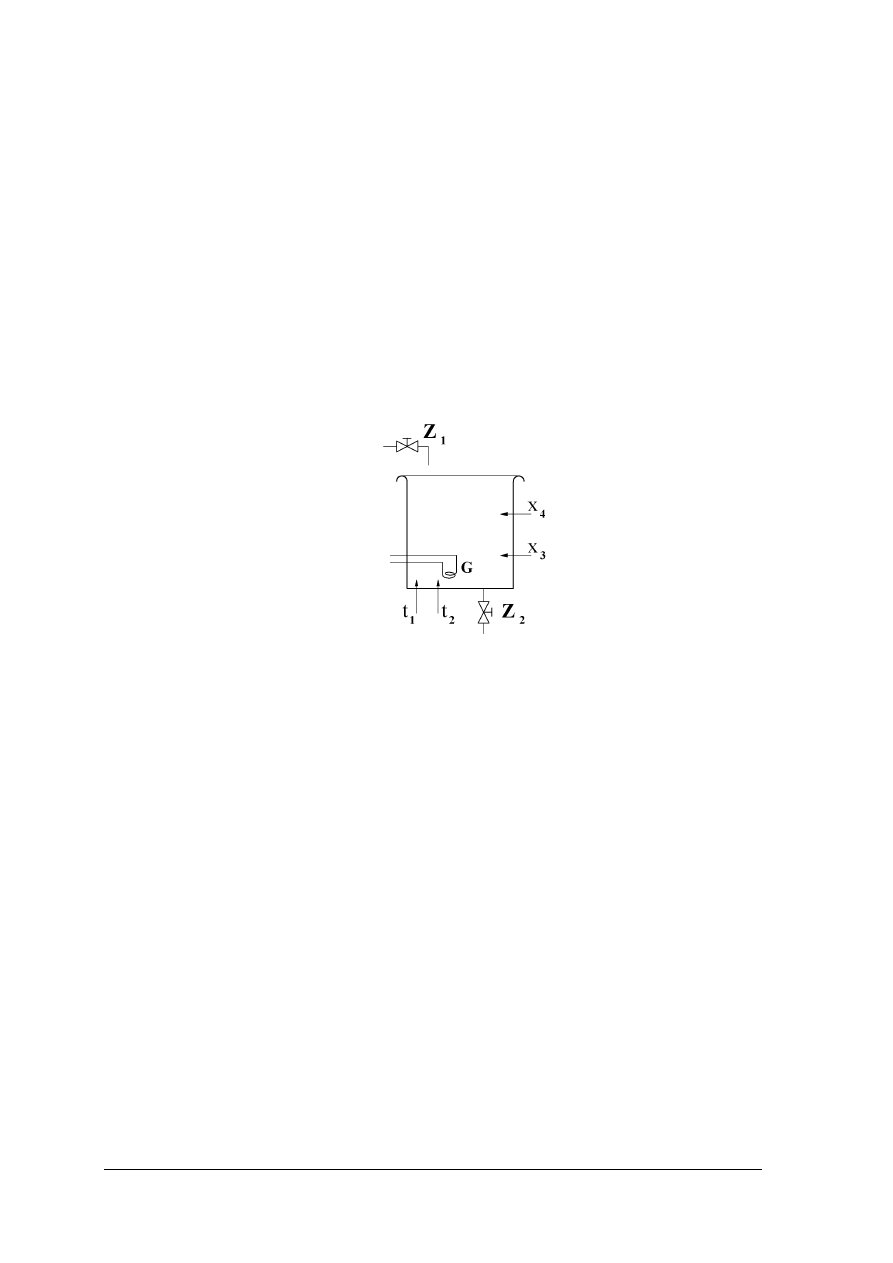
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

–

stanowisko do łączenia układów,

–

katalogi elementów elektronicznych,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 3

Na podstawie opisu słownego działania układu napisz tablicę prawdy potrzebną do

realizacji układu kombinacyjnego sterującego zaworami Z

i Z

oraz grzałką G.

Rysunek przedstawia zbiornik, w którym podgrzewana jest woda. Woda do zbiornika

doprowadzana jest woda zaworem Z

, jej poziom sygnalizowany jest za pomocą dwóch

czujników x

dla poziomu minimalnego i x

dla poziomu maksymalnego. Temperaturę wody

sygnalizują natomiast czujniki t

– temperatura minimalna i t

– temperatura maksymalna.

Grzałka G może być załączona, gdy w zbiorniku jest minimalny poziom wody. Zawór
Z

otwierany jest wówczas gdy poziom wody jest większy od minimalnego a jej temperatura

T spełnia zależność t

< T < t

Rysunek do ćwiczenia 3. Schemat poglądowy zbiornika

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) określić zmienne wejściowe,
3) określić zmienne wyjściowe,
4) stworzyć tablicę prawdy opisującą działanie układu,
5) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 4

Zaprojektuj, a następnie zbuduj układ prostego kodera 2–bitowego kodu binarnego na

kod 1 z 4, używając dwuwejściowych bramek NAND. Zbadaj działanie zmontowanego
układu.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) zapisać tablicę działania kodera 2–bitowego kodu binarnego na kod 1 z 4,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

3) narysować schemat ideowy kodera,
1) zgromadzić potrzebne elementy i urządzenia,
4) zmontować układ kodera z bramek dwuwejściowych NAND,
5) zbadać działanie kodera próbnikiem stanów logicznych, podając na wejścia sygnały

zgodnie z tablicą działania kodera,

6) sformułować wnioski i sporządzić sprawozdanie z ćwiczenia.

Uwaga! Przed załączeniem napięcia zasilania układ musi sprawdzić nauczyciel.

Wyposażenie stanowiska pracy:

–

3 układy UCY 7400N,

–

zasilacz napięcia stałego +5 V,

–

próbnik stanów logicznych,

–

stanowisko do łączenia układów,

–

literatura wskazana przez nauczyciela,

–

katalogi elementów elektronicznych,

–

materiały i przybory do pisania.

Ćwiczenie 5

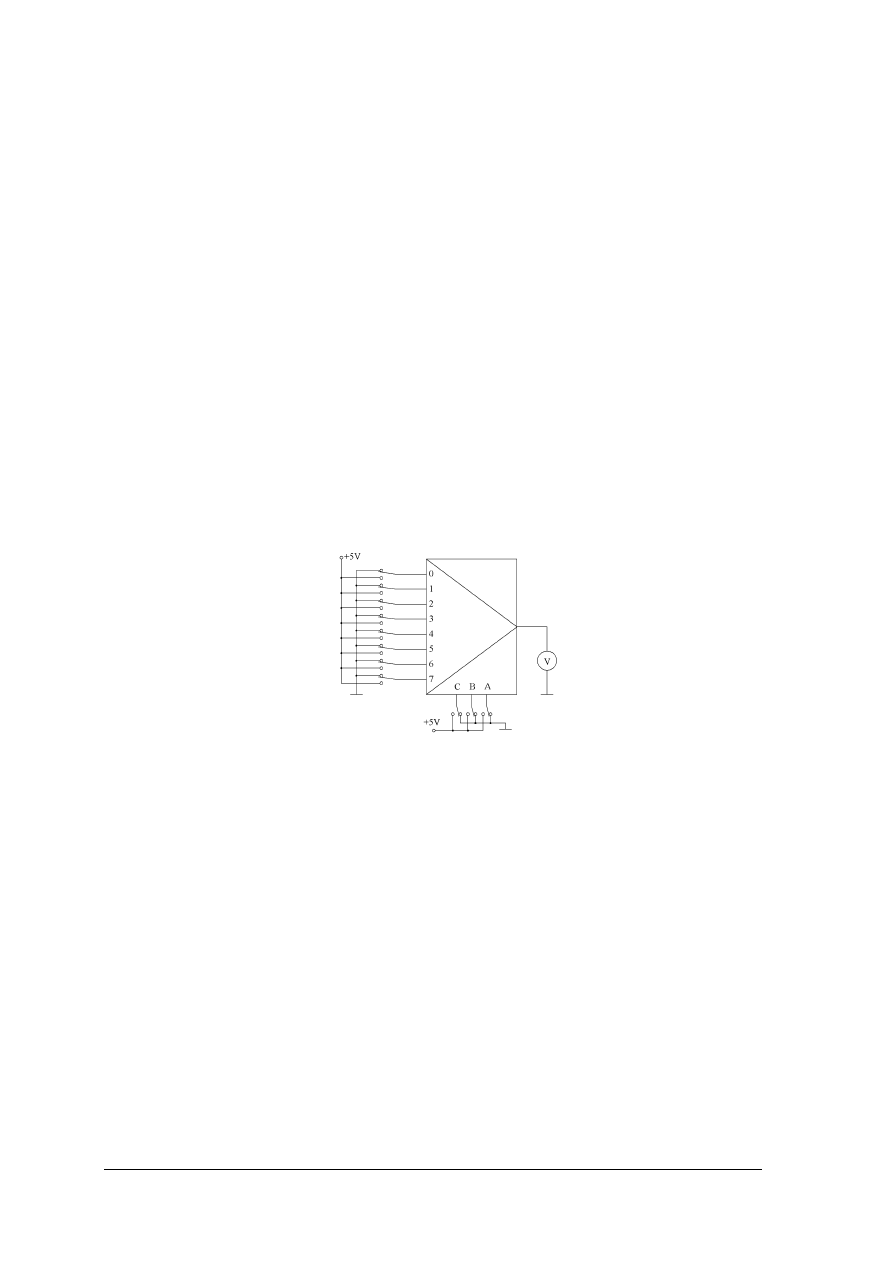
Zbadaj właściwości funkcjonalne multipleksera.

Rysunek do ćwiczenia 5. Schemat układu do badania właściwości funkcjonalnych multipleksera

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) zapisać tablicę działania multipleksera,
3) zgromadzić potrzebne elementy i urządzenia,
4) zmontować układ z rysunku,
5) zbadać działanie układu: zadając na wejścia adresowe kombinacje sygnałów cyfrowych,

na odpowiednie wejście 1 logiczną (na pozostałe wejścia należy podać 0 logiczne),
sprawdzać zgodność działania multipleksera z zapisami w tablicy,

6) sformułować wnioski i sporządzić sprawozdanie z ćwiczenia.

Uwaga! Przed załączeniem napięcia zasilania układ musi sprawdzić nauczyciel.

Wyposażenie stanowiska pracy:

–

układ UCY 74151,

–

zasilacz napięcia stałego +5 V,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

–

11 przełączników dwupozycyjnych,

–

multimetr uniwersalny,

–

stanowisko do łączenia układów,

–

literatura wskazana przez nauczyciela,

–

katalogi elementów elektronicznych,

–

materiały i przybory do pisania.

Ćwiczenie 6

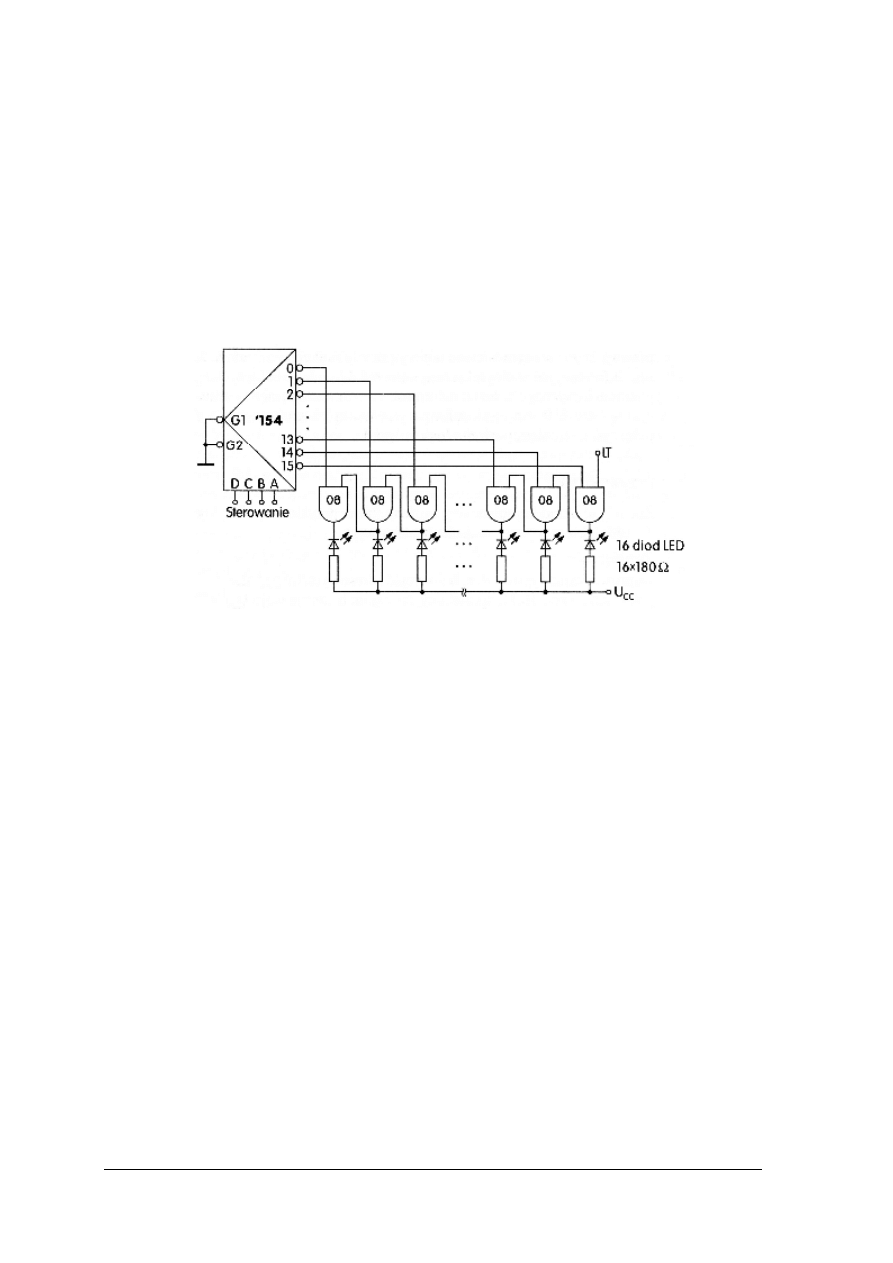
Zbuduj układ wskaźnika diodowego tzw. linijki świetlnej sterowanej z demultipleksera

i zbadaj jego działanie.

Rysunek do ćwiczenia 6. Schemat układu sterującego linijką świetlną [1, s. 207]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) zapisać tablicę działania demultipleksera, określając dla każdej kombinacji sygnałów

wejściowych, która z diod LED powinna się zaświecić,

3) zgromadzić potrzebne elementy i urządzenia,
4) zmontować układ z rysunku,
5) zbadać działanie układu: zadając na wejścia adresowe kombinacje sygnałów cyfrowych,

sprawdzać zgodność świecenia diod z zapisami w tablicy działania demultipleksera,

6) sformułować wnioski i sporządzić sprawozdanie z ćwiczenia.

Uwaga! Przed załączeniem napięcia zasilania układ musi sprawdzić nauczyciel.

Wyposażenie stanowiska pracy:

–

2 układy UCY 7408,

–

układ UCY 74154,

–

16 rezystorów 180

Ω

–

16 diod LED

–

zasilacz napięcia stałego +5 V,

–

próbnik stanów logicznych,

–

stanowisko do łączenia układów,

–

literatura wskazana przez nauczyciela,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

–

katalogi elementów elektronicznych,

–

materiały i przybory do pisania.

4.4.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) stworzyć tablicę prawdy na podstawie opisu słownego działania układu

kombinacyjnego?

2) zapisać postać funkcji logicznej dla danej tablicy prawdy?

3) stworzyć tablicę Karnaugha dla na podstawie tablicy prawdy?

4) sklejać grupy tablicy Karnaugha?

5) zapisać postać funkcji wynikającą ze sklejenia grup?

6) zbudować układ kombinacyjny realizujący określoną funkcję logiczną

i sprawdzić jego działanie?

7) sterować demultiplekserem wskaźnik informacji cyfrowej?

8) zbudować układ prostego kodera?

9) opisać działanie komparatora?

10) scharakteryzować budowę sumatorów?

11) zbudować prosty układ sumatora dwóch liczb dwubitowych?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.5. Układy sekwencyjne

4.5.1. Materiał nauczania

Przerzutniki

Przerzutniki to układy służące do zapamiętywania wartości wybranych zmiennych

logicznych. Przerzutnik posiada co najmniej dwa wejścia i zazwyczaj dwa wyjścia

Q i Q . Wejścia mogą być:
–

zegarowe zwane również synchronizującymi lub wyzwalającymi, oznaczone C (ang.
Clock),

–

informacyjne,

–

programujące: ustawiające w stan wysoki - oznaczone S lub PR (ang. Set lub PReset),
ustawiające w stan niski nazywane zerującym - oznaczone R lub CLR (ang. Reset lub
CLeaR).

Działanie przerzutnika opisuje się za pomocą:
–

tablicy przejść, która określa kolejny stan przerzutnika w zależności od aktualnego stanu
jego wejść i wyjść;

–

tablicy charakterystycznej, będącej bardziej skomplikowaną postacią tablicy przejść:

–

tablicy wzbudzeń, która określa jaki powinien być stan wejść informacyjnych, aby
przerzutnik przeszedł z jednego stanu w drugi;

–

wykresu czasowego.

Przerzutniki dzielimy na:
–

asynchroniczne, które nie posiadają wejścia zegarowego,

–

synchroniczne, które reagują na informacje podaną na wejścia informacyjne tylko
w obecności aktywnego sygnału zegarowego (stan wejść informacyjnych powinien być
wówczas ustalony).

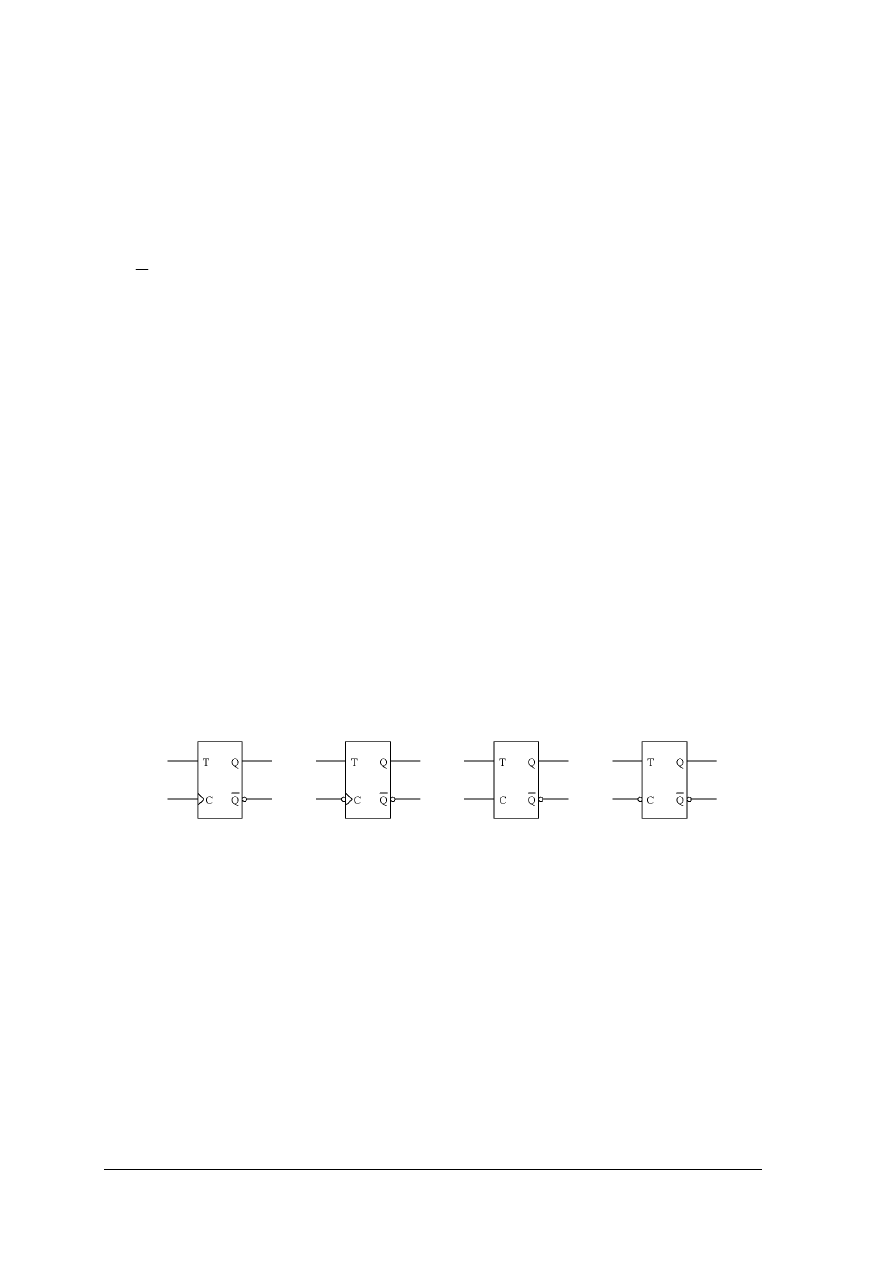
Przerzutniki synchroniczne mogą być wyzwalane poziomem niskim lub wysokim sygnału
zegarowego, albo jego zboczem opadającym bądź narastającym.

Rys. 18. Symbole przerzutników typu T wyzwalanych a) zboczem narastającym, b) zboczem opadającym,

c) poziomem wysokim, d) poziomem niskim [1, s. 123]`

Przerzutniki służą do budowy układów sekwencyjnych między innymi liczników i rejestrów

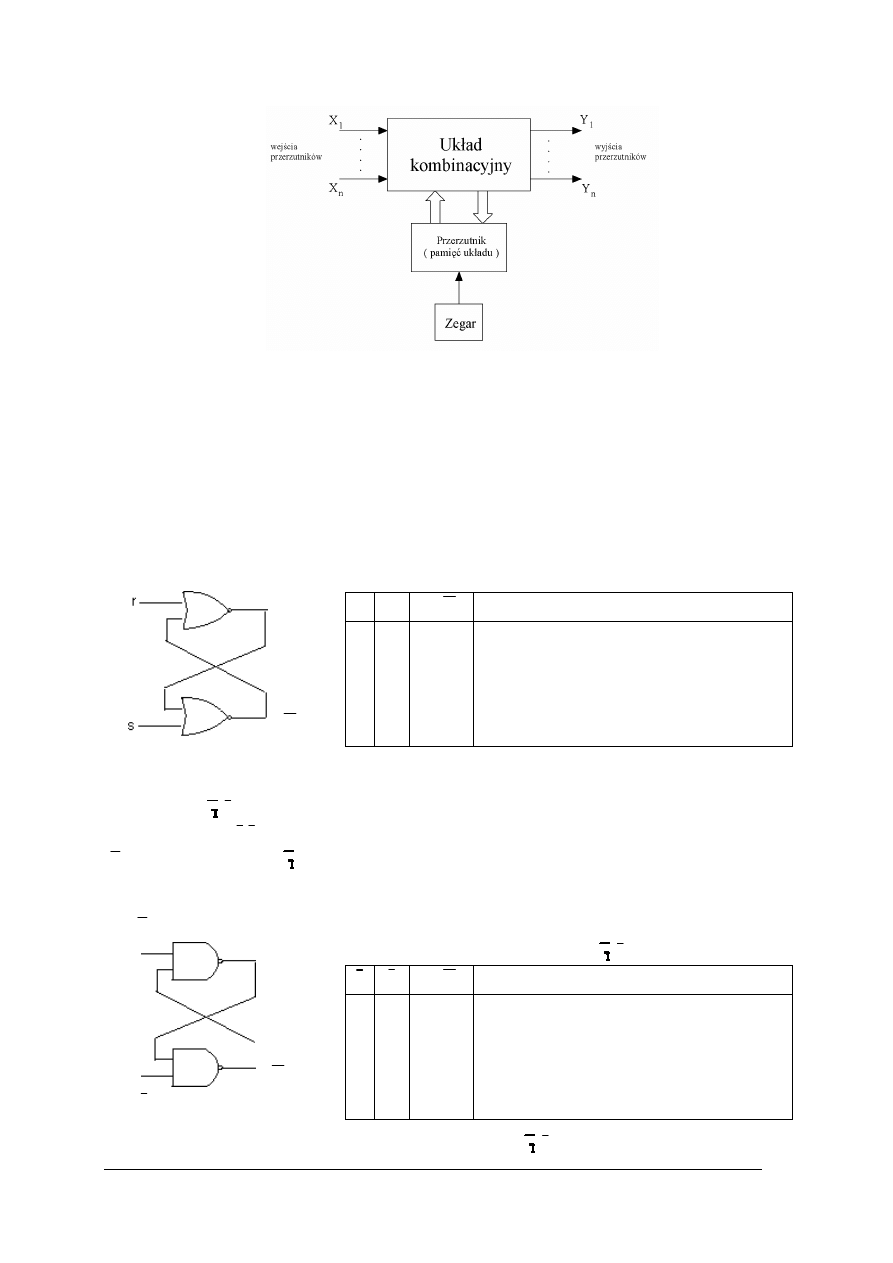
Układy sekwencyjne

Układy sekwencyjne są układami kombinacyjnymi wyposażonymi w pamięć. Stan wyjść

w układzie sekwencyjnym zależy od słowa wejściowego oraz od poprzednich stanów
wyjściowych. Elementem pamiętającym w układzie sekwencyjnym jest przerzutnik.
Jednocześnie przerzutnik jest najprostszym układem sekwencyjnym.

Układy sekwencyjne dzielimy na synchroniczne i asynchroniczne. Stan układu

synchronicznego zmienia się przy aktywnym sygnale synchronizującym, natomiast stan
układu asynchronicznego pozostaje tak długo niezmienny, jak długo nie zmienia się stan jego
wejść.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 19. Schemat poglądowy sekwencyjnego układu synchronicznego [1, s. 33]

Przerzutniki asynchroniczne

Przerzutnik r s

Przerzutnik rs zbudowany jest z dwóch bramek NOR, posiada dwa wejścia

s – ustawiające oraz r – zerujące. Aktywnym stanem logicznym tego przerzutnika jest
jedynka. Wymuszenie jedynki na obu wejściach jest stanem zabronionym natomiast podanie
zera na oba wejścia powoduje zapamiętanie informacji wpisanej do przerzutnika.

Tabela 4. Stany stabilne przerzutnika r s

Rys. 20. Schemat logiczny przerzutnika r s. [1, s. 117]

Przerzutnik

Przerzutnik r s zbudowany jest z dwóch bramek NAND, posiada dwa wejścia

– ustawiające oraz

– zerujące. Aktywnym stanem logicznym tego przerzutnika jest

zero. Wymuszenie zera na obu wejściach jest stanem zabronionym natomiast podanie jedynki
na oba wejścia powoduje zapamiętanie informacji wpisanej do przerzutnika

Tabela 5. Stany stabilne przerzutnika

Rys. 21. Schemat logiczny przerzutnika

[1, s. 119]

Q Q

Stan stabilny

1
1
0

1
0
1

0 0
0 1
1 0
0 1

1 0

Stan wejść logicznie zabroniony

Przerzutnik ustawiony w stan 0
Przerzutnik ustawiony w stan 1

Pamiętanie stanu 0

Pamiętanie stanu 1

Q Q

Stan stabilny

0
0
1

0
1
0

1 1
0 1
1 0
0 1

1 0

Stan wejść logicznie zabroniony

Przerzutnik ustawiony w stan 0
Przerzutnik ustawiony w stan 1

Pamiętanie stanu 0

Pamiętanie stanu 1

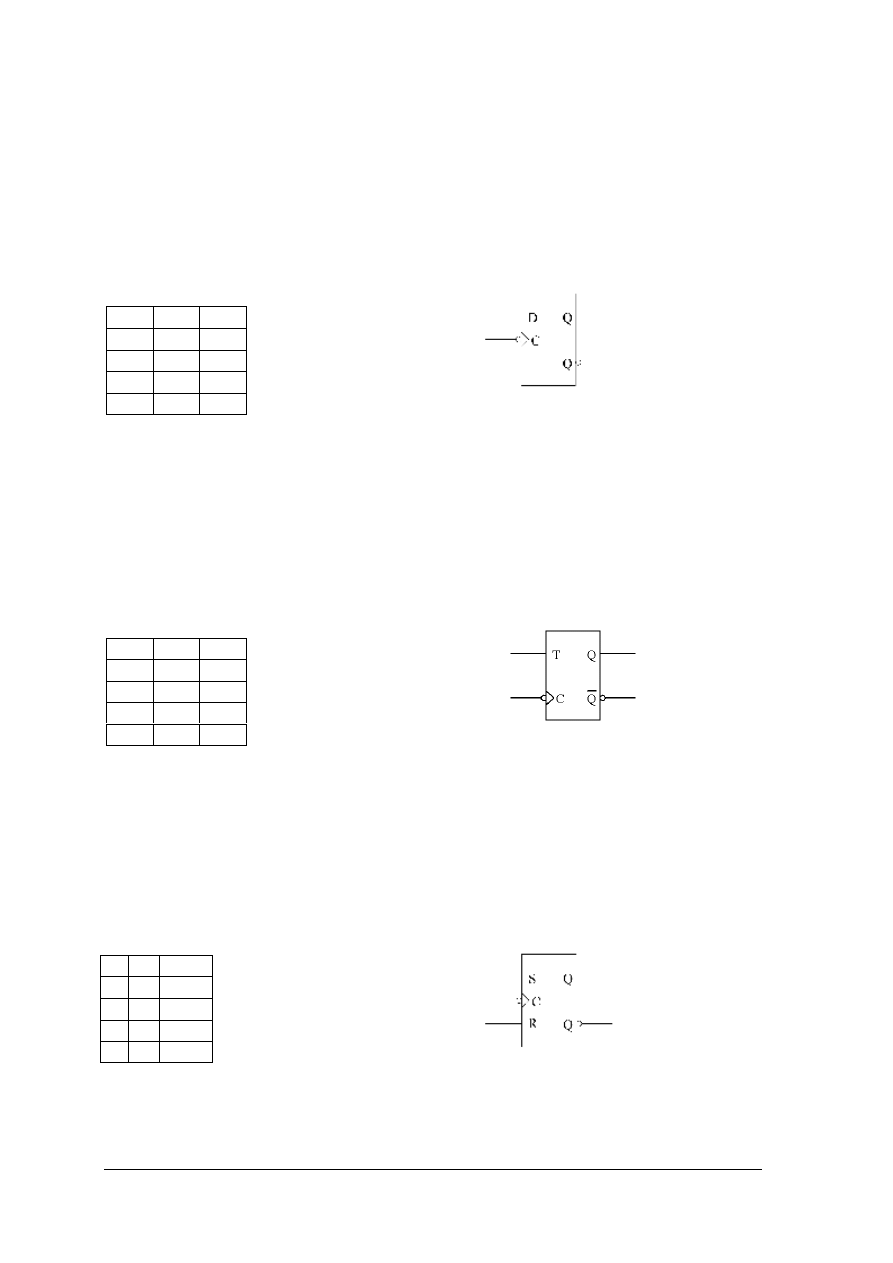
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Przerzutniki synchroniczne

Przerzutnik synchroniczny typu D

Przerzutnik synchroniczny typu D posiada jedno wejście informacyjne D oraz wejście

zegarowe. Przy aktywnym sygnale zegarowym informacja z wejścia D zostaje przepisana
na wyjście Q.

Q aktualny stan wyjścia przerzutnika
Q

następny stan wyjścia przerzutnika

Rys. 22. Przerzutnik D wyzwalany zboczem opadającym a) tablica wzbudzeń, b) symbol graficzny [1, s. 122]

Przerzutnik synchroniczny typu T

Przerzutnik synchroniczny typu T posiada jedno wejście informacyjne T oraz wejście

zegarowe C. Zmiana stanu wyjścia przerzutnika na przeciwny następuje przy aktywnym
sygnale zegarowym i jedynce logicznej na wejściu T.

Q aktualny stan wyjścia przerzutnika
Q

następny stan wyjścia przerzutnika

Rys. 23. Przerzutnik T wyzwalany zboczem opadającym a) tablica wzbudzeń, b) symbol graficzny [1, s. 123]

Przerzutnik synchroniczny typu RS

Przerzutnik synchroniczny typu RS posiada dwa wejścia informacyjne S oraz R i wejście

zegarowe C. Stan 11 na wejściach informacyjnych jest stanem zabronionym.

Q aktualny stan wyjścia przerzutnika
Q

następny stan wyjścia przerzutnika

Rys. 24. Przerzutnik RS wyzwalany zboczem opadającym a) tablica wzbudzeń, b) symbol graficzny [1, s. 123]

Q Q

S R

0 0

0 –

0 1

1 0

0 1

1 1

– 0

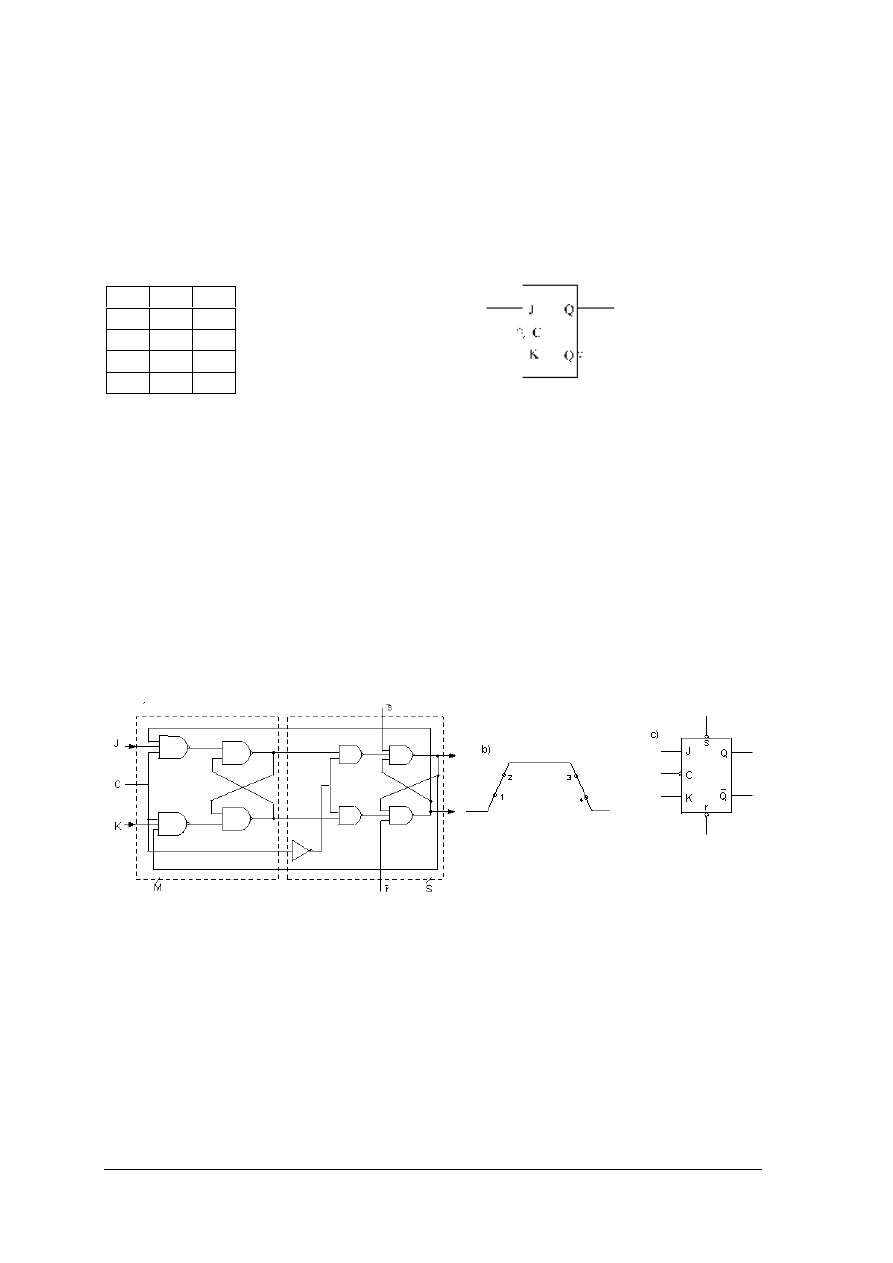
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Przerzutnik synchroniczny typu JK

Przerzutnik synchroniczny typu JK posiada dwa wejścia informacyjne J oraz K i wejście

zegarowe C. Wejście J = 1 ustawia przerzutnik w stan 1, natomiast wejście K = 1 ustawia
przerzutnik w stan 0. Stan 11 na wejściach informacyjnych powoduje zmianę stanu wyjścia
przerzutnika na przeciwny.

Q aktualny stan wyjścia przerzutnika
Q

następny stan wyjścia przerzutnika

Rys. 25. Przerzutnik JK wyzwalany zboczem opadającym a) tablica wzbudzeń, b) symbol graficzny [1, s. 123]

Przerzutnik dwutaktowy typu JK

Do ustawienia stanu przerzutnik dwutaktowego wymagane są dwa kolejne zbocza

impulsu zegarowego. Przerzutnik JK zwany popularnie przerzutnikiem Master–Slave (czyt.
Master-Slejw); składa się z dwóch przerzutników połączonych kaskadowo, pierwszy
przerzutnik układu to część Master, przerzutnik drugi to część Slave. Działanie rzeczywistego
przerzutnika Master–Slave można rozdzielić na cztery fazy. W punkcie 1 impulsu
zegarowego następuje przerwanie połączenia między częścią Master i częścią Slave, z kolei
w punkcie 2 zostają otwarte wejścia bramek dla sygnałów J i K; następuje zapamiętanie wejść
części Master, wreszcie w punkcie 4 ma miejsce przepisanie wartości zmiennych
wyjściowych przerzutnika Master do przerzutnika Slave, tzn. na wyjściu układu.

Rys. 26. Przerzutnik JK Master–Slave: a) schemat logiczny, b) symbol graficzny [1, s. 131]

Liczniki

Licznik jest sekwencyjnym układem czasowym, służącym do zliczania i zapamiętywania

liczby impulsów podawanych na jego wejście zliczające. Podstawowym parametrem licznika
jest pojemność określają ilość impulsów N jakie może on zliczyć:

≤

n określa ilość przerzutników użytych do budowy licznika a tym samym ilość jego wyjść
i nazywana jest długością licznika. Liczniki o różnych długościach można łączyć kaskadowo,
wówczas otrzymuje się licznik, którego pojemność jest iloczynem pojemności połączonych
liczników. Stan licznika, od którego rozpoczyna się zliczanie, nazywamy stanem
początkowym licznika.

J K

0 –

1 –

– 1

– 0

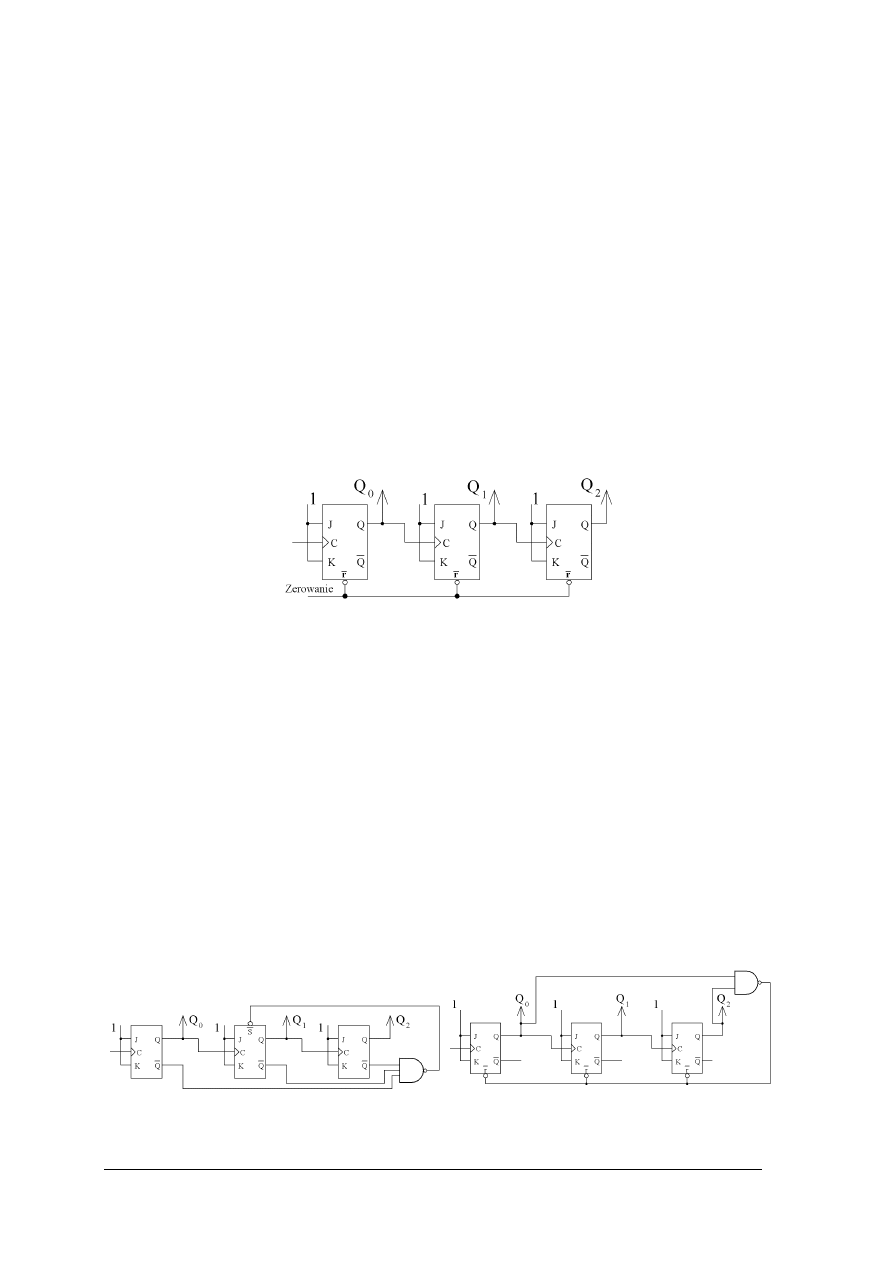
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Licznik który, przechodzi wszystkie stany cyklicznie nazywamy modulo N, natomiast taki
który przechodzi przez wszystkie stany jednokrotnie i pozostaje w stanie ostatnim nazywamy
licznikiem do N.
Rozróżniamy liczniki:
–

dodające czyli liczące w przód, które po każdym impulsie zwiększają zapamiętaną liczbę
o jeden,

–

odejmujące czyli liczące w tył, które po każdym impulsie zmniejszają zapamiętaną liczbę
o jeden,

–

dwukierunkowe czyli liczące w przód i w tył zwane rewersyjnymi.

Ze względu na sposób wprowadzania impulsów zliczanych liczniki dzielimy na:
–

szeregowe czyli asynchroniczne,

–

równoległe czyli synchroniczne.

Liczniki asynchroniczne zbudowane są z przerzutników synchronicznych połączonych

kaskadowo. Impulsy zliczane podawane są na wejście zegarowe pierwszego przerzutnika,
a poszczególne przerzutniki zmieniają swoje stany kolejno (wejście zegarowe kolejnego
przerzutnika jest wysterowane wyjściem przerzutnika poprzedniego).

Rys. 27. Schemat licznika asynchronicznego o pojemności 8

W celu uzyskania licznika o pojemności N < 2

można skrócić cykl liczenia, ustawić

warunek początkowy różny od 0 (maksymalnej ilości impulsów dla licznika liczącego w tył)
lub opuścić wybrane stany licznika. Dwa pierwsze sposoby są najpopularniejszymi
rozwiązaniami stosowanymi w licznikach szeregowych.
by skrócić cykl liczenia należy:
–

dla zadanej pojemności N połączyć w kaskadę n przerzutników,

–

z ostatniej sekwencji stanów odpowiadającej zadanej pojemności N, utworzyć sygnał
sprzężenia zwrotnego zerujący licznik (podawany na wejścia zerujące wszystkich
przerzutników).

Aby ustawić warunek początkowy różny od 0 (maksymalnej ilości impulsów dla licznika
liczącego w tył) należy:
–

dla zadanej pojemności N połączyć w kaskadę n przerzutników,

–

z ostatniej sekwencji stanów odpowiadającej utworzyć sygnał sprzężenia zwrotnego
ustawiający stan początkowy licznika (podawany na wejścia ustawiające określonych
przerzutników).

Rys. 28. Schemat licznika asynchronicznego liczącego w przód [6, s. 117], a) z niezerowym warunkiem

początkowym, b) ze skróconym cyklem liczenia [3, s. 116]

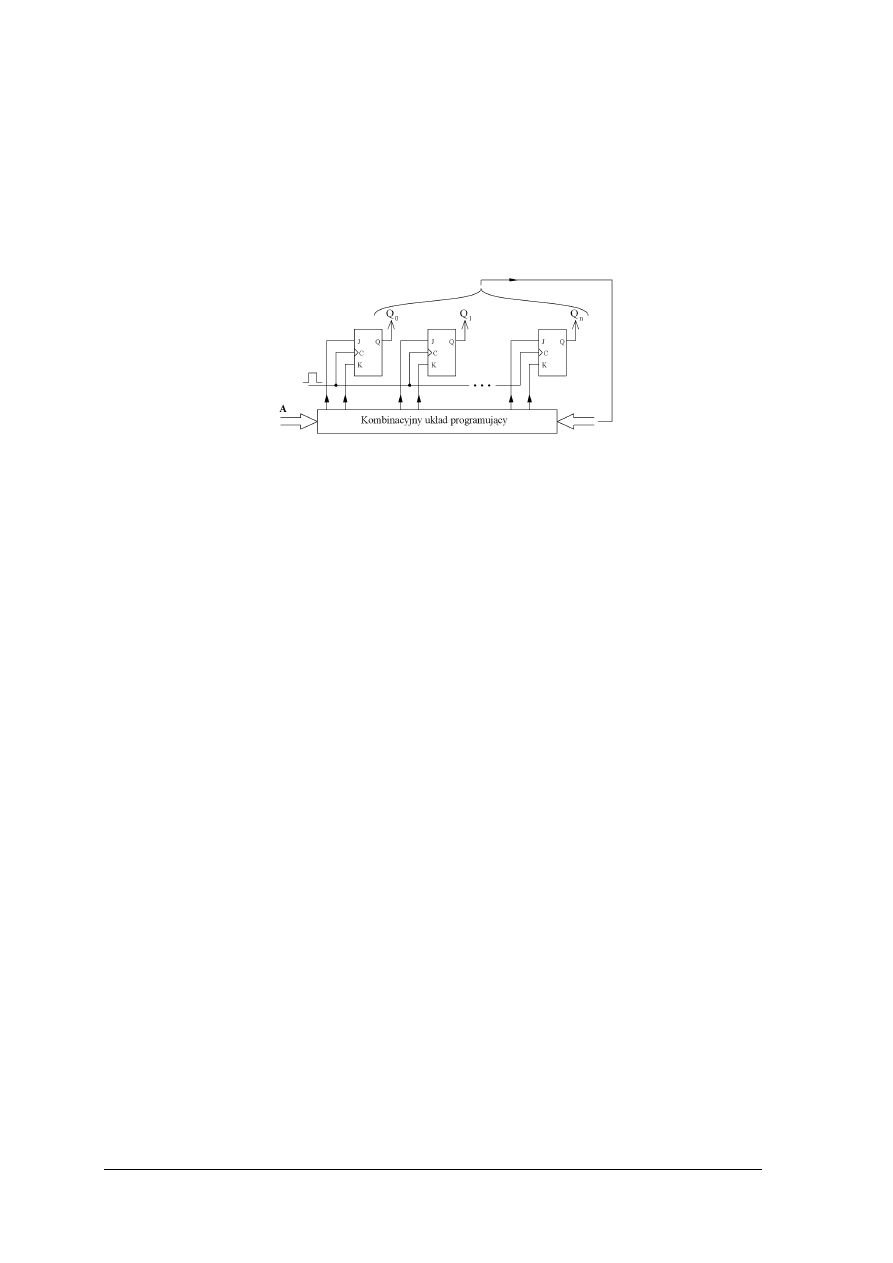
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Liczniki szeregowe są proste do zaprojektowania, natomiast ich podstawową wadą jest długi
czas propagacji sygnału.

Liczniki

synchroniczne

zbudowane

są

przerzutników

synchronicznych

i kombinacyjnego układu programującego określającego funkcje informacyjnych zmiennych
wejściowych. Zmiana stanów poszczególnych przerzutników odbywa się jednocześnie w takt
impulsów wprowadzanych na równolegle do wejścia zegarowego każdego przerzutnika.

Rys. 29. Schemat blokowy licznika synchronicznego [3, s.120]

Projektowanie liczników synchronicznych składa się z następujących etapów:
–

stworzenia tablicy wzbudzeń licznika,

–

stworzenia tablicy Karnaugha dla wejścia informacyjnego każdego przerzutnika,

–

minimalizacji tablic Karnaugha i określeniu na tej podstawie funkcji logicznej
określającej wejścia informacyjne,

–

narysowaniu schematu licznika (wraz z kombinacyjnym układem programującym).

Rejestry

Rejestry to układy składające się z zespołu przerzutników służące do przechowywania

informacji w systemie cyfrowym. Jeżeli rejestr zbudowany jest z przerzutników
synchronicznych to nazywamy go synchronicznym, natomiast rejestry zbudowane
z rzerzutników asynchronicznych noszą nazwę asynchronicznych.

Podstawowe parametry rejestrów to:

–

długość rejestru określająca liczbę bitów jaka może być przechowywana w rejestrze, jest
ona zawsze równa liczbie przerzutników, z których zbudowany jest rejestr,

–

szybkość pracy rejestru.

Ze względu na sposób wprowadzania i wyprowadzania informacji rejestry dzielimy na:
–

równoległe (PIPO, ang. Parallel Imput-Parallel Output), w których wprowadzanie
i yprowadzanie informacji odbywa się równolegle,

–

równoległo–szeregowe (PISO, ang. Parallel Imput-Serial Output), w których
wprowadzanie informacji odbywa się równolegle a wyprowadzanie szeregowo,

–

szeregowo–równoległe (SIPO, ang. Serial Imput-Parallel Output), w których
wprowadzanie informacji odbywa się szeregowo a wyprowadzanie równolegle,

–

szeregowe (SISO, ang. Serial Imput-Serial Output), w których wprowadzanie
i wyprowadzanie informacji odbywa się szeregowo.

W rejestrach w których informacja wprowadzana jest lub wyprowadzana szeregowo, zachodzi
konieczność jej przesuwania w prawo lub w lewo są to rejestry przesuwające. Rejestry, które
umożliwiają przesuwanie informacji w obu kierunkach to rejestry rewersyjne.

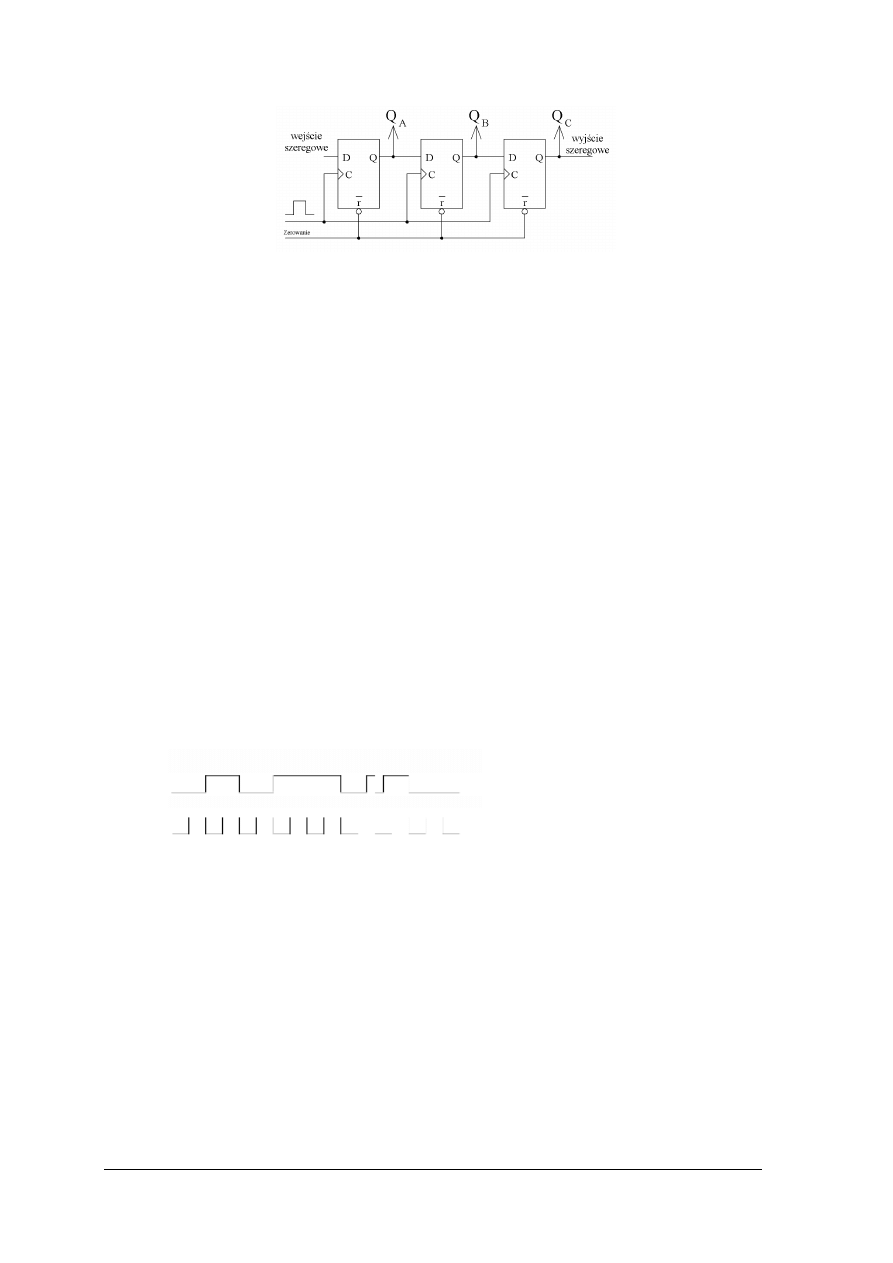
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Rys. 30. Rejestr zbudowany z trzech przerzutników D z wejściem szeregowym oraz wyjściami równoległymi

i zeregowym. [1, s.254]

4.5.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany ćwiczeń.

1. Jak dzielimy przerzutniki?
2. Jakie wejścia posiadają przerzutniki?
3. Czym charakteryzują się układy sekwencyjne?
4. Jaka jest różnica w działaniu przerzutnika synchronicznego i asynchroniczny?
5. Co oznacza nazwa przerzutnik dwutaktowy?
6. Jakie są podstawowe parametry liczników?
7. Czym różnią się licznika asynchroniczne od synchronicznych?
8. Jakie jest przeznaczenie rejestrów?
9. Jak klasyfikujemy rejestry?
10. Jak działa rejestr przesuwający?

4.5.3. Ćwiczenia

Ćwiczenie 1

Narysuj przebieg na wyjściu przerzutnika synchronicznego T wyzwalanego zboczem

opadającym, na podstawie przebiegu sygnału na wejściu informacyjnym T oraz wejściu
zegarowym C.

T

C

Rysunek do ćwiczenia 1. Przebiegi sygnałów na wejściu informacyjnym T

oraz wejściu zegarowym C przerzutnika synchronicznego T

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) napisać tablicę wzbudzeń przerzutnika T,
3) narysować przebieg wyjściowy przerzutnika, na podstawie przebiegu sygnału na wejściu

informacyjnym T oraz wejściu zegarowym C i tablicy wzbudzeń,

4) zaprezentować wyniki pracy.

Wyposażenie stanowiska pracy:

–

literatura wskazana przez nauczyciela,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

–

materiały i przybory do pisania.

Ćwiczenie 2

Zbadaj działanie przerzutnika asynchronicznego

s .

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,

2) narysować schemat logiczny przerzutnika asynchronicznego

s ,

3) zapisać tablicę wzbudzeń przerzutnika asynchronicznego

s ,

4) narysować schemat układu do badania działania przerzutnika asynchronicznego

s ,

5) zmontować układ przerzutnika asynchronicznego

s ,

6) zmontować układ do badania przerzutnika asynchronicznego

s według

zaproponowanego schematu,

7) zmierzyć napięcie na wyjściach przerzutnika zmieniając na wejściu stany logiczne

zgodnie z tablicą wzbudzeń,

8) sformułować wnioski i sporządzić sprawozdanie z ćwiczenia.

Wyposażenie stanowiska pracy:

–

2 bramki NAND (z układu UCY 7400N),

–

zasilacz napięcia stałego +5 V,

–

2 multimetry cyfrowe,

–

stanowisko do łączenia układów,

–

literatura wskazana przez nauczyciela,

–

katalogi elementów elektronicznych,

–

materiały i przybory do pisania.

Ćwiczenie 3

Zaprojektuj licznik asynchroniczny o pojemności 8 na przerzutnikach JK. Zmontuj

zaproponowany układ i zaobserwuj na oscyloskopie przebiegi na jego wyjściach Q

, Q

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) narysować schemat ideowy licznik asynchroniczny o pojemności 8 budowany

z przerzutników JK,

3) narysować schemat układu do badania licznika,
4) zgromadzić potrzebne elementy i urządzenia,
5) zmontować układ według zaproponowanego schematu,
6) zaobserwować przebiegi na wyjściach licznika Q

, Q

, podając na wejście zegarowe

przebieg prostokątny o napięciu 5 V i częstotliwości 10 kHz,

7) sformułować wnioski i sporządzić sprawozdanie z ćwiczenia.

Uwaga! Przed załączeniem napięcia zasilania układ musi sprawdzić nauczyciel.

Wyposażenie stanowiska pracy:

–

dwa układy ‘74109,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

–

zasilacz napięcia stałego +5 V,

–

generator funkcyjny,

–

oscyloskop dwukanałowy,

–

stanowisko do łączenia układów,

–

literatura wskazana przez nauczyciela,

–

katalogi elementów elektronicznych,

–

materiały i przybory do pisania.

Ćwiczenie 4

Zaprojektuj rejestr synchroniczny czterobitowy na przerzutnikach typu D, z wejściem

szeregowym oraz z wyjściem szeregowym i równoległym. Zmontuj zaproponowany układ
i zbadaj jego działanie.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) narysować schemat ideowy rejestru,
3) dobrać z katalogu elementów elektronicznych układy scalone, które można wykorzystać

do budowy rejestru,

4) uzasadnić przyjęte rozwiązanie,
5) zgromadzić potrzebne elementy i urządzenia,
6) zmontować układ rejestru według zaproponowanego schematu,
7) zbadać działanie rejestru: podając informację na wejście szeregowe oraz pojedyncze

impulsy prostokątne napięcia o wartości 5 V na wejście zegarowe, obserwować za
pomocą próbnika stanów logicznych stany wyjść równoległych i wyjścia szeregowego.

8) zaprezentować wyniki swojej pracy.

Wyposażenie stanowiska pracy:

–

układy UCY 74174, UCY 74175, UCY 74273,

–

zasilacz 5 V,

–

przerzutnik bistabilny,

–

próbnik stanów logicznych,

–

literatura wskazana przez nauczyciela,

–

katalogi elementów elektronicznych,

–

materiały przybory do pisania.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.5.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) narysować schemat logiczny przerzutnika asynchronicznego rs?

2) opisać działanie przerzutnika asynchronicznego rs?

3) rozróżnić typ przerzutnika na podstawie symbolu graficznego?

4) napisać tablicę przejść lub wzbudzeń dla dowolnego przerzutnika

asynchronicznego?

5) narysować przebieg wyjściowy przerzutnika na podstawie przebiegów

na jego wejściach informacyjnych i zegarowy?

6) zbudować prosty licznik asynchroniczny i zbadać jego działanie?

7) rozróżnić na podstawie schematu ideowego licznik synchroniczny

od asynchroniczny?

8) zbudować prosty rejestr określonego typu i zbadać jego działanie?

9) rozpoznać na podstawie schematu ideowego typ rejestru?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4.6. Podstawy techniki mikroprocesorowej

4.6.1. Materiał nauczania

Podczas współpracy urządzeń cyfrowych i analogowych zachodzi konieczność

przetwarzania sygnałów cyfrowych na analogowe i analogowych na cyfrowe.

Przetworniki cyfrowo-analogowe C/A

Zdaniem przetwornika C/A jest przetworzenie liczby na proporcjonalne do niej napięcie.

Najprostszym przetwornikiem C/A może być przekaźnik sterowany sygnałem cyfrowym.
Wyróżnia się zasadniczo trzy metody przetwarzania cyfrowo-analogowego:
–

równoległą, gdzie dzielnik napięcia dostarcza wszystkich możliwych napięć, a dekoder
1z n powoduje zamknięcie tego klucza, któremu odpowiada napięcie wyjściowe;

–

wagową, gdzie każdemu bitowi przyporządkowany jest jeden klucz, a napięcie
wyjściowe jest sumowane za pomocą rezystorów o odpowiednich wagach;

–

zliczania, gdzie stosuje się jeden klucz, który jest okresowo zamykany i otwierany,
wytworzone impulsy prądu powodują ładowani się kondensatora do napięcia
proporcjonalnego do liczby zamknięć klucza.

Najczęściej stosowana jest metoda wagowa, ponieważ wymaga zastosowania tylko jednego
klucza.

Rys. 31. Metody przetwarzania cyfrowo-analogowego a) równoległa, b) wagowa, c) zliczania [6, s. 631]

Przetworniki analogowo-cyfrowe

Zadaniem przetwornika analogowo-cyfrowego jest przetwarzanie napięcia wyjściowego

na proporcjonalna do niego liczbę. Najprostszym przetwornikiem A/C może być komparator
lub dyskryminator. Podobnie jak w przetwarzaniu cyfrowo-analogowym wyróżnia się
zasadniczo trzy metody przetwarzania cyfrowo-analogowego:
–

równoległą (bezpośredniego porównania), gdzie napięcie wejściowe jest porównywane
jednocześnie z n napięciami odniesienia, w wyniku otrzymuje się dwa napięcia
odniesienia między, którymi zawarte jest napięcie przetwarzane, ponieważ dla każdej
cyfry potrzebny jest jeden komparator, koszt tej metody jest duży, ale cyfrę wynikową
otrzymuje się w jednym kroku,

–

wagową (kolejnych przybliżeń), gdzie rozpoczyna się porównanie od najwyższej pozycji
ustalając, czy napięcie wejściowe jest większe, czy mniejsze od odpowiadającemu tej
pozycji napięciu odniesienia, jeśli jest większe przyjmuje się wartość największej pozycji
równa 1 i odejmuje się napięcie odniesienia, a następnie z wynikiem powtarza się
operację dla kolejnej pozycji niższej itd., w jednym kroku nie uzyskuje się całego
wyniku, ale w tylu ile pozycji ma liczba,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

–

zliczania, gdzie zlicza się ile razy należy dodać napięcie odniesienia odpowiadające
najniższej pozycji, aby otrzymać napięcie wejściowe, wynik jest równy liczbie kroków.
Metoda zliczania jest najprostsza, ale też najwolniejsza.

Procesor

Procesor zwany też jednostką centralną CPU (ang. Central processing Unit) przetwarza

dane binarne poprzez poddanie ich prostym operacjom logicznym. Obecnie procesory są
wykonane w postaci jednego elementu dużej skali integracji zwanego mikroprocesorem.
Mogą one mieć różną organizację zależna od przeznaczenia, ale każdy mikroprocesor posiada
jednostkę sterującą i jednostkę arytmetyczno-logiczną, z którymi stowarzyszone są
odpowiednie rejestry.

Producenci mikroprocesorów określają rodzaj operacji, jakie może on wykonać w postaci

listy rozkazów (instrukcji). Mikroprocesor wykonuje na słowach wielobitowych operacje
przewidziane listą rozkazów. Obecnie najczęściej wykorzystuje się mikroprocesory operujące
na słowach 32– i 64–bitowych. Rozkazy i dane przesyłane są wielobitową szyną nazywana
magistrala danych (ang. Data Bus), natomiast mikroprocesor określa adres źródła i miejsce
przeznaczenia za pomocą magistrali adresowej (ang. Address Bus). Mikroprocesor
współpracuje z urządzeniami zewnętrznymi za pośrednictwem sygnałów sterujących
tworzących magistralę sygnałów sterujących. Wyróżnia się dwie fazy pracy mikroprocesora
pobranie rozkazu i wykonanie rozkazu.

Jednostka arytmetyczno-logiczna ALU (ang. Arithmetic Logic Unit) jest blokiem

funkcjonalnym przeznaczonym do wykonywania operacji arytmetycznych i logicznych na
liczbach n–bitowych. Operacje logiczne są realizowane przez ALU na odpowiadający sobie
parach bitów słów wejściowych. Układ jednostki arytmetyczno-logicznej posiada:
–

wejścia wyboru funkcji ustawione na nich słowo umożliwia zrealizowanie
odpowiadającej mu funkcji,

–

wejście rodzaju funkcji – wartości logiczne na tym wejściu decydują czy będą
realizowane funkcje logiczne czy mieszane,

–

wejścia danych dla dwóch liczb n–bitowych,

–

wyjścia wyniku, gdzie generowany jest wynik operacji,

–

wyjście przeniesienia używane przy realizacji funkcji arytmetycznych,

–

wyjście komparatora sygnalizujące równość liczb podanych na wejścia danych,

–

wyjścia wykorzystywane do przyspieszania pracy działanie przy kaskadowym połączeniu
kilku układów ALU.

Rys. 32. Symbol graficzny ALU [1, s. 233]

Pamięci

Pamięci są układami służącymi do przechowywania informacji w postaci ciągu słów

bitowych. Wykonuje się jako układy o bardzo dużym stopniu scalenia w technice TTL, ECL,
CMOS i NMOS. Pamięć podzielona jest na komórki (rejestry), każda z nich posiada swój

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

adres umożliwiający dostęp do zawartej w niej informacji. Liczba bitów w komórce określa
organizację pamięci czyli sposób dostępu do informacji. Zazwyczaj komórki pamięci
zawierają 8 bitów (choć mogą mieć 4 bity), wówczas mówimy o organizacji słowowej typu
N 8

⋅

(N 4

⋅

), gdzie N oznacza ilość komórek. Jeśli pamięć ma komórki jednobitowe mówimy,

że jest to pamięć bitowa.

Organizacja pamięci wiąże się z podstawowym parametrem pamięci jakim jest

pojemność P, określająca jak wiele informacji można w niej przechowywać. Pojemność
pamięci określa się w bitach [b], ze względu na bardzo szybki postęp technologiczny
umożliwiający wykonywanie pamięci o dużych pojemnościach, powszechnie używa się
pamięci o pojemnościach wyrażanych w kilobitach [Kb] (1 Kb = 2

b = 1024 b) lub

megabitach [Mb] (1 Mb = 1 K K

⋅

b = 2

b = 1048576 b).

Przykład
Pamięć o 10 wejściach adresowych i komórkach 8–bitowych czyli długości słowa 1 bajt (1 B)
ma pojemność P = 2

B = 1 KB

Pamięć tej samej pojemności może być zorganizowana na kilka sposobów zależna od ilości
słów i ich długości.

Przykład
Pamięć o pojemności 4Kb można posiadać organizację:
–

512 8

⋅

czyli 512 słów o długości 8 bitów,

–

1024 4

⋅

czyli 1024 słowa o długości 4 bity,

–

4096 1

⋅

czyli 4096 słów o długości 1 bit.

Rys. 33. Przykłady organizacji pamięci 4 Kb

Układy pamięci mogą posiadać następujące wejścia i wyjścia:
–

wejścia adresowe umożliwiające dostęp do określonych komórek,

–

wejścia sterujące między innymi są to: wejście uaktywniające pamięć CS (ang. Chip
Select) lub CE (ang. Chip Enable), wejście zezwalające na zapis WR (ang. WRite) lub
WE (ang. Write Enable), wejście zezwalające na odczyt RD (ang. ReaD) lub OE (ang.
Output Enable), wejście strobujące adresów ALE (ang. Addres Latch Enable), RAS (ang.
Row Addres Select), CAS (ang. Column Addres Select),

–

wejścia/wyjścia danych (informacyjne D).

Pamięci dzielimy na:
–

pamięci odczyt – zapis, popularnie zwane RAM (ang. Random-Access Memory),

–

pamięci stałe ROM (ang. Read-Only Memory) – tylko do odczytu.

Parametry dynamiczne pamięci

Podstawowe parametry dynamiczne pamięci to czasy: dostępu, cyklu i blokowania.
Czas dostępu t

jest to czas liczony od wystąpienia nowego adresu do pojawienia się na

wyjściach układu zawartości komórki pamięci o tym adresie.

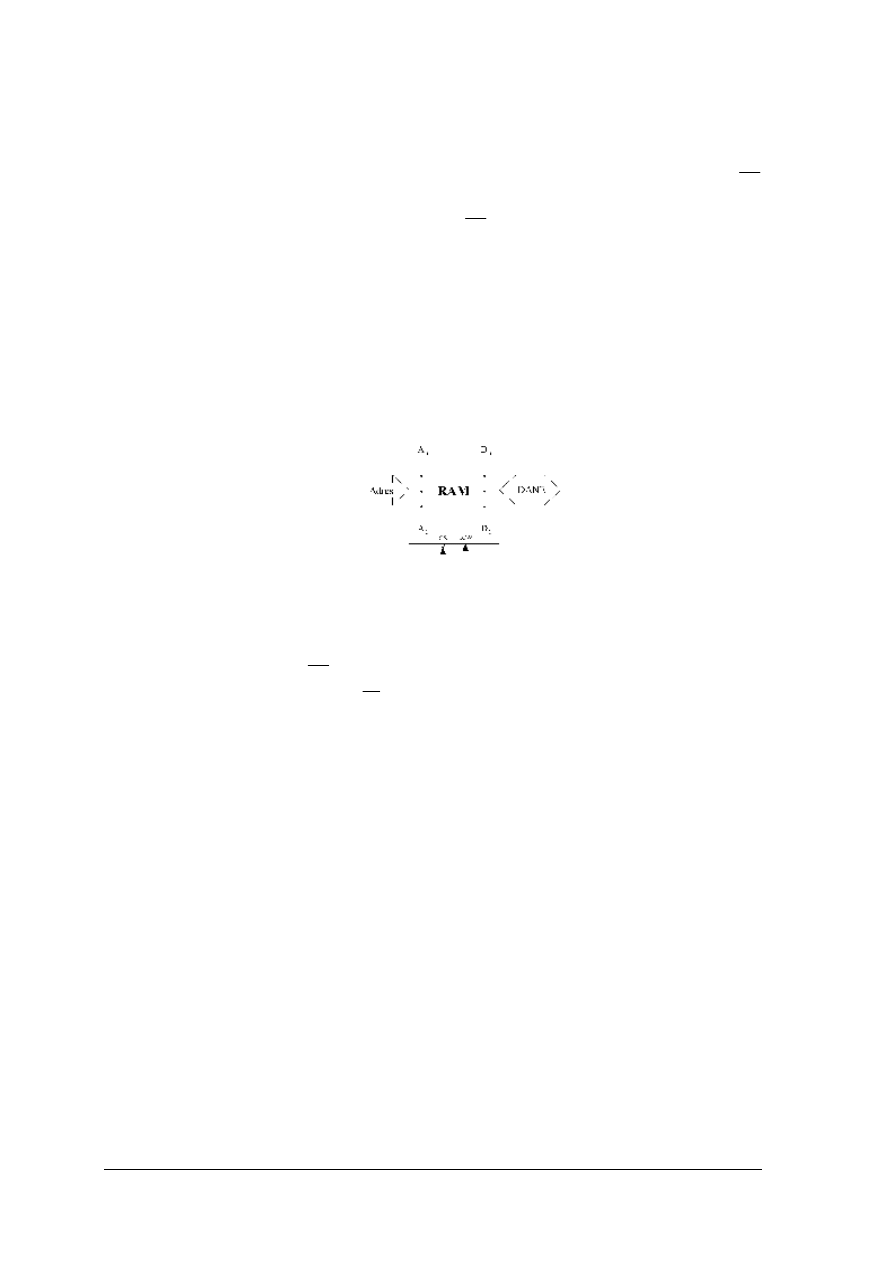
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Czas cyklu to minimalny odstęp czasu między kolejnymi prawidłowo zapisami i/lub

odczytami pamięci. Rozróżnia się czasami czas cyklu zapisu, cyklu odczytu i cyklu odczyt–
zapis.

Czas blokowania to odstęp czasu liczony od zmiany stanu wejścia wybierającego CS do

chwili przejścia wyjść/wejść danych do stanu wielkiej impedancji. Czas odblokowania jest

liczony od zmiany stanu wejścia wybierającego CS do chwili przejścia wejść/wyjść danych
do trybu pracy dwustanowej.
Dla bezkolizyjnej współpracy kilku bloków pamięci trójstanowych o połączonych wyjściach
czas blokowania tych układów powinien być krótszy niż czas odblokowania.

Pamięć RAM

Pamięć RAM jest zespołem rejestrów równoległych. Informacja może być zapisywana

w dowolnym rejestrze lub odczytywana z dowolnego rejestru dlatego pamięć ta nazywa się
pamięcią o dostępie bezpośrednim.

Rys. 34. Symbol graficzny pamięci RAM [1, s. 264]

Pamięć RAM posiada:
–

wejścia adresowe A

... A

–

wejście uaktywniające CS ,

–

wejście wyboru trybu pracy R/ W ,

–

wejścia/wyjścia danych D

... D

Pamięć RAM wykonuje się jako układy:
–

bipolarne TTL i ECL charakteryzujące się małymi pojemnościami, dużymi prądami
zasilającymi i małą szybkością działania (porównywalnie szybkie z CMOS są pamięci
ECL),

–

unipolarne CMOS i NMOS: statyczne SRAM (ang. Static Random Access Memory) oraz
dynamiczne DRAM (ang. Dynamic Random Access Memory) – obecnie DDRAM.

Pamięci dynamiczne DRAM wymagają okresowego odświeżania zawartych informacji, mogą
one posiadać wewnętrzny układ odświeżania. Obecnie powszechnie stosowane są pamięci
DDRAM.

Pamięć ROM

Pamięć ROM to pamięć stała, której zawartość podczas eksploatacji jest niezmienna, raz

zapisana informacja jest trwale przechowywana i może być wielokrotnie odczytywana.
Pamięć ROM jest cyfrowym układem kombinacyjnym.
Pamięci stałe mogą być programowane:
–

przez wytwórcę podczas produkcji – pamięci MROM,

–

przez użytkownika za pomocą specjalnych programatorów w sposób trwały, bez
możliwości wykasowania zapisanej informacji – pamięci PROM (ang. Programmable
Read-Only Memory), wykonywane zazwyczaj jako układy bipolarne,

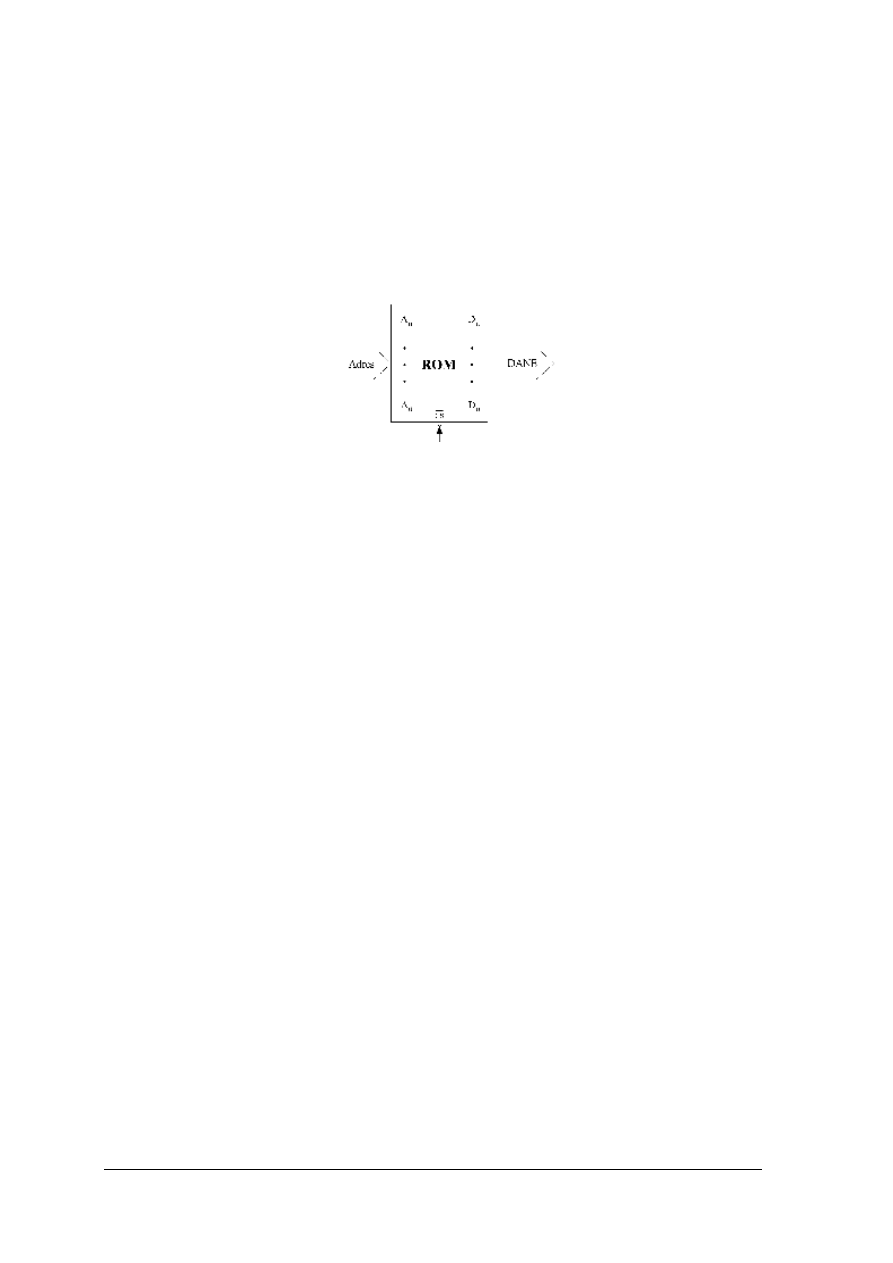
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

– przez użytkownika w sposób prawie trwały, z możliwością wykasowania zapisanej

informacji – pamięci EPROM (ang. Erasable Programmable Read-Only Memory),
wykonywane zazwyczaj jako układy unipolarne.

Pamięci EPROM mogą być:
–

zapisywane i kasowane elektrycznie – te pamięci noszą nazwę EEPROM (ang. Electrical
Erasable Programmable Read-Only Memory),

–

zapisywane metodą elektryczna, a kasowane promieniami X lub promieniami
ultrafioletowymi.

Rys. 35. Symbol graficzny pamięci ROM [1, s.264]

Komputer zawiera kilka różnych rodzajów pamięci, które generalnie można podzielić na

dwie grupy: chwilowe i stałe.
Pamięci chwilowe używane są przez komputer tylko w czasie pracy. Podstawowa jest pamięć
operacyjna (obecnie DDRAM), w której znajduje się system operacyjny i wszystkie inne
programy niezbędne do pracy komputera. System operacyjny jest na stałe zapisany na dysku
twardym, a przy każdym uruchomieniu komputera przepisuje się go automatycznie
do pamięci operacyjnej. Jest to tzw. „bootowanie”. Od wielkości i szybkości pamięci
operacyjnej zależy w dużej mierze szybkość działania komputera.

Pamięć „cache” jest dodatkową małą, podręczną pamięcią usytuowaną jak najbliżej

procesora, przechowująca dane potrzebne w danym momencie do pracy procesora. Zazwyczaj
ma dwa poziomy L1 znajdujący się wewnątrz procesora i L2 na zewnątrz.

Pamięci stałe to przede wszystkim dysk twardy oraz dyski optyczne typu CD (ang.

Compact Disc) i DVD (ang. Digital Video Device) do jednokrotnego (typu R, ROM) lub
wielokrotnego zapisu - typu RW (ang. ReWritable).
Coraz częściej stosowane są również przenośne pamięci RAM, z użytku natomiast wychodzą
dyskietki, na których stosowano magnetyczny zapis informacji.

Układy wejścia/wyjścia

Układy wejścia/wyjścia służą do wymiany danych pomiędzy komputerem a urządzeniami

zewnętrznymi. Ze względu na przeznaczenie rozróżnia się:
–

układy wejść cyfrowych (różnego rodzaju równoległe, szeregowe, buforowane
i niebuforowane) umożliwiające wprowadzenie danych z różnych nadajników informacji
cyfrowej np.: przekaźników, sygnalizatorów granicznych, cyfrowych przetworników
pomiarowych pamięci zewnętrznych,

–

układy wyjść cyfrowych (różnego rodzaju równoległe, szeregowe, buforowane
i niebuforowane) umożliwiające wyprowadzenie danych do różnych odbiorników
informacji cyfrowej np.: elementów nastawczych sterowanych cyfrowo, drukarek,
wyświetlaczy cyfrowych, monitorów ekranowych,

–

układy wejść analogowych (przetworniki A/C) przetwarzające sygnały analogowych
przetworników pomiarowych (np. temperatury, ciśnienia), na ciągi informacji cyfrowej,

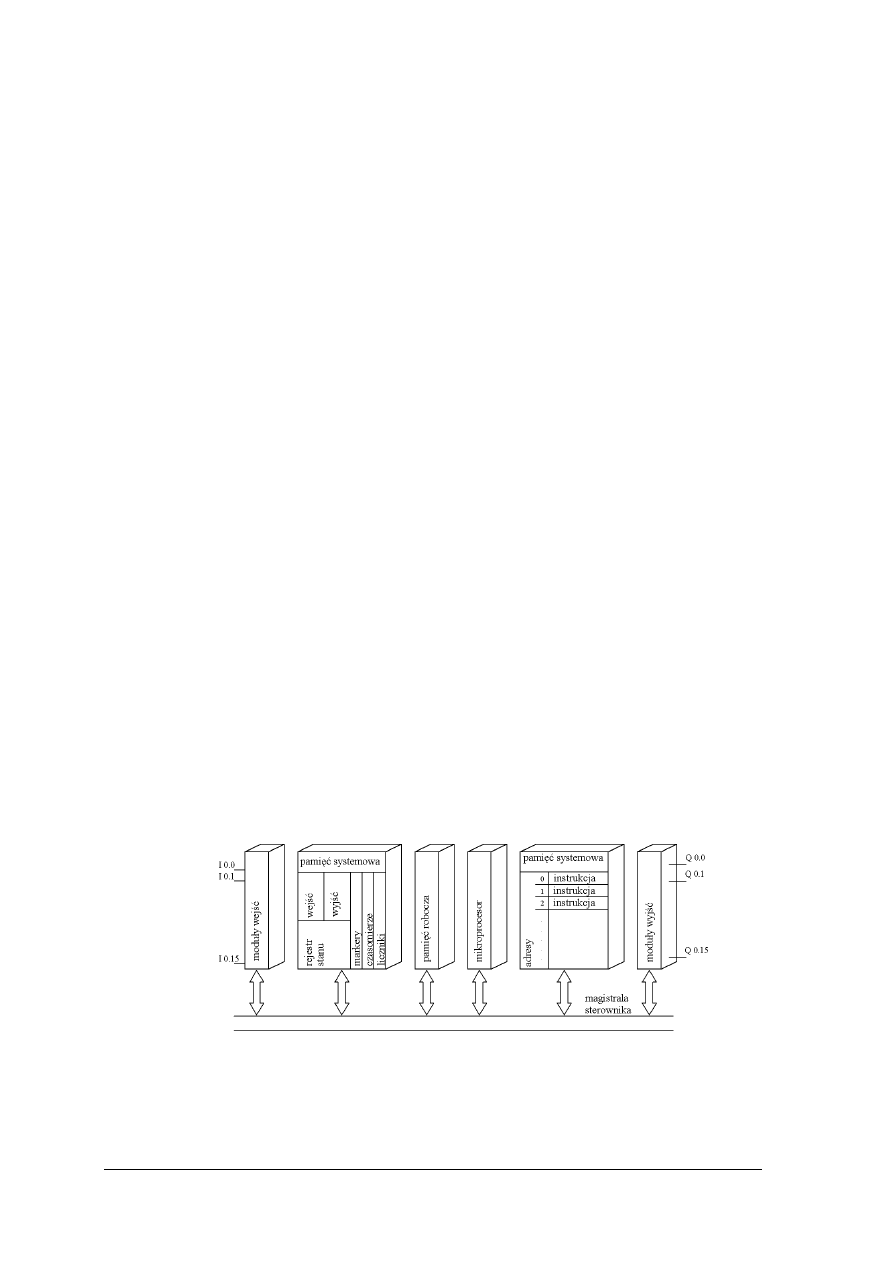
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

–

układy wyjść analogowych (przetworniki C/A) przetwarzające ciągi informacji cyfrowej
generowane przez mikroprocesor na sygnały analogowe sterujące analogowymi
elementami wykonawczymi np. zaworami regulacyjnymi.

Urządzenia zewnętrzne

Urządzenia zewnętrzne połączone z są z komputerem, a konkretnie z magistralą

rozszerzeń za pomocą interfejsu czyli karty dopasowującej.

Urządzenia wejściowe służą do zbierania i przetwarzania informacji. Najbardziej

rozpowszechnione to klawiatura i mysz czyli urządzenie wskazujące przeznaczone do
wydawania poleceń oraz zaznaczania tekstów i obrazów na ekranie. Urządzenia wejściowe to
również skaner i kamera cyfrowa pozwalające na przesłanie do komputera obrazu w postaci
cyfrowej. Wykorzystywane w grach komputerowych joysticki, zwykle dołączone do
specjalnego gniazda, są również zewnętrznymi urządzeniami wejściowymi.

Urządzenia wyjściowe umożliwiają wskazanie i gromadzenie przetworzonych danych,

podstawowe do monitor ekranowy, drukarka czy głośniki.

Systemy mikroprocesorowe w automatyce i zastosowaniach przemysłowych

Systemy mikroprocesorowe mają szerokie zastosowanie w układach automatyki

przemysłowej. Przede wszystkim wszelkiego rodzaju maszyny oraz całe linie produkcyjne
sterowane są za pomocą sterowników mikroprocesorowych czyli wysokospecjalizowanych
komputerów. Za ich pośrednictwem ustawiane są parametry procesu przemysłowego
określające warunki i sposób wykonania wyrobu, a w konsekwencji jego parametry, jakość
i właściwości. Sterowniki „zbierają” informacje z wszelkiego rodzaju czujników
pomiarowych, aparatury pomiarowej i na ich podstawie wypracowują sygnały sterujące dla
urządzeń wykonawczych.

Powszechnie w systemach automatyki przemysłowej stosowane są uniwersalne

sterowniki programowalne PLC (ang. Programmable Logic Controller), które mogą być
wykonane w postaci kompaktowej lub modułowej, pozwalającej na modernizację
z rozszerzeniem możliwości urządzenia.

Sterownik PLC zbudowany jest podobnie jak komputer z: układu zasilania napięciowego

(zasilacza), modułu sygnałów wejściowych, jednostki centralnej z mikroprocesorem (CPU),
bloku pamięci, modułu sygnałów wyjściowych. Układ zasilania napięciowego to zazwyczaj
zasilacz napięcia stałego +24 V.

Rys. 36. Schemat blokowy sterownika PLC [5, s. 168]

Dla obsługi skomplikowanych procesów przemysłowych zazwyczaj nie wystarczy jeden

sterownik. Poszczególne jednostki produkcyjne są wówczas sterowane poprzez sterowniki

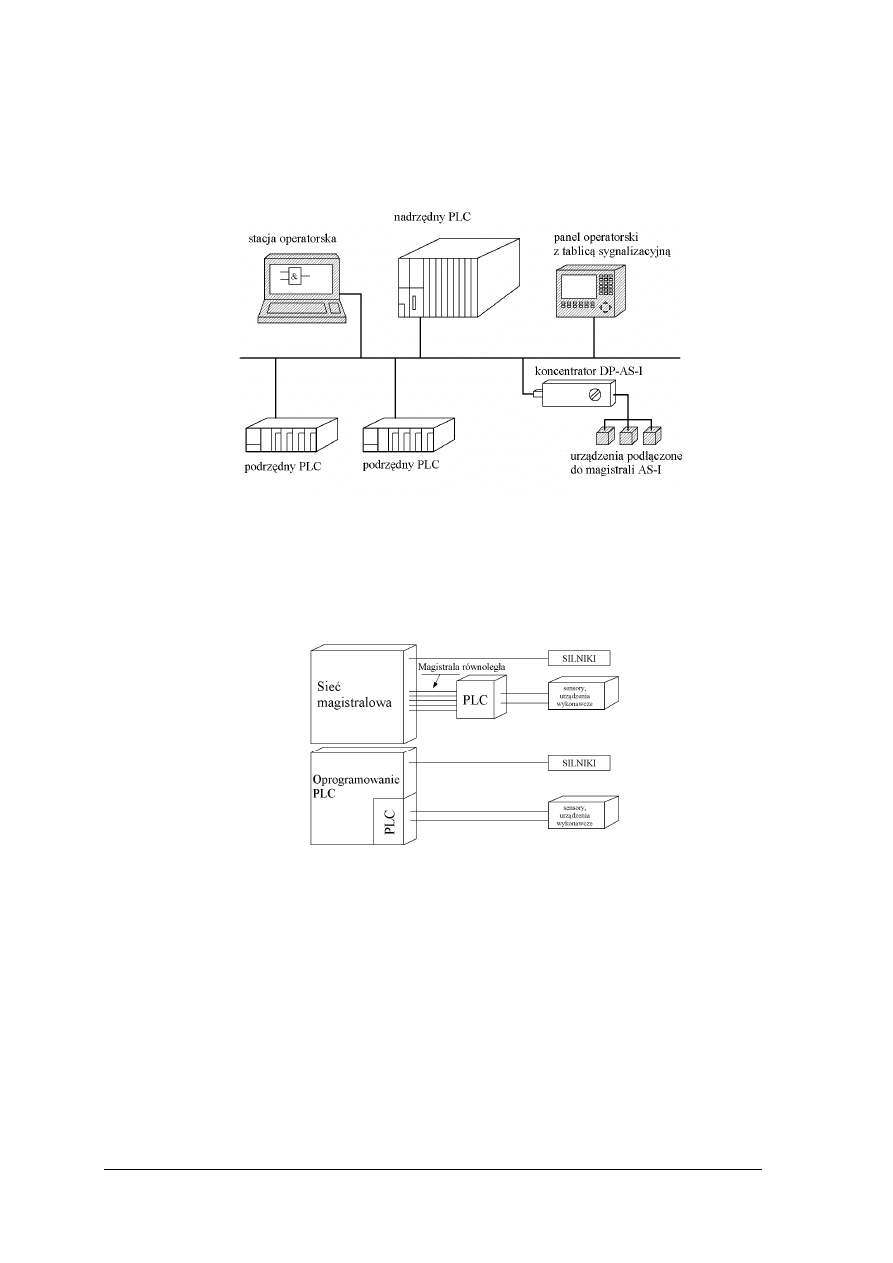
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

lokalne, podrzędne (Slave), połączone przy pomocy sieci np. PROFIBUS–DP ze
sterownikiem nadrzędnym (Master), który zarządza całym systemem. Do magistrali może być
podłączonych wiele innych urządzeń jak np. stacje i panele operatorskie, inne sieci np.
pozwalające na współpracę z urządzeniami pomiarowymi i wykonawczymi.

Rys. 37. Schemat blokowy sieci sterowników [5, s. 166]

Sterownik PLC może też być zintegrowany z innym układem sterowania cyfrowego.

Często integruje się tylko wybrane moduły sterownika z systemem operacyjnym układu
sterowania cyfrowego.

Rys. 38. Schemat blokowy układu zintegrowanego sterownika [5, s. 167]

4.6.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1. Jak działa przetwornik cyfrowo-analogowy?
2. Jakie są metody przetwarzania analogowo-cyfrowego?
3. Jakie dwa podstawowe układy posiada procesor?
4. Jakie zadania wykonuje ALU?
5. Jak dzielimy pamięci półprzewodnikowe?
6. Czym różni się pamięć SRAM od pamięci DRAM?
7. Co oznacza organizacja pamięci?
8. Jakiego typu pamięci stosuje się w komputerach?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

9. Jakie są zadania układów wejścia/wyjścia?
10. Jakie znasz urządzenia zewnętrzne komputera?
11. Jakie urządzenia mikroprocesorowe stosuje się w układach automatyki przemysłowej?

4.6.3. Ćwiczenia

Ćwiczenie 1

Narysuj symbole graficzne pamięci ROM o pojemności 8 Kb i organizacji: 1024 8

⋅

2048 4

⋅

, 8192 1

⋅

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) narysować symbole graficzne pamięci ROM o określonych pojemnościach,
3) zaprezentować wyniki swojej pracy.

Wyposażenie stanowiska pracy:

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 2

Określ programowo, a następnie fizycznie typ i wielkość zainstalowanej w komputerze

pamięci operacyjnej.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) sprawdzić w sposób programowy typ i wielkość pamięci operacyjnej,
3) zdemontować obudowę komputera,
4) zlokalizować pamięć operacyjną,
5) zdemontować układ pamięci,
6) odczytać jego parametry,
7) zamontować układ pamięci,
8) zamontować obudowę komputera,
9) zaprezentować wyniki swojej pracy.

Wyposażenie stanowiska pracy:

–

komputer PC,

–

komplet wkrętaków,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

Ćwiczenie 3

Określ parametry sterownika PLC na podstawie dokumentacji technicznej. Jakimi

urządzeniami może on sterować?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1) przeanalizować treść zadania,
2) zapoznać się z przygotowaną dokumentacją techniczną sterownika,
3) wypisać dane techniczne,
4) wyjaśnić do sterowania jakimi urządzeniami może służyć ten typ sterownika.

Wyposażenie stanowiska pracy:

−

dokumentacja techniczna sterownika PLC,

–

literatura wskazana przez nauczyciela,

–

materiały i przybory do pisania.

4.6.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1) wyjaśnić zasadę działania przetwornika analogowo-cyfrowego?

2) wyjaśnić zasadę działania przetwornika cyfrowo-analogowego?

3) scharakteryzować rolę mikroprocesora w komputerze?

4) scharakteryzować podstawowe różnice pomiędzy pamięciami ROM

i RAM?

5) określić organizację pamięci na podstawie jej symbolu graficznego?

6) określić typ pamięci operacyjnej zainstalowanej w komputerze?

7) narysować symbol graficzny pamięci o określonej organizacji?

8) dobrać urządzenie zewnętrzne komputera do określonych zadań?

9) określić rolę sterownika PLC w systemie automatyki przemysłowej?

10) określić parametry sterownika PLC na podstawie dokumentacji

technicznej?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5. SPARWDZIAN OSIĄGNIĘĆ

INSTRUKCJA DLA UCZNIA

1. Przeczytaj uważnie instrukcję zanim zaczniesz rozwiązywać zadania.
2. Podpisz imieniem i nazwiskiem kartę odpowiedzi.
3. Test składa się z 20 zadań dotyczących elementów i układów cyfrowych. Zadania od nr 1 do

nr 15 są z poziomu podstawowego. Zadania od nr 16 do nr 20 są z poziomu
ponadpodstawowego

4. Zadania zawierają cztery odpowiedzi, z których tylko jedna jest poprawna. Wybraną

odpowiedź zakreśl znakiem X

5. Jeśli uznasz, że pomyliłeś się i wybrałeś nieprawidłową odpowiedź, to otocz ją kółkiem,

a prawidłową odpowiedź zaznacz znakiem X.

6. Pracuj samodzielnie, bo tylko wtedy będziesz mógł sprawdzić poziom swojej wiedzy.
7. Jeśli jakieś zadanie sprawi Ci trudność, rozwiąż inne i ponownie spróbuj rozwiązać

trudniejsze.

8. Przed wykonaniem każdego zadania przeczytaj bardzo uważnie polecenie.
9. Odpowiedzi udzielaj tylko na załączonej karcie odpowiedzi.
10. Na rozwiązanie wszystkich zadań masz 60 minut.

Powodzenia!

ZESTAW ZADAŃ TESTOWYCH

1. Wynik sumy logicznej jest równy 0 jeśli

a) wszystkie operandy są równe 0.
b) wszystkie operandy są równe 1.
c) jeśli przynajmniej jeden operand jest równy 0.
d) jeśli przynajmniej jeden operand jest równy 1.

2. Wynik zanegowanego iloczynu logicznego jest równy 0 jeśli

a) wszystkie operandy są równe 0.
b) wszystkie operandy są równe 1.
c) jeśli przynajmniej jeden operand jest równy 0.
d) jeśli przynajmniej jeden operand jest równy 1.

3. Funkcją logiczną nie jest

a) negacja.
b) komparacja.
c) koniunkcja.
d) alternatywa.

4. Bramka AND realizuje

a) negację.
b) sumę logiczną.
c) iloczyn logiczny.
d) koniunkcję.

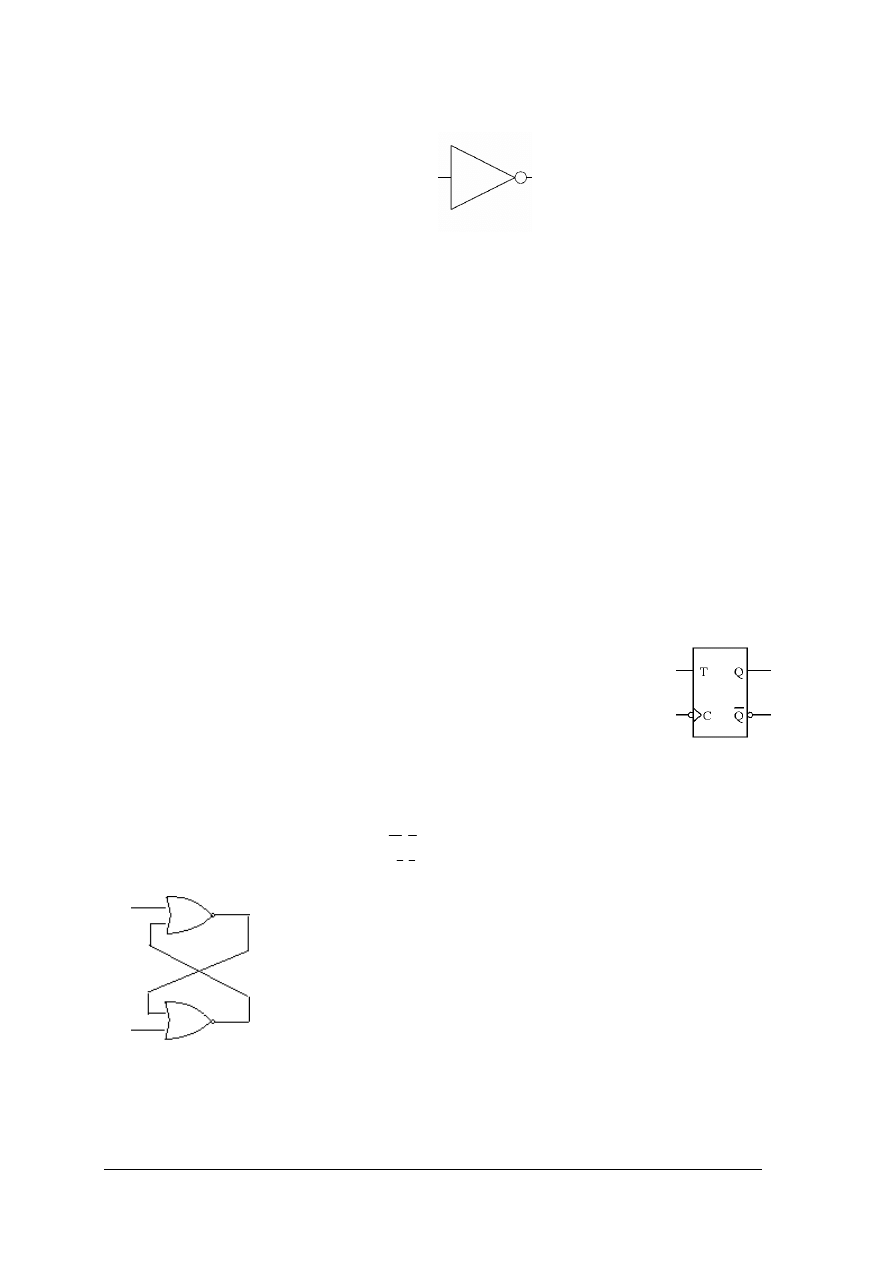
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5. Rysunek przedstawia symbol graficzny bramki

a) NOT.
b) AND.
c) Ex – OR.
d) NOR.

6. Nazwą technologii wykonania układów scalonych nie jest oznaczenie

a) TTL.
b) CMOS.
c) DTL.
d) ULY.

7. Podstawą systemu heksadecymalnego jest liczba

a) 16.
b) 8.
c) 10.
d) 2.

8. Jakich wejść nie posiada przerzutnik asynchroniczny

a) informacyjnych.
b) zegarowych.
c) ustawiających.
d) zerujących.

9. Rysunek przedstawia symbol graficzny

a) przerzutnika synchronicznego T wyzwalanego poziomem wysokim.
b) przerzutnika synchronicznego T wyzwalanego zboczem

narastającym.

c) przerzutnika synchronicznego T wyzwalanego poziomem niskim.
d) przerzutnika synchronicznego T wyzwalanego zboczem opadający.

10. Rysunek przedstawia schemat logiczny

a) przerzutnika synchronicznego RS.
b) przerzutnika asynchronicznego r s.

c) przerzutnika synchronicznego R S .

d) przerzutnika asynchronicznego r s .

11. Działania układów kombinacyjnych nie przedstawia się za pomocą

a) tablicy prawdy.
b) opisu słownego.
c) wykresów czasowych.
d) postaci kanonicznej funkcji.

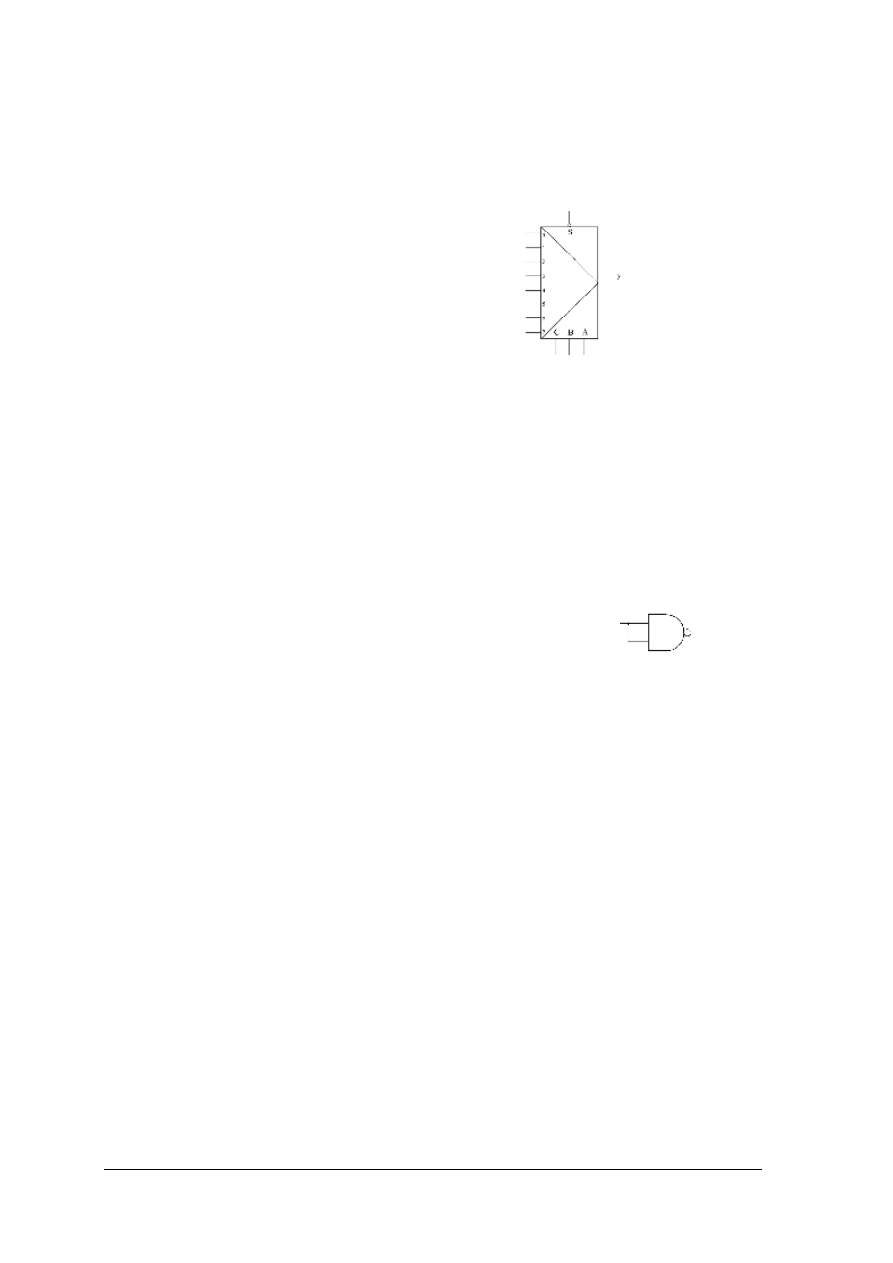
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

12. Układami komutacyjnymi są

a) sumatory.
b) demultipleksery.
c) rejestry.
d) liczniki.

13. Rysunek przedstawia symbol graficzny

a) demutipleksera.
b) multipleksera.
c) komparatora.
d) sumatora.

14. Pamięć tylko do odczytu to

a) RAM.
b) SRAM.
c) DDRAM.
d) ROM.

15. Rejestry pozwalające na szeregowe wprowadzania i wyprowadzanie danych to rejestry

a) równoległe.
b) szeregowo–równoległe.
c) równoległo–szeregowe.
d) szeregowe.

16. Rysunek przedstawia

a) negację zrealizowaną bramce NAND.
b) negację zrealizowaną bramce AND.
c) zanegowany iloczyn.
d) zanegowaną sumę.

17. Liczba 173

zapisana w systemie binarnym ma postać

a) 10001010

b) 11101010

c) 10101101

d) 10101110

18. Liczba 1000 1001 0011

zapisana w kodzie BCD, to liczba dziesiętna równa

a) 895.
b) 985.
c) 398.
d) 893.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

19. Rysunek przedstawia schemat licznika

a) asynchronicznego trzybitowego liczącego w przód.
b) synchronicznego trzybitowego liczącego w przód.
c) asynchronicznego trzybitowego liczącego w tył.
d) synchronicznego trzybitowego liczącego w tył.

20. Rysunek przedstawia pamięć o organizacji

a) 1024 x 4.
b) 4096 x 2.
c) 512 x 8.
d) 4096 x 1.