MATLAB

PODSTAWY PROGRAMOWANIA

Ćwiczenia 5

FUNKCJE

Wydział Inżynierii Lądowej i Środowiska
Katedra Mechaniki Budowli i Mostów

copyleft by Marcin Kujawa & Łukasz Smakosz

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

2/15

Funkcje

Funkcją nazywamy ciąg instrukcji zapisany w oddzielnym pliku. Jej realizacja
zachodzi po wprowadzeniu nazwy funkcji oraz uporządkowanego ciągu
argumentów oddzielonych przecinkami i

ograniczonych okrągłymi

nawiasami.

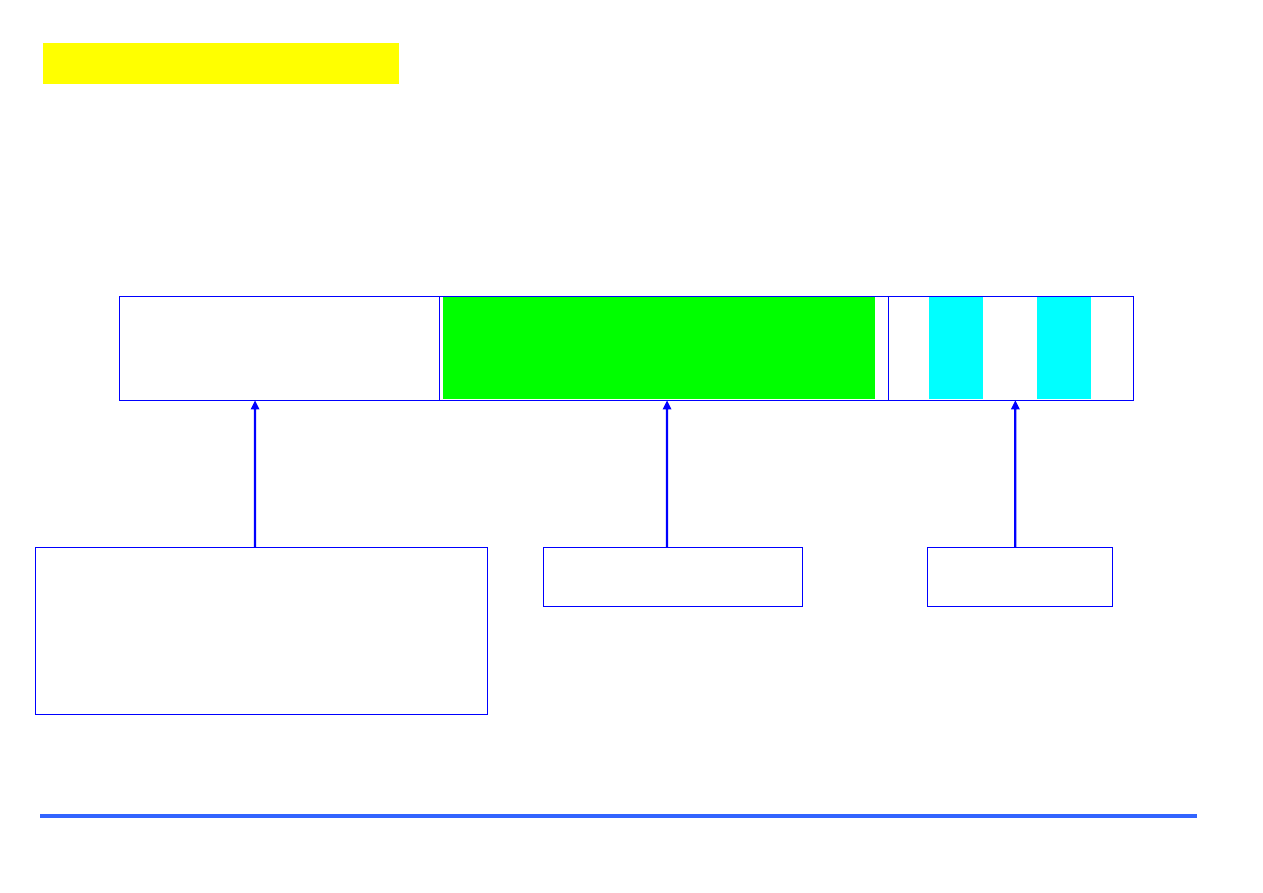
B=ones(2,3)

Podstawienie - wynik działania
funkcji, czyli jej wartość, zostanie
podstawiony za zmienną B. W tym
przypadku wynikiem działania
funkcji jest macierz składająca się
z jedynek. Wymiary macierzy
określają podane w okrągłych
nawiasach argumenty.

Nazwa

funkcji,

pokrywa się z

nazwą pliku,
który zawiera

realizowany w

funkcji ciąg

instrukcji.

Argumenty, czyli dane
niezbędne do realizacji funkcji.
Podaje się je w określonej
kolejności i oddziela
przecinkami. Muszą mieć
odpowiednią postać, np. skalar,
wektor, macierz czy tekst -
zależnie od typu funkcji.

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

3/15

Przykłady funkcji

a=sin(x)

Argument x może być skalarem, wektorem lub macierzą. Wynik działania funkcji,
podstawiony za a, ma tę samą postać oraz wymiar.

c=det(B)

Argument B musi być macierzą kwadratową. Wynik działania funkcji, podstawiony
za c, jest wyznacznikiem tej macierzy.

b=input(

'Komunikat'

,

's'

)

Funkcja ma dwa argumenty typu tekstowego - pierwszy jest komunikatem, który
wyświetli się na ekranie, drugi mówi, że zmienna b, za którą został podstawiony ciąg
znaków wprowadzony przez użytkownika, jest typu tekstowego.

d=menu(

'tytul menu'

,

'opcja1'

,

'opcja2'

)

Wszystkie argumenty są typu tekstowego i oznaczają, kolejno, nazwę menu oraz jego
opcji. Wynik, podstawiony za zmienną d, jest numerem wybranej opcji.

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

4/15

Przykłady funkcji

[m,n]=size(A)

Argument A może być macierzą dowolnych rozmiarów. Wynikiem działania funkcji
są dwie liczby, podstawione za m i n, będące, kolejno, liczbą wierszy i kolumn
macierzy A.

[x,y]=meshgrid(X,Y)

Argumenty X i Y są wektorami jednakowej długości. Wynikiem działania funkcji są
dwie macierze, podstawione za x i y, będące zbiorem współrzędnych siatki węzłów.

disp(

'Komunikat'

)

Funkcja ma jeden argument typu tekstowego. Wynikiem działania funkcji jest
komunikat, który pojawia się na ekranie po jej wywołaniu.

plot(x,y)

Argumenty x i y są wektorami lub macierzami o jednakowych rozmiarach. Wynikiem
działania funkcji jest wykres przyporządkowujący elementom wektora x elementy
wektora y.

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

5/15

Własne funkcje

W Matlabie istnieje możliwość definiowania własnych funkcji i
wykorzystywania ich jako części programów i skryptów.

Przy tworzeniu i korzystaniu z własnych funkcji trzeba pamiętać o tym, że
różnią się one od skryptów składnią oraz sposobem pobierania danych.
Tworzone przez użytkownika funkcje mają ściśle określoną składnię pierwszej
aktywnej (nie będącej komentarzem) linii pliku.

Uwagi:

 W celu pobierania danych od użytkownika podczas tworzenia pliku

funkcji nie wykorzystujemy funkcji input.

 W pliku przed instrukcją function nie powinny znajdować się żadne inne

komendy.

 W pliku funkcji nie należy wykorzystywać komendy clear.


Plik funkcji musi znajdować się w tym samym katalogu, co korzystający
z funkcji skrypt.

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

6/15

Przykład:
Napisz funkcję, która oblicza wartość n!.

% Funkcja wyznacza wartosc n!

function

[wynik]=silnia(n)

% pierwsza aktywna linia kodu

wynik=1;

for

i=1:n

wynik=wynik*i;

end

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

7/15

Przykład:
Napisz funkcję, która oblicza wartość n!.

% Funkcja wyznacza wartosc n!

function

[wynik]=silnia(n)

% pierwsza aktywna linia kodu

wynik=1;

for

i=1:n

wynik=wynik*i;

end

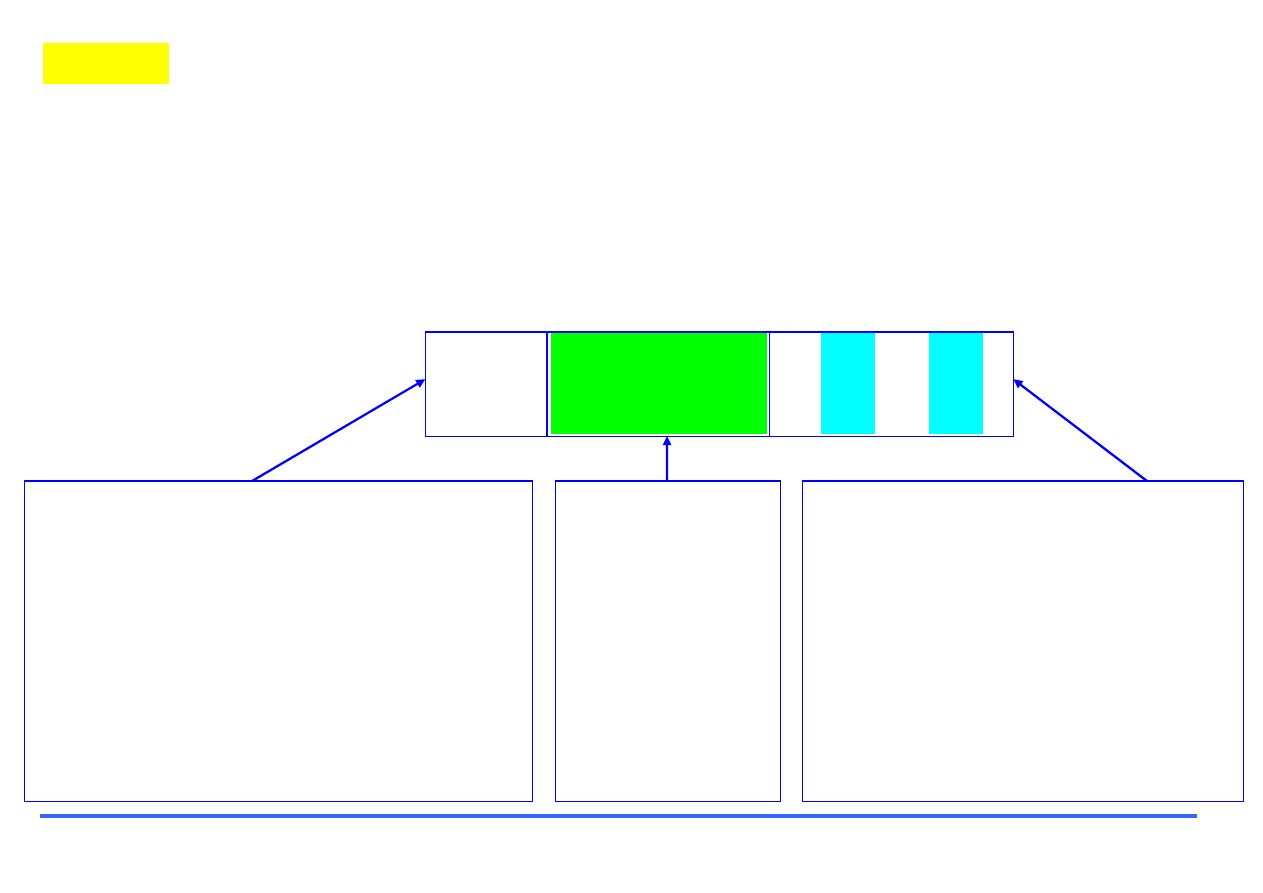
Instrukcja
otwierająca
plik funkcji.

Zmienna, która
zostanie wyświetlona
jako wynik
działania funkcji.

Nazwa funkcji, musi być taka
sama jak nazwa pliku.
W tym przykładzie plik należy
zapisać pod nazwą

silnia

.m

Zmienna, która jest argumentem
funkcji. Przy pisaniu pliku należy
ją traktować jako daną.

Ciąg instrukcji realizowany w ramach funkcji.
Argumenty funkcji należy w nim traktować jako

dane

, zmienne zdefiniowane jako

wyniki

powinny

być jedynym widocznym efektem działania funkcji.

Każda

linia kodu, która mogłaby wyświetlić coś na

ekranie, powinna być zakończona średnikiem.

Definiowanie własnej funkcji

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

8/15

Przykład:
Napisz skrypt, który wykorzystuje stworzoną funkcję. Niech skrypt akceptuje
tylko n, będące liczbami naturalnymi.

% Skrypt wyznacza wartosc n!

clear, clc

n1=input(

'podaj wartosc n: '

);

while

n1<=0 | n1~=round(n1)

clc

n1=input(

'wprowadz liczbe naturalna! '

)

end

ns=silnia(n1)

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

9/15

Przykład:
Napisz skrypt, który wykorzystuje stworzoną funkcję. Niech skrypt akceptuje
tylko n, będące liczbami naturalnymi.

% Skrypt wyznacza wartosc n!

clear, clc

n1=input(

'podaj wartosc n: '

);

while

n1<=0 | n1~=round(n1)

clc

n1=input(

'wprowadz liczbe naturalna! '

)

end

ns=silnia(n1)

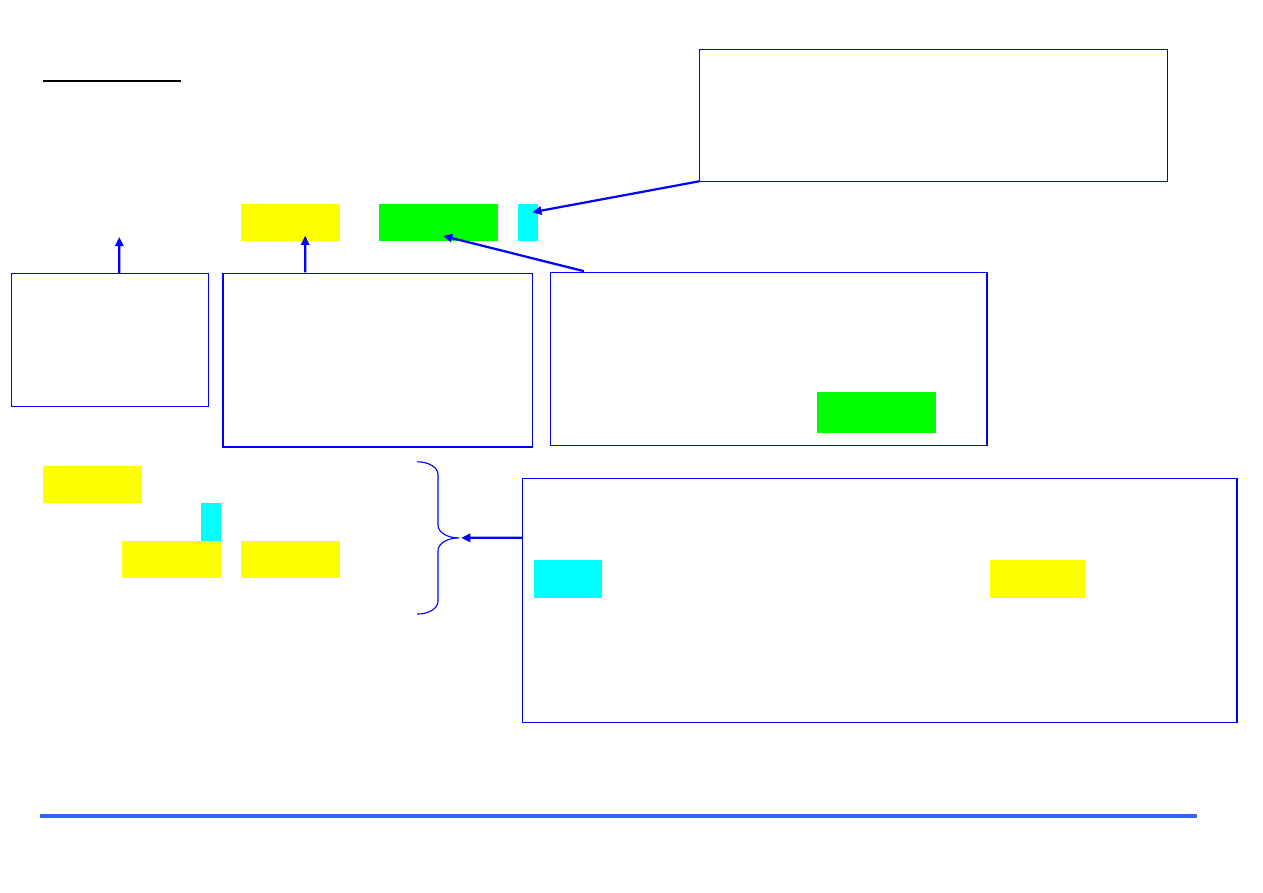
Pętla wewnętrzna aktywuje się
tylko wtedy kiedy wprowadzona
wartość nie jest liczbą naturalną.

Realizacja własnej funkcji

Zmienna

, wstawiona w miejsce argumentu funkcji

silnia

, zostanie

potraktowana jako

dana

dla ciągu instrukcji w pliku funkcji.

Za ns został podstawiony wynik funkcji

silnia

.

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

10/15

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Stwórz funkcję obliczającą pole koła w zależności od jego promienia. Następnie
stwórz skrypt wykorzystujący tę funkcję i kontrolującą czy wprowadzony
promień jest liczbą nieujemną.

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

11/15

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Stwórz funkcję obliczającą pole koła w zależności od jego promienia. Następnie
stwórz skrypt wykorzystujący tę funkcję i kontrolującą czy wprowadzony
promień jest liczbą nieujemną.

Definicja funkcji:

% Funkcja wyznacza pole kola

function

[field]=pole(r)

field=pi*r^2;

Realizacja skryptu z funkcją:

clear, clc

promien=input(

'podaj wartosc promienia: '

);

while

promien<0

clc

promien=input(

'wprowadz liczbe nieujemna! '

);

end

pole_kola=pole(promien)

Nazwa pliku:

pole

.m

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

12/15

Funkcje wielu wartości

Funkcja może mieć więcej niż jeden wynik - żeby uzyskać te wyniki należy
zastosować specjalny typ podstawienia. Przykładami takich funkcji są size oraz
meshgrid

.

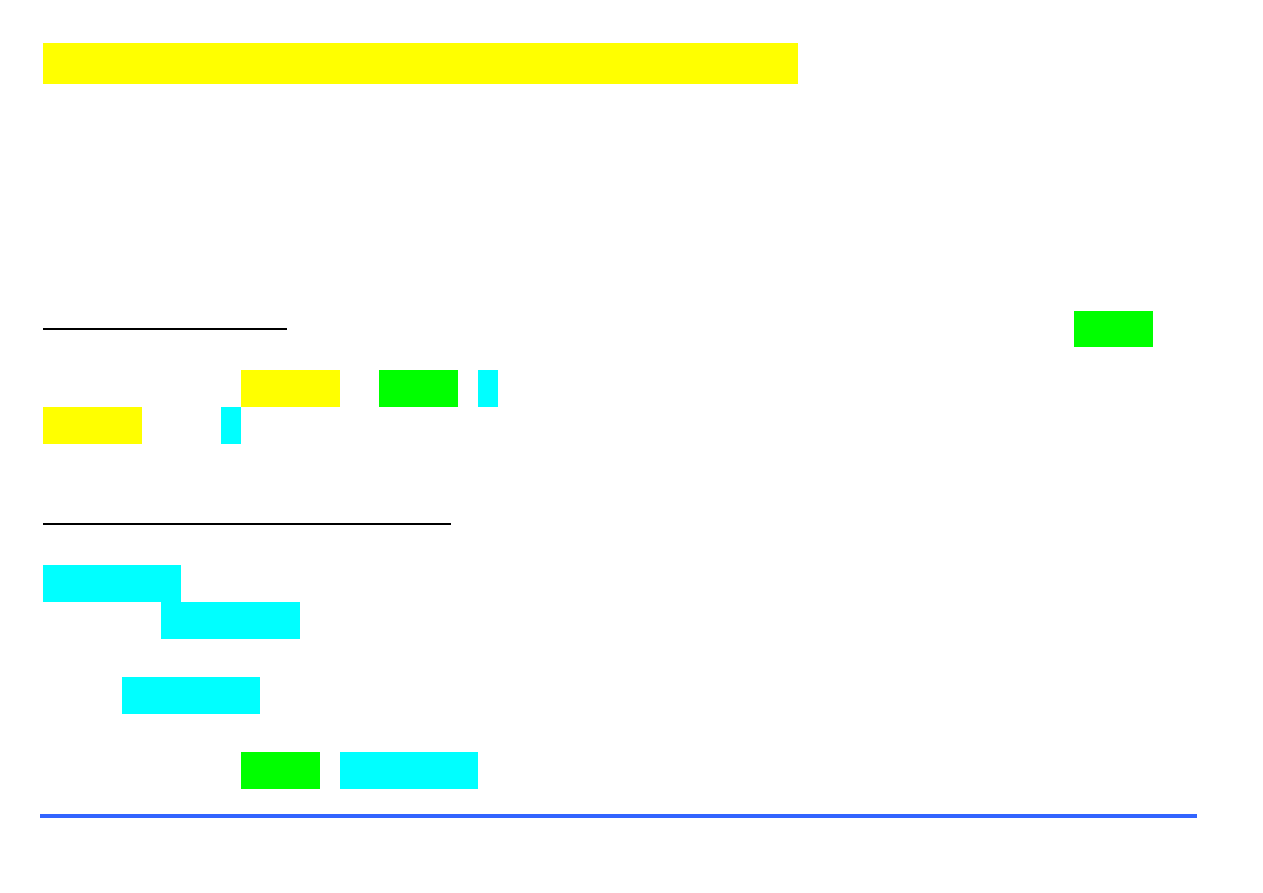
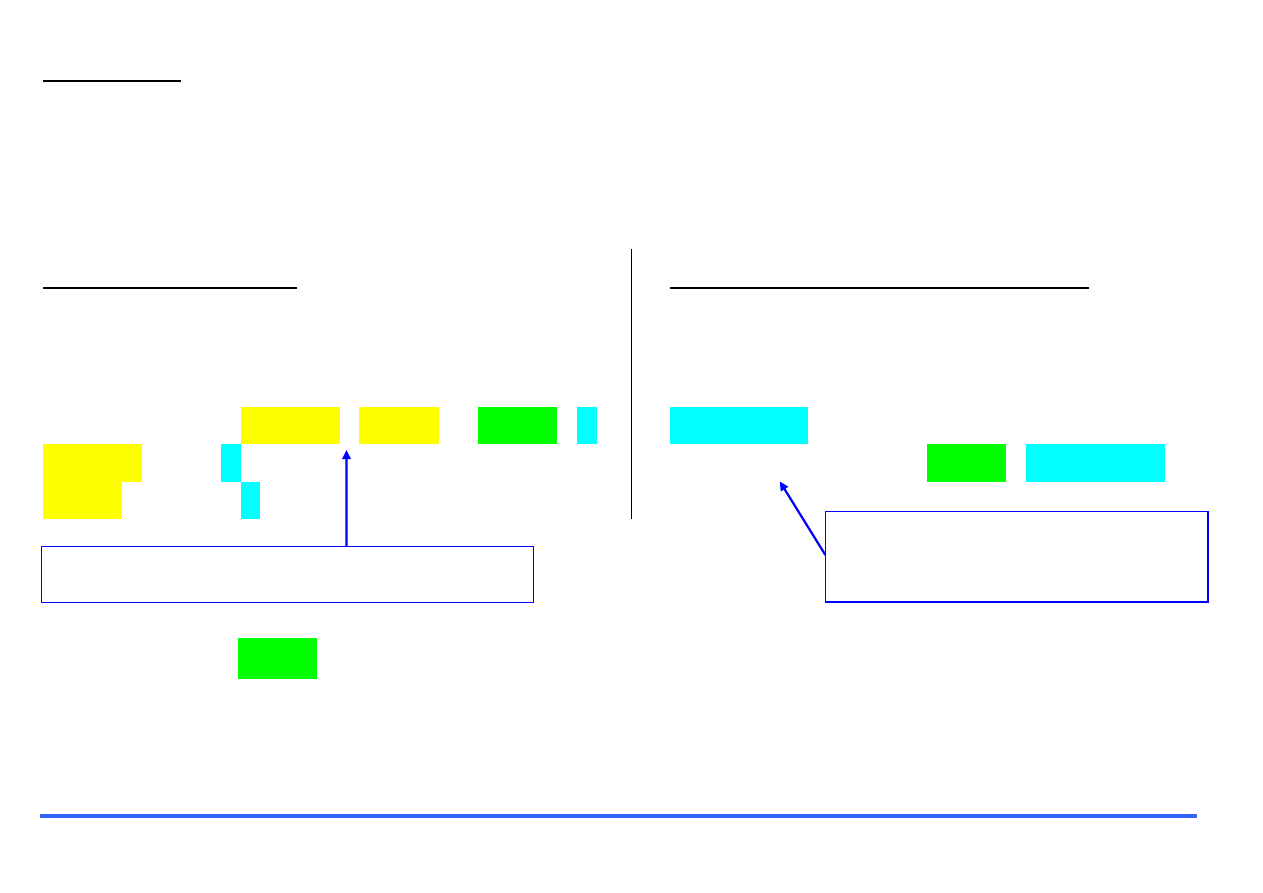
[x,y]=meshgrid(X,Y)

Podstawienie - dwa wyniki
działania funkcji, czyli jej
wartości, zostaną podstawione
za zmienne x i y.

Nazwa funkcji

Argumenty

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

13/15

Przykład:
Stwórz funkcję obliczającą pole i obwód koła w zależności od jego promienia
oraz prosty skrypt ją realizujący.

Definicja funkcji:

% Funkcja wyznacza pole i
obwod kola

function

[field,peri]=kolo(r)

field=pi*r^2;

peri=2*pi*r;

Realizacja skryptu z funkcją:

clear, clc

promien=input(

'promien: '

);

[pole,obwod]=kolo(promien)

Kolejne wyniki działania funkcji.

Podstawienie za kolejne
wyniki działania funkcji.

Nazwa pliku:

kolo

.m

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

14/15

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Stwórz funkcję obliczającą pierwiastki równania kwadratowego postaci

. Następnie stwórz prosty skrypt wykorzystujący tę funkcję.

MATLAB

 5. Funkcje  2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

15/15

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Stwórz funkcję obliczającą pierwiastki równania kwadratowego postaci

. Następnie stwórz prosty skrypt wykorzystujący tę funkcję.

Definicja funkcji:

% Funkcja wyznacza pierw.
rown. kwadratowego

function

[x1,x2]=kwad(a,b,c)

delta=b^2-4*a*c;

x1=(-b-sqrt(delta))/2/a;

x2=(-b+sqrt(delta))/2/a;

Realizacja skryptu z funkcją:

clear, clc

a=1;

b=0;

c=-4;

[x1,x2]=kwad(a,b,c)

Nazwa pliku:

kwad

.m