MATLAB

PODSTAWY PROGRAMOWANIA

Ćwiczenia 3

WIZUALIZACJA DANYCH - WYKRESY

Wydział Inżynierii Lądowej i Środowiska
Katedra Mechaniki Budowli i Mostów

copyleft by Marcin Kujawa & Łukasz Smakosz

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

2/23

Operacje na łańcuchach

Zmienna typu łańcuchowego jest to zmienna zawierająca dane tekstowe. Definiuje się
ją poprzez ograniczenie wprowadzanego tekstu apostrofami.

Uwaga: Przy kopiowaniu gotowych skryptów należy pamiętać o tym, że Matlab nie rozpoznaje
apostrofu drukarskiego używanego jako domyślny w edytorach tekstowych!

Przykład:

Zdefiniuj wektor b zawierający frazę ‘matlab jest super’. Stwórz macierz B, której
kolejne wiersze zawierają kolejne słowa tej frazy. Wykonaj transpozycję dla wektora b i
macierzy B.

clear, clc

b=

'matlab jest super'

B=[

'matlab'

;

'jest**'

;

'super*'

]

b'

B'

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

3/23

Operacje na łańcuchach

Zmienną typu łańcuchowego można wykorzystać do wyświetlania na ekranie
wskazówek dla użytkownika. Wykorzystuje się ją w tym celu jako argument funkcji
input.

Przykład:

clear, clc

a=input(

'Jak sie nazywasz? '

,

's'

)

% 's' oznacza, ze zmienna zostanie zapisana jako lancuch

b=input(

'Jaki jest Twoj ulubiony kolor? '

,

's'

)

c=input(

'Z jaka predkoscia leci jaskolka bez obciążenia? '

)

% brak 's' oznacza, ze zmienna zostanie zapisana jako
liczba

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

4/23

Operacje na łańcuchach

Zmienną typu łańcuchowego można wykorzystać do wyświetlania na ekranie
wskazówek dla użytkownika. Wykorzystuje się ją w tym celu jako argument funkcji
input.

Przykład:

clear, clc

s1=

'Jak sie nazywasz? '

;

s2=

'Jaki jest Twoj ulubiony kolor? '

;

s3=

'Z jaka predkoscia leci jaskolka bez obciążenia? '

;

a=input(s1,

's'

)

b=input(s2,

's'

)

c=input(s3)

Alternatywny zapis

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

5/23

Operacje na łańcuchach

W zmiennej typu łańcuchowego można zawrzeć instrukcję, która będzie traktowana
jak łańcuch tekstowy, ale może być wykonana przy użyciu funkcji eval.

Przykład:

clear, clc

a=input(

'Wprowadz funkcje zmiennej x: '

,

's'

)

% a zostanie przypisana zmienna tekstowa

x=input(

'Wprowadz wartosc x: '

)

% pod x zostanie podstawiona liczba

disp(

'Wartosc f(x) wynosi:'

)

eval(a)

% matlab wykona instrukcje ze zmiennej tekstowej o

ile ma ona prawidlowa skladnie

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

6/23

Wykresy dwuwymiarowe funkcji

Funkcja plot

plot(x)

– rysuje wektor x w funkcji indeksu, w przypadku macierzy traktuje ją jak

zestaw wektorów

plot(x,y)

– wykreśla wektor y w funkcji wektora x; gdy x lub y jest macierzą to

wektor jest rysowany odpowiednio w funkcji kolumn lub wierszy

plot(x,y,s)

– wykreśla jak funkcja plot(x,y) ale dodatkowo pozwala wybierać

kolor, rodzaj linii i symbole punktów

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

7/23

Przykład:

 Wykreśl wektor y=x

2

w funkcji wektora x o elementach od 0 do 10.

 Wykreśl ten wykres w kolorze niebieskim zaznaczając go krzyżykami.

 Wykreśl funkcje y=x

2

oraz y=2x

2

w jednym układzie współrzędnych.

x=[0:10];, y=x.^2;

% generacja wektorow x i y

plot(x,y)

% kreślenie wykresu funkcji y(x)

plot(x,y,

'bx'

)

% kreślenie wykresu z dod. oznaczeniami

plot(x,y,

'bx'

,x,y*2,

'r*'

)

% kreślenie 2 wykresow

Funkcja fplot

fplot(F,P)

– wykreśla funkcję F daną w postaci łańcucha na przedziale P.

Przykład:
Wykreśl wykres funkcji 2sin(x) w przedziale od 0 do 2π.

fplot(

'2*sin(x) '

,[0 2*pi])

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

8/23

Opisywanie wykresów

title (

'Nazwa wykresu'

)

– wstawia tytuł na wykresie

grid on

– włącza wyświetlanie siatki

xlabel(

'1 oś'

)

– wstawia podpis dla osi poziomej w układzie płaskim

ylabel(

'2 oś'

)

– wstawia podpis osi pionowej w układzie płaskim

zlabel(

'3 oś'

)

– wstawia podpis dla trzeciej osi w układzie przestrzennym

text(m,n,

'Opis'

)

– wstawia opis na wykresie w punkcie o wsp. (m,n)

Niestandardowe znaki w opisie wykresów

Do wypisywania niestandardowych znaków wykorzystywana jest składnia
TeX. Przykładowo:

text(0.2,0.4,

'\alpha^{3/2}'

)

– wstawia tekst w punkcie (0.2,0.4).

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

9/23

Skalowanie osi wykresów

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

10/23

Przykład:
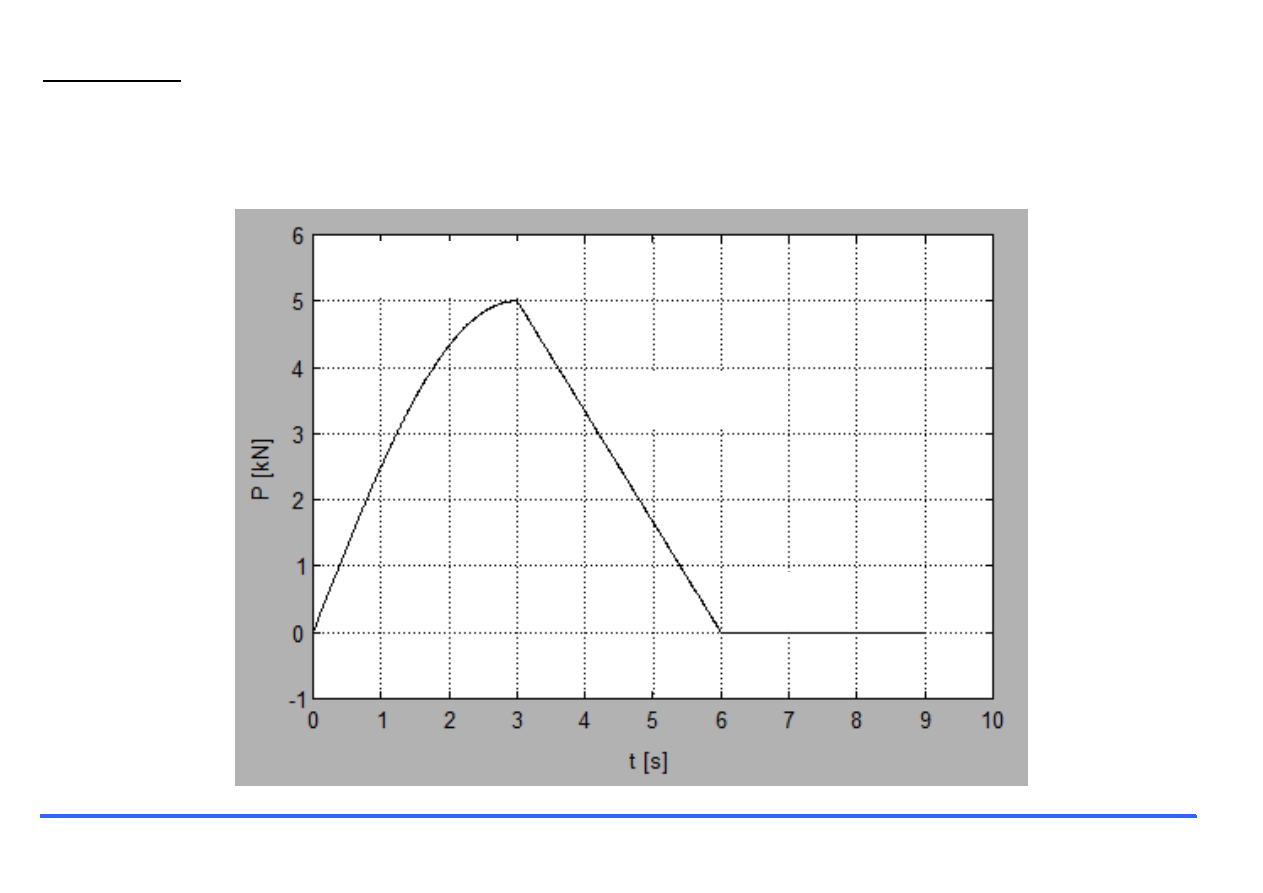
Stwórz skrypt, którego wynikiem będzie wykres przedstawiony na rysunku:

y(x)=5*sin(x*pi/6)

y(x)=-5/3*x+10

y(x)=x*0

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

11/23

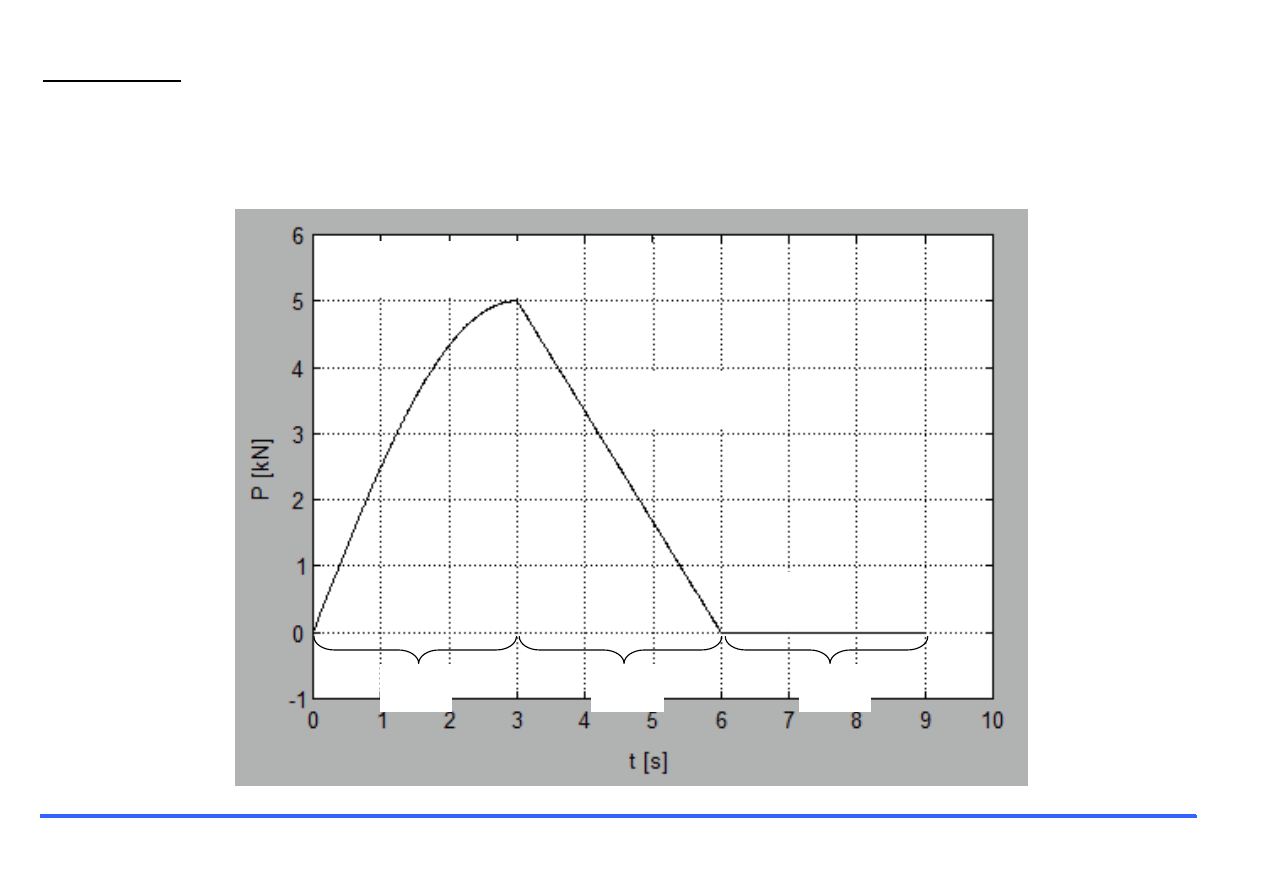
Przykład:
Stwórz skrypt, którego wynikiem będzie wykres przedstawiony na rysunku:

x1

x2

x3

y(x)=5*sin(x*pi/6)

y(x)=-5/3*x+10

y(x)=x*0

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

12/23

clear, clc, clf

k=0.01;

% steruje zageszczeniem punktow wykresu

% definicja odcinkow dziedziny

x1=[0:k:3];, x2=[3:k:6];, x3=[6:k:9];

% definicja odcinkow przeciwdziedziny

y1=5*sin(x1*pi/6);, y2=-5/3*x2+10;, y3=0*x3;

% zlozenie dziedziny i przeciwdziedziny

x=[x1 x2 x3];, y=[y1 y2 y3];

plot(x,y,

'k'

)

grid

on

% siatka

xlabel(

't [s]'

)

% opis osi poziomej

ylabel(

'P [kN]'

)

% opis osi pionowej

axis([0,10,-1,6])

% zakres osi

%opisy na wykresie

text(0.5,5.5,

'y(x)=sin(x*pi/6)'

)

text(4.5,3.5,

'y(x)=-5/3*x+10'

)

text(6.5,0.5,

'y(x)=x*0'

)

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

13/23

Otwieranie wielu okien graficznych

figure(m)

–

otwiera nowe okno graficzne o numerze m

close

–

zamyka okno aktywne

cla

–

czyści bieżący wykres

clf

–

czyści aktywne okno graficzne

Rysowanie wykresów w jednym układzie współrzędnych

hold

on

–

wstrzymuje czyszczenie okna graficznego

hold

off

–

przywraca tryb domyślny (każdorazowe czyszczenie okna).

Rysowanie wielu wykresów w jednym oknie graficznym

subplot(m,n,p)

– wyświetla

wykres w oknie graficznym o wymiarach m × n

na pozycji numer p

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

14/23

ZADANIE DO WYKONANIA NA ZAJĘCIACH

 Narysuj wykresy funkcji

20

kolorem czarnym

przerywany i

20

2

kolorem fioletowym kropkowany.

 Umieść je w jednym układzie współrzędnych.

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

15/23

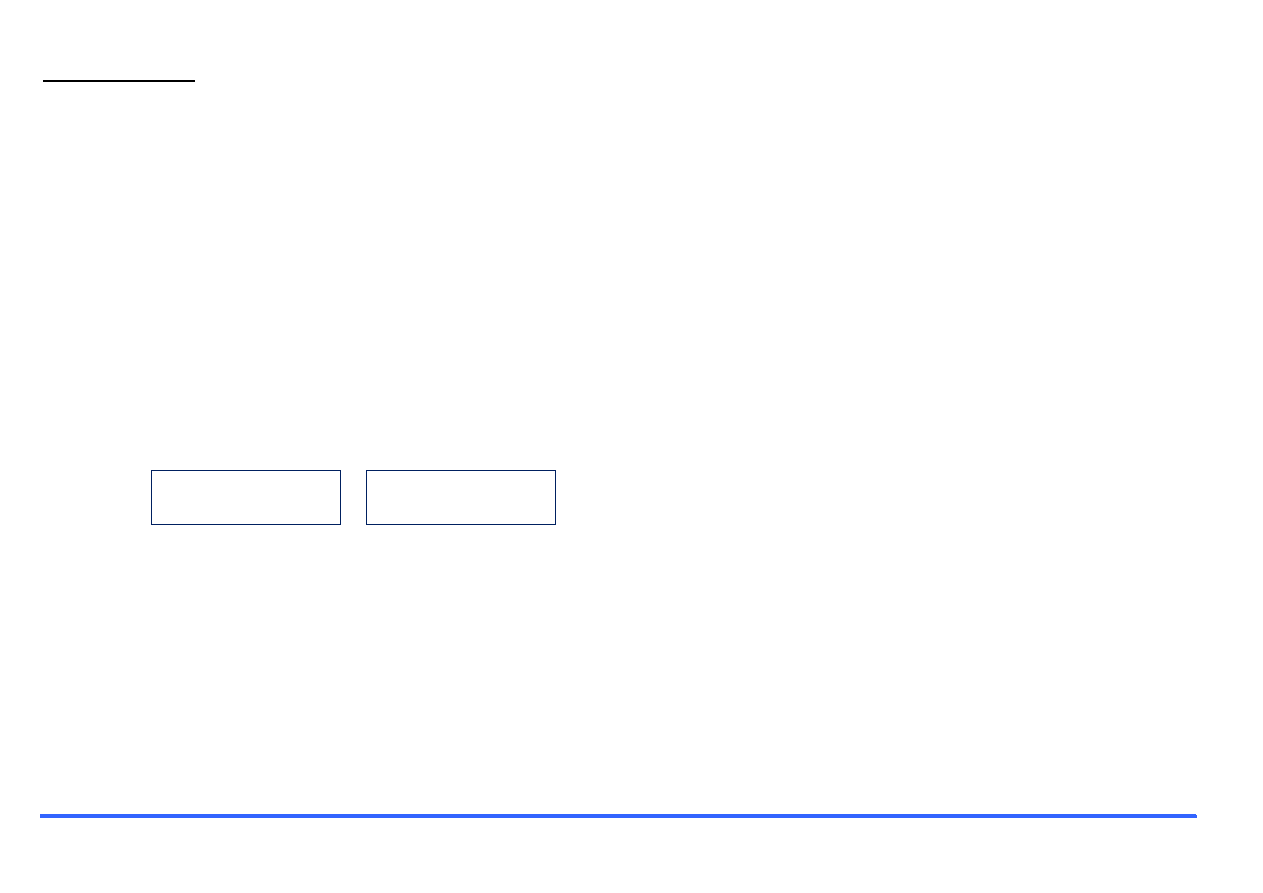
Sposób 1.:

clear, clc, clf

k=0.1;

% steruje zageszczeniem punkow wykresu

x=[0:k:10];

% przeciwdziedzina, op. tablicowa!!

y=20*sin(x)+x.^2;, y2=20*sin(2*x)+x.^2;

plot(x,y,

'k--'

)

text(7,100,

'y(x)=20sin(x)+x^2'

)

% opis

hold

on

% zatrzymuje wczesniejsze dane graficzne

plot(x,y2,

'mo'

)

text(3,45,

'y(x)=20sin(2x)+x^2'

)

% opis

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

16/23

Sposób 2.:

clear, clc, clf

k=0.1;

% steruje zageszczeniem punkow wykresu

x=[0:k:10];

% przeciwdziedzina, op. tablicowa!!

y=20*sin(x)+x.^2;, y2=20*sin(2*x)+x.^2;

plot(x,y,

'k--'

,x,y2,

'mo'

)

% 2 wykresy w 1 plot

text(7,100,

'y(x)=20sin(x)+x^2'

)

% opis

text(3,45,

'y(x)=20sin(2x)+x^2'

)

% opis

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

17/23

Funkcje hist, stairs, bar, stem

Przykład:
Wykreśl wektor y=sin(x) w funkcji wektora x o elementach od -5 do 5
wykorzystując powyższe polecenia.

clear, clc, clf
x=[-5:5];, y=sin(x);

figure(1), hist(y)
figure(2), stairs(x,y)
figure(3), bar(x,y)
figure(4), stem(x,y)

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

18/23

Rysowanie linią łamaną

Za pomocą komend line(x,y) oraz fill(x,y) można tworzyć wielokąty
poprzez połączenie współrzędnych zebranych w wektorach x i y.

Przykład:
Narysuj kontur trójkąta prostokątnego o bokach długości 3, 4 i 5. Kąt prosty
trójkąta ustaw w punkcie o współrzędnych (0,0). W osobnym oknie narysuj ten
sam trójkąt wypełniony kolorem żółtym.

clear, clc, clf
x=[0, 4, 0, 0];

% wektor wsp. x

y=[0, 0, 3, 0];

% wektor wsp. y

figure(1)
line(x,y);
axis([-1,5,-1,4])

figure(2)
fill(x,y,

'y'

);

axis([-1,5,-1,4])

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

19/23

Grafika trójwymiarowa

plot3(x,y,z)

–

rysuje w przestrzeni krzywą opisaną przez wektory x, y i z

[x,y]=meshgrid(X,Y)

–

tworzy macierze x i y opisujące położenie węzłów

na płaszczyźnie opisanej przez wektory X i Y

mesh(x,y,z)

–

rysuje siatkę powierzchni opisanej przez macierze x, y i z

surf(x,y,z)

–

rysuje powierzchnię opisaną przez macierze x, y i z

shading

–

funkcja umożliwiająca wybór typu cieniowania powierzchni spośród

opcji

flat

,

interp

,

faceted

X=[0:a]

Y=[0:b]

0

a

b

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

20/23

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Dla x z zakresu od -5 do 5 narysuj w przestrzeni krzywą opisaną równaniami:

3

4 ,

10

2 .

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

21/23

ZADANIE DO WYKONANIA NA ZAJĘCIACH

Dla x z zakresu od -5 do 5 narysuj w przestrzeni krzywą opisaną równaniami:

3

4 ,

10

2 .

clear, clc

x=[-5:0.1:5];
y=3+cos(4*x);
z=10*sin(y/2)+2*x.^2;

plot3(x,y,z)

% generacja krzywej w przestrzeni

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

22/23

Rysowanie powierzchni

Przykład:
Narysuj powierzchnię opisaną równaniem

dla

, ∈ 〈 1,1〉,

przyjmij odpowiednią gęstość dziedziny. Zastosuj różne typy cieniowania,
wykresy zestaw ze sobą za pomocą funkcji subplot.

clear, clc

k=0.1;

% gestosc siatki

X=[-1:k:1];, Y=[-1:k:1];

% generacja wektorow

[x,y]=meshgrid(X,Y);

% generacja siatki wezlow

z=exp(-x.^2-y.^2);

% potegowanie tablicowe!!

Generacja danych

MATLAB

 3. Wizualizacja danych – wykresy



2013/2014

Marcin Kujawa



Łukasz Smakosz



Politechnika Gdańska



WILiŚ



Katedra Mechaniki Budowli i Mostów

23/23

subplot(2,2,1)

% siatka, wyk. 1 w oknie 2x2

mesh(x,y,z);
title(

'siatka'

)

subplot(2,2,2)

% powierzchnia, wyk. 2 w oknie 2x2

surf(x,y,z);, shading

flat

title(

'shading flat'

)

subplot(2,2,3)

% powierzchnia, wyk. 3 w oknie 2x2

surf(x,y,z);, shading

faceted

title(

'shading faceted'

)

subplot(2,2,4)

% powierzchnia, wyk. 4 w oknie 2x2

surf(x,y,z);, shading

interp

title(

'shading interp'

)