Procesy cieplne inzynieria Zajr Nieznany

Wersja robocza.

Opracował: Jacek Wołkowiak

Materiały do ćwiczeń dla grup, w których prowadzę zajęcia.

Proszę założyć zeszyt i wykonać wszystkie zadania (zadania pisane kursywą należy wykonać

samodzielnie).

Procesy cieplne.

Na zajęciach poznamy dwa mechanizmy przenoszenia ciepła:

1) przewodzenie;

2) konwekcja i wnikanie.

Na wykładach jeszcze jeden – promieniowanie.

Wymiana ciepła występuje wtedy, gdy istnieje równica temperatur w rozpatrywanym

systemie i następuje wtedy wymiana energii – przy czym elementy systemu o większej

temperaturze oddają energię elementom o temperaturze niższej. Różnica temperatur jest więc

siłą napędową procesów wymiany ciepła.

Definicje:

Q – strumień ciepła [W];

q – gęstość strumień ciepła lub jednostkowy strumień ciepła [W/m

];

S – powierzchnia wymiany ciepła [m

];

T – temperatura [K];

Przewodzenie

Równanie Fouriera dla jednorodnego przewodzenia ciepła przez ściankę płaską prostopadle

do jej powierzchni w kierunku x podczas ustalonego przepływu ciepła przyjmuje postać:











(1)

gdzie:

 - grubość ścianki [m];

T – przyłożona różnica temperatur na grubości  [K];

 - współczynnik przewodzenia ciepła [W/mK].

Natomiast przez ściankę cylindryczną:











(2)

gdzie:

l – długość rury [m];

, d

– średnice rury na odcinku przewodzenia, odpowiednio większa i mniejsza [m]

Zadanie 1.

Oblicz strumień ciepła przewodzony przez płytę o wymiarach 2x4 [m] i grubości 2 [cm]

wykonana z materiału o współczynniku przewodzenia ciepła równym 40 [W/mK], jeżeli

skrajnych powierzchniach płyty przyłożono temperatury 20 i 100 [°C].

Ile wynosi temperatura w połowie grubości płyty?

Dane:

= 20 [°C]

= 100 [°C]

A = 2 [m]

B = 4 [m]

 = 0,02 [m]

 = 40 [W/mK]

Obliczamy powierzchnię wymiany ciepła:

 

8 m







Obliczamy strumień ciepła z równania (1)

 

1280

100









– temperatura w szukanym miejscu [K]

Przekształćmy równanie (1) do postaci:



















gdzie:





stąd:

 

1280000









Zadanie 2

Dla danych z zadania 1 obliczyć temperaturę w 1/3 i 2/3 grubości.

Wprowadźmy pojęcie średnicy średniej – średnia logarytmiczna:

log

śr





(3)

Teraz do równania (2) za

wprowadźmy

log

śr



(z równania 3). Otrzymamy:

log

śr













(4)

Proszę zwrócić uwagę, że:





log

śr













gdzie:

śr

– średnia powierzchnia wymiany ciepła [m

];

 - grubość ścianki cylindrycznej[m].

Stąd otrzymujemy postać równania dla cylindra jak dla ścianki płaskiej (1):





śr







(5)

Zadanie 3.

Oblicz strumień ciepła przewodzony przez cylinder o wymiarach d

= 7 [cm], d

= 9 [cm] i

wysokości 30 [cm] wykonany z materiału o współczynniku przewodzenia ciepła równym 40

[W/mK], jeżeli na skrajnych powierzchniach cylindra przyłożono temperatury 20 i 100 [°C].

Ile wynosi temperatura w połowie grubości ścianki cylindra?

Dane:

= 20 [°C]

= 100 [°C]

= 0,07 [m]

= 0,09 [m]

l = 0,3 [m]

 = (0,09-0,07)/2 = 0,01[m]
 = 40 [W/mK]

Obliczamy średnice średnią logarytmiczną z równania (3):

 

śr

0796

log







Obliczamy średnią powierzchnie wymiany ciepła:

 

075

0796

śr







Obliczamy strumień ciepła z równania (5)

 

100

075









Temperaturę w środku grubości cylindra liczymy identycznie jak w zadaniu 1.

śr



















gdzie:

= 0,08 [m] (w połowie grubości ścianki cylindra średnica wynosi 0,08 [m])

Ale zwróćmy uwagę, że zmienia nam się średnia powierzchnia wymiany ciepła, ponieważ:

0749

log











śr

stąd:





005

0705











śr





więc:

 

0705

005

24000









Zadanie 4

Dla danych z zadania 3 obliczyć temperaturę w 1/3 i 2/3 grubości.

Zadanie 5

Proszę zastanowić się jak rozwiązaliby Państwo zadania 1 – 4, gdyby równanie (1)

przekształcono do postaci:



















Wnikanie

Strumień ciepła przenoszony podczas wnikania jest opisany równaniem Newtona:









(6)

gdzie:

α – współczynnik wnikania ciepła [W/m

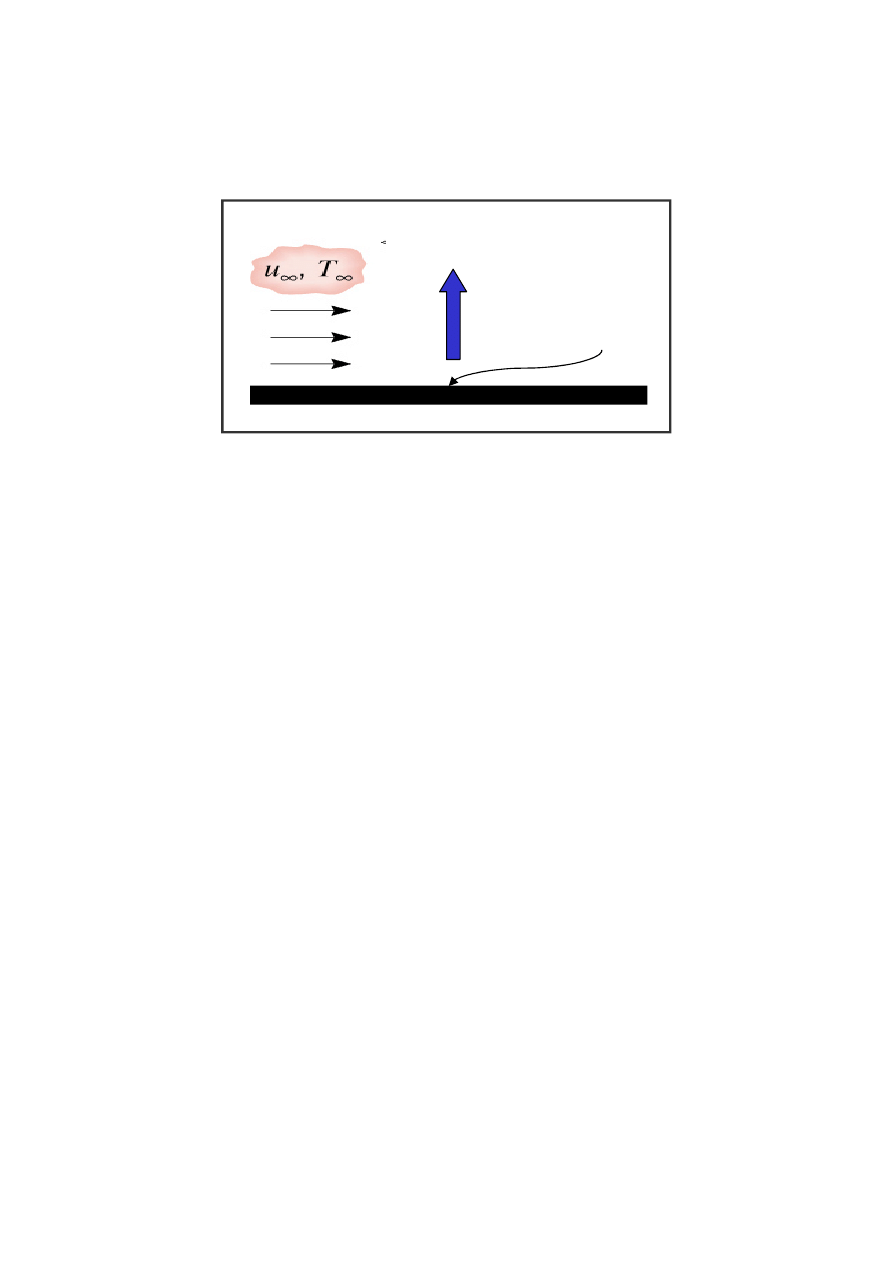
Zastanówmy się, jaka różnica temperatur występuje w równaniu (6).

Najczęściej omawiany przypadek wnikania ciepła występuje podczas wymiany ciepła

pomiędzy ścianką stałą, a przepływającym koło niej płynem. Spójrzmy na rysunek.

Nad gorącą płytą o temperaturze ścianki T

przepływa zimne powietrze, które w pewnej

odpowiednio dużej odległości od płyty ma temperaturę T



(w odpowiednio dużej odległości

od płyty temperatura powietrza jest stała i równa T



). Możemy założyć, że całkowity spadek

temperatury następuje w pewnej warstewce przyściennej, natomiast w rdzeniu płynu

temperatura jest stała - intensywne mieszanie płynu podczas ruchu (wymiana ciepła na

zasadzie konwekcji) powoduje występowanie niewielkich tylko różnic temperatur w rdzeniu

płynu w odróżnieniu od warstewki przyściennej, gdzie dominuje wymiana ciepła na zasadzie

przewodzenia. Grubość tej warstewki zależy od kilku czynników, o których szerzej na

wykładzie.

Równanie (6) zapiszemy w postaci:









gdy





















(7)

Dwa przypadki – pierwszy dla gorącej ścianki, a drugi dla gorącego powietrza.

Proszę zwrócić uwagę, że powierzchnią wymiany ciepła jest zawsze powierzchnia

międzyfazowa (w naszym przypadku powierzchnia ścianki).

Zadanie 6

Oblicz strumień ciepła, który wnika od gorącej płyty o wymiarach 4x10 [m] do powietrza o

temperaturze 30 [°C]. Temperatura ścianki płyty (po stronie powietrza) wynosi 100 [°C].

Współczynnik wnikania ciepła ma wartość 30 [W/m

K].



= 30 [°C]

= 100 [°C]

A = 4 [m]

B = 10 [m]

konwekcja

 = 30 [W/m

Obliczamy powierzchnię wymiany ciepła:

 

40 m







Obliczamy strumień ciepła z równania (7)





 

100









Zadanie 7

Oblicz strumień ciepła, który wnika od gorącej rury o wymiarach D = 10 [cm] i długości L =

100 [cm] do powietrza o temperaturze 30 [°C]. Temperatura ścianki rury (po stronie

powietrza) wynosi 100 [°C]. Współczynnik wnikania ciepła ma wartość 30 [W/m

K].

Wprowadźmy teraz pojęcie gęstości strumienia ciepła (jednostkowego strumienia ciepła).



(8)

gdzie:

q – gęstość strumień ciepła lub jednostkowy strumień ciepła [W/m

]

Równania (1) i (6) będą miały postać:



















(9)

Do obliczenia gęstości strumienia ciepła nie jest potrzebna znajomość powierzchni wymiany

ciepła.

Zadanie 1 i 7 mogą wyglądać następująco:

Oblicz jednostkowy strumień ciepła przewodzony przez płytę wykonana z materiału o

współczynniku przewodzenia ciepła równym 40 [W/mK], jeżeli skrajnych powierzchniach

płyty przyłożono temperatury 20 i 100 [°C].

Ile wynosi temperatura w połowie grubości płyty?

Oblicz jednostkowy strumień ciepła, który wnika od gorącej rury do powietrza o temperaturze

30 [°C]. Temperatura ścianki rury (po stronie powietrza) wynosi 100 [°C]. Współczynnik

wnikania ciepła ma wartość 30 [W/m

K].

Obliczenia prowadzimy korzystając ze wzorów (9) zamiast (1) i (6).

Reszta się nie zmienia.

Opór cieplny

Wprowadźmy kolejne pojęcie – opór cieplny, które ułatwi nam wykonywanie rachunków

przy rozwiązywaniu pewnych typów zadań.

Równania przewodzenia i wnikania ciepła (1) i (6) można zapisać w ogólnej postaci:





(10)

gdzie:

R – opór cieplny [K/W]

Porównując równania (1) oraz (6) z równaniem (10) otrzymujemy:

1. opór cieplny dla przewodzenia









(11)

2. opór cieplny dla wnikania







(12)

Opory cieplne możemy sumować, jeżeli połączone są szeregowo (połączenia równoległe

oporów nie zostaną omówione na ćwiczeniach):









sum

...

Ważne! Każdy opór czy suma oporów występują we wzorze (10) dla

T przyłożonej na

„skrajach” oporu lub ich sumy. Ilustruje to poniższy przykład.

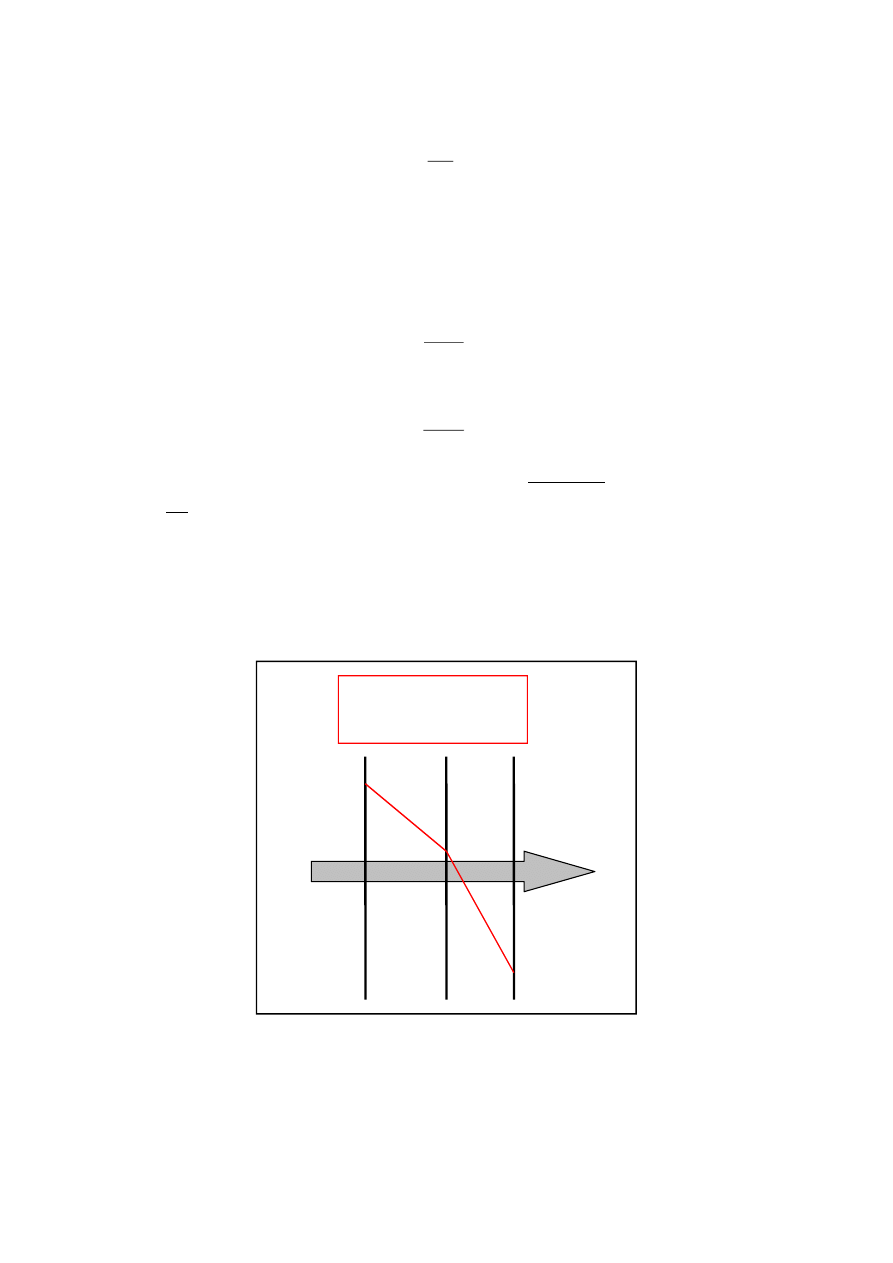
Płyta złożona z dwóch warstw A i B:

Jeżeli pierwsza warstwa posiada grubość



i wykonana jest z materiału o



, natomiast druga

posiada grubość



i wykonana jest z materiału o



to strumień ciepła Q przewodzony przez

tą płytę można opisać równaniem:

T

= T

-T

T

= T

-T















gdzie:























Proszę zauważyć, że strumień ciepła jest stały dla każdej warstwy jak i dla ich sumy (czyli

całej płyty).

Powierzchnia wymiany ciepła S dla płyty jest stała i wynosi długość x szerokość tej płyty.

Inaczej ma się rzecz dla warstwy cylindrycznej. Tu średnia powierzchnia wymiany ciepła jest

różna dla kolejnych warstw.

Zadanie 8

Rura stalowa (λ= 46,5 [W/mK)]) o średnicy D = 60×3 [mm] jest izolowana warstwą korka

(λ= 0,047 [W/mK]) o grubości 30 [mm] z zewnątrz izolowana jest jeszcze warstwą sowielitu

(λ= 0,098 [W/mK]) o grubości 40 [mm]. Temperatura ścianki rury wynosi -175 [°C] (minus

175 [°C]), zaś temperatura zewnętrznej powierzchni izolacji równa się 10 [°C]. Oblicz straty

„zimna” (tzn. strumień ciepła) przez odcinek rury o długości 1 m.

Jak zmieni się strumień ciepła (strata „zimna”), jeżeli warstwa wewnętrzna zostanie

wykonana z sowielitu (s=40 mm), a warstwa zewnętrzna z korka (s=30 mm)?

Obliczenia prowadzimy osobno dla kolejnych warstw tak jakby inne w ogóle nie istniały.

Warstwy są cylindryczne więc powierzchnie liczymy ze wzoru:

śr





log



L – długość 1 [m]

Średnicę średnią logarytmiczną liczymy ze wzoru (3) w postaci:

śr

log





a opór cieplny ze wzoru (11) w postaci ogólnej:







stal

 = 46,5

= 0,054

= 0,06

 = 0,003

057

log



śr

179



śr

000361



korek

 = 0,047

= 0,06

= 0,12

 = 0,03

0866

log



śr



śr

348



sowielit

 = 0,098

= 0,12

= 0,2

 = 0,04

157

log



śr



śr



Strumień równa się:

 









gdzie:

ΔT = 10 – (-175) = 185 [K]

Po zamianie miejsc:

stal

--> d

= 0,054 d

= 0,06

 = 0,003

sowielit

--> d

= 0,06 d

= 0,14

 = 0,04

korek

--> d

= 0,14 d

= 0,2

 = 0,03

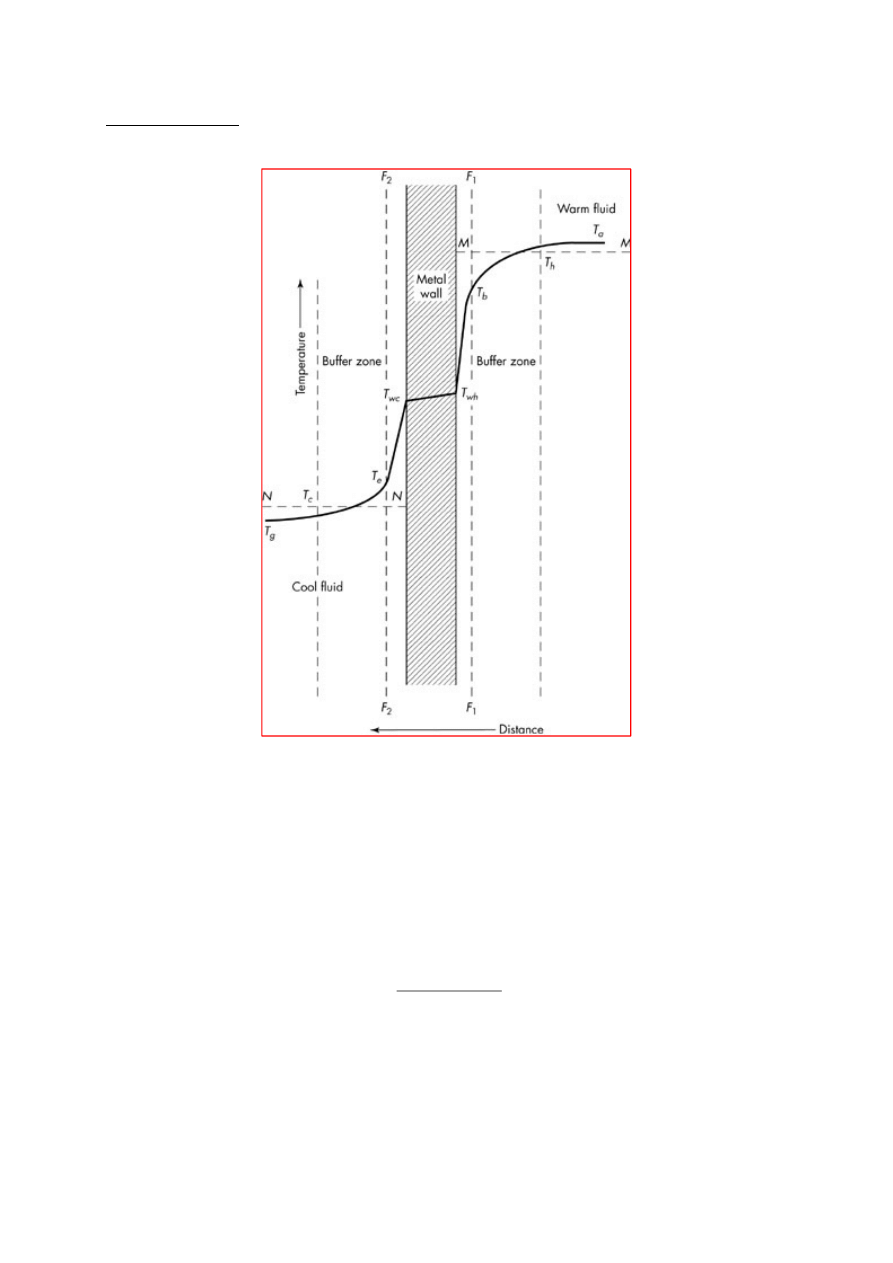
Przenikanie ciepła

Spójrzmy na rysunek:

Strumień ciepła przenoszony jest przez ściankę od gorącego płynu (po prawej na rysunku) do

zimnego płynu. Tak więc mamy połączenie szeregowe trzech oporów:

1. wnikanie od gorącego płynu do ścianki

2. przewodzenie przez ściankę

3. wnikanie od ścianki do zimnego płynu.

Przenoszony strumień jest równy:







gdzie:



























Jeżeli mamy do czynienia ze ścianką płaską to powierzchnia S jest stała i możemy ją

wyłączyć z oporów (dla ścianek cylindrycznych również wyłączymy, ale już średnią

powierzchnię S

śr

liczoną identycznie jak poprzednio ze średniej średnicy). Otrzymamy:























(13)

gdzie:













(14)

Oznaczenia:

z – indeks odnoszący się do czynnika zimnego;

g - indeks odnoszący się do czynnika gorącego;

k – współczynnik przenikania ciepła [ W/m

K].

Zadanie 9

Jaki jest udział oporów cieplnych wnikania i przewodzenia ciepła w procesie przenikania w

następujących warunkach: t

=90 [

C], 

=4000 [W/m

K], s=4 [mm],

=10 [W/mK], t

=30

[

C], 

=1000 [W/m

K], Q=2000 [W]? Obliczyć powierzchnię wymiany ciepła.

Dane:

A – czynnik gorący

B – czynnik zimny

Obliczmy współczynnik przenikania ciepła korzystając z równania (14)





606

1000

004

4000



















Obliczmy powierzchnie wymiany ciepła korzystając z równania (13)





]

[

055

606

2000















Obliczmy wszystkie opory i ich sumę:

01818

055

1000

007273

055

004

004545

055

4000































calk









Udziały kolejnych oporów to ich stosunek do sumy razy 100 %:

Udział oporu wnikania od czynnika gorącego:

 

100





calk

Udział oporu przewodzenia przez ściankę:

 

100





calk

Udział oporu wnikania do czynnika zimnego:

 

100





calk

Zadanie 10

Narysować schemat rozkładu temperatur i obliczyć jednostkowy strumień ciepła oraz

temperatury ściany płaskiej o grubości s

=3 mm wykonanej ze stali kwasoodpornej λ

= 14,6

[W/m·°C] dla następujących danych: t

=95 [°C], α

= 1200 [W/m

K], t

= 88 [°C],

= 850 [W/m

K]. Po stronie czynnika B na ścianie powstaje warstwa osadu s

=0,2 [mm];

= 0,24 [W/m·°C].

Wymienniki ciepła

Wymiennikiem nazwiemy każdy aparat, który służy do przekazywania ciepła między płynem

gorącym i zimnym.

Do tej pory temperaturę płynu uznawaliśmy za stałą, jednak w wypadku obliczeń

wymienników ciepła temperatura płynu będzie się zmieniać na drodze wymiany ciepła.

temperatura zimnego czynnika rośnie

temperatura gorącego czynnika maleje

W wymiennikach ciepła płyn gorący, który przepływa wzdłuż przepony (wymienniki

przeponowe) oddaje ciepło, które przenika przez przeponę do płynu zimnego. W

konsekwencji temperatura płynu gorącego spada natomiast zimnego rośnie.

Strumienie ciepła, które płyn gorący oddaje, a płyn zimny przyjmuje podczas wymiany ciepła

w wymienniku opisujemy równaniami:

g
p

z
p















(15)

gdzie:

, Q

– strumienie ciepła: przyjęty przez płyn zimny i oddany przez płyn gorący [W];

– ciepło właściwe płynu w temperaturze średniej tego płynu [J/kgK];

T – wzrost/spadek temperatury płynu w wymienniku [K];

Q – strumień ciepła wymieniony w wymienniku pomiędzy płynami [W].

Zadanie 11

W aparacie przeponowym oziębia się 6000 [kg/h] soku owocowego o c

= 3,75 [kJ/kg·K] od

temperatury 55 [°C] do 10 [°C]. Nośnikiem ciepła jest woda lodowa o c

= 4,19 [kJ/kg·K] o

temperaturze początkowej 2 [°C], przetłaczana z wydajnością 3-krotnie większą od

wydajności przepływu soku.

Obliczyć ilość ciepła wymienianego w aparacie i temperaturę końcową wody.

Dane:

= 6000 [kg/h] = 1,67 [kg/s]

g
p

c = 3750 [J/kgK]

z
p

c = 4190 [J/kgK]

Obliczamy masowe natężenie przepływu czynnika zimnego:

= 3

G

= 5 [kg/s]

Wymiennik ciepła

T ,

wyl

T ,

Całkowite zmiany temperatur obu czynników możemy opisać równaniami:

wyl













(16)

gdzie:

indeks wl – wlot do wymiennika

indeks wyl – wylot z wymiennika

Ważne!

T zawsze jest dodatnie, więc od wyższej temperatury odejmujemy niższą.

Stąd:

T

= 55 -10 = 45 [°C]

Obliczamy ilość ciepła wymienianego w aparacie z równań (15):

 

281250

3750







oraz spadek temperatury czynnika zimnego:

 

z
p

4190

281250 











W końcu temperaturę czynnika zimnego na wylocie z wymiennika z równań (16):













wyl

[°C]

Czasami czynnikiem grzewczym (gorącym) jest para wodna, która oddaje ciepło podczas

skraplania. Takie wymienniki nazywamy skraplaczami. Para wodna podczas skraplania nie

zmienia swojej temperatury (skrapla się w stałej temperaturze równej temperaturze

wrzenia/skraplania w danym ciśnieniu skraplania). Równania (15) zapiszemy w postaci:





z
p























(17)

gdzie:

r – ciepło parowania/skraplania [J/kg];

i 

- entalpia właściwa pary [J/kg];

i

- entalpia skroplin [J/kg].

Ważne! W równaniu (17) założyliśmy, że skraplająca się para jest nasycona, a odprowadzane

skropliny posiadają temperaturę wrzenia, stąd różnica entalpii właściwych równa jest ciepłu

parowania/skraplania.

Zadanie 12

Do jakiej temperatury w wymienniku ciepła zostanie ogrzany sok o c

= 3,75 [kJ/kg·K] i

temperaturze początkowej 10 [°C] przepływający z wydajnością 2 [kg/s]. Nośnikiem ciepła

jest skraplająca się pod ciśnieniem 2 [bar] para wodna. W procesie powstało 20 [kg] skroplin

w ciągu 3 [min].

Dane:

= 2 [kg/s]

z
p

c = 3750 [J/kgK]

Obliczamy wydajność, z która skrapla się para:

180

20 



skroplin

[kg/s]

Określamy wartość ciepła parowania:

r = 2201100 [J/kg]

Obliczamy ilość ciepła wymienianego w aparacie z równań (17):

 

244566

2201100







oraz spadek temperatury czynnika zimnego:

 

z
p

3750

244566 











W końcu temperaturę czynnika zimnego na wylocie z wymiennika z równań (16):













wyl

[°C]

Bilansowanie płynu mamy za sobą. Teraz wróćmy do procesu wymiany ciepła, a konkretnie

do przenikania ciepła. Na wstępie wspomniałem, że w wymienniku ciepło przenika od

czynnika gorącego do zimnego przez ściankę przepony. Co więcej strumień ciepła, który

oddaje płyn gorący, a pobiera płyn zimny jest równe ciepłu wymienionemu w wymienniku w

procesie przenikania opisanym równaniem (13).







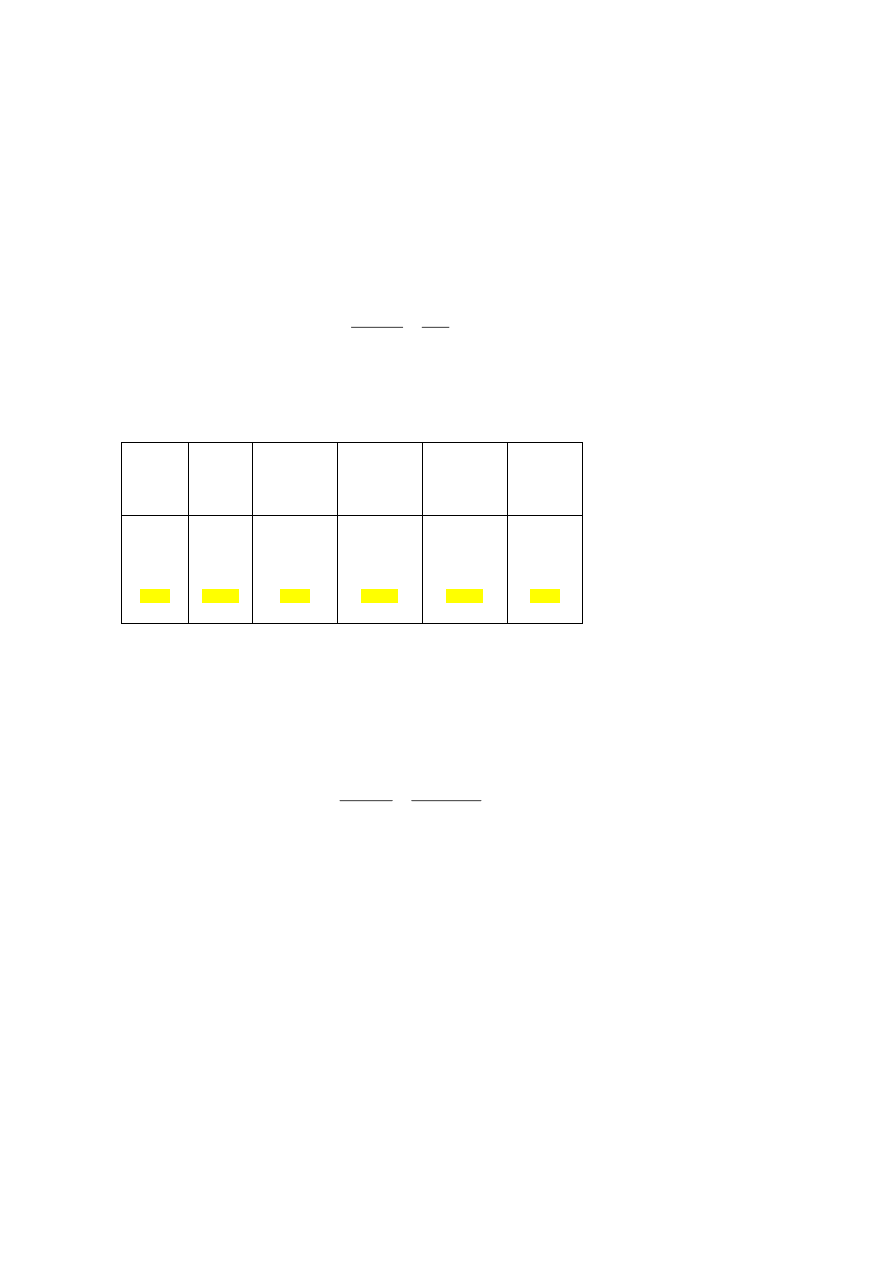
Tablica parowa ze strony katedry.

Ciśnienie

[bar abs]

Temp.

t [°C]

Entalpia wody

i' [kJ/kg]

Ciepło

parowania

r [kJ/kg]

Entalpia pary

i" [kJ/kg]

Objętość
właściwa

v [m

/kg]

0,90

96,71

405,15

2265,7

2670,9

1,869

1,00

99,63

417,46

2258,0

2675,5

1,694

1,013

100,00

419,04

2257,0

2676,0

1,673

1,513

111,61

468,3

2225,6

2693,9

1,149

2,013

120,42

505,6

2201,1

2706,7

0,881

2,513

127,62

536,1

2181,0

2717,1

0,714

Powstaje tylko jedno pytanie – „jak określić różnicę temperatur pomiędzy gorącym, a

zimnym płynem skoro są one zmienne w wymienniku?”

Wprowadzimy średnią różnicę temperatur – średnią logarytmiczną, tak jak w przypadku

średnic cylindra.

śr















log

(18)

gdzie:

T

– różnica temperatur na początku wymiennika;

T

– różnica temperatur na końcu wymiennika.

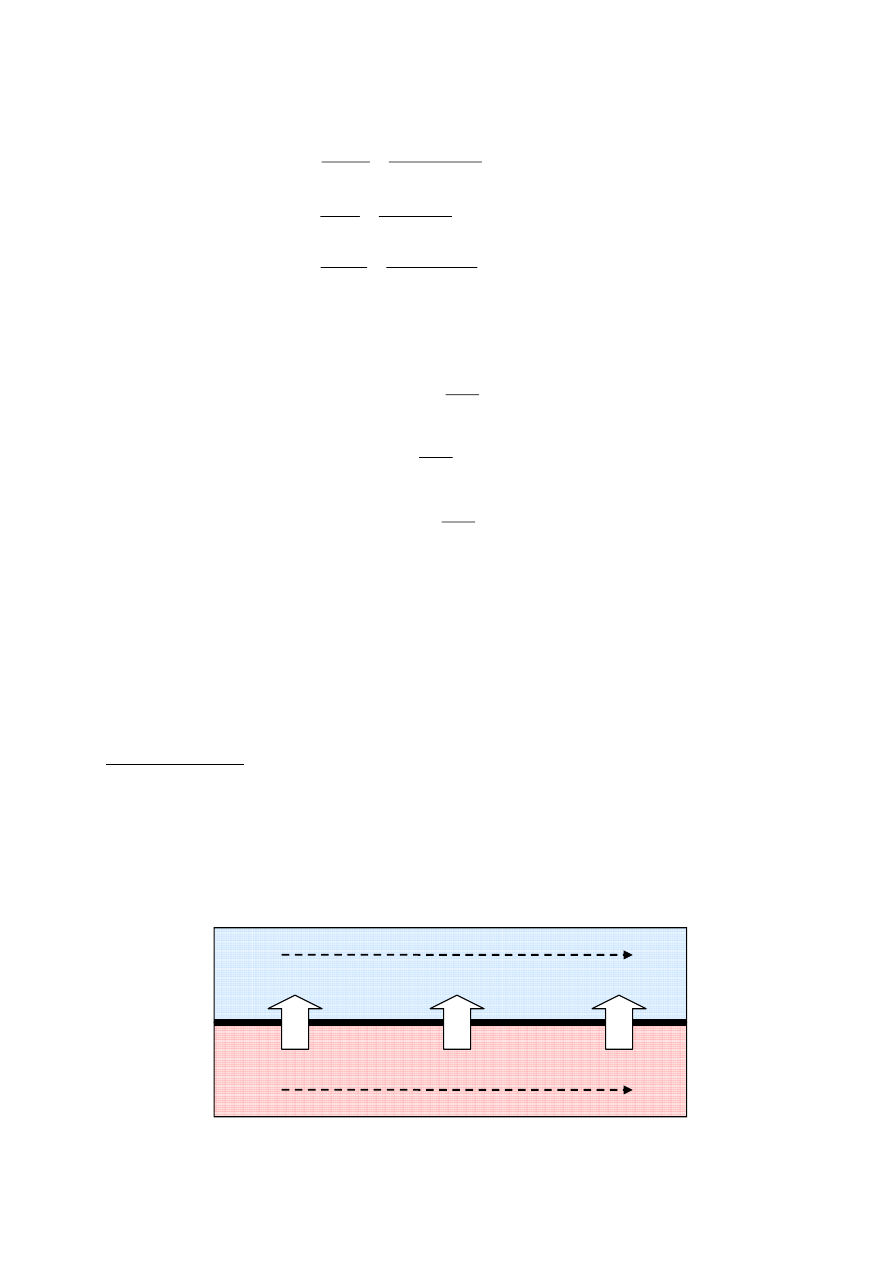
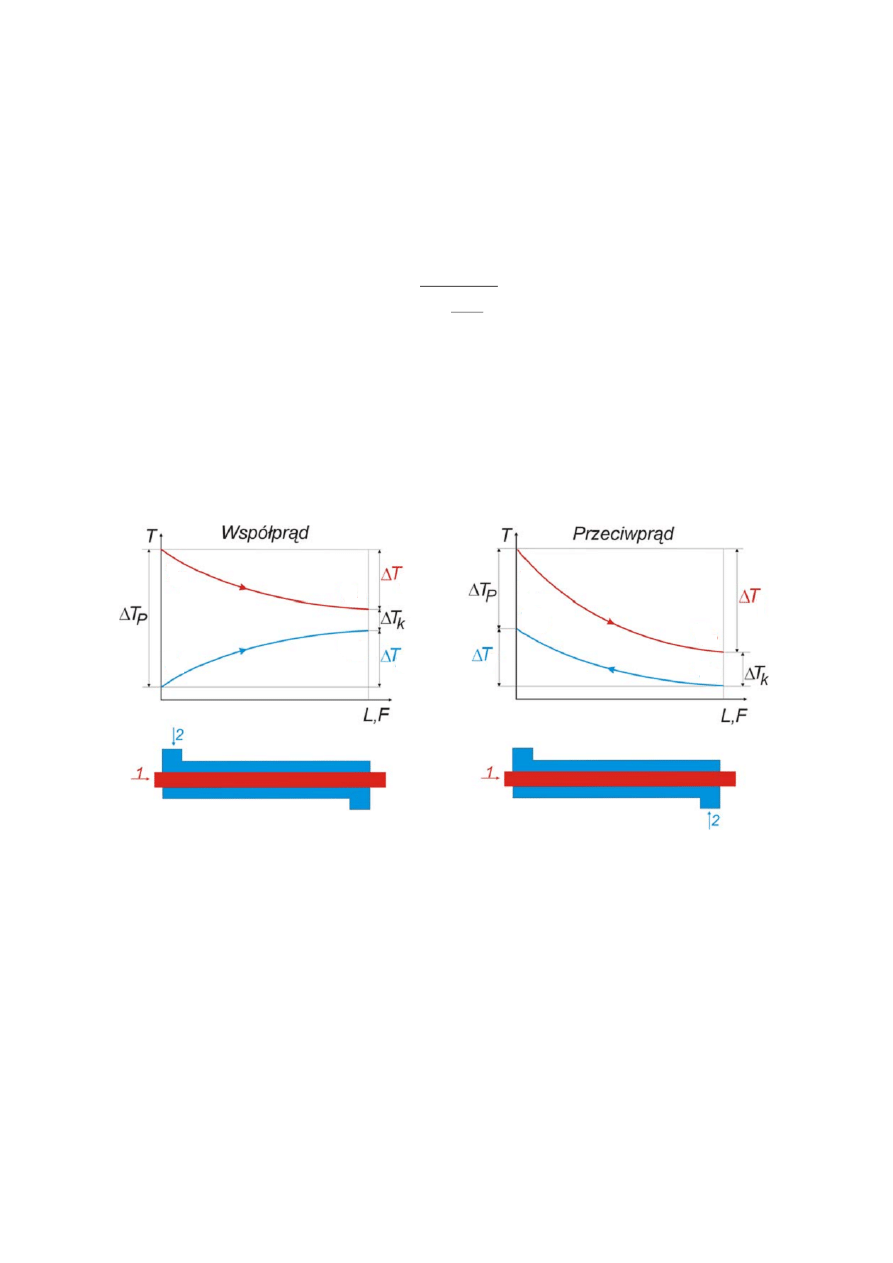
Jakimi zależnościami będą opisane te różnice zależy od tzw. trybu prowadzenia procesu.

Wyróżniamy dwa szczególne: współprąd i przeciwprąd. Spójrzmy na rysunek:

- dla współprądu

wyl













(19)

- dla przeciwprądu

wyl













(20)

Dla skraplacza nie wyróżniamy trybów i różnice na początku i końcu wymiennika opiszemy

równaniami:

wyl

pary













(21)

gdzie:

pary

– temperatura wrzenia/skraplania w danym ciśnieniu skraplania [K]

Zadanie 13

W przeciwprądowym podgrzewaczu należy podgrzać 2100 [l/h] mleka od temperatury

20 [

C] do temperatury 50 [C] za pomocą 3600 [l/h] gorącej wody o temperaturze 80 [C].

Współczynnik przenikania ciepła wynosi 180 [W/m

K]. Obliczyć niezbędną powierzchnię

wymiany ciepła.

Gęstość mleka 1027 [kg/m

], wody 983 [kg/m

Ciepło właściwe mleka 3,9 [kJ/kgK], wody 4,18 [kJ/kgK].

Zadanie 14

Należy ochłodzić 2 [m

/h] cieczy o gęstości

= 1010 [kg/m

] i cieple właściwym

c = 3,84 [kJ/kgK] od temperatury 80 [°C] do temperatury 40 [

C] za pomocą 4000 [l/h]

zimnej wody o temperaturze 4 [

C]. Współczynnik przenikania ciepła wynosi 220 [W/m

K].

Jaka powinna być powierzchnia wymiany ciepła przy zastosowaniu współprądu, a jaka przy

zastosowaniu przeciwprądu?

Gęstość wody 1000 [kg/m

], ciepło właściwe wody c

=4,18 [kJ/kgK].

Zadanie 15

W aparacie przeponowym trzeba podgrzać produkty spożywcze c

=3,68 [kJ/kgK] od

temperatury 16 [

C] do 92 [C]. Wydajność przepływu produktu 13500 [kg/h]. Nośnikiem

ciepła jest woda (=1000 [kg/m

], c

= 4,19 [kJ/kgK]) o temperaturze początkowej 98 [

C],

płynąca z natężeniem 25 [m

/h]. Przepona aparatu wykonana jest ze stali kwasoodpornej

(s=1,6 [mm],

=16,8 [W/mK]). Sporządzić bilans cieplny układu i wykres temperatur

wymiennika ciepła oraz obliczyć powierzchnię ogrzewalną aparatu pracującego w

Tablica parowa ze strony katedry.

Ciśnienie

[bar abs]

Temp.

pary

[°C]

Entalpia wody

i' [kJ/kg]

Ciepło

parowania

r [kJ/kg]

Entalpia pary

i" [kJ/kg]

Objętość
właściwa

v [m

/kg]

0,90

96,71

405,15

2265,7

2670,9

1,869

1,00

99,63

417,46

2258,0

2675,5

1,694

1,013

100,00

419,04

2257,0

2676,0

1,673

1,513

111,61

468,3

2225,6

2693,9

1,149

2,013

120,42

505,6

2201,1

2706,7

0,881

2,513

127,62

536,1

2181,0

2717,1

0,714

przeciwprądzie. W obliczeniach należy przyjąć wartości współczynnika wnikania ciepła po

stronie wody 4350 [W/m

K], a po stronie produktu wielkość niższą o 30%. Obliczenia należy

wykonać dla przepony czystej oraz pokrytej warstwą osadu po stronie produktu s=0,08 [mm],
=0,68 [W/mK].

Bilans ciepła we wszystkich powyższych zadaniach możemy opisać równaniami (15):

g
p

z
p















Proszę zauważyć, że znamy trzy temperatury, wydajności przepływu obu czynników oraz

ciepła właściwe.

Ważne! Ciepło właściwe oznaczamy c, c

, c

. Ja oznaczam c

, ale na wykładach i w zadaniach

na egzaminie może być oznaczone c lub c

Ostatnie równanie informuje o równości strumieni ciepła, stąd możemy napisać, że:

log

śr

g
p

z
p



















(22)

gdzie:

Q – strumień ciepła, który oddaje płyn gorący, a pobiera płyn zimny jest wymieniony w

wymienniku w procesie przenikania [W].

Rozwiązanie zadania z wymiennika ciepła to obliczenie jego powierzchni (czasami tylko

długości). W tym celu skorzystamy z ostatniego równania w (22):

log

śr













(23)

Widzimy, że aby obliczyć powierzchnię wymiany ciepła w wymienniku musimy znać

wartość współczynnika przenikania ciepła k, strumień ciepła Q oraz średnią różnice

temperatur

T

śr.log

1. Strumień ciepła Q obliczymy z bilansu ciepła, z równania bilansowego dla czynnika o

znanych obu temperaturach wlotowej i wylotowej.

Zadanie 13. czynnik zimny (mleko)





70092

3900

1027

3600

2100

















z
p

[W]

Zadanie 14. czynnik gorący (nie nazwany)





86186

3840

1010

3600















g
p

[W]

Zadanie 15. czynnik zimny (produkt spożywczy)





1048800

3680

3600

13500















z
p

[W]

Jeżeli była podana wydajność objętościowa to przeliczałem na masowa mnożąc przez gęstość

czynnika.

2. Współczynnik przenikania ciepła obliczymy z równania (14)

Zadanie 13. znane k = 180 [W/m

Zadanie 14. znane k = 220 [W/m

Zadanie 15. obliczamy z równania (14)

Dwa przypadki:

- pierwszy bez osadu:





151

1530

4350





















stal









- drugi z osadem:





1296

4350























osad

stal













Proszę zauważyć, że równanie (14) możemy zapisać w postaci ogólnej:















(24)

Sumujemy wszystkie opory przewodzenia, jeżeli przepona składa się z kilku warstw.

3. Średnia różnica temperatur opisana jest równaniem (18)

Do jej obliczenia konieczna jest znajomość wartości wszystkich czterech temperatur oraz

trybu prowadzenia procesu przeciwprąd/współprąd.

Czwartą (brakującą) temperaturę obliczymy z drugiego równania bilansowego (wartość Q

już znamy --> patrz punkt 1).

Zadanie 13.

4180

983

3600

70092

log









































































śr

wyl

g
p

Zadanie 14.

4180

1000

3600

4000

86186

































wyl

z
p

Dwa przypadki:

- współprąd

log









































śr

wyl

- przeciwprąd

log









































śr

wyl

Średnia logarytmiczna różnica temperatur w przeciwprądzie będzie zawsze większa.

Zadanie 15.

4190

1000

3600

1048800

log







































































śr

wyl

g
p

Na końcu korzystając z równania (23) obliczmy powierzchnie wymiany ciepła w naszym

wymienniku/-ach (dla każdego przypadku w zadaniach 14 i 15).

Zadanie 13.

180

70092

log













śr

]

Zadanie 14.

220

86186

log













śr

wspolprad

]

220

86186

log













śr

przeciwpra

]

Zadanie 15.

1530

1048800

log













śr

osadu

bez

]

1296

1048800

log













śr

osadem

]

Zadanie 16

Do dyspozycji jest rurowy wymiennik ciepła o powierzchni ogrzewalnej 9,50 m

. Trzeba

sprawdzić, czy aparat ten można zastosować do podgrzewania zadanego produktu (o gęstości
= 1010 [kg/m

] i cieple właściwym c = 3,84 [kJ/kgK]) w następujących warunkach:

natężenie przepływu produktu 1,15 kg/s, temperatura początkowa produktu 12 °C,

temperatura końcowa 65°C. Przepona wymiennika wykonana jest z rur kwasoodpornych D =

38 x 1,0 mm o

= 17 W/(m °C). Nośnikiem ciepła jest para wodna o temperaturze skraplania

120°C przy współczynniku wnikania ciepła od pary do powierzchni rury równym

=3800

W/(m°C). Współczynnik wnikania po stronie produktu można przyjąć jako równy

=1750

W/(m °C).