1

Ćwiczenie 2

POMIARY MOCY

1. Wprowadzenie

Moc (praca w jednostce czasu) pobierana przez urządzenie elektryczne wynosi:

I

U

P

⋅

=

(1.1)

Jest to po prostu (praca/ładunek)*(ładunek/czas). Dla napięcia mierzonego w woltach

[V], oraz prądu w amperach [A], jednostką mocy jest wat [W]. Waty są to dżule na sekundę
(1W=1J/s).
Energia (związana z mocą) zamienia się zazwyczaj w ciepło lub pracę mechaniczną
(silniki), energię promieniowania (lampy, nadajniki), lub w energię zmagazynowaną (baterie,
kondensatory).

1.1. Moc w obwodach prądu stałego

W układach prądu stałego mówi się jedynie o mocy czynnej. Z tego względu bilans

mocy jest tu stosunkowo prosty. Moc czynna w ogólnym przypadku jest iloczynem prądu,
napięcia i kosinusa kąta przesunięcia między nimi. Przy prądzie stałym trudno mówić o
przesunięciu w fazie między prądem i napięciem. Z tego względu można powiedzieć, że moc
czynna równa jest iloczynowi prądu i napięcia. W obwodach z prądem stałym praktyczne
znaczenie mają jedynie rezystory. Moc rozpraszana w rezystorze wyznaczona może być na
podstawie zależności (1.1). Stosując prawo Ohma można otrzymać następujące zależności:

R

I

P

2

=

i

R

U

P

2

=

(1.2)

Moc prądu stałego mierzy się bezpośrednio watomierzem elektrodynamicznym, lub

pośrednio – metodą techniczną poprzez pomiar prądu i napięcia w obwodzie.

1.2. Moc prądu przemiennego

W obwodach prądu przemiennego pojęcie mocy używane jest w różnych odmianach

definicyjnych. Chwilowa moc dostarczana do obwodu jednofazowego wyrażana jest na
podstawie chwilowych wartości napięcia i prądu:

)

(

)

(

)

(

t

i

t

u

t

p

⋅

=

(1.3)

Przy prądzie sinusoidalnym przebiegi prądu i(t) i napięcia u(t) w ogólnym przypadku

nie są ze sobą w fazie, lecz są przesunięte. Prąd i napięcie określić można na podstawie
poniższych zależności:

)

sin(

)

(

0

u

t

U

t

u

ϕ

ω

+

=

(1.4)

2

)

sin(

)

(

0

i

t

I

t

i

ϕ

ω

+

=

(1.5)

Gdzie

u

ϕ

,

i

ϕ

- fazy początkowe przesunięcia odpowiednio: napięcia i prądu.

Po uwzględnieniu zależności (1.4) i (1.5) w równaniu (1.3), otrzymamy następującą

zależność na moc chwilową:

[

]

)

2

cos(

)

cos(

2

1

)

sin(

)

sin(

0

0

0

0

i

u

i

u

i

u

t

I

U

t

I

t

U

p

ϕ

ϕ

ω

ϕ

ϕ

ϕ

ω

ϕ

ω

+

+

−

−

=

+

+

=

(1.6)

Uwzględniając, że

2

0

U

U =

, oraz

2

0

I

I =

(co jest słuszne tylko dla przebiegów

sinusoidalnych)

1

, oraz wprowadzając pojęcie kąta przesunięcia fazowego (zwanego kątem

mocy)

i

u

ϕ

ϕ

ϕ

−

=

, wyrażenie na moc chwilową przyjmie postać:

)

2

cos(

cos

ϕ

ω

ϕ

−

−

=

t

UI

UI

p

(1.7)

Drugi składnik powyższego równania określa moc oscylującą z podwójną pulsacją

ω

2 wokół stałej wartości

ϕ

cos

UI

. Wartość ta równa jest co do wartości średniej mocy

chwilowej, wyznaczonej w okresie T:

∫

=

=

T

UI

pdt

P

0

cos

ϕ

(1.8)

Wielkość określona wzorem (1.8) nosi nazwę mocy czynnej. Jednostką mocy czynnej

jest wat (1[W]). To właśnie energia elektryczna związana z mocą czynną (inaczej: „mocą
użyteczną”) zamieniana jest na inny rodzaj energii (np. energię cieplną, mechaniczną,
chemiczną, świetlną, itp.).

Moc w układach reaktancyjnych

Moc chwilowa (1.3) dostarczana do dowolnego elementu zawsze wyrażana jest

iloczynem prądu i napięcia

. Jednak w układach reaktancyjnych, gdzie U i I nie są

proporcjonalne nie można ich po prostu pomnożyć przez siebie. W wyniku takiego działania
może dojść do nieprawidłowości. Na przykład znak iloczynu może zmienić się na przeciwny
dla jednego okresu przebiegu zmiennego. Pokazano to na rys. 1.1, który przedstawia
przebiegi prądu i napięcia w układzie kondensatora zasilanego ze źródła napięcia
przemiennego (rys. 2.3).

1

Należy zaznaczyć, iż w naszych rozważaniach wielkości

0

0

iI

U

są wartościami maksymalnymi napięcia i

prądu, natomiast

UiI

są wartościami skutecznymi. Związki łączące te dwie wielkości słuszne są jedynie dla

przebiegów sinusoidalnych.

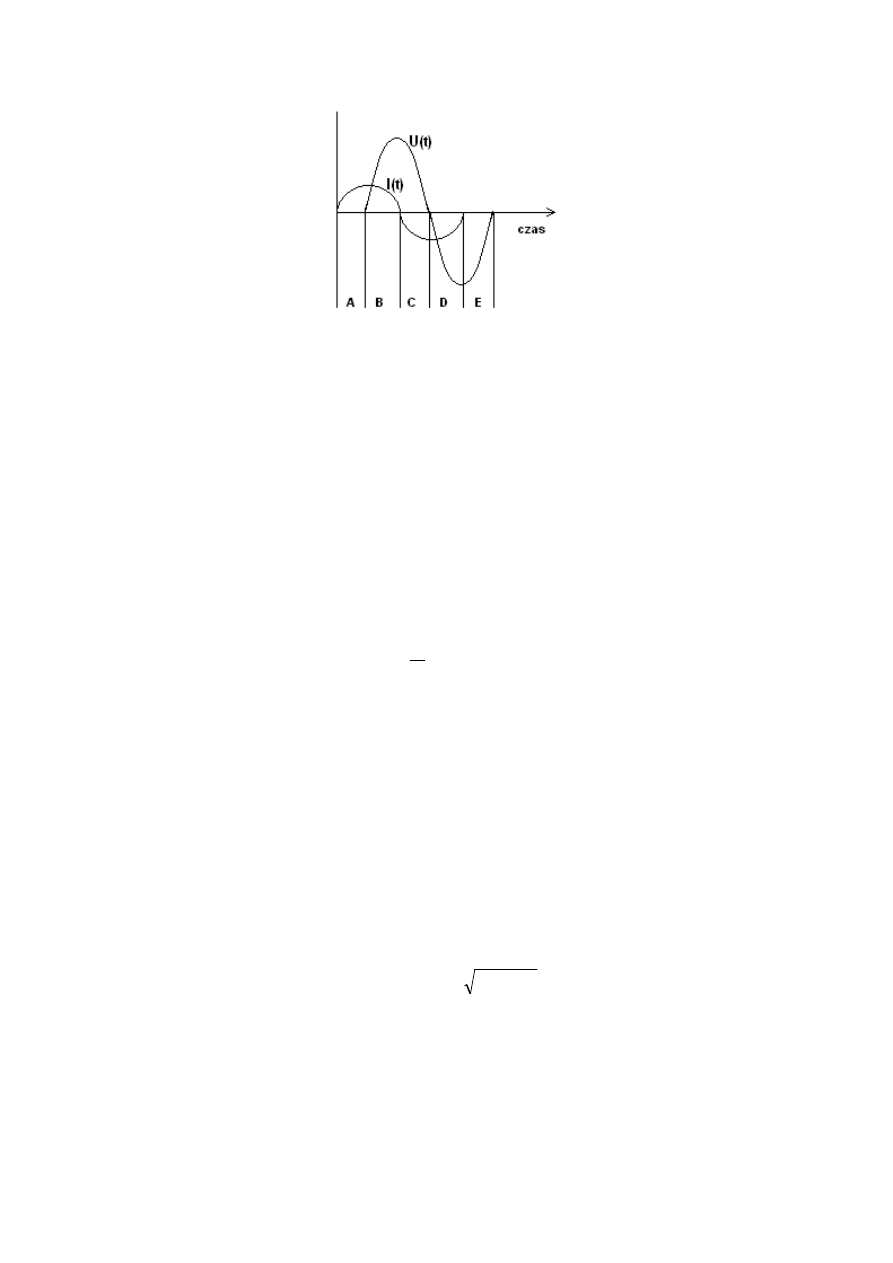
3

Rys. 1.1. Dla układów sinusoidalnych prąd płynący przez kondensator wyprzedza

napięcie o 90˚.

W przedziałach czasowych B i D moc dostarczana jest do kondensatora, powodując

jego ładowanie. Energia zgromadzona powiększa się (moc jest prędkością zmian energii). W
przedziałach C i E moc dostarczana do kondensatora jest ujemna – następuje jego
rozładowanie.

Średnia moc w całym okresie zmian dla pokazanego przykładu równa jest zeru.

Stwierdzenie to jest słuszne dla dowolnych czysto reaktancyjnych elementów i ich
kombinacji.

W ogólnym przypadku moc średnia wydzielana w dowolnym układzie może być

wyznaczana poprzez określenie pola powierzchni pod krzywą określoną iloczynem

i

u ⋅

, oraz

wyznaczenie średniej wartości tego iloczynu:

∫

=

T

dt

t

i

t

u

T

P

0

)

(

)

(

1

(1.10)

Do elementów reaktancyjnych odnosi się pojęcie mocy biernej, definiowanej jako:

ϕ

sin

UI

Q =

(1.11)

Jednostką mocy biernej jest 1 var. Wielkość ta nie ma fizycznego wyjaśnienia. W

odróżnieniu od energii czynnej, energia bierna nie jest rozpraszana w odbiorniku.
Odpowiadająca jej moc bierna pozostaje w układzie źródło-odbiornik powodując dodatkowe
obciążenie linii zasilającej. Mimo to jest ona potrzebna do wytworzenia np. zmiennego pola
magnetycznego w urządzeniach takich jak transformatory, silniki elektryczne itp.

Przebiegi czasowe mocy nie nadają się do praktycznych zastosowań. Wprowadzono

pojęcie mocy pozornej (

S), definiowanej jako iloczyn wartości skutecznych prądu i napięcia:

2

2

Q

P

UI

S

+

=

=

(1.12)

Na podstawie zależności (1.9), (1.11) i (1.12) można zauważyć, że wielkości P, Q i S są

bokami trójkąta prostokątnego o kącie ostrym

ϕ. Nazwano go trójkątem mocy (rys. 1.2).

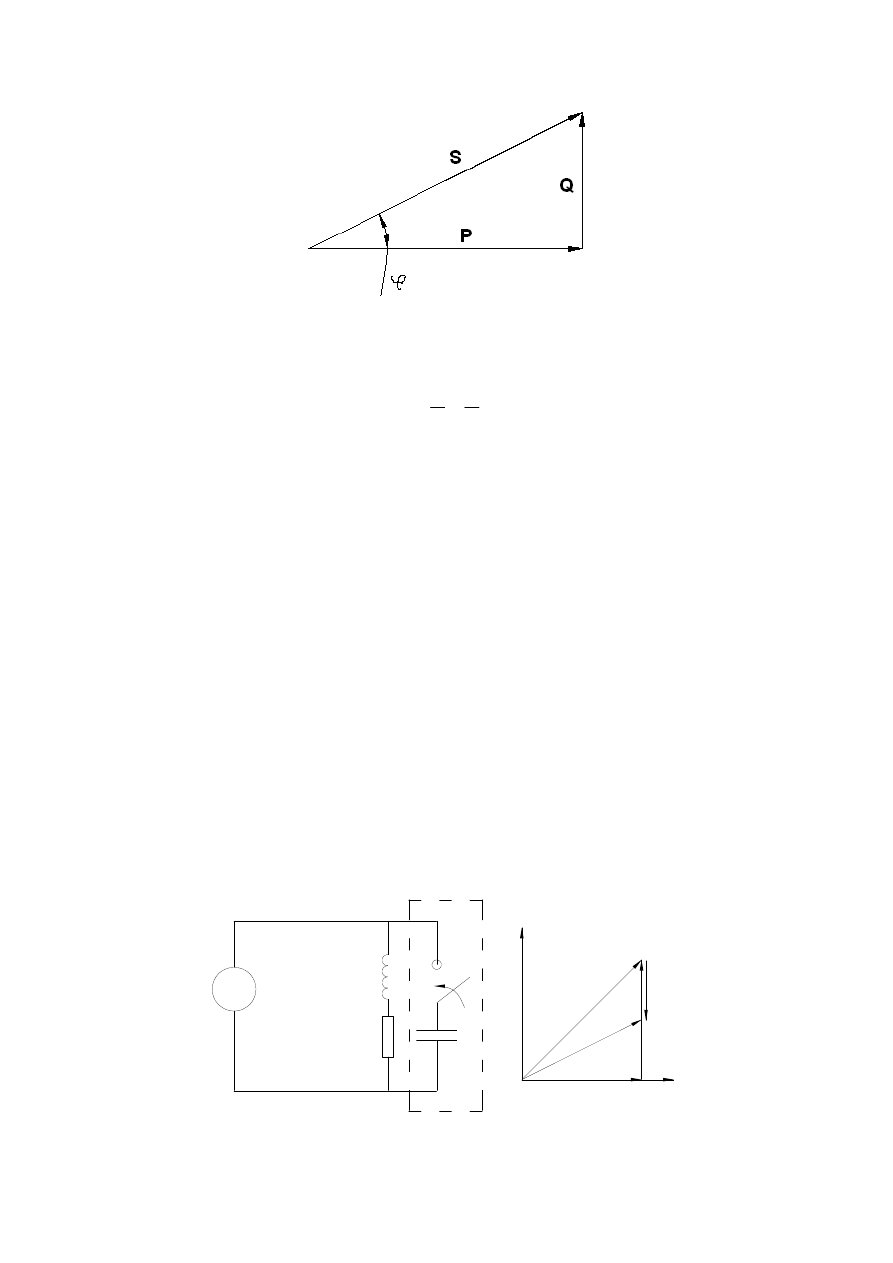
4

Rys. 1.2. Trójkąt mocy

Na rys. 1.2 widoczny jest kąt mocy (

ϕ

). Kosinus tego kąta zwany jest

współczynnikiem mocy:

Z

R

S

P =

=

ϕ

cos

(1.13)

Współczynnik mocy jest kosinusem przesunięcia fazy między napięciem i prądem.

Zmienia się od zera (dla układu czysto reaktancyjnego), do jedności (dla układu czysto
rezystancyjnego). Jeżeli współczynnik mocy jest mniejszy od 1, w układzie znajdują się
elementy reaktancyjne.

Z reguły dążymy do sytuacji, w której współczynnik mocy będzie jak największy. Jak

już wspomniano powyżej, moc bierna nie jest bezpośrednio zamieniana na inne formy
energii. Nadmiar mocy biernej nie jest pożądany w systemie elektroenergetycznym.
Powoduje on bowiem obniżenie sprawności generatorów, oraz zwiększenie prądów w liniach
zasilających przy danych mocach czynnych odbiorników. W konsekwencji wzrastają straty w
przesyle energii.

Większość odbiorników energii elektrycznej ma charakter rezystancyjno – indukcyjny.

Wymagają więc dostarczenia mocy czynnej i biernej – indukcyjnej. W konsekwencji
współczynnik

ϕ

cos maleje. Stąd powstał problem poprawiania współczynnika mocy, inaczej

kompensacji mocy biernej.

Moce bierne indukcyjne (

L

Q

) i pojemnościowe (

C

Q ) są w przeciwfazie (są

przesunięte o 180˚) i jeżeli występują jednocześnie w obwodzie, to następuje ich
kompensacja. Kompensacja mocy biernej najczęściej realizowana jest za pomocą baterii
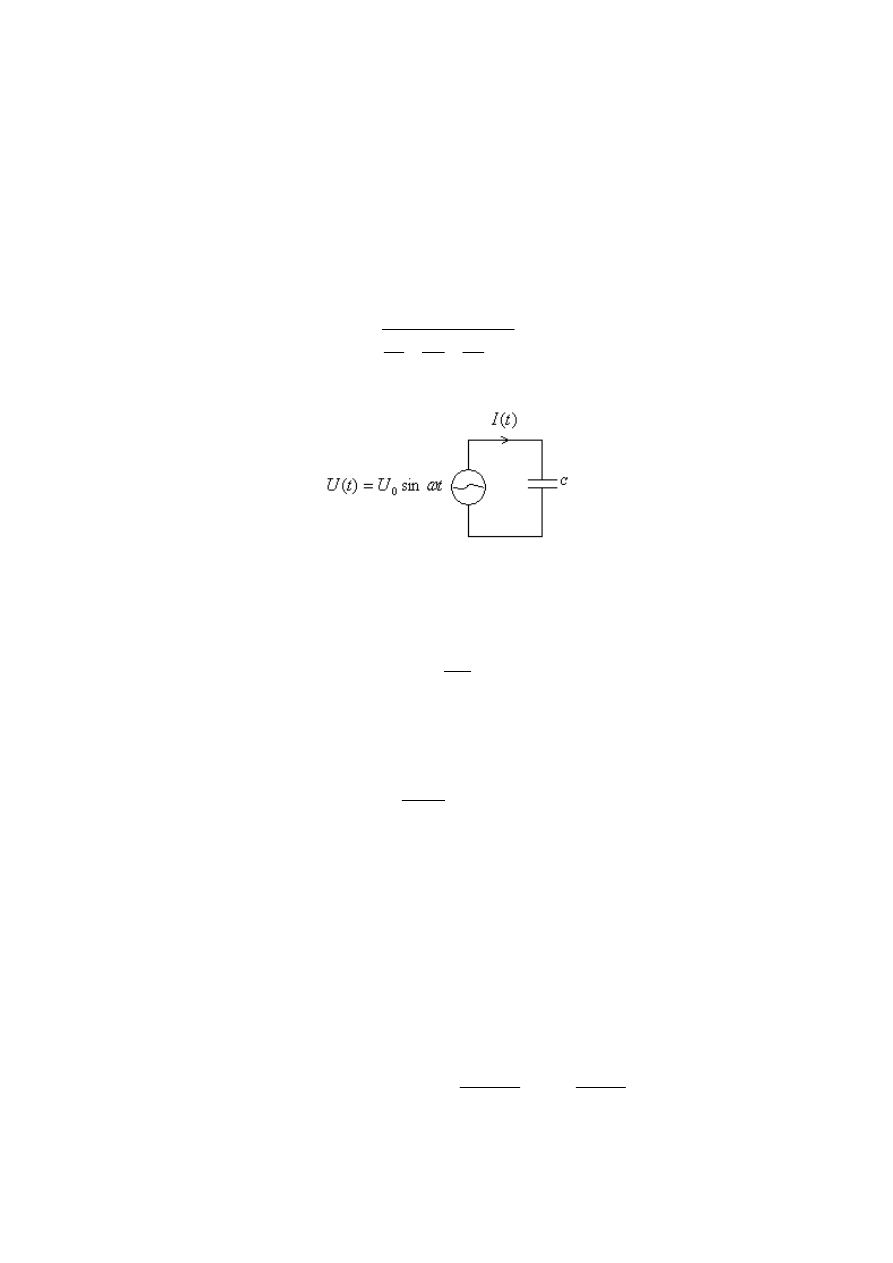
kondensatorów dołączanej równolegle do odbiornika indukcyjnego (rys. 1.3). Dzięki temu
kondensatory dostarczają odpowiednią ilość mocy biernej pojemnościowej.

Re

Im

P

S

1

=P

+j

Q

L1

R

L

L

~

Q

L1

Q

c1

S

2

=P

+j(

Q

L1

-

Q

C1

)

C

a)

b)

Rys. 1.3. Kompensacja mocy biernej.

5

2. Odbiorniki

2.1. Rezystory

Rezystory są elementami pasywnymi, charakteryzujące się tym, iż prąd przez nie

płynący jest wprost proporcjonalny do napięcia występującego na ich końcach. Prawo to nie
jest absolutnie uniwersalne dla wszystkich obiektów. Na przykład prąd płynący przez
świetlówkę jest nieliniową funkcją występującego na niej napięcia (do pewnego poziomu
prąd neonówki jest zerowy, a po przekroczeniu tej wartości – gwałtownie rośnie). Każdy
rezystor wykonany jest z jakiegoś materiału przewodzącego (węgla, folii metalowej, drutu o
małej przewodności właściwej, itp) z drutowymi wyprowadzeniami po obu stronach.
Charakteryzuje się on rezystancją:

I

U

R

/

=

(2.1)

Gdy

U wyrazimy w woltach a I w amperach, wartość R otrzymamy w omach. Zależność (2.1)

zwana jest prawem Ohma.

Z definicji (2.1) wynika kilka prostych wniosków:
- Rezystancja dwóch rezystorów połączonych szeregowo (rys. 2.1.a) wynosi:

2

1

R

R

R

+

=

(2.2)

Łącząc rezystory szeregowo zawsze otrzymamy rezystor o większej wartości rezystancji.

- Rezystancja dwóch rezystorów połączonych równolegle (rys. 2.1.b) wynosi:

2

1

2

1

R

R

R

R

R

+

⋅

=

lub

2

1

1

1

1

R

R

R

+

=

(2.3)

Łącząc rezystory równolegle zawsze otrzymamy rezystor o mniejszej wartości rezystancji.

R

1

R

2

R

1

R

2

a)

b)

Rys. 2.1. Połączenia rezystorów. a)szeregowe; b) równoległe.

2.2. Elementy reaktancyjne

Cewki indukcyjne i kondensatory są bezużyteczne w obwodach prądu stałego. Wraz z

rezystorami, elementy te tworzą triadę pasywnych elementów liniowych (amplituda sygnału
wyjściowego jest proporcjonalna do sygnału wejściowego) stanowiących podstawę
wszystkich układów elektronicznych.

6

Układy z kondensatorami i cewkami są bardziej skomplikowane niż układy

rezystorowe, gdyż ich parametry zależą od częstotliwości. Poza tym na elementach tych
występuje przesunięcie pomiędzy napięciem i prądem.

Prawo Ohma określone zależnością (2.1) może być uogólnione na układy zawierające

kondensatory i cewki. Pojęcie rezystancji musi zostać jednak rozszerzone na wielkość zwaną
„impedancją” (nazwijmy ją uogólnioną rezystancją). Cewki i kondensatory muszą być
rozpatrywane na płaszczyźnie liczb urojonych. Elementy te charakteryzowane są za pomocą
reaktancji będącej „rezystancją urojoną (na płaszczyźnie liczb zespolonych)”.

Mówiąc inaczej:

2

2

tan

tan

cja

reak

cja

rezys

impedancja

+

=

2.2.1. Kondensatory

Kondensatory charakteryzują się następującą właściwością:

CU

Q =

(2.4)

Kondensator o pojemności C faradów i napięciu U woltów pomiędzy jego

wyprowadzeniami zawiera Q kulombów ładunku zmagazynowanego na jednej okładzinie i

–Q kulombów na drugiej.
Kondensatory nie mogą rozpraszać mocy choć może przez nie płynąć prąd. Fakt ten

tłumaczy się tym, iż prąd i napięcie na kondensatorze przesunięte są w fazie o 90˚.
Po zróżniczkowaniu równania definicyjnego, otrzymujemy wzór na prąd kondensatora:

dt

dU

C

I =

(2.5)

Widać stąd, iż prąd kondensatora nie jest wprost proporcjonalny do napięcia (tak jak w

rezystorze), lecz do szybkości jego zmian (pochodnej napięcia względem czasu). Ponadto,
również odmiennie niż dla rezystora traktowana jest moc (iloczyn napięcia i prądu) związana
z przepływem prądu. Nie zamienia ona się w ciepło, lecz jest magazynowana jako
wewnętrzna energia pola elektrycznego kondensatora. Całą tą energię można uzyskać z
powrotem w czasie rozładowywania.

Łącząc kondensatory równolegle, należy pamiętać, iż ich wypadkowa pojemność jest

sumą pojemności poszczególnych kondensatorów. Można to łatwo udowodnić na podstawie
poznanych zależności (2.4). Niech U będzie napięciem na kondensatorach połączonych
równolegle (rys. 2.2) (pamiętamy, że napięcie na gałęziach połączonych równolegle jest
takie samo).

Rys. 2.2. Połączenie równoległe kondensatorów

7

W takim przypadku można napisać na podstawie (2.4):

(

)

U

C

C

C

U

C

U

C

U

C

Q

Q

Q

Q

U

C

cała

cała

...

...

...

3

2

1

3

2

1

3

2

1

+

+

+

=

+

+

+

=

+

+

+

=

=

(2.6)

lub:

...

*

4

2

1

C

C

C

C

cała

+

+

=

(2.7)

Dla kondensatorów połączonych szeregowo wzór na pojemność całkowitą układu ma

taką samą postać jak wzór na rezystancję zastępczą rezystorów połączonych równolegle:

...

1

1

1

1

3

2

1

+

+

+

=

C

C

C

C

cała

(2.8)

Rys. 2.3. Analiza częstotliwościowa

Jeżeli do kondensatora jak w układzie na rys. 2.3 doprowadzone zostanie napięcie

sinusoidalne, to prąd w tym obwodzie będzie równy:

t

U

C

dt

dU

C

t

I

ω

ω

cos

)

(

0

=

=

(2.9)

W tym przypadku mamy prąd o amplitudzie I, wyprzedzający w fazie napięcie o 90˚.

Jeżeli rozważać tylko amplitudy, pomijając zależności fazowe, to prąd jest równy:

C

U

I

ω

/

1

=

(2.10)

Prąd zachowuje się tak jakbyśmy mieli do czynienia z rezystancją zależną od

częstotliwości (

C

ω

/

1

), przesuniętą dodatkowo w fazie o 90˚.

Przyjmując konwencję liczb zespolonych, możliwe jest znalezienie reaktancji

kondensatorów:

)

Re(

)

(

0

t

j

e

U

t

U

ω

=

(2.11)

Korzystając z zależności (2.5) otrzymujemy:













=













−

=

−

=

c

t

j

t

j

X

e

U

C

j

e

U

t

C

U

t

I

ω

ω

ω

ω

ω

0

0

0

Re

/

Re

sin

)

(

(2.12)

8

Czyli:

C

j

X

C

ω

1

−

=

(2.13)

Wielkość opisana wzorem (2.13) jest reaktancją kondensatora dla częstotliwości

π

ω

2

=

f

. Warto zauważyć, iż dla prądu stałego, reaktancja kondensatora równa jest

nieskończoności, co oznacza, iż nie popłynie przez niego prąd.

2.2.2. Cewki indukcyjne

Cewki są w rzeczywistości przeciwieństwem kondensatorów. Prędkość zmian prądu

płynącego przez cewkę zależy od panującego na niej napięcia. Równanie definiujące cewkę
ma postać:

dt

dI

L

U

=

(2.14)

Prąd płynący przez cewkę nie jest wprost proporcjonalny do spadku napięcia na

cewce. Moc związana z przepływem prądu (iloczyn prądu i napięcia) nie zamienia się w
ciepło, lecz jest magazynowana jako energia pola magnetycznego wytwarzanego przez
cewkę. Całą tą energię otrzymuje się z powrotem, gdy przerwie się przepływ prądu przez
cewkę.

Poszukując reaktancji cewki, można przeprowadzić podobną analizę jak dla

kondensatora. Powinniśmy wtedy otrzymać:

L

j

X

L

ω

=

(2.15)

2.2.3. Uogólnione prawo Ohma

Zachowując poprzednio podane konwencje dotyczące reprezentacji prądów i napięć,

prawo Ohma przyjmuje prostą postać:

Z

U

I

=

(2.16)

Należy pamiętać, że we wzorze (2.16) występują teraz wielkości zespolone. Napięcie

reprezentowane przez U występuje na impedancji Z powodując przepływ prądu
reprezentowany przez I. Dla zespolonej impedancji elementów połączonych szeregowo lub
równolegle stosuje się te same zasady co dla rezystancji:

...

3

2

1

+

+

+

=

Z

Z

Z

Z

(połączenie szeregowe)

(2.17)

...

1

1

1

1

3

2

1

+

+

+

=

Z

Z

Z

Z

(połączenie równoległe)

(2.18)

9

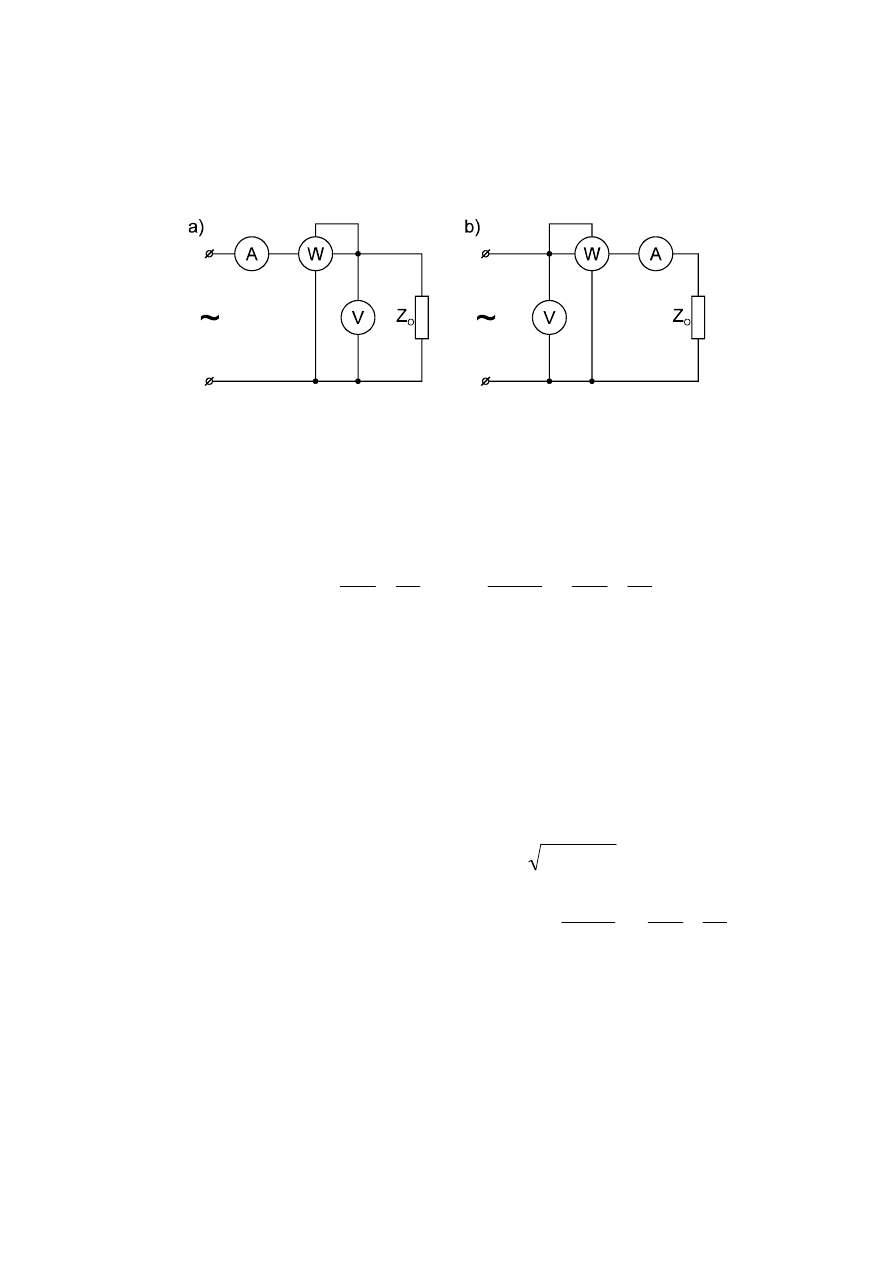
2.3. Pomiar mocy odbiorników jednofazowych metodą techniczną

Pomiar ten przeprowadza się za pomocą watomierza, woltomierza i amperomierza w

układzie jak na rys.2.4.a lub 2.4.b.

Rys.2.4. Schemat układu do pomiaru mocy prądu jednofazowego:

a) układ dla odbiorników o małej impedancji Z

0

;

b) układ dla odbiorników o dużej impedancji Z

0

W układzie jak na rys.2.4.a moc czynna mierzona za pomocą watomierza jest większa od

mocy czynnej odbiornika o moc wydzielaną w woltomierzu i obwodzie napięciowym
watomierza

























+

+

=













+

+

=

v

wn

v

v

wn

v

w

R

R

Z

U

R

R

U

P

P

1

1

cos

1

1

0

0

2

2

0

ϕ

(2.19)

przy czym R

wn

, R

v

- rezystancja odpowiednio obwodu napięciowego watomierza i

woltomierza, Z

0

- impedancja odbiornika.

W układzie jak na rys.1.8.b moc mierzona watomierzem jest większa od mocy czynnej

odbiornika o moc wydzielaną w obwodzie prądowym watomierza i w amperomierzu.

[

]

)

(

cos

)

(

0

0

2

2

0

a

wi

a

a

wi

a

w

R

R

Z

I

R

R

I

P

P

+

+

=

+

+

=

ϕ

(2. 20)

przy czym R

wi

, R

a

- rezystancja odpowiednio obwodu prądowego watomierza i

amperomierza, Z

0

- impedancja odbiornika.

Wybór określonego układu musi być dokonany tak, aby zminimalizować dodatkowe moce

mierzone. I tak układ a) powinien być stosowany przy małych, zaś układ b) przy dużych
impedancjach odbiornika. Jako impedancję graniczną umożliwiającą podział na małą i dużą

impedancję można w przybliżeniu przyjąć wartość równą

wi

wn

R

R

⋅

.

Przy prawidłowym wyborze układu moce pobierane przez przyrządy pomiarowe są

znacznie mniejsze od mocy odbiornika, gdyż: w układzie a)

v

wn

R

R

Z

1

1

cos

0

0

+

>>

ϕ

oraz w

układzie b)

a

wi

R

R

Z

+

>>

0

0

cos

ϕ

.

Moc czynną mierzoną za pomocą watomierza wyznacza się ze wzoru

α

w

w

k

P =

(2.21)

gdzie k

w

- stała watomierza [W/dz],

α - liczba działek odpowiadająca wychyleniu

wskazówki miernika.

Stałą watomierza wyznacza się następująco

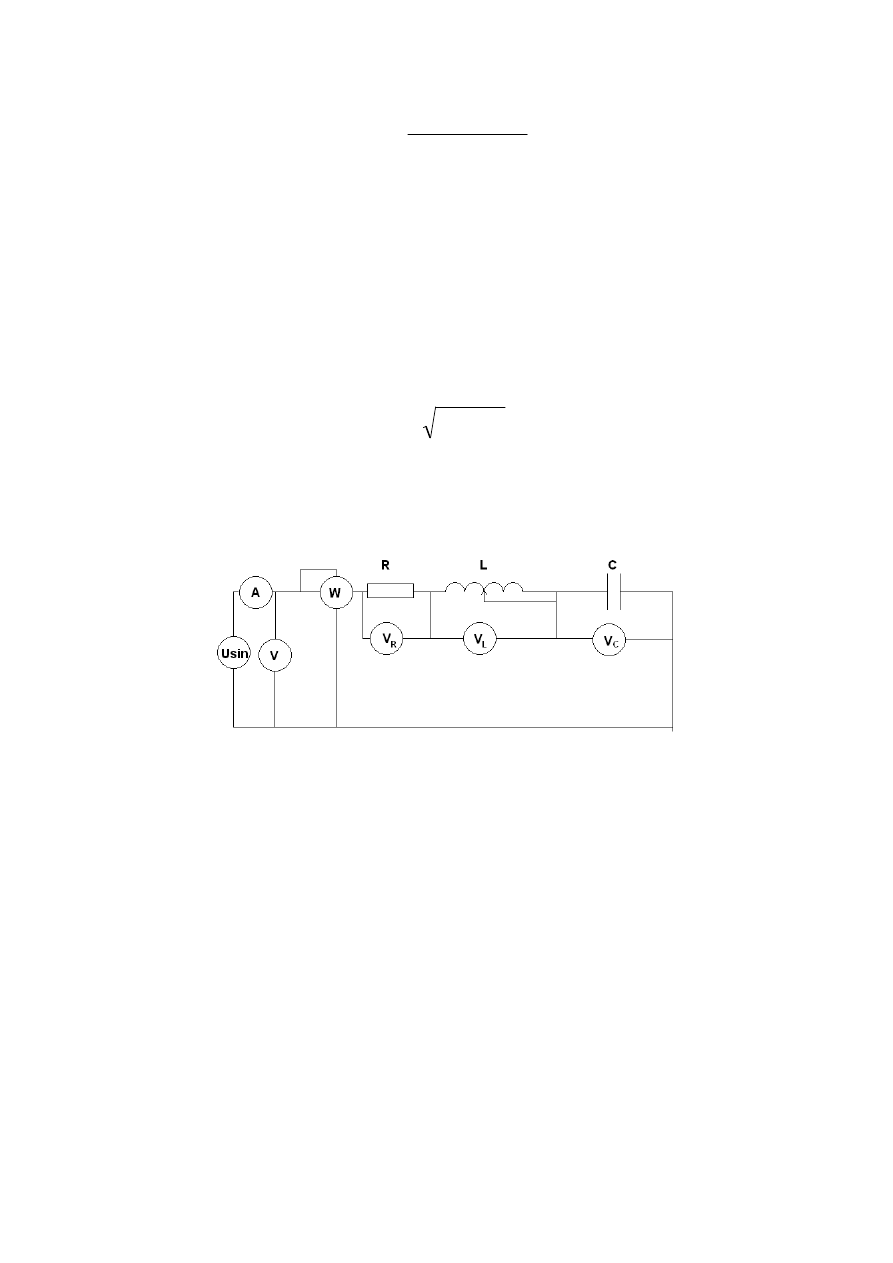
10

zn

zn

zn

zn

w

I

U

k

α

ϕ

cos

=

(2.22)

gdzie U

zn

, I

zn

- znamionowa wartość odpowiednio napięcia i prądu zakresów watomierza,

cos

ϕ

zn

- znamionowy współczynnika mocy watomierza (jeżeli nie jest podany tzn., że

cos

ϕ

zn

=1),

α

zn

- znamionowa liczba działek skali watomierza.

W celu uniknięcia przeciążenia obwodu napięciowego lub prądowego watomierza włącza

się zawsze woltomierz i amperomierz.

Na podstawie wskazań woltomierza i amperomierza można wyznaczyć moc pozorną

odbiornika

a

v

I

U

S =

0

(2.23)

oraz moc bierną

2

2

0

w

P

S

Q

−

=

(2.24)

3. Badania laboratoryjne

Pomiary wykonujemy zgodnie z protokołem dostarczonym przez prowadzącego.
Korzystamy z obwodu jednofazowego, składającego się z elementów R, L, C.

1) W pierwszej kolejności wykonujemy obwód jedynie z elementami R. Należy zmierzyć

moc czynną, napięcie na źródle zasilania, prąd w obwodzie, oraz spadek napięcia na
rezystancji.
Na podstawie znanych zależności należy wyznaczyć wartość mocy pozornej, biernej,
wartość współczynnika mocy i dokładną rezystancję opornika. Należy skomentować
wyniki.

2) Badania układu RL. Do istniejącego obwodu należy dołączyć regulowaną

indukcyjność. Podczas pomiarów należy zmieniać wartość indukcyjności i notować
wskazania mierników. Z otrzymanych wyników należy wykonać obliczenia mocy
czynnej, biernej i pozornej w obwodzie, oraz wartości współczynnika mocy w
zależności od indukcyjności cewki. Wyniki skomentować. Odpowiedzieć na pytanie w
jaki sposób cewka wpływa na parametry pracy układu.

3) Badania układu RLC. W tym przypadku do obwodu RL należy dołączyć baterię

kondensatorów. W pierwszej kolejności należy wykonać pomiary dla zerowej
wartości indukcyjności. W kolejnych próbach należy zwiększać wartość indukcyjności
i notować wskazania mierników. Na podstawie wyników należy obliczyć wartości P,
Q, S, R, X, cosφ. Odpowiedzieć na pytanie, w jaki sposób kondensator wpływa na
pracę układu. Narysować wykres wektorowy dla układu. W jaki sposób można
sumować wartości R, X, P, Q, S w obwodzie składającym się z elementów R, L, C?