Rozwiązania zadań otwartych i schematy punktowania
Strona 1 z 14
Klucz odpowiedzi do zadań zamkniętych
i schemat oceniania zadań otwartych
Klucz odpowiedzi do zadań zamkniętych
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18 19 20
D C D A
A
B
D C C
D
B
C
A
B
B
D
B
C
A
A
Schemat oceniania zadań otwartych
Zadanie 21. (2pkt)
Rozwiąż nierówność
2
2
3
2
0
x
x
.
Rozwiązanie
Obliczamy wyróżnik i pierwiastki trójmianu kwadratowego
2
2
3
2
x
x
9 4
2 2
25
,
5
,
1
3 5
2
4
x
,
2
3 5
1
4
2
x
.
Szkicujemy wykres trójmianu kwadratowego
2
2
3
2
y
x
x
,
-1
1
2
3
-1
1
2
3
y
0
x
1
2
_ _
z którego odczytujemy zbiór rozwiązań rozwiązywanej nierówności
1
2
,
2,
x
.
Schemat oceniania
Zdający otrzymuje ............................................................................................................1 pkt
gdy:
obliczy lub poda pierwiastki trójmianu kwadratowego
1
2
x
,
2
1
2
x
i na tym
poprzestanie lub błędnie zapisze zbiór rozwiązań nierówności
albo
rozłoży trójmian kwadratowy na czynniki liniowe, np.
1
2
2
2
x
x
i na tym
poprzestanie lub błędnie zapisze zbiór rozwiązań nierówności
albo
zapisze nierówność w postaci równoważnej
3
5
4
4
x
i na tym poprzestanie lub błędnie
zapisze zbiór rozwiązań nierówności
albo
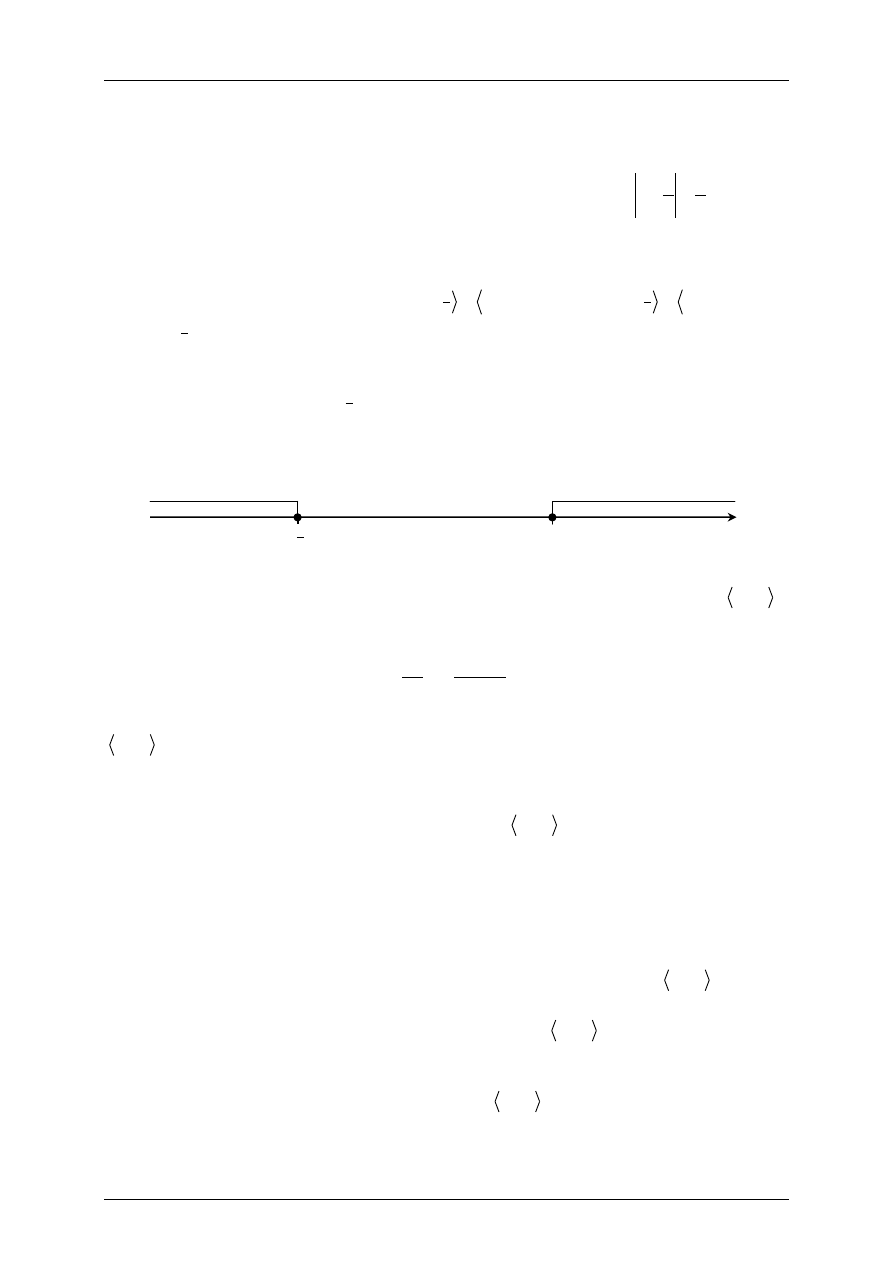
Rozwiązania zadań otwartych i schematy punktowania
Strona 2 z 14
popełni błąd rachunkowy przy obliczaniu wyróżnika lub pierwiastków trójmianu
kwadratowego (ale otrzyma dwa różne pierwiastki) i konsekwentnie do popełnionego
błędu rozwiąże nierówność
albo
błędnie przekształci nierówność do postaci równoważnej, np. zapisze
3
5
4
4
x
i konsekwentnie do popełnionego błędu rozwiąże nierówność.
Zdający otrzymuje ............................................................................................................2 pkt
gdy:
poda zbiór rozwiązań nierówności:
1
2
,
2,
lub
1
2
,
2,
x
lub
(
1
2
x
lub
2
x
)
albo
sporządzi ilustrację geometryczną (oś liczbowa, wykres) i zapisze zbiór rozwiązań
nierówności w postaci:
1
2
x
,
2
x
albo
poda zbiór rozwiązań nierówności w postaci graficznej z poprawnie zaznaczonymi
końcami przedziałów.
Zadanie 22. (2 pkt)
Oblicz największą wartość funkcji kwadratowej
2
( )
2
16
15
f x
x
x
w przedziale
2,3
.
Rozwiązanie
Pierwsza współrzędna wierzchołka paraboli będącej wykresem funkcji f jest równa
16
4
2
2
2
w
b
x
a
.
Stąd i z ujemnego znaku współczynnika stojącego przy
2
x wnioskujemy, że w przedziale
2,3
funkcja f jest rosnąca. Zatem największa wartość funkcji f w tym przedziale jest
równa
2
3
2 3
16 3 15
18 48 15 15
f
.
Odpowiedź: Największa wartość funkcji f w przedziale
2,3
jest równa 15.
Schemat punktowania
Zdający otrzymuje ............................................................................................................1 pkt
gdy:
obliczy pierwszą współrzędną wierzchołka paraboli będącej wykresem funkcji f
albo
zapisze wzór funkcji f w postaci kanonicznej i stwierdzi, że w przedziale
2,3
funkcja
jest rosnąca (wystarczy, że stwierdzi, że jest monotoniczna, o ile w dalszej części
rozwiązania oblicza wartości na obu krańcach przedziału
2,3
)
i na tym poprzestanie lub dalej popełnia błędy.
Zdający otrzymuje ............................................................................................................2 pkt
gdy obliczy największą wartość funkcji w przedziale
2,3
: 15.
x
1
2
2
Rozwiązania zadań otwartych i schematy punktowania
Strona 3 z 14
Zadanie 23. (2pkt)
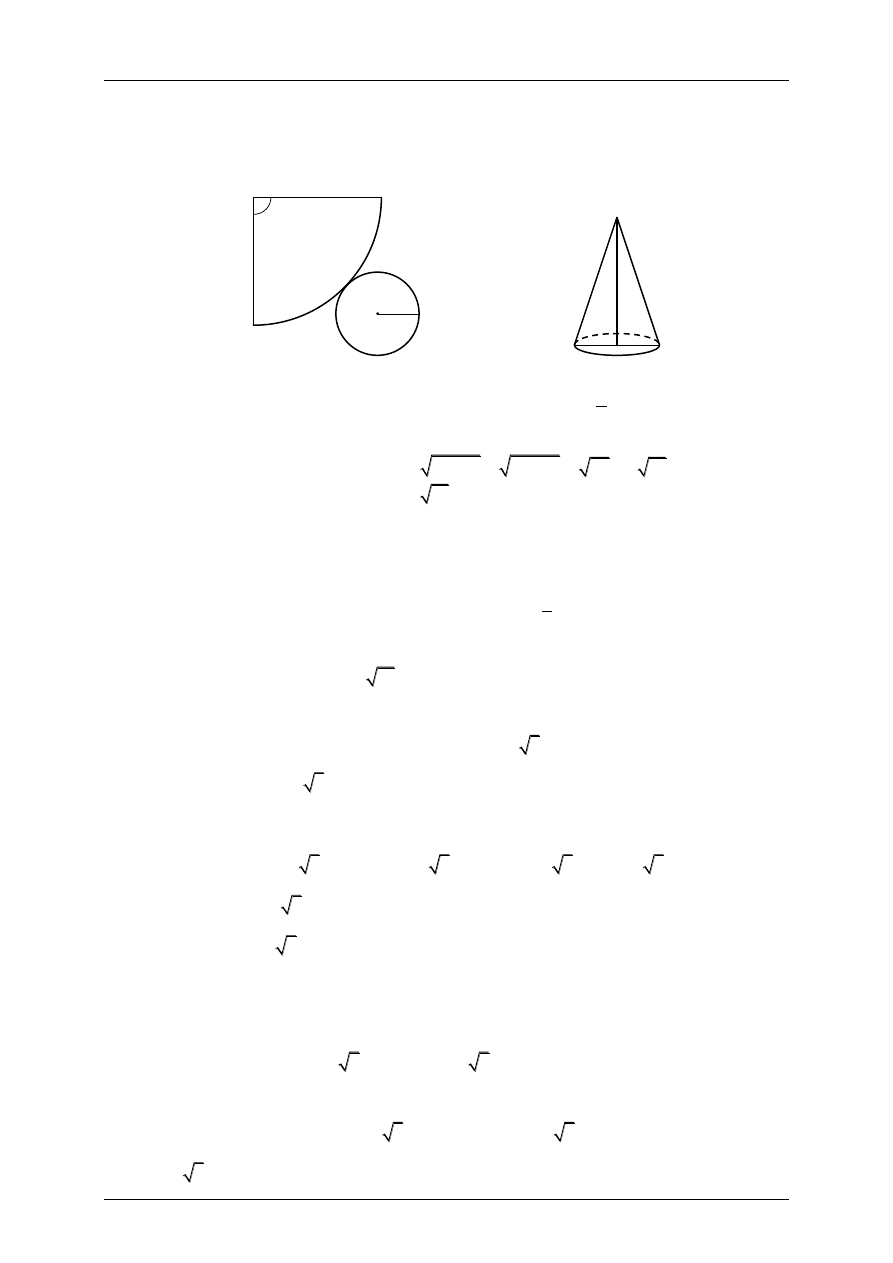
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest ćwiartką koła o promieniu 8 cm.
Oblicz wysokość tego stożka.
Rozwiązanie
Ponieważ powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest ćwiartką koła
o promieniu 8 cm, więc pole powierzchni bocznej stożka jest równe
2
1
8
16
4
.
Zatem ze wzoru na pole powierzchni bocznej stożka otrzymujemy
8 16
r
. Stąd
2
r
.
Z twierdzenia Pitagorasa otrzymujemy
2
2
2
2
8
8
2
60
2 15
h
r
.
Odpowiedź: Wysokość stożka jest równa 2 15 cm.
Schemat punktowania
Zdający otrzymuje ............................................................................................................1 pkt
gdy zapisze związek pozwalający obliczyć promień podstawy stożka, np. wykorzysta wzór na
pole powierzchni bocznej stożka i zapisze równanie
2
1
8
8
4
r
.
Zdający otrzymuje ............................................................................................................2 pkt
gdy obliczy wysokość stożka:
2 15
h
.
Zadanie 24. (2pkt)
Ciąg
n
a
jest określony dla
1
n
wzorem
2
4 3
n
a
n
. Sprawdź, którym wyrazem tego
ciągu jest liczba
2
2
3
2
3
.
Rozwiązanie
Po zastosowaniu wzoru na kwadrat sumy i wykonaniu redukcji otrzymujemy
2
2
2
3
2
3
9
4 4 3 3
16 4 3
4
4 3
.
Zatem liczba
2
2
3
2
3
jest czwartym wyrazem ciągu
n
a
.
Odpowiedź:
2
2
4
3
2
3
a
.
Schemat punktowania
Zdający otrzymuje ............................................................................................................1 pkt
gdy poprawnie zastosuje wzór skróconego mnożenia na kwadrat sumy i na tym zakończy lub
dalej popełnia błędy:
2
2
3
2
3
9
4 4 3 3
.
Zdający otrzymuje ............................................................................................................2 pkt
gdy doprowadzi wyrażenie
2
2
3
2
3
do postaci 16 4 3
i zapisze, że
2
2
4
3
2
3
a
.
r
8
h
8
8
.
r
Rozwiązania zadań otwartych i schematy punktowania
Strona 4 z 14
Zadanie 25. (2pkt)
Udowodnij, że dla dowolnych liczb rzeczywistych x, y, z takich, że
3
x
y
z
prawdziwa
jest nierówność
2
2
2
3
x
y
z
.
Dowód
I sposób rozwiązania
Z założenia
3
x
y
z
otrzymujemy
3
z
x
y
. Wobec tego tezę możemy zapisać
w sposób równoważny
2
2
2
3
3
x
y
x
y
,
2
2
2
9 6
3
x
y
x
y
x
y
,
2
2
2
2
9 6
6
2
3
x
y
x
y
x
xy
y
,
2
2
2
2
2
6
6
6
0
x
xy
y
x
y
2
2
3
3
3
0
x
xy
y
x
y
,
2
2
3
3
3
0
x
y
x
y
y
.
Otrzymaliśmy w ten sposób nierówność kwadratową z niewiadomą x. Wyróżnik trójmianu
stojącego po lewej stronie tej nierówności jest równy
2
2
2
2
3
4 1
3
3
6
9 4
12
12
y
y
y
y
y
y
y
2
2
2
3
6
3
3
2
1
3
1
0
y
y
y
y
y
dla każdej
y
R
.
To, wraz z dodatnim współczynnikiem przy
2
x oznacza, że nierówność kwadratowa jest
prawdziwa dla dowolnej liczby
x
R
.
Uwaga
Prawdziwość otrzymanej nierówności
2
2
3
3
3
0
x
xy
y
x
y
możemy też udowodnić
zapisując ją w postaci równoważnej jej nierówności prawdziwej w sposób oczywisty.
Pokażemy dwa takie sposoby:
a)
2
2
3
3
3
0
x
xy
y
x
y
,
2
2
2
1
2
1
1 0
x
x
y
y
xy
x
y
,
2
2
1
1
1
1
0
x
y
x y
y
,
2
2
1
1
1
1
0
x
y
x
y
,
2
2
2
1
1
3
1
2
1
1
1
1
0
2
4
4
x
x
y
y
y
,
2
2
1
3
1
1
1
0
2
4
x
y
y
.
Nierówność ta jest prawdziwa dla dowolnych liczb rzeczywistych x, y.
b)
2
2
1
1
1
1
0
x
y
x
y
,
2
2
2
2
1
1
1
1
1
1
1
1
1
1
0
2
2
2
2
x
x
y
y
x
y
,
2
2
2
2
1
1
1
1
2
1
1
1
1
1
0
2
2
2
x
x
y
y
x
y
2
2
2
1
1
1
1
1
1
1
0
2
2
2
x
y
x
y
.
Podobnie jak poprzednio uzyskujemy nierówność prawdziwą w sposób oczywisty.
Rozwiązania zadań otwartych i schematy punktowania
Strona 5 z 14
II sposób rozwiązania
Podstawiając
1
x
a
,
1
y
b
,
1
z
c
możemy zapisać założenie w postaci
1
1
1
3
a
b
c
, czyli
0
a b c
, zaś tezę możemy zapisać w sposób
równoważny w postaci kolejno:
2
2
2
1
1
1
3
a
b
c
,
2
2
2
2
2
2
0
a
a b
b c
c
,
2
2
2
2
a
b
c
a b c
.
Ostatnia nierówność jest, wobec założenia
0
a b c
, równoważna nierówności
2
2
2
0
a
b
c
,
która jest prawdziwa dla dowolnych liczb rzeczywistych.
III sposób rozwiązania
Dla dowolnych liczb rzeczywistych x, y, z prawdziwe są nierówności
2
0
x
y
,
2
0
y
z
,
2
0
z
x
,
czyli
2
2
2
x
y
xy
,
2
2
2
y
z
yz
,
2
2
2
z
x
zx
.
Dodając te nierówności stronami otrzymujemy
2
2
2
2
2
2
2
2
2
x
y
z
xy
yz
zx
.
Ponieważ z założenia
3
x
y
z
, więc
2
2
2
2
2
2
9
x
y
z
xy
yz
zx
.
Stąd
2
2
2
2
2
2
9
xy
yz
zx
x
y
z
.
Otrzymujemy zatem
2
2
2
2
2
2
2
2
2
9
x
y
z
x
y
z
,
2
2
2
3
3
3
9
x
y
z
,
2
2
2
3
x
y
z
,
co należało udowodnić.
IV sposób rozwiązania
Dla liczb nieujemnych x, y, z prawdziwa jest nierówność między średnią arytmetyczną
i średnią kwadratową
2
2
2
3
3
x
y
z
x
y
z
.
Jeżeli natomiast któraś z liczb x, y, z jest ujemna, to ta nierówność również jest prawdziwa.
Stąd i z założenia, że
3
x
y
z
dostajemy
2
2
2
1
3
x
y
z
.
Podnosząc obie strony te nierówności do kwadratu, a następnie mnożąc je przez 3 dostajemy
tezę.
Rozwiązania zadań otwartych i schematy punktowania
Strona 6 z 14
Schemat punktowania
Zdający otrzymuje ............................................................................................................1 pkt
gdy
zapisze nierówność w postaci równoważnej jej nierówności kwadratowej
2
2
3
3
3
0
x
y
x
y
y
i zapisze, że otrzymana nierówność to nierówność
kwadratowa lub obliczy wyróżnik trójmianu kwadratowego
2
2
3
3
3
x
y
x
y
y
albo
zapisze nierówność w postaci równoważnej
2
2
1
1
1
1
0
x
y
x
y
albo
zastosuje podstawienie
1
x
a
,
1
y
b
,
1
z
c
i zapisze założenie w postaci
0
a b c
oraz tezę w postaci
2
2
2
1
1
1
3
a
b
c
albo
zapisze równość
2
2
2
2
2
2
9
xy
yz
zx
x
y
z
wynikająca z założenia oraz
wykaże prawdziwość nierówności
2
2
2
2
2
2
2
2
2
x
y
z
xy
yz
zx
(wystarczy, że powoła się na znaną nierówność , prawdziwą dla dowolnych liczb
rzeczywistych x, y, z)
albo
zastosuje nierówność między średnią arytmetyczną i średnią kwadratową i zapisze
nierówność
2
2
2
3
3
x
y
z
x
y
z
(nawet bez rozpatrywania znaków liczb x, y, z)
i na tym poprzestanie lub dalej popełnia błędy.
Zdający otrzymuje ............................................................................................................2 pkt
gdy przeprowadzi pełne rozumowanie.
Zadanie 26. (2pkt)
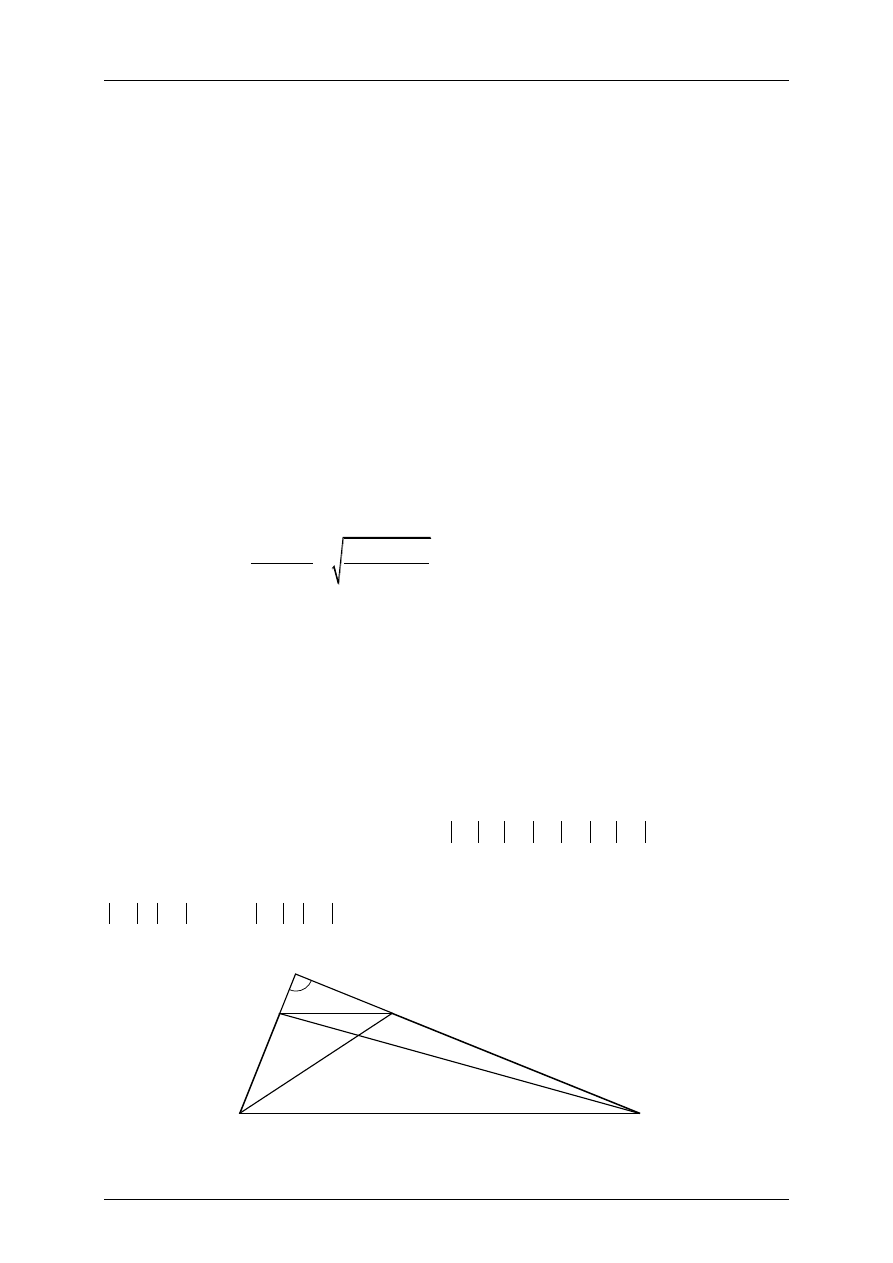
Wykaż, że jeżeli ramiona AD i BC trapezu ABCD o podstawach AB i CD zawierają się
w prostych prostopadłych (zobacz rysunek), to
2
2
2
2
AB
CD
AC
BD
.
Rozwiązanie
Niech E oznacza punkt przecięcia prostych AD i BC (przyjęliśmy za rysunkiem, że
AB
CD
. Gdyby AB
CD
, to punkt E leżałby po drugiej stronie prostej CD, zaś
rozumowanie nie zmieniłoby się).
Z twierdzenia Pitagorasa zastosowanego kolejno do trójkątów ABE, DCE, ACE, BED
otrzymujemy równości
A
B
C
D
E
.
Rozwiązania zadań otwartych i schematy punktowania
Strona 7 z 14
(1)
2
2
2
AB
AE
BE
,
(2)
2
2
2
CD
DE
CE
,
(3)
2
2
2
AC
AE
CE
,
(4)
2
2
2
BD
DE
BE
.
Zatem
(1),(2)
2
2
2
2
2
2
AB
CD
AE
BE
DE
CE
(3),(4)
2
2
2
2
2
2
AE
CE
DE
BE
AC
BD
.
To kończy dowód.
Schemat punktowania
Zdający otrzymuje ............................................................................................................1 pkt
gdy zapisze równości wynikające z twierdzenia Pitagorasa pozwalające udowodnić tezę,
np.:
2
2
2
AB
AE
BE
,
2
2
2
CD
DE
CE
,
2
2
2
AC
AE
CE
,
2
2
2
BD
DE
BE
i na tym poprzestanie lub dalej popełnia błędy.
Zdający otrzymuje ............................................................................................................2 pkt
gdy przeprowadzi pełne rozumowanie.
Rozwiązania zadań otwartych i schematy punktowania
Strona 8 z 14
Zadanie 27. (4pkt)
Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz
prawdopodobieństwo zdarzenia, że otrzymamy liczbę spełniającą jednocześnie trzy
następujące warunki:
(1)
liczba jest podzielna przez 25,
(2)
cyfry dziesiątek i setek są nieparzyste,
(3)
cyfra dziesiątek jest nie większa niż cyfra setek.
Rozwiązanie
Zdarzeniem elementarnym jest wylosowanie liczby naturalnej czterocyfrowej, więc zbiór
wszystkich zdarzeń elementarnych ma postać
1000,1001,1002,
,9999
. Liczba
wszystkich liczb w tym zbiorze jest równa
9999 999
9000
.
Niech A oznacza zdarzenie, że wylosowana liczba ze zbioru
spełnia jednocześnie warunki
(1), (2) i (3). Liczba jest podzielna przez 25, więc jej dwucyfrowa końcówka to 00, 25, 50 lub
75. Ponieważ z (2) warunku wynika, że cyfra dziesiątek jest nieparzysta, więc końcówką
może być jedynie 50 lub 75. Cyfra setek jest nieparzysta i cyfra dziesiątek jest od niej nie
większa. Mamy zatem następujące trzycyfrowe końcówki liczby: 550, 750, 950, 775, 975.
Cyfrą tysięcy jest dowolną cyfrą spośród dziewięciu cyfr: 1, 2, 3, 4, 5, 6, 7, 8, 9. Zatem
9 5
A
.
Prawdopodobieństwo zdarzenia A jest zatem równe
9 5
1
9000
200
A
P A
.
Schemat punktowania
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania .........................................................................................................................1 pkt
Obliczenie liczby wszystkich zdarzeń elementarnych:
9000
albo
poprawne rozpatrzenie jednego z podanych warunków, np. obliczenie liczby
wszystkich końcówek dwucyfrowych liczb naturalnych podzielnych przez 25 lub ich
wypisanie.
Rozwiązanie, w którym jest istotny postęp .....................................................................2 pkt
Obliczenie liczby wszystkich zdarzeń elementarnych oraz poprawne rozpatrzenie
jednego z podanych warunków, np. obliczenie liczby wszystkich końcówek
dwucyfrowych liczb naturalnych podzielnych przez 25 lub ich wypisanie
albo
poprawne rozpatrzenie co najmniej dwóch warunków ale nie obliczenie liczby
wszystkich zdarzeń elementarnych lub obliczenie jej z błędem.
Pokonanie zasadniczych trudności zadania ....................................................................3 pkt
Obliczenie liczby wszystkich zdarzeń elementarnych oraz obliczenie liczby zdarzeń
elementarnych sprzyjających zdarzeniu A:
9 5
A
.
Rozwiązanie pełne ..............................................................................................................4 pkt
Obliczenie prawdopodobieństwa zdarzenia A:
1
200
P A
.
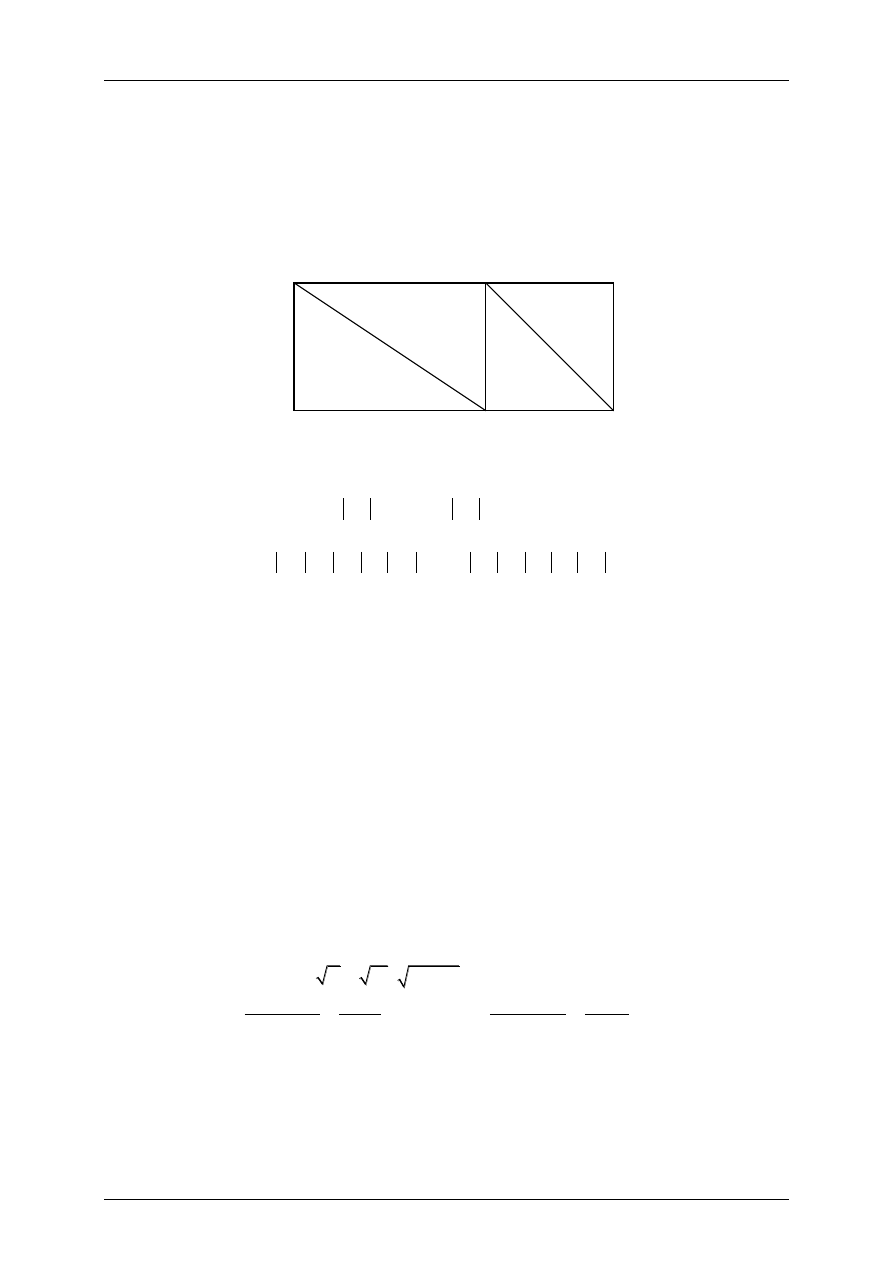
Rozwiązania zadań otwartych i schematy punktowania
Strona 9 z 14
Zadanie 28. (5pkt)
Prostokątny pas wykładziny dywanowej o wymiarach 3,6 m na 7,5 m należy przeciąć
prostopadle do dłuższego boku tak, aby przekątne otrzymanych dwóch prostokątnych
kawałków różniły się o 1,5 m. Oblicz wymiary większego z otrzymanych kawałków.
Rozwiązanie:
Oznaczmy przez x nieznany wymiar większego z kawałków. Przekątna tego kawałka jest
dłuższa od przekątnej mniejszego z kawałków.
Nieznany wymiar mniejszego kawałka i długość przekątnej tego kawałka są równe
odpowiednio
7,5
EB
x
,
1,5
FB
d
.
Z twierdzenia Pitagorasa dla trójkąta AED i dla trójkąta EBF otrzymujmy
2
2
2
DE
AE
AD
oraz
2
2
2
FB
EB
EF
,
2
2
2
3, 6
d
x
oraz
2
2
2
1,5
7,5
3, 6
d
x
.
Drugie równanie zapisujemy w postaci
2
2
2
3
2, 25
56, 25 15
3, 6
d
d
x
x
.
Stąd i z pierwszego równania mamy
2
2
3
2, 25
56, 25 15
d
d
x d
,
15
3
54
x
d
,
5
18
x d
,
5
18
d
x
.
Podstawiając w miejsce d w pierwszym równaniu
5
18
x
otrzymujemy równanie z jedną
niewiadomą
2
2
2
5
18
3, 6
x
x
,
2
2
25
180
324 12,96
x
x
x
,
2
24
180
311, 04
0
x
x
.
2
180
4 24 311, 04 180 180 4 4 6 311, 04
4 45 4 45 4 4 6 311, 04 16 45 45 6 311, 04
16 158, 76
,
16
158, 76
4 12, 6
50, 4
180 50, 4
129, 6
2, 7
48
48
x
lub
180 50, 4
230, 4
4,8
48
48
x
.
Pierwsze z otrzymanych rozwiązań nie spełnia warunków zadania, gdyż wówczas mielibyśmy
5
18
5 2, 7 18
4,5
0
d
x
.
Zatem wymiary większego z otrzymanych kawałków są równe 3,6 m na 4,8 m.
A
C
B
D
F
E
3,6
7,5
x
d
Rozwiązania zadań otwartych i schematy punktowania
Strona 10 z 14
Schemat punktowania
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania ..............................................................................................................................
1 pkt
Przyjęcie oznaczeń i zapisanie jednego z równań wynikających z treści zadania, np.:
2
2
2
3, 6
d
x
, gdzie x oznacza nieznany wymiar większego z kawałków, zaś d długość
przekątnej tego kawałka.
Rozwiązanie, w którym jest istotny postęp ........................................................................... 2
pkt
Zapisanie układu równań pozwalającego obliczyć wymiary większego z kawałków, np.:
2
2
2
2
2
2
3, 6
1,5
3, 6
7,5
d
x
d
x
.
Pokonanie zasadniczych trudności zadania .......................................................................... 3
pkt
Doprowadzenie układu do równania z jedną niewiadomą (x albo d), np.:
2
2
2
5
18
3, 6
x
x
.
Rozwiązanie zadania do końca lecz z usterkami, które jednak nie przekreślają
poprawności rozwiązania (np. błędy rachunkowe) ........................................................4 pkt
Doprowadzenie do równania kwadratowego z jedną niewiadomą (x albo d), np.:
2
24
180
311, 04
0
x
x
.
Rozwiązanie bezbłędne ........................................................................................................... 5
pkt
Obliczenie nieznanego wymiaru większego kawałka: 4,8 m.
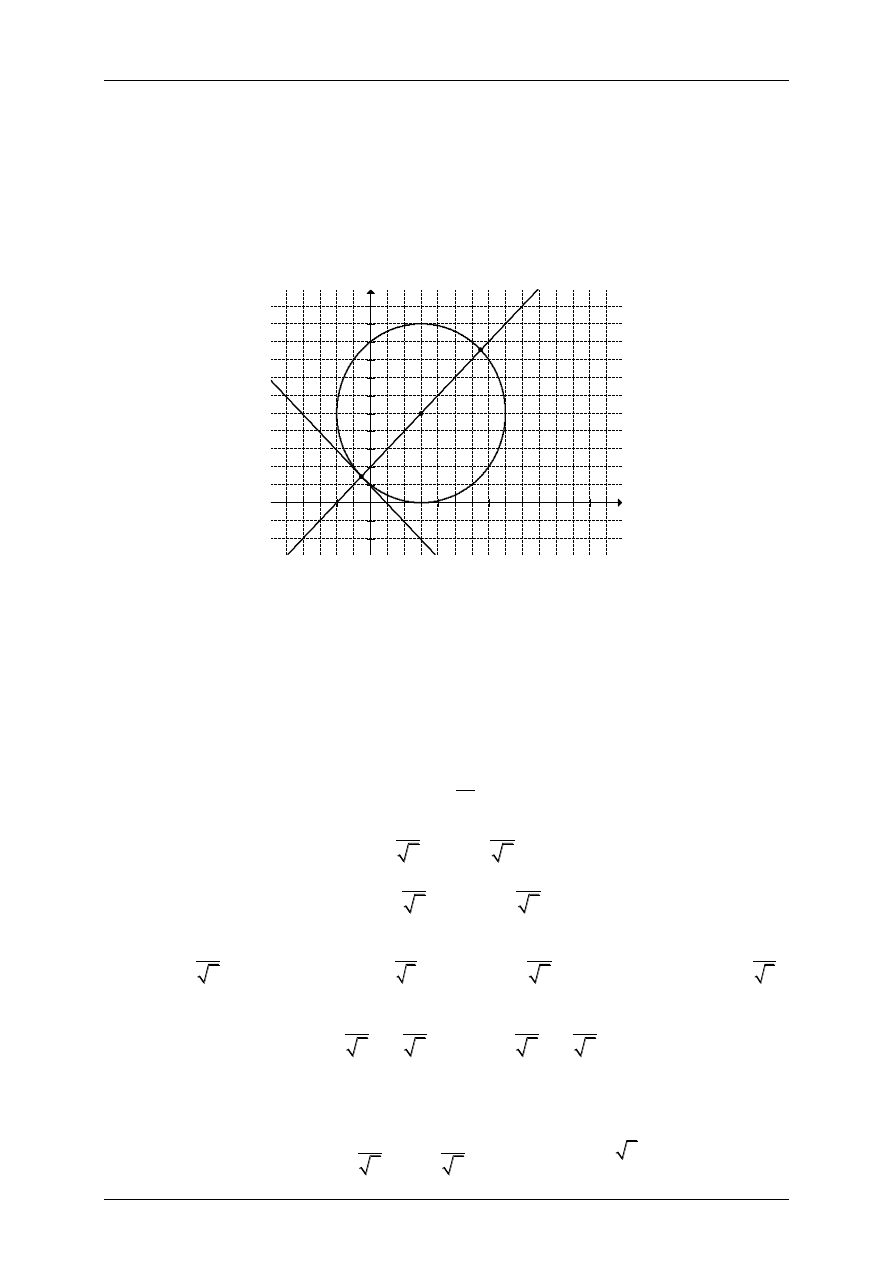
Rozwiązania zadań otwartych i schematy punktowania
Strona 11 z 14
Zadanie 29. (4pkt)
Prosta o równaniu
2
y
x
przecina okrąg o równaniu
2
2
3
5
25
x
y
w punktach
A i B. Oblicz współrzędne punktów A i B oraz wyznacz równanie stycznej do danego okręgu,
przechodzącej przez jeden z tych punktów.
Rozwiązanie
Środkiem okręgu o równaniu
2
2
3
5
25
x
y
jest punkt
3,5
S
, a promień tego
okręgu jest równy
5
r
. Narysujmy ten okrąg wraz z prostą k o równaniu
2
y
x
.
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
-2
-1
1
2
3
4
5
6
7
8
9
10
11
x
y
A
B
S
k
Współrzędne punktów przecięcia prostej k z okręgiem obliczmy rozwiązując układ równań
2
2
3
5
25
2
x
y
y
x
.
Stąd otrzymujemy równanie
2
2
3
2 5
25
x
x
,
2
2
3
3
25
x
x
,
2
2
3
25
0
x
,
2
25
3
0
2
x
,
5
5
3
3
0
2
2
x
x
,
5
3
2
x
lub
5
3
2
x
Gdy
5
3
2
x
, to wtedy
5
2 5
2
y
x
, a gdy
5
3
2
x
, to wówczas
5
2 5
2
y
x
.
Zatem prosta k przecina okrąg w punktach
5
5
3
,5
2
2
A
,
5
5
3
,5
2
2
B
.
Zauważmy, że środek S okręgu leży na prostej k, gdyż
3 2
5
. Oznacza to, że styczna do
okręgu przechodząca przez punkt A lub przez punkt B jest prostopadła do prostej k.
Równanie stycznej do okręgu przechodzącej przez A ma zatem postać
5
5
3
5
2
2
y
x
, czyli
8 5 2
y
x
.
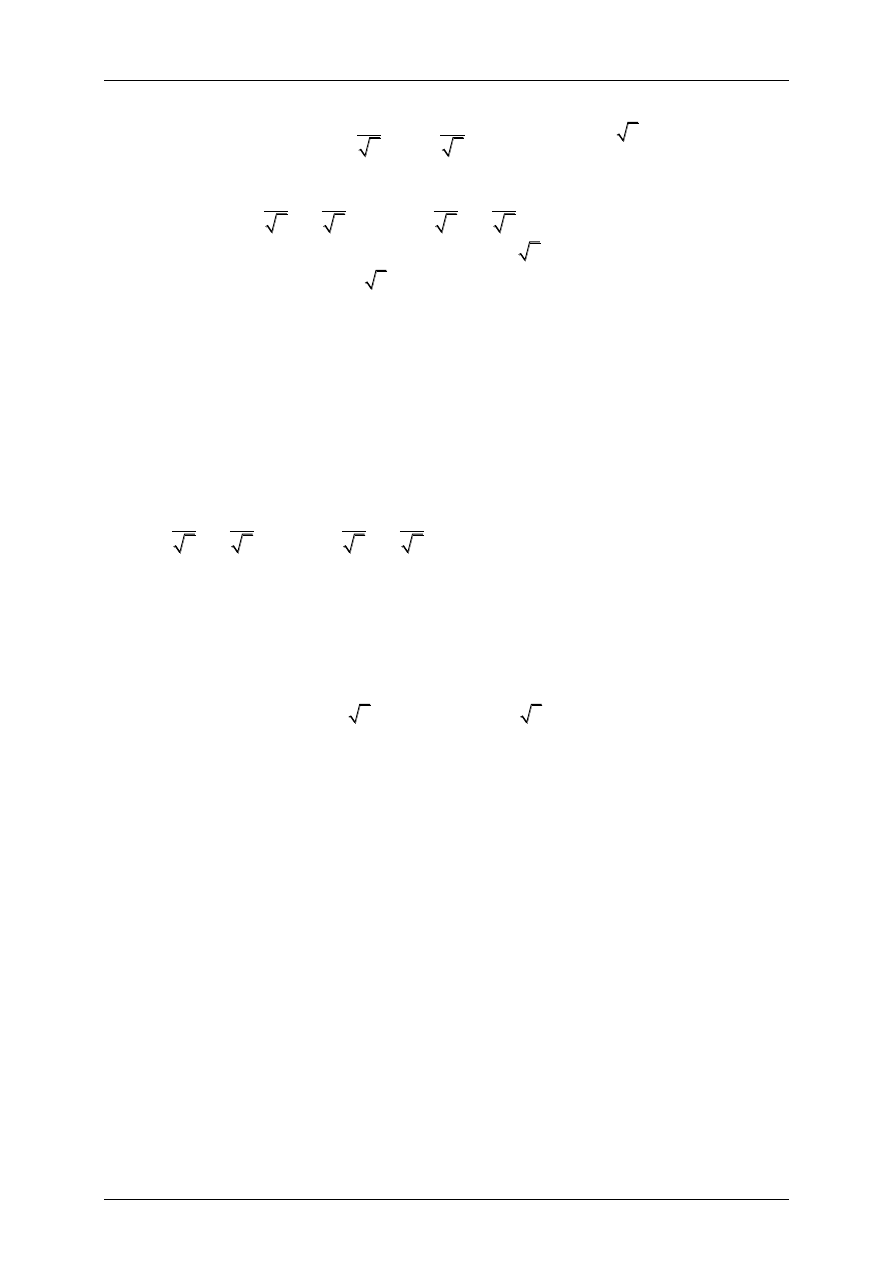
Rozwiązania zadań otwartych i schematy punktowania
Strona 12 z 14
Równanie stycznej do okręgu przechodzącej przez B ma postać
5
5
3
5
2
2
y
x
, czyli
8 5 2
y
x
.
Odpowiedź.
5
5
3
,5
2
2
A
,
5
5
3
,5
2
2
B
, styczna do danego okręgu
poprowadzona przez punkt A ma równanie
8 5 2
y
x
, a styczna poprowadzona przez
punkt B ma równanie
8 5 2
y
x
.
Schemat punktowania
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania ..............................................................................................................................
1 pkt
Doprowadzenie układu równań
2
2
3
5
25
x
y
i
2
y
x
do równania
kwadratowego z jedną niewiadomą, np.:
2
2
3
2 5
25
x
x
.
Rozwiązanie, w którym jest istotny postęp ........................................................................... 2
pkt
Rozwiązanie układu równań i zapisanie współrzędnych punktów A i B:
5
5
3
,5
2
2
A
,
5
5
3
,5
2
2
B
.
Pokonanie zasadniczych trudności zadania .......................................................................... 3
pkt
Obliczenie współczynnika kierunkowego stycznej do danego okręgu przechodzącej przez punkt
A lub przez punkt B:
1
.
Rozwiązanie pełne ................................................................................................................... 4
pkt
Wyznaczenie równania
stycznej do danego okręgu przechodzącej przez punkt A
(lub przez punkt B):
8 5 2
y
x
( lub
8 5 2
y
x
).
Rozwiązania zadań otwartych i schematy punktowania
Strona 13 z 14
Zadanie 30. (5pkt)
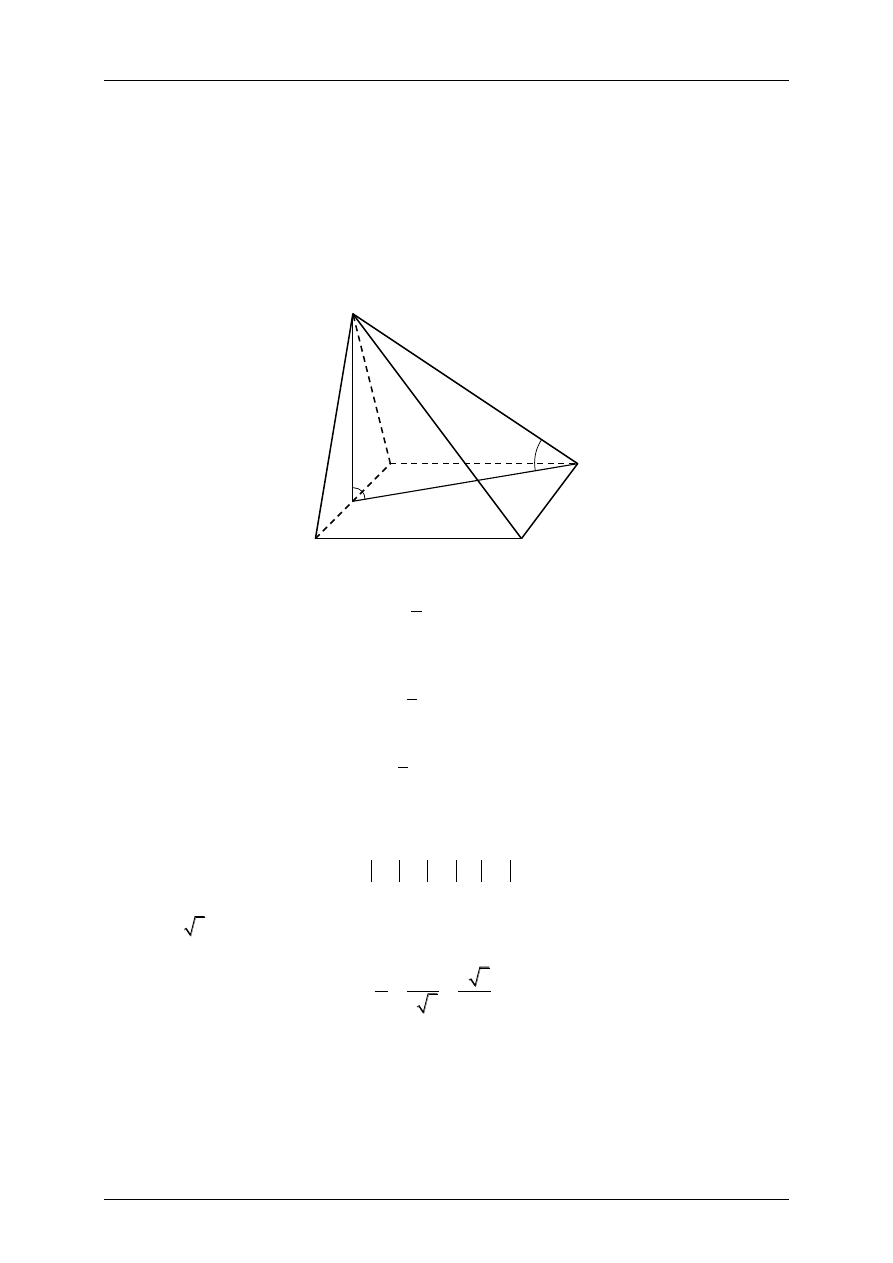
Podstawą ostrosłupa ABCDS jest kwadrat ABCD. Wysokość SE ściany bocznej ADS jest
jednocześnie wysokością ostrosłupa, a punkt E jest środkiem krawędzi AD (zobacz rysunek).
Pole ściany ADS jest równe 12 cm
2
, a objętość ostrosłupa jest równa 48 cm
3
. Oblicz miarę kąta
nachylenia krawędzi bocznej CS do płaszczyzny podstawy ostrosłupa. Wynik zaokrąglij do
1
.
Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku. Zaznaczmy też kąt
między krawędzią boczną CS
ostrosłupa a płaszczyzną jego podstawy. Jest to kąt ostry w trójkącie prostokątnym ECS
o kącie prostym przy wierzchołku E.
Pole ściany bocznej ADS jest równe 12, więc możemy zapisać równanie
1
12
2
ah
.
Wykorzystując podaną objętość ostrosłupa zapisujemy drugie równanie z tymi samymi
niewiadomymi a i h
2
1
48
3
a h
.
Z pierwszego równania otrzymujemy
24
ah
, więc stąd i z drugiego równania dostajemy
1
24
48
3
a
,
6
a
.
Zatem
6
24
h
, czyli
4
h
.
Z twierdzenia Pitagorasa dla trójkąta prostokątnego EDC otrzymujemy
2
2
2
EC
ED
CD
,
2
2
2
3
6
45
p
.
Stąd
3 5
p
.
Obliczmy tangens kąta
w trójkącie ECS
4
4 5
tg
0,5963
15
3 5
h
p
.
Z tablic odczytujemy miarę kąta
zaokrągloną do
1
31
.
Odpowiedź:
31
.
A
B
C
D
S
E
.
a
a
b
h
p
Rozwiązania zadań otwartych i schematy punktowania
Strona 14 z 14
Schemat punktowania
Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania ..............................................................................................................................
1 pkt
Zapisanie jednego z równań:
1
12
2
ah
,
2
1
48
3
a h
, gdzie a oznacza długość krawędzi
podstawy ostrosłupa, zaś h wysokość ostrosłupa i jednocześnie wysokość ściany bocznej
ADS.
Rozwiązanie, w którym jest istotny postęp ........................................................................... 2
pkt
Zapisanie układu równań pozwalającego obliczyć
długość krawędzi podstawy ostrosłupa oraz
wysokość ostrosłupa
:
1
12
2
ah
oraz
2
1
48
3
a h
.
Pokonanie zasadniczych trudności zadania .......................................................................... 3
pkt
Zaznaczenie kąta nachylenia
krawędzi bocznej CS do płaszczyzny podstawy ostrosłupa
oraz
obliczenie
długości krawędzi podstawy ostrosłupa i wysokości ostrosłupa:
6
a
,
4
h
.
Uwaga
Jeżeli zdający zaznaczy zły kąt
nachylenia
krawędzi bocznej CS do płaszczyzny podstawy
ostrosłupa, to za całe rozwiązanie zadania może otrzymać co najwyżej 2 punkty.
Rozwiązanie zadania do końca, lecz z usterkami, które jednak nie przekreślają
poprawności rozwiązania (np. błędy rachunkowe) ........................................................4 pkt
Obliczenie wartości funkcji trygonometrycznej kąta
i błędne odczytanie miary kąta
albo
obliczenie wartości funkcji trygonometrycznej kąta
z błędem rachunkowym
i konsekwentne podanie miary kąta
.
Rozwiązanie bezbłędne ........................................................................................................... 5
pkt
Odczytanie miary kąta
:
31
.